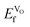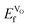Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A computational study of the electronic properties, ionic conduction, and thermal expansion of Sm1−xAxCoO3 and Sm1−xAxCoO3−x/2 (A = Ba2+, Ca2+, Sr2+, and x = 0.25, 0.5) as intermediate temperature SOFC cathodes†
Emilia
Olsson
 a,
Xavier
Aparicio-Anglès
a,
Xavier
Aparicio-Anglès
 a and
Nora H.
de Leeuw
a and
Nora H.
de Leeuw
 *ab
*ab
aDepartment of Chemistry, University College London, WC1H 0AJ, London, UK
bSchool of Chemistry, Cardiff University, Main Building, Park Place, CF10 3AT, Cardiff, UK. E-mail: deleeuwn@cardiff.ac.uk
First published on 17th May 2017
Abstract
The substitutional doping of Ca2+, Sr2+, and Ba2+ on the Sm-site in the cubic perovskite SmCoO3 is reported to improve both electronic and ionic conductivities for applications as solid oxide fuel cell (SOFC) cathodes. Hence, in this study we have used density functional theory (DFT) calculations to investigate dopant configurations at two different dopant concentrations: 25 and 50%. To preserve the electroneutrality of the system, we have studied two different charge compensation mechanisms: the creation of oxygen vacancies, and electronic holes. After examining the electronic structure, charge density difference, and oxygen vacancy formation energies, we concluded that oxygen vacancy charge compensation is the preferred mechanism to maintain the electroneutrality of the system. Furthermore, we found that the improvement of the electronic conduction is not a direct consequence of the appearance of electron holes, but a result of the distortion of the material, more specifically, the distortion of the Co–O bonds. Finally, molecular dynamics were employed to model ionic conduction and thermal expansion coefficients. It was found that all dopants at both concentrations showed high ionic conduction comparable to experimental results.
1. Introduction
Solid oxide fuel cells (SOFC) are important potential replacements of traditional power sources, and offer a clean and efficient chemical-to-electrical energy conversion process.1–3 However, to make these devices more widely available and applicable, their operating temperature and costs have to be lowered. One of the most pressing issues is the need to develop new cathode materials that are capable of operating at intermediate temperatures (500–900 °C), with high electrical and catalytic efficiencies at these lower temperatures, i.e. intermediate temperature SOFC (IT-SOFC). The factor influencing the efficiency of IT-SOFC cathodes is the catalytic efficiency towards the oxygen reduction reaction, which depends on the surface oxygen reduction and oxygen bulk diffusion. These reactions are oxygen vacancy assisted, whereby high oxygen vacancy concentrations are favorable. The main task of the IT-SOFC cathode is then to provide an efficient pathway for the reduced oxygen through the cathode bulk to the electrolyte, as well as being able to transport electrons.1 Therefore, IT-SOFC cathodes are required to have high ambipolar conductivity in the form of mixed electronic and ionic conductivity (MIEC).4 Furthermore, it is critical that the cathode is chemically compatible with the electrolyte, and that all components have similar thermal expansion coefficients, so as to have physical compatibility.Unlike traditional cathode materials such as La1−xSrxMnO3−δ (LSM), which loses efficiency at these low temperatures due to polarization resistance, cobalt-based perovskites have shown better performance and have been suggested as suitable materials for IT-SOFC,5 as their reported properties include better mixed ionic and electronic conduction, low polarization resistance, and lower overpotentials.6,7 Their higher ionic conductivity is a consequence of the lower activation energies required for the oxygen to migrate via oxygen vacancies, which are induced when substituting Sm3+ by a divalent cation (A).6–13 Upon doping, the overall charge of the system can be compensated via two different charge compensation schemes. On the one hand, oxygen vacancies (VO) can be generated, as described in eqn (1), according to the Kröger–Vink notation:14
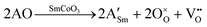 | (1) |
On the other hand, the charge can be compensated with the creation of electron holes, as expressed in eqn (2).13,15–17
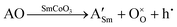 | (2) |
While the oxygen vacancy compensation mechanism is widely used to explain the formation of oxygen vacancies, and thus the increase in the ionic conductivity, the hole compensation mechanism has been suggested to explain the increase in the electronic conductivity.16,17 Although there is no strong evidence, it is believed that both mechanisms coexist in the material. The increase in the electronic conductivity seems to be related with the spin transition observed in cobalt, from low spin to either high (HS, t42ge2g), intermediate (IS, t52ge1g), or mixed spin (LS/IS, IS/HS).8 This leads to magnetic domains, metallic electronic structure, and the cobalt ions coexisting in different spin states.8 Another improvement that doped SmCoO3 cathodes present with respect to LSMO, is that although they do not couple well with yttria-stabilized zirconia (YSZ) as the electrolyte material, they show better compatibility with ceria-based electrolytes such as gadolinium-doped ceria (GDC).6,10
Although experimental studies conducted on Sm1−xAxCoO3−x/2 indicate that they could be promising materials for IT-SOFC cathodes, questions remain why samarium cobaltates show better performance than doped lanthanum manganite.2 Hence, in this paper, we investigate three common SmCoO3 dopants; Ca2+, Sr2+, and Ba2+, at two different dopant concentrations (x); x = 0.25, and 0.5. Using a combination of density functional theory and molecular dynamics simulations, we have investigated two different charge compensation schemes, the electronic and magnetic structure, oxygen diffusion, and the thermal expansion coefficients. On the basis of these calculations, we then compare the different Sm1−xAxCoO3−x/2 systems to gain an understanding of how the dopant species and its concentration influences the oxygen conduction and the materials’ properties. The results have been compared to experiment, and especially the compatibility with traditional electrolytes has been kept in mind when evaluating which dopant and concentration are most suitable for IT-SOFC cathode applications.
2. Computational details
In this study, we have employed two different methodologies to model the Sm1−xAxCoO3−x/2 systems; density functional theory (DFT) calculations and interatomic potential-based molecular dynamics (MD). DFT has been used to study the energetics and the electronic structure of the different dopant configurations, whereas MD is used to study thermal properties and oxygen diffusion at different temperatures.2.1. Density functional theory calculations
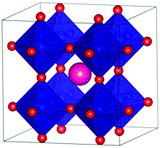
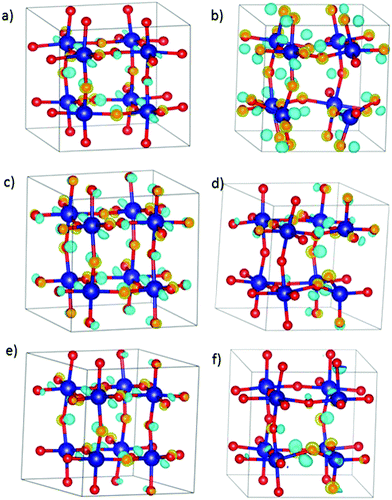
DFT calculations were performed with the Vienna ab initio simulation package, VASP (version 5.4.1).18–21 The projector-augmented wave method (PAW) was applied to describe the ion-electron interaction.22 Based on convergence tests, the plane wave energy cut-off for SmCoO3 was set to 500 eV. Spin-polarized calculations were performed with the Perdew–Burke–Ernzerhof (PBE)23,24 functional under electronic and ionic self-consistence, with convergence criteria of 10−5 eV and 10−3 eV Å−1 respectively. The following valence electrons for the atomic species involved were taken into account: Sm (5s25p66s2), Sr (4s24p65s2), Ba (5s25p66s2), Ca (3s23p64s2), Co (4s23d7), and O (2s22p4). The tetrahedron method with Blöchl corrections for smearing25 together with a 4 × 4 × 4 Γ-centered Monkhorst–Pack grid was applied.26 Bader charges27 were calculated using the Henkelman algorithm.28 When non-stoichiometric bulk materials were modelled without charge compensation via oxygen vacancies, a homogeneous background charge was added to counteract the resulting charge. This makes the system overall charge-neutral and avoids a diverging Coulomb interaction.29,30 To correct the electron self-interaction problem arising from the d-electrons of Co,31–33 we have used the on-site Coulombic interaction (DFT+U), considering a Hubbard parameter of 3 eV using the Dudarev approximation.34,35 Finally, the crystal structure used was the 2 × 2 × 2 Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m pseudo cubic cell (Fig. 1) as this has been shown to be sufficient to reproduce the properties of the system.34 These materials have average cubic structures at high temperatures, with local Jahn–Teller distortions on the CoO-octahedra.36
m pseudo cubic cell (Fig. 1) as this has been shown to be sufficient to reproduce the properties of the system.34 These materials have average cubic structures at high temperatures, with local Jahn–Teller distortions on the CoO-octahedra.36
2.2. Molecular dynamics calculations
All MD simulations were performed using the DL_POLY 4.07 code,37 with a 20 × 20 × 20 supercell simulated under NPT conditions, using a Nosé–Hoover thermostat.38 All statistics were collected after a system equilibration of 13 ps, with an added 100 ps production phase. The time step for both phases was 0.5 fs. The Ewald summation was employed to account for the electrostatic interactions, whereas the Verlet algorithm evaluated the atomic motions. We have used the Buckingham potential, within the Born model for ionic solids,39,40 to describe the short-range interactions between atoms.41 This potential is described in eqn (3), where r defines the distance between ions i and j, and A, ρ, and C are empirically fitted parameters.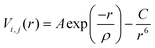 | (3) |
In addition, we have considered the shell model to describe the electronic polarization of the atoms (α), where the ions are modeled as cores with a harmonic spring (k) connected to a massless shell with charge Y. The cores represent the nuclei and core electrons of the ions, whereas the shell represents the valence electrons. The relation is presented in eqn (4).
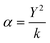 | (4) |
The interatomic potentials used in this work are taken from the Cherry et al. library, as they have previously been used to model ionic conductivity in perovskites.42–45 The Sm3+–O2− interatomic potential parameters had to be derived separately since they were not available for this potential model. To that end, we have used the GULP code46–49 to fit them according to the structural data for cubic and orthorhombic SmCoO3, as well as Sm2O3. The fitting results are presented in Table S1 of the ESI,† which show that the derived model perfectly replicates the structural properties of all different phases and materials considered. The full set of interatomic potentials used is presented in Table 1 below.
| Interaction | Short range interactions | Shell model | |||||
|---|---|---|---|---|---|---|---|
| A (eV) | ρ (Å) | C (eV Å6) | Y (e) | k (eV Å−2) | Ref. | ||
| Sm3+–O2− | 1252.94 | 0.3590 | 0.00 | Sm3+ | −0.250 | 173.90 | |
| Co3+–O2− | 1329.82 | 0.3087 | 0.00 | Co3+ | 2.040 | 196.30 | 42 |
| O2−–O2− | 22764.30 | 0.1490 | 43.00 | O2− | −2.389 | 42.00 | 42 |
| Ba2+–O2− | 4818.42 | 0.3067 | 0.00 | Ba2+ | 1.831 | 34.05 | 44 |
| Ca2+–O2− | 1090.40 | 0.3437 | 0.00 | Ca2+ | 3.135 | 110.20 | 45 |
| Sr2+–O2− | 959.10 | 0.3721 | 0.00 | Sr2+ | 3.251 | 71.70 | 45 |
3. Results and discussion
3.1. Dopant configurations
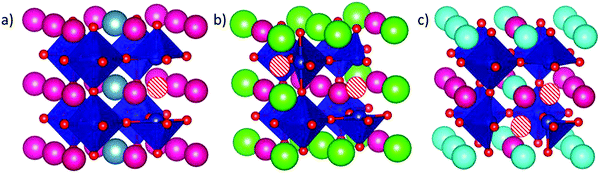
To evaluate the position of the A2+ and the VO, we have used the Site-Occupancy Disorder program (SOD).50 SOD uses the symmetry operations of the non-doped bulk system to determine all the non-equivalent substitutions. At this stage, we should then use SOD again to determine the non-equivalent positions for the oxygen vacancy in the doped system. However, due to the high number of resulting configurations (around 250 configurations in total), we first determined the most stable dopant configuration in doped SmCoO3 without VO. We found three inequivalent configurations for x = 0.25, and six for x = 0.50 (ESI,† Fig. S1). Since SOD does not provide any information about the relative stability of the different bulks, we optimized all the different distributions using VASP, for all the different dopants: Ca2+, Sr2+, and Ba2+. After optimization, the most stable dopant distribution per dopant and concentration was used to determine the positions of the oxygen vacancies. We found that all systems with x = 0.25 had the same most stable dopant vacancy configuration, whereas Sr- and Ba-doped systems for x = 0.5 had different configurations from the Ca-doped system at the same concentration. The reason for this difference was attributed to size-effects, as Ca2+ is the smallest dopant. The final configurations for each cation and concentration are depicted in Fig. 2, and a full description of the energetics can be found in the ESI.†3.2. Electronic and magnetic structures
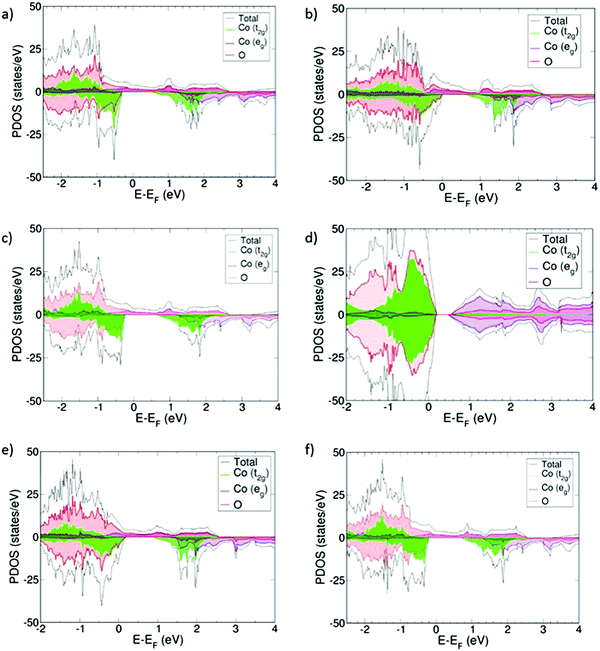
Projected density of states (PDOS) for the oxidized systems (Sm1−xAxCoO3) with x = 0.25 and 0.5 are collected in Fig. 3. All materials, with the exception of Sm0.50Sr0.50CoO3, show the same common features. Upon doping, the systems become half-metallic, thus indicating that they all become electronic conductors. This conduction mainly occurs through the Co eg orbitals, which are hybridized with the O 2p-orbitals. We modelled different magnetic structures for all the different systems, and in all cases the ferromagnetic ground state was the most stable. This magnetic structure is evidenced in the PDOS by the fact that α- and β-densities are not symmetrical. The change in the magnetic structure is attributed to the LS to IS transition observed in the cobalt centers and listed in Table 2, where Co3+ transitions from LS (μCo = 0 μB) to IS with μCo ≈ 2 μB. Cobalt charges (qCo) do not vary markedly with increasing x, whereas qO decreases by ≥0.04 e going from x = 0.25 to x = 0.5. This trend has also been observed for La1−xSrxFeO3, and was suggested to indicate hole delocalization on the oxygen sub-lattice,16 although there is no clear evidence in the PDOS of the existence of this electronic hole near the Fermi level (EF).| A | Sm0.75A0.25CoO3 | Sm0.75A0.25CoO2.88 | Sm0.5A0.5CoO3 | Sm0.5A0.5CoO2.75 | |
|---|---|---|---|---|---|
| Ca | μ Co (μB) | 1.8 | 0.13, 2.1 | 1.7 | 0.1, 2.0, 2.1 |
| μ Co* (μB) | 1.8 | 1.9, 2.0, 2.6 | |||
| q Co (e) | 1.36 | 1.21–1.32 | 1.36 | 1.23–1.32 | |
| q Co* (e) | 1.25 | 1.05–1.33 | |||
| q O (e) | −1.11 ± 0.02 | −1.13 ± 0.1 | −1.07 ± 0.02 | −1.11 ± 0.07 | |
| Sr | μ Co (μB) | 1.8 | 0.1, 2.1 | 0.01, 0.03, 0.04, 0.05 | 1.8, 2.0, 1.9, 2.2 |
| μ Co* (μB) | 1.8 | 1.9, 2.1 | |||
| q Co (e) | 1.38 | 1.23–1.32 | 1.33 | 1.32–1.37 | |
| q Co* (e) | 1.26 | 1.14–1.24 | |||
| q O (e) | −1.12 ± 0.02 | −1.13 ± 0.06 | −1.05 ± 0.02 | −1.14 ± 0.06 | |
| Ba | μ Co (μB) | 1.9 | 0.1, 2.1, 2.2 | 1.9 | 2.4, 3.1, 2.1, 0.4 |
| μ Co* (μB) | 1.7 | 2.3, 2.0 | |||
| q Co (e) | 1.40 | 1.22–1.30 | 1.40 | 1.28–1.48 | |
| q Co* (e) | 1.29 | 1.22–1.26 | |||
| q O (e) | −1.13 ± 0.03 | −1.14 ± 0.1 | −1.09 ± 0.04 | −1.15 ± 0.1 | |
For the specific case of Sm0.50Sr0.50CoO3, it is still a conductor since the cobalt t2g orbitals are found both above and below EF, but its electronic structure reveals that the t2g/eg crystal field splitting still applies for this material despite the doping (Fig. 3d). Accordingly, the magnetic moment of cobalt atoms is about 0 and no significant change in the cobalt charge is observed.
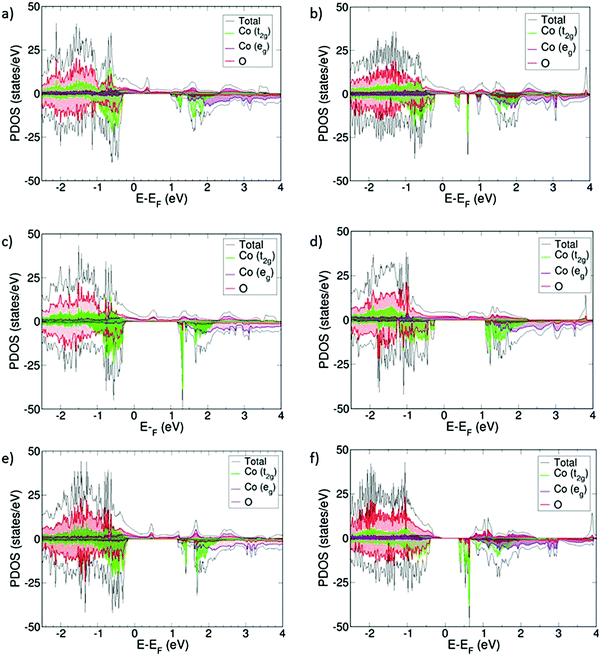
For the VO compensated systems, the PDOS are collected in Fig. 4. Now, without exception, all systems become half-metallic, thus indicating that they also become electronic conductors. The VBM is a mixture of O 2p, Co t2g, and Co eg, as opposed to the oxidized systems where Co eg-states were mainly present at the CBM and above. Again, the conduction mainly occurs through the Co eg-orbitals, which are hybridized with the O 2p-orbitals.
The presence of VO induces different magnetic moments in the cobalt centers. Those who are next to the VO keep the same magnetic moment observed in the oxidized systems, around 1.8 μB, whereas the rest of the cobalt atoms show different values, ranging from 0 to 2.2 μB. All magnetic moments show spin in the same direction, indicating that the doped systems with oxygen vacancies become ferromagnetic (Table 2). Sm0.50Ba0.50CoO2.75 has the highest μCo, indicating that Co3+ is in the IS/HS spin state. This mixing of μCo is in agreement with experimental results on doped SmCoO3.8
The presence of VO in the lattice gives different cobalt spin states within the system, but not cobalt mixed valence, which has also been noted experimentally for x > 0.2.51 This finding would imply that the charge compensation is fully completed through VO compensation, without remaining negative charge in VO. A similar result was found for VO formation in the undoped SmCoO3.34 However, the subtle difference in qCo between the oxidized and VO compensated systems is worth noting. The difference in total qCo in the two different charge compensation schemes for the same A and x is, however, larger. ΔCa,0.25 = 0.70 e, ΔCa,0.50 = 0.91 e, ΔSr,0.25 = 0.78 e, ΔSr,0.50 = 0.33 e, ΔBa,0.25 = 0.92 e, and ΔBa,0.50 = 0.65 e. This could possibly indicate the presence of an electron hole on the cobalt atoms, but we would then expect charges closer to 2 e. Therefore, we consider that due to how the Bader charges are partitioned, and that ΔA,x do not sum to a whole electron, no certain conclusion can be drawn.
Since the analysis of the density of states, and the variation of the cobalt magnetic moments and Bader charges do not provide clear evidence of the actual existence of an electron hole to compensate the charge of the system, we have examined their possible presence by calculating the charge density difference (Δρ) according to eqn (5).
| Δρ = ρSm1−xAxCoO3−x/2 + nρ0 − ρSm1−xAxCoO3 | (5) |
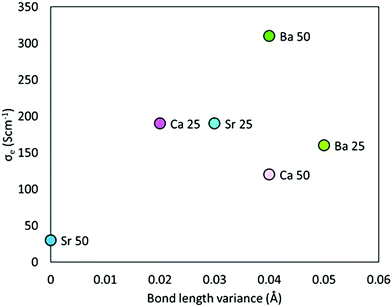
The question still remains though, why A2+-doped SmCoO3 becomes an electronic conductor. The key to understand this behavior can be seen in Sm0.50Sr0.50CoO3, which is almost diamagnetic and still shows eg/t2g splitting. Examining the geometric structure of Sm0.50Sr0.50CoO3, we realize that there are no distortions in the Co–O bond lengths (see full list in Table S4 in ESI†), and thus no CoO6-octahedral distortions. Therefore, the crystal field splitting is still intact, which explains why Sm0.50Sr0.50CoO3 has not become at least half metallic. From this finding, we can conclude that any doping that induces structural distortion in SmCoO3, will alter the electronic structure, i.e. will break the crystal field splitting, and the Co d-orbitals will be closer in energy, as well as more hybridized with O 2p-orbitals, turning the system into an electrical conductor. To prove this, hypothesis we calculated the 0 K electronic conductivity (σe) for all Sm1−xAxCoO3, and plotted them as a function of Co–O bond length variance. The variance was set as the difference between the shortest and the longest Co–O distance, according to Table S4 in ESI.† The larger the spread in Co–O bond lengths, the higher the electronic conductivity. The trend is presented in Fig. 6. Although it is not a perfect linear dependence, it is indicative enough to conclude that conductivity in Sm-site doped SmCoO3 is a direct consequence of the distortion induced by doping the system, rather than being a consequence of any electron hole.
3.3. Oxygen vacancy formation energy
To calculate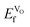 (Table 3), we have employed the method developed by Zhang and Northrup (eqn (6)),54,55
(Table 3), we have employed the method developed by Zhang and Northrup (eqn (6)),54,55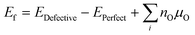 | (6) |
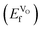 for the most stable configuration. Other VO-configurations are included in ESI
for the most stable configuration. Other VO-configurations are included in ESI
VO formation in these doped materials is spontaneous, i.e. negative 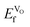 , as expected considering the oxygen vacancy charge compensation scheme. Moreover, as mentioned for the hole compensation, dopant-size effects appear to exist when the systems obtain more ACoO3 character at the higher dopant concentrations, leading to opposing trends in
, as expected considering the oxygen vacancy charge compensation scheme. Moreover, as mentioned for the hole compensation, dopant-size effects appear to exist when the systems obtain more ACoO3 character at the higher dopant concentrations, leading to opposing trends in 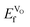 at the higher concentration. This trend has previously been observed for AMnO3, with
at the higher concentration. This trend has previously been observed for AMnO3, with 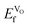 decreasing going from CaMnO3, via SrMnO3, and to BaMnO3.63 However, as all
decreasing going from CaMnO3, via SrMnO3, and to BaMnO3.63 However, as all 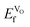 are negative, the effect would not be noticeably different between the different materials. Furthermore, the negative
are negative, the effect would not be noticeably different between the different materials. Furthermore, the negative 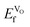 does indicate that oxygen could spontaneously leave the lattice, which would eventually lead to breakdown of the material. Material breakdown is known in the literature to occur at high temperatures, which are, however, outside the IT-SOFC range.64,65 It is also worth noting that the oxygen vacancy formation energies (corresponding to eqn (1)) are much lower in all cases than the hole formation energies (corresponding to eqn (2)), which would indicate that oxygen vacancy formation is the most probable compensation scheme under equilibrium conditions.
does indicate that oxygen could spontaneously leave the lattice, which would eventually lead to breakdown of the material. Material breakdown is known in the literature to occur at high temperatures, which are, however, outside the IT-SOFC range.64,65 It is also worth noting that the oxygen vacancy formation energies (corresponding to eqn (1)) are much lower in all cases than the hole formation energies (corresponding to eqn (2)), which would indicate that oxygen vacancy formation is the most probable compensation scheme under equilibrium conditions.
Compared to SmCoO3, which had an 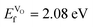 , we can conclude that doping clearly favors the formation of spontaneous vacancies. It is also worth mentioning that at high temperatures, SmCoO3 has a C-type antiferromagnetic structure.68 Thus, we also calculated
, we can conclude that doping clearly favors the formation of spontaneous vacancies. It is also worth mentioning that at high temperatures, SmCoO3 has a C-type antiferromagnetic structure.68 Thus, we also calculated 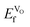 for the high-temperature structure, and found this to be 1.43 eV. Furthermore, for comparison, we calculated
for the high-temperature structure, and found this to be 1.43 eV. Furthermore, for comparison, we calculated 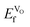 for the traditional high-temperature SOFC cathode material La0.75Sr0.25MnO3−d (LSM), which is 1.82 eV. We thus see that VO formation in Sm1−xAxCoO3−x/2 is energetically more favorable than in LSM. Thus, all of these systems show excellent potential as ionic conductors, but these results are not conclusive as to which x or A2+ leads to the highest oxygen conduction. Next, we have therefore used MD to evaluate the oxygen diffusion and ionic conduction. Please note that all the results below are for the systems in the VO compensated scheme.
for the traditional high-temperature SOFC cathode material La0.75Sr0.25MnO3−d (LSM), which is 1.82 eV. We thus see that VO formation in Sm1−xAxCoO3−x/2 is energetically more favorable than in LSM. Thus, all of these systems show excellent potential as ionic conductors, but these results are not conclusive as to which x or A2+ leads to the highest oxygen conduction. Next, we have therefore used MD to evaluate the oxygen diffusion and ionic conduction. Please note that all the results below are for the systems in the VO compensated scheme.
3.4. Association energy
Another important property to assess is the dopant-VO-cluster interaction energy (Eint), which is calculated (eqn (7)) as the difference in Ef of the defect cluster (Epairf), and the sum of Ef for the two individual defects (Eisolated![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) defectsf).58
defectsf).58Eint = Epairf − ∑Eisolated![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) defectsf defectsf | (7) |
Negative values (e.g. −0.67 eV for Ca-doping) indicate an energetic benefit for the defects to be associated, whereas positive values (e.g. 0.06 eV for Sr-doping and 0.20 eV for Ba-doping) indicate the tendency for the defects to dissociate. Thus, trapping of VO may occur near a Ca-dopant site at low temperatures, although at operating temperatures, either intermediate or high, this barrier will be easy to overcome and should not noticeably influence oxygen migration.
3.5. Oxygen migration and conduction
Oxygen diffusion in perovskite oxides undergoes a vacancy hopping mechanism and is temperature dependent. Diffusion can be calculated using Fick's first law, assuming steady state diffusion. For steady state diffusion, the diffusion flux (J), which is the number of atoms diffusing per unit area and time, along a given direction (x, y, or z) is proportional to the concentration (C) gradient (eqn (8)).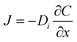 | (8) |
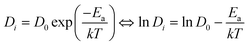 | (9) |
| 〈r2(t)〉 = 6Dit + Bi | (10) |
According to the MSD representation depicted in Fig. S1 of the ESI,† cation diffusion is limited and reaches equilibrium shortly after equilibration, whereas the oxygen MSD clearly increases with time (Fig. S2 in ESI†). DO for oxygen was calculated according to eqn (10), and showed that in general the highest oxygen conductivity is found at temperatures higher than 1000 K, and for CaxSm1−xCoO3−x/2 at 1500 K. Moreover, all materials show higher oxygen diffusion (even at low temperatures) than the traditional cathode material La0.5Sr0.5MnO3−d, which has a experimentally measured DO of 3 × 10−12 cm2 s−1 at 900 °C (1173 K),69 as compared to the calculated value of 2.87 × 10−7 cm2 s−1 for Sm0.5Ca0.5CoO2.75 at 1200 K (Table S5, ESI†).
The highest oxygen diffusion is reached when the system is doped with Ca2+, which can be explained by the fact that Ca2+ is also the system with the smallest of the tested dopants. Relating diffusion to activation energy (Fig. 7 and Table 4), Ea decreases with increasing x, indicating that higher dopant concentrations favor oxygen migration, as has previously been reported for Sr-doping of LaMnO3 and LaCoO3.41
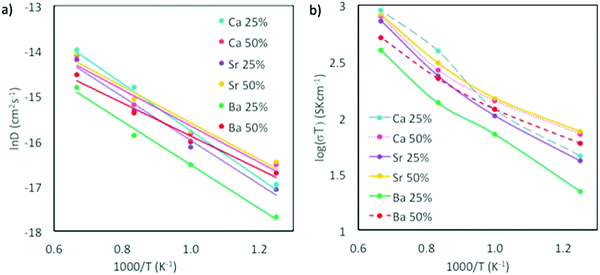 | ||
| Fig. 7 (a) Arrhenius plots for oxygen diffusion, and (b) ionic conductivity for CaxSm1−xCoO3−d, BaxSm1−xCoO3−d and SrxSm1−xCoO3−d. Temperature range is 800–1500 K. | ||
| System | E a, x = 0.25 (eV) | E a, x = 0.50 (eV) |
|---|---|---|
| BaxSm1−xCoO3−d | 0.42 | 0.32 |
| CaxSm1−xCoO3−d | 0.45 | 0.36 |
| SrxSm1−xCoO3−d | 0.42 | 0.35 |
| SmCoO3 | 0.93 | |
Ionic conduction (σO) is challenging to measure experimentally since both electronic and ionic conductivities are normally hard to differentiate.10 Thus, theoretical calculations have proved to be very useful in directly comparing σO between different systems. σO is calculated from DO through the Nernst–Einstein equation10 (eqn (11)).
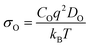 | (11) |
3.6. Thermal expansion coefficient
In addition to ionic conductivity, another vital property of SOFC cathodes is the thermal expansion coefficient (TEC). The cathode requires a TEC that is compatible with the electrolyte, as incompatibility will lead to SOFC cell breakdown. Common SOFC electrolytes include YSZ, LSGM, and GDC, which have TEC of 10.0–12.5 × 10−6 K−1.70 TEC for SmCoO3 (17.7 × 10−6 K−1) itself is incompatible with these electrolytes, and thus to reduce TEC, doping is vital.67 DFT+U results showed that the lattice volume increases with increasing x, thus inducing negative chemical pressure, as all dopants have a higher ionic radius than Sm3+; Sm3+(0.96 Å) < Ca2+(1.00 Å) < Sr2+(1.18 Å) < Ba2+(1.35 Å).71 The largest volume increase for all x is seen for Ba2+, and the least for Ca2+, which behavior has previously been reported in molecular dynamics studies of Sr-doped SmCoO3.72 The volume expansion in relation to temperature was then calculated with MD, and the linear thermal expansion coefficient extracted (Table 5).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 66
66
| System | TEC, x = 0.25 (10−6 K−1) | TEC, x = 0.50 (10−6 K−1) |
|---|---|---|
| CaxSm1−xCoO3−d | 23.3 | 24.2 |
| SrxSm1−xCoO3−d | 22.7 | 30.9 |
| BaxSm1−xCoO3−d | 23.7 | 30.0 |
| System | TEC, x = 0 (10−6 K−1) |
|---|---|
| SmCoO3 | 17.1 |
The TECs are in alignment with previous results for cobalt-based SOFC cathodes, which normally have higher TEC than SOFC electrolytes.70 To overcome this incompatibility between these cathodes and traditional electrolytes, Co-site doping with transition metals might be necessary. Such doping has been shown to decrease cathode TEC in for example La1−xSrxCoO3−x/2.73 However, this is outside the scope of this paper.
Comparing all the above calculated properties of Sm1−xAxCoO3−x/2, it can be seen that Ca-doping gives the highest DO, among the lowest Ea, highest ionic conduction, and more compatible TEC at intermediate temperatures (800–1000 K). Sr-Doping, however, gives higher ionic conduction at lower temperature (x = 0.50), but due to this composition a much higher TEC. Thus, Ca-doping might be more practical for IT-SOFC cathode applications.
4. Conclusion
The electronic properties and ionic conduction of potential IT-SOFC cathode materials have been modeled using DFT+U and MD calculations. Evaluation of two charge compensation schemes suggests that oxygen vacancy compensation is the more likely for these materials. Furthermore, the change in electronic structure upon doping has been linked directly to distortions in the Co–O bonds. Structural distortions break the octahedral crystal field splitting, which provokes a spin transition in Co that leads to a change in the electronic structure, making the doped SmCoO3 a conductor.However, we have found that the ionic conductivity in doped SmCoO3 is two times higher at intermediate temperatures than in LSM, with Ca2+, x = 0.25, reporting the best results, in agreement with experimental findings. Finally, thermal expansion coefficients were also calculated, and were found to be in the same range as lanthanum-based cathode materials, but still too high for perfect compatibility with the traditional electrolyte materials. One way to overcome this deficiency could be the introduction of additional Co-site dopants, which is the topic of future studies.
Acknowledgements
The authors acknowledge the Engineering and Physical Sciences Research Council (EPSRC) for financial support (Grants references EP/K016288/1 and EP/K001329/1). We also acknowledge the use of the UCL Legion High Performance Computing Facility (Legion@UCL), as well as the use of the UCL Grace High Performance Computing Facility (Grace@UCL), and associated support services, in the completion of this work. Finally, via our membership of the UK's HPC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202), this work made use of the facilities of ARCHER, the UK's national high-performance computing service, which is funded by the Office of Science and Technology through EPSRC's High End Computing Programme. DL_POLY_4 is a molecular dynamics simulation package written by I. T. Todorov and W. Smith, and has been obtained from STFC's Daresbury Laboratory via the website http://www.ccp5.ac.uk/DL_POLY. N. H. d. L. thanks the Royal Society for an Industry Fellowship. E. O. gratefully acknowledges EPSRC funding from the Centre for Doctoral Training in Molecular Modelling and Materials Science (EP/G036675/1).References
- S. M. Haile, Acta Mater., 2003, 51, 5981–6000 CrossRef CAS.
- M. M. Kuklja, E. A. Kotomin, R. Merkle, Y. A. Mastrikov and J. Maier, Phys. Chem. Chem. Phys., 2013, 15, 5443–5471 RSC.
- B. C. Steele and A. Heinzel, Nature, 2001, 414, 345–352 CrossRef CAS PubMed.
- A. Aguadero, L. Fawcett, S. Taub, R. Woolley, K.-T. Wu, N. Xu, J. A. Kilner and S. J. Skinner, J. Mater. Sci., 2012, 47, 3925–3948 CrossRef CAS.
- Y. Choi, D. S. Mebane, M. C. Lin and M. Liu, Chem. Mater., 2007, 19, 1690–1699 CrossRef CAS.
- H. Fukunaga, M. Koyama, N. Takahashi, C. Wen and K. Yamada, Solid State Ionics, 2000, 132, 279–285 CrossRef CAS.
- X. Jiang, Q. Xu, Y. Shi, X. Li, W. Zhou, H. Xu and Q. Zhang, Int. J. Hydrogen Energy, 2014, 39, 10817–10823 CrossRef CAS.
- T. N. Vasil’chikova, T. G. Kuz’mova, A. A. Kamenev, A. R. Kaul’ and A. N. Vasil’ev, JETP Lett., 2013, 97, 34–37 CrossRef.
- I. Fullarton, J. Jacobs and H. Van Benthem, Ionics, 1995, 1, 51–58 CrossRef CAS.
- T. C. Yeh, J. L. Routbort and T. O. Mason, Solid State Ionics, 2013, 232, 138–143 CrossRef CAS.
- C. Xia, W. Rauch, F. Chen and M. Liu, Solid State Ionics, 2002, 149, 11–19 CrossRef CAS.
- B. Wei, K. Chen, C. C. Wang, Z. Lü and S. P. Jiang, Electrochim. Acta, 2015, 174, 327–331 CrossRef CAS.
- S. Pawar and K. Shinde, J. Mater., 2013, 2013, 6 Search PubMed.
- F. A. Kröger and H. J. Vink, Solid State Phys., 1956, 3, 307–435 Search PubMed.
- A. M. Deml, V. Stevanović, C. L. Muhich, C. B. Musgrave and R. O’Hayre, Energy Environ. Sci., 2014, 7, 1996 CAS.
- A. M. Ritzmann and A. B. Muñoz-García, Chem. Mater., 2013, 25, 3011–3019 CrossRef CAS.
- A. M. Ritzmann, J. M. Dieterich and E. A. Carter, Phys. Chem. Chem. Phys., 2016, 18, 12260–12269 RSC.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- P. E. Blöchl, O. Jepsen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 16223–16233 CrossRef.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Oxford, 1990 Search PubMed.
- G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- G. Pacchioni, J. Chem. Phys., 2008, 128, 182505 CrossRef PubMed.
- H.-P. Komsa, T. T. Rantala and A. Pasquarello, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 45112 CrossRef.
- T. Geng, Z. Han and S. Zhuang, Phys. B, 2010, 405, 3714–3716 CrossRef CAS.
- P. Ravindran, A. Kjekshus, H. Fjellvåg, A. Delin and O. Eriksson, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 64445 CrossRef.
- P. Ravindran, R. Vidya, H. Fjellvåg and A. Kjekshus, J. Cryst. Growth, 2004, 268, 554–559 CrossRef CAS.
- E. Olsson, X. Aparicio-Anglès and N. H. De Leeuw, J. Chem. Phys., 2016, 145, 14703 CrossRef PubMed.
- S. Dudarev, G. Botton and S. Savrasov, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
- S. Zhang, N. Han and X. Tan, RSC Adv., 2015, 5, 760 RSC.
- I. T. Todorov, W. Smith, K. Trachenko and M. T. Dove, J. Mater. Chem., 2006, 16, 1911–1918 RSC.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef.
- M. Born and J. Mayer, Phys. B, 1932, 75, 1–18 CAS.
- J. E. Mayer, J. Chem. Phys., 1933, 1, 270–279 CrossRef CAS.
- M. S. Islam, M. Cherry and C. R. A. Catlow, J. Solid State Chem., 1996, 124, 230–237 CrossRef CAS.
- M. Cherry, M. S. Islam and C. R. A. Catlow, J. Solid State Chem., 1995, 118, 125–132 CrossRef CAS.
- M. S. D. Read, M. S. Islam, G. W. Watson, F. King and F. E. Hancock, J. Mater. Chem., 2000, 10, 2298–2305 RSC.
- T. S. Bush, J. D. Gale, C. R. A. Catlow and P. D. Battle, J. Mater. Chem., 1994, 4, 831 RSC.
- G. V. Lewis and C. R. A. Catlow, J. Phys. C: Solid State Phys., 1985, 18, 1149–1161 CrossRef CAS.
- J. D. Gale, J. Chem. Soc., Faraday Trans., 1997, 93, 629–637 RSC.
- J. D. Gale and A. L. Rohl, Mol. Simul., 2003, 29, 291–341 CrossRef CAS.
- J. D. Gale, Z. Kristallogr., 2005, 220, 552–554 CAS.
- J. D. Gale, Philos. Mag. B, 1996, 73, 3–19 CrossRef CAS.
- R. Grau-Crespo, S. Hamad, C. R. A. Catlow and N. H. De Leeuw, J. Phys.: Condens. Matter, 2007, 19, 256201 CrossRef.
- Y. Orikasa, T. Ina, T. Nakao, A. Mineshige, K. Amezawa, M. Oishi, H. Arai, Z. Ogumi and Y. Uchimoto, J. Phys. Chem. C, 2011, 115, 16433–16438 CAS.
- A. L. Shluger, K. P. McKenna, P. V. Sushko, D. M. Ramo and A. V. Kimmel, Modell. Simul. Mater. Sci. Eng., 2009, 17, 84004 CrossRef.
- E. A. Kotomin, R. I. Eglitis, A. V. Postnikov, G. Borstel and N. E. Christensen, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 11–15 CrossRef.
- S. T. Murphy and N. D. M. Hine, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 1–18 Search PubMed.
- S. Zhang and J. Northrup, Phys. Rev. Lett., 1991, 67, 2339–2342 CrossRef CAS PubMed.
- H. Raebiger, S. Lany and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 45209 CrossRef.
- T. Tanaka, K. Matsunaga, Y. Ikuhara and T. Yamamoto, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 205213 CrossRef.
- P. G. Sundell, M. E. Björketun and G. Wahnström, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 104112 CrossRef.
- Z. Alahmed and H. Fu, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 224101 CrossRef.
- E. Heifets, S. Piskunov, E. A. Kotomin, Y. F. Zhukovskii and D. E. Ellis, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 115417 CrossRef.
- Y.-L. Lee, J. Kleis, J. Rossmeisl and D. Morgan, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 224101 CrossRef.
- J. Buckeridge, D. O. Scanlon, A. Walsh and C. R. A. Catlow, Comput. Phys. Commun., 2014, 185, 330–338 CrossRef CAS.
- A. M. Ritzmann, M. Pavone, A. B. Muñoz-García, J. A. Keith and E. A. Carter, J. Mater. Chem. A, 2014, 2, 8060–8074 CAS.
- C. Persson, Y. J. Zhao, S. Lany and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 1–14 CrossRef PubMed.
- A. Marthinsen, C. Faber, U. Aschauer, N. A. Spaldin and S. M. Selbach, MRS Commun., 2016, 1–26 Search PubMed.
- R. Liu, D. Xu, S. Li, Z. Lü, Y. Xue, D. Wang and W. Su, Front. Chem. China, 2006, 1, 398–401 CrossRef.
- S. W. Baek, J. H. Kim and J. Bae, Solid State Ionics, 2008, 179, 1570–1574 CrossRef CAS.
- E. Olsson, X. Aparicio-Anglès and N. H. de Leeuw, J. Chem. Phys., 2016, 145, 224704 CrossRef PubMed.
- S. P. Jiang, J. Mater. Sci., 2008, 43, 6799–6833 CrossRef CAS.
- J. A. Kilner and M. Burriel, Annu. Rev. Mater. Res., 2014, 44, 365–393 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- M. A. Farhan and M. J. Akhtar, J. Phys.: Condens. Matter, 2010, 22, 75402 CrossRef PubMed.
- J. H. Kim, S.-W. Baek, C. Lee, K. Park and J. Bae, Solid State Ionics, 2008, 179, 1490–1496 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Calculated and experimental lattice parameters for cubic and orthorhombic SmCoO3, as well as Sm2O3 using interatomic potentials (Table S1), a description of the Goldschmidt factor and its calculated values (Table S2), the relative energies of the different dopant configurations (Table S3), lattice parameters, and interatomic distances in the dopant systems for the most stable configurations (Table S4), and a discussion of the solution energy (Table S5). Furthermore, graphical representations of all oxygen vacancy-dopant configurations and their oxygen vacancy formation energies are included in Fig. S1–S3. In Tables S6 and S7, Bader charges have been collected, and mean square displacement plots are presented in Fig. S4 and S5. Table S8 contains all diffusion coefficients used to calculate ionic conductivity and activation energies. See DOI: 10.1039/c7cp01555k |
| This journal is © the Owner Societies 2017 |