Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Molecular organization in the twist–bend nematic phase by resonant X-ray scattering at the Se K-edge and by SAXS, WAXS and GIXRD†
W. D.
Stevenson
a,
Z.
Ahmed
b,
X. B.
Zeng
 *a,
C.
Welch
b,
G.
Ungar
*ac and
G. H.
Mehl
*b
*a,
C.
Welch
b,
G.
Ungar
*ac and
G. H.
Mehl
*b
aDepartment of Materials Science and Engineering, University of Sheffield, Sheffield S1 3JD, UK. E-mail: x.zeng@shef.ac.uk
bDepartment of Chemistry, University of Hull, Hull HU6 7RX, UK
cDepartment of Physics, Zhejiang Sci-Tech University, Hangzhou 310018, China
First published on 3rd May 2017
Abstract
Using a magnetically aligned liquid crystal mixture containing a novel Se-labelled dimer and the difluoroterphenyl dimer DTC5C7, the twist–bend nematic phase (Ntb) was studied by the resonant scattering of hard X-rays and by conventional small and wide-angle X-ray scattering (SAXS, WAXS). Resonant diffraction spots indicated a helix with a 9–12 nm pitch in the Ntb phase and an unprecedentedly high helix orientation. This enabled deconvolution of global and local order parameters. These findings, combined with the simultaneously recorded resonant and non-resonant SAXS and WAXS data, allowed us to construct a locally layered molecular model of the Ntb phase, where the average twisted conformation of each molecule was idealised as a helical segment, matching the local heliconical director field. The dimers were found to be less bent in the Ntb phase than in their minimum energy conformation, and straightening further with increasing temperature. It is proposed that on further heating their low bend angle allows the transition to the normal nematic phase, where the molecules can freely move longitudinally, without the need to perform screw-like motion as in the Ntb phase. At the low-temperature end, the increasing molecular twist becomes unsustainable, leading to a transition to a smectic phase, where no twist is required.
The nematic–nematic liquid crystal (LC) transition, first reported in main-chain LC polyethers1,2 and later in bent LC dimers,3–22 is commonly observed when mesogens are angled to each other (bent conformation) by a semi-flexible spacer, such as an odd-numbered oligomethylene chain. Prediction of the nematic–nematic transition in 197623 predates even the first experimental observation in 1992,1 but the more recent theoretical framework provided by Dozov24 and Memmer25 has become the basis of reference. On transition from the higher temperature nematic (N), it is proposed that the mesogens preferentially select a lower energy ground state with a locally bent director field, thereby enabling a closer packing of bent molecular conformations. To fill space, the local director bend is accompanied by twist or splay deformations, giving rise to two alternative bent nematic ground states: helical twist–bend nematic (Ntb) and oscillating splay–bend nematic (Nsb).24 Of importance to this work is the Ntb model. Currently, the Ntb phase is described as a nematic continuum featuring an average heliconical director field. The mesogens are thought to glide fluidly along the helical axis, possess no long-range positional order and complete a full rotation in just a few molecular lengths. Both left- and right-handed domains are expected.
Historically, the Ntb model has proven difficult to unambiguously validate by experimental means. Topological characterisation methods, e.g. opto-electric studies,3,4 have shown inversely handed domains and switching speeds consistent with a nano-scale pitch. A nano-scale pitch was also suggested by AFM5 and freeze fracture TEM;6,7 though in both cases, the imaging was performed below the stability range of the Ntb phase, and doubts remained as to whether the surface imaging was representative of the bulk. The structure of the Ntb phase was also unclear from NMR,8 Raman scattering9 and conventional X-ray scattering.10 However, recently, helical periodicity within the Ntb phase was directly identified in a bulk sample by resonant X-ray scattering at the carbon absorption edge (K-edge).11 A resonant Bragg ring was observed in the Ntb phase originating from an 8–10 nm long helical pitch. Such observation of orientational periodicity is possible only at the absorption edge of the atoms, where X-ray scattering becomes sensitive to the symmetry of bound orbitals, i.e. where the atomic form factor changes from scalar to a complex tensor.26–28
Although the helical pitch has now been confirmed by carbon RXS, many questions about the Ntb phase remain unanswered. The three principal subjects of debate regard the orientational order parameter, the manner in which the molecules pack into the helix and whether or not the molecules are locally layered. However, carbon RXS is unable to provide answers to these questions, because the low energy ‘soft’ X-rays (∼0.3 keV) required for carbon resonance imposes severe experimental constraints; for example, the beamline must be fully windowless in high vacuum and the sample must be held between thin, fragile substrates, preventing alignment by external fields.11 Moreover, soft X-ray scattering allows access to only a limited range of reciprocal space, excluding the scattering at larger wave vectors (q), which holds information on molecular conformation and packing.
Here, we avoided the drawbacks of carbon RXS by studying the Ntb phase using harder X-rays at the selenium K-edge (12.658 keV). For this purpose, a selenoether dimer was specially synthesised. In addition to resonant diffraction from the heliconical Ntb structure, we extend the previous work by simultaneously recording the non-resonant scattering at larger q. Furthermore, we aligned the Ntb phase using a magnetic field and, for the first time, obtained direct information on the orientation of the helical axis and, simultaneously, that of the molecules. This enabled us to obtain new details about the molecular conformation and packing in the Ntb phase. Combined resonant and non-resonant small- and wide-angle X-ray scattering (SAXS and WAXS) data on the perfectly aligned sample, together with the results from grazing incidence X-ray diffraction (GIXRD), allowed us to construct a more detailed model of the Ntb phase. This includes twisted molecular conformations matching the shape of the local heliconical director field, as well as local molecular layering. We also present herein the first quantitative data on the helical domain size in bulk Ntb.
Sample preparation and phase behaviour
The selenoether dimer compound DTSe (Fig. 1a) was synthesised as described in the ESI.† DTSe does not exhibit the Ntb phase, but did so when mixed with the previously studied compound DTC5C7 (Fig. 1a).12,13 The miscibility of the two compounds was examined qualitatively by bringing them into contact under crossed polarisers. A composition gradient was formed, which was most evident at 114 °C. Fig. 1b shows the central N phase separating the Ntb phase of the DTC5C7-rich region (left) and the Smectic-C (SmC) phase of the DTSe-rich region (right). | ||
| Fig. 1 (a) The molecular structure of DTC5C7 (n = 7, X = CH2) and DTSe (n = 9, X = Se). (b) Optical textures observed between cross polarizers at 114 °C for a contact preparation, showing the change from Ntb, to N, to SmC phase with increasing concentration of DTSe in the binary mixture. Scale bar = 100 μm. (c) Phase diagram of DTC5C7 and DTSe. The experimental points are the DSC peak temperatures on first heating (note: a metastable smectic forms in pure DTC5C7 on cooling12). C1 = DTC5C7 crystal, C2 = DTSe crystal. The dashed vertical line indicates Se45, and the horizontal line 114 °C. | ||
The binary phase diagram (Fig. 1c) was determined by differential scanning calorimetry (DSC) and polarised optical microscopy. Each mixture was prepared by dissolving weighed amounts of DTC5C7 and DTSe in dichloromethane and freeze drying after mixing in solution. The diagram shows a stable Ntb region between 0 and ca 60 mol% DTSe. For our RXS investigation we selected a mixture containing 45 mol% DTSe, henceforth referred to as Se45.
Resonant X-ray scattering
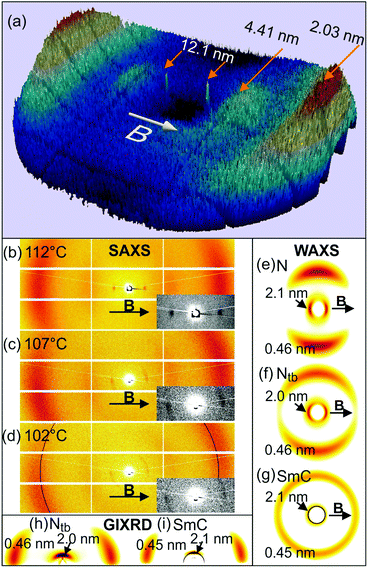
The RXS investigation of Se45 was performed on beamline I22 of the Diamond Light Source. The sample was held in a 1 mm glass capillary, positioned perpendicular to a 1 T magnetic field. The sample was heated and cooled using thermostated nitrogen gas. Se45 was investigated in each of its phases using X-ray energies above and below the Se K-edge (Er = 12.658 keV). Two Pilatus 2 M detectors were simultaneously employed to cover the range of ∼0.3 nm−1 ≤ q ≤ 15 nm−1. Additional non-resonant SAXS and WAXS experiments were carried out at station BM28 (ESRF) using a MAR165 CCD camera.The sample was first cooled from the isotropic to the Ntb phase (105 °C), where the incident energy (Ei) was increased in increments of 5 eV from 12.608 to 12.708 keV. Throughout this energy range, two broad SAXS maxima were observed at q = 1.44 and 3.16 nm−1, corresponding to average spacings of 4.4 (d1) and 2.0 nm (d2) (Fig. S5 and Table S2, ESI†). These spacings are comparable to the average (DTSe and DTC5C7) dimer length (4.5 nm) and centre-to-centre mesogen distance (2.1 nm) within Se45. These two SAXS maxima are believed to arise from localised smectic-like layering, usually driven by π–π-interactions between aromatic mesogens and often referred to as cybotactic nematic correlations.29 A non-resonant diffuse WAXS maximum at q = 13.7 nm−1 corresponds to a “d-spacing” of 0.46 nm, suggesting an average lateral intermolecular distance of 0.51 nm.29 However at X-ray energies satisfying |Ei − Er| ≤ 5 eV, an additional Bragg peak was observed at q = 0.62 nm−1, attributed to resonant diffraction from a helical pitch p of 10.1 nm (Fig. S5, ESI†). The resonant peak was strongest at Ei = Er.
Temperature dependence of the resonance effect
Temperature dependence of the resonance effect was investigated by cooling the sample through each of its LC phases with Ei = Er. The resonant peak was observed exclusively in the Ntb phase and at the biphasic boundaries. As shown in Fig. 2a, the resonant peak appeared at the onset of the Ntb phase (115 °C), reaching a maximum intensity at 112 °C, with p = 12.1 nm. With decreasing temperature, the resonant peak shifted to larger q, indicating a reducing pitch length (Fig. 2b). The radial full width at half maximum (FWHM) of the resonant peak initially increased, indicating a broadening distribution of p, before decreasing again at the onset of the SmC phase. The resonance effect was lost with further cooling into the SmC phase. These findings are summarised numerically in Table S2 (ESI†).At 112 °C, the sharp resonant peaks were exactly on the meridian (Fig. 3a and b), defined as the axis through the beam centre, parallel to the magnetic field. This indicates that the helical axis of the bulk sample was highly oriented with the field. The diffuse SAXS peaks were azimuthally spread (arc-like), but were also centred on the meridian (Fig. 3a–c). As mentioned above, these SAXS features arise from local smectic-like layering of dimers. The azimuthal arcing of the SAXS maxima indicates that the short-range layers are not all perpendicular to the helical axis.
On cooling from 112 °C, the intensity maxima of all three SAXS peaks simultaneously shifted away from the meridian; the lower the temperature, the larger the shift, see Fig. 3b–d. The resonant peak began to broaden azimuthally, indicating decreasing orientational order of the Ntb phase. Phase orientation was lost entirely in the SmC phase – see the sharp Bragg ring in Fig. 3d. The lamellar phase is assumed to be SmC (tilt angle ∼24°) because the layer height (4.12 nm) is shorter than the length of both dimer types in the mixture. The WAXS maxima similarly rotated and spread azimuthally, before becoming a diffuse halo in the SmC (Fig. 3e–g).
The temperature dependency of the pitch length was reported by C. Zhu et al.,11 who measured p of CB7CB to vary between 8 and 10 nm. However in their work, the reflection was usually split over a wider q-range, possibly due to a surface confinement effect. The increased p of Se45 (9–12 nm) is attributed to the larger molecular lengths of DTC5C7 and DTSe.
Structural correlation and orientational order
At 112 °C, the azimuthal FWHM of the resonant peak was ∼12°, indicating that the orientational order parameter of the global helical axis (S0) must be close to 1 ((3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2
cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6° − 1)/2 = 0.98, taking 12°/2 = 6° as the mean deviation angle of the local helical directors to the external field). This is in fact an underestimation as it assumes no contribution from other peak broadening factors, such as the structural correlation lengths. However, the mesogens are tilted (tilt angle θ) in respect to the helical axis, which means that a second order parameter S1 = 〈3
6° − 1)/2 = 0.98, taking 12°/2 = 6° as the mean deviation angle of the local helical directors to the external field). This is in fact an underestimation as it assumes no contribution from other peak broadening factors, such as the structural correlation lengths. However, the mesogens are tilted (tilt angle θ) in respect to the helical axis, which means that a second order parameter S1 = 〈3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2
cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ − 1〉/2 is required to account for this angular distribution. The overall orientational order parameter S of the Ntb phase, measureable by classical means, is therefore S0·S1, which quantifies the orientational distribution of the helical domains and the tilt angle distribution of the mesogens inside each domain. We have shown that S0 of the Ntb phase can be close to 1 and that it decreases with temperature, but even in the case of perfect helical alignment, the classically measured orientational order parameter will be small because S1 ≪ 1, due to θ ≫ 0° (see next section on the molecular-level model and Fig. 4). The fundamental limitation imposed by S1 may account for the low orientational order parameter (〈P2〉 ∼ 0.4–0.6) often reported within the Ntb phase of bent dimers.8–10,14–16
θ − 1〉/2 is required to account for this angular distribution. The overall orientational order parameter S of the Ntb phase, measureable by classical means, is therefore S0·S1, which quantifies the orientational distribution of the helical domains and the tilt angle distribution of the mesogens inside each domain. We have shown that S0 of the Ntb phase can be close to 1 and that it decreases with temperature, but even in the case of perfect helical alignment, the classically measured orientational order parameter will be small because S1 ≪ 1, due to θ ≫ 0° (see next section on the molecular-level model and Fig. 4). The fundamental limitation imposed by S1 may account for the low orientational order parameter (〈P2〉 ∼ 0.4–0.6) often reported within the Ntb phase of bent dimers.8–10,14–16
Assuming perfect orientational order of the helical axis (reasonable at 112 °C where S0 ≃ 1), the intensity distribution of the resonant peak can be attributed to structural correlations parallel and perpendicular to the helical axis. In a nematic LC, one may assume that correlation decays exponentially with distance r, i.e. ∝exp(−r/ξ). Under this assumption, the scattered intensity in reciprocal space is well reproduced by Lorentzian profiles of the form Imax/(1 + Δq‖2ξ‖2 + Δq⊥2ξ⊥2),30–32 where ξ‖ and ξ⊥ are the correlation lengths parallel and perpendicular to the helical axis. By least squares fitting of a Lorentzian profile to the intensity around the resonant peak at 112 °C (I vs. Δq‖ and I vs. Δq⊥), and after making corrections for instrumental broadening (Fig. 2c), we obtained ξ‖ = 33 nm and ξ⊥ = 18 nm. Alternatively, using the FWHM of the Lorentzian fit (Δq = 2/ξ), the Scherrer equation τ = 2Kπ/Δq can be used to estimate the size of the coherent heliconical domain. If the shape factor (K) is set to unity, then τ = πξ and the longitudinal and transverse helical domain sizes are estimated to be 104 nm (24 molecular lengths) and 57 nm (112 molecular widths). Note that both values are underestimates: the calculations assumed that the breadth of the resonant peak arose entirely from structural correlation. However, the distribution of p and the orientational imperfection also contribute to the peak breadth, as discussed above. At temperatures below 112 °C, ξ⊥ can no longer be determined due to the increased contribution of S0 ≪ 1 to azimuthal peak broadening. Similarly the increasing distribution of p with reducing temperature prevents accurate measurement of ξ‖. However it would appear that ξ‖ reduces as the Ntb phase progresses, until reaching the onset of the SmC phase, where the quasi-long-range positional order sets in ref. 33. For the SmC phase, measurement of Δq‖d2 is limited by the instrumental resolution (0.005 nm−1), indicating a correlation length >400 nm.
As mentioned previously, the two broad SAXS peaks are respectively linked to short-range correlations between the dimers and mesogens. These correlations must be (on average) in the direction of the helical axis because the two broad SAXS peaks remain aligned with the resonant peak at all times, despite the reducing influence of the magnetic field with cooling. At temperatures close to the N–Ntb boundary, the inter-mesogen correlation length along the helical axis can be estimated from 2/Δq‖d2 (Table S2, ESI†) as ∼1.7 nm.
Molecular-level model
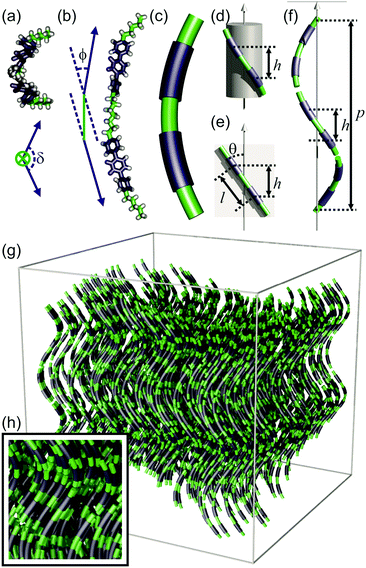
The existing models of the Ntb phase describe an average helical director field inside a nematic continuum, but lack consideration of local molecular packing. Here, we propose a locally layered molecular-level model of the Ntb phase, in line with the newly presented information discussed above. In this model, the ideal average conformation of the molecules (DTC5C7 and DTSe) resembles the shape of a helical segment (Fig. 4a–c), which enables each component of the dimer to match the heliconical path of the Ntb director field (Fig. 4f). In the real dynamic system, there is a multitude of conformations. However in the following geometric construction we assume, for simplicity, the molecular conformation that follows the ideal shape of a helical segment, representing the conformational average, and show that it is energetically feasible.The local director field along the helical axis can be defined mathematically as:
n = sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(−2πz/p)i + sin cos(−2πz/p)i + sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(−2πz/p)j + cos sin(−2πz/p)j + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θk θk | (1) |
h = l![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(θ) cos(θ) | (2) |
Using the experimental values of the rotation and tilt angles, one may also calculate the bend angle between the two mesogens of a dimer. If the two rod-like mesogens are respectively defined by unit vectors n1 and n2 (see Fig. S7), it can be shown geometrically (ESI†) that:
| sin(ϕ/2) = sin(θ)·sin(πh/p) | (3) |
For the dimer molecules, another important parameter is its twist angle δ, i.e. the angle between the two mesogens when projected along the spacer axis (Fig. 4a). Using our model, it could be calculated that the twist angle was 129° at 115 °C, and 125° at 105 °C (Section S5.3, ESI†). These values are far from the 0° twist angle for an all-trans conformation of the spacer.
In comparison to our model, a molecular dynamic simulation of the Ntb phase formed by the cyanobiphenyl dimer CB7CB was carried out by D. Chen et al. in a periodic bounding box of size 5.6 × 5.6 × 8.0 nm.7 According to this, the average external bend angle ϕ of the dimer was ∼47°, significantly larger than estimated from our model of Se45. Vanakaras and Photinos34 used a very simplified molecular model of two rod-like units (representing the two mesogens in the dimer) with a fixed core–core distance between them, and predicted that a bend angle of ∼60° and a twist angle also of ∼60° would be best for the formation of the Ntb phase.
The results presented here (low bending angle and high twist angle of the dimer) suggest that in order to follow a heliconical path, the molecules must adopt a higher energy conformation in which the arms are twisted about the spacer axis and are closer to parallel than in the minimum energy conformation of an isolated molecule. Molecular modelling (ESI,† Section S6) has shown that this can be achieved by changing the torsion angles of C–C bonds in the spacer, such as the molecule shown in Fig. 4a and b. In the Ntb phase, it is likely that this distortion energy is compensated by the entropy associated with the retained positional freedom of the dimers. The increasing ϕ on cooling is therefore expected, as lower energy conformations are preferred at lower temperatures. Furthermore, eqn (3) shows that p ∝ 1/ϕ. On cooling, as ϕ increases, the helical pitch p is reduced. On further cooling, when the translational entropy gain becomes insufficient to outweigh the energy cost of the distortion of the spacer, the system transforms to the SmC. The true nature of this smectic phase is still under investigation. There would be little advantage in chirality synchronization if it turns out to be a standard SmC phase, as longitudinal translational contribution to entropy is minor in a smectic anyway. A further likely consequence of the continuous change in helical pitch on cooling is a breakup into smaller domains, resulting in loss of the initial high orientational order of the helical axis, and thus also resulting in poor alignment in the SmC.
At the high-T end, as ϕ decreases and the dimer straightens further, the helix unwinds at the Ntb–N transition as longitudinal motion no longer requires the molecules to follow the helical path. The drop in ϕ at the transition is indicated by the reduction in azimuthal spread of the WAXS arcs in Fig. 3e and f.
The establishment of long-range homochirality in the Ntb phase appears to be a unique example of entropy-driven chirality synchronisation in achiral systems. Chirality synchronisation occurs where cooperativity in the choice of same-sense conformation in many molecules lowers the free energy, see recent reviews.35,36 As far as we know, in all other reported cases the reduction in free energy means in fact lowering the interaction energy through closer packing.
In summary, using a specially synthesised selenium-containing compound, we have presented the first RXS experiment on the Ntb phase using hard X-rays, which allowed sample alignment. Resonant Bragg reflection at Se absorption edge revealed a temperature dependent helical pitch of 9–12 nm. Of the two orientational order parameters required for the Ntb phase, we found that of the helical axis, measured here for the first time, to reach an unprecedented value of S0 = 0.98–1.00. Simultaneous recording of the resonant and the higher q non-resonant scattering, impossible with carbon RXS, and the knowledge that the non-resonant features come from perfectly aligned helices, allowed us to determine the tilt angle of the mesogens relative to the helical axis, as well as the bend angle of the dimers. We thus obtained a molecular-level model of the Ntb phase. According to this, the mesogen arms of the dimer are closer to parallel than in the minimum energy conformation, and are twisted about the spacer axis. Furthermore we found that, while the segregation of the aromatic and aliphatic moieties in layers is only local, the coherently diffracting heliconical domains size is of the order of 0.1 μm.
Acknowledgements
We acknowledge funding from the joint NSF-EPSRC PIRE program ‘‘RENEW’’ (EP/K034308), the Leverhulme Trust (RPG-2012-804) and the EPSRC (EP/M015726) and (EP/J004480) for ZA and CW and the EPSRC NMSF, Swansea for high resolution mass spectra. GU is grateful for the award of State Specially Recruited Expert from the Government of China. For help with the synchrotron experiments we thank Prof. N. Terrill at I22, Diamond Light Source, and Drs O. Bikondoa, L. Bouchenoire, S. Brown, P. Thompson and D. Wermeille of the XMaS beamline BM28 at ESRF.References
- G. Ungar, V. Percec and M. Zuber, Macromolecules, 1992, 25, 75 CrossRef CAS.
- G. Ungar, V. Percec and M. Zuber, Polym. Bull., 1994, 32, 325 CrossRef CAS.
- V. P. Panov, R. Balachandran, M. Nagaraj, J. K. Vij, M. G. Tamba, A. Kohlmeier and G. H. Mehl, Appl. Phys. Lett., 2011, 99, 261903 CrossRef.
- C. Meyer, G. R. Luckhurst and I. Dozov, Phys. Rev. Lett., 2013, 111, 067801 CrossRef CAS PubMed.
- E. Gorecka, M. Salamonczyk, A. Zep, D. Pociecha, C. Welch, Z. Ahmed and G. H. Mehl, Liq. Cryst., 2015, 42, 1 CrossRef CAS.
- V. Borshch, Y.-K. Kim, J. Xiang, M. Gao, A. Jákli, V. P. Panov, J. K. Vij, C. T. Imrie, M. G. Tamba, G. H. Mehl and O. D. Lavrentovich, Nat. Commun., 2013, 4, 2635 CAS.
- D. Chen, J. H. Porada, J. B. Hooper, A. Klittnick, Y. Shen, M. R. Tuchband, E. Korblova, D. Bedrov, D. M. Walba, M. A. Glaser, J. E. Maclennan and N. A. Clark, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 15931 CrossRef CAS PubMed.
- L. Beguin, J. W. Emsley, M. Lelli, A. Lesage, G. R. Luckhurst, B. A. Timimi and H. Zimmermann, J. Phys. Chem. B, 2012, 116, 7940 CrossRef CAS PubMed.
- Z. Zhang, V. P. Panov, M. Nagaraj, R. J. Mandle, J. W. Goodby, G. R. Luckhurst, J. C. Jones and H. F. Gleeson, J. Mater. Chem. C, 2015, 3, 10007 RSC.
- K. Adlem, M. Čopič, G. R. Luckhurst, A. Mertelj, O. Parri, R. M. Richardson, B. D. Snow, B. A. Timimi, R. P. Tuffin and D. Wilkes, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 022503 CrossRef CAS PubMed.
- C. Zhu, M. R. Tuchband, A. Young, M. Shuai, A. Scarbrough, D. M. Walba, J. E. Maclennan, C. Wang, A. Hexemer and N. A. Clark, Phys. Rev. Lett., 2016, 116, 147803 CrossRef PubMed.
- N. Sebastián, M. G. Tamba, R. Stannarius, M. R. de la Fuente, M. Salamonczyk, G. Cukrov, J. Gleeson, S. Sprunt, A. Jákli, C. Welch, Z. Ahmed, G. H. Mehl and A. Eremin, Phys. Chem. Chem. Phys., 2016, 18, 19299 RSC.
- S. A. Pardaev, S. Shamid, M. G. Tamba, C. Welch, G. H. Mehl, J. T. Gleeson, D. Allender, J. V. Selinger, B. D. Ellman, A. Jakli and S. Sprunt, Soft Matter, 2016, 12, 4472 RSC.
- C. Meyer, G. R. Luckhurst and I. Dozov, J. Mater. Chem. C, 2015, 3, 318 RSC.
- V. P. Panov, M. Nagaraj, J. K. Vij, Yu. P. Panarin, A. Kohlmeier, M. G. Tamba, R. A. Lewis and G. H. Mehl, Phys. Rev. Lett., 2010, 105, 167801 CrossRef CAS PubMed.
- A. Hoffmann, A. G. Vanakaras, A. Kohlmeier, G. H. Mehl and D. J. Photinos, Soft Matter, 2015, 11, 850 RSC.
- S. M. Salili, C. Kim, S. Sprunt, J. T. Gleeson, O. Parri and A. Jákli, RSC Adv., 2014, 4, 57423 RSC.
- M. G. Tamba, S. M. Salili, C. Zhang, A. Jákli, G. H. Mehl, R. Stannarius and A. Eremin, RSC Adv., 2015, 5, 11207 RSC.
- P. A. Henderson and C. T. Imrie, Liq. Cryst., 2011, 38, 1407 CrossRef CAS.
- M. Cestari, E. Frezza, A. Ferrarini and G. R. Luckhurst, J. Mater. Chem., 2011, 21, 12303 RSC.
- P. K. Challa, V. Borshch, O. Parri, C. T. Imrie, S. N. Sprunt, J. T. Gleeson, O. D. Lavrentovich and A. Jákli, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 060501 CrossRef CAS PubMed.
- M. Cestari, S. Diez-Berart, D. A. Dunmur, A. Ferrarini, M. R. de la Fuente, D. J. B. Jackson, D. O. Lopez, G. R. Luckhurst, M. A. Perez-Jubindo, R. M. Richardson, J. Salud, B. A. Timimi and H. Zimmermann, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 031704 CrossRef CAS PubMed.
- R. Meyer, in Molecular Fluids, ed. R. Balian and G. Weil, Gordon and Breach, New York, 1976 Search PubMed.
- I. Dozov, Europhys. Lett., 2001, 56, 247 CrossRef CAS.
- R. Memmer, Liq. Cryst., 2002, 29, 483 CrossRef CAS.
- D. H. Templeton and L. K. Templeton, Acta Crystallogr., 1980, A36, 237–241 CrossRef CAS.
- W. A. Hendrickson, Science, 1991, 254, 51 CAS.
- J.-L. Hodeau, V. Favre-Nicolin, S. Bos, H. Renevier, E. Lorenzo and J.-F. Berar, Chem. Rev., 2001, 101, 1843 CrossRef CAS PubMed.
- A. de Vries, Mol. Cryst. Liq. Cryst., 1970, 10, 219 CrossRef CAS.
- G. J. Brownsey and A. J. Leadbetter, Phys. Rev. Lett., 1980, 44, 24 CrossRef.
- K. K. Chan, P. S. Pershan and L. B. Sorensen, Phys. Rev. A: At., Mol., Opt. Phys., 1986, 34, 2 Search PubMed.
- S. H. Hong, R. Verduzco, J. C. Williams, R. J. Twieg, E. DiMasi, R. Pindak, A. Jákli, J. T. Gleeson and S. Sprunt, Soft Matter, 2010, 6, 4819 RSC.
- P. S. Pershan, Structure of Liquid Crystal Phases, World Scientific Publishing Ltd, 1988 Search PubMed.
- A. G. Vanakaras and D. J. Photinos, Soft Matter, 2016, 12, 2208 RSC.
- C. Tschierske and G. Ungar, ChemPhysChem, 2016, 17, 9 CrossRef CAS PubMed.
- E. Yashima, N. Ousaka, D. Taura, K. Shimomura, T. Ikai and K. Maeda, Chem. Rev., 2016, 116, 13752 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp01404j |
| This journal is © the Owner Societies 2017 |