Coherent electronic and nuclear dynamics in a rhodamine heterodimer–DNA supramolecular complex

Abstract

Elucidating the role of quantum coherences in energy migration within biological and artificial multichromophoric antenna systems is the subject of an intense debate. It is also a practical matter because of the decisive implications for understanding the biological processes and engineering artificial materials for solar energy harvesting. A supramolecular rhodamine heterodimer on a DNA scaffold was suitably engineered to mimic the basic donor–acceptor unit of light-harvesting antennas. Ultrafast 2D electronic spectroscopic measurements allowed identifying clear features attributable to a coherent superposition of dimer electronic and vibrational states contributing to the coherent electronic charge beating between the donor and the acceptor. The frequency of electronic charge beating is found to be 970 cm⁻¹ (34 fs) and can be observed for 150 fs. Through the support of high level ab initio TD-DFT computations of the entire dimer, we established that the vibrational modes preferentially optically accessed do not drive subsequent coupling between the electronic states on the 600 fs of the experiment. It was thereby possible to characterize the time scales of the early time femtosecond dynamics of the electronic coherence built by the optical excitation in a large rigid supramolecular system at a room temperature in solution.

---

Introduction

One of the most surprising and significant advances in the study of the photosynthetic light-harvesting process is the discovery that electronic energy transfer can involve long-lived electronic coherences at physiologically relevant conditions. In this picture, coherent superpositions of excited states sample the energy landscape in a more efficient way, reaching more effectively the reaction center.¹ This is in contrast with the conventional purely classical mechanism typically described as a random hopping process. Central to the understanding of coherent dynamics has been the development of new ultrafast spectroscopic techniques, in particular two-dimensional electronic spectroscopy (2DES).²

2DES is now the primary tool to obtain clear and definitive experimental proofs of coherence effects whose signature is oscillations in the signal amplitude as a function of the delay time between laser pulses, conventionally identified as ‘population’ or ‘waiting’ time t₂. Long time (1 ps) persisting oscillations have been recorded in the 2D spectra of several biological complexes and have been interpreted as due to quantum coherent mechanisms of energy transport.^3–7 The persistence of these oscillations for times much longer than what is estimated by spectral line widths, predicting electronic dephasing times not longer than 100 fs,⁸ initiated a lively debate about their origin and the mechanism enabling this persistence.^9–14 Does the coupling with vibrations extend, sustain or destroy electronic coherences is still an open question.

Light induced coherent dynamics is also the key to molecular quantum information processing^15–17 and to parallel computations by observables.^18–20 In these applications too, the control over the mechanisms regulating the lifetime of coherences is crucial.

We combine here advanced data analysis techniques together with high-level excited states dynamics modeling to characterize the time scale of the early time coherences between two moieties assembled in a hetero-dimer. To clarify how different vibrational modes influence the dynamical response upon coherent electronic excitation by short fs pulses, we engineered a simplified model system, a rhodamine dimer assembled on a DNA double-strand template (BP28, Fig. 1). The DNA scaffold allows control over the distance between the two monomers, and therefore over their coupling, and provides a rather rigid environment for the dimer tethered between the 3′ and 5′ ends of the DNA strands. The chromophores are a carboxytetramethylrhodamine (TAMRA) and a sulphorhodamine (RHO). The investigation of the molecular system structure by classical and quantum mechanical modelling shows that the non-covalent dimer is stable and the inter-chromophore distance of about 3.7 Å allows an efficient electronic coupling. In contrast to previous studies on covalently coupled dimers,^21,22 here the chromophores involved remain distinguishable and assembled in a supra-molecular fashion (i.e. coupled through self-assembling non-covalent forces), like in biological complexes. Such a tailoring allows following the coherent dynamics between the donor TAMRA and the acceptor RHO upon coherent optical excitation in 2DES experiments.

Fig. 1 Structure of the dimeric system. (a) Schematic representation of the studied species (red = TAMRA–DNA; blue = RHO–DNA). (b) Molecular equilibrium geometry of BP28 as obtained from MD simulations. The color legend is the same of panel (a). (c) Zoom on the dimeric structure, water molecules within 5 Å from the dyes are explicitly shown.

Specific exciting conditions have been engineered so as to obtain a spectral filter selecting the relevant molecular levels involved in the dynamics. Moreover, the development of advanced data analysis tools able to extract the information embedded in complex 2D spectra with a higher degree of accuracy allows disentangling the different time scales of the experimental data. Thereby we provide a clear identification of off-diagonal features whose dynamics along the population time could be ascribed to the evolution of electronic coherences, clearly distinguished from quantum beats having vibrational origin. The comparison with monochromophoric control samples¹⁸ (Fig. 1a) confirmed this identification. By electronic coherence we mean a coherent superposition of vibrational states belonging to different electronic states of the dimer, here S₁ and S₂, which are localized on different moieties. This should be distinguished from vibrational coherences, originating from non stationary vibrational wavepacket motion on a single electronic state (Section S1.5 of ESI†).

Our analysis of the experimental data is supported and supplemented by a modeling approach centered on characterizing the structural properties of the entire weakly bound dimer by molecular dynamics (MD) simulations and its electronic and vibronic properties by high level ab initio TD-DFT computations including solvation. The detailed analysis of the excited states of the dimer identifies the electronic and vibrational states that are coherently excited by the fs pulse and provides understanding on the electronic coherence and the excited nuclear degrees of freedom. The RHO moiety is primarily excited in the S₁ state of the dimer while it is TAMRA that is primarily excited in the S₂ one. The S₁–S₂ transition density is delocalized over the two moieties, and is responsible for the observed electronic coherence between the donor and the acceptor. The complex nature of the frequency beating identified experimentally requires the investigation of the vibrational response of the dimer electronic states in the Franck Condon (FC) region.

The vibrational modes preferentially optically accessed in the FC region are in-plane xanthene modes. These are rigid planar modes that do not distort the geometry of the dimer and do not involve modulations of the distances and of the electronic coupling between the two rhodamine moieties. Unlike in more complex systems,^11,23 these modes do not induce vibronic mixing between the electronic states. Modes that could induce mixing between the electronic states have a much lower frequency, <50 cm⁻¹. On the 600 fs time scale of the experiment, the electronic coherence that is probed is due to the coherent excitation and is not further altered by non-adiabatic couplings driven by nuclear motions or by coupling to the solvent. In this rather rigid system, it is therefore possible to characterize the time scales of a coherent vibronic wave packet created by a controlled coherent excitation. The detailed analysis of the electronic and vibrational structure of the dimer were then used to build a simplified model Hamiltonian that allows the simulation of the observed 2D spectra and its interpretation in terms of relevant excitation pathways (i.e. Feynman diagrams). In this model, the environment is described by coupling each monomer to a Brownian oscillator bath. Thereby we provide valuable information on the coherent electronic charge beating, crucial for the subsequent steps of energy migration in complex systems.

Energy levels of the rhodamine dimer

Fig. 2a shows the absorption spectra of the dimer BP28 and of the monochromophoric control samples TAMRA–DNA and RHO–DNA in water solutions, together with the BP28 spectrum obtained from the model excitonic Hamiltonian. The computed spectra of monochromophoric samples are reported in ESI.† The blue-shifted most intense absorption appearing in the dimer spectrum confirms that the DNA template forces the two rhodamines to lie in close proximity promoting the formation of a weakly coupled excitonic dimer with a nearly co-facial geometry²⁴ (Fig. 1b). Our MD simulations show that dimer complex is stable and remains exposed to the aqueous environment so that the electronic states and the vibrational modes of the dimeric structure are not significantly perturbed by interacting with the DNA template (Fig. 1b and c). This can be explained by the presence of rather long aliphatic linkers and the limited flexibility of the DNA double helix on the length scale of few base-pairs.²⁵

Fig. 2 Experimental and theoretical characterization of the energy levels of the dimer system. (a) Absorption spectra in aqueous Hepes buffer of BP28 (black), TAMRA–DNA (red), and RHO–DNA (blue). The dashed black line is the spectrum computed using the exciton-vibrational model Hamiltonian. The laser spectral profile used for the excitation in 2DES is also reported (shaded grey area). (b) Diagram of the energy levels derived by experiments and by ab initio modelling, and used for the calculation of the linear and 2DES response of the dimeric system. S₁ (S₂) vibronic sublevels are reported in blue (red) to highlight the higher degree of localization on RHO (TAMRA) moiety. Solid (dashed) lines denote ground (excited) vibrational states. Only four of the identified bands (e₂–e₅) fall within the exciting bandwidth used in 2DES. (c) Huang–Rhys factors of the modes of the S₁ excited state of the dimer. The three main groups of vibrations (200–600, 600–1000 and 1000–1900 cm⁻¹) are highlighted with different colours.

The excitonic nature of BP28 is confirmed by the circular dichroism (CD) spectrum (Fig. S1.1.1, ESI†), which presents the typical shape expected for an excitonic dimer, with two exciton bands of opposite sign and similar in magnitude.²⁶ In order to identify the number and the nature of the states contributing to the photophysical behavior of the dimer, we performed a joint experimental–theoretical analysis of the linear optical response. From the global fitting of the experimental absorption, emission, and CD spectra we identify six bands contributing to the spectra centered at energies: e₁ = 17 010 cm⁻¹, e₂ = 17 610 cm⁻¹, e₃ = 17 990 cm⁻¹, e₄ = 18 500 cm⁻¹, e₅ = 18 980 cm⁻¹, and e₆ = 20 080 cm⁻¹ as shown in Fig. 2.

DFT computations (CAM-B3LYP-D/6-311G(d,p)) of the ground electronic state equilibrium geometry followed by TD-DFT calculation of the excited electronic states at the same level allow identifying e₁ and e₅ with the ground vibrational states of the S₁ and S₂ electronic states of the dimer, respectively. Solvation effects on the optical transitions are well described by a continuum model. Interactions of the chromophores with specific water molecules by H-bond formation do not affect the energy of the lowest electronic transitions, in agreement with previous results, see ESI,† Section S2.3.^27,28 The computed value of the S₁–S₂ energy gap ranges from 1640 cm⁻¹ to 2450 cm⁻¹ depending on the solvation model used (linear PCM, state specific PCM, ONIOM) in very good agreement with the e₁–e₅ experimental one (1970 cm⁻¹). For all solvation models, both the S₁ and S₂ states are mainly composed of excitations from the HOMO, HOMO−1 orbitals to the LUMO and LUMO+1 orbitals of the dimer. The occupied orbitals are delocalized on the two chromophores while the LUMO and LUMO+1 correspond to the LUMO of RHO and of the TAMRA monomer, respectively (see Fig. S3.2.6, ESI†). The S₁–S₂ transition density responsible for the electronic coherence is delocalized on RHO and TAMRA, see Fig. S3.2.14 (ESI†).

The study of optically accessed vibrations upon the S₀ → S₁ electronic transition allows relating the experimentally identified bands centered at e₂, e₃, and e₄ with transitions to excited normal modes of S₁ state. The vibronic structure is computed using a time-dependent formalism.^29,30Fig. 2c shows the most important modes associated with the electronic transition S₀ → S₁ and the corresponding Huang–Rhys factor (HR) for BP28. This analysis identifies two groups of high-frequency modes contributing to the spectral width of the absorption, the first group includes modes between 600 cm⁻¹ and 1000 cm⁻¹ while the second group is formed by higher frequency modes in the range 1200–1650 cm⁻¹. We thus assign the absorption bands at e₂ and e₃ to transitions to two vibrationally excited states of the first group of modes and the band at e₄ to a transition to the vibrationally excited state of a mode around 1500 cm⁻¹. A more precise identification is not possible given that the line shape of the absorption profile results from the convolution of many active modes having similar nature and HR factors, and thus not fully distinguishable.

2D spectroscopy

2D spectra of the two control samples and of the dimer solutions were recorded using the exciting laser band shown in Fig. 2a. This band covers the region in the absorption spectrum of the dimer where the absorption bands centered at e₅, e₄, e₃, and e₂ are located. The central wavelength of the pulses was chosen in order to act as a frequency filter.^21,31 In this way the specific features due to the dynamics of the coherences between e₅ and other lower energy states could be isolated from the vibrational dynamics on the ground electronic state and on first excited state S₁. The relative contributions of specific optically active modes to the 2D response are determined by the dynamics resulting from interaction with the three 20 fs laser pulses and therefore differ from those given by the Huang–Rhys factors. Below, we retain the bands of states centered at e₃, e₄ and e₅ in the analysis of the components of the photon-echo signal and of the 2D maps. The energy of e₂ corresponds to the edge of the laser bandwidth where no spectral dynamics can be reliably observed. The components of the 2D signals can be explained on the basis of two optically active vibrational modes of S₁ (e₃ and e₄) and the vibrational ground state of S₂ (e₅).

The comparison with monochromophoric dyes allows unambiguously establishing which of the observed dynamics are unique to the excitonic system. Similarly to earlier studies on small organic molecules,^18,32,33 both TAMRA–DNA and RHO–DNA present 2D spectra exhibiting features associated with the first electronic excited state and optically active vibrational modes in the energy range 200–1500 cm⁻¹.

The 2D spectra of the BP28 dimer present a number of dynamically evolving on- and off-diagonal peaks, pinpointed in Fig. 3b. Their position, in some case hidden in the broadening, has been assessed through the comparison with the experimental and theoretical analysis of the linear and Raman spectra (ESI,† S1.5). Particularly interesting are the cross peak CP53 and the corresponding weaker symmetric peak above diagonal, CP35. These signals are not present in the spectra of monochromophoric dyes and are located at approximately 1000 cm⁻¹ far from the diagonal, in agreement with the energy separation between e₅ and e₃ states, but also with a ground state vibration at about 970 cm⁻¹ (g₂, Fig. S1.5.1, ESI†). This is also true for all the other cross-peaks identified in the maps (CP54, CP34 and CP43): the corresponding (ω₁–ω₃) coordinates could indeed be associated with superposition of excited states e_i–e_j or with ground state vibrations. Moreover the signal at these positions is characterized by a complex beating pattern along t₂ (see Fig. 3a). This oscillating amplitude bears information on the dynamics of the superposition of the states giving rise to off-diagonal features and therefore is a valuable tool to assess their nature. A full analysis of the behavior of the signal at CP35 will be described below.

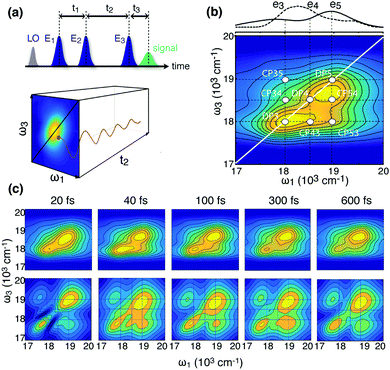Fig. 3 2D electronic spectroscopy. (a) Pulse sequence in the 2DES experiment and pictorial representation of the matrix dataset obtained with a 2DES experiment; the two frequency axes ω₁ and ω₃ are obtained by Fourier transforming the delay times t₁ and t₃, respectively. Coherent dynamics is manifested as oscillations of the signal amplitude at given coordinates on the ω₁–ω₃ map as a function of t₂ (more details in ESI,† S1.3). (b) Example of absolute rephasing 2D map recorded for BP28 at t₂ = 40 fs. The main diagonal and off-diagonal features are pinpointed. The numbers refer to the energy levels defined in Fig. 2. To facilitate the identification of the states giving rise to the signals in the 2D map, the absorption spectrum (solid line) and the exciting laser band (dashed line) are reported for comparison in the top panel. (c) Comparison of experimental (upper line) and simulated (lower line) absolute rephasing spectra at selected values of t₂. The maps are normalized to their maxima.

To identify the main frequencies contributing to the overall beating behavior in the evolution of the 2D maps, the Fourier transform (FT) along the t₂ time coordinate (t₂ → ω₂) is performed on the oscillating residuals. The result is a three-dimensional (ω₁, ω₂, ω₃) spectrum. In Fig. 4a we plot the results obtained integrating this 3D (ω₁, ω₂, ω₃) spectrum along the ω₁ and ω₃ dimensions for BP28 and the monochromophoric control samples. This provides a 1D Fourier spectrum showing the components that on average contribute the most to the overall beating behavior of the whole 2D maps in the t₂ time range studied. For both monochromophoric samples, the frequencies found in the Fourier spectrum are in good agreement with the Raman spectra of the dyes, confirming their attribution to vibrational modes in the ground or in the excited state. The Fourier spectrum of BP28 exhibits components also present in monochromophoric control samples that could be easily attributed to purely vibrational modes of the rhodamines skeleton. In addition, a signal at about 970 cm⁻¹ is clearly identifiable above noise level in the Fourier spectrum of the dimer but not in the Fourier spectra of the two monochromophoric samples.

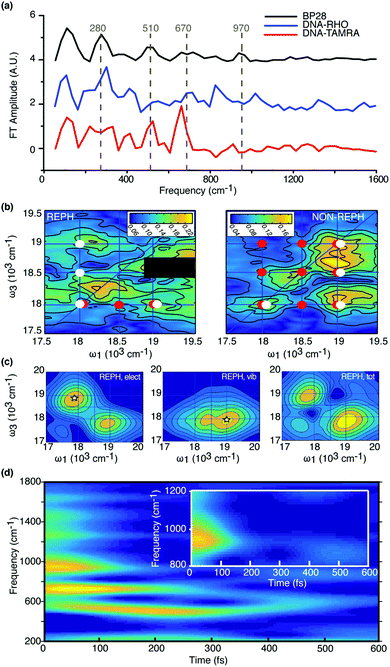Fig. 4 Beating analysis of the 2D data. (a) Experimental Fourier spectra of BP28 (black), DNA–TAMRA (red) and DNA–RHO (blue). The most relevant beating components in BP28 are identified (dashed grey lines). (b) Experimental Fourier maps at ω₂ = 970 cm⁻¹ obtained analyzing the rephasing (left) and non-rephasing (right) portion of the signal. The contributions in the 2D maps arising from the ground state vibrational coherence g₀–g₂ are denoted by red dots, whereas white dots pinpoint the contributions of the e₃–e₅ electronic coherence (in the rephasing map, the signal covered by the black box is due to a spurious contribution, see ESI,† 1.5. (c) Theoretical analysis of the different contributions to the spectral beating in the rephasing signal at 970 cm⁻¹ as detailed in the text, left: electronic contribution, middle: vibrational, right: all contributions included. The maps are obtained by integrating selected Liouville pathways along t₂. Relative intensities are in arbitrary units. (d) Time–frequency plot of the beating recorded at CP35 position showing how the amplitude of the different frequency components evolves in time. The inset shows an enlargement of the spectral region where the 970 cm⁻¹ mode contributes. Details on the TFT parameters in ESI.†

To have a simple model for the interpretation of the beating components distributed in the 2D spectra,^21,34 we built an excitonic model Hamiltonian treating each monomer as a two electronic state system with a single, optically active, vibrational mode. The excitonic dimer model has been previously discussed in the context of non-linear optical response of molecular dimers in ref. 35–38. The energy of the excited state, the frequency and the Frank–Condon factor of the active mode were chosen to reproduce the absorption spectrum of each monomer, including the vibronic shoulder (see Fig. S2.4.1, ESI†). In principle, more than one vibrational mode can be included in the phenomenological Hamiltonian, as shown in Fig. S2.4.2 (ESI†). The choice of one active mode per monomer provides a reasonable agreement with the experimental absorption spectra in the region of interest while keeping a minimum number of fitting parameters in the model. Once the three-state model (GS, S₁v = 0, S₁v = 1) of each monomer is parametrized, a four by four Hamiltonian (eqn (T4.3) of the ESI†) is obtained for the excited state manifold of the dimer, made of S₁v = 0 and S₁v = 1 for each monomer. The only remaining tunable parameter in the four by four Hamiltonian is the strength of the electronic coupling between the RHO and the TAMRA moiety. We chose an electronic coupling constant J of 1100 cm⁻¹ because it is consistent with the electronic gap calculated by TD-DFT and the value experimentally measured. This value leads to a good agreement of the absorption profile of the dimer in the energy range covered by the laser pulse (the calculated absorption profile is compared to the experimental one in Fig. 2a). While the model Hamiltonian gives an explicit description of the coupling with the selected intramolecular vibrational modes,³⁹ the other degrees of freedom of the environment are treated collectively as Brownian oscillators.⁴⁰ Each monomer is coupled to a bath composed of a fast and a slower component whose reorganization energies and relaxation rates were tuned to fit the linear absorption of both monomers and dimer (see Fig. S2.4.1 of the ESI†).

The diagonalization of the model Hamiltonian generates four vibronic states of the dimer. The four-state picture only provides a semi-quantitative physical description of the one-exciton manifold of the dimer because, as calculated from the full quantum mechanical treatment, a large number of vibronic states contribute to the response. We can interpret the four-state model as an effective representation of the many-state system that allows simulating the main components of the system dynamics that are relevant to the non-linear optical response. The three lowest eigenstates of the vibronic dimer Hamiltonian are mainly composed of RHO states while the highest energy level is mainly composed of TAMRA states (see Table S4.2, ESI†). We identify the lowest and the highest energy levels of the four-state model with the ground vibrational states of S₁ and S₂ of the dimer (e₁ and e₅ in Fig. 2). The other two intermediate states that have a high weight on the RHO moiety correspond well to the e₃ and e₄ states identified by the experimental fit. The vibronic dimer model only leads to 4 eigenstates of the dimer and does not take the state e₂ into account. Therefore, it fails to describe the lower energy part of the dimer absorption spectrum (see Fig. 2a). The description of the low energy part of the linear absorption can be improved by including explicitly more vibrational modes at the cost of introducing additional parameters. Here, we limit our attention to the states e₃–e₅ that are probed in the 2D photon echo spectra (see Fig. 3b). Therefore, the four by four Hamiltonian was sufficient to provide an effective representation of the vibronic structure of the dimer in the spectral region covered by the pulse as shown by the good agreement between the calculated and experimental absorption spectrum in this region (grey area in Fig. 2a). In the light of the TD-DFT results the states e₃ and e₄ are interpreted as an effective representation of the two manifolds of high-energy vibronic states of S₁ (dark blue and light blue in Fig. 2c).

Spectra calculations have been carried out in the perturbative and impulsive limits whose applicability is well understood^21,41 and is consistent with the sub-15 fs pulse duration of the experiment, see Section S2.5 of ESI†). In the calculation of the 2D maps, the three effective vibrational modes of S₁ identified in the fitting of the linear response have been assumed to also be present in the electronic ground state (g₁, g₂ and g₃ in Fig. S2.4.1, ESI†). Based on the solutions of the vibronic model, the rephasing part of the 2D response of BP28 has been calculated for different values of the population time t₂ and compared with the experimental response in Fig. 3c. The key features of the numerical results are in good agreement with the experimental maps. More details on the computations of the 2D maps can be found in the ESI,† S2.5.

Spectral signatures of inter-exciton electronic coherence

The current experimental protocols to distinguish between electronic or vibrational coherences are based on the study of the frequency and amplitude distribution of their oscillations in rephasing and non rephasing maps and the comparison with Raman spectra.^2,10,38,42 Therefore, to verify the origin of the 970 cm⁻¹ beating and justify its possible attribution to an electronic e₅–e₃ coherence, the so-called Fourier maps or oscillation maps have been determined. In these maps the amplitude and phase distribution of each ω₂ frequency component contributing to the beating is plotted in a 2D spectrum as a function of ω₁ and ω₃ frequencies.^38,40

Fig. 4b shows the Fourier maps at ω₂ = 970 cm⁻¹ for the rephasing and nonrephasing portion of the signal. The distribution of the signals in these maps is particularly complex. This is because the distribution of the levels within the exciting bandwidth (Fig. 2b) is such that the oscillations at a frequency of about 970 cm⁻¹ can arise both from a vibrational coherence (g₀–g₂, Fig. S1.5.1, ESI†) in the electronic ground state as well as from the evolution of the electronic coherence e₅–e₃. An additional complication comes from the fact that the energy of the transition e₅–g₂ (18 010 cm⁻¹) corresponds, within our experimental resolution, to the energy difference between e₃–g₀ (17 990 cm⁻¹). All the Feynman diagrams corresponding to the two possible contributions (vibrational g₀–g₂ and electronic e₃–e₅, respectively) have been identified (Fig. S1.5.2, ESI†) and the coordinates at which they contribute have been pinpointed as colored dots in Fig. 4b. Because the limited bandwidth does not include e₁, we do not observe the excited state vibration e₁–e₃, therefore the signal above diagonal (CP35) in the rephasing spectrum can only be explained with an e₅–e₃ electronic coherence (S1.5 of ESI†). The presence of such signal is an indubitable proof of the electronic nature of the 34 fs beating frequency. The simulated maps shown in Fig. 4c support this attribution. It is indeed possible to analyze separately the different contributions that beats at this frequency during the population time t₂ by computing the FT spectrum of selected Liouville pathways corresponding to the evolution of the electronic e₅–e₃, or the vibrational g₀–g₂ coherence during t₂. Simulations confirmed that g₀–g₂ vibrational coherence (middle panel of Fig. 4c) has intensity comparable with the electronic coherence (left panel) but it affects only the spectral region below the diagonal, so that in the full spectrum (right panel) the cross peak above the diagonal is the signature of the electronic coherence e₃–e₅.

More information on the nature of the 970 cm⁻¹ component can be found analyzing how it evolves in time. This analysis requires to overcome the limitations of conventional methods based on Fourier Transforms and to move to a time–frequency transform (TFT) approach, capable of maintaining both frequency and time resolution.⁴³Fig. 4d shows the TFT analysis performed by a suitably developed algorithm based on the use of a modified smoothed-pseudo-Wigner-Ville transform.⁴³ The analysis of the oscillations recorded at coordinates associated with CP35, where only the electronic contribution is relevant, allows estimating the damping time of the 970 cm⁻¹ component, i.e. how the 34 fs oscillation decays upon interactions with the environment. Despite the interference artifacts appearing in the TFT,⁴³ it is clear that the lower energy beating components are characterized by long damping times, >1 ps, as expected for vibrational coherences.⁴⁴ The signal at 970 cm⁻¹ is instead characterized by a considerably shorter damping time and, in agreement with time–frequency indetermination principle, by a larger bandwidth. The TFT plot shows that this component spans a frequency interval of about 100 cm⁻¹, from which a lifetime of about 100 fs can be estimated, in agreement with the observed damping time (inset in Fig. 4d). Moreover, since this component contributes only for the first 150 fs after photoexcitation, its amplitude in the overall FT analysis (see for example Fig. 4a) is necessarily weaker than other frequencies contributing for the whole investigated time window. The electronic coherence does not survive long enough to be classified as ‘long-lived’ and no signatures of persistent oscillations at this frequency could be found at the position CP35 in the spectra. Moreover, the populations in e₃ and e₅ are found constant over the 600 fs span by t₂ (Fig. S1.6.1, ESI†) This suggests that the coupling with nuclear motions or the environment are not acting so as to increase the lifetime of the beating signal. Nonetheless, 150 fs is an unexpected long time for an electronic coherence, considering the ambient temperature and the aqueous environment. Both observations could be justified by considering the nature of the environment and the in plane character of the vibrational modes coupled with the optical transitions.

Experimental

Sample preparation

The sequences of the oligonucleotides in the studied samples were suitably designed to self-assemble in a strongly coupled dimer configuration. The final synthesis was commissioned to Integrated DNA Technologies that provided the oligonucleotides with HPLC purity grade. The samples were prepared dissolving the oligonucleotides in an aqueous solution containing HEPES buffer at pH = 7.5 and a nucleic acid concentration of 25 μM in order to have absorbance values appropriate for 2DES experiments (A = 0.2 in a 1 mm path-length cuvette). Simulated melting curve analysis confirmed that at 25 °C the fraction of unpaired bases is lower than 4% and that the yield of the hybridized product is higher than 99%.

2D electronic spectroscopy

2D electronic spectra were measured with a diffractive optic-based inherently phase-stabilized four-wave mixing set-up.^45,46 Double modulation lock-in detection for additional noise reduction and sensitivity enhancement was also implemented.⁴⁷ The exciting pulses are produced by a non-collinear optical parametric amplifier (TOPAS-white, Light Conversion) pumped by an amplified Ti:sapphire oscillator (Libra, Coherent) at 3 kHz repetition rate. The resulting pulse is temporally compressed and spectrally shaped by a pulse shaper (Dazzler, Fastlite). The pulse duration is compressed down to a temporal FWHM of sub-15 fs, determined by frequency resolved optical gating (FROG) measures on the solvent. Neutral density filters attenuated the pulses energy until 5 nJ per pulse at the sample position. In our experiments, t₂ was scanned from 0 to 600 fs in steps of 5 fs and for each value of t₂ the coherence time t₁ was scanned from 0 to 70 fs in steps of 0.26 fs. Both the rephasing and non rephasing parts of the 2D signal were acquired.² To ensure the reliability of the measures, at least 3 different sets of measures in different days were performed on each sample and then averaged. The experimental error on the 2D map intensity intensities is estimated to be about 5% from repeated measurements. All measurements were performed under ambient temperatures (295 K).

The result of a 2D measurement is a series of 2D maps, each one recorded at a fixed second inter-pulse delay t₂, allowing for a correlation of excitation (ω₁) and emission (ω₃) frequencies. One of the advantages of 2DPE is that it can directly reveal couplings and energy transfer pathways by mapping coupled states onto off-diagonal signals, far from the main diagonal congested region, where the main part of the system dynamics is concentrated. Moreover, the technique is sensitive to the presence of coherent mechanisms in the relaxation processes, manifested as oscillations of the signal amplitude at diagonal and off-diagonal positions with characteristic frequencies corresponding to energy differences between coupled states.^48,49 See ESI,† S1.3 for a more detailed technical description.

Theoretical methods

Classical molecular dynamics of the supramolecular aggregate in explicit solvent was performed to sample the configurational space of the whole system (see S2.1, ESI†). The molecular equilibrium geometry of the isolated chromophores and the dimer was optimized at the DFT level and excited states calculated within the TD-DFT formalism. Frequency calculations at the equilibrium geometry give access to the vibrational normal modes of the ground electronic state. The simulation of the vibronic structure is carried out using a time-domain formalism²⁹ based on Fourier transform of the Lax's autocorrelation function³⁰ within the multi-mode parallel harmonic oscillator model.⁵⁰ Huang–Rhys (HR) parameters (or coupling strengths) of vibrational modes and the corresponding linear absorption line-shape were computed with all necessary parameters taken from the DFT calculations. Further details of the quantum chemistry modelling are given in S2.2 (ESI†). The role of solvation and of the DNA backbone was studied with PCM and ONIOM models. The theoretical characterization of the linear optical response of the two chromophores and of the dimeric species is reported in S2.3 (ESI†). We then built a vibronic dimer Hamiltonian^51,52 as recently proposed for describing the non-linear optical response, based on the ab initio results and experimental evidence.^9,35,36 Details about the vibronic dimer model are given in S2.4 (ESI†). The simulation of the 2D response is based on the non-linear response function formalism in the third order of perturbation theory.^48,53 The response function for the dimeric system is given in S2.5 (ESI†).

Conclusions

To capture key features of coherent dynamics we have investigated the electronic response created by optical fs excitation in a non-covalently, weakly bound, engineered dimer. The distance between the two moieties is controlled through the supporting DNA scaffold. It was possible to tailor the electronic coupling between the two moieties so that the two electronic states involved in the wave packet created by the optical excitation are mainly localized each on a specific moiety with enough delocalization on the other moiety that electronic coherence can be built by the fs optical excitation. In this way, we could explore the fast beatings of an electronic coherence in a model system including implications for other systems and in particular to information transduction and processing.^18–20

Through a careful analysis of the different contributions to the experimental 2D maps it was possible to identify oscillating features unambiguously ascribed to the evolution of a coherent superposition of electronic states localized on the donor and acceptor moieties. A combined approach merging full ab initio calculations of electronic states and molecular vibrations with an effective four state model Hamiltonian was used to simulate experimental responses and identify the relevant time scales. Other approaches, like the solution of the hierarchical equation of motion^54,55 including environment spectral density calculated along classical trajectories^39,56 allow including all the vibrational degrees of freedom in the spectral density and in the computation of the optical response. By solving a vibronic dimer Hamiltonian we followed a different strategy providing a simplified and phenomenological treatment of the system dynamics. Only one vibrational mode for each monomer was explicitly included in the Hamiltonian while the other states were described as a Brownian oscillator bath. The calculations led to a clear identification of the most relevant excitation pathways contributing to the 2D spectra dynamics. Using the TD-DFT computations, we were able to provide a full characterization of the nuclear motions corresponding to the vibrational modes more directly involved in the coherent superposition of electronic and vibrational states built by the optical excitation.

The electronic coherence is directly created by the interaction with the laser pulses and no vibronic mixing between the dimeric electronic states S₁ and S₂ driven by nuclear motion takes place in the time-window of the experiment. Therefore, it was possible to follow the frequency (970 cm⁻¹) and the duration (150 fs) of the beatings of the optically induced electronic coherence without the additional complexity brought by vibronic coupling mediated by nuclear motion, making a step further toward a closer and more rigorous understanding of the role of optically induced electronic coherence in the subsequent steps of energy migration. Indeed, the analysis of the vibrational motion in the dimer suggests that the non-adiabatic coupling inducing energy and charge transfer will occur on a longer time scale than that probed in this experiment.

Our approach allowed establishing that the modes accessed during the electronic transitions are rigid modes that do not distort the geometry of the dimer and do not modulate distances and electronic coupling between the two rhodamine moieties. This is a critical input towards engineering molecular systems supporting electronic coherence and thus quantum-enhanced energy transport. The vibrational modes are specific to the molecules investigated and thus the behavior found for the rhodamine dimer is not immediately applicable without change of details to other systems (biomimetic or biological). However, rhodamines, like chlorophylls and porphyrins, present a relatively rigid and π-extended structure. The possibility that in the latter molecules the presence of similar modes could also be relevant in the coherent electronic dynamics is therefore likely. In addition, the generation of the coherence by fs optical excitation could be controlled by the laser pulse characteristics, like its polarization, duration, and strength offering the ability of tailoring the initial state for inducing subsequent selective energy migration.

Conflict of Interest

There are no conflicts of interest to declare.

Acknowledgements

This work is supported by FP7 FET EC project MULTI (317707) and ERC Starting Grant QUENTRHEL (278560). FR acknowledges support from the Fonds National de la Recherche Scientifique (FNRS), Belgium and BF acknowledges the support of the Italian Ministero dell'Istruzione, Università e Ricerca through the grant Rita Levi Montalcini – 2013. FR, KK, PR and BF acknowledge support from the Consortium des Equipements de Calcul Intensif (CECI) for computational resources (FNRS 2.5020.11).

Notes and references

1. A. Chenu and G. D. Scholes, Annu. Rev. Phys. Chem., 2015, 66, 69–96.
2. E. Collini, Chem. Soc. Rev., 2013, 42, 4932–4947.
3. E. Collini, C. Y. Wong, K. E. Wilk, P. M. G. Curmi, P. Brumer and G. D. Scholes, Nature, 2010, 463, 644–647.
4. G. S. Engel, T. R. Calhoun, E. L. Read, T.-K. Ahn, T. Mancal, Y.-C. Cheng, R. E. Blankenship and G. R. Fleming, Nature, 2007, 446, 782–786.
5. G. Panitchayangkoon, D. V. Voronine, D. Abramavicius, J. R. Caram, N. H. C. Lewis, S. Mukamel and G. S. Engel, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 20908–20912.
6. B. Whaley and G. Milburn, New J. Phys., 2015, 17, 100202.
7. S. Hoyer, F. Caruso, S. Montangero, M. Sarovar, T. Calarco, M. B. Plenio and K. B. Whaley, New J. Phys., 2014, 16, 045007.
8. M. Wendling, T. Pullerits, M. A. Przyjalgowski, S. I. E. Vulto, T. J. Aartsma, R. van Grondelle and H. van Amerongen, J. Phys. Chem. B, 2000, 104, 5825–5831.
9. N. Christensson, H. F. Kauffmann, T. Pullerits and T. Mančal, J. Phys. Chem. B, 2012, 116, 7449–7454.
10. V. Tiwari, W. K. Peters and D. M. Jonas, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 1203–1208.
11. A. W. Chin, J. Prior, R. Rosenbach, F. Caycedo-Soler, S. F. Huelga and M. B. Plenio, Nat. Phys., 2013, 9, 113–118.
12. F. Fassioli, A. Olaya-Castro and G. D. Scholes, J. Phys. Chem. Lett., 2012, 3, 3136–3142.
13. P. Brumer and M. Shapiro, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 19575–19578.
14. T. Mančal and L. Valkunas, New J. Phys., 2010, 12, 065044.
15. B. Whaley, A. R. Dinner, S. A. Rice and S. Kais, Advances in Chemical Physics, Quantum Information and Computation for Chemistry, John Wiley & Sons, 2014, vol. 154.
16. J. Yuen-Zhou, J. J. Krich, I. Kassal, A. S. Johnson and A. Aspuru-Guzik, Quantum information and wavepackets, IOP Publishing, 2014.
17. H. Stephan, S. Mohan and K. B. Whaley, New J. Phys., 2010, 12, 065041.
18. B. Fresch, M. Cipolloni, T.-M. Yan, E. Collini, R. D. Levine and F. Remacle, J. Phys. Chem. Lett., 2015, 6, 1714–1718.
19. B. Fresch, D. Hiluf, E. Collini, R. D. Levine and F. Remacle, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 17183–17188.
20. T.-M. Yan, B. Fresch, R. D. Levine and F. Remacle, J. Chem. Phys., 2015, 143, 064106.
21. A. Halpin, P. J. M. Johnson, R. Tempelaar, R. S. Murphy, J. Knoester, T. L. C. Jansen and R. J. D. Miller, Nat. Chem., 2014, 6, 196–201.
22. D. Hayes, G. B. Griffin and G. S. Engel, Science, 2013, 340, 1431–1434.
23. J. Lim, D. Paleček, F. Caycedo-Soler, C. N. Lincoln, J. Prior, H. von Berlepsch, S. F. Huelga, M. B. Plenio, D. Zigmantas and J. Hauer, Nat. Commun., 2015, 6, 7755.
24. R. W. Chambers, T. Kajiwara and D. R. Kearns, J. Phys. Chem., 1974, 78, 380–387.
25. B. Fresch and F. Remacle, Phys. Chem. Chem. Phys., 2014, 16, 14070–14082.
26. W. W. Parson, Modern Optical Spectroscopy, Springer, Heidelberg, 2007.
27. P. V. Komarov and V. G. Plotnikov, J. Lumin., 2012, 132, 1139–1143.
28. J. J. Szymczak, T. Müller and H. Lischka, Chem. Phys., 2010, 375, 110–117.
29. E. J. Heller, Acc. Chem. Res., 1981, 14, 368–375.
30. M. Lax, J. Chem. Phys., 1952, 20, 1752–1760.
31. P. Kjellberg, B. Brüggemann and T. Pullerits, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 024303.
32. A. Nemeth, F. Milota, T. Mančal, V. Lukeš, J. Hauer, H. F. Kauffmann and J. Sperling, J. Chem. Phys., 2010, 132, 184514.
33. N. Christensson, F. Milota, J. Hauer, J. Sperling, O. Bixner, A. Nemeth and H. F. Kauffmann, J. Phys. Chem. B, 2011, 115, 5383–5391.
34. H. Park, N. Heldman, P. Rebentrost, L. Abbondanza, A. Iagatti, A. Alessi, B. Patrizi, M. Salvalaggio, L. Bussotti, M. Mohseni, F. Caruso, H. C. Johnsen, R. Fusco, P. Foggi, P. F. Scudo, S. Lloyd and A. M. Belcher, Nat. Mater., 2016, 15, 211–216.
35. S. Polyutov, O. Kühn and T. Pullerits, Chem. Phys., 2012, 394, 21–28.
36. A. Chenu, N. Christensson, H. F. Kauffmann and T. Mančal, Sci. Rep., 2013, 3, 2029.
37. J. M. Womick and A. M. Moran, J. Phys. Chem. B, 2011, 115, 1347–1356.
38. V. Butkus, L. Valkunas and D. Abramavicius, J. Chem. Phys., 2014, 140, 034306.
39. M. Aghtar, J. Strümpfer, C. Olbrich, K. Schulten and U. Kleinekathöfer, J. Phys. Chem. Lett., 2014, 5, 3131–3137.
40. V. Butkus, L. Valkunas and D. Abramavicius, J. Chem. Phys., 2012, 137, 044513.
41. D. Zigmantas, E. L. Read, T. Mančal, T. Brixner, A. T. Gardiner, R. J. Cogdell and G. R. Fleming, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 12672–12677.
42. V. Butkus, D. Zigmantas, D. Abramavicius and L. Valkunas, Chem. Phys. Lett., 2013, 587, 93–98.
43. A. Volpato and E. Collini, Opt. Express, 2015, 23, 20040–20050.
44. E. Hack and J. R. Huber, Int. Rev. Phys. Chem., 1991, 10, 287–317.
45. T. Brixner, T. Mančal, I. V. Stiopkin and G. R. Fleming, J. Chem. Phys., 2004, 121, 4221–4236.
46. T. Brixner, I. V. Stiopkin and G. R. Fleming, Opt. Lett., 2004, 29, 884–886.
47. R. Augulis and D. Zigmantas, Opt. Express, 2011, 19, 13126–13133.
48. M. Cho, Two-Dimensional Optical Spectroscopy, CRC Press, 2009.
49. A. M. Brańczyk, D. B. Turner and G. D. Scholes, Ann. Phys., 2014, 526, 31–49.
50. P. S. Rukin, A. Y. Freidzon, A. V. Scherbinin, V. A. Sazhnikov, A. A. Bagaturyants and M. V. Alfimov, Phys. Chem. Chem. Phys., 2015, 17, 16997–17006.
51. F. C. Spano, Acc. Chem. Res., 2010, 43, 429–439.
52. F. C. Spano, J. Clark, C. Silva and R. H. Friend, J. Chem. Phys., 2009, 130, 074904.
53. S. Mukamel, Principles of Nonlinear Optical Spectroscopy, Oxford University Press, 1995.
54. A. Ishizaki and G. R. Fleming, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 17255–17260.
55. C. Lambert, F. Koch, S. F. Völker, A. Schmiedel, M. Holzapfel, A. Humeniuk, M. I. S. Röhr, R. Mitric and T. Brixner, J. Am. Chem. Soc., 2015, 137, 7851–7861.
56. M. K. Lee and D. F. Coker, J. Phys. Chem. Lett., 2016, 7, 3171–3178.

---

Footnotes

† Electronic supplementary information (ESI) available: Additional experimental data and computational details. See DOI: 10.1039/c7cp01334e

‡ Present address: Federal Scientific Research Centre “Crystallography and Photonics” Photochemistry Center, Russian Academy of Sciences, ul. Novatorov 7a, Moscow, 119421, Russia.

---