H₂ binding to the active site of [NiFe] hydrogenase studied by multiconfigurational and coupled-cluster methods

Abstract

[NiFe] hydrogenases catalyse the reversible conversion of molecular hydrogen to protons and electrons. This seemingly simple reaction has attracted much attention because of the prospective use of H₂ as a clean fuel. In this paper, we have studied how H₂ binds to the active site of this enzyme. Combined quantum mechanical and molecular mechanics (QM/MM) optimisation was performed to obtain the geometries, using both the TPSS and B3LYP density-functional theory (DFT) methods and considering both the singlet and triplet states of the Ni(II) ion. To get more accurate energies and obtain a detailed account of the surroundings, we performed calculations with 819 atoms in the QM region. Moreover, coupled-cluster calculations with singles, doubles, and perturbatively treated triples (CCSD(T)) and cumulant-approximated second-order perturbation theory based on the density-matrix renormalisation group (DMRG-CASPT2) were carried out using three models to decide which DFT methods give the most accurate structures and energies. Our calculations show that H₂ binding to Ni in the singlet state is the most favourable by at least 47 kJ mol⁻¹. In addition, the TPSS functional gives more accurate energies than B3LYP for this system.

---

Introduction

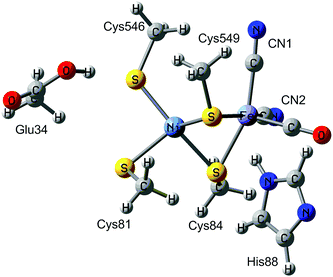
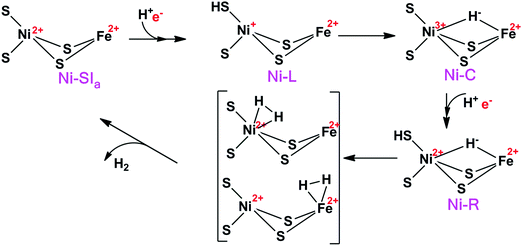
Hydrogenases are metalloenzymes that catalyse the reversible cleavage of H₂ to protons and electrons. They are widespread in nature and found in bacteria, archaea, and some eukaryotes.¹ They can be classified into [NiFe], [FeFe], and [Fe] hydrogenases based on the metal-ion content in the active sites. The binuclear active site of [NiFe] hydrogenases is shown in Fig. 1. The iron ion is coordinated by one carbon monoxide and two cyanide molecules. Moreover, two thiolates from Cys-84 and 549 (the residues are numbered according to the enzyme from Desulfovibrio vulgaris Miyazaki F²) bridge the two metals. Two additional cysteine ligands (Cys-81 and 546) coordinate terminally to the nickel ion. This gives a penta-coordinate iron ion and a tetra-coordinate nickel ion, which are ready to bind an additional ligand during the reaction mechanism (H₂ or H⁻) or as an inhibitor (e.g. OH⁻ or CO). Typically, the [NiFe] hydrogenases also contain three iron–sulfur clusters and an octahedral Mg²⁺ site.

Fig. 1 The active site of [NiFe] hydrogenases.

The [NiFe] hydrogenases have been extensively studied by spectroscopic,^1,3,4 electrochemical,⁵ biomimetic,^6,7 and computational methods.^8–14 Based on these studies, a tentative reaction mechanism has been suggested, shown in Fig. 2. The Fe ion is supposed to remain in the low-spin +II state throughout the reaction. In the Ni-SI_a state, the Ni ion is in the +II oxidation state, without any extra ligand. Then, one electron and one proton are added to form the Ni-L state, in which the proton probably is bound to the S atom of the terminal Cys-546 residue. Next, the proton takes up two electrons from the Ni ion to form a hydride ion and moves to a bridging position between the two metals, thereby forming the Ni-C state. After that, another H⁺/e⁻ pair is added, resulting in the Ni-R state, in which the proton again goes to Cys-546. Next, a H–H bond is formed between the hydride and the proton, giving a H₂ complex. Finally, the hydrogen molecule is released, regenerating the Ni-SI_a state, which is ready to start a new reaction cycle.

Fig. 2 The putative reaction mechanism of [NiFe] hydrogenases.

In this mechanism, one of the key questions is how H₂ binds to the active site. Previous studies have suggested two different binding modes (Fig. 2), viz. binding to Ni or binding to Fe. Moreover, the ground state of the Ni ion is not clear when H₂ binds to the active site. Experimentally, the evidence is varying. Carbon monoxide, which is a competitive inhibitor of H₂, binds to Ni.¹⁵ Likewise, a likely binding path for H₂ has been identified by xenon binding experiments and it ends at the Ni ion.^16,17 On the other hand, from an organometallic perspective, Fe is the expected binding site of H₂.¹⁸ This would also explain the unusual choice of Fe ligands (CO and CN), which enforces a low-spin state on Fe and enhances H₂ activation.¹⁹

Likewise, previous theoretical studies have given varying and often conflicting results, as is described in Table 1. In the first QM-cluster studies with minimal models, only H₂ binding to Fe in the singlet state was reported.^20,21 QM-cluster calculations with the density-functional theory (DFT) B3LYP method and somewhat larger models gave the same results and no local minimum for H₂ bound to Ni was found.¹⁰ However, in the transition state for H–H cleavage, H₂ moved to mainly bind to Ni, but with one atom bridging to Fe (Ni–H distance of 1.68 and 1.77 Å and a Fe–H distance of 1.80 Å). Wu and Hall made a systematic study of the H₂ binding to QM-cluster models of varying sizes. They also pointed out that Ni^II can attain either a low-spin singlet state or a high-spin triplet state.²² For their smallest model (42 atoms), they found only Fe binding. However, with a larger model (103 atoms), they could find both binding modes in the singlet state. It turned out that H₂ preferred to bind to Fe in the triplet state and to Ni in the singlet state. However, the triplet state was always more stable by 5–52 kJ mol⁻¹. If Ni was oxidised to low-spin Ni(III), both binding modes were found, but binding to Fe was preferred by 1–21 kJ mol⁻¹.

Table 1 H₂ binding to the active site of [NiFe] hydrogenase in previous computational studies. For each model, the most stable spin state and binding mode are marked in bold face (if both were studied)

Ref.	Approach	DFT method	# QM atoms	Ni spin state	Binding site
21	QM-cluster	B3LYP	19	Singlet	Fe
20	QM-cluster	B3LYP	30	Singlet	Fe
10	QM-cluster	B3LYP	57	Singlet	Fe
22	QM-cluster	B3LYP	42	Singlet	Fe
				Triplet	Fe
			103	Singlet	Fe, Ni
				Triplet	Fe
			105	Singlet	Ni
				Triplet	Fe
23	QM-cluster	B3LYP	30	Singlet	Fe, Ni
				Triplet	Fe
		BP86		Singlet	Fe, Ni
				Triplet	Fe
	QM/MM	B3LYP	30	Singlet	Fe, Ni
				Triplet	Fe
		BP86		Singlet	Ni
				Triplet	Fe, Ni
13	QM-cluster	BP86	290	Singlet	Ni
				Triplet	Fe, Ni
			122	Singlet	Ni
				Triplet	Fe
			30	Singlet	Fe
24	QM-cluster	BP86, PBE, TPSS	30	Singlet	Fe
				Triplet	Fe
		B3LYP		Singlet	Fe
				Triplet	Fe

---

Hillier and coworkers performed both QM-cluster and QM/MM calculations with a minimal QM system in both spin states and employing two DFT functionals BP86 and B3LYP.²³ The results were somewhat varying, but the QM-cluster calculations indicated that Fe-binding mode was most favourable, whereas Ni binding was preferred in most QM/MM calculations (except with B3LYP in the triplet state). Moreover, in the Fe-binding mode in the QM/MM structures, one of the H atoms bridged to Ni (1.82–2.11 Å distance). In all B3LYP calculations, the triplet state was most stable, whereas the opposite was true for the BP86 functional.

Recently, H₂ binding to the Ni-SI state was studied by Bruschi et al. with the BP86 functional using models of three different sizes.¹³ For the largest model (290 atoms), H₂ was found to bind only to Ni in the singlet state, whereas it could bind to either Ni or Fe centre if the enzyme was in the triplet state (but Fe binding was 7 kJ mol⁻¹ more stable). The triplet state was found to be 36 and 39 kJ mol⁻¹ less stable than the singlet state when H₂ was binding to Ni or Fe, respectively. For the medium-size model (122 atoms), H₂ was predicted to bind only to Ni in the singlet state and only to Fe in the triplet state. Again, the singlet state was found to be more stable than triplet state (by 42 kJ mol⁻¹). For the minimal model (30 atoms), only H₂ binding to Fe was observed if the complex was fully optimised. However, if all non-hydrogen atoms were fixed to the positions in the largest model, H₂ binding to Ni was only observed. The same minimal model was used by Varganov et al. to examine H₂ binding with four DFT functionals, PBE, BP86, TPSS, and B3LYP.²⁴ In all cases, they obtained similar geometries and predicted that H₂ binds to Fe in both the singlet and triplet states. The singlet state was most stable with the three pure functionals, whereas the triplet state was more stable with B3LYP.

Thus, it can be concluded that the H₂ binding mode and energetics are very sensitive to the size of the QM region, as well as the DFT method employed and the spin state of the Ni ion. Most previous studies have indicated that H₂ binding to Fe is more favourable. However, QM-cluster calculations with large models, as well as QM/MM optimisations, in both cases with the BP86 functional, have instead suggested that H₂ prefers to bind to Ni. Likewise, the spin ground state depends on the DFT method employed: pure functionals suggest the singlet state, whereas the hybrid B3LYP functional instead favours the triplet state. Apparently, more accurate calculations are needed to settle the preferred binding mode and spin state for the H₂ complex.

Two years ago, we studied the geometries and singlet–triplet energy splitting for the Ni-SI_a state²⁵ using coupled-cluster calculations with singles, doubles and (perturbatively treated) triples (CCSD(T)),^26,27 multiconfigurational second-order perturbation theory with a complete active-space wavefunction (CASPT2)²⁸ as well as restricted active-space theory (RASPT2).²⁹ We also benchmarked various DFT methods to describe the geometries and singlet–triplet differences. TPSS was found to be a proper method for this system. In this paper, CCSD(T) and density matrix renormalisation group (DMRG) CASPT2 calculations^30–32 were performed to study the H₂ binding in the active site of [NiFe] hydrogenase based on structures obtained by QM/MM optimisation. We also used big-QM³³ calculations to estimate the influence of the surroundings.

Methods

Models

The calculations were started from our previous QM/MM structure of the Ni-SI_a state of [NiFe] hydrogenase.¹⁴ It was based on the 1.4 Å crystal structure from D. vulgaris Miyazaki F (PDB code 1H2R).² The structure of the Ni-SI_a state is shown in Fig. 1. H₂ was then added to the active site, giving a total of 56 989 atoms. The protonation states of all residues were the same as in the previous structure of the deprotonated Ni-SI_a state.¹⁴ In this paper, two binding modes of H₂ were examined, viz. binding to Ni or to Fe (Fig. 2).

For the DFT and DMRG-CASPT2 calculations, we used models of three different sizes, shown in Fig. 3, whereas for the CCSD(T) calculations, only the minimal model 1 could be afforded. Model 3 (47 atoms) contained the Ni and Fe ions with their first sphere ligands (CO, two CN⁻, and four Cys residues, modelled by CH₃S⁻), an acetic-acid model of Glu-34, an imidazole model of His-88, and the H₂ molecule. It was taken from structures optimised with QM/MM. Model 2 (30 atoms) was obtained from these structures by deleting the acetic-acid and imidazole groups, whereas model 1 (18 atoms) was obtained by replacing the methyl groups by a proton, employing a S–H bond length of 1.34 Å. Thus, only single-point calculations in vacuum were performed.

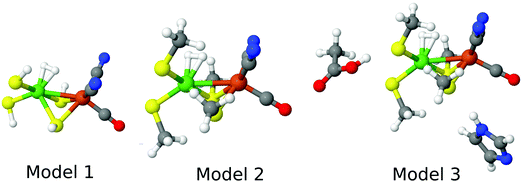Fig. 3 The three models for the DFT and DMRG calculations, showing the state in which H₂ binds to Ni.

QM calculations

DFT calculations were performed with the Turbomole 7.0 software.³⁴ We employed two DFT methods, TPSS³⁵ and B3LYP^36–38 with the def2-QZVPD^39,40 basis set. They represent typical and widely used examples of one pure and one hybrid DFT functionals. The calculations were sped up by expanding the Coulomb interactions in an auxiliary basis set, the resolution-of-identity (RI) approximation.^41,42 Empirical dispersion corrections were included with the DFT-D3 approach, standard zero-damping, and optimised parameters for each DFT method,^43,44 as implemented in Turbomole. The triplet state was obtained with UHF formalism. Spin contamination was small (〈S²〉 = 2.007–2.014).

DMRG-CASPT2 calculations^30–32 were performed with BLOCK code^45–50 interfaced with MOLCAS 8.1.⁵¹ ANO-RCC basis sets were employed: [7s6p4d3f2g1h] for Ni and Fe,⁵² [5s4p2d1f] for S,⁵³ [4s3p2d1f] for C, N, and O, and [3p1s] for H.⁵⁴ The number of renormalized states (m) was 1000 in all calculations. We used the default sweep schedule implemented in BLOCK, i.e. the initial DMRG iterations were done with a small m value to approximately converge the DMRG wavefunction, whereas the later iterations were carried out with the full m. A small amount of perturbative noise (ε = 10⁻⁴ in BLOCK) was added to the wavefunction in the initial iterations to prevent it from being trapped in a local minimum. The orbital ordering was automatized by minimising the quantum entanglement using a genetic algorithm.⁵⁵ In all DMRG-CASPT2 calculations, the four-particle reduced density matrices were obtained by a cumulant reconstruction based on the two- and three-particle reduced density matrices, neglecting the four-cumulant (the DMRG-cu(4)-CASPT2 approximation; this approach will be called DMRG-CASPT2 throughout this article).³¹ DMRG-cu(4)-CASPT2 calculations with m = 1000 have been shown to work well for several transition-metal models with medium-sized active spaces, including [NiFe] hydrogenase models.⁵⁶ All DMRG-CASPT2 calculations were performed with the standard ionization-potential electron-affinity (IPEA) Hamiltonian shift of 0.25 a.u.⁵⁷ An imaginary level shift of 0.1 a.u.⁵⁸ was used to avoid weak intruder states and to improve convergence of the perturbational treatment. The core electrons of the C, N, O, and S atoms were kept frozen in the perturbational treatment, whereas all valence electrons were correlated. To investigate the impact of the Fe and Ni semi-core (3s,3p) correlation, we performed calculations both with and without the 3s and 3p electrons correlated. Scalar relativistic effects were included using a standard second-order Douglas–Kroll–Hess Hamiltonian.

Spin-restricted CCSD(T) calculations^26,27 were carried out with the MOLPRO 2012.1 software.⁵⁹ These calculations employed the same basis set as the DMRG calculations. We also performed calculations both with and without the 3s and 3p electrons correlated for the Ni and Fe ion. The CCSD(T) calculations are too demanding to be used with model 2 and 3. Therefore, the CCSD(T) energies presented in this paper for models 2 and 3 were obtained by adding the difference between the CCSD(T) and DMRG-CASPT2 result for model 1 to the DMRG-CASPT2 energies (without the 3s, 3p semi-core correlation) for these models:

E^CCSD(T)_{model 2 or 3} = E^CASPT2_{model 2 or 3} + E^CCSD(T)_model 1 − E^CASPT2_model 1 (1)

We will see below that the correction (last two terms in eqn (1)) is rather small, 0–13 kJ mol⁻¹.

Thermal corrections to the Gibbs free energy (ΔΔG_therm; including the zero-point vibrational energy) were calculated at 298.15 K and 1 atm pressure using an ideal-gas rigid-rotor harmonic-oscillator approach⁶⁰ from vibrational frequencies calculated for model 3 in vacuum at the TPSS/def2-SV(P) level of theory. To obtain more stable results, low-lying vibrational modes (below 100 cm⁻¹) were treated by a free-rotor approximation, using the interpolation model suggested by Grimme and implemented in the thermo program.⁶¹

QM/MM calculations

QM/MM calculations were performed with the ComQum software.^62,63 In this approach, the protein and solvent are split into two subsystems: system 1 (the QM region) was relaxed by QM methods and it consisted of model 3 in Fig. 3. System 2 consisted of all the remaining parts of the protein and the solvent (577 crystal-water and 14 311 bulk-water molecules). It was kept fixed at the equilibrated crystal structure. Our previous study of [NiFe] hydrogenase showed that the dynamic effect of the surrounding protein (obtained by calculating QM/MM free energies) is restricted (up to 21 kJ mol⁻¹).²⁵

In the QM calculations, system 1 was represented by a wavefunction, whereas all the other atoms were represented by an array of partial point charge, one for each atom, taken from MM libraries. Thereby, the polarization of the QM system by the surrounding protein is included in a self-consistent manner (electronic embedding). When there is a bond between system 1 and 2 (a junction), the hydrogen link-atom approach was employed: the QM system was capped with hydrogen atoms (hydrogen link atoms, HL), the positions of which are linearly related to the corresponding carbon atoms (carbon link atom, CL) in the full system.^62,64 All atoms were included in the point-charge model, except the CL atoms.⁶⁵

The total QM/MM energy in ComQum was calculated as^62,63

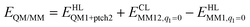where E^HL_QM1+ptch2 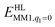is the QM energy of the QM system truncated by HL atoms and embedded in the set of point charges modelling systems 2 (but excluding the self-energy of the point charges). is the MM energy of the QM system, still truncated by HL atoms, but without any electrostatic interactions. Finally, 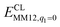is the classical energy of all atoms in the system with CL atoms and with the charges of the QM system set to zero (to avoid double counting of the electrostatic interactions). By this approach, which is similar to the one used in the ONIOM method,⁶⁶ error caused by truncation of the QM system should cancel.

The geometry optimisation was continued until the energy change between two iterations was less than 2.6 J mol⁻¹ (10⁻⁶ a.u.) and the maximum norm of the Cartesian gradients was below 10⁻³ a.u. The QM calculations were performed with Turbomole 7.0 software.³⁴ Geometry optimisations were performed with the TPSS³⁵ and B3LYP^36–38 functionals in combination with def2-SV(P)⁶⁷ basis set, including empirical dispersion corrections with the DFT-D3 approach.⁶⁸ The MM calculations were performed with Amber software,⁶⁹ using the Amber ff14SB force field.⁷⁰

Big-QM calculations

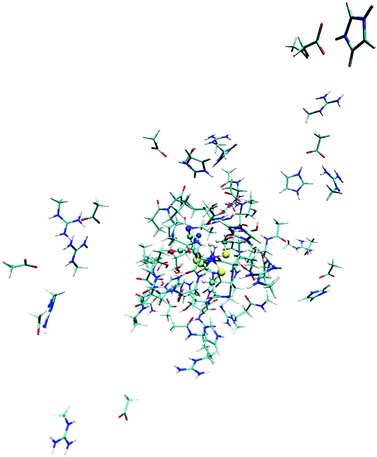
Previous studies of [NiFe] hydrogenase have shown that both QM-cluster and QM/MM energies strongly depend on the size of QM system.^13,65,71 To avoid this problem, we have developed the big-QM approach to obtain converged results:³³ the QM system was extended with all residues with at least one atom within 4.5 Å of model 2 in Fig. 3 and junctions were moved at least two residues away. In addition, all charged groups buried inside the protein were included, but the three iron–sulfur clusters were omitted to avoid convergence problems, which according to our previous calculations can be done without compromising the energies.^33,72 This gave a QM system of 819 atoms, shown in Fig. 4.¹⁴ All the big-QM calculations were performed on coordinates from the QM/MM calculations and with a point-charge model of surroundings, because this gave the fastest calculations in our previous tests.³³ They also employed the multipole-accelerated resolution-of-identity J approach (marij keyword). Two different functionals, TPSS and B3LYP, with def2-SV(P) basis set, were used (the same as in the QM/MM optimisations).

Fig. 4 Atoms included in the big-QM calculations.

To this big-QM energy, we added the DFT-D3 dispersion correction, calculated for the same big QM system with Becke–Johnson damping,⁴⁴ third-order terms, and default parameters for the TPSS or B3LYP functional using dftd3 program.^43,44,68 We also included a standard QM/MM correction for this large QM system (eqn (2), but with the big-QM region).

Reported final energies are the big-QM energies, including dispersion and the MM correction (E^TPSS/SV(P)_bigQM/MM). This energy was extrapolated to the CCSD(T) level using QM calculations on model 3 in gas phase and thermal corrections were added:

G_tot = E^TPSS/SV(P)_bigQM/MM + E^CCSD(T)_model 3 − E^TPSS/SV(P)_model 3 + ΔΔG_therm (3)

Results and discussion

In this paper, we study the binding of H₂ to the active site of [NiFe] hydrogenase, addressing three questions: Does H₂ prefer to bind to Fe or Ni? Does the binding take place in the singlet or the triplet state? Which DFT functional gives the more reliable energies? This is done by employing two accurate QM methods, CCSD(T) and DMRG-CASPT2. We start by discussing geometries for the structures obtained with two DFT functionals, TPSS and B3LYP. Then, we analyse the orbitals from DMRG calculations. Finally, the relative energies of different binding modes and spin states will be compared.

Geometries

Structures were first optimised by QM/MM, using the 47-atom QM system of model 3 in Fig. 3. The QM/MM optimisations were performed with the TPSS and B3LYP functionals using the def2-SV(P) basis set. For the singlet (low-spin) state, two binding modes of H₂ were located (shown in Fig. 5) with both functionals. In the first mode, H₂ binds side-on to Ni (this mode will be called ¹Ni–H₂ in the following). In the second mode (¹Fe–H₂), H₂ binds side-on to Fe, but one of the two H atoms bridges the two metal ions, with a Ni–H distance that is similar to (and sometimes even shorter than) the two Fe–H distance. In the triplet (high-spin) state, only the Fe binding mode could be found (³Fe–H₂). No further structures could be located, in spite of thorough tries. If the same models are optimised in vacuum (without the protein), the same structures were obtained, except the ¹Ni–H₂ structure with B3LYP (H₂ dissociates for all three models) and the ¹Ni–H₂ structure with TPSS and model 1 (H₂ moves to Fe). However, if model 3 is enhanced with the sidechain of Val-83 and the connecting backbone to Cys-84, the ¹Ni–H₂ state could be found also with B3LYP.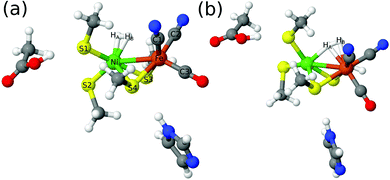

Fig. 5 The two binding modes of H₂ to the active site of [NiFe] hydrogenase: (a) H₂ binding to Ni (Ni–H₂); (b) H₂ binding to Fe (Fe–H₂) with H_A partly bridging to Ni.

Key bond distances are collected in Table 2. Both functionals predict that the H_A–H_B bond length (H_A and H_B are the two atoms in H₂) is longer in the [NiFe] hydrogenase models (0.80–0.92 Å) than for free H₂ (0.76 Å for both functionals) and therefore activated for H–H bond cleavage. However, the B3LYP H_A–H_B bond lengths are 0.05 Å shorter than those obtained with TPSS for all states. Moreover, the H_A–H_B bond is 0.02 Å longer in the singlet state than in the triplet state and 0.05 Å longer when H₂ binds to Ni than when it binds to Fe in the singlet state. Thus, the longest and most activated H–H bond is observed for the TPSS structure of the ¹Ni–H₂ state.

Table 2 Bond distances in X-ray structures and QM/MM optimised structures

	X-ray structure			TPSS			B3LYP
	4U9H^73	4U9I^73	1H2R ^2	^1Ni–H2	^1Fe–H2	^3Fe–H2	^1Ni–H2	^1Fe–H2	^3Fe–H2
HA–HB	—	—	—	0.92	0.87	0.85	0.87	0.82	0.80
Ni–HA	—	—	—	1.59	1.71	1.87	1.62	1.86	2.16
Ni–HB	—	—	—	1.65	2.49	2.66	1.68	2.65	2.65
Fe–HA	—	—	—	3.12	1.97	1.84	3.08	1.91	1.85
Fe–HB	—	—	—	2.33	1.72	1.71	2.34	1.78	1.78
Ni–Fe	2.57	2.58	2.60	2.76	2.58	2.70	2.76	2.71	2.89
Ni–S1	2.18	2.17	2.24	2.23	2.25	2.24	2.24	2.27	2.28
Ni–S2	2.24	2.23	2.32	2.28	2.23	2.28	2.30	2.23	2.27
Ni–S3	2.21	2.22	2.33	2.26	2.22	2.33	2.27	2.26	2.39
Ni–S4	2.54	2.55	2.43	2.43	2.33	2.31	2.50	2.35	2.42
Fe–S3	2.26	2.27	2.29	2.36	2.32	2.35	2.36	2.36	2.37
Fe–S4	2.31	2.32	2.36	2.38	2.44	2.43	2.37	2.46	2.46
Fe–C1	1.88	1.87	—	1.88	1.88	1.87	1.90	1.90	1.90
Fe–C2	1.91	1.89	—	1.89	1.89	1.90	1.93	1.92	1.92
Fe–C3	1.75	1.73	—	1.70	1.73	1.73	1.72	1.75	1.74

---

The metal–H bonds are also longer with B3LYP than with TPSS, typically by 0.03–0.07 Å, but the difference is less systematic. In the Ni–H₂ structures, both Ni–H bonds are short, 1.59–1.68 Å, with H_A being 0.06 Å closer than H_B. This is caused by the fact that H_B is weakly interacting also with Fe, at a distance of 2.33–2.34 Å. The Fe–H₂ structures are more varying, depending both on the functional and the spin state, but they all have two short Fe–H bonds, a shorter Fe–H_B of 1.71–1.78 Å and a longer Fe–H_A bond of 1.84–1.97 Å. The H_A atom also forms a bond to Ni, with a varying bond length of 1.71–2.16 Å. The Ni–H_B distance is rather large, 2.49–2.66 Å. The Ni–H_A bond is shortest in the TPSS ¹Fe–H₂ structure, in which it is actually shorter than both the Fe–H bonds (and the Fe–H_A bond is longest among the four Fe–H₂ structures). The Ni–H_A bond is 1.86 Å in the corresponding B3LYP structure, which is in between the two Fe–H bond lengths. It is of a similar length in the TPSS ³Fe–H₂ structure, but both Fe–H bonds are shorter. The same is true in the B3LYP triplet structure, but in this case, the Ni–H_A distance is appreciably longer, 2.16 Å, giving a structure with the most similar Fe–H bond lengths, 1.78 and 1.85 Å. Thus, the ¹Ni–H₂ structure has the longest H–H bond and shortest H–metal bond, implying that the two H atoms have stronger interactions with the metal than in the other two states. This could be favourable for catalysis.

The Ni–Fe distance is quite varying, 2.58–2.89 Å. For the singlet structures, it is longer when H₂ binds to Ni than when it binds to Fe. The Ni–S bonds are typically 2.22–2.30 Å, often ∼0.02 Å longer for B3LYP than TPSS. However, one (singlet) or two (triplet) of the bridging Cys ligands give longer distances (up to 2.50 Å). The Fe–S bonds are typically 2.32–2.38 Å, but one bond is 2.43–2.46 Å when H₂ binds to Fe. The calculated S–metal distances are reasonably close to what is found in available crystal structures (the difference is no more than 0.1 Å). The Fe–C bond lengths are similar in all structures and 0.02–0.03 Å longer for B3LYP than for TPSS. They are in excellent agreement with experimental data.

Several precautions have been taken to ensure that the presented structures are accurate and reliable. First, we reoptimised the B3LYP structures starting from the corresponding TPSS structures and vice versa to ensure that the reported differences are significant. Second, the structures were reoptimised by QM/MM calculations, in which all residues with at least one atom within 6 Å of any atom in the QM region were relaxed by MM. This did not change the structures significantly, and the same binding modes were still located. Third, the observation that only the Fe–H₂ binding mode is found for the triplet state is in accordance with all previous studies, except the QM-cluster calculations with a 290-atom model, for which also the ³Ni–H₂ state was reported.¹³ Therefore, we performed QM/MM optimisations, using a 298-atom QM region (we use [NiFe] hydrogenase from a different species, so a few residues are different). However, we could still not locate the ³Ni–H₂ state, even if the Ni–H_A and Ni–H_B bonds were initially restrained to the distances in their study. On the other hand, we could find the ¹Fe–H₂ state with the same QM/MM method and the 298-atom QM region, although this state was not found in the previous study.

Orbital analysis in the DMRG calculations

In the DMRG calculations, we used the three models shown in Fig. 3. In all three models, the same active space was employed. For the singlet state, the active space contained the two H₂ 1s orbitals, five Ni 3d orbitals, five Fe 3d orbitals, and a second set of correlating d orbitals for each occupied metal orbital (which is often referred to as 3d′) to account for the so-called double-shell effect (four on Ni and three on Fe).⁷⁴ In addition, three bonding orbitals between Ni, Fe, and their ligands were included. Thus, the active space consisted of 22 electrons in 22 orbitals.

The active orbitals from the DMRG calculation are shown in Fig. 6 for the ¹Ni–H₂ state, obtained from the QM/MM optimisation with the TPSS functional. Three doubly occupied orbitals (orbitals 1, 3, and 8) show interactions between H₂ and the Ni ion. The first two orbitals involve the H–H σ bonding orbital interacting with a Ni 3d orbital and ligand bonding orbital, whereas the third involves the H–H σ* antibonding orbital interacting with another Ni 3d orbital. There is also a weak interaction between the H–H σ* antibonding orbital and the Fe 3d orbital in orbital 8. Similar orbitals were obtained for the same state with the B3LYP structures (Fig. S1, ESI†).

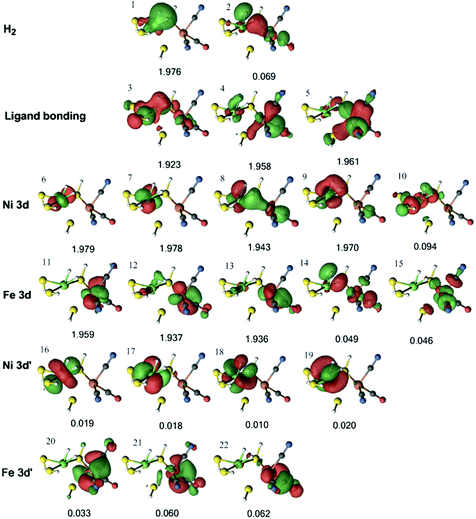Fig. 6 Active natural orbitals and their occupation numbers resulting from the DMRG calculation of the ¹Ni–H₂ state for model 1, optimised with the TPSS method.

Next, we studied the ¹Fe–H₂ state obtained from the QM/MM optimisations with both the TPSS and B3LYP functionals. The orbitals for the former are collected in Fig. 7, whereas the orbitals of the latter are shown in Fig. S2 (ESI†). It can be seen from Fig. 7 that the H–H σ bonding orbital interacts with Ni in orbitals 7, with Fe in orbital 3, and with both metals in orbital 1.

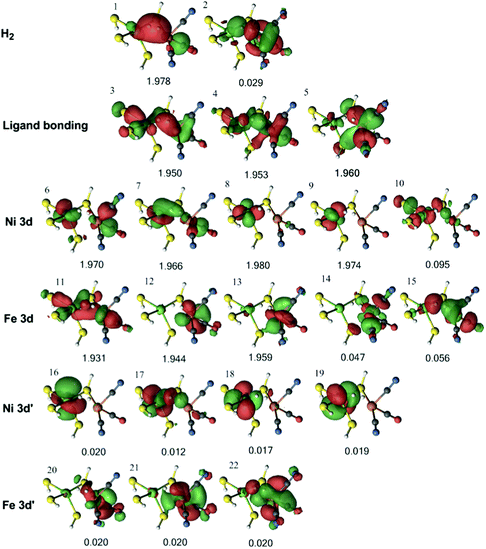Fig. 7 Active natural orbitals and their occupation numbers resulting from the DMRG calculation of Fe–H₂ species in the singlet state for model 1, optimised with the TPSS method.

For the triplet ³Fe–H₂ state, four 3d orbitals can be involved in metal–ligand bonding (two singly occupied Ni 3d orbitals and two empty Fe 3d orbitals), whereas in the singlet state there are only three such orbitals (one empty Ni 3d orbital and two empty Fe 3d orbitals). Therefore, an extra ligand orbital was included in the active space. Moreover, as all five Ni 3d are occupied in the triplet state (instead of four in the singlet states), the active space was also extended with an extra 3d′ orbital. This gives an active space of 24 electrons in 24 orbitals (Fig. 8). The H–H σ bonding orbital interacts only weakly with Ni (orbital 1). On the other hand, there is a strong interaction between H₂ and Fe in orbital 6 and a weaker interaction also in orbital 14.

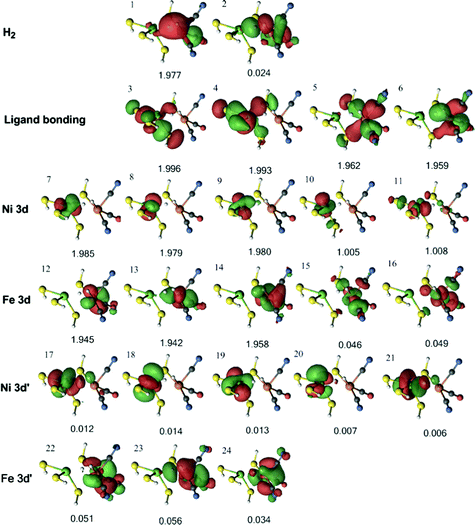Fig. 8 Active natural orbitals and their occupation numbers resulting from the DMRG calculation of the triplet ³Fe–H₂ state for model 1, optimised with the TPSS method.

Energies

Next, we focus on the energies. We have studied the three states (¹Ni–H₂, ¹Fe–H₂ and ³Fe–H₂) using QM/MM geometries obtained with either the TPSS or the B3LYP method with the def2-SV(P) basis set. All energies discussed come from single-point energies calculated on these six QM/MM structures. Energies were calculated with four different methods: TPSS-D3 and B3LYP-D3 with the much larger def2-QZVPD basis set, as well as CCSD(T) and DMRG-CASPT2 with the even larger ANO-RCC basis set. The calculations were performed on the three models in Fig. 2 in vacuum (CCSD(T) calculations could be afforded only for model 1). The relative energies of the six states are shown in Table 3, always using the ¹Ni–H₂ state as the reference. In the CCSD(T) calculations, the 3s,3p correlation effect of the metal atoms was included. In a recent study, we have demonstrated that CASPT2 often fails to correctly describe the contribution of 3s,3p correlation energetics.⁷⁵ Therefore, in the DMRG-CASPT2 results shown in Table 3, the 3s,3p correlation was not obtained with perturbation theory, but it was taken from CCSD(T) calculations with and without 3s,3p correlation. A table comparing the CASPT2 and CCSD(T) relative energies obtained with or without metal 3s,3p correlation is provided in the ESI† (Table S1). For the present relative energies, the effect of the 3s,3p correlation was quite small, up to 13 kJ mol⁻¹, and the difference in 3s,3p correlation between CCSD(T) and DMRG-CASPT2 was 4–7 kJ mol⁻¹.

Table 3 Relative energies of the three H₂ adducts (kJ mol⁻¹), calculated by four different levels of theory: TPSS/def2-QZVPD, B3LYP/def2-QZVPD, CCSD(T), and DMRG-CASPT2. Models of three different sizes were employed, based on QM/MM structures optimised with TPSS or B3LYP. The ¹Ni–H₂ structure was used as the reference. The last two rows show the results from the original QM/MM structure optimisations

Model	QM method	TPSS structure			B3LYP structure
		^1Ni–H2	^1Fe–H2	^3Fe–H2	^1Ni–H2	^1Fe–H2	^3Fe–H2
a CCSD(T) calculations with valence electrons and the metal 3s,3p semi-core correlated. b DMRG-CASPT2 calculation with the metal 3s,3p correlation effect taken from CCSD(T). c Energies obtained from both DMRG-CASPT2 and CCSD(T) data according to eqn (1).
1	TPSS	0	25.6	3.1	0	20.7	1.8
	B3LYP	0	23.6	−38.1	0	9.7	−55.2
	CCSD(T)^a	0	18.1	4.1	0	8.9	−10.8
	DMRG-CASPT2^b	0	11.9	−8.7	0	8.8	−12.3
2	TPSS	0	34.0	25.4	0	32.7	29.0
	B3LYP	0	31.3	−18.8	0	20.9	−30.7
	CCSD(T)^c	0	39.2	46.0	0	26.7	27.8
	DMRG-CASPT2	0	33.0	33.2	0	26.6	26.3
3	TPSS	0	18.5	13.0	0	18.8	16.0
	B3LYP	0	17.1	−30.0	0	8.4	−42.5
	CCSD(T)^c	0	17.3	38.8	0	12.0	26.1
	DMRG-CASPT2	0	11.1	26.0	0	12.0	24.6
QM/MM	TPSS	0	32.5	40.0	0	37.2	13.4
	B3LYP	0	30.9	−3.6	0	26.5	−8.9

---

We first discuss results obtained with model 1, i.e. the smallest model, in which the cysteine residues are modelled by SH⁻. For this model, we could obtain energies with all four methods, TPSS, B3LYP, CCSD(T), and DMRG-CASPT2. The occupation numbers in Fig. 6–8 and Fig. S1–S3 (ESI†) show that all three studied states are essentially single configurational (they differ by less 0.09 from 0, 1, or 2). This is also supported by the T₁, D₁, and %TAE diagnostics⁷⁶ for the CCSD(T) calculations, shown in Table S2 (ESI†). They are similar to our previous CCSD(T) calculations on bimetallic [NiFe] hydrogenase models.²⁵ Therefore, we will use the CCSD(T) results as the reference.

From Table 3, it can be seen that TPSS predicts ¹Ni–H₂ as the most stable binding mode, but only 3 kJ mol⁻¹ more stable than the ³Fe–H₂ state and 26 kJ mol⁻¹ more stable than the ¹Fe–H₂ state. The TPSS results are in satisfactory agreement with CCSD(T) in predicting the most stable binding mode. DMRG-CASPT2 overestimates the stability of the ³Fe–H₂ state by 13 kJ mol⁻¹ compared to CCSD(T). On the other hand, B3LYP gives quite different results, strongly favouring the triplet ³Fe–H₂ state (by 55 kJ mol⁻¹ for the B3LYP structure). For the B3LYP structures, CCSD(T) and DMRG-CASPT2 partially fix this problem by significantly destabilising the triplet state compared to B3LYP, reducing the energy difference between ¹Ni–H₂ and ³Fe–H₂ by ∼40 kJ mol⁻¹. However, this destabilisation is not large enough to bring the ¹Ni–H₂ state back as the ground state. On the other hand, the CCSD(T) and DMRG-CASPT2 energy results agree within 2 kJ mol⁻¹ for the B3LYP structures. Thus, the two ab initio methods give quite similar results, but it is not clear whether ¹Ni–H₂ or ³Fe–H₂ is the most stable structure. Fortunately, this ambiguity disappears for the larger and more realistic models.

For models 2 and 3, no CCSD(T) calculations could be afforded. Instead, the CCSD(T) results in Table 3 were simply obtained by correcting the DMRG-CASPT2 results with the difference of the CCSD(T) and DMRG-CASPT2 results for model 1 (eqn (1)). From Table 3, it can be seen that the ³Fe–H₂ state is strongly destabilised with the larger models. It is now the least stable state, 26–46 kJ mol⁻¹ less stable than the ¹Ni–H₂ state, according to the combined CCSD(T) and DMRG-CASPT2 energies. B3LYP still favours the triplet state, but these energies are wrong by 58–69 kJ mol⁻¹, according to the ab initio data.

The DMRG-CASPT2 energies change by up to 22 kJ mol⁻¹ when model 2 is increased to model 3 (i.e. adding models of two second-sphere residues, hydrogen-bonding to the active site), showing that the energies strongly depend on the surrounding protein. To more accurately model the surroundings, we have used the big-QM approach. Our big-QM model included 819 atoms (Fig. 4), which is much more than in previous studies of H₂ binding to [NiFe] hydrogenase (19–290 atoms, cf.Table 1). It can be seen from Table 4 that the big-QM energies (E^TPSS/SV(P)_bigQM/MM) favour the ¹Ni–H₂ state by 50 and 53 kJ mol⁻¹ compared to the ¹Fe–H₂ and ³Fe–H₂ states. These large energy differences come mainly from the QM energy contribution: the MM corrections (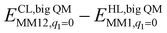) are small, 2–3 kJ mol⁻¹ (owing to the large big-QM region), whereas the dispersion contributions are 9–11 kJ mol⁻¹. This energy (obtained at the TPSS/def2-SV(P) level) should be corrected by the CCSD(T) and DMRG-CASPT2 results for models 1 and 3. These corrections are slightly larger than in Table 3 because they start from TPSS calculations with the def2-SV(P) basis set. Finally, thermal corrections to Gibbs free energy were added (ΔΔG_therm), obtained from frequency calculations on the isolated model 3. They favour the ³Fe–H₂ state by 7 kJ mol⁻¹. With all corrections added (G_tot in Table 4), ¹Ni–H₂ is 47 and 78 kJ mol⁻¹ more stable than the other two states.

Table 4 Relative energies of the three H₂ adducts (kJ mol⁻¹) based on big-QM calculations at the TPSS/def2-SV(P) level. The calculations were performed on QM/MM structures obtained with TPSS

	^1Ni–H2	^1Fe–H2	^3Fe–H2
E ^HL,big QMQM1+ptch2	0	42.2	45.6
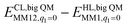
	0	−1.7	−2.8
DFT-D3 dispersion	0	9.2	10.5
E ^TPSS/SV(P)bigQM/MM	0	49.7	53.3
ΔΔGtherm	0	0.4	−7.1
G tot (eqn (3))	0	47.3	78.3

---

Conclusions

In this paper, we have studied the binding of H₂ to the active site of [NiFe] hydrogenase with coupled-cluster CCSD(T) and DMRG-CASPT2 methods. The geometries were optimised by standard QM/MM methods, using the TPSS and B3LYP functionals, combined with the def2-SV(P) basis set. In addition, big-QM/MM calculations were performed to accurately estimate the effect of the surroundings. Several important results have been obtained.

First, we show that the singlet state is appreciably more stable than the triplet state. For the minimal model 1, the energy difference is small and for structures optimised with B3LYP, the triplet state was actually the most stable. However, with the more realistic models 2 and 3, the triplet state was 26–46 kJ mol⁻¹ less stable than the ¹Ni–H₂ state. Including the entire protein with the big-QM/MM approach, the difference increased to 78 kJ mol⁻¹, which is so large that the triplet state can be discarded. Thus, the triplet state is even less stable for the H₂ adduct than for the Ni-SI_a state, for which our previous studies with CCSD(T), CASPT2, and RASPT2 methods indicated that the singlet state was 24 kJ mol⁻¹ more stable than the triplet state in the protein.²⁵

Second, we show that H₂ prefers to bind to Ni, rather than to Fe. For the singlet state, we find both binding modes in QM/MM optimisations with both small (30-atom) and large (298-atom) QM regions, whereas for the triplet state, only the Fe–H₂ state is found. For the isolated models 1–3, the ¹Fe–H₂ state is 9–39 kJ mol⁻¹ less stable than the ¹Ni–H₂ state. In the protein, the difference increases to 47 kJ mol⁻¹. This finally settles the old controversy of the binding mode of H₂ to [NiFe] hydrogenase (cf.Table 1). Our conclusion is supported by the crystal structure of CO inhibited [NiFe] hydrogenase and the suggested H₂ binding paths.^15–17

Third, we have compared the performance of two DFT methods, TPSS and B3LYP, with the CCSD(T) and DMRG-CASPT2 results. For the energy difference between the two singlet binding modes (¹Fe–H₂ and ¹Ni–H₂), both functionals give accurate results with errors of less than 12 kJ mol⁻¹ (B3LYP slightly better, with a mean absolute deviation, MAD, of 4 kJ mol⁻¹, compared to 7 kJ mol⁻¹ for TPSS). This is actually similar to the accuracy of DMRG-CASPT2. However, for the singlet–triplet energy splitting, the errors are much larger. TPSS is appreciably more accurate than B3LYP with MAD and maximum errors of 10 and 21 kJ mol⁻¹, respectively, compared to 58 and 69 kJ mol⁻¹ for B3LYP. Thus, we recommend the TPSS method for [NiFe] hydrogenase energetics. DMRG-CASPT2 reproduce the CCSD(T) energies even better with MAD and maximum errors of 7 and 13 kJ mol⁻¹.

With all these important points settled regarding the H₂ complex of [NiFe] hydrogenase, we are now ready to study the full reaction mechanism of the enzyme with QM/MM methods.

Acknowledgements

This investigation has been supported by grants from the Swedish research council (project 2014-5540), the Flemish Science Foundation (FWO, project G.0863.13), the China Scholarship Council (project 201406360045), and COST through Action CM1305 (ECOSTBio) and the short-term scientific mission (COST-STSM-CM1305-30814). The computations were performed on computer resources provided by the Swedish National Infrastructure for Computing (SNIC) at Lunarc at Lund University and by the VSC (Flemish Supercomputer Center), funded by the Hercules Foundation and the Flemish Government-department EWI.

References

1. W. Lubitz, H. Ogata, O. Ruediger and E. Reijerse, Chem. Rev., 2014, 114, 4081.
2. Y. Higuchi, H. Ogata, K. Miki, N. Yasuoka and T. Yagi, Structure, 1999, 7, 549.
3. A. L. De Lacey, V. M. Fernandez, M. Rousset and R. Cammack, Chem. Rev., 2007, 107, 4304.
4. W. Lubitz, E. Reijerse and M. van Gastel, Chem. Rev., 2007, 107, 4331.
5. K. A. Vincent, A. Parkin and F. A. Armstrong, Chem. Rev., 2007, 107, 4366.
6. V. I. Bakhmutov, Eur. J. Inorg. Chem., 2005, 245.
7. C. Tard and C. J. Pickett, Chem. Rev., 2009, 109, 2245.
8. H.-J. Fan and M. B. Hall, J. Biol. Inorg. Chem., 2001, 6, 467.
9. M. Bruschi, G. Zampella, P. Fantucci and L. De Gioia, Coord. Chem. Rev., 2005, 249, 1620.
10. P. E. M. Siegbahn, J. W. Tye and M. B. Hall, Chem. Rev., 2007, 107, 4414.
11. M. Kampa, W. Lubitz, M. van Gastel and F. Neese, J. Biol. Inorg. Chem., 2012, 17, 1269.
12. T. Kraemer, M. Kamp, W. Lubitz, M. van Gastel and F. Neese, ChemBioChem, 2013, 14, 1898.
13. M. Bruschi, M. Tiberti, A. Guerra and L. De Gioia, J. Am. Chem. Soc., 2014, 136, 1803.
14. G. Dong and U. Ryde, J. Biol. Inorg. Chem., 2016, 21, 383.
15. H. Ogata, Y. Mizoguchi, N. Mizuno, K. Miki, S. Adachi, N. Yasuoka, T. Yagi, O. Yamauchi, S. Hirota and Y. Higuchi, J. Am. Chem. Soc., 2002, 124, 11628.
16. Y. Montet, P. Amara, A. Volbeda, X. Vernede, E. C. Hatchikian, M. J. Field, M. Frey and J. C. Fontecilla-Camps, Nat. Struct. Biol., 1997, 4, 523.
17. A. Volbeda and J. C. Fontecilla-Camps, Dalton Trans., 2003, 4030.
18. G. J. Kubas, Metal Dihydrogen and σ-Bond Complexes: Structure, Theory and Reactivity, Kluwer Academic/Plenum Publishers, Dordrecht, Netherlands, 2001.
19. P. E. M. Siegbahn and M. R. A. Blomberg, Oxidative addition reactions, in Theoretical Aspects of Homogeneous Catalysis, Applications of Ab Initio Molecular Orbital Theory, ed. P. W. N. M. van Leeuwen, J. H. van Lenthe and K. Morokuma, Kluwer Academic/Plenum Publishers, Dordrecht, Netherlands, 1993, pp. 15–63.
20. S. Q. Niu, L. M. Thomson and M. B. Hall, J. Am. Chem. Soc., 1999, 121, 4000.
21. M. Pavlov, M. R. A. Blomberg and P. E. M. Siegbahn, Int. J. Quantum Chem., 1999, 73, 197.
22. H. Wu and M. B. Hall, C. R. Chim., 2008, 11, 790.
23. P. Jayapal, M. Sundararajan, I. H. Hillier and N. A. Burton, Phys. Chem. Chem. Phys., 2008, 10, 4249.
24. D. S. Kaliakin, R. R. Zaari and S. A. Varganov, J. Phys. Chem. A, 2015, 119, 1066.
25. M. G. Delcey, K. Pierloot, Q. M. Phung, S. Vancoillie, R. Lindh and U. Ryde, Phys. Chem. Chem. Phys., 2014, 16, 7927.
26. P. J. Knowles, C. Hampel and H. J. Werner, J. Chem. Phys., 1993, 99, 5219.
27. J. D. Watts, J. Gauss and R. J. Bartlett, J. Chem. Phys., 1993, 98, 8718.
28. K. Andersson, P.-Å. Malmqvist and B. O. Roos, J. Chem. Phys., 1992, 96, 1218.
29. P.-Å. Malmqvist, K. Pierloot, A. R. M. Shahi, C. J. Cramer and L. Gagliardi, J. Chem. Phys., 2008, 128, 204109.
30. Y. Kurashige and T. Yanai, J. Chem. Phys., 2011, 135, 094104.
31. Y. Kurashige, J. Chalupsky, T. N. Lan and T. Yanai, J. Chem. Phys., 2014, 141, 174111.
32. S. R. White, Phys. Rev. Lett., 1992, 69, 2863.
33. L. Hu, P. Söderhjelm and U. Ryde, J. Chem. Theory Comput., 2013, 9, 640.
34. TURBOMOLE V7.0 2015, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007; available from http://www.turbomole.com.
35. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401.
36. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098.
37. C. T. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785.
38. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
39. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297.
40. D. Rappoport and F. Furche, J. Chem. Phys., 2010, 133, 134105.
41. K. Eichkorn, O. Treutler, H. Öhm, M. Häser and R. Ahlrichs, Chem. Phys. Lett., 1995, 240, 283.
42. K. Eichkorn, F. Weigend, O. Treutler and R. Ahlrichs, Theor. Chem. Acc., 1997, 97, 119.
43. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
44. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456.
45. G. K. L. Chan and M. Head-Gordon, J. Chem. Phys., 2002, 116, 4462.
46. S. Sharma and G. K. L. Chan, J. Chem. Phys., 2012, 136, 124121.
47. R. Olivares-Amaya, W. F. Hu, N. Nakatani, S. Sharma, J. Yang and G. K. L. Chan, J. Chem. Phys., 2015, 142, 034102.
48. G. K. L. Chan, J. Chem. Phys., 2004, 120, 3172.
49. D. Ghosh, J. Hachmann, T. Yanai and G. K. L. Chan, J. Chem. Phys., 2008, 128, 014107.
50. D. Zgid and M. Nooijen, J. Chem. Phys., 2008, 128, 014107.
51. F. Aquilante, J. Autschbach, R. K. Carlson, L. F. Chibotaru, M. G. Delcey, L. De Vico, I. F. Galvan, N. Ferre, L. M. Frutos, L. Gagliardi, M. Garavelli, A. Giussani, C. E. Hoyer, G. Li Manni, H. Lischka, D. X. Ma, P.-Å. Malmqvist, T. Muller, A. Nenov, M. Olivucci, T. B. Pedersen, D. L. Peng, F. Plasser, B. Pritchard, M. Reiher, I. Rivalta, I. Schapiro, J. Segarra-Marti, M. Stenrup, D. G. Truhlar, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, V. P. Vysotskiy, O. Weingart, F. Zapata and R. Lindh, J. Comput. Chem., 2016, 37, 506.
52. B. O. Roos, R. Lindh, P.-Å. Malmqvist, V. Veryazov and P. O. Widmark, J. Phys. Chem. A, 2005, 109, 6575.
53. B. O. Roos, R. Lindh, P.-Å. Malmqvist, V. Veryazov and P. O. Widmark, J. Phys. Chem. A, 2004, 108, 2851.
54. P. O. Widmark, P.-Å. Malmqvist and B. O. Roos, Theor. Chim. Acta, 1990, 77, 291.
55. G. Moritz, B. A. Hess and M. Reiher, J. Chem. Phys., 2005, 122, 024107.
56. Q. M. Phung, S. Wouters and K. Pierloot, J. Chem. Theory Comput., 2016, 12, 4352.
57. G. Ghigo, B. O. Roos and P.-Å. Malmqvist, Chem. Phys. Lett., 2004, 396, 142.
58. N. Forsberg and P.-Å. Malmqvist, Chem. Phys. Lett., 1997, 274, 196.
59. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, W. Györffy, D. Kats, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nicklaß, D. P. O'Neill, P. Palmieri, D. Peng, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson and M. Wang, MOLPRO, version 2012.1, a package of ab initio programs, 2012, see http://www.molpro.net.
60. J. Frank, Introduction to computational chemistry, Wiley, Chichester, 2017, pp. 454–464.
61. S. Grimme, Chem. – Eur. J., 2012, 18, 9955.
62. U. Ryde, J. Comput.-Aided Mol. Des., 1996, 10, 153.
63. U. Ryde and M. H. M. Olsson, Int. J. Quantum Chem., 2001, 81, 335.
64. N. Reuter, A. Dejaegere, B. Maigret and M. Karplus, J. Phys. Chem. A, 2000, 104, 1720.
65. L. Hu, P. Söderhjelm and U. Ryde, J. Chem. Theory Comput., 2011, 7, 761.
66. M. Svensson, S. Humbel, R. D. J. Froese, T. Matsubara, S. Sieber and K. Morokuma, J. Phys. Chem., 1996, 100, 19357.
67. A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571.
68. dftd3 software, http://www.thch.uni-bonn.de/tc/index.php?section=downloads&subsection=DFT-D3&lang=english.
69. D. A. Case, V. Babin, J. T. Berryman, R. M. Betz, Q. Cai, D. S. Cerutti, T. E. Cheatham, III, T. A. Darden, R. E. Duke, H. Gohlke, A. W. Goetz, S. Gusarov, N. Homeyer, P. Janowski, J. Kaus, I. Kolossváry, A. Kovalenko, T. S. Lee, S. LeGrand, T. Luchko, R. Luo, B. Madej, K. M. Merz, F. Paesani, D. R. Roe, A. Roitberg, C. Sagui, R. Salomon-Ferrer, G. Seabra, C. L. Simmerling, W. Smith, J. Swails, R. C. Walker, J. Wang, R. M. Wolf, X. Wu and P. A. Kollman, AMBER14, University of California, San Francisco, 2014.
70. J. A. Maier, C. Martinez, K. Kasavajhala, L. Wickstrom, K. E. Hauser and C. Simmerling, J. Chem. Theory Comput., 2015, 11, 3696.
71. L. Hu, J. Eliasson, J. Heimdal and U. Ryde, J. Phys. Chem. A, 2009, 113, 11793.
72. S. Sumner, P. Söderhjelm and U. Ryde, J. Chem. Theory Comput., 2013, 9, 4205.
73. H. Ogata, K. Nishikawa and W. Lubitz, Nature, 2015, 520, 571.
74. K. Andersson and B. O. Roos, Chem. Phys. Lett., 1992, 191, 507.
75. K. Pierloot, Q. M. Phung and A. Domingo, J. Chem. Theory Comput., 2017, 13, 537.
76. W. Y. Jiang, N. J. DeYonker and A. K. Wilson, J. Chem. Theory Comput., 2012, 8, 460.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp01331k

---