Open Access Article
Open Access ArticleExtra electronic outer-shell peculiarities accessible under a joint XPS and DFT study†
A. R.
Cholach
 *a,
I. P.
Asanov
bc,
A. A.
Bryliakova
a and
A. V.
Okotrub
bc
*a,
I. P.
Asanov
bc,
A. A.
Bryliakova
a and
A. V.
Okotrub
bc
aBoreskov Institute of Catalysis, Akademik Lavrentiev Ave 5, Novosibirsk 630090, Russian Federation. E-mail: cholach@catalysis.ru
bNikolaev Institute of Inorganic Chemistry, Akademik Lavrentiev Ave 3, Novosibirsk 630090, Russian Federation
cNovosibirsk State University, Pirogov Str 2, Novosibirsk 630090, Russian Federation
First published on 22nd May 2017
Abstract
Electronic configuration of chemically bound atoms at the surface, including adsorbed species, or in the bulk of a solid contains a set of natural traps for energy absorption provided by valence band transitions or plasmon oscillations. The core level excitation of any origin is generally coupled with those traps, forming a multichannel route for nonradiative energy dissipation. Using an example of Pt and graphite-based materials, the study shows experimental tracing over these channels by means of elastic electron scattering and X-ray photoelectron spectroscopy. As a complement to the experimental data, calculations of the density of states provide information on chemical behavior and local geometry of the atoms in a sample.
Introduction
Intrinsic properties of a sample can be fortunately exposed in specific responses to a core-level excitation. For example, the following effects have been detected and have become the basis of advanced techniques under the tuneable synchrotron irradiation: X-ray absorption fine structure (XAFS), resonant inelastic X-ray scattering (RIXS), resonant photoemission (RPES) and Auger electron (RAES) spectroscopies.1 The XAFS appears both near the photoionization threshold (NEXAFS) and in the extended region far beyond the absorption edge (EXAFS) and reveals the vacant state structure and local geometry, respectively, of the sample.2 The RIXS, which is enabled by the energy and momentum transferred by a photon near the absorption edge, exhibits the intrinsic excitations of the material.3 RPES and RAES investigate the local electronic structure and electron correlations in a system, respectively.4Similar effects were also discovered under the electron impact as another source of the resonant core-level excitation:5,6 a fine structure above the threshold in elastic scattering spectra, which corresponds to the valence state structure of adsorbed species, substrate atoms, and plasmon oscillations. Experimental evidence for conjugate electron excitation (CEE) occurring in ever-present satellites is obtained in the Disappearance Potential spectra from various adsorbed layers, while theoretical evidence is ground in the CEE mechanism, which occurs in a combination of well-known electron transitions. Indeed, shake-up plasmons are usual objects in X-ray Photoelectron (XPS) and Auger Electron Spectroscopies (AES).7,8 The valence band ionization of comparable efficiency for substrate atoms and adsorbed species is the basis of Ultraviolet Photoelectron Spectroscopy (UPS).9 CEE replicas above different thresholds in DAPS spectra confirm that core levels are identical with regard to the excitations.5,6 Therefore, the CEE phenomena form a multichannel route for nonradiative energy dissipation within the DAPS probing depth of 2–3 monolayers (ML) and do not break the general concepts in the field of electron–solid interaction. The present study verifies similar effects in the bulk of model graphite-based samples under the non-resonant X-ray core level excitation.
Experimental
The Disappearance Potential spectroscopy (DAPS) is based on the threshold core-level excitation of a target atom by an electron beam with time-based energy Ep.10 Whenever an accelerating potential overcomes the core level energy, a part of scattered electrons disappears from the elastic current I, providing a spectral dip in the dependence of dI(Ep)/dEp on Ep. The spectrum appears at Ep equal to the difference between the core and the vacant state energy, while its shape is determined by the self-convolution of the vacant density of states (DOS), to which the core and primary electrons move. Adsorption of gases was performed at 300 K on the Auger-clean Pt(100)-(1 × 1) surface obtained by an NO receipt;11 exposures are in Langmuir units (1 L = 10−6 Torr s). The Fermi level EF in DAPS spectra corresponds to the incident electron energy 314.8 eV close to the Pt4d5/2 eigenvalue.12 Other experimental details and methods of spectrum treatment can be found elsewhere.5,6The XPS studies were performed on a Phoibos 150 SPECS spectrometer using monochromatized Al Kα radiation (1486.7 eV). Other experimental details, the low-temperature synthesis technique, and characterization of highly orientated pyrolytic graphite (HOPG), pristine and fluorinated C2F can be found elsewhere.13,14 The Br2 embedding into C2F was performed as in ref. 15 and resulted in the ∼C2FBr0.15 stoichiometric composition.
Theoretical
Geometric parameters and DOS of used unit cells were calculated within the Density Functional Theory (DFT) using the Quantum Espresso software16 and the non-local exchange–correlation functional in the Perdew–Burke–Ernzerhof parameterization.17 The interactions between ionic cores and electrons were described by the Projected Augmented Wave (PAW) method18 with the kinetic energy cutoff Ecut = 40 Ry (320 Ry for the charge-density cutoff) for a plane-wave basis set. The Gaussian spreading for the Brillouin-zone integration was 0.02 Ry; the Marzari–Vanderbilt cold smearing was used.19 Pure graphite was modeled with a two-layer slab using a C24 unit cell with the optimized lattice parameters a = 2.46 Å × 3 and b = 2.46 Å × 2. Half-fluorinated graphite C2F was modeled with a two-layer slab using a C24F12 unit cell with the optimized lattice parameters a = 2.51 Å × 3 and b = 2.46 Å × 2, where F is attached to C atoms on both sides of the slab. DFT calculations have found this structure to be energetically most favourable,20 whereas experimental data indicate another C2F configuration.21 Moreover, the common feature of each phase is the presence of fluorinated and unfluorinated carbons, which determines the DOS structure in similar energy regions. The empty space of 40 Bohr in the Z-direction was accepted to neglect the interaction between the slabs. The Brillouin zone was integrated on a 20 × 20 × 1 grid of Monkhorst–Pack k-points.22 The accuracy was verified by testing the energy convergence. The default number of bands (NB) for the C24 unit cell is shown to result in a DOS structure that is close to the relevant data on graphite and graphene.23–26 However, in this study, we accepted NB = 384 and 288 for C24 and C24F12 unit cells, respectively; these larger NBs preserve the structure of the occupied valence band (VB) and enable a larger vacant DOS energy, providing better agreement between the model and the experimental data. DFT calculations were performed for the unit cells with the Bernal and hexagonal (Hex) structures.20 Trial DFT runs for the Hex C24 unit cell have not revealed a perceptible DOS change under the van der Waals (vdW) interaction, except a slight change in pz.26 The atomic composition of unit cells C24F12Br2 was chosen on the basis of the stoichiometric composition of the sample C2FBr0.15 used in XPS studies. The work function φ = 4.6 eV23 was accepted for each of the C24-based unit cells.The Pt DOS was calculated using the Perdew–Burke–Ernzerhof functional27 and the PAW with the optimized lattice constant 3.99 Å. In this case, Ecut = 40 Ry and a 12 × 12 × 12 grid of Monkhorst–Pack k-points were applied.
CEE effect in the near-surface layer
Conventional DAPS theory directs the core and primary electrons to vacant states around EF.16 The larger the spectral dip is, the larger the vacant DOS is, whereas the lack of vacant DOS results in no signal.10 Moreover, DAPS is certainly sensitive to other channels of elastic electron consumption related specifically to the CEE phenomena and consists of independent shake-off and shake-up VB transitions, each coupled with the threshold core level excitation of a target atom. These channels of energy dissipation can be approximated as an electron transition from the ground DOS σVB to the vacant DOS σVac, whose probability W(E) is in proportion to convolution on the absolute energy relative to EF with a matrix element f(E, σ):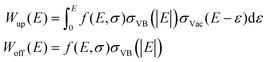 | (1) |
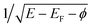 at the energies below, at, and above the vacuum level, respectively,30 where φ = 5.6 eV is a Pt(100) work function.31 This behavior provides the resonant character of CEE and multiple tracing over adsorbed species, including hydrogen atoms and reaction intermediates.5,6 A shake-off CEE satellite due to the adsorbed species is a distinct peak with the 1–2 eV base-width and coverage-proportional intensity, located at a given ionization potential above each threshold. The DAPS spectra in Fig. 1 particularly exhibit 1π, 5σ, and 4σ valence states of the adsorbed CO molecule and the σ state of Had species, which fit published UPS data.32–35 Similar accordance has been found for adsorbed O, N, NO, and NH particles.6
at the energies below, at, and above the vacuum level, respectively,30 where φ = 5.6 eV is a Pt(100) work function.31 This behavior provides the resonant character of CEE and multiple tracing over adsorbed species, including hydrogen atoms and reaction intermediates.5,6 A shake-off CEE satellite due to the adsorbed species is a distinct peak with the 1–2 eV base-width and coverage-proportional intensity, located at a given ionization potential above each threshold. The DAPS spectra in Fig. 1 particularly exhibit 1π, 5σ, and 4σ valence states of the adsorbed CO molecule and the σ state of Had species, which fit published UPS data.32–35 Similar accordance has been found for adsorbed O, N, NO, and NH particles.6
The theoretical Pt shake-off spectrum in Fig. 1(a) was constructed from DFT calculations via the following sequence: VB inversion (because of Woff(E) in eqn (1) and, therefore, the larger the σVB, the larger the spectral dip), differentiation, and shifting to the higher energy by φPt. A substantial contribution of the adsorbed layer into DAPS spectra (as compared with substrate atoms) is a result of the exceptional surface sensitivity of the DAPS, whose probing depth is determined by half the electron mean free path in a solid and thus is restricted to 2–3 ML.
The theoretical Pt shake-up spectrum in Fig. 1(b) corresponds to the convolution of the partial d states by eqn (1). The simulated Pt shake-up and shake-off spectra in Fig. 1 are close to each other because of strongly localized vacant states at EF and 1D DOS at the vacuum level, respectively, and because of the domination of the equal dzx, dzy, and dxy states in the total Pt DOS.26 Close similarity between experimental and simulated spectral fragments in Fig. 1 implies regular involvement of Pt DOS into events, similar matrix elements f(E, σ) for different partial densities of states (pDOS) in eqn (1), and no symmetry ban for CEE transitions. Furthermore, Fig. 1(b) traces adsorbed hydrogen atoms, which is not available for AES and XPS. It is worth noting that none of the CEE satellites in the DAPS spectra could be assigned to the transition from the valence band of adsorbed species to the vacant state of the adjacent substrate atom.5,36 In contrast to VB CEE features, the surface plasmon disappears while the bulk plasmon decreases on coverage, as shown in Fig. 1(b), due to screening by the adsorbed layer.5 Multiple plasmon excitations are also detected at energy points aliquot to the bulk plasmon energy in Fig. 1(b).5 The agreement between the calculated and experimental data in Fig. 1 confirms that both vacancies, at EF and at the vacuum level, are appropriate spots for the allocation of excited electrons under CEE transitions. Present examination accentuates the generality of the CEE effect under inelastic electron scattering by any adsorbed system, bringing to light the outer shell structure of near-surface atoms, while the Auger effect discloses the inner shell peculiarities. CEE control seems to be an additional tool of a standard electron analyzer for fingerprinting the adsorbed layer at the atomic-molecular level and an alternative to the RPES, which requires tunable synchrotron irradiation and fine analytical instrumentation.4 In addition, the elastic electron scattering basically provides the vacant state structure and geometrical parameters, similar to NEXAFS and EXAFS, respectively.37 In prospect, the CEE control should empower the localization of adsorbed species over a composite surface. Indeed, relevant satellites accompany the threshold excitation of only such a surface atom that is chemically bound to the adsorbed particle, while core level energies are easily distinguishable. The following CEE regularities are thus verified.
• Shake-up transitions include ground and excited states of the same atom and probably have no symmetry prohibition.
• Shake-off excitations are available for both the substrate atom and the adsorbed species, although the former is the only over-energy carrier. The infinite free 1D DOS at the vacuum level is a common spot of VB destination. There is no symmetry ban for shake-off transitions, whose satellite structure above the threshold is a σVB mirror-image with respect to EF in eqn (1) shifted to higher energy by the work function.
• The plasmon oscillation is evidence for the collective CEE of free electrons.
CEE effect in the bulk of a solid
CEE phenomena have been successfully traced within the DAPS probing depth of 2–3 ML. The fundamental affinity between the electronic structure of near-surface and bulk atoms assumes similar channels of electron energy dissipation accompanying the core level excitation, irrespective of it occurring by primary electrons or X-ray irradiation. Therefore, the photoelectron can lose a part of its energy for CEE processes and result in a fine XPS spectral structure providing the outer shell peculiarities. By analogy with DAPS measurements, CEE in a multicomponent substance under the non-resonant X-ray core level excitation should include the following:• Shake-off VB transitions to the vacuum level, where pDOS should be considered through possible differences in the matrix elements in eqn (1). The same ground state (VB), the common point of destination (1D DOS), and enough energy excess of any photoelectron, a former core electron, should result in analogous energy losses in XPS spectra of different target components.
• Shake-up VB transitions to free states, with the preferable convolution of the pDOS of the same atom. The unified VB of chemically bound atoms probably gives no preference for a photoelectron to detach the energy for a particular CEE transition. Then, similar fine structures are again expected in XPS spectra of different sample components.
• Plasmon oscillations, if any.
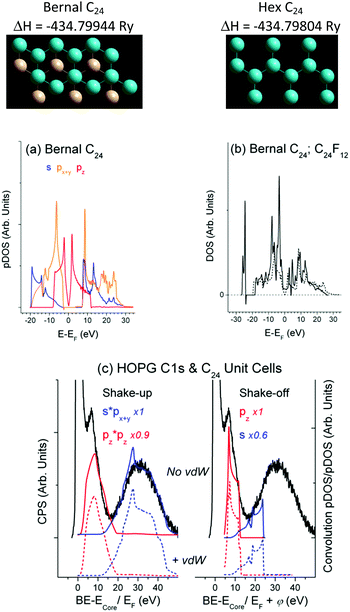
XPS HOPG vs. DFT C24 unit cell
DFT runs revealed that the DOSs obtained for the C24 unit cells with the Bernal and Hex structure are similar and close to the DOS of graphite/graphene (Fig. 2(a and b)). The optimized C–C bond length dC–C = 1.42 Å fits to that of graphite, whereas the interlayer distance dlayer = 3.96 Å is somewhat larger (3.35 Å for graphite), which could be expected for the bilayer unit cells without vdW interaction. Accounting for the vdW interaction has resulted in dlayer = 3.34 Å for the Hex C24 unit cell. It has also led to the negligible change in DOS as compared with Fig. 2(a) and, therefore, to the same (as in Fig. 2(c)) CEE transitions that are responsible for the energy losses. The current study focuses on the DOS structure, whose similarity makes it admissible to confront XPS and DFT data related to bulk material and a suitable unit cell, respectively, omitting the vdW correlation.Conventional satellites at higher energy sides of XPS spectra truly indicate the photoelectron energy consumption. The CEE approach enables complete description of the HOPG XPS C1s spectrum by the combination of shake-up and shake-off transitions (Fig. 2(c)). The matrix elements f(E, σ) in eqn (1) were accepted to be unity for a W(E) basis set, while the Y-scale magnification in Fig. 2(c) evaluates f(E, σ) as a contribution of a particular CEE transition into calculated energy consumption to fit the experimental photoelectron energy losses. As in the case of Pt (Fig. 1), the shake-off probability W(E)off is a σVB mirror-image with respect to EF shifted by φ to higher energy. The satellite ∼5.5 eV in Fig. 2(c) is usually assigned to a π plasmon responsible for the π → π* transition,38 although the classic plasmon stands for collective oscillations of the free electrons missing in HOPG according to Fig. 2(b) and ref. 24. Moreover, this satellite rather originates from shake-off than from shake-up pz transition (Fig. 2(c)).
XPS C2F vs. DFT C24F12
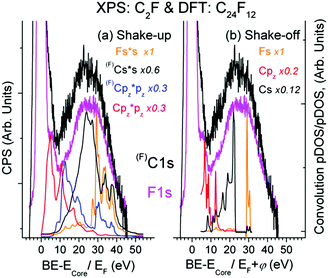
As seen from Fig. 3, there is expected similarity between higher energy tails of (F)C1s (C is bound to F atom) and F1s XPS spectrum, in which the background of multiple external and surface energy losses has been subtracted according to ref. 39.Fine XPS spectral structures above 10 eV conform well to shake-up (Fig. 3(a)) and shake-off (Fig. 3(b)) transitions. The feature ∼5.4 eV is usually assigned to conjugated π bonds in a chain of C atoms;14 it fits the shake-up Cpz transition and naturally accompanies the C1s spectrum since the π bond is localized exclusively at the Csp2 atom, not bound to F. Finding a similar satellite in the F1s spectrum is rather remarkable from the viewpoint of classical theory (because F atoms are not involved in the π bond), but is quite in line with the CEE model. The base line shift in Fig. 3 relative to C1s = 285.1 eV (C is not bound to F) does not contradict the DFT data, but enables the other shake-off transitions ((F)Cpy, Fpy, Fpz) to contribute to the ∼5.4 eV feature. The formation energy of the Bernal unit cell is by 0.008 eV higher than that of the Hex C24F12 cell, while pDOSs of both structures are very similar. A sizable DOS at EF shown in Fig. 2(b) accepts plasmon oscillations that can give the energy loss at 9.1 or 12.9 eV for 1 or 2 free electrons per a C2F fragment, respectively.
XPS C2F + Br2vs. DFT C24F12Br2
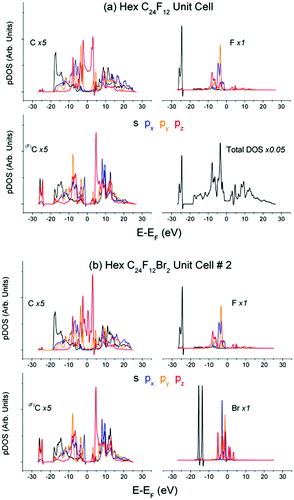
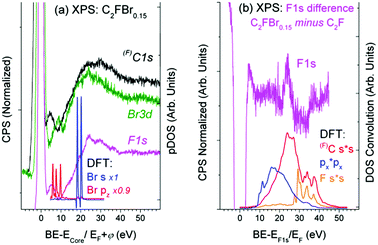
Partial DOS of the pristine C24F12 unit cell in Fig. 4(a) undergoes little change in comparison with that of C24F12Br2 in Fig. 4(b). The XPS spectra in Fig. 5(a), obtained after the Br2 intercalation, correspond to the stoichiometric composition C2FBr0.15 and reveal the lack of new features as compared with Fig. 3. Energy losses in the F1s spectrum are less pronounced than those in C1s; however, both spectra are in agreement with the same CEE transitions as before the Br2 embedding. The Bromine pz- and s- shake-off transition conforms well to the non-resolved ∼9.5 eV peak and the ∼20 eV shoulder in Fig. 5(a), respectively. The higher energy part of the XPS Br3d spectrum is similar to that of F1s and C1s, but it does not correspond to any CEE within Br pDOS. This probably indicates a bonding between a Br2 molecule and the C2F frame that is enough to provide the Br3d photoelectron energy losses via the CEE transitions in pDOS of C and F.The difference F1s spectrum in Fig. 5(b) exhibits a distinct structure, which conforms to shake-up transitions of the pDOS responsible for C–F bonding, which can be interpreted as the C–F bond strengthening. It seems reasonable because Br2 embedding weakens the interactions between carbon layers, which should be accompanied with the balanced enrichment of the occupied DOS of C and F. The difference XPS C1s spectrum shows similar, but less pronounced, features (Fig. 5(b)).
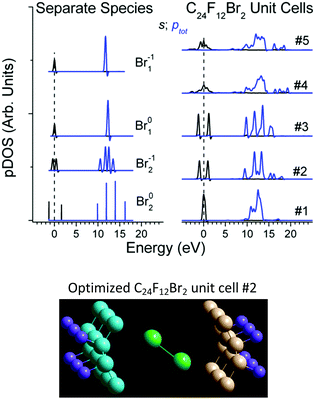
The DFT studies were performed for the Bernal and Hex C24F12Br2 unit cells #1–4 at the extreme entry angles α0 = 0° and α0 = 90° between the Br–Br axis and carbon planes (Table 1). The calculations revealed that the Br2 embedding enlarges the interlayer distance, but insignificantly affects the pDOS of C and F. The latter conforms to the chemical inertness of the pristine C2F cell and to the low Br content in the product substance C2FBr0.15.40 Another DFT run for Bernal unit cell #5 at α0 = 52° (about optimal α for Hex #2) resulted in new optimized parameters in Table 1. Both atomic (No. 1, 4 and 5) and molecular (No. 2 and 3 in Table 1) states of intercalated Br2 are available, and each of the local structures seems appropriate. No preference can be given to a particular case at this phase of the conventional DFT study. Moreover, each of the five unit cells is characterized by the specific Br pDOS structure (Fig. 6). Further processing was attempted to choose the appropriate cell out of the five unit cells in Table 1.‡
| Parameter | #1 | #2 | #3 | #4 | #5 |
|---|---|---|---|---|---|
| a Each value corresponds to C triplet representing the plane.26 b A set answers the zigzag arrangement of carbon planes; compare to dlayer = 4.08; 5.52 and 3.75; 3.98 Å for the Hex and Bernal C24F12 unit cell, respectively.26 | |||||
| α 0 | 0° | 90° | 0° | 90° | 52° |
| α | 0.2° | 23.7° | 6.2° | 0.1° | 0.7° |
| 2.4° | 24.2° | 8.9° | 9.9° | 0.9° | |
| 50.8° | 20.2° | 24.2° | 22.4° | ||
| 78.0° | 31.4° | 29.9° | |||
| d BrBr (Å) | 3.24 | 2.45 | 2.37 | 3.18 | 3.34 |
| d layer (Å) | 4.88 | 6.74 | 7.38 | 5.70 | 5.11 |
| 6.32 | 8.21 | 7.39 | 5.98 | 5.82 | |
| 6.02 | 6.74 | ||||
| 〈Es〉 (eV) | −13.24 | −14.61 | −15.08 | −15.34 | −15.10 |
| 〈Ep〉 (eV) | −1.58 | −2.55 | −2.75 | −2.66 | −2.49 |
| Δ s–p (eV) | 11.66 | 12.06 | 12.32 | 12.68 | 12.61 |
| ΔH (eV) | 0 | 0.79 | 0.42 | 1.28 | 0.74 |
| Δ s–p Deviation (eV) | |||||
| Br02 | 1.39 | 0.99 | 0.73 | 0.37 | 0.44 |
| Br2−1 | 0.4 | 0 | −0.26 | −0.62 | −0.55 |
| Br01 | 0.62 | 0.22 | −0.04 | −0.4 | −0.33 |
| Br1−1 | 0.07 | −0.33 | −0.59 | −0.95 | −0.88 |
First, DFT examinations of separate species revealed a pronounced difference Δs–p = 0.2–1.3, which is far beyond the accuracy of calculations (0.01 eV), between the weighted average energy 〈Es,p〉 of the Br s- and p-DOS (Table 2). The energy 〈Es,p〉 was determined as E, 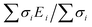 , and middle of
, and middle of 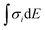 for the Br atom with single, several localized, and diffused s- and p-DOS, respectively.
for the Br atom with single, several localized, and diffused s- and p-DOS, respectively.
| (eV) | Br02 | Br2−1 | Br01 | Br1−1 |
|---|---|---|---|---|
| 〈Es〉 | −20.49 | −13.43 | −12.37 | −11.91 |
| 〈Ep〉 | −7.44 | −1.37 | −0.09 | −0.18 |
| Δ s–p | 13.05 | 12.06 | 12.28 | 11.73 |
| d BrBr (Å) | 2.29 | 2.85 | — | — |
Second, the empirical parameter Δs–p was taken as a descriptor of the Br state, in the same way as the apparent binding energy determines the oxidation rate in XPS practice. The smallest deviations Δs–p of 0.02, 0, and 0.04 eV make cells #1, 2, and 3, preferable, respectively (Table 1). Third, in the case of the large distance dBrBr (the Br–Br bond is lost), the difference Δs–p in a cell should be close to that of separate Br1. Otherwise (i.e. the Br–Br bond retains), the difference Δs–p should be close to that of Br2 species. In this case, dBrBr for cell #1 (3.24 Å) and for cell #2 (2.45 Å) corresponds to the lack of the Br–Br bond in Br1−1 and to dBrBr in Br02 (2.29 Å), respectively (Table 1).
On the contrary, cell #3 should be ruled out because its dBrBr = 2.37 Å implies that the Br–Br bond is retained, while the Br01 specimen with nearest Δs–p has no bond. Finally, cell #2 is preferred over cell #1 with respect to the formation energy (Table 1). In addition, the reaction C24F12 + Br2 → C24F12Br2 is found endothermic for cell #1 in contrast to others.26
The optimal unit cell (cell # 2, Fig. 6) corresponds to the enlargement of the interlayer distance by 2–4 Å under Br2 embedding into C24F12 and to the angles 24–78° between the Br–Br axis and various planes of the C-skeleton. These results agree well with experimental X-ray absorption studies that have reported the angles 20°–30° and the molecular Br2 state for similar systems.15,41
The CEE control by the joint XPS and DFT efforts can be characterized by the following obvious, verified or probable resources.
• The comparison of extended XPS spectra with theoretical CEE transitions can provide the local geometry and bond types in a sample with the use of conventional DFT facilities.
• The occurrence and consequence of bonding between atoms can be enabled because the core level excitation of a given atom is accompanied by CEE satellites of the next one only within the integrated valence band. Examination of the adsorbed layer and strong metal–support interaction at grazing incident can also be promising.
• The multiple CEE control (around various XPS peaks) should improve the reliability of data interpretation, while individual sets of the core level energies facilitate the study of multicomponent materials.
• Similarly to DAPS data,5 hydrogen tracing as a CEE satellite above the core level energy of the other sample component does not contradict XPS principles.
• The energy loss spectrum is linked up to the XPS peak and does not depend on the apparent core level energy; therefore, CEE control is available for samples of any conductivity.
• The valence band structure in XPS spectra, being affected by the primary irradiation, differs from that obtained by non-destructive or theoretical methods. Currently, the VB does not undergo the incident X-ray impact, but absorbs a part of photoelectron energy necessary for the resonant transition; therefore, CEE control is a non-destructive method.
• The extensive use of XPS and DFT techniques makes the CEE analysis accessible.
Regular plasmons in AES and XPS spectra, as well as assignment of XPS, RPES and NEXAFS spectra in terms of π, σ → π*, σ* or the Highest Occupied → the Lowest Unoccupied Molecular Orbital transitions,42,43 are obvious CEE manifestations. The energy dissipation, which follows the core level excitation, is the general trend of electron systems. Auger electron transitions are particular cases of such an event which results from filling the core hole. The CEE phenomena form another natural route of relaxation—by the photoelectron energy redistribution through the valence band. It is worth noting that CEE events are enabled because the former core and VB electrons belong to the same configuration and therefore can be hardly detectable by electron energy loss spectroscopy, while AES spectra are usually complicated by a large number of background features. The current study focuses on the DAPS and omits allied threshold excitation techniques of the Auger Electron and Soft X-ray Appearance Potential Spectroscopies (AEAPS, SXAPS) because of the following reasons. DAPS data are considered enough to develop the methodology for a surface science study. Furthermore, AEAPS and SXAPS follow the core hole decay, which is inevitably complicated by the electron–core hole interaction. In contrast, the DAPS fixes the moment of core hole origination, when the electron–core hole interaction has not occurred or is minimal. The same is the case for photoelectron energy losses in XPS spectra, because the events of photon energy absorption and shake-off/shake-up electron energy dissipation can proceed at once or shortly, eliminating or minimizing the electron–core hole interaction, respectively.
Conclusions
The possibility to generate extra data by conventional techniques is truly desirable. This study highlights a rational model that gives a chance to realize this desire using ordinary XPS and DFT outputs. The model is based on the following statements. First, there are natural traps for the resonant energy absorption in the electronic configuration of atoms in a solid, such as shake-off, shake-up transitions, and plasmon oscillations; there is electronic affinity between the near-surface and bulk atoms. Second, the core level excitation of any origin forms multiple channels for the energy dissipation by filling those traps. Third, the relaxation can be traced experimentally, as the energy losses in XPS and DAPS spectra, and theoretically, via the convolution of the valence band DOS. The model does not conflict with general concepts of electron–solid interaction and has been well verified in model studies of Pt and graphite-based materials.Acknowledgements
This study has been supported by the Russian Foundation for Basic Research (Grants 17-03-00049 and 16-03-00048). The authors thank D. V. Pinakov for the preparation of C2F samples and Siberian supercomputer centre for granting their facilities for quantum-chemical calculations.Notes and references
- J. Sá, High resolution XAS/XES: analyzing electronic structures of catalysis, CRC Press, Boca Raton, 2014 Search PubMed.
- G. Bunker, Introduction to XAFS: A Practical Guide to X-ray Absorption Fine Structure Spectroscopy, Cambridge University Press, Cambridge, 2010 Search PubMed.
- L. Ament, M. van Veenendaal, T. Devereaux, J. Hill and J. van den Brink, Rev. Mod. Phys., 2011, 83, 705 CrossRef CAS.
- P. Brühwiler, O. Karis and N. Mårtensson, Rev. Mod. Phys., 2002, 74, 703 CrossRef.
- A. Cholach and V. Tapilin, J. Chem. Phys., 2013, 138, 104201 CrossRef PubMed.
- A. Cholach and V. Tapilin, Appl. Surf. Sci., 2001, 180, 173 CrossRef CAS.
- D. Briggs and M. Seach, Practical Surface Analysis by Auger and X-ray Photoelectron Spectroscopy, Wiley & Sons, NY, 1983 Search PubMed.
- D. Woodruff and T. Delchar, Modern Techniques of Surface Science, Cambridge Univ. Press, Cambridge, 1994 Search PubMed.
- J. Rabalais, Principles of Ultraviolet Photoelectron Spectroscopy, Wiley, NY, 1977 Search PubMed.
- J. Kirschner, Electron-excited core level spectroscopes, Springer, Berlin, 1977 Search PubMed.
- G. Brodén, G. Briden and H. Bonzel, Surf. Sci., 1978, 72, 45 CrossRef.
- CRC Handbook of Chemistry and Physics, ed. D. Lide, CRC Press, Boca Raton, 2005 Search PubMed.
- I. Asanov, A. Okotrub, A. Gusel’nikov, I. Yushina, D. Vyalikh and L. Bulusheva, Carbon, 2014, 82, 446 CrossRef.
- I. Asanov, L. Bulusheva, M. Dubois, N. Yudanov, A. Alexeev, T. Makarova and A. V. Okotrub, Carbon, 2013, 59, 518 CrossRef CAS.
- N. Bausk, S. Erenburg, N. Yudanov and L. Mazalov, J. Struct. Chem., 1996, 37, 913 CrossRef.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- J. Perdew, A. Ruzsinszky, G. Csonka, O. Vydrov, G. Scuseria, L. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- P. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- N. Marzari, D. Vanderbilt, A. De Vita and M. Payne, Phys. Rev. Lett., 1999, 8, 3296 CrossRef.
- C.-H. Hu, P. Zhang, H.-Y. Liu, S.-Q. Wu, Y. Yang and Z.-Z. Zhu, J. Phys. Chem. C, 2013, 117, 3572 CAS.
- A. Okotrub, N. Yudanov, I. Asanov, D. Vyalikh and L. Bulusheva, ACS Nano, 2013, 7, 65 CrossRef CAS PubMed.
- H. Monkhorst and J. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef.
- N. Ooi, A. Rairkar and J. Adams, Carbon, 2006, 44, 231 CrossRef CAS.
- O. Sedelnikova, L. Bulusheva and A. Okotrub, Synth. Met., 2010, 160, 1848 CrossRef CAS.
- H. Nejati and M. Dadsetani, Micron, 2014, 67, 30 CrossRef CAS PubMed.
- Supplement (Optimized atomic coordinates, DOS and views for the C24, C24F12 and C24F12Br2 unit cells).
- J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- A. Rother and K. Scheerschmidt, Ultramicroscopy, 2009, 109, 154 CrossRef CAS PubMed.
- D. Gingrich, Practical Quantum Electrodynamics, CRC Press, NY, 2006 Search PubMed.
- C. Kittel, Introduction to solid state physics, Wiley, 2005 Search PubMed.
- B. Pennemann, K. Oster and K. Wandelt, Surf. Sci., 1991, 249, 35 CrossRef CAS.
- H. Bonzel and T. Fischer, Surf. Sci., 1975, 51, 213 CrossRef CAS.
- A. Ramstad, F. Strisland, S. Raaen, A. Borg and C. Berg, Surf. Sci., 1999, 440, 290 CrossRef CAS.
- M. Bartram, B. Koel and E. Carter, Surf. Sci., 1989, 219, 467 CrossRef CAS.
- J. Demuth, Surf. Sci., 1977, 65, 369 CrossRef CAS.
- A. Cholach, Chemical Physics Research Developments, Nova Sci. Publ., NY, 2011, pp. 149–173 Search PubMed.
- M. den Boer, T. Einstein, W. Elam, R. Park, L. Roelofs and G. Laramore, Phys. Rev. Lett., 1980, 44, 496 CrossRef CAS.
- E. Taft and H. Phillipp, Phys. Rev., 1965, 138, A197 CrossRef.
- S. Tougaard and I. Chorkendorff, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 35, 6570 CrossRef CAS.
- L. Bulusheva, V. Tur, E. Fedorovskaya, I. Asanov, D. Pontiroli, M. Riccò and A. Okotrub, Carbon, 2014, 78, 137 CrossRef CAS.
- J. Feldman, W. Elam, A. Ehrlich, E. Skelton, D. Dominguez, D. Chung and F. Lytle, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 7961 CrossRef CAS.
- O. Sedelnikova, L. Bulusheva, I. Asanov, I. Yushina and A. Okotrub, Appl. Phys. Lett., 2014, 104, 161905 CrossRef.
- K.-D. Tsuei, J.-Y. Yuh, C.-T. Tzeng, R.-Y. Chu, S.-C. Chung and K.-L. Tsang, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 15412 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Optimized atomic coordinates, density of states and relevant views for the C24, C24F12 and C24F12Br2 unit cells are available in ref. 26. See DOI: 10.1039/c7cp00900c |
| ‡ A similar processing may be useful for identification of the state of the atoms in other compounds whereas its theoretical rationalizing is beyond this paper. |
| This journal is © the Owner Societies 2017 |