 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Does water belong to the homologous series of hydroxyl compounds H(CH2)nOH?
Jolanta
Świergiel
 * and
Jan
Jadżyn
* and
Jan
Jadżyn
Institute of Molecular Physics, Polish Academy of Sciences, M. Smoluchowskiego 17, PL-60-179 Poznań, Poland. E-mail: swiergiel@ifmpan.poznan.pl
First published on 20th March 2017
Abstract
The main objective of this paper is to find a source of anomalously high value of the equilibrium permittivity of water. The source is identified to be the unusually high deformation polarizability. The conclusion follows from the analysis of the behavior of the orientational entropy increment induced by an external electric field applied to the liquids belonging to the homologous series of hydroxyl compounds H(CH2)nOH at the end of which water is located. The finding reflects the “indecision” of water about its dielectric relationship with the alcohol family: the value of the permittivity of water absolutely does not fit into alcohols (is too high), while the dipolar orientation effects (which normally determine the permittivity level) fit into alcohols quite well. It results from the presented experimental data that among all the diversity of intermolecular hydrogen-bonded structures existing in liquid water, predominant are the polar entities, i.e. the structures which more or less resemble the chains. Otherwise, the dipolar orientational effects would behave in a quite different way than what is observed in the experiment. The result is convergent with the conclusion of Wernet et al., based on the high-performance X-ray studies of water (Science, 2004).
1 Introduction
It is a truism that water is the most important liquid on Earth. However, one should add simultaneously that it is the most complex liquid known even though it is composed of one of the simplest molecules in nature, H–O–H. The relative simplicity of water molecules refers, however, to the situation when the molecules are isolated from each other. Being in contact, the water molecules spontaneously link together by the hydrogen bonds O–H⋯O. The uniqueness of the H2O molecule is that each of its atoms is able to create such a hydrogen bond with an adjacent molecule, while the oxygen atom can form two bonds using two of its free electron pairs. So, in total, the water molecule can participate in four bonds O–H⋯O. Indeed, water is dominated by hydrogen bonds. The energy of a single hydrogen bond is relatively low, because it accounts for about 10% of the energy of a typical covalent bond, but a large amount of such linkages makes the hydrogen bonds a serious energetic player in water, comparable to the energy of thermal excitation of molecules (kT). Competition between these two energies causes continuous disintegration and re-formation of hydrogen bonds, which makes the molecular dynamics of water really exceptional.In brief, the existence of the directional hydrogen bonds basically determines the structure of water and the continuous cracking of the bonds and re-linking molecules determine the dynamics of water on the microscopic level. These unique molecular properties result in many unique macroscopic properties of water, which determine all the nature on Earth. Understanding these properties has been the subject of intense research for over a hundred years.1–3
The present paper concerns one of the topics in discussion about the properties of water, namely the inclusion of water in the homologous series of hydroxyl compounds H(CH2)nOH and looks at the properties of water from the perspective of alcohols. One should realize that the molecules of alcohols contain in their structure a hydrophobic part, which, however, gradually disappears as n decreases. Anyway, for n = 0, the series H(CH2)nOH formally ends as water. In reality, however, the transition from n = 1 to n = 0 is not so simple. After subtraction of the CH2 group from the methanol molecule, the remaining hydrogen atom adopts totally different properties. Now, the hydrogen, linked to the oxygen atom in the molecule of water, has acidic properties and is capable of forming a hydrogen bond. So, the quantitative change involves here a qualitative change. Besides, the transition from n = 1 to n = 0 is accompanied by an increase of the electric dipole moment of single molecules from 1.65 D (alcohols) to 1.85 D (water), which reflects the difference in polarity of C–H and O–H bonds.
At the beginning, let us have a look at several well-known properties of water in light of the properties of several alcohols which are nearest to water (from methanol to pentanol). Fig. 1 presents two physical quantities: the molar volumes4,5 (a) and the dielectric relaxation time6–8 (b), measured for the homologous series of hydroxyl compounds H(CH2)nOH, n = 0–5, at a constant temperature (25 °C). As is clear from the pictures, in both cases water certainly belongs to the series of alcohols. For the molar volumes, the situation seems to be expected, because an increase in the bonding ability of water molecules in comparison to alcohols cannot influence the molar volume of water too much, if one takes into account the relative weakness of the hydrogen bonds.
 | ||
| Fig. 1 The molar volume4,5 (a) and the principal dielectric relaxation time6–8 (b) (at 25 °C) of the homologous series of hydroxyl compounds H(CH2)nOH: water (0) and aliphatic alcohols: methanol (1), ethanol (2), propanol (3), butanol (4) and pentanol (5). | ||
In the case of the dielectric relaxation time, the situation is a bit different because the dielectric spectrum of the hydroxyl compounds is, in general, composed of several absorption bands.9,10 And recently, the number of bands has even increased due to the development of the terahertz techniques.11–14 Here, it is important to notice that among the dielectric absorption bands which are recorded for hydroxyl compounds, one band strongly dominates over the others. In general, that band constitutes more than 90% of the total dielectric absorption of hydroxyl compounds. That main dynamic dielectric contribution is a well-known Debye-type band which is related to the collective relaxation of the dipole moments of molecular self-assemblies composed of i molecules, at a given moment t, 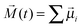 , where
, where ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) i is the dipole moment vector of a single molecule. In the case of water, that main dielectric absorption band is situated at about 20 GHz, and the corresponding relaxation time τD equals 8.32 ps.6Fig. 1b depicts just the main dielectric relaxation times τD recorded for the hydroxyl compounds6–8 of different numbers of n. However, the theoretical shape of the τD(n) dependence for hydroxyl compounds is not known, but the experimental data presented in Fig. 1b show that water and alcohols present consistent dependence on n.
i is the dipole moment vector of a single molecule. In the case of water, that main dielectric absorption band is situated at about 20 GHz, and the corresponding relaxation time τD equals 8.32 ps.6Fig. 1b depicts just the main dielectric relaxation times τD recorded for the hydroxyl compounds6–8 of different numbers of n. However, the theoretical shape of the τD(n) dependence for hydroxyl compounds is not known, but the experimental data presented in Fig. 1b show that water and alcohols present consistent dependence on n.
As seen in Fig. 2, one cannot say the same about behavior of the viscosities of the compounds under discussion.15,16 Here, the water, in any way, cannot be included in the viscosity line determined by alcohols (n ≥ 1). One could say this is fortunate, because the continuation of the viscosity evolution occuring within the alcohols would end up in the superfluidity of water at room temperature.
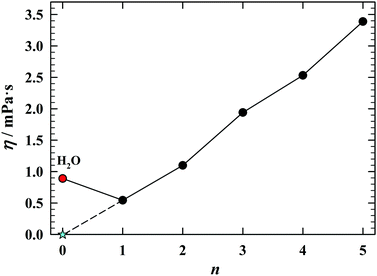 | ||
| Fig. 2 The viscosity15,16 of hydroxyl compounds H(CH2)nOH, n = 0–5, at 25 °C. If water were in the homologous series of alcohols, it would be superfluid at room temperature. | ||
At the end of this introduction let us have a look on the phase diagram of the hydroxyl compounds under consideration. As can be seen in Fig. 3, both m.p. and b.p. of water absolutely do not fit the alcohol data. For water, the real temperatures of the phase transitions are anomalously high. Being in the alcohol regime, water should melt and boil at −84 °C and 43 °C, respectively. So, the anomalous behavior of water does not refer only to the homologous series of H2O, H2S, H2Se, H2Te and H2Po.17 However, as is also observed from Fig. 3, water, as compared with the depicted alcohols, has the narrowest temperature range of existence as a liquid. Propanol offers a liquid state over a temperature range twice as large as that of water.
Of course, numerous other strange anomalies in the behavior of water are known and discussed in the literature.18–20
In this paper, we will focus on the dipolar orientational effects in water, as the final element in our chain of hydroxyl compounds. Among the experimental data presented above, those from Fig. 1b present rather unexpected consistency of the dielectric relaxation times τD of water and alcohols, so, one can suspect that it may result from some coincidences. In this paper, we will verify the conclusions resulting from Fig. 1b, by examining the dipolar orientation effects induced by the static electric field applied to liquids. The static field causes the orientation ordering of the dipolar entities actually existing in a given liquid, while in the fields of high frequencies these entities exhibit their presence as relaxors. Since both experiments, static and dynamic, involve the same molecular objects, the conclusions resulting from these distant frequency regions should be consistent with each other.
Our studies of the dipolar effects may help in solving two hot topics relevant to the understanding of water. The first topic concerns the effective shape of the hydrogen-bonded entities formed by molecules of alcohols and water. Here, we would like to address the conclusions resulting from the studies of X-ray absorption spectroscopy and X-ray Raman scattering, performed for water by Wernet et al.21 The authors have concluded that the chain-like hydrogen-bonded entities are formed by the molecules of water. This conclusion has been recently classified as one of the myths about water.22
The second topic is related to the theoretical simulations of the properties of water, in particular the simulations of the high value of its static permittivity εS23–32 (78 at 25 °C). We hope that our results will lead to something important in this subject.
The methodology of our studies is based on the fact that the ordering of molecular dipoles by the static electric field causes a decrease of the entropy of a liquid. The effect is available in experiment and can be determined on the basis of temperature dependence of the static permittivity of the studied liquid. The theoretical basis of the orientational entropy effects induced by the probing electric field in dipolar liquids was first developed by H. Fröhlich.33
2 Experimental section
2.1 Materials
Alcohols were purchased from Acros Organics with a declared purity of 99.9%. The liquids were stored over molecular sieves (4 Å) several weeks before the measurements. Water of high purity – deionized reagent grade III (conductivity 1.5 μS cm−1 at 20 °C) from Acros Organics was used without further treatment.2.2 Methods
The complex permittivity spectra were recorded using an HP 4194A impedance/gain phase analyzer in the frequency range from 100 Hz to 5 MHz. The measurements were performed in the temperature range from 5 °C to 50 °C. At first, the samples were cooled down (approximately with 1 °C min−1) to 5 °C and next the measurements were performed for increasing temperature. The temperature of the measuring cell was controlled with a “Scientific Instruments” device, model 9700, within ±2 × 10−3 °C. The details of the used experimental set-up and the procedure of determination of the permittivity values can be found in a recent paper.343 Results and discussion
Fig. 4 presents the temperature dependences of the static permittivity of water and five alcohols. Strikingly, there is a big jump in the permittivity value occurring at the transition from methanol to water (at 5 °C the difference is about 48). But let us analyze exactly how, under the isothermal conditions, the static permittivity of the hydroxyl compounds H(CH2)nOH evolves with n. Because, for comparison purposes, an analysis of the molar quantities is more comfortable and more safe for interpretation, we will first analyze the behavior of the molar static dielectric susceptibility (χM) of the investigated liquids:| χM = (εS − 1)VM, | (1) |
 | ||
| Fig. 4 Temperature dependences of the static permittivity (εS) of neat hydroxyl compounds H(CH2)nOH. The numbers in the picture denote the number (n) of CH2 groups in the alkyl chain of molecules. | ||
Fig. 5a clearly shows that the static dielectric susceptibility of water does not belong to the susceptibility line created by alcohols. The χM(1 ≤ n ≤ 5) dependence extrapolated to n = 0 leads to the value of χ(star)M = 1.18 × 10−3 m3 mol−1, which is essentially lower than the experimental one (1.39 × 10−3 m3 mol−1). The permittivity calculated from the extrapolated susceptibility, ε(star)S = (χ(star)M/VM) + 1, is equal to about 66 (Fig. 5b) and is lower by about 12 from the measured permittivity value (the extrapolated susceptibility and permittivity, are marked in Fig. 5 as stars). It seems to be important to notice here that the permittivity value of about 66 appears in part of the papers devoted to the simulations of the static permittivity of water.23 The problem of the origin of the permittivity excess from 66 to the actual value 78 (all at 25 °C), is one of the fundamental and unresolved issues in the understanding of water at the molecular level. In the hope of finding some important information in this regard, let us examine the dipolar orientation effects as seen through the temperature behavior of the static permittivities of the studied hydroxyl compounds. The orientational effect reflects the actual state of the molecular self-assembly process at the given temperature, whereas the evolution of that effect with temperature reveals the direction of that process.
But before presenting the results in detail, a short comment should be added about the still commonly used Kirkwood correlation factor,35gK, as a detector of dipolar couplings in liquids. The factor is defined as the square of the ratio of the apparent dipole moment per one molecule of the studied dipolar liquid (μapp) and the dipole moment (μ1) of a single molecule (monomer) of the compound:
| gK = (μapp/μ1)2. | (2) |
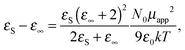 | (3) |
The factor gK reflects the predominant type of intermolecular interaction occurring in polar liquids. In the case when the dipole–dipole correlations are negligible, μapp is equal to the dipole moment of a single molecule, μ1, and the Kirkwood factor gK = 1. The case of gK < 1 corresponds to the antiparallel dipolar correlation which leads to the reduction of the dipole moment per molecule and the case of gK > 1 reflects the parallel dipoles correlation with enhancement of the apparent molecular dipole moment. It is natural that with increasing temperature of a studied system, the Kirkwood correlation factor tends to 1, independent of the type of the dipolar interaction.
As is apparent from the eqn (3), the physical quantity which essentially determines the value of μapp is the difference between the static and high-frequency permittivities of the studied compound, εS − ε∞. The basic problem is that we can precisely determine εS, but not ε∞. The difficulties are related both to the accuracy of measurement of the permittivity in high frequencies as well as to the numerical processing of the experimental data. The detailed discussion of that problem was presented in a recent paper.37 Here, we show only the difficulties with the description of the dipolar situation in water, when one uses the Kirkwood correlation factor.
On Fig. 6 are shown some literature values of ε∞6,38,39 for water and for the first three alcohols.6 The figure depicts also the squared refractive index (nD2) of hydroxyl compounds, measured for the sodium D line.5,40
 | ||
| Fig. 6 The high-frequency permittivities (ε∞) of water and methanol, ethanol and propanol (full points).6,38,39 The open points are the refractive index squared of hydroxyl compounds H(CH2)nOH (n = 0–5).5,40 The data refer to the temperature of 25 °C. | ||
The static permittivity of water (εS = 78.36, at 25 °C) is known with a relatively high accuracy, while the high-frequency permittivity, ε∞, as is clearly seen in Fig. 6, can be estimated with a considerable margin. The value of ε∞ for water, resulting from an assumption used in the literature that ε∞ ≈ 1.1nD2 (10% represents the atomic polarizability) amounts ε∞ ≈ 1.954, while, as seen in Fig. 6, the numerical analysis of the dielectric relaxation spectrum can lead to a value as high as ε∞ ≈ 5.16.39 The first option gives for the Kirkwood correlation factor the value gK = 2.56 (quite strong parallel dipolar association), while the latter value gives gK = 0.77 (significant antiparallel coupling). For ε∞ ≈ 4.596 (full circle for n = 0 in Fig. 6), gK = 0.90 (moderate antiparallel association of dipoles) and for ε∞ ≈ 3.9638 (full square for n = 0 in Fig. 6), gK = 1.11 (moderate parallel association of dipoles). Of course, such discrepancies are not acceptable. In practice, the problem of an appropriate determination of ε∞ concerns nearly all polar liquids, although the differences between 1.1nD2 and ε∞ are not always as dramatic as in the case of water. But whatever the experimental circumstances, the anomalously large difference between nD2 and ε∞ of water seems to be real and we will get back to that problem later.
As shown in numerous papers,41–45 an alternative method which reveals the state of dipolar aggregation of molecular dipoles in liquids is also related to the liquid permittivity, but only with its static part, εS. Namely, it was shown first by Fröhlich in 195833 and next by Becker,46 Landau, Lifshitz and Pitaevskii47 and Scaife,48 that the probing electric field, applied to the dipolar liquid, induces an increment of the thermodynamic quantities (internal energy, entropy and Helmholtz free energy), which are quite simply related to the static permittivity of a liquid, εS, its temperature derivative, dεS/dT, and the square of the electric field strength E. For the purposes of this work, we are interested in the change of entropy, which is dependent exclusively on the permittivity temperature derivative:
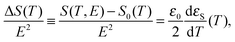 | (4) |
It is obvious that an ordering of the dipolar entities forced by electric field leads to decrease of the orientational entropy of the tested liquid, i.e. the entropy increment is negative. The change of the temperature definitely differentiates the ways of the molecular self-assembling: with lowering temperature the increment increases (in its absolute value) for the dipoles parallel self-association (a positive slope) and |ΔS| decreases for the antiparallel coupling of molecular dipoles (a negative slope). The temperature independence of the entropy increment virtually means that the dipolar correlations in a given liquid can be neglected.
Like in the case of the static permittivity, for interpretation purposes, we will refer to the entropy increment per mole of the molecules of the studied liquid, ΔS(T)VM(T)E−2.
Fig. 7 presents the temperature dependences of the increments of the molar orientational entropy for the studied hydroxyl compounds. A brief overview of the results shows that the tested fluids behave quite similarly. For all compounds, the entropy increment is negative, and its slope in temperature dependence is positive. Two main conclusions follow from Fig. 7. (i) The negative value of the entropy increment indicates that the dominant effect caused by an applied electric field is the ordering of the dipolar entities actually existing in the liquids. (ii) The positive slope of the increment reflects the gradual increase of the polarity of the entities with decreasing temperature. This is a typical temperature behavior of liquids where relatively weak intermolecular interactions, especially hydrogen bonds, lead to the formation of polar supramolecular polymers. Increase of the negative orientational entropy, which is observed with decreasing temperature, is a consequence of an increase of the degree of supramolecular polymerization in the tested liquids.
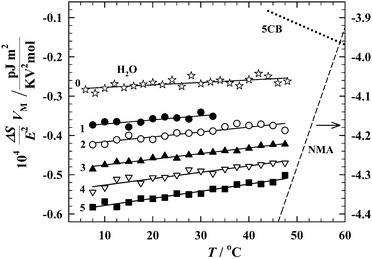 | ||
| Fig. 7 Temperature dependences of the increments of molar orientational entropy for water (0) and aliphatic alcohols [from methanol (1) to pentanol (5)]. For comparison, the dependences for two radically different self-associated liquids are traced in the picture: N-methylacetamide (NMA),49 the molecules of which form strongly elongated (head-to-tail) hydrogen-bonded chains and n-pentylcyanobiphenyl (5CB),41 the mesogenic dipolar liquid where the antiparallel dimers strongly dominate. | ||
The experiment described here allows one to distinguish between supramolecular polymers in which the molecules are hydrogen-bonded in two different ways. The first way, the cyclic way, leads to reduction in the polarity of the molecular assembly in comparison to the polarity of non-linked molecules, and with decreasing temperature the reduction intensifies because the cyclic assemblies include more molecules. The second way, the chain-like way, leads to an opposite temperature effect: an increase in the polarity of the molecular assembly with decreasing temperature. Of course, both of these ways can be realized simultaneously, especially in such a complex liquid like water, and what is observed in the experiment is the resultant of all possible ways of molecular self-assembly.
The experimental data presented in Fig. 7 prove that in the tested hydroxyl compounds, including water, the resultant molecular supramolecular assemblies are of chain-like type. However, one must realize the scale of the problem we are dealing with here. In Fig. 7 are traced the temperature dependences of the molar entropy for the two exceptional liquids which represent the above discussed extreme ways of molecular self-aggregation. N-Methylacetamide (NMA)49 is well known for its huge self-association in the form of the hydrogen-bonded quasi-linear supramolecular polymers. The second compound is n-pentylcyanobiphenyl (5CB),41 the classical nematogenic liquid, strongly self-associated in antiparallel dimers due to the dipole–dipole couplings. As can be seen in the picture, the temperature behavior of the hydroxyl compounds certainly resembles NMA, but the scale of the orientational effects in alcohols and water is really small.
Further analysis of our results will concern only details, however, details of great importance. As seen in Fig. 7, the increment of the entropy is negative for all compounds, but its absolute value is steadily increasing with increasing n. It undoubtedly means that the resultant polarities of the hydrogen bonded molecular associates are gradually increasing when going from water to pentanol. So, the experiment shows the direction in which the population of the cyclic self-assemblies with partially or even totaly reduced dipole moment decreases. As expected, the highest number of the hydrogen bonded cyclic entities can be found in water, but even here these cyclic entities do not prevail on the chain-like associates.
Fig. 8 shows how in studied hydroxyl compounds develops the process of formation of the more and more polar (i.e. the chain-like) self-associates: under the isothermal conditions, that process increases monotonically with increasing the length of the alkyl chain. A weak odd–even effect is observed for low values of n. As is clearly evident from Fig. 8, from the point of view of the orientational processes, the water certainly belongs to the alcohol family. So, the behavior of the dielectric relaxation time, as presented in Fig. 1b, is not accidental. The behavior of the dielectric relaxation time is consistent with the dipolar orientational picture seen at the low frequencies of the probing electric field.
Thus, our studies reveal the following singularity in the dielectric properties of water: its static permittivity does not fit to the permittivities of alcohols (Fig. 5), while the dipolar orientational effects in water, which give a decisive contribution to the permittivity, behave consistently with alcohols (Fig. 8). The understanding of that apparent contradiction can lead through the assumption of an exceptionally high atomic polarizability of water. It is probably the only assumption which can be physically justified. The deformational polarizabilities are induced in the direction of an applied electric field, and thus, are not involved in the ordering process, but, of course, they make a contribution to the static permittivity of liquids. The contribution of the atomic polarizability to the total deformational polarizability can be roughly estimated taking into account the experimental values of nD2, which represent the electronic polarizability, and ε∞, which represents the total deformation polarizability (atomic + electronic). As depicted in Fig. 6, the high-frequency permittivity of water is about twice as large as the square of the refractive index, ε∞ ≈ 2nD2, i.e. the atomic polarizability is more or less equal to the electronic polarizability. In “normal” liquids, the atomic polarizability amounts only to about 10% of the electronic polarizability.
Our experiment enabled one to separate the share of the permanent and induced dipoles in the equilibrium permittivity of water. This result can have an impact on the assumptions made for the computer simulations of the physical properties of water, in particular of its permittivity. Because the molecular simulations for water are being developed for nearly half a century and the number of papers published on this topic is impressive, we will limit ourselves here to one remark. The intermolecular potentials which are commonly used for water involve rigid structures. As was mentioned above, such simulations often lead to a water static permittivity value of about 66. The convergence of that value with the permittivity extrapolated from the homologous series of alcohols, marked as an asterisk in Fig. 5b, appears to be not accidental.
A part of the simulations which takes into account the broad range of the effects of deformational polarizability of water,25,26,29 leads to results much more approximate to the experimental values and concerns not only the permittivity but also other basic physical properties of water. Such simulations consume, however, much more computing time. The results presented in this work seem to prove that it is worth paying attention and devoting a long period of time to learn the secrets of the most important liquid.
4 Conclusions
There is no clear answer to the question posed in the title of this paper. It was, however, to be expected, given the complexity and uniqueness of water. However, failure of water with respect to some rules prescribed by the alcohols, helped us to realize something very important. Namely, the discrepancy between the permittivity of water and alcohols, on the one hand, and the consistency in the dipolar orientation effects occurring in the both systems, on the other hand, revealed an anomalously high polarizability of water as the main cause of the (too) high value of its permittivity.In addition, the presented studies have demonstrated that among the self-assemblies formed in water, certainly of a great diversity, the predominant entities are the hydrogen-bonded chain-like polar structures which undergo ordering by an external electric field, reducing in that manner the entropy of the liquid. The finding has resulted from the analysis of behavior of the static permittivity of hydroxyl coumpounds which has been precisely measured at different temperatures. Temperature evolution of the derivative dεS/dT quite clearly indicates that in liquid water the averaged structures are the polar (thus elongated) intermolecular entities.
References
- P. Ball, H2O: A Biography of Water, Phoenix Press, London, 2000 Search PubMed.
- J. Russo and H. Tanaka, Nat. Commun., 2014, 5, 3556 CrossRef PubMed.
- C. Fishman, The Big Thirst: The Secret Life and Turbulent Future of Water, Free Press, 2012 Search PubMed.
- Å. U. Burman and K. H. U. Ström, J. Chem. Eng. Data, 2008, 53, 2307–2310 CrossRef.
- J. Ortega, J. Chem. Eng. Data, 1982, 27, 312–317 CrossRef CAS.
- J. Barthel, K. Bachhuber, R. Buchner and H. Hetzenauer, Chem. Phys. Lett., 1990, 165, 369–373 CrossRef CAS.
- T. Shinomiya, Bull. Chem. Soc. Jpn., 1989, 62, 908–914 CrossRef CAS.
- Y. Dutuit, J. L. Salefran, A. M. Bottreau, R. Chahine and T. K. Bose, Adv. Mol. Relax. Processes, 1982, 23, 75–95 CrossRef CAS.
- V. Raicu and Y. Feldman, Dielectric Relaxation in Biological System, Physical Principles, Methods and Applications, Oxford University Press, 2015 Search PubMed.
- J. C. Dore and J. Teixeira, Hydrogen-Bonded Liquids, Kluwer, Dordrecht, 1991 Search PubMed.
- T. Fukasawa, T. Sato, J. Watanabe, J. Hama, W. Kunz and R. Buchner, Phys. Rev. Lett., 2005, 95, 197802 CrossRef PubMed.
- I. Popov, P. B. Ishai, A. Khamzin and Y. Feldman, Phys. Chem. Chem. Phys., 2016, 18, 13941–13953 RSC.
- N. Q. Vinh, M. S. Sherwin, S. J. Allen, D. K. George, A. J. Rahmani and K. W. Plaxco, J. Chem. Phys., 2015, 142, 164502 CrossRef CAS PubMed.
- C. Rønne, P.-O. Åstrand and S. R. Keiding, Phys. Rev. Lett., 1999, 82, 2888–2891 CrossRef.
- B. González, N. Calvar, E. Gómez and A. Domínguez, J. Chem. Thermodyn., 2007, 39, 1578–1588 CrossRef.
- M. I. Aralaguppi, C. V. Jadar and T. M. Aminabhavi, J. Chem. Eng. Data, 1999, 44, 216–221 CrossRef CAS.
- B. Cabane and R. Vuilleumier, C. R. Geosci., 2005, 337, 159–171 CrossRef CAS.
- J. Teixeira, A. Luzar and S. Longeville, J. Phys.: Condens. Matter, 2006, 18, S2353–S2362 CrossRef CAS.
- J. Swenson and J. Teixeira, J. Chem. Phys., 2010, 132, 014508 CrossRef PubMed.
- A. Nilsson and L. G. M. Pettersson, Nat. Commun., 2015, 6, 8998 CrossRef CAS PubMed.
- Ph. Wernet, D. Nordlund, U. Bergmann, M. Cavalleri, M. Odelius, H. Ogasawara, L. Å. Näslund, T. K. Hirsch, L. Ojamäe, P. Glatzel, L. G. M. Pettersson and A. Nilsson, Science, 2004, 304, 995–999 CrossRef CAS PubMed.
- A. K. Soper, Pure Appl. Chem., 2010, 82, 1855–1867 CrossRef CAS.
- G. Raabe and R. J. Sadus, J. Chem. Phys., 2011, 134, 234501 CrossRef PubMed.
- M. Sprik and M. L. Klein, J. Chem. Phys., 1988, 89, 7556–7560 CrossRef CAS.
- I. M. Svishchev and T. M. Hayward, J. Chem. Phys., 1999, 111, 9034–9038 CrossRef CAS.
- G. Lamoureux, E. Harder, I. V. Vorobyov, B. Roux and A. D. MacKerell Jr., Chem. Phys. Lett., 2006, 418, 245–249 CrossRef CAS.
- J. Li, Z. Zhou and R. J. Sadus, J. Chem. Phys., 2007, 127, 154509 CrossRef PubMed.
- P. Paricaud, M. M. Predota, A. A. Chialvo and P. T. Cummings, J. Chem. Phys., 2005, 122, 244511 CrossRef PubMed.
- I. M. Svishchev, P. G. Kusalik, J. Wang and R. J. Boyd, J. Chem. Phys., 1996, 105, 4742–4750 CrossRef.
- S. Riniker, A.-P. E. Kunz and W. F. Van Gunsteren, J. Chem. Theory Comput., 2011, 7, 1469–1475 CrossRef CAS PubMed.
- G. A. Cisneros, K. T. Wikfeldt, L. Ojamäe, J. Lu, Y. Xu, H. Torabifard, A. P. Bartók, G. Csányi, V. Molinero and F. Paesani, Chem. Rev., 2016, 116, 7501–7528 CrossRef CAS PubMed.
- H. J. Strauch and P. T. Cummings, Mol. Simul., 1989, 2, 89–104 CrossRef.
- H. Fröhlich, Theory of Dielectrics, Clarendon Press, Oxford, 2nd edn, 1958 Search PubMed.
- J. Świergiel and J. Jadżyn, J. Chem. Eng. Data, 2012, 57, 2271–2274 CrossRef.
- J. G. Kirkwood, J. Chem. Phys., 1939, 7, 911–919 CrossRef CAS.
- C. J. F. Böttcher and P. Bordewijk, Theory of Electric Polarization: Dielectric in Time-Dependent Fields, Elsevier, Amsterdam, 1992 Search PubMed.
- J. Świergiel, I. Płowaś and J. Jadżyn, J. Mol. Liq., 2016, 220, 879–882 CrossRef.
- T. Sato and R. Buchner, J. Phys. Chem. A, 2004, 108, 5007–5015 CrossRef CAS.
- U. Kaatze and V. Uhlendorf, Z. Phys. Chem. Neue Fol., 1981, 126, 151–156 CrossRef CAS.
- C.-P. Lin, G.-H. Lai and C.-H. Tu, J. Chem. Eng. Data, 2013, 58, 3265–3274 CrossRef CAS.
- J. Jadżyn, G. Czechowski, C. Legrand and R. Douali, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 041705 CrossRef PubMed.
- J. Jadżyn and G. Czechowski, J. Phys. Chem. B, 2007, 111, 3727–3729 CrossRef PubMed.
- J. Jadżyn, U. Sokołowska and J.-L. Déjardin, J. Phys. Chem. B, 2007, 112, 9050–9052 CrossRef PubMed.
- J. Świergiel, J. Jadżyn and L. Bouteiller, J. Phys. Chem. B, 2010, 114, 737–741 CrossRef PubMed.
- G. P. Johari, J. Chem. Phys., 2016, 145, 164502 CrossRef CAS PubMed.
- R. Becker, Electromagnetic fields and interactions, Blackie and Son, London, 1964 Search PubMed.
- L. D. Landau, E. M. Lifshitz and L. P. Pitaevskii, Electrodynamics of continuous media, Pergamon Press, Oxford, 2nd edn, 1984 Search PubMed.
- B. K. P. Scaife, Principles of Dielectrics, Clarendon Press, Oxford, 1998 Search PubMed.
- J. Świergiel and J. Jadżyn, Phys. Chem. Chem. Phys., 2011, 13, 3911–3916 RSC.
| This journal is © the Owner Societies 2017 |



