Open Access Article
Open Access ArticleThe role of thermodynamic stability in the characteristics of the devitrification front of vapour-deposited glasses of toluene
Joan
Ràfols-Ribé
 ,
Marta
Gonzalez-Silveira
,
Marta
Gonzalez-Silveira
 *,
Cristian
Rodríguez-Tinoco†
*,
Cristian
Rodríguez-Tinoco†
 and
Javier
Rodríguez-Viejo
*
and
Javier
Rodríguez-Viejo
*
Grup de Nanomaterials i Microsistemes, Physics Department, Universtitat Autònoma de Barcelona, 08193 Bellaterra, Spain. E-mail: marta.gonzalez@uab.cat; javier.rodriguez@uab.cat
First published on 3rd April 2017
Abstract
Physical vapour deposition (PVD) has settled in as an alternative method to prepare glasses with significantly enhanced properties, providing new insights into the understanding of glass transition. One of the striking properties of some PVD glasses is their transformation into liquid via a heterogeneous mechanism that initiates at surfaces/interfaces. Here, we use membrane-based fast-scanning nanocalorimetry (104 K s−1) to analyse the variables that govern the transformation mechanism of vapour-deposited toluene glasses with different stabilities. Thin films ranging from 20 to 250 nm were prepared at deposition temperatures between 0.70 and 1.15 times the glass transition temperature. We show how a propagating growth front is the initial transformation mechanism in all the vapour deposited samples, revealing a clear tendency to faster front velocities for less stable samples. Contrary to other glass-formers such as indomethacin, toluene shows a one-to-one relationship between limiting fictive temperature and front velocity. We associate this behaviour with the much simpler molecular geometry of toluene, which would prevent the presence of strong preferential molecular arrangements in the glass. However, the propagation distance of the growth front before the homogenous transformation mechanism dominates the transition is found to be dependent on the preparation conditions rather than on the thermal stability of the glass. Understanding the link between the growth variables and the properties of PVD glasses is crucial for finding and developing potential applications of this type of glass.
Introduction
The discovery of highly stable glasses in 20071,2 offered new insights into the field of glasses. Prepared by physical vapour deposition, some properties of these glasses can be easily tuned by changing the substrate temperature and the deposition rate. When the substrate temperature is around 0.85 times the glass transition temperature (Tg), the produced glasses, also named as ultrastable glasses (UG), exhibit enhanced properties, such as low enthalpy,3–5 high kinetic stability,5,6 low heat capacities6,7 or high density.8,9 Apparently, at this particular substrate temperature and at low deposition rates, when molecules reach the substrate they become part of a mobile surface layer having time to explore their best configuration state before getting buried by the following ones.2,3,10 By changing either deposition rate or substrate temperature, the molecules are trapped in higher energy configurations, producing less stable glasses.11,12Another striking property that vapour deposited glasses exhibit is a heterogeneous transformation mechanism into the supercooled liquid state,13–17 at least for the first stages of the transformation, in contrast to the homogeneous transformation observed in glasses prepared by quenching the liquid. It has been proposed that, in ultrastable glasses, the molecules are so tightly packed that the transformation begins where the mobility is higher, i.e. at surfaces and/or interfaces.10,18 This phenomenon was already predicted by random first order transition (RFOT) theory,19,20 facilitated kinetic Ising model calculations21,22 and vapour deposition simulations.23 Experimentally, this phenomenon has also been observed using a variety of techniques in several systems, e.g. secondary mass ion spectroscopy (SIMS),13,24 ellipsometry,25 AC-calorimetry,6,26 differential scanning calorimetry17 and fast-scanning nanocalorimetry.17,27 Both theory and experiments show a direct relation between the growth front velocity and the mobility of the supercooled liquid.17,20,28 Experimental studies found that this velocity depends on the inverse of the relaxation time of the liquid to a power that is slightly below one.24 Recently, it was shown using fast-scanning nanocalorimetry that the same relationship holds across a very wide temperature range, from Tg up to 75 K above Tg, corresponding to 12 orders of magnitude in relaxation time in the case of indomethacin (IMC).17
One of the advantages of physical vapour deposition is the possibility of tailoring the stability of the produced glass by tuning the deposition conditions. It was recently observed that not only highly stable glasses transform via a heterogeneous mechanism, but, in general, vapor-deposited glasses with lower stability also start the transformation process via a growth front.25,27,28 Walters et al.28 and Dalal et al.25 measured respectively the front velocity of glasses of TPD and IMC with different stabilities by ellipsometry close to ambient temperature. Rodríguez-Tinoco et al. used fast-scanning nanocalorimetry to measure the growth front velocity of IMC glasses spanning a broad range of stabilities.27 It was found that the velocity at which the front propagates in glasses of different stabilities, including the ultrastable glass, had the same temperature dependence. However, the absolute value of the growth front velocity depends on the stability of the glass. This result was in contrast with both RFOT and pinning models, which foresee a strong temperature dependence of the growth front velocity but a small influence of the stability,19,29 determined in our case by the deposition temperature.
The thermodynamic stability of a glass is typically quantified by means of the limiting fictive temperature, calculated by integration of the specific heat curve.30 Several studies have reached the conclusion, though, that this parameter does not univocally determine some properties of the glass.31 In this context, we established in a previous work27 that the growth front velocity of a transforming glass of IMC could not be determined considering only its limiting fictive temperature, but two different dependences arose, depending on whether the glass was deposited above or below 0.85Tg. According to previous studies,8,32,33 IMC vapour deposited glasses exhibit certain molecular anisotropy that depends on the deposition conditions. From the correlation between growth front velocity and molecular anisotropy in IMC glassy films, it was inferred that the arrangement of the molecules in the glass can also play a role in the transformation velocity. Since this behaviour may depend on the size and structural symmetry of the molecule it is necessary to analyse other molecules before general conclusions can be established. Yokoyama showed that molecular orientation in organic glasses is directly related to the shape of the molecules;34 more planar or linear molecules tend to align parallel to the substrate under certain deposition conditions, while more bulky or compact molecules tend to have random orientation producing more isotropic glasses. Depending on the deposition temperature, molecules can also tend to align perpendicular to the substrate, as was shown for different organic molecules by Ediger and co-workers.9,32 According to Yokoyama's classification, toluene is a compact molecule with a low aspect ratio, so less preferred orientation of the molecules as a function of substrate temperature is expected. However, Ishii et al. found a small anisotropic peak in the WAXS data obtained for stable glasses of toluene.35 Quantum chemical calculations performed by the same authors36 indicate that some molecular arrangements are more energetically favourable, in accordance with the WAXS results. Fukusawa et al.37 suggested that vapour deposited glasses of ethylbenzene, a very similar molecule to toluene, obtained at temperatures close to Tg were densely packed due to the formation of certain dimers, as would happen with toluene. However, according to Yokoyama's classification the molecular packing anisotropy of a toluene glassy film, if any, should be small.
There is the remaining question whether anisotropy has any relation with the ability to form stable glasses. In this regard, Dawson et al.38 showed that it is possible to obtain ultrastable glasses from molecules that do not present anisotropy when deposited as thin films and, more recently, Chua et al.39 proved how completely symmetrical molecules can also form ultrastable glasses. Another example can be found in toluene if we assume that anisotropy is expected to be small in thin film glasses of this molecule. Previous reports have already shown that it is possible to grow toluene glasses of different stabilities from the vapour phase by tuning either the substrate temperature5,6,40–43 or the deposition rate.6,43 Although there is no complete agreement between different studies on the optimum deposition temperature, in all cases there is a clear increase of the stability,5,6 the density42 or even the quality41 of the glass for deposition temperatures between 0.80Tg and 0.94Tg, with Tg = 117 K being the glass transition temperature of a conventional glass of toluene.44
In this work, we show that the first stage of the transformation of vapour-deposited toluene glasses into the liquid state is heterogeneous and occurs via a parallel growth front. The velocity of this front has a clear dependence on the relaxation time of the corresponding super cooled liquid at that temperature. These results agree with previous findings for toluene at lower measuring temperatures and for other organic molecules. However, in contrast to earlier papers that focused on anisotropic molecules we show that the growth front velocity for vapour-deposited toluene glasses correlates well with the limiting fictive temperature of the glass, which in turn is determined by the deposition temperature. By comparison to previous data we infer that this behaviour could be related to a lower degree of molecular packing anisotropy in toluene glasses. Finally, the cross-over length, the transformed thickness achieved by the front before the homogeneous transformation starts, is measured and discussed in relation to the deposition and fictive temperature. While we see a one-to-one correlation between growth front velocity and limiting fictive temperature, there are remarkable differences in the cross-over length depending on the preparation conditions of the glasses.
Experimental method
Anhydrous toluene (purity 99.8%) dried over molecular sieves and packaged under an argon atmosphere was purchased from Cymit Quimica and placed in a Pyrex container which was afterwards connected to a high vacuum pre-chamber. Extra purification of the source material was achieved by applying several sequences of freeze–pump–thaw cycles. Samples were grown in an UHV chamber under a base pressure of 5 × 10−9 mbar using a high-precision leak valve to control the vapour flow from the pre-chamber. Vapour was injected through a copper pipe connected to the leak valve. The deposition rate was monitored using a quartz microbalance located near the sample. A liquid nitrogen cold trap was installed both to improve the vacuum quality and to cool down the sample holder and the quartz microbalance.Thin films of toluene, with thicknesses ranging from 20 to 250 nm, were grown at 0.32 ± 0.02 nm s−1 and measured in situ by means of quasi-adiabatic nanocalorimetry in differential mode. This technique uses membrane-based microcalorimeters and high heating rates (2.7–3.5 × 104 K s−1, for this work) achieving high sensitivities.45,46 Voltage raw data were converted into heat capacity curves following the procedure explained elsewhere.47 A 100 nm aluminium plate was evaporated on the sensing area of the device in order to obtain a homogeneous thermal profile across the sample.48
Thin film glasses of different stabilities were prepared by changing the substrate temperature (Td) between 82 K and 135 K. The deposition temperature was determined by supplying a specific constant intensity to the microcalorimeter. The sample mass was calculated by dividing the heat capacity in the supercooled liquid range by the specific heat capacity data of liquid toluene reported in the literature by Yamamuro et al.44
After performing a temperature scan of the as-deposited sample, a low stability glass was created by passive cooling of the supercooled liquid at ca. 500 K s−1. We denote this glass as fast-cooled (FC) and, since it is a reversible process, heat capacity curves of this type of glass are the result of the averaging of multiple scans.
Results and discussion
Determination of the transformation mechanism
We have measured the heat capacity of thin layers of toluene glass, ranging from 20 nm to 250 nm, by means of quasi-adiabatic fast-scanning nanocalorimetry.45 The samples have been deposited at substrate temperatures between 82 and 135 K, corresponding respectively to 0.70Tg and 1.15Tg, with Tg = 117 K being the glass transition temperature of a conventional glass of toluene.44 Specific heat curves of the samples deposited at 82.6 K, 104.0 K, 133.8 K and after passive cooling of the liquid (FC) have been obtained by dividing the heat capacity curves by the corresponding mass (left panels in Fig. 1). As previously observed for indomethacin thin film glasses,17,27 when using this type of representation, the onset temperature of the glass transition shifts depending on the thickness of the film for the as-deposited vapour deposited films, while in the case of the fast-cooled glass there is no observable shift. In the case of indomethacin, this behaviour was shown to be related to the transformation mechanism.17 The specific heat curves of samples transforming via a homogenous bulk mechanism show a complete overlap regardless of their thickness, as in the case of the fast-cooled glass. On the other hand, if the glass transition is not a homogeneous process, mass normalization yields curves with different onset temperatures. Previous experimental reports on other organic glasses have shown that some vapour deposited glasses transform into the supercooled liquid following a parallel growth front that starts in the regions of faster mobility, mainly the surface and the interface with the substrate.13,14,16,17,24 An ad hoc normalization procedure of the heat capacity curves that considers the surface of the sample allows the identification of this transformation mechanism. This normalization procedure has been explained elsewhere.17 Briefly, it consists on separating the different contributions of the experimental heat capacity: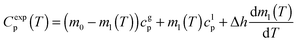 | (1) |
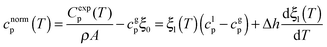 | (2) |
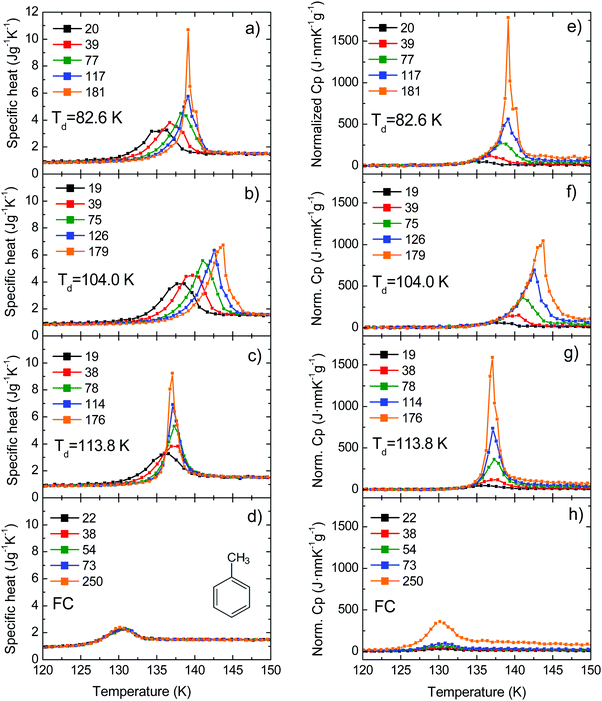 | ||
| Fig. 1 (left panels) Specific heat curves for films obtained at different deposition temperatures: (a) 82.6 K (0.70Tg), (b) 104.0 (0.89Tg) K and (c) 113.8 (0.97Tg); and (d) after fast cooling the super-cooled liquid. (right panels) Curves obtained by normalizing the same heat capacity data using eqn (2). The legend indicates the thickness of the films in nm. Panel (d) shows a schematic representation of the toluene molecule. | ||
Right panels in Fig. 1 show the resulting curves after applying the normalization presented in eqn (2). In the case of a heterogeneous transformation mechanism consisting of parallel fronts that advance at a constant rate, i.e. independent of the thickness of the film, the onset of the normalized curves should collapse while this mechanism is dominating the transformation. This is clearly the case for samples deposited at 104 K (Fig. 1f), where the onset of all the curves collapse into a single onset irrespectively of their thicknesses. If the sample is thick enough, during the progression of the front the homogeneous transformation is triggered and this normalization procedure is no longer valid. This is the case of samples deposited at 82.6 K and 113.8 K (Fig. 1e and g respectively) for which the onsets of the normalized curves overlap up to a certain temperature. Above that temperature, the bulk transformation is triggered and the front normalization procedure starts to underestimate the transformed fraction, which, in the case of homogeneous bulk processes, depends on the total mass of the sample. This combined heterogeneous and homogeneous transformation mechanism has been observed experimentally for IMC,26 TNB49 and methyl-m-toluate,11,16 but has also been predicted by simulations based on facilitated kinetic Ising models21,22 and random pinning models.29
Effect of liquid mobility on the transformation rate
As mentioned above, if the transformation of the samples takes place via a parallel growth front the ad hoc normalization procedure presented in eqn (2) yields heat capacity curves that overlap independently of their thickness. Solving the proposed differential equation for ξl(T) using the experimental data, the growth front velocity can be calculated as a function of temperature as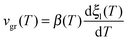 | (3) |
Previous studies have shown that the transformation rate is mainly driven by the mobility of the adjacent newly formed liquid layer.17,24 Specifically, for many organic glasses it has been found that the transformation rate follows a relation with τα, the relaxation time of the supercooled liquid:11
| vgr = Cτα−γ | (4) |
In Fig. 2a we can see a log–log representation of the front velocity versus the relaxation time of liquid toluene for samples deposited at different substrate temperatures. We have used the relaxation time of the liquid derived by Hatase,50 which follows a VFT relationship, τ = τ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(DT0/(T − T0)), with DT0 = 434 K, T0 = 104 K and τ0 = 6.3 × 10−13 s. We see that in this representation of the data, all the stabilities can be fitted by parallel straight lines with a common slope of −0.92 ± 0.06 and a factor C that depends on the deposition conditions. The exponent γ is similar in different organic compounds,11,16 indicating that the dependence of the growth front velocity on the liquid relaxation time is nearly independent of the molecular nature of the forming material. Still, toluene and ethylbenzene show the values of γ closest to one. An interesting experiment would be checking whether other small and/or symmetric molecules show the same trend.
exp(DT0/(T − T0)), with DT0 = 434 K, T0 = 104 K and τ0 = 6.3 × 10−13 s. We see that in this representation of the data, all the stabilities can be fitted by parallel straight lines with a common slope of −0.92 ± 0.06 and a factor C that depends on the deposition conditions. The exponent γ is similar in different organic compounds,11,16 indicating that the dependence of the growth front velocity on the liquid relaxation time is nearly independent of the molecular nature of the forming material. Still, toluene and ethylbenzene show the values of γ closest to one. An interesting experiment would be checking whether other small and/or symmetric molecules show the same trend.
 | ||
| Fig. 2 (a) Logarithm of the growth front velocity corresponding to the samples grown at the indicated deposition temperatures versus the logarithm of the relaxation time of the supercooled liquid, which has been calculated using the VFT equation with the values given by Hatase et al.50 The lines are fits of the expression vgr = Cτ−γ considering the exponent as a common fit parameter. (b) Logarithm of the front velocity as a function of temperature for the samples deposited at 104.2 and 110.4 K and at a deposition rate of 0.35 nm s−1. Dashed green and red lines correspond to the fit of the data shown in panel (a) extended to lower temperatures. Star symbols correspond to data obtained by Ahrenberg et al.6 by means of AC-calorimetry at low temperatures. Ahrenberg's films were grown at 2 nm s−1 and at a deposition temperature of 105 K. The grey continuous line is a representation of the expression vgr = Cτ−γ using gamma = 0.92 and a prefactor C that fits both our 104.2 and 110.4 K data and the 105 K data from Ahrenberg et al.,6 using a line width of around ±13%. The inset shows the same data but as a function of the relaxation time of the liquid. | ||
The high heating rates imposed during the measurement of the heat capacity of the system when using fast-scanning nanocalorimetry permit to push the transition towards much higher temperature values, accessing the properties of the system in a temperature range unreachable by using conventional techniques. In order to check whether this relation between growth front and relaxation time of the liquid holds for an extended range of temperatures also in the case of toluene, we incorporate in Fig. 2b the data obtained by Ahrenberg et al.6 using AC-nanocalorimetry for glasses of toluene deposited at 105 K. Their data correspond to their most stable glass, deposited at 2 nm s−1 and 105 K. Our samples, on the other hand, were prepared at 0.35 nm s−1. However, according to previous work this change in the deposition rate should not represent a major change in the stability of toluene thin film glasses.5,6 We therefore assume that the characteristics of their glass will lie in between the ones we deposited at 104.2 K and 110.4 K. We also plot in Fig. 2b a representation of the function vgr = Cτ−γ using gamma = 0.92 and a prefactor C that fits both our 104.2 and 110.4 K data and the 105 K data from Ahrenberg et al.6 within a tolerance of ±13%. Considering this uncertainty, we can see a good match of our high temperature data and Ahrenberg's low temperature data, spanning the relationship between liquid relaxation time and front velocity up to Tg + 25 K, equivalent to 8 orders of magnitude in relaxation time. Still, our technique cannot distinguish between the existence of one or two fronts, coming from the surface and the interface with the substrate, and thus, our growth rate values can differ up to a factor 2 when compared with those obtained by other techniques which can distinguish the evolution of single fronts.13 Our front velocities are comparable to previous fast scanning calorimetry measurements from Bhattacharya et al.43 on toluene thin films. Although they deposit at a higher temperature (112 K) than our most stable glass and at much faster rates (15 nm s−1), the velocities they measure for films thinner than 250 nm are of the same order of magnitude than ours, although their data do not follow the same linear relation in the log–log plot of Fig. 2a.
Effect of glass properties on the transformation rate
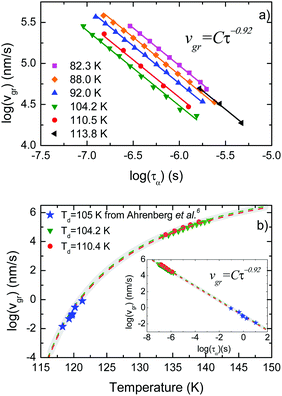
In Fig. 3a we present data on the limiting fictive temperature of toluene vapour deposited glasses as a function of deposition temperature. The values of limiting fictive temperature have been obtained from the intersection of the enthalpy curves of supercooled liquid and glass.30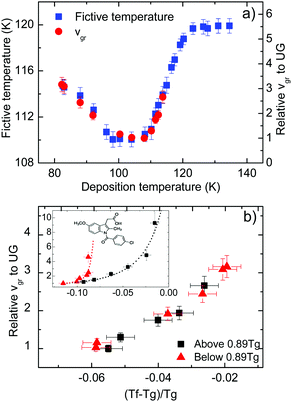 | ||
| Fig. 3 (a) Limiting fictive temperature (left axis, squares) and growth front velocity expressed relative to the slowest value (corresponding to Td = 108 K in this case, right axis, circles) as a function of deposition temperature. (b) Growth front velocity relative to the slowest value as a function of the difference between fictive temperature and glass transition temperature normalized by Tg, that is (Tf − Tg)/Tg. The different symbols indicate if the glasses have been grown at a deposition temperature above (squares) or below (triangles) 0.89Tg. Inset: Equivalent representation for indomethacin data, adapted from Rodríguez-Tinoco et al.27 | ||
Fig. 3a also shows the velocity of the growth front relative to the slowest velocity, corresponding to the glasses deposited at 108 K. Using the appropriate scale factor, we can see good agreement between limiting fictive temperature, i.e. thermodynamic stability, and front velocity. In a previous report on indomethacin vapour deposited glasses27 we showed that there was no one-to-one relation between front velocity and limiting fictive temperature. We observed that two branches emerged when considering the dependence between these two magnitudes for glasses deposited below and above the temperature producing the maximum stability (inset in Fig. 3b). In fact, for equal limiting fictive temperature (287.0 K ± 0.5 K), the samples deposited below 0.89Tg presented higher velocities, up to a factor 3.5.27 We show in Fig. 3b an equivalent representation for toluene. In this figure, we can see that there is no significant difference in the growth front velocity when depositing below and above 0.89Tg, and that the transformation rate appears to mostly depend on the limiting fictive temperature of the glass.
We note that the range of deposition temperatures is different for both systems. The lowest deposition temperature for toluene in this study was 0.70Tg, while in the case of IMC we reached 0.63Tg and, in fact, the IMC glass showing the largest divergence in growth front velocities was deposited at this temperature. However, as can be seen in Fig. 3b (main figure and inset) the behaviour of the two molecular glasses is clearly different. In the case of toluene, films grown at low Td have limiting fictive temperatures closer to Tg and show similar growth front velocities to those grown above Tg with identical Tf′. In addition, preliminary measurements of the growth front velocity on other long-shaped molecules (not shown here) confirm the appearance of two well-defined branches supporting the trend observed in Fig. 3b.
In the aforementioned study on indomethacin glasses, we associated the difference between the two branches with the orientation of the molecules, based on birefringence measurements by Dalal et al.8 Apparently, the more oriented were the molecules, the faster was the transformation front. Walters et al. also showed that vapor-deposited glasses of TPD with the same density but deposited above and below 0.85Tg transformed at different rates.28 It should be emphasized that TPD is a highly anisotropic molecule and the molecular alignment in these glasses also depend on the deposition temperature. If molecular orientation plays a role in the velocity of the front, the absence or a small contribution of anisotropy would result in a transformation rate that would only depend on the stability of the glass, which is indeed what we can see in Fig. 3b for toluene. WAXS measurements by Ishii et al.35 on toluene glasses deposited at 0.89Tg show a small anisotropic peak, which they associate with the formation of certain dimers more energetically favourable. However, the presence of these dimers does not imply necessarily that toluene molecules tend to align with a preferred orientation when deposited at different temperatures. According to previous work from Yokoyama et al.,34 small or no preferred orientation should be expected from a small molecule such as toluene. Therefore, we rationalize our finding that the growth front velocity is mainly determined by the fictive temperature as an indication that toluene films exhibit a lower degree of molecular ordering that should be manifested in a smaller change of the birefringence or order parameter as the deposition temperature is changed in the vicinity of Tg.
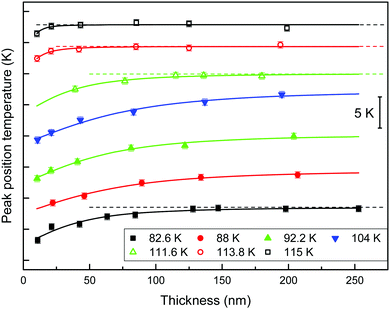
Effect of glass properties on the cross-over length
We define the cross-over length, ξco, as the distance travelled by the front before the homogeneous mechanism dominates the transformation. This distance can be inferred from the specific heat curves. When the film is thick enough, the glass transition simultaneously occurs in the whole volume of the sample, and therefore the transformed fraction is proportional to the total mass. In this way, if glasses are thicker than the cross-over length, the mass normalized specific heat curves show a temperature value of the maximum of the glass transition peak that remains constant, independent of their thickness. We therefore infer the cross-over length by representing the position of the maximum of the glass transition peak as a function of the thickness of the films. While there is a temperature shift of the peak position, the heterogeneous mechanism will still have a significant impact on the transformation. Fig. 4 shows the position of the maximum of the glass transition peak as a function of the thickness of the films for glasses grown at different deposition temperatures. The curves have been vertically shifted for clarity. To facilitate the interpretation of the results we have plotted the glasses with similar fictive temperature with the same symbol and colour. Data from glasses deposited above 0.89Tg are plotted using void symbols and we have used filled symbols for glasses deposited below 0.89Tg. Irrespective of the deposition temperature the position of the glass transition peak shifts to higher temperatures as thickness increases and tends to stabilize at a certain thickness when bulk transformation sets in. As a guide to the eye, the different data sets from Fig. 4 have been fitted with the same function. We can use the derivative of this function to provide a rough estimation of the cross-over length. Considering the asymptotic nature of the function, we have defined the cross-over length as the thickness at which the derivative of the function is equal to 0.002 K nm−1, i.e. when the change in the position of the glass transition peak is equal to 0.2%. Table 1 presents the calculated values of cross-over length together with the corresponding deposition and limiting fictive temperatures.| T d (K) | 82.6 | 88.0 | 92.2 | 104.0 | 110.8 | 111.6 | 112.6 | 113.8 | 115.0 |
| T f′ (K) | 114.7 | 113.8 | 112.6 | 110.0 | 110.9 | 112.3 | 113.0 | 113.9 | 114.8 |
| ξ co (nm) | 200 ± 30 | >200 | >200 | >200 | 200 ± 30 | 200 ± 30 | 115 ± 30 | 77 ± 30 | 53 ± 20 |
The first conclusion that one can extract from the figure is that the cross-over length strongly depends on the deposition temperature. Glasses deposited between 0.75 and 0.90Tg, in agreement with the range of deposition temperatures for maximum stability,5,6,40 achieve thicker cross-over lengths. For higher and lower deposition temperatures, the homogeneous transformation mechanism starts at lower temperatures, dominating the transformation before the front has travelled a longer distance. In a previous study, Bhattacharya et al. found that stable toluene glasses transformed via a front mechanism up to thicknesses of around 2 μm.43 With our technique, we are limited in film thickness, so it is not possible for us to determine the cross-over length maximum for stable glasses.
Even though we do not see variations in the growth front velocity between glasses grown at different deposition temperatures but encoded with the same limiting fictive temperature, we do observe remarkable changes in their cross-over lengths. The cross-over length depends on the velocity of the front but also on the dynamics of the transformation mechanism in the remaining volume of glass.22,29 If the front velocity is univocally determined by Tf′, as our data in Fig. 3b suggest, but the cross-over length is not, then the homogeneous transformation will not be determined by Tf′ alone. In particular, glasses deposited at 115.0 K and 82.6 K having Tf′ = (114.7 ± 0.5) K transform via a heterogeneous mechanism up to ca. 50 nm and 200 nm, respectively, while having similar front velocities. Since, as we have defined it, the cross-over length represents the length that the front propagates before the bulk transformation dominates, the variation of cross-over length can be related to a change in the onset temperature of the bulk glass. It is important to emphasize that the limiting fictive temperature provides information on the average thermodynamic stability of the glass and it has been previously shown for IMC glasses that Tf′ and density, both of them average magnitudes, show a good correlation.27 The intriguing question is: why two glasses with comparable thermodynamic average stability may show different onset temperatures for the bulk transformation? In the ongoing debate of what happens to the relaxation time below Tg, there are some studies that reveal a two equilibration time scenario.51,52 Cangialosi et al. in a recent study about the enthalpy recovery in polymers aged at low temperatures for long periods of time reported the existence of two relaxation mechanisms. According to these authors, the differences in the formation of the glass would be reflected in their devitrification behaviours. Extrapolating their results, we speculate that it may be the case that glasses deposited well below Tg are densified by a different mechanism compared with those deposited close to Tg, at the equilibrium line. This theory could explain the different devitrification temperatures for glasses with the same limiting fictive temperature but deposited close or far from Tg. Data from Fig. 3a can be further analysed using this new perspective. The dependence of fictive temperature with deposition temperature is clearly different on both sides of the minimum. While close to Tg the dependence is strong, a milder dependence can be observed at lower temperatures. Considering the divergence of relaxation times at temperatures close to T0 (T0 = 104 K for toluene50), a much stronger dependence of the limiting fictive temperature should be expected for glasses deposited below 0.89Tg, unless a different mechanism would dominate the formation of the glass. We are cautious since this interpretation seems to be in contrast with recent results from Zhang et al.,53 which show complete decoupling between surface and bulk dynamics. Enhanced surface mobility with respect to bulk appears to be the origin of the high stability of vapour deposited glasses.10,18 A deeper understanding of the bulk transformation mechanism in stable glasses as a function of the deposition temperature is needed to extract further conclusions.
Thermodynamic stability minimum
As can be seen in Fig. 3a, glasses deposited between 110 K and 120 K have a limiting fictive temperature that coincides with their deposition temperature. In previous work, it was shown that the properties of a glass deposited at substrate temperatures between 0.85Tg and Tg are the expected for the supercooled liquid at that temperature, which would indicate equilibration between glassy and liquid states.8 In general, the lowest temperature of this equilibrium temperature range depends on the deposition rate, i.e. for some molecules slower deposition rates yield a smaller low temperature limit.7 On the other hand, the upper limit of this temperature range is not necessarily the conventional Tg, but it is determined by the cooling rate imposed between the deposition temperature and the measurement temperature. It is possible to obtain glasses which are in equilibrium with the liquid above Tg if the cooling rate is fast enough. Consequently, above this upper temperature limit the stability of the resulting glass will become independent of the deposition temperature. In our case, glasses are grown in the range from 0.7 to 1.15Tg (82 to 130 K) and passively cooled at a rate of ca. 500 K s−1. Cooling from a high temperature liquid at this rate results in a glass with a Tf′ of ca. 120 K. Thus, if the deposition temperature is higher than 120 K, the resulting glass will always have, with this cooling rate, a Tf′ of 120 K regardless of the deposition temperature, as can be seen in Fig. 3a.Conclusions
We have used fast scanning quasi-adiabatic nanocalorimetry to characterize the glass transition in toluene glasses obtained by physical vapour deposition at different substrate temperatures. These vapour deposited glasses transform into the supercooled liquid state via a heterogeneous transformation that starts at the surface/interfaces of the sample. As has been demonstrated for other organic molecules, the propagation velocity of this transformation front is strongly dominated by the mobility of the supercooled liquid molecules. A linear relation holds between the logarithm of the front velocity and the logarithm of the relaxation time of the liquid for an extended temperature range, covering 8 orders of magnitude in the case of toluene. The most thermodynamically stable glasses present the slowest transformation rates. Contrary to previous observations in vapour deposited glasses of indomethacin, where the orientation of the molecules seemed to affect the transformation rate, in the case of toluene the stability of the glass and the mobility of the liquid determine the growth front velocity. Surprisingly, this behaviour is not reproduced for the cross-over length. We see up to a 4-fold change for the cross-over length of glasses with the same thermal stability but prepared at different deposition temperatures. A possible explanation for this behaviour could be the existence of two different mechanisms of glass formation at temperatures close and far from Tg. A thorough analysis of the homogeneous (bulk) glass transition in a large deposition temperature range would be necessary to confirm or refute this hypothesis. Our study suggests a prominent relation between molecular geometry, and therefore anisotropy of the produced glass, and transformation velocity. Further measurements of the growth front velocity as a function of stability for molecules of different shapes would help quantifying this correlation.Acknowledgements
This work was financially supported by the Spanish Ministry of Economy and Competitiveness and the European Regional Development Fund through projects MAT2013-40896-P and MAT2016-79579-R. Joan Ràfols Ribé is also in receipt of a FPU grant from the Spanish Ministry of Education, Culture and Sport. We thank the support in the microfabrication of the calorimeters by Ll. Abad from IMB-CNM-CSIC and the technical assistance of Theo Bijvoets.References
- K. L. Kearns, S. F. Swallen, M. D. Ediger, T. Wu and L. Yu, J. Chem. Phys., 2007, 127, 154702 CrossRef PubMed.
- S. F. Swallen, K. L. Kearns, M. K. Mapes, Y. S. Kim, R. J. McMahon, M. D. Ediger, T. Wu, L. Yu and S. Satija, Science, 2007, 315, 353–356 CrossRef CAS PubMed.
- K. L. Kearns, S. S. F. Swallen and M. D. Ediger, J. Phys. Chem. B, 2008, 112, 4934–4942 CrossRef CAS PubMed.
- S. L. L. M. Ramos, M. Oguni, K. Ishii and H. Nakayama, J. Phys. Chem. B, 2011, 115, 14327–14332 CrossRef CAS PubMed.
- E. Leon-Gutierrez, A. Sepúlveda, G. Garcia, M. T. Clavaguera-Mora and J. Rodríguez-Viejo, Phys. Chem. Chem. Phys., 2010, 12, 14693–14698 RSC.
- M. Ahrenberg, Y. Z. Chua, K. R. Whitaker, H. Huth, M. D. Ediger and C. Schick, J. Chem. Phys., 2013, 138, 24501 CrossRef CAS PubMed.
- Y. Z. Chua, M. Ahrenberg, M. Tylinski, M. D. Ediger and C. Schick, J. Chem. Phys., 2015, 142, 54506 CrossRef CAS PubMed.
- S. S. Dalal, Z. Fakhraai and M. D. Ediger, J. Phys. Chem. B, 2013, 117, 15415–15425 CrossRef CAS PubMed.
- S. S. Dalal, D. M. Walters, I. Lyubimov, J. J. de Pablo and M. D. Ediger, Proc. Natl. Acad. Sci. U. S. A., 2015, 201421042 Search PubMed.
- L. Zhu, C. W. Brian, S. F. Swallen, P. T. Straus, M. D. Ediger and L. Yu, Phys. Rev. Lett., 2011, 106, 256103 CrossRef CAS PubMed.
- M. Tylinski, A. Sepúlveda, D. M. Walters, Y. Z. Chua, C. Schick and M. D. Ediger, J. Chem. Phys., 2015, 143, 244509 CrossRef CAS PubMed.
- K. Ishii, H. Nakayama, T. Okamura, M. Yamamoto and T. Hosokawa, J. Phys. Chem. B, 2003, 107, 876–881 CrossRef CAS.
- S. F. Swallen, K. Traynor, R. J. McMahon and M. D. Ediger, Phys. Rev. Lett., 2009, 102, 65503 CrossRef PubMed.
- A. Sepúlveda, S. F. Swallen and M. D. Ediger, J. Chem. Phys., 2013, 138, 12A517 CrossRef PubMed.
- A. Sepúlveda, E. Leon-Gutierrez, M. Gonzalez-Silveira, M. T. Clavaguera-Mora and J. Rodríguez-Viejo, J. Phys. Chem. Lett., 2012, 3, 919–923 CrossRef PubMed.
- A. Sepúlveda, M. Tylinski, A. Guiseppi-Elie, R. Richert and M. D. Ediger, Phys. Rev. Lett., 2014, 113, 45901 CrossRef PubMed.
- C. Rodríguez-Tinoco, M. Gonzalez-Silveira, J. Ràfols-Ribé, A. F. Lopeandía, M. T. Clavaguera-Mora and J. Rodríguez-Viejo, J. Phys. Chem. B, 2014, 118, 10795–10801 CrossRef PubMed.
- S. S. Dalal, A. Sepúlveda, G. K. Pribil, Z. Fakhraai and M. D. Ediger, J. Chem. Phys., 2012, 136, 204501 CrossRef PubMed.
- A. Wisitsorasak and P. G. Wolynes, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 22308 CrossRef PubMed.
- P. G. Wolynes, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 1353–1358 CrossRef CAS PubMed.
- S. Léonard and P. Harrowell, J. Chem. Phys., 2010, 133, 244502 CrossRef PubMed.
- R. Gutierrez and J. P. Garrahan, J. Stat. Mech.: Theory Exp., 2016, 2016, 74005 Search PubMed.
- I. Lyubimov, M. D. Ediger and J. J. de Pablo, J. Chem. Phys., 2013, 139, 144505 CrossRef PubMed.
- A. Sepúlveda, S. F. Swallen, L. A. Kopff, R. J. McMahon and M. D. Ediger, J. Chem. Phys., 2012, 137, 204508 CrossRef PubMed.
- S. S. Dalal and M. D. Ediger, J. Phys. Chem. B, 2015, 119, 3875–3882 CrossRef CAS PubMed.
- K. L. Kearns, M. D. Ediger, H. Huth and C. Schick, J. Phys. Chem. Lett., 2010, 1, 388–392 CrossRef CAS.
- C. Rodríguez-Tinoco, M. Gonzalez-Silveira, J. Ràfols-Ribé, A. F. Lopeandía and J. Rodríguez-Viejo, Phys. Chem. Chem. Phys., 2015, 17, 31195–31201 RSC.
- D. M. Walters, R. Richert and M. D. Ediger, J. Chem. Phys., 2015, 142, 134504 CrossRef PubMed.
- G. M. Hocky, L. Berthier and D. R. Reichman, J. Chem. Phys., 2014, 141, 224503 CrossRef PubMed.
- C. T. Moynihan, A. J. Easteal, M. A. Bolt and J. Tucker, J. Am. Ceram. Soc., 1976, 59, 12–16 CrossRef CAS.
- H. N. Ritland, J. Am. Ceram. Soc., 1956, 39, 403–406 CrossRef CAS.
- S. S. Dalal and M. D. Ediger, J. Phys. Chem. Lett., 2012, 3, 1229–1233 CrossRef CAS PubMed.
- K. J. Dawson, L. Zhu, L. Yu and M. D. Ediger, J. Phys. Chem. B, 2011, 115, 455–463 CrossRef CAS PubMed.
- D. Yokoyama, J. Mater. Chem., 2011, 21, 19187 RSC.
- K. Ishii and H. Nakayama, Phys. Chem. Chem. Phys., 2014, 16, 12073–12092 RSC.
- K. Omori, H. Nakayama and K. Ishii, Chem. Lett., 2014, 43, 1803–1805 CrossRef.
- K. Fukasawa, T. Takahashi, T. Matsunami, H. Nakayama and K. Ishii, in AIP Conference Proceedings, American Institute of Physics AIP, 2013, vol. 1518, pp. 296–299.
- K. Dawson, L. A. Kopff, L. Zhu, R. J. McMahon, L. Yu, R. Richert and M. D. Ediger, J. Chem. Phys., 2012, 136, 94505 CrossRef PubMed.
- Y. Z. Chua, M. Tylinski, S. Tatsumi, M. D. Ediger and C. Schick, J. Chem. Phys., 2016, 144, 244503 CrossRef CAS PubMed.
- E. Leon-Gutierrez, A. Sepúlveda, G. Garcia, M. T. Clavaguera-Mora and J. Rodríguez-Viejo, Phys. Chem. Chem. Phys., 2016, 18, 8244–8245 RSC.
- R. S. Smith, R. A. May and B. D. Kay, J. Phys. Chem. Lett., 2015, 6, 3639–3644 CrossRef CAS PubMed.
- K. Ishii, H. Nakayama, R. Moriyama and Y. Yokoyama, Bull. Chem. Soc. Jpn., 2009, 82, 1240–1247 CrossRef CAS.
- D. Bhattacharya and V. Sadtchenko, J. Chem. Phys., 2014, 141, 94502 CrossRef PubMed.
- O. Yamamuro, I. Tsukushi, A. Lindqvist, S. Takahara, M. Ishikawa and T. Matsuo, J. Phys. Chem. B, 1998, 102, 1605–1609 CrossRef CAS.
- E. León-Gutierrez, G. Garcia, A. F. Lopeandía, J. Fraxedas, M. T. Clavaguera-Mora and J. Rodríguez-Viejo, J. Chem. Phys., 2008, 129, 181101 CrossRef PubMed.
- A. F. Lopeandía, J. Rodríguez-Viejo, M. Chacón, M. T. Clavaguera-Mora and F. J. Muñoz, J. Micromech. Microeng., 2006, 16, 965–971 CrossRef.
- M. Molina-Ruiz, Nanocalorimetric studies of size effects in magnetic oxides and formation kinetics in silicides, PhD dissertation, Universitat Autònoma de Barcelona, 2014.
- C. Rodríguez-Tinoco, Calorimetric study of vapour deposited glasses: beyond conventional stability and temperature limits, PhD dissertation, Universitat Autònoma de Barcelona, 2016.
- K. R. Whitaker, M. Ahrenberg, C. Schick and M. D. Ediger, J. Chem. Phys., 2012, 137, 154502 CrossRef PubMed.
- M. Hatase, M. Hanaya, T. Hikima and M. Oguni, J. Non-Cryst. Solids, 2002, 307–310, 257–263 CrossRef CAS.
- D. Cangialosi, V. M. Boucher, A. Alegría and J. Colmenero, Phys. Rev. Lett., 2013, 111, 95701 CrossRef PubMed.
- D. Cangialosi, J. Phys.: Condens. Matter, 2014, 26, 153101 CrossRef CAS PubMed.
- Y. Zhang and Z. Fakhraai, Phys. Rev. Lett., 2017, 118, 66101 CrossRef PubMed.
Footnote |
| † Present Address: Institute of Physics, University of Silesia, ulica Uniwersytecka 4, 40-007 Katowice, Poland. |
| This journal is © the Owner Societies 2017 |