Open Access Article
Open Access ArticleMaterials space of solid-state electrolytes: unraveling chemical composition–structure–ionic conductivity relationships in garnet-type metal oxides using cheminformatics virtual screening approaches†
Natalia
Kireeva
 *ab and
Vladislav S.
Pervov
c
*ab and
Vladislav S.
Pervov
c
aFrumkin Institute of Physical Chemistry and Electrochemistry Russian Academy of Sciences, Leninsky Prospect, 31a, 119071, Moscow, Russia. E-mail: nkireeva@gmail.com; kireeva@phyche.ac.ru; Tel: +7 4959554666
bMoscow Institute of Physics and Technology (State University), Institutsky per., 9, 141700, Dolgoprudny, Russia
cKurnakov Institute of General and Inorganic Chemistry Russian Academy of Sciences, Leninsky Prospect, 31a, 119071, Moscow, Russia
First published on 26th July 2017
Abstract
The organic electrolytes of most current commercial rechargeable Li-ion batteries (LiBs) are flammable, toxic, and have limited electrochemical energy windows. All-solid-state battery technology promises improved safety, cycling performance, electrochemical stability, and possibility of device miniaturization and enables a number of breakthrough technologies towards the development of new high power and energy density microbatteries for electronics with low processing cost, solid oxide fuel cells, electrochromic devices, etc. Currently, rational materials design is attracting significant attention, which has resulted in a strong demand for methodologies that can accelerate the design of materials with tailored properties; cheminformatics can be considered as an efficient tool in this respect. This study was focused on several aspects: (i) identification of the parameters responsible for high Li-ion conductivity in garnet structured oxides; (ii) development of quantitative models to elucidate composition–structure–Li ionic conductivity relationships, taking into account the experimental details of sample preparation; (iii) circumscription of the materials space of solid garnet-type electrolytes, which is attractive for virtual screening. Several candidate compounds have been recommended for synthesis as potential solid state electrolyte materials.
1. Introduction
Solid state inorganic electrolytes enable a number of breakthrough technologies towards the development of new high power and energy density microbatteries for electronics with low processing cost,1 solid oxide fuel cells,2 electrochromic devices,1,3,4 and many others. The organic electrolytes of most current commercial rechargeable Li-ion batteries (LiBs) are flammable, toxic and have limited electrochemical energy windows. All-solid-state battery technology promises improved safety, cycling performance, electrochemical stability and possibility of device miniaturization. Additionally, solid electrolytes would enhance the energy density by reviving metallic Li anodes technology. In recent decades, a large number of inorganic materials, including LISICONs-like and NASICONs-like compounds, perovskites, antiperovskites, garnets, argyrodites, Li nitrides, halides and hydrides, and LIPONs, with both crystalline and amorphous structures as well as their composite structures have been investigated experimentally and theoretically as potential solid electrolyte candidates.5–12Rational materials design to accelerate materials development processes is attracting much attention, initiated to some extent by growing interest in alternative green energy storage and conversion technologies,13–21 which has resulted in a strong demand for methodologies that can ascertain materials candidates with tailored properties; cheminformatics (or materials informatics) can be used as an efficient tool in this respect.14–20,22–39
There are a number of requirements40 that materials must satisfy to be used as solid electrolytes in all-solid-state batteries: high total Li+-ion conductivity (σLi > 10−4) with a transference number close to unity (σLi/σtotal ≈ 1), a high electrochemical stability window (∼6 V) with elemental Li or Li alloy, negligible electronic conductivity (σe < 10−10), retention of the electrode/electrolyte interface during cycling, environmental safety of materials, negligible solid-state electrode–electrolyte interface charge transfer resistance, chemical stability over the operation temperature range, etc.
The current study is aimed at identifying the parameters responsible for high Li-ion conductivity in the garnet-structured oxide family of solid electrolytes that are attractive candidates for high power and energy all-solid state Li ion batteries41 due to a number of benefits, including their high Li ion conductivities, stability against Li anodes, and small grain boundary resistance. This study considers the total Li-ion conductivity as the target property, focusing on the development of quantitative models to elucidate chemical composition–structure–ionic conductivity relationships and endeavoring to consider materials synthesis and processing information (experimental method, effects of temperature, time and atmosphere of sintering, etc.). Other specified requirements for electrolytes are expected to be satisfied by the intrinsic properties of garnet type oxides.
The study was carried out by applying machine learning approaches related to two different groups of methods. The Li ion transport characteristics of the collected data were analyzed by combining regression analysis, thus elucidating the composition–structure–ionic conductivity relationships and surveying garnet-related structures for promising compositions with data visualization techniques, known in computer-aided molecular design as chemography or cartography approaches; this provided a bird's eye view of the materials space of solid electrolytes, which is attractive for virtual screening. Both groups of methods29,42–46 are based on the chemical similarity principle, which claims similar property values for similar compounds; the latter methods posit a correspondence between the positioning of the compounds in the chemical space defined by the ensemble of selected parameters (descriptors) that are identified to be responsible for the target properties and the structural similarity.
Among the most promising garnet-type solid electrolytes are Al3+, Ga3+ and Fe3+-stabilized Li7La3Zr2O12 (LLZO). These compounds are the object of increasing attention due to their high Li ionic conductivities and interesting phase structure behavior in response to doping. It was recently shown that Ga3+- and Fe3+-stabilized LLZO can crystallize in alternative cubic space group I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3d (No. 220) to the cubic polymorph great while considered as the only (SG Ia
3d (No. 220) to the cubic polymorph great while considered as the only (SG Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d; No. 230). The reasons for the phase transition and formation of this SG are related to the site preferences of Ga3+ and Fe3+ cations, which may be related to size factors.47 Several studies have been published on the local structure and site occupancy preferences of Al3+ and Ga3+ substituents.48–52 Thus, another aim of this study is an attempt to offer insight on the relative 24d and 96h site occupancy by dopants using grid search and setting-up ionic radii values of Al3+ and Ga3+ cations for each compound. The correspondence of predicted by the model ionic conductivity values with known experimental ones served as a criterion for establishing relative 24d and 96h site occupancy.
d; No. 230). The reasons for the phase transition and formation of this SG are related to the site preferences of Ga3+ and Fe3+ cations, which may be related to size factors.47 Several studies have been published on the local structure and site occupancy preferences of Al3+ and Ga3+ substituents.48–52 Thus, another aim of this study is an attempt to offer insight on the relative 24d and 96h site occupancy by dopants using grid search and setting-up ionic radii values of Al3+ and Ga3+ cations for each compound. The correspondence of predicted by the model ionic conductivity values with known experimental ones served as a criterion for establishing relative 24d and 96h site occupancy.
2. Methodology
Despite the substantial progress in materials informatics, only a few published studies are closely related to the objects of our research. In ref. 16, the authors apply density functional theory computation and an artificial neural network for modeling Li ion transport (migration energy) in tavorite-type structures in order to optimize these well-known cathode material structures for application as solid-state electrolyte materials. Using cathode and solid electrolyte related to the same structural type would be beneficial in order to decrease possible interface resistance. Structural information (lattice parameters, ion effective charges, intra- and interpolyhedron parameters) obtained as a result of DFT computations have been used as descriptor values. Candidate compositions have been proposed. In ref. 15 and 17, a combination of DFT with machine learning methods (partial least squares or artificial neural networks) was used for virtual screening of olivine-type materials for solid electrolyte applications (with Li ion hopping energy as a predicted property). Similar with previous study of the same group, they perform the screening of olivine-related compounds for compositions with suppressed electronic contribution in conductivity value. In ref. 14, first principles calculations were combined with support vector regression for modeling Li ion conductivity values in LISICON-type materials; diffusion coefficients, transition temperatures, formation free energies of solid solutions and average volumes of disordered structures were used as descriptor values.The details of our study are organized as separate paragraphs and are given below.
2.1. Data and descriptors
The main dataset encompasses information related to garnet-type oxide structures exhibiting high total conductivities at ambient temperature, desirable chemical and electrochemical stabilities, small grain boundary resistances, and Li transference numbers close to unity, which make them of substantial interest for use as solid electrolytes in all-solid-state batteries. This information includes the total Li-ion conductivities (sum of the bulk and grain boundary contributions), corresponding activation energy values, unit cell parameters if available, experimental details of synthesis, resulting product densities, types of pressure (uniaxial or isostatic) if available, etc. of garnet-type structure metal oxides with the general formula A3B2(XO4)3, whose A, B, X – eight, six and four oxygen coordinated cation sites are known to crystallize into crystal structures in two cubic space groups (Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d; No. 230 and I
d; No. 230 and I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3d) as well as one tetragonal space group (I41/acd; No. 142).
3d) as well as one tetragonal space group (I41/acd; No. 142).
The distribution of the initial dataset according to reported experimental values of their total ionic conductivities as well as the taxonomy of the data in use are given in Fig. 1. This data is provided as ESI.†
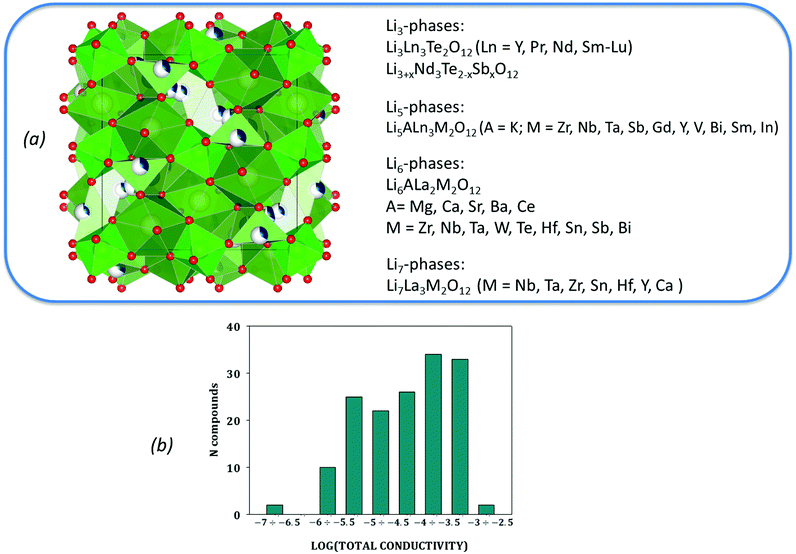 | ||
| Fig. 1 The taxonomy of the collected data (a) with its distribution according to reported experimental values of total ionic conductivity (b). | ||
At the dataset preparation stage, only compounds with total ionic conductivity values evaluated at ambient temperatures were included (data measured at high temperatures have been omitted). Also we removed the compounds related to tetragonal crystal structure if the information about this compound as about the cubic polymorph has been represented in other publications from the data. Another reason for data removal is observed data variance. Even for compounds obtained using the same synthesis methodology, one can see that the evaluated Li ion total conductivity values varied in a wide range up to several orders of magnitude (see Fig. 2 and Table 1).
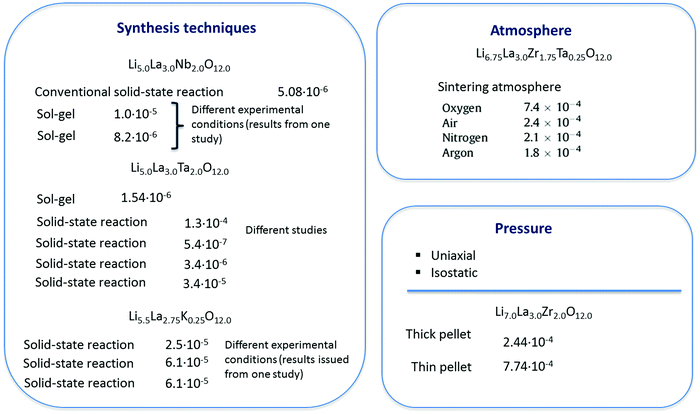 | ||
| Fig. 2 The impact of experimental technique on the electrochemical performance of solid electrolytes: reported total conductivity values (S cm−1) as a function of processing method. | ||
| Ref. | Precursors | Syn. conditions | Lattice const | Additional comments | E a (eV) | σ total (S cm−1) |
|---|---|---|---|---|---|---|
| Li5La3Nb2O12 | ||||||
| 79 | Solid-state reaction Li2CO3, La2O3, Nb2O3 | Calcination 700 °C (12 h) → 900 °C (12 h) sintering 1000 °C (12 h) | — | Isostat. pressure 2.5 ton | 0.6 | 7.49 × 10−6 |
| 80 | Solid-state reaction LiNO3 (10% excess), La2O3, Nb2O5 | Heating 700 °C (6 h) sintering 900 °C (24 h) → 1000 °C to 1100 °C (6 h) | 12.718 | Isostat. pressure 300 kN | 0.6 | 5.08 × 10−6 |
| 81 | Sol–gel, LiOH, LaAc3·1.5H2O, N2O5, HOOC–COOH, EDTA (5 mol%) | Pre-calcination 700 °C (6 h), sintering 700 °C to 1000 °C (6 h) | 12.805 | Uniaxial pressure 5 MPa | — | 1.00 × 10−5 |
| 81 | Sol–gel, LiOH, LaAc3·1.5H2O, N2O5, HOOC–COOH, EDTA (5 mol%) | Pre-calcination 900 °C (6 h), sintering 700 °C to 1000 °C (6 h) | 12.805 | Uniaxial pressure 5 MPa | — | 8.20 × 10−6 |
| 82 | Solid-state reaction La2O3, LiOH·H2O (10% excess) and Nb2O5 | Heating 700 °C (6 h) → annealing 900 °C (24 h) | 12.762 | Isostat. pressure | 0.43 | 8.00 × 10−6 |
| 83 | Solid-state reaction La(NO3)3·6H2O, LiOH·H2O, Nb2O5 | 700 °C (24 h) → 800 °C (24 h) → 850 °C (12 h) → sintering 950 °C (24 h) | 12.762 | Isostat. pressure | 0.43 | 8.00 × 10−6 |
| 84 | Solid-state reaction Li2CO3, La2O3, Nb2O5, Co(NO3)2·6H2O, NiCO3 | 700 °C (12 h); sintering 900 °C to 1000 °C (12 h) | 12.814 | Isostat. pressure | 0.56 | 5.70 × 10−6 |
| 84 | Solid-state reaction Li2CO3, La2O3, Nb2O5, Co(NO3)2·6H2O, NiCO3 | 700 °C (12 h); 800 °C (12 h); 950 °C (24 h) | 12.818 | Isostat. pressure | 0.55 | 2.30 × 10−5 |
| 84 | Solid-state reaction Li2CO3, La2O3, Nb2O5, Co(NO3)2·6H2O, NiCO3 | 700 °C (12 h); 800 °C (12 h); sintering 1000 °C (24 h) | 12.8 | Isostat. pressure | 0.55 | 4.40 × 10−5 |
| 85 | Solid-state reaction LiNO3, La2O3, Nb2O3 | 700 °C (12 h) → 700 °C (12 h) → sintering 950 °C (24 h) | — | Isostat. pressure | 0.51 | 2.54 × 10−7 |
| 85 | Ion-exchange reaction | — | Isostat. pressure | 0.35 | 3.63 × 10−6 | |
| Li5La3Ta2O12 | ||||||
| 86 | Sol–gel synthesis, ethylene glycol, acetic acid·2H2O, Ta(OCH2CH3)5, (La(NO3)3·6H2O) | Solution heating 120 °C, dry gel heating 300 °C, calcination 700 °C to 900 °C (5 h) sintering 900 °C (5 h) | — | Relative dens. 70%; press. 300 MPa | 0.57 | 1.54 × 10−6 |
| 87 | Solid-state reaction, LiNO3, La(OH)3, Ta2O5 | Calcination 700 °C (12 h), sintering 1000 °C to 1200 °C (24 h) | — | Relative dens. 70% | — | 1.30 × 10−4 |
| 88 | Solid-state reaction, LiOH·6H2O, Ta2O5, La2O3 | Heating 700 °C (12 h), 800 °C (24 h), 950 °C (24 h step 50 °C), sintering 850 °C (24 h) | 12.823 | Relative dens. 71% | 0.62 | 5.40 × 10−7 |
| 83 | Solid-state reaction La(NO3)3·6H2O, LiOH·H2O, Nb2O5 | 700 °C (24 h) → 800 °C (24 h) → 850 °C (12 h) → sintering 950 °C (24 h) | 12.766 | 0.56 | 3.40 × 10−6 | |
| 89 | Solid-state reaction LiOH·H2O, Ta2O5, La2O3 | Heating 900 °C (10 h) → 900 °C (10 h), sintering 36 h | 12.831 | Relative dens. 94%, uniaxial pressure 5 ton | — | 3.40 × 10−5 |
| Li6BaLa2Ta2O12 | ||||||
| 90 | Solid-state reaction LiOH (10 weight % excess), Ta2O5, La2O3, Ba(NO3)2 | Heating 700 °C (6 h) → 900 °C (12 h) | 12.997 | Relative dens. 70%, isostat. pressure | 0.47 | 1.50 × 10−5 |
| 91 | Solid-state reaction Li2CO3, La2O3, Ta2O5, BaCO3 | Calcination 700 °C (6 h), 1000 °C (12 h), sintering 1000 °C (4 h) | 13.001 | Relative dens. 67%, pressure 0.2 GPa | 0.44 | 1.30 × 10−5 |
| 92 | Sol–gel reaction, Li2CO3, La2O3, Ta(OC2H5)5, BaCO3 | Calcination 650 °C to 850 °C (6 h), sintering 900 °C (4 h) | 12.995 | Relative dens. 96% | 0.4 | 1.69 × 10−5 |
| 93 | Solid-state reaction LiNO3, La2O3, Ta2O5, Ba(NO3)2 | Heating 700 °C (12 h), sintering 950 °C (24 h) | 12.98 | Isostat. pressure | 0.41 | 1.22 × 10−5 |
| 94 | Solid-state reaction LiNO3, La2O3, Ta2O5, Ba(NO3)2 | Heating 700 °C (12 h), sintering 900 °C (24 h) | 12.975 | Isostat. pressure | 0.42 | 1.51 × 10−4 |
| 95 | Solid-state reaction LiOH·H2O, La2O3, Ta2O5, Ba(NO3)2 | Heating 700 °C (6 h), sintering 900 °C (24 h) | 12.946 | Isostat. pressure | 0.4 | 4.00 × 10−5 |
The decisions in this case were made ad hoc, i.e. considering each situation individually (compounds under consideration were removed in cases of discrepancy with a prominent number of observations for the same compound obtained using the same synthesis method). One more reason for exclusion was an estimated relative density of the sample (<50%) that was essentially different from most of the observations in the data.
In fact, the problem of data curation, which is well-known in cheminformatics, bioinformatics and chemogenomics,53–55 acquires special importance here due to the necessity to analyze the reasons for such discrepancies. It acquires a wider meaning and combines aspects related to the critical assessment of published experimental data56–59 with the problem of controllable design of materials with desired characteristics; this is of practical importance, for example, in the design of hybrid electrolyte/Li metal anode structures in which garnet-based solid state electrolytes (SSE) have porous/dense bilayer structures with porous sublayers as a host for infiltrated lithium metal anodes60 (the possibility to rationally design products with specified characteristics is highly desirable and requires a clear understanding of the relationships between the synthesis method/conditions and final product characteristics).
The attempt to explicitly analyze the impact of materials synthesis information on the materials properties was the reason for including descriptors to encode materials synthesis information as well as for using several computational procedures reflected in different corresponding data sets that were issued from the initial data or coincide with it.
Thus, two different data preparation protocols have been used: in accordance with the first one, in cases where several compounds are present, only the first compound in the list was stored irrespective of the synthesis method or other experimental conditions (123 compounds). This was also performed for the alternative computations, where only the compounds obtained by conventional solid-state reactions have been included (106 compounds). In parallel, we decided to average out the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σtot values in cases where several compounds were present.
σtot values in cases where several compounds were present.
Another difference has been specified for the development of models involving space filling parameters (see below), where only compounds with available information on their lattice constants have been considered (the data set encompasses 98 compounds).
The whole dataset used in combination with descriptors encoding materials synthesis information encompasses 168 compounds.
Several types of parameters related to different categories were used as descriptors for the model development. Most of these are geometry-based and stem from the interrelations of constituent element radii with geometric principles of ion packing as well as currently published studies where the most well known specific chemistries and structural type parameters responsible for Li ion conductivity were related to the geometrical point of view61 (Fig. 3).
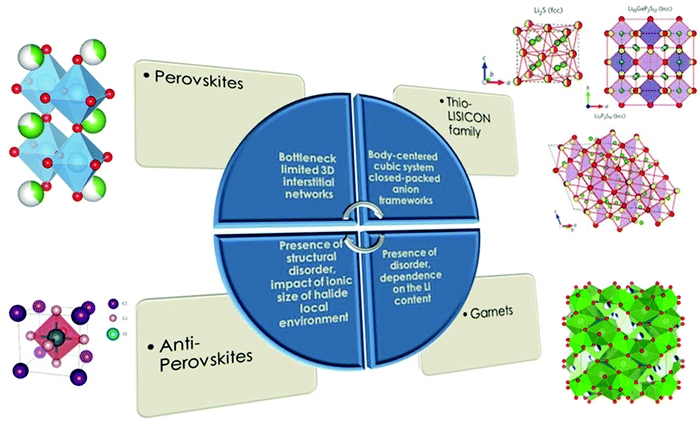 | ||
| Fig. 3 Parameters designated for specific chemistries and structural types of solid electrolytes responsible for Li-ion conductivity values (part of the figure is reproduced with permission from Macmillan Publishers Ltd Nature Materials (Nat. Mater., 2015, 14, 1026–1031), copyright (2015)62 and the Royal Society of Chemistry63). | ||
Constitutional (compositional) descriptors describe the composition of compounds per formula unit (pfu), taking into account the corresponding structure type by means of the compound fingerprint bit string. For each cation type (in the case of garnet-related structures, tetrahedrally, octahedrally or dodecahedrally coordinated), three positions in this string are allocated. The first one is the position of the cation most commonly accommodated in the given site; the remaining two are reserved for substitution elements. The same scheme is used for other descriptors.
Shannon ionic radii values take into account the coordination environment of the metal cation in the structure and, for less trivial cases concerned with alternative coordination, “optimized” ionic radii values where metal cations can be found in different coordinations (see details in the computational procedures section).
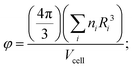 | (1) |
Atomic X-ray scattering factor is the only parameter in this study that is directly concerned with atomic electron configuration and radial electron density distribution. The corresponding values for chemical elements have been taken from ref. 69.
2.2. Machine learning methods
Support vector machines (SVM)70 were used in this study for regression model development. Support vector regression (SVR) is a commonly used supervised machine learning method which is related to methods of structural risk minimization71 (arranging the trade-off between model complexity and predictive error), realizing this principle by constructing an optimal hyperplane in order to minimize a special introduced ε-insensitive loss function where an optimization problem is solved using the methods of quadratic programming.The logarithm of total ionic conductivity was taken as a target predicted property. SVM models were obtained using LIBSVM software72 with epsilon-SVR and radial basis function (RBF) kernel functions. The predictive performance of each model was optimized in a grid search by varying three parameters: C = 2−5, 2−3…215, ε = 0.0001, 0.001…10 (internal parameters of the method) and γ = 2−15, 2−13…23 (parameter of the RBF kernel). The models with optimized parameters providing the best SVM performance on the cross-validation tuning set (part of the training) were validated on the corresponding test set.
The predictive performances of the developed regression models were assessed using the ten-fold external cross-validation (10-CV) procedure, where the entire dataset is divided into ten non-overlapping pairs of training and test sets of compounds (only the training set compounds are involved in model development, followed by application of the obtained models to the test set compounds in order to evaluate the predictive ability of the models). The determination coefficient R2, root mean squared error RMSE, and mean absolute error MAE were accepted in this study as the statistical parameters assessing the ability of the models to quantitatively reproduce the experimental data. They are calculated and related as follows:
| R2 = 1 − ∑(Ypred − Yexp)2/∑(Yexp − 〈Y〉exp)2 | (2) |
| RMSE = (∑(Yexp − Ypred)2/n)1/2 | (3) |
| MAE = ∑|Yexp − Ypred|/n | (4) |
In this study, t-Distributed Stochastic Triplet Embedding73 has been used as the chemography technique. We chose this approach due to our interest in the concept that underlies this probabilistic method, which is based on a system of judgments that are close to human ones when performing a comparison of objects based on the principle “everything is relative” using similarity triplet supervision (A is more similar to B than C) in the framework of the stochastic neighbor approach. Thus, the sum of the log probabilities over all triplets of compounds in the training data is maximized:
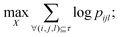 | (5) |
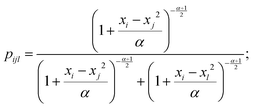 | (6) |
The choice of this technique finally appeared to be justifiable because it resulted in better data visualization performance compared to several alternative data visualization approaches; these results were omitted, as they were assumed to be excessive. The number of considered triplets (N = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) and the number of principal components (n = 4) of Principal Component Analysis (PCA)74 that are recommended for use in this realization were optimized during the process of model development.
000) and the number of principal components (n = 4) of Principal Component Analysis (PCA)74 that are recommended for use in this realization were optimized during the process of model development.
2.3. Heuristic elucidation of relative site preference of Al3+ and Ga3+
Garnet-type structure metal oxides have the general formula A3B2(XO4)3, where A, B, X – eight, six and four oxygen coordinated cation sites are known to crystallize into crystal structures in two cubic space groups (Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d; No. 230 and I
d; No. 230 and I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3d) as well as one tetragonal space group (I41/acd; No. 142). The tetragonal low-temperature phase exhibits low RT total conductivity values and thus cannot be considered as a material for solid state electrolytes. The cubic polymorphs can be stabilized at RT by the introduction of supervalent dopants (to date, Al3+, Ga3+ and Fe3+), which results in the formation of Li vacancies in the lattice to maintain general electroneutrality. The questions of site preferences and local compound coordinations for these cations remain of interest because they can be closely related to questions such as phase transitions between two observable cubic modifications in a given metal oxide type related to symmetry lowering. The experimental information on the local coordination and the site preferences is quite discordant. The most recent MAS NMR study51 using very high magnetic fields showed that Al3+ and Ga3+ have almost the same site preferences, which indicates that other parameters are responsible for the twofold efficiency of Ga3+ doping.
3d) as well as one tetragonal space group (I41/acd; No. 142). The tetragonal low-temperature phase exhibits low RT total conductivity values and thus cannot be considered as a material for solid state electrolytes. The cubic polymorphs can be stabilized at RT by the introduction of supervalent dopants (to date, Al3+, Ga3+ and Fe3+), which results in the formation of Li vacancies in the lattice to maintain general electroneutrality. The questions of site preferences and local compound coordinations for these cations remain of interest because they can be closely related to questions such as phase transitions between two observable cubic modifications in a given metal oxide type related to symmetry lowering. The experimental information on the local coordination and the site preferences is quite discordant. The most recent MAS NMR study51 using very high magnetic fields showed that Al3+ and Ga3+ have almost the same site preferences, which indicates that other parameters are responsible for the twofold efficiency of Ga3+ doping.
We decided to check if it is possible to offer insight on the relative site occupancy by adjusting the related descriptor parameters from the known experimental ionic conductivity values and analyzing the corresponding correlations. This effort appeared interesting due to the simplicity of the idea. It was believed that the agreement between the theoretical and observed experimental data could enable the use of this additional information for predicting the Li ion conductivities of new “virtual” compounds.
The descriptors (constitutional descriptors, Shannon ionic radii and octahedral factors) were changed in order to reflect the site occupancy preferences of the considered metal cations as well as the introduced threshold values, which can be related to the relative occupancy of tetrahedral and octahedral sites. A simple grid search was performed by adjusting the internal parameters corresponding to the threshold values of the pfu values of the doping cations (0.01, 0.05, 0.1, etc.) for the cation sites (which were exceeded corresponding to changes in tetrahedral and octahedral occupancy) as well as the values corresponding to information on the relative site preferences of each doping substituent and their ionic radii values, e.g. if the amount of substituent cation A (pfu) exceeds the given threshold value, this cation begins to occupy the distorted octahedral 96h site according to the depiction of the descriptors (adjusting this value), thus corresponding to the adjustment of the relative site preference parameters (the tetrahedrally coordinated 24d site was considered by default).
3. Results and discussion
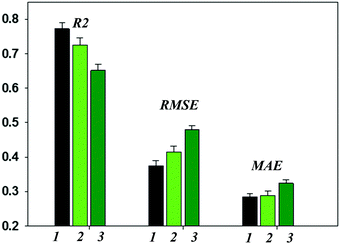
This study addressed several aspects, such as the possibility of using the models developed here for virtual screening of new garnet-related electrolytes, using the experimental information as characteristics heavily defining the final product properties, heuristic elucidation of the relative site preferences of Al3+ and Ga3+ metal cations, etc.Reasonable levels of predictive ability of the models have been achieved; however, some limitations remain. Using experimental details implicitly as model parameters yields unanticipated results in a given realization. Another serious limitation is the desensitization of the model by choosing one “frozen” Li ionic radius value corresponding to the tetrahedral coordination and leaving aside the information considered in ref. 75. Additional models taking into account different possible Li+ coordinations and, particularly, workarounds to consider Li+/H+ exchange if this occurs resulted in no improvement of the achieved predictive ability. Herewith, the reached predictivity provides a means of asserting the obtained models as a valid method for virtual screening of new garnet-type SSEs. Thus, the predictive ability of the regression models is represented in Fig. 4 as a function of the protocol of computations (details are presented in the Methodology (Data and descriptors) paragraph). The given values of R2 characterizing the general model performance and the corresponding predictive error values (RMSE and MAE) are averaged over the results of 100 individual models (shuffling compounds followed by re-building of the models). As is shown, the predictive errors appear to be adequate for the requirements of models suitable for the virtual screening of new compounds. Thus, for the first data set R2, the RMSE and MAE values are 0.778, 0.372 and 0.283, respectively. The results of the models in predicting the external test set compounds are generally in line with this assertion. Meanwhile, significant discrepancies in the experimental and predicted log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σtot values were observed for some compounds. The impact of the descriptors on the predictive ability of the models was analyzed using the SVD-USE program (developing multiple linear regression models); their contributions to the complete descriptors pool were demonstrated to be almost equal. Artificially reducing the number of descriptors emphasized the compositional descriptors (notably, tetrahedrally and dodecahedrally coordinated cations) and octahedral factors and their analogues for alternative coordinations. A general analysis and discussion of the obtained results is given below, and the prediction errors are examined.
σtot values were observed for some compounds. The impact of the descriptors on the predictive ability of the models was analyzed using the SVD-USE program (developing multiple linear regression models); their contributions to the complete descriptors pool were demonstrated to be almost equal. Artificially reducing the number of descriptors emphasized the compositional descriptors (notably, tetrahedrally and dodecahedrally coordinated cations) and octahedral factors and their analogues for alternative coordinations. A general analysis and discussion of the obtained results is given below, and the prediction errors are examined.
3.1. Experimental data analysis
An important point that should be discussed is the intrinsic variance in the experimental data. Understanding the sources of this discrepancy in the experimental results for the same compounds obtained in different studies appears to be important, as it is related to a number of miscellaneous problems arising from the questions of synthesis route selection (the impact of the method, as in ref. 76, where, for a given example, two synthesis methods are used with controversial results for the electrochemical characteristics for the same cathode material, or the effect of the experimental conditions, as in ref. 77), to reach the reaction-by-design concept,78 the problem of reproducibility of research, the accessibility of published negative results, etc. Preliminary endeavors to explain the sometimes significant discrepancies in the experimental data have been undertaken: the experimental details, lattice constant values and activation energies for LLNO, LLTO and LBLTO, the most investigated compounds, are represented in line with their total conductivity values (Table 1). Unfortunately, the processing-property interrelation is not always evident. The encoding of experimental information in parameters thus attempting to unravel composition–processing–structure–ionic conductivity relationships for garnet-type oxides using machine learning techniques was an inception (the results are represented in one of the paragraphs below).3.2. Predictive ability of models
Among the most promising garnet-type solid electrolytes are Al3+, Ga3+ and Fe3+-stabilized Li7La3Zr2O12 (LLZO). These compounds are objects of increasing attention due to their high Li ionic conductivities and interesting phase structure behaviors in response to doping. It was recently shown that Ga3+- and Fe3+-stabilized LLZO can crystallize in alternative cubic space group I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3d (No. 220) to the cubic polymorph great while considered as the only (SG Ia
3d (No. 220) to the cubic polymorph great while considered as the only (SG Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d; No. 230). The reasons for the phase transition and the formation of this SG are related to the site preferences of Ga3+ and Fe3+, which are possibly due to size factors.47
d; No. 230). The reasons for the phase transition and the formation of this SG are related to the site preferences of Ga3+ and Fe3+, which are possibly due to size factors.47
Here, we briefly summarize the obtained property prediction results for Al3+, Ga3+ and Fe3+-stabilized Li7La3Zr2O12 (LLZO). The total conductivity values for most of the Al3+ and Ga3+-stabilized compounds were predicted sufficiently accurately. However, the effects of Al3+ and Ga3+ co-doping remained unexplained by models. Thus, for two of three Li6.4Al0.2−xGaxLa3Zr2O12 compounds,96 the differences between the experimental and predicted log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σtot values exceeded 0.5.
σtot values exceeded 0.5.
As an alternative to Al3+, Ga3+ and Fe3+ doping, stabilized cubic LLZO polymorph is a super-valent substitution with highly charged ferroactive cations (Ta5+, Nb5+, W6+, Mo6+, V5+etc.) on Zr4+ sites which are assumed not to hinder the Li ion diffusion pathways (unlike tetrahedral site doping) and, hence, can be considered as more efficient. Here, one can attribute the difficulty of prediction of the compounds to the simultaneous presence of Nb5+ and V5+ cations in the structure.97 The disagreement between the experimental and predicted values was acceptable (∼0.2 in log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σtot) for Li5La3Nb2−xVxO12 (x = 0.05, 0.1) and steeply increased for Li5La3Nb2−xVxO12 (x = 0.15, 0.2, 0.25). Formation of secondary phases has been observed for Li5La3Nb2−xVxO12 (x = 0.2, 0.25).
σtot) for Li5La3Nb2−xVxO12 (x = 0.05, 0.1) and steeply increased for Li5La3Nb2−xVxO12 (x = 0.15, 0.2, 0.25). Formation of secondary phases has been observed for Li5La3Nb2−xVxO12 (x = 0.2, 0.25).
The predictions for Li7La3Hf2O12 compounds98 were not sufficiently accurate, possibly due to discrepancies in the experimental total conductivity values published in ref. 98 and 99.
The relatively poor conductivity prediction for Li6.8La3Zr1.8Sb0.2O12 may be related to the “cliff” property that appeared in the experimental conductivity values from ref. 100. This observation can be related with discrepancy in the relative density of this sample as well as in the difference in the total conductivity assessment where this compound was the only for which impedance plot was resolved into bulk, grain boundary and electrode resistance, for other compounds total conductivity value was evaluated as the inverse of the resistivity.
Finally, the predicted conductivity for Li5La3Ta2O12 from ref. 101 was very different from its corresponding experimental value.
The total conductivities for Ba-substituted LLT compounds (Li5+xBaLa2Ta2O11.5+0.5x)102 were systematically underestimated by models that included the difference in the experimental temperatures, the oxygen nonstoichiometry of these compounds or their instability to moisture.103 In contrast, the total conductivities of Gd3+-substituted LLN79 were overestimated by the models, except those for LLN-Gd60 (impurity phases were observed for this particular compound). The incorrect predictions for these compounds as well as for supervalent (Ce4+)-substituted LLZO Li6.6La2.6Ce0.4Zr2O12104 remain unexplained.
3.3. Heuristic elucidation of the relative site preferences of Al3+ and Ga3+ cations
Here, some ambiguous results are discussed. This ambiguity is a result of both the simplified method offering insight on the relative site occupancies and adjusting the parameters of the related descriptors using known experimental ionic conductivity values (the correspondence between the predicted and experimental values was considered as a congruence criterion) followed by analyzing the corresponding correlations with predictions, as well as the character of the results obtained.The greatest consistency with experimental total conductivity values was obtained as a result of a grid search performed with the following parameters:
(i) If the amount of substituent cation A (pfu) exceeds the threshold value of 0.1 for Ga3+ and 0.01 for Al3+ (almost all the compounds), the tetrahedrally coordinated 24d sites 0.1 and 0.2 are occupied, respectively, assuming that 0.9 and 0.8 of Ga3+ and Al3+ are accommodated by the octahedrally coordinated 96h site.
(ii) Increasing the threshold value for Al3+ to 0.1 blurred the occupancies of Ga3+ and Al3+ to the ranges of 0.1 to 0.4 and 0.2 to 0.5, respectively.
(iii) Further increasing the threshold for Ga3+ resulted in changes of the occupation of the tetrahedrally coordinated 24d sites to 0.7 and 0.5 for Ga3+ and Al3+, respectively.
The results presented here that were not confirmed to be in agreement with experimental observation (although the published experimental data on the local coordination and the site preferences are quite discordant) should still be discussed, as they led to improvement of the predictive performance of the models. Thus, the R2, RMSE and MAE values for the optimized model are as high as 0.81, 0.34, and 0.26, respectively. The predicted vs. experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σtot values are represented in Fig. 5.
σtot values are represented in Fig. 5.
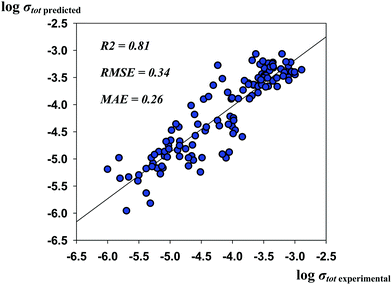 | ||
Fig. 5 The predicted vs. experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σtot values for the optimized “best” model during heuristic elucidation of the relative site preferences of Al3+ and Ga3+ cations. σtot values for the optimized “best” model during heuristic elucidation of the relative site preferences of Al3+ and Ga3+ cations. | ||
The evaluation of statistical relevance of the observed improvement of the predictive ability of the models is not sufficiently correct. First, a different descriptor set was used for model development; second, it is hindered by the number of Al3+ and Ga3+-stabilized LLZO compounds available. However, the analysis of the property prediction revealed a significant improvement in the predictive ability of the model. First, the effects of Al3+ and Ga3+ co-doping, which remained unexplained in previous calculations, appeared to be described precisely here. Thus, finally, no outlier-by-prediction Al3+ and Ga3+-doped compounds were observed. Second, the general predictive ability of the models was increased.
3.4. Using experimental information as descriptors
A description of the descriptor types is given in the data and descriptors paragraph. By analyzing the data, one can see that a variety of synthesis methods have been used for sample preparation (conventional solid-state reactions, sol–gel, modified sol–gel combustion, Pechini, polymerized complex, co-precipitation, microwave assisted, etc.) with different experimental conditions that highly impact the final microstructure and, consequently, the Li-ion conductivity. Additionally, even for compounds obtained using the same experimental synthesis method, one can see that the evaluated Li ion total conductivity value varied in a wide range up to several orders of magnitude (see Table 1 and Fig. 2). Therefore, the concept of using the synthesis information explicitly as descriptors refining the predictivity of the model was itself feasible. However, its implementation appeared to be unsatisfying. The case where only the sintering step was encoded resulted in models with moderate predictive performance (at least, for regression models), as shown in Fig. 4. Similarly, distinguishing the data issued from the solid-state reactions and encoding most of the processing history (if possible in principle105) did not improve the total conductivity predictions. Additionally, its apparent shortcomings include: first, the non-optimal method chosen to encode information as descriptor values; second, the disparity between the number of compounds obtained using conventional solid-state reactions and all other approaches en bloc; and finally, the consideration of similar reported materials synthesis and processing information for compounds with different property values (Table 1).3.5. Other computational protocols
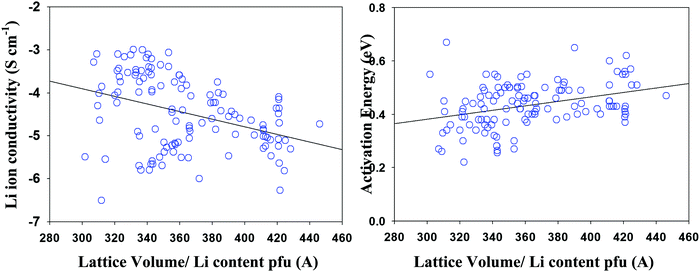
Involving space filling parameter as descriptors' type to models' development provides no improvement of model predictive ability that is in a combination with reduced number of compounds in the data set (as a result of missing structural data in a number of studies) made its application inexpedient. Fig. 6 represents the Li ion conductivity and activation energies as a function of the normalized lattice volume parameter, demonstrating a similar situation where using lattice volume value as a descriptor parameter despite observed correlations also appeared to be unfeasible.“Averaged property” computations were performed as a shortcut for the data selection procedure in cases where it was necessary to choose one compound among many. Ideally, it has to be performed entirely by the expert opinion which is not always possible due to the coincident description of the published experimental data. Thus, this study can be considered as some sort of the compromise between the undertaken efforts of such data evaluation and final quite rustic implementation. The results of the performed procedure demonstrate similar predictive performance to the first type of model computation.
We additionally attempted to distinguish compounds that can be potentially instable to moisture. Thus, the possible instability of garnet structures to moisture has been related to accommodation of the tetrahedral and octahedral sites by Li+. Recently, it was shown that increasing Li content results in the re-distribution of Li ions among tetrahedrally coordinated 24d sites and octahedrally coordinated 96h sites, increasing accommodation of the latter.75 It was also reported that compounds with high Li content can be especially sensitive to moisture. Conjoining the given observations, we considered this by means of corresponding adjustment of the descriptor values. The obtained results show no improvement in the predictive performance of the models, which can be interpretable as superfluous information (the described behavior is already reflected in a roundabout way in the compositional descriptors, which provide one of the greatest contributions to the models), as an infeasibility to consider complex problems using the given approach, or, finally, as further indication of the lack of impact of Li+/H+ exchange on the total conductivity values.
3.6. Prediction of the external test set
The external test set encompasses all Ga3+-substituted compounds (with known experimental values of total ionic conductivity) detached from the initial data set (these compounds were preliminarily excluded from the training data used for development of the models), Fe3+-substituted compounds,47 and several out-of-bag compounds not included in the initial data set77,106–109 as well as the suggested “virtual” garnet-type compounds substituted with Zn2+, Ni2+, Cu2+, Sc3+, Cr3+, and Rb+ cations. Here, Ga3+-substituted compounds were detached from the initial data in order to check if the developed models have predictive ability for compounds containing “new” dopants different from those in the training set.The results of the external test set predictions are represented in Table 2. It should be pointed out that for the suggested “virtual” compounds, high predicted total conductivity values alone are not sufficient, as these compounds may exhibit also electronic conductivity, which makes them infeasible for application as materials for solid state electrolytes.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σtot) for the “virtual” and synthesized compounds of the external test set
σtot) for the “virtual” and synthesized compounds of the external test set
| Compound name | Experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σtot (S cm−1) σtot (S cm−1) |
Predicted log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σtot (S cm−1) σtot (S cm−1) |
|---|---|---|
| Li6.4Ga0.2La3Zr2O12 | −3.40 | −3.25 |
| Li6.15La3Zr1.75Ta0.25Ga0.2O12 | −3.39 | −3.37 |
| Li6.55La3Zr2Ga0.15O12 | −2.89 | −3.18 |
| Li6.4La3Zr2Ga0.2O12 | −3.05 | −3.25 |
| Li6.1La3Zr2Ga0.3O12 | −4.15 | −3.42 |
| Li5.5La3Zr2Ga0.5O12 | −4.00 | −3.89 |
| Li6.4Al0.15Ga0.05La3Zr2O12 | −3.42 | −3.71 |
| Li6.4Al0.1Ga0.1La3Zr2O12 | −3.20 | −3.69 |
| Li6.4Al0.05Ga0.15La3Zr2O12 | −3.97 | −3.66 |
| Li6.4Ga0.2La3Zr2O12 | −3.93 | −3.25 |
| Li6.25La3Zr2Ga0.25O12 | −3.46 | −3.33 |
| Li6.7Fe0.1La3Zr2O12 | −3.16 | |
| Li6.46Fe0.18La3Zr2O12 | −3.25 | |
| Li6.52Fe0.16La3Zr2O12 | −3.23 | |
| Li6.4Fe0.2La3Zr2O12 | −3.28 | |
| Li6.25Fe0.25La3Zr2O12 | −3.36 | |
| Li6.1Fe0.3La3Zr2O12 | −3.45 | |
| Li6.7Cr0.1La3Zr2O12 | −3.22 | |
| Li6.7Ni0.1La3Zr2O12 | −3.10 | |
| Li6.7Cu0.1La3Zr2O12 | −3.84 | |
| Li7.25La2.875Rb0.125Zr2O12 | −3.23 | |
| Li7.5La2.75Rb0.25Zr2O12 | −3.41 | |
| Li7.75La2.62Rb0.375Zr2O12 | −3.62 | |
| Li6.7La3Zr1.9Zn0.1O12 | −3.30 | |
| Li6.35La3Nb1.375Sc0.625O12 | −3.86 | −3.74 |
| Li6.52Al0.08La3Zr1.75Ta0.25O12 | −3.11 | −3.26 |
| Li6.5La3Sn1.5Ta0.5O12 | −3.62 | −3.78 |
| Li6.65Ga0.15La3Zr1.9Sc0.1O12 | −2.74 | −2.90 |
| Li6.9La3Zr1.9Bi0.1O12 | −3.36 | |
| Li6.6La3Zr1.8Mo0.2O12 | −3.29 | −3.31 |
3.7. Visualization of the chemical space of solid-state electrolytes
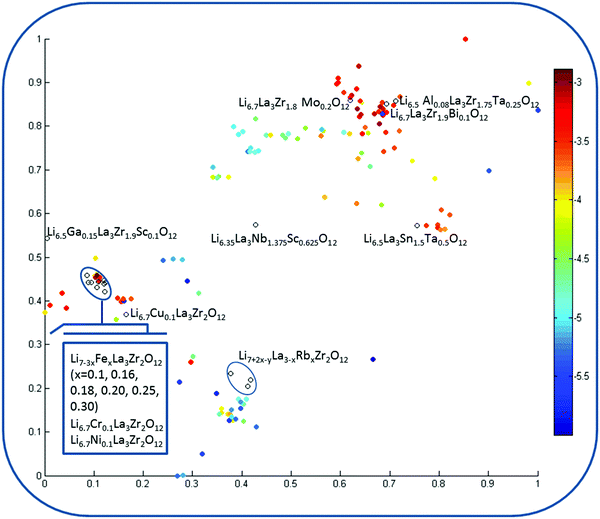
Visualization of the chemical space of garnet-type solid electrolytes was performed using t-stochastic triplet embedding (t-STE) (Fig. 7). Each point in the obtained map is an individual compound; the color corresponds to the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σtot value. The external test set compounds are represented by black circles. One can see that almost all of these compounds are situated in the area corresponding to high log
σtot value. The external test set compounds are represented by black circles. One can see that almost all of these compounds are situated in the area corresponding to high log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σtot values. The distribution of the compounds is in agreement with the SVR conductivity prediction. The reasonable separation of the areas of chemical space in accordance with the log
σtot values. The distribution of the compounds is in agreement with the SVR conductivity prediction. The reasonable separation of the areas of chemical space in accordance with the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σtot value of the compounds confirms the appropriateness of the choice of descriptors for elucidating composition–structure–property relationships because t-STE is related to unsupervised techniques where the information on the property value is not involved in the process of the model development itself and is engaged only for final data visualization of the already obtained model if needed. One can see that among the proposed compounds, only Rb+-substituted LLZO is projected to the areas of the low total conductivity space. All the other “virtual” compounds form a distinct cluster joined with the Ga3+ and Al3+-stabilized LLZO compounds.
σtot value of the compounds confirms the appropriateness of the choice of descriptors for elucidating composition–structure–property relationships because t-STE is related to unsupervised techniques where the information on the property value is not involved in the process of the model development itself and is engaged only for final data visualization of the already obtained model if needed. One can see that among the proposed compounds, only Rb+-substituted LLZO is projected to the areas of the low total conductivity space. All the other “virtual” compounds form a distinct cluster joined with the Ga3+ and Al3+-stabilized LLZO compounds.
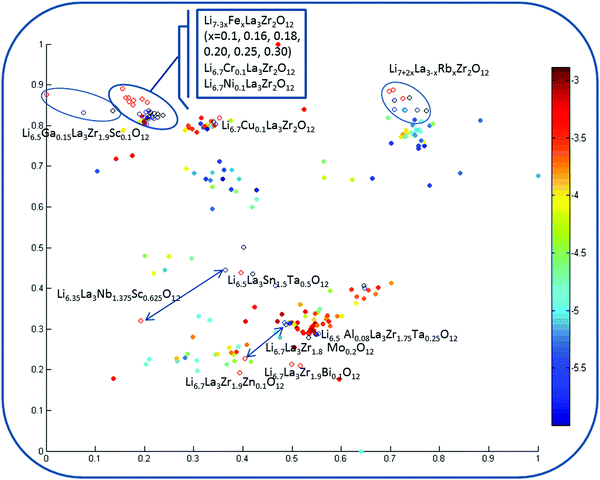
Fig. 8 corresponds to the model involving experimental information as an additional descriptor pool and reflecting the analysis from the viewpoint of the impact of these parameters on the property space. First of all, one can observe the significantly lowest discrepancy for the data visualization models among the considered property spaces defined by the descriptors in use compared with the regression models, where this difference was substantial. Second, one can see the relatively reduced area corresponding to high log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σtot values.
σtot values.
Two cases for three descriptor pools are considered: two types of normalization where (i) parameters responsible for the materials synthesis information were scaled to union variance in order to avoid the dominant contribution of any or (ii) re-weighted (by multiplying by 2) parameters for (a) virtual compounds that have been generated as synthesized by conventional one-step solid state reactions (sintering temperature 1100 °C; time 36 h; represented as black mark points in the figure); (b) the same data obtained via two-stage sintering processes (the sintering conditions have been taken from published studies – sintering temperature 900 °C/1100 °C; time 24/6 h; labeled by red guide-marks); (c) finally, the descriptor pool corresponding to sol–gel synthesis with experimental conditions conforming with published studies (sintering temperature 1200 °C; time 36 h; compounds represented as blue circles), i.e. the same candidate compounds in the map are distinguished by different color coding related to the synthesis conditions. Results of the second normalization scheme are given in Fig. 8 because they appeared to be more meaningful (in the models using the descriptor scaling to union variance scheme, the weight of the experimental information is minimized).
To sum up, reasonable levels of predictive ability of the models have been achieved. The predictive errors (RMSE and MAE) are comparable with the variance in the total conductivities for the same compounds extracted from different publications. The observed limitations of the predictive ability of the models can be concerned with different aspects. Obviously, one of the most valuable stages is the selection of descriptors. Here, we have used a simple and even naive approach that is based mostly on “geometrical” insights into the problem. However, the predictive performance of the developed models argues that they were sufficiently successful that it would be reasonable to extend these efforts to answer a number of pivotal questions that were not addressed here. Another serious limitation of the developed models is related to the ionic radii of Li. Thus, the problem considered in ref. 75 was ignored here and the models were desensitized by choosing one frozen ionic radius value corresponding to tetrahedral coordination. Moreover, using the information in ref. 75 in test computations had no impact on the predictive ability of the models.
Additionally, the collected data has not been used sufficiently. Thus, information on the activation energy, pressure, use of the hot pressure approach, formation of secondary phases, and precursors used as well as the relative densities of the obtained samples have not been included in this study.
4. Conclusions
Several types of parameters related to different categories have been used as descriptors to develop a model to identify the descriptors that are responsible for high Li-ion conductivity in garnet-structured oxides; most of the identified parameters were geometry-based and stemmed from the interrelations of constituent element radii with geometric principles of ion packing.The Li ion transport characteristics of garnet-structured oxides were analyzed combining regression analysis by support vector regression (SVR), thus unraveling the composition–structure–ionic conductivity relationships and surveying garnet-related structures for promising compositions with t-stochastic triplet embedding (t-STE), which is related to the group of approaches known in computer-aided molecular design as chemography or cartography methods and which circumscribes the materials space of solid electrolytes; this is attractive for virtual screening. A reasonable level of predictive ability of the models was achieved (the statistical parameters R2, RMSE and MAE of the SVR model are as high as 0.778, 0.372 and 0.283, respectively). The predictive errors (RMSE and MAE) are comparable with the variance in the total conductivities for the same compounds extracted from different publications. The observed limitations of the predictive ability of the models can involve different aspects, such as the choice of descriptors or the intrinsic variance in the experimental data. The models obtained by t-STE demonstrate clear allocation of the areas of chemical space in accordance with the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σtot value of the compounds; this confirms the appropriateness of the chosen descriptors for elucidating composition–structure–property relationships and enables an intuitively understandable method of structure optimization. Both models were used to evaluate the log
σtot value of the compounds; this confirms the appropriateness of the chosen descriptors for elucidating composition–structure–property relationships and enables an intuitively understandable method of structure optimization. Both models were used to evaluate the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σtot values for the candidate compounds recommended for synthesis.
σtot values for the candidate compounds recommended for synthesis.
Heuristic elucidation of the relative site preferences of Al3+ and Ga3+ cations was attempted. The character of the obtained results has been discussed. We attempted to distinguish compounds that can be potentially instable to moisture. The possible instability of garnet structures to moisture was related to tetrahedral and octahedral site accommodation by Li+. Unfortunately, the results obtained are not sufficient for any conclusions.
Several candidate compounds have been recommended for synthesis as potential solid state electrolyte materials.
Acknowledgements
The authors are grateful to the Russian Foundation for Basic Research (Project No. 17-03-00835) for their support. NK acknowledges Dr Vitaly Solov'ev and Dr E. V. Makhonina for their helpful comments.References
- J. F. M. Oudenhoven, L. Baggetto and P. H. L. Notten, Adv. Energy Mater., 2011, 1, 10–33 CrossRef CAS.
- J. B. Goodenough and P. Singh, J. Electrochem. Soc., 2015, 162, A2387–A2392 CrossRef CAS.
- J. Jensen and F. C. Krebs, Adv. Mater., 2014, 26, 7231–7234 CrossRef CAS PubMed.
- X. Xia, Z. Ku, D. Zhou, Y. Zhong, Y. Zhang, Y. Wang, M. J. Huang, J. Tu and H. J. Fan, Mater. Horiz., 2016, 3, 588–595 RSC.
- J. C. Bachman, S. Muy, A. Grimaud, H.-H. Chang, N. Pour, S. F. Lux, O. Paschos, F. Maglia, S. Lupart, P. Lamp, L. Giordano and Y. Shao-Horn, Chem. Rev., 2016, 116, 140–162 CrossRef CAS PubMed.
- R. Chen, W. Qu, X. Guo, L. Li and F. Wu, Mater. Horiz., 2016, 3, 487–516 RSC.
- P. Knauth, Solid State Ionics, 2009, 180, 911–916 CrossRef CAS.
- E. Quartarone and P. Mustarelli, Chem. Soc. Rev., 2011, 40, 2525–2540 RSC.
- Y. Ren, K. Chen, R. Chen, T. Liu, Y. Zhang and C.-W. Nan, J. Am. Ceram. Soc., 2015, 98, 3603–3623 CrossRef CAS.
- S. Stramare, V. Thangadurai and W. Weppner, Chem. Mater., 2003, 15, 3974–3990 CrossRef CAS.
- V. Thangadurai, S. Narayanan and D. Pinzaru, Chem. Soc. Rev., 2014, 43, 4714–4727 RSC.
- V. Thangadurai, D. Pinzaru, S. Narayanan and A. K. Baral, J. Phys. Lett., 2015, 6, 292–299 CAS.
- P. Dey, J. Bible, S. Datta, S. Broderick, J. Jasinski, M. Sunkara, M. Menon and K. Rajan, Comput. Mater. Sci., 2014, 83, 185–195 CrossRef CAS.
- K. Fujimura, A. Seko, Y. Koyama, A. Kuwabara, I. Kishida, K. Shitara, C. A. J. Fisher, H. Moriwake and I. Tanaka, Adv. Energy Mater., 2013, 3, 980–985 CrossRef CAS.
- R. Jalem, T. Aoyama, M. Nakayama and M. Nogami, Chem. Mater., 2012, 24, 1357–1364 CrossRef CAS.
- R. Jalem, M. Kimura, M. Nakayama and T. Kasuga, J. Chem. Inf. Model., 2015, 55, 1158–1168 CrossRef CAS PubMed.
- R. Jalem, M. Nakayama and T. Kasuga, J. Mater. Chem. A, 2014, 2, 720–734 CAS.
- M. S. Park, I. Park, Y.-S. Kang, D. Im and S.-G. Doo, Phys. Chem. Chem. Phys., 2016, 18, 26807–26815 RSC.
- E. O. Pyzer-Knapp, K. Li and A. Aspuru-Guzik, Adv. Funct. Mater., 2015, 25, 6495–6502 CrossRef CAS.
- E. O. Pyzer-Knapp, G. N. Simm and A. Aspuru Guzik, Mater. Horiz., 2016, 3, 226–233 RSC.
- D. J. Scott, P. V. Coveney, J. A. Kilner, J. C. H. Rossiny and N. M. N. Alford, J. Eur. Ceram. Soc., 2007, 27, 4425–4435 CrossRef CAS.
- P. V. Balachandran, J. Theiler, J. M. Rondinelli and T. Lookman, Sci. Rep., 2016, 5, 13285 CrossRef PubMed.
- S. Curtarolo, G. L. W. Hart, M. B. Nardelli, N. Mingo, S. Sanvito and O. Levy, Nat. Mater., 2013, 12, 191–201 CrossRef CAS PubMed.
- M. de Jong, W. Chen, R. Notestine, K. Persson, G. Ceder, A. Jain, M. Asta and A. Gamst, Sci. Rep., 2016, 6, 34256 CrossRef CAS PubMed.
- P. E. Dolgirev, I. A. Kruglov and A. R. Oganov, AIP Adv., 2016, 6, 085318 CrossRef.
- V. C. Epa, A. L. Hook, C. Chang, J. Yang, R. Langer, D. G. Anderson, P. Williams, M. C. Davies, M. R. Alexander and D. A. Winkler, Adv. Funct. Mater., 2013, 24, 2085–2093 CrossRef.
- R. Gomez-Bombarelli, J. Aguilera-Iparraguirre, T. D. Hirzel, D. Duvenaud, D. Maclaurin, M. A. Blood-Forsythe, H. S. Chae, M. Einzinger, D.-G. Ha, T. Wu, G. Markopoulos, S. Jeon, H. Kang, H. Miyazaki, M. Numata, S. Kim, W. Huang, S. I. Hong, M. Baldo, R. P. Adams and A. Aspuru-Guzik, Nat. Mater., 2016, 15, 1120–1127 CrossRef CAS PubMed.
- F. Hase, S. Valleau, E. Pyzer-Knapp and A. Aspuru-Guzik, Chem. Sci., 2016, 7, 5139–5147 RSC.
- O. Isayev, D. Fourches, E. N. Muratov, C. Oses, K. Rasch, A. Tropsha and S. Curtarolo, Chem. Mater., 2015, 27, 735–743 CrossRef CAS.
- N. N. Kiselyova, A. V. Stolyarenko, V. V. Ryazanov, O. V. Senko and A. A. Dokukin, Russ. J. Inorg. Chem., 2016, 61, 604–609 CrossRef CAS.
- C. S. Kong, W. Luo, S. Arapan, P. Villars, S. Iwata, R. Ahuja and K. Rajan, J. Chem. Inf. Model., 2012, 52, 1812–1820 CrossRef CAS PubMed.
- T. C. Le, H. Yin, R. Chen, Y. Chen, L. Zhao, P. S. Casey, C. Chen and D. A. Winkler, Small, 2016, 12, 3568–3577 CrossRef CAS PubMed.
- Y. Liu, D. A. Winkler, V. C. Epa, B. Zhang and B. Yan, Nano Res., 2015, 8, 1293–1308 CrossRef CAS.
- A. O. Oliynyk, E. Antono, T. D. Sparks, L. Ghadbeigi, M. W. Gaultois, B. Meredig and A. Mar, Chem. Mater., 2016, 28, 7324–7331 CrossRef CAS.
- S. Srinivasan, S. R. Broderick, R. Zhang, A. Mishra, S. B. Sinnott, S. K. Saxena, J. M. LeBeau and K. Rajan, Sci. Rep., 2016, 5, 17960 CrossRef PubMed.
- A. W. Thornton, D. A. Winkler, M. S. Liu, M. Haranczyk and D. F. Kennedy, RSC Adv., 2015, 5, 44361–44370 RSC.
- D. A. Winkler, Toxicol. Appl. Pharmacol., 2016, 299, 96–100 CrossRef CAS PubMed.
- H. Xu, R. Liu, A. Choudhary and W. Chen, J. Mech. Design., 2015, 137, 051403 CrossRef.
- U. Zavyalova, M. Holena, R. Schlögl and M. Baerns, ChemCatChem, 2011, 3, 1935–1947 CrossRef CAS.
- J. B. Goodenough and Y. Kim, Chem. Mater., 2010, 22, 587–603 CrossRef CAS.
- X. Han, Y. Gong, K. Fu, X. He, G. T. Hitz, J. Dai, A. Pearse, B. Liu, H. Wang, G. Rubloff, Y. Mo, V. Thangadurai, E. D. Wachsman and L. Hu, Nat. Mater., 2016, 16, 572–580 CrossRef PubMed.
- J.-L. Reymond, Acc. Chem. Res., 2015, 48, 722–730 CrossRef CAS PubMed.
- N. Kireeva, I. Baskin, H. Gaspar, D. Horvath, G. Marcou and A. Varnek, Mol. Inf., 2012, 31, 301–312 CrossRef CAS PubMed.
- N. Kireeva, S. L. Kuznetsov and A. Y. Tsivadze, Ind. Eng. Chem. Res., 2012, 51, 14337–14343 CrossRef CAS.
- K. Klimenko, G. Marcou, D. Horvath and A. Varnek, J. Chem. Inf. Model., 2016, 56, 1438–1454 CrossRef CAS PubMed.
- M. Reutlinger and G. Schneider, J. Mol. Graphics Modell., 2012, 34, 108–117 CrossRef CAS PubMed.
- R. Wagner, G. J. Redhammer, D. Rettenwander, G. Tippelt, A. Welzl, S. Taibl, J. Fleig, A. Franz, W. Lottermoser and G. Amthauer, Chem. Mater., 2016, 28, 5943–5951 CrossRef CAS PubMed.
- C. Bernuy-Lopez, W. Manalastas, J. M. Lopez del Amo, A. Aguadero, F. Aguesse and J. A. Kilner, Chem. Mater., 2014, 26, 3610–3617 CrossRef CAS.
- M. A. Howard, O. Clemens, E. Kendrick, K. S. Knight, D. C. Apperley, P. A. Anderson and P. R. Slater, Dalton Trans., 2012, 41, 12048–12053 RSC.
- R. Jalem, M. J. D. Rushton, W. Manalastas, M. Nakayama, T. Kasuga, J. A. Kilner and R. W. Grimes, Chem. Mater., 2015, 27, 2821–2831 CrossRef CAS.
- D. Rettenwander, J. Langer, W. Schmidt, C. Arrer, K. J. Harris, V. Terskikh, G. R. Goward, M. Wilkening and G. Amthauer, Chem. Mater., 2015, 27, 3135–3142 CrossRef CAS.
- J. Wolfenstine, J. Ratchford, E. Rangasamy, J. Sakamoto and J. L. Allen, Mater. Chem. Phys., 2012, 134, 571–575 CrossRef CAS.
- D. Fourches, E. Muratov and A. Tropsha, J. Chem. Inf. Model., 2010, 50, 1189–1204 CrossRef CAS PubMed.
- D. Fourches, E. Muratov and A. Tropsha, Nat. Chem. Biol., 2015, 11, 535 CrossRef CAS PubMed.
- D. Fourches, E. Muratov and A. Tropsha, J. Chem. Inf. Model., 2016, 56, 1243–1252 CrossRef CAS PubMed.
- R. D. Chirico, M. Frenkel, J. W. Magee, V. Diky, C. D. Muzny, A. F. Kazakov, K. Kroenlein, I. Abdulagatov, G. R. Hardin, W. E. Acree, J. F. Brenneke, P. L. Brown, P. T. Cummings, T. W. de Loos, D. G. Friend, A. R. H. Goodwin, L. D. Hansen, W. M. Haynes, N. Koga, A. Mandelis, K. N. Marsh, P. M. Mathias, C. McCabe, J. P. O’Connell, A. Pádua, V. Rives, C. Schick, J. P. M. Trusler, S. Vyazovkin, R. D. Weir and J. Wu, J. Chem. Eng. Data, 2013, 58, 2699–2716 CrossRef CAS.
- C. M. Powers, K. A. Mills, S. A. Morris, F. Klaessig, S. Gaheen, N. Lewinski and C. Ogilvie Hendren, Beilstein J. Nanotechnol., 2015, 6, 1860–1871 CrossRef CAS PubMed.
- C. O. Hendren, C. M. Powers, M. D. Hoover and S. L. Harper, Beilstein J. Nanotechnol., 2015, 6, 1752–1762 CrossRef CAS PubMed.
- I. Cortés-Ciriano and A. Bender, ChemMedChem, 2016, 11, 57–71 CrossRef PubMed.
- C. Wang, Y. Gong, B. Liu, K. Fu, Y. Yao, E. Hitz, Y. Li, J. Dai, S. Xu, W. Luo, E. D. Wachsman and L. Hu, Nano Lett., 2017, 17, 565–571 CrossRef CAS PubMed.
- Z. Deng, Y. Mo and S. P. Ong, NPG Asia Mater., 2016, 8, e254 CrossRef CAS.
- Y. Wang, W. D. Richards, S. P. Ong, L. J. Miara, J. C. Kim, Y. Mo and G. Ceder, Nat. Mater., 2015, 14, 1026–1031 CrossRef CAS PubMed.
- Z. Lu, C. Chen, Z. M. Baiyee, X. Chen, C. Niu and F. Ciucci, Phys. Chem. Chem. Phys., 2015, 17, 32547–32555 RSC.
- W. Li, E. Ionescu, R. Riedel and A. Gurlo, J. Mater. Chem. A, 2013, 1, 12239–12245 CAS.
- K. M. Ok, P. S. Halasyamani, D. Casanova, M. Llunell, P. Alemany and S. Alvarez, Chem. Mater., 2006, 18, 3176–3183 CrossRef CAS.
- N. M. Halberstam, I. I. Baskin, V. A. Palyulin and N. S. Zefirov, Mendeleev Commun., 2002, 12, 185–186 CrossRef.
- M. Nele, A. Vidal, D. L. Bhering, J. Carlos Pinto and V. M. M. Salim, Appl. Catal., A, 1999, 178, 177–189 CrossRef CAS.
- O. Wodo, S. Broderick and K. Rajan, MRS Bull., 2016, 41, 603–609 CrossRef.
- Database on properties of chemical elements “Elements”, http://phases.imet-db.ru/elements/main.aspx.
- O. Ivanciuc, in Reviews in Computational Chemistry, ed. T. R. C. Kenny and B. Lipkowitz, 2007, pp. 291–400 Search PubMed.
- V. N. Vapnik, The Nature of Statistical Learning Theory, 2000 Search PubMed.
- C.-C. Chang and C.-J. Lin, LIBSVM: a library for support vector machines, 2001, software available at http://www.csie.ntu.edu.tw/~cjlin/libsvm.
- L. Maaten, Proceedings of the IEEE International Workshop on Machine Learning for Signal Processing, 2012 Search PubMed.
- Principal Component Analysis, ed. I. T. Jolliffe, Springer, New York, 2002 Search PubMed.
- T. Thompson, A. Sharafi, M. D. Johannes, A. Huq, J. L. Allen, J. Wolfenstine and J. Sakamoto, Adv. Energy Mater., 2015, 5, 1500096 CrossRef.
- N. Li, R. An, Y. Su, F. Wu, L. Bao, L. Chen, Y. Zheng, H. Shou and S. Chen, J. Mater. Chem. A, 2013, 1, 9760–9767 CAS.
- C. Deviannapoorani, S. Ramakumar, M. M. Ud Din and R. Murugan, RSC Adv., 2016, 6, 94706–94716 RSC.
- A. J. Martinolich and J. R. Neilson, Chem. Mater., 2017, 29, 479–489 CrossRef CAS.
- M. M. Ahmad and M. M. Al-Quaimi, Phys. Chem. Chem. Phys., 2015, 17, 16007–16014 RSC.
- S. Narayanan and V. Thangadurai, J. Power Sources, 2011, 196, 8085–8090 CrossRef CAS.
- H. Peng, Q. Wu and L. Xiao, J. Sol-Gel Sci. Technol., 2013, 66, 175–179 CrossRef CAS.
- V. Thangadurai and W. Weppner, J. Am. Ceram. Soc., 2005, 88, 411–418 CrossRef CAS.
- V. Thangadurai, H. Kaack and W. J. F. Weppner, J. Am. Ceram. Soc., 2003, 86, 437–440 CrossRef CAS.
- V. Thangadurai and W. Weppner, J. Solid State Chem., 2006, 179, 974–984 CrossRef CAS.
- L. Truong and V. Thangadurai, Chem. Mater., 2011, 23, 3970–3977 CrossRef CAS.
- Y. X. Gao, X. P. Wang, W. G. Wang and Q. F. Fang, Solid State Ionics, 2010, 181, 33–36 CrossRef CAS.
- M. Kotobuki and K. Kanamura, Ceram. Int., 2013, 39, 6481–6487 CrossRef CAS.
- C. R. Mariappan, K. I. Gnanasekar, V. Jayaraman and T. Gnanasekaran, J. Electroceram., 2013, 30, 258–265 CrossRef CAS.
- Y. Wang and W. Lai, Electrochem. Solid-State Lett., 2012, 15, A68–A71 CrossRef CAS.
- W. G. Zeier, S. Zhou, B. Lopez-Bermudez, K. Page and B. C. Melot, ACS Appl. Mater. Interfaces, 2014, 6, 10900–10907 CAS.
- J. Awaka, N. Kijima, Y. Takahashi, H. Hayakawa and J. Akimoto, Solid State Ionics, 2009, 180, 602–606 CrossRef CAS.
- I. Kokal, K. V. Ramanujachary, P. H. L. Notten and H. T. Hintzen, Mater. Res. Bull., 2012, 47, 1932–1935 CrossRef CAS.
- R. Murugan, V. Thangadurai and W. Weppner, J. Electrochem. Soc., 2008, 155, A90–A101 CrossRef CAS.
- R. Murugan, V. Thangadurai and W. Weppner, Appl. Phys. A: Mater. Sci. Process., 2008, 91, 615–620 CrossRef CAS.
- V. Thangadurai and W. Weppner, Adv. Funct. Mater., 2005, 15, 107–112 CrossRef CAS.
- D. Rettenwander, G. Redhammer, F. Preishuber-Pflügl, L. Cheng, L. Miara, R. Wagner, A. Welzl, E. Suard, M. M. Doeff, M. Wilkening, J. Fleig and G. Amthauer, Chem. Mater., 2016, 28, 2384–2392 CrossRef CAS PubMed.
- W. H. Kan, L. Truong and V. Thangadurai, Ionics, 2014, 21, 373–379 CrossRef.
- T. Zaiss, M. Ortner, R. Murugan and W. Weppner, Ionics, 2010, 16, 855–858 CrossRef CAS.
- A. Gupta, R. Murugan, M. P. Paranthaman, Z. Bi, C. A. Bridges, M. Nakanishi, A. P. Sokolov, K. S. Han, E. W. Hagaman, H. Xie, C. B. Mullins and J. B. Goodenough, J. Power Sources, 2012, 209, 184–188 CrossRef CAS.
- S. Ramakumar, L. Satyanarayana, S. V. Manorama and R. Murugan, Phys. Chem. Chem. Phys., 2013, 15, 11327–11338 RSC.
- Y. X. Gao, X. P. Wang, W. G. Wang and Q. F. Fang, Solid State Ionics, 2010, 181, 33–36 CrossRef CAS.
- R. Murugan, V. Thangadurai and W. Weppner, Appl. Phys. A: Mater. Sci. Process., 2008, 91, 615–620 CrossRef CAS.
- C. Galven, G. Corbel, F. Le Berre and M.-P. Crosnier-Lopez, Inorg. Chem., 2016, 55, 12872–12880 CrossRef CAS PubMed.
- E. Rangasamy, J. Wolfenstine, J. Allen and J. Sakamoto, J. Power Sources, 2013, 230, 261–266 CrossRef CAS.
- L. Cheng, J. S. Park, H. Hou, V. Zorba, G. Chen, T. Richardson, J. Cabana, R. Russo and M. Doeff, J. Mater. Chem. A, 2014, 2, 172–181 CAS.
- L. Buannic, B. Orayech, J.-M. López Del Amo, J. Carrasco, N. A. Katcho, F. Aguesse, W. Manalastas, W. Zhang, J. Kilner and A. Llordés, Chem. Mater., 2017, 29, 1769–1778 CrossRef CAS.
- Y. Matsuda, Y. Itami, K. Hayamizu, T. Ishigaki, M. Matsui, Y. Takeda, O. Yamamoto and N. Imanishi, RSC Adv., 2016, 6, 78210–78218 RSC.
- H. Nemori, Y. Matsuda, M. Matsui, O. Yamamoto, Y. Takeda and N. Imanishi, Solid State Ionics, 2014, 266, 9–12 CrossRef CAS.
- X. Liu, Y. Li, T. Yang, Z. Cao, W. He, Y. Gao, J. Liu, G. Li and Z. Li, J. Am. Ceram. Soc., 2017, 100, 1527–1533 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: The collected data used in this study. See DOI: 10.1039/c7cp00518k |
| This journal is © the Owner Societies 2017 |