Effect of chirality on monoacylglycerol ester monolayer characteristics: 3-monostearoyl-sn-glycerol

Abstract

The effect of chirality on the thermodynamic behavior, the morphological features, and the 2D lattice structures of 3-monostearoyl-sn-glycerol monolayers is studied. The present study focusses on the influence of the alkyl chain length on the chiral discrimination. Surface pressure–area (π–A) isotherms, Brewster angle microscopy (BAM), and particularly, grazing incidence X-ray diffraction (GIXD) are the experimental basis of the presented results. The π–A isotherms of the enantiomeric 3-monostearoyl-sn-glycerol monolayers measured between 25 and 38 °C resemble those of the racemic 1-monostearoyl-rac-glycerol monolayers, thus indicating small energetic differences between the enantiomeric and the racemic forms. The absolute ΔS values increase as the temperature decreases and thus, the ordering of the condensed phase increases at lower temperatures. The extrapolation to zero ΔS provides a critical temperature T_c of 42.1 °C (315.3 K), above which the monolayer cannot be compressed into the condensed state. Despite the great tendency of the 3-monostearoyl-sn-glycerol domains to develop irregular deviations in shape and inner texture, regular domains similar to those of the racemic monoacylglycerol esters are also formed. GIXD measurements performed over a large range of lateral pressures at four different temperatures (5, 10, 15 and 20 °C) indicate the dominance of the chiral nature. Contour plots with three clearly separated diffraction signals are observable in a large pressure range which is shifted to higher lateral pressures with increasing temperature. The comparison with the contour plots of the homologous 3-monopalmitoyl-sn-glycerol monolayers reveals the stronger dominance of the chiral nature with increasing alkyl chain length and thus, demonstrates the stronger influence of the lattice symmetry. The lattice data obtained by fitting the contour plots with 3 or 2 peaks demonstrate the resemblance to orthorhombic structures with NN tilted molecules at low pressures and NNN tilted molecules at high pressures. The temperature and alkyl chain length dependence of the distortion at zero tilt angle, d₀, of the enantiomeric and racemic monoacylglycerols shows an increased influence of chirality on the lattice distortion for the shorter-chain compound (equivalent to increased temperature). This demonstrates that lattice distortion and lattice symmetry are differently influenced by chirality.

---

Introduction

Chiral objects are abundant in nature and are operative in many biological systems at both microscopic as well as macroscopic levels. Therefore, chirality-based model systems are of permanent interest. Design and characterization of molecules which can form attractive and sophisticated hierarchical chiral nanoarchitectures have been the focus of the current attention in order to mimic natural chiral nanostructures.^1–3

Defined amphiphilic monolayers at the air/water interface have been used as promising model approaches for a better understanding of specific phenomena of inherently complex biological and technological processes.^4–7 Monoacylglycerols have been frequently used for model studies of the enantiomeric and racemic monolayers of monoglycerol ethers,^8–10 esters,^11–15 amines,^16,17 and amides¹⁸ using BAM, fluorescence microscopy and GIXD.

Monoacylglycerol esters are ubiquitous in a large diversity of biological and applied systems.^19–21 They are composed of a glycerol backbone linked by an ester group to an alkyl chain. The alkyl chain located at the end of the glycerol backbone gives rise to an optically active carbon atom in the C-2 position. Palmitoyl and stearoylglycerol esters have been the most examined saturated monoacylglycerol ester monolayers for understanding their role in inherently complex biological processes and solid lipid nanoparticles for drug delivery systems.^22–24

In recent papers,^25,26 systematic studies of the racemic 1-monopalmitoyl-rac-glycerol and 1-monostearoyl-rac-glycerol monolayers in the accessible temperature and pressure regions resulted in the construction of the generic π–T phase diagram of racemic monoacylglycerol monolayers on the basis of the individual phase diagrams of the racemic 1-monopalmitoyl-rac-glycerol and 1-monostearoyl-rac-glycerol monolayers. It is interesting to refer to the first evidence for symmetry breaking in a monolayer of a racemic surfactant. An oblique intermediate phase occurs surprisingly between the orthorhombic lattices with the NN and NNN tilt directions in the low-temperature range of 1-monostearoyl-rac-glycerol monolayers.

In particular, 1-monopalmitoyl-rac-glycerol monolayers display regular mesoscopic domains with perfect topography that allowed the geometric analysis of the inner segment structure. These domains are subdivided into seven segments of different uniform brightness that meet in a center, at which the alkyl chain tilt azimuth jumps by a defined angle of ∼51 deg. The alkyl chains have different azimuthal orientation in each segment. Based on the geometric analysis of this domain texture, it was concluded that the alkyl chains are tilted along the bisector of each segment and that the segment boundaries are along the next-nearest neighbor directions.^12,13 A similar mesoscopic domain topography was found in other homologous 1-monoacyl-glycerol monolayers.

These general insights into the monolayer characteristics of the racemic monoacylglycerols represent a good prerequisite to compare the racemic and enantiomeric main characteristics of monoacylglycerols for conducting a general survey of the effect of chirality-dependent interactions in the chiral monoacylglycerol monolayers. The objective of the present work is to characterize the influence of chirality on the thermodynamic behavior, morphological features, and 2D lattice structures of 3-monostearoyl-sn-glycerol monolayers.

Experimental

For the monolayer experiments, 3-monostearoyl-sn-glycerol (Sigma, purity ≥99 mol%) dissolved in heptane/ethanol (9 : 1) (Merck p.a. grade) was spread on ultrapure water with a specific resistance of 18.2 MΩ cm, obtained from a Millipore desktop system.

The equilibrium surface pressure–molecular area (π–A) isotherms, recorded at a compression rate of ≤10 Ų (molecule min)⁻¹, were measured using an experimental setup consisting of a self-made, computer-interfaced film balance²⁷ using the Wilhelmy method with a roughened glass plate to measure the surface tension with an accuracy of ±0.1 mN m⁻¹ and the molecular area with ±0.5 Ų. BAM measurements were carried out using the Nanofilm-UltraBAM, Accurion GmbH, Göttingen. Detailed information about the BAM method is given elsewhere (see, e.g., ref. 27–29 and references therein).

The grazing incidence X-ray diffraction (GIXD) measurements were performed at the BW1 beamline, HASYLAB (Hamburg, Germany). In the experimental setup, a Langmuir film balance equipped with a movable barrier and a Wilhelmy plate for monitoring the lateral pressure was placed in a helium-flushed container with Kapton windows transparent for X-rays. A monochromatic X-ray beam (λ = 1.304 Å) is adjusted to strike the water surface at a grazing incidence angle slightly below the critical angle for total reflection to produce an evanescent wave, which propagates with high sensitivity along the surface and has a penetration depth of 8 nm. It illuminates an approximately 2 × 50 mm² monolayer surface and can be diffracted by lateral structures in the monolayer. The trough is slowly laterally moved during the experiment, to avoid sample damage by the strong X-ray beam. A linear position-sensitive detector (PSD, OEM-100-M, Braun, Garching, Germany) measured the diffracted signal and was rotated to scan the in-plane Q_xy component values of the scattering vector. The vertical channels of the PSD measured the out-of-plane Q_z component of the scattering vector between 0 and 0.85 Å⁻¹.

The analysis of the obtained diffraction patterns provides information about the lattice structure of the monolayer. The Bragg peaks, obtained by integration of the scattering intensity (corrected for polarization, effective area, and Lorentz factor) over a certain Q_z window, and the Bragg rods, obtained by the integration of the scattering intensity over a certain Q_xy window, provide information about the unit cell dimensions (lattice parameters a, b, c, in-plane area A_xy, cross-sectional area A₀, tilt angle t). The in-plane lattice repeat distances, d, of the ordered structures in the monolayer were calculated from the Bragg peak positions: d = 2π/Q_xy. The in-plane coherence length, L_xy, was approximated from the full-width at half-maximum (fwhm) of the Bragg peaks using L_xy ∼ 0.9(2π)/fwhm(Q_xy). The thickness of the scattering unit can be estimated from the fwhm of the Bragg rod using 0.9(2π)/fwhm(Q_z). More details are presented in the literature.^30–32

Results and discussion

The experimental π–A isotherms of the 3-monostearoyl-sn-glycerol monolayers spread on pure water and measured at different temperatures in the range between 25 and 38 °C are presented in Fig. 1.

Fig. 1 π–A isotherms of 3-monostearoyl-sn-glycerol monolayers spread on water and measured in the temperature range between 25 °C and 38 °C.

Generally, the features of the π–A isotherms of 1-monostearoyl-rac-glycerol resemble those of usual monolayers of amphiphiles.³³ According to the rather long alkyl chain (C₁₈) the main phase transition is shifted to the high-temperature range (>30 °C). At T < 30 °C, the shape of the isotherm, which does not show an inflection point, indicates that the condensed phase already exists at nearly zero pressure in coexistence with a fluid phase (gaseous, G) directly after spreading. At T > 30 °C, the isotherms show a clear inflection at the first-order phase transition point (A_e) from the fluid (liquid-expanded, LE) phase to the condensed phase. The extension of the following phase transition region (A < A_e) decreases in the usual way as the temperature increases. In this region, the slope of the isotherm is very small and approximated nearly to be horizontal at lower temperatures (curves 2 and 3). The characteristics of the π–A isotherms of the chiral 3-monostearoyl-sn-glycerol are similar to those of the racemic 1-monostearoyl-rac-glycerol monolayers.²⁵

The temperature dependence of the phase transition pressure (π_t) provides information about the thermodynamic characteristics for the transition between the fluid and condensed phases. Fig. 2 shows the π_t–T relationship of 3-monostearoyl-sn-glycerol monolayers on water. The slope dπ_t/dT of the linear fit to the experimental data amounts to 0.39592 mN (m K)⁻¹. At temperatures of 35 and 38 °C, the transition pressure of the racemate is 0.2 and 0.6 mN m⁻¹, respectively, slightly larger compared to that of the corresponding pure enantiomer, whereas at 30 °C it reaches already 0 mN m⁻¹, which means, 0.7 mN m⁻¹ smaller than that of the corresponding enantiomer.

Fig. 2 Temperature dependence of the main phase transition pressure, π_t of 3-monostearoyl-sn-glycerol monolayers on water. ● 3-Monostearoyl-sn-glycerol; ▲ 1-monostearoyl-rac-glycerol.

Evaluating the temperature dependence of the phase transition pressure (π_t) gives access to important thermodynamic parameters such as the transition entropy. The entropy change ΔS of the phase transition was calculated using the two-dimensional Clapeyron equation

where A_e is the molecular area at the onset of the phase transition at π_t, and A_c is the area of the corresponding condensed phase at the same lateral pressure. The temperature dependence of the entropy change, ΔS, is presented in Fig. 3.

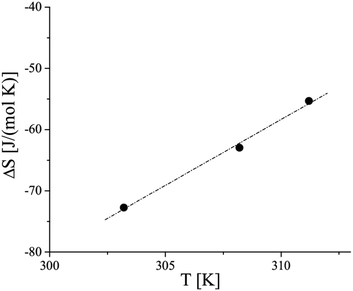Fig. 3 Temperature dependence of the entropy change at the LE/LC phase transition of 3-monostearoyl-sn-glycerol monolayers on water.

According to the exothermic nature of the main phase transition at compression of amphiphilic monolayers, negative ΔS values are obtained. The absolute ΔS values increase as the temperature decreases, indicating the increase of the condensed phase ordering at lower temperatures. The linear fit and extrapolation to zero ΔS provide the critical temperature T_c of 63.9 °C (337.1 K), above which the monolayer cannot be compressed into the condensed state. It is interesting to note that shorter chain homologues provide essentially lower T_c values having smaller differences between the enantiomeric (42.1 °C (315.3 K)) and racemic (49.2 °C (322.4 K)) forms.

The extended two-phase coexistence region (A < A_e) provides reasonable conditions for studying the domain morphology using Brewster angle microscopy at 35 °C. Typical examples are shown in Fig. 4. The mostly regular domains are subdivided into 7 optimal segments similar to the racemic monoacylglycerol esters. The different reflectivity of the segments indicates a jump-like change in the azimuthal tilt at the segment boundaries. However, in all these domains, the shape deviates already from circular, and also the inner textures show certain irregularities, such as different sizes of the segments and some shift of the contact point from the center. Despite the examples presented, the tendency to develop irregular deviations in shape and inner texture of the condensed phase domains is rather high. At further compression, the irregular structures coalesce to larger entities having several segment centers with different and often mutual segments. The reason (maybe anisotropic line tension) for the observed different positions of the segment center is not understood. Possibly, this behavior is determined by a directional effect of the growth rate of the domains.

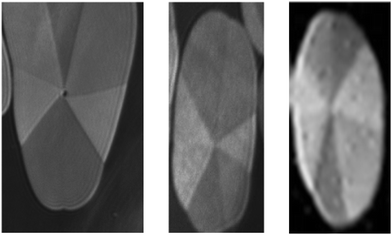Fig. 4 Examples of 3-monostearoyl-sn-glycerol domains subdivided into seven segments. Compression rate = 1 Ų (min molecule)⁻¹, T = 35 °C, image height = 1400 μm.

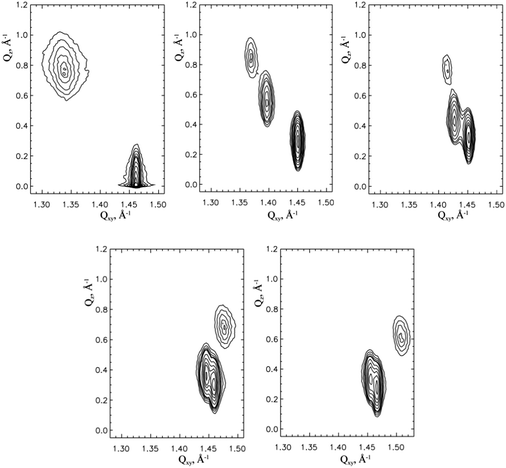
In the present study, we focused mainly on the GIXD experiments which provide insight into the characteristic features of the lattice structure of condensed monolayer phases in the Angstrom scale. GIXD measurements of 3-monostearoyl-sn-glycerol monolayers were performed over a large range of lateral pressures at four different temperatures (5, 10, 15 and 20 °C) to obtain reliable two-dimensional lattice structures in the accessible temperature and surface pressure ranges. At all pressures, the diffracted intensity is plotted as contour lines of equal intensity versus the in-plane component Q_xy and the out-of-plane component Q_z of the scattering vector. According to the chiral nature of 3-monostearoyl-sn-glycerol, three diffraction signals indicating generally an oblique lattice structure are expected to be seen at all pressures.

Fig. 5 shows the contour plots obtained at 5 °C and 2, 10, 20 (top) and 40, 50 mN m⁻¹ (bottom). The three diffraction signals are perfectly separated at 10 and 20 mN m⁻¹ and are also reasonably separated up to pressures of 40 mN m⁻¹. However, at limiting pressures of 2 and 50 mN m⁻¹ two diffraction signals strongly overlap, so that at a pressure of 2 mN m⁻¹ the contour plot resembles that of NN tilted orthorhombic structures, and at 50 mN m⁻¹ it is similar to that of NNN tilted orthorhombic structures. The Bragg peak positions, their full-widths at half-maximum and all lattice parameters obtained at 5 °C and different surface pressures are listed in Table 1.

Fig. 5 GIXD contour plots of the corrected diffraction intensities as a function of the in-plane Q_xy and out-of-plane Q_z components of the scattering vector for 3-stearoyl-sn-glycerol monolayers at 5 °C and different pressures (top: 2, 10, 20 mN m⁻¹; bottom: 40, 50 mN m⁻¹; from left to right).

Table 1 (A) Bragg peak (Q_xy) and Bragg rod (Q_z) positions and the corresponding full-widths at half-maximum of 3-stearoyl-sn-glycerol monolayers at different surface pressures π and 5 °C. (B) Lattice parameters of 3-stearoyl-sn-glycerol monolayers at 5 °C

(A)
π (mN m^−1)	Q xy (1) (Å^−1)	Q z (1) (Å^−1)	Q xy (2) (Å^−1)	Q z (2) (Å^−1)	Q xy (3) (Å^−1)	Q z (3) (Å^−1)
π is the surface pressure; a, b, c, and α, β, γ are the lattice parameters of the unit cell; t is the polar tilt angle; Axy is the molecular area; A0 is the cross-section area of the alkyl chain; lattice distortion.
1	1.448	0.173	1.335	0.754	1.314	0.925
	0.009	0.21	0.028	0.21	0.022	0.21
2	1.451	0.181	1.354	0.745	1.333	0.926
	0.010	0.21	0.026	0.21	0.026	0.21
10	1.450	0.294	1.396	0.540	1.369	0.834
	0.012	0.21	0.020	0.21	0.021	0.21
20	1.451	0.339	1.427	0.442	1.415	0.781
	0.012	0.21	0.015	0.21	0.026	0.21
30	1.453	0.338	1.449	0.442	1.425	0.781
	0.010	0.21	0.007	0.21	0.025	0.21
40	1.478	0.691	1.459	0.338	1.445	0.353
	0.032	0.21	0.013	0.21	0.013	0.21
50	1.508	0.628	1.466	0.298	1.455	0.329
	0.029	0.21	0.011	0.21	0.013	0.21

---

(B)
π (mN m^−1)	a (Å) b (Å) c (Å)	α (deg) β (deg) γ (deg)	Distortion	t (deg)	A xy (Å^2)	A 0 (Å^2)
1	5.141 5.224 5.666	123.8 122.4 113.7	0.123331	37.9	24.6	19.4
2	5.104 5.181 5.556	123.4 122.0 114.6	0.106774	36.5	24.0	19.3
10	5.039 5.135 5.337	122.5 120.8 116.7	0.068238	32.2	23.1	19.5
20	5.010 5.049 5.138	121.1 120.3 118.6	0.029902	29.3	22.2	19.4
30	4.962 5.006 5.027	120.7 119.8 119.4	0.015433	26.4	21.6	19.4
40	4.924 4.965 5.019	120.9 120.1 119.0	0.022229	24.9	21.4	19.4
50	4.847 4.883 5.023	121.4 120.7 117.8	0.043941	22.7	20.9	19.3

---

Fig. 6 displays the contour plots measured at 10 °C and 2, 10, 20 mN m⁻¹ (top) and 30, 40, 50 mN m⁻¹ (bottom). Here, the three diffraction signals are clearly separated at 10 and 20 mN m⁻¹ and satisfactorily separated at 30 mN m⁻¹. Again, at the limiting pressures two diffraction signals strongly overlap. At 2 mN m⁻¹, the contour plot resembles that of NN tilted orthorhombic structures and at 40 and 50 mN m⁻¹ it is similar to that of the NNN tilted orthorhombic structures. The lattice characteristics calculated at 10 °C are listed in Table 2.

Fig. 6 GIXD contour plots of the corrected diffraction intensities as a function of the in-plane Q_xy and out-of-plane Q_z components of the scattering vector for 3-stearoyl-sn-glycerol monolayers at 10 °C and different pressures (top: 2, 10, 20 mN m⁻¹; bottom: 30, 40, 50 mN m⁻¹; from left to right).

Table 2 (A) Bragg peak (Q_xy) and Bragg rod (Q_z) positions and the corresponding full-widths at half-maximum of 3-stearoyl-sn-glycerol monolayers at different surface pressures π and 10 °C. (B) Lattice parameters of 3-stearoyl-sn-glycerol monolayers at 10 °C

(A)
π (mN m^−1)	Q xy (1) (Å^−1)	Q z (1) (Å^−1)	Q xy (2) (Å^−1)	Q z (2) (Å^−1)	Q xy (3) (Å^−1)	Q z (3) (Å^−1)
π is the surface pressure; a, b, c, and α, β, γ are the lattice parameters of the unit cell; t is the polar tilt angle; Axy is the molecular area; A0 is the cross-section area of the alkyl chain; lattice distortion.
2	1.449	0.128	1.329	0.790	1.311	0.919
	0.010	0.21	0.028	0.21	0.023	0.21
5	1.454	0.126	1.350	0.755	1.330	0.931
	0.010	0.21	0.024	0.21	0.028	0.21
7	1.454	0.163	1.360	0.726	1.340	0.889
	0.007	0.21	0.024	0.21	0.028	0.21
10	1.453	0.179	1.370	0.697	1.345	0.876
	0.011	0.21	0.029	0.21	0.024	0.21
20	1.451	0.310	1.417	0.484	1.384	0.793
	0.013	0.21	0.020	0.21	0.023	0.21
30	1.453	0.332	1.437	0.404	1.419	0.736
	0.014	0.21	0.0	0.21	0.0	0.21
40	1.462	0.668	1.457	0.318	1.452	0.350
	0.012	0.21	0.047	0.21	0.017	0.21
50	1.485	0.602	1.470	0.299	1.462	0.303
	0.049	0.21	0.013	0.21	0.019	0.21

---

(B)
π (mN m^−1)	a (Å) b (Å) c (Å)	α (deg) β (deg) γ (deg)	Distortion	t (deg)	A xy (Å^2)	A 0 (Å^2)
2	5.152 5.223 5.695	123.9 122.7 113.4	0.128742	38.0	24.7	19.5
5	5.106 5.183 5.582	123.5 122.2 114.3	0.112797	36.2	24.1	19.5
7	5.117 5.155 5.553	123.0 122.4 114.6	0.106749	35.9	24.0	19.4
10	5.073 5.167 5.480	123.2 121.5 115.3	0.094740	35.0	23.7	19.4
20	5.004 5.123 5.246	122.3 120.1 117.6	0.054577	30.1	22.7	19.6
30	4.992 5.055 5.111	121.2 120.0 118.8	0.027337	27.5	22.1	19.6
40	4.967 4.977 5.001	120.3 120.1 119.6	0.008143	25.0	21.5	19.5
50	4.896 4.919 4.973	120.7 120.2 119.1	0.018523	22.1	21.0	19.5

---

Fig. 7 shows the contour plots measured at 15 °C and 2, 10, 20, mN m⁻¹ (top) and 30, 40 mN m⁻¹ (bottom). At this temperature, the three diffraction peaks are clearly separated at 20 mN m⁻¹ and reasonably separated at 40 mN m⁻¹. Here, due to two overlapping diffraction peaks the contour plots at low pressures of <10 mN m⁻¹ resemble that of NN tilted orthorhombic structures, and at 40 mN m⁻¹ the contour plot is similar to that of NNN tilted orthorhombic structures. All characteristic GIXD data obtained for 15 °C are listed in Table 3.

Fig. 7 GIXD contour plots of the corrected diffraction intensities as a function of the in-plane Q_xy and out-of-plane Q_z components of the scattering vector for 3-stearoyl-sn-glycerol monolayers at 15 °C and different pressures (top: 2, 10, 20 mN m⁻¹; bottom: 30, 40 mN m⁻¹; from left to right).

Table 3 (A) Bragg peak (Q_xy) and Bragg rod (Q_z) positions and the corresponding full-widths at half-maximum of 3-stearoyl-sn-glycerol monolayers at different surface pressures π and 15 °C. (B) Lattice parameters of 3-stearoyl-sn-glycerol monolayers at 15 °C

(A)
π (mN m^−1)	Q xy (1) (Å^−1)	Q z (1) (Å^−1)	Q xy (2) (Å^−1)	Q z (2) (Å^−1)	Q xy (3) (Å^−1)	Q z (3) (Å^−1)
π is the surface pressure; a, b, c, and α, β, γ are the lattice parameters of the unit cell; t is the polar tilt angle; Axy is the molecular area; A0 is the cross-section area of the alkyl chain; lattice distortion.
0.5	1.452	0.084	1.316	0.812	1.301	0.895
	0.010	0.21	0.041	0.21	0.011	0.21
2	1.457	0.077	1.326	0.808	1.310	0.961
	0.012	0.21	0.030	0.21	0.032	0.21
10	1.457	0.097	1.359	0.739	1.342	0.835
	0.010	0.21	0.026	0.21	0.024	0.21
17	1.462	0.140	1.395	0.650	1.373	0.790
	0.010	0.21	0.026	0.21	0.023	0.21
20	1.460	0.182	1.403	0.594	1.378	0.776
	0.011	0.21	0.022	0.21	0.019	0.21
30	1.460	0.293	1.440	0.422	1.410	0.715
	0.013	0.21	0.019	0.21	0.022	0.21
40	1.471	0.295	1.460	0.319	1.443	0.614
	0.017	0.21	0.017	0.21	0.026	0.21
50	1.482	0.237	1.475	0.307	1.474	0.544
	0.018	0.21	0.070	0.21	0.017	0.21

---

(B)
π (mN m^−1)	a (Å) b (Å) c (Å)	α (deg) β (deg) γ (deg)	Distortion	t (deg)	A xy (Å^2)	A 0 (Å^2)
0.5	5.172 5.231 5.772	124.2 123.2 112.6	0.143701	38.2	25.0	19.6
2	5.144 5.206 5.721	124.1 123.0 112.9	0.138421	37.6	24.7	19.5
10	5.090 5.154 5.526	123.2 122.1 114.7	0.104514	34.8	23.8	19.6
17	5.022 5.102 5.347	122.6 121.1 116.2	0.076416	31.9	23.0	19.5
20	5.012 5.103 5.310	122.5 120.8 116.7	0.068982	30.7	22.9	19.6
30	4.959 5.065 5.135	121.8 119.8 118.4	0.040377	27.0	22.1	19.6
40	4.926 4.984 5.021	121.0 119.9 119.1	0.022321	23.1	21.4	19.6
50	4.896 4.909 4.922	120.3 120.0 119.7	0.006250	19.8	20.9	19.6

---

Finally, Fig. 8 shows the contour plots measured at 20 °C and 2, 10, 20 mN m⁻¹ (top) and 30 40, 50 mN m⁻¹ (bottom). Here, the three diffraction peaks are clearly separated only at 30 mN m⁻¹. Due to two overlapping diffraction peaks the contour plots at ≤20mN m⁻¹ resemble that of NN tilted orthorhombic structures and at ≥40 mN m⁻¹ NNN tilted orthorhombic structures. The lattice characteristics calculated at 20 °C are listed in Table 4.

Fig. 8 GIXD contour plots of the corrected diffraction intensities as a function of the in-plane Q_xy and out-of-plane Q_z components of the scattering vector for 3-stearoyl-sn-glycerol monolayers at 20 °C and different pressures (top: 2, 10, 20 mN m⁻¹; bottom: 30, 40, 50 mN m⁻¹; from left to right).

Table 4 (A) Bragg peak (Q_xy) and Bragg rod (Q_z) positions and the corresponding full-widths at half-maximum of 3-stearoyl-sn-glycerol monolayers at different surface pressures π and 20 °C. (B) Lattice parameters of 3-stearoyl-sn-glycerol monolayers at 20 °C

(A)
π (mN m^−1)	Q xy (1) (Å^−1)	Q z (1) (Å^−1)	Q xy (2) (Å^−1)	Q z (2) (Å^−1)	Q xy (3) (Å^−1)	Q z (3) (Å^−1)
π is the surface pressure; a, b, c, and α β, γ are the lattice parameters of the unit cell; t is the polar tilt angle; Axy is the molecular area; A0 is the cross-section area of the alkyl chain; lattice distortion (from left to right).
2	1.456	0.089	1.324	0.781	1.321	0.870
	0.011	0.21	0.062	0.21	0.033	0.21
10	1.463	0.065	1.355	0.708	1.343	0.849
	0.011	0.21	0.029	0.21	0.021	0.21
20	1.473	0.089	1.402	0.619	1.387	0.757
	0.011	0.21	0.027	0.21	0.022	0.21
25	1.479	0.114	1.426	0.549	1.405	0.663
	0.009	0.21	0.032	0.21	0.024	0.21
30	1.476	0.187	1.440	0.465	1.411	0.652
	0.016	0.21	0.024	0.21	0.023	0.21
35	1.482	0.235	1.462	0.373	1.429	0.607
	0.019	0.21	0.025	0.21	0.037	0.21
40	1.484	0.230	1.472	0.333	1.444	0.562
	0.023	0.21	0.024	0.21	0.029	0.21
50	1.489	0.210	1.484	0.298	1.464	0.508
	0.016	0.21	0.024	0.21	0.022	0.21

---

(B)
π (mN m^−1)	a (Å) b (Å) c (Å)	α (deg) β (deg) γ (deg)	Distortion	t (deg)	A xy (Å^2)	A 0 (Å^2)
2	5.163 5.175 5.691	123.5 123.3 113.2	0.132073	36.9	24.6	19.6
10	5.089 5.134 5.544	123.2 122.4 114.3	0.111333	34.2	23.8	19.7
20	4.997 5.051 5.306	122.4 121.4 116.2	0.075239	29.7	22.6	19.7
25	4.946 5.020 5.206	122.2 120.8 117.0	0.061589	27.0	22.1	19.7
30	4.923 5.020 5.153	122.1 120.2 117.6	0.053077	26.1	21.9	19.7
35	4.883 4.995 5.064	121.9 119.3 118.7	0.042302	23.1	21.5	19.7
40	4.872 4.967 5.007	121.5 119,7 118.8	0.032234	21.4	21.2	19.7
50	4.862 4.918 4.921	121.0 119.7 119.3	0.015747	19.2	20.8	19.6

---

Similar to the homologous 3-monopalmitoyl-sn-glycerol monolayers,³⁴ the contour plots show a shift of the three clearly separated diffraction signals, which indicate the dominance of the chiral nature, to higher lateral pressures with an increase in temperature from 5 to 20 °C. It is interesting to note that the comparison with the contour plots of the 3-monopalmitoyl-sn-glycerol monolayers indicates the stronger influence of the chiral nature in the homologous 3-monostearoyl-sn-glycerol monolayers, i.e. with the increase of the alkyl chain length from C16 to C18. This dominance of the lattice symmetry is seen in the contour plots of Fig. 5–8 having a larger pressure range with three separated diffraction peaks.

In particular, all contour plots at pressures smaller or higher than those showing three clearly separated diffraction signals resemble the contour plots of the corresponding racemic 1-monostearoyl-rac-glycerol monolayers.²⁵ This is demonstrated by one example comparing the results by fitting the contour plots which resemble those of NN tilted or NNN tilted orthorhombic structures with 3 or 2 peaks.

Fig. 9 shows the results obtained at 10 °C at 2 mN m⁻¹. As can be seen, the contour plot resembles that of the NN tilted orthorhombic structures. The diffracted intensity plotted as a function of the in-plane scattering vector component Q_xy (Bragg peak) and as a function of the out-of-plane scattering vector component Q_z (Bragg rod) of the contour plot (top) can be perfectly fitted using both 3 (middle) and 2 (bottom) peaks with the consequence that the effect of chirality is small in these structures, as also demonstrated by the similarity of the lattice parameters presented in Table 5.

Fig. 9 GIXD data of 3-monostearoyl-sn-glycerol monolayers on water at 10 °C and 2 mN m⁻¹. Top: The diffracted intensity is plotted as a contour plot of the corrected diffraction intensities as a function of the in-plane Q_xy and out-of-plane Q_z components of the scattering vector. Middle and bottom: The diffracted intensity is plotted as a function of the in-plane scattering vector component Q_xy (Bragg peak, left) and as a function of the out-of-plane scattering vector component Q_z (Bragg rod, right). Fitting 3 peaks (middle) and 2 peaks (bottom) indicates reasonable agreement.

Table 5 (A) Comparison between fitting 3 or 2 peaks to the experimental data. Bragg peak (Q_xy) and Bragg rod (Q_z) positions and the corresponding full-widths at half-maximum of 3-stearoyl-sn-glycerol monolayers at 2 and 50 mN m⁻¹ at 10 °C on the basis of oblique and orthorhombic lattices. (B) Comparison of the lattice parameters of 3-stearoyl-sn-glycerol monolayers at 2 and 50 mN m⁻¹ at 10 °C obtained on the basis of oblique and orthorhombic lattices

(A)
Lattice type	π (mN m^−1)	Q xy (1) (Å^−1)	Q z (1) (Å^−1)	Q xy (2) (Å^−1)	Q z (2) (Å^−1)	Q xy (3) (Å^−1)	Q z (3) (Å^−1)
π is the surface pressure; a, b, c, and α, β, γ are the lattice parameters of the unit cell; t is the polar tilt angle; Axy is the molecular area; A0 is the cross-section area of the alkyl chain; lattice distortion.
Oblique	2	1.449 0.010	0.128 0.21	1.329 0.028	0.790 0.21	1.311 0.023	0.919 0.21
Orthorhombic	2	1.449 0.010	0 0.21	1.322 0.046	0.847 0.21
Oblique	50	1.485 0.049	0.602 0.21	1.470 0.013	0.299 0.21	1.462 0.019	0.303 0.21
Orthorhombic	50	1.495 0.040	0.607 0.22	1.467 0.025	0.304 0.22

---

(B)
Lattice type	π (mN m^−1)	a (Å) b (Å) c (Å)	α (deg) β (deg) γ (deg)	Distortion	t (deg)	A xy (Å^2)	A 0 (Å^2)
Oblique	2	5.70 5.22 5.15	113.5 122.7 123.9	0.128742	38	24.7	19.5
Orthorhombic	2	5.682 5.184 5.184	113.5 123.2 123.2	0.125798	37.5	24.6	19.6
Oblique	50	4.97 4.92 4.89	119.1 120.2 120.7	0.018523	22.1	21.0	19.5
Orthorhombic	50	4.978 4.884 4.884	118.7 120.6 120.6	0.025366	22.1	20.9	19.4

---

In the other example obtained at 10 °C at a high surface pressure of 50 mN m⁻¹ (Fig. 10), the contour plot can be perfectly described again by 2 as well as by 3 peaks. That means, the effect of chirality on the contour plots, which resemble that of the NNN tilted orthorhombic structures, is small (see Table 5).

Fig. 10 GIXD data of 3-monostearoyl-sn-glycerol monolayers on water at 10 °C and 50 mN m⁻¹. Top: The diffracted intensity is plotted as a contour plot of the corrected diffraction intensities as a function of the in-plane Q_xy and out-of-plane Q_z components of the scattering vector. Middle and bottom: The diffracted intensity is plotted as a function of the in-plane scattering vector component Q_xy (Bragg peak, left) and as a function of the out-of-plane scattering vector component Q_z (Bragg rod, right). Fitting 3 peaks (middle) and 2 peaks (bottom) indicates perfect agreement.

The cross-sectional area, A₀, is approximately constant over the large surface pressure range measured, only slightly affected by temperature and amounts to values of 19.4 mN m⁻¹ at 5 °C, 19.5 Ų at 10 °C, 19.6 Ų at 15 °C, and 19.7 Ų at 20 °C indicating a slightly increased rotation of the alkyl chains. As typical for many amphiphilic monolayers and also found in other racemic and enantiomeric monoacylglycerol monolayers, the tilt angle with respect to the surface normal, t, decreases with increasing pressure. The transition pressure π_t into a non-tilted phase can be calculated if the condensed isotherms exhibit linear relations between pressure and molecular area and the cross-sectional area, A₀, is approximately constant at all measured temperatures. Plotting 1/cos(t) vs. the lateral pressure and extrapolating toward 1/(cos t) = 1 allows the determination of the tilting transition pressure, π_m (Fig. 11, left).³⁵ The pressure needed to reach the non-tilted state decreases with increasing temperature. The values are quite high and cannot be experimentally reached (67.9 mN m⁻¹ at 5 °C, 66.1 mN m⁻¹ at 10 °C, 60.5 mN m⁻¹ at 15 °C and 58.7 mN m⁻¹ at 20 °C).

Fig. 11 3-Monostearoyl-sn-glycerol monolayers at 5, 10, 15 and 20 °C. (Left) Dependence of the tilt angle of the alkyl chains (t) represented as 1/cos(t) on the lateral surface pressure (π). Extrapolation of 1/cos(t) to 1 gives the transition surface pressure (π_t) at which the tilt angle becomes zero, whereas extrapolation to π = 0 yields the maximum tilt angle (t₀) of the chains. (Right) Lattice distortion d versus sin²(t). The extrapolation to zero tilt yields the d₀ value.

Nevertheless, the comparison with the values obtained for the corresponding racemic 1-monostearoyl-rac-glycerol is of interest (see Table 6A). The values of the chiral 3-monostearoyl-sn-glycerol are slightly smaller than those of the corresponding racemic compound. Table 6A shows also the value calculated for the homologues enantiomeric 3-monopalmitoyl-sn-glycerol and racemic 1-monopalmitoyl-rac-glycerol. Generally, these π_m values are considerably lower than those of the longer chain homologues, but they also cannot be experimentally reached. However, a tendency is seen that the π_m values increase with increasing temperature.

Table 6 (A) Transition surface pressure, π_m of chiral and racemic monoacylglycerols, at which the tilt angle becomes zero, obtained at different temperatures. (B) Distortion at zero-tilt angle, d₀, of chiral and racemic monoacylglycerols at different temperatures

(A)
Monoacylglycerol	π m, mN m^−1
	5 °C	10 °C	15 °C	20 °C
3-Monostearoyl-sn-glycerol	67.9	66.1	60.5	58.7
1-Monostearoyl-rac-glycerol	72.8	68.6	60.6	49.8
3-Monopalmitoyl-sn-glycerol	46.8	53.8	54.4
1-Monopalmitoyl-rac-glycerol	53.0	56.2	56.7

---

(B)
Monoacylglycerol	d 0
	5 °C	10 °C	15 °C	20 °C
3-Monostearoyl-sn-glycerol	−0.14067	−0.10258	−0.05993	−0.03107
1-Monostearoyl-rac-glycerol	−0.13952	−0.12074	−0.06328	−0.03491
3-Monopalmitoyl-sn-glycerol	−0.03523	−0.02791	−0.02014
1-Monopalmitoyl-rac-glycerol	−0.038	0	0

---

The lattice distortion d versus sin²(t) plot is shown in Fig. 11, right, at the four investigated temperatures. The Landau theory predicts that the tilt contribution to the distortion is proportional to sin²(t).³⁶ Therefore, plotting the lattice distortion measured along an isotherm as a function of sin²(t) and extrapolating to zero tilt allows the separation of the tilt contribution from other contributions to the distortion, such as herringbone packing or chirality. At all temperatures measured, the d₀ values are smaller than 0 (Table 6B). The absolute d₀ values decrease with increasing temperature. Table 6B shows that an analogous decrease of the absolute d₀ values with increasing temperature was also found for the homologous racemic 1-monostearoyl-rac-glycerol and the corresponding 3-monopalmitoyl-sn-glycerol and 1-monopalmitoyl-rac-glycerol.³⁴ The smaller absolute d₀-values of the C16-glycerols indicate the strong influence of the temperature on the lattice distortion. The cross-sectional area increases with increasing temperature from 19.4 Ų at 5 °C to 19.7 Ų at 20 °C. As shown in the generic phase diagram of racemic monoacylglycerol monolayers, decreasing alkyl chain length is equivalent to increasing temperature.²⁶ The actual temperature in the 1-monopalmitoyl-rac-glycerol experiments has to be shifted up by 16 K to be directly compared with the 1-monostearoyl-rac-glycerol experiments.

Plotting the d₀ values in this way (Fig. 12) shows a perfect agreement between the racemic C18 and C16 monolayers, and the linear fit yields 298.7 K (25.5 °C) as the limiting temperature for observing zero d₀ values in the 1-monostearoyl-rac-glycerol experiments. In light of generic behavior this temperature can be translated into 282.7 K (9.5 °C) for 1-monopalmitoyl-rac-glycerol. Indeed, at 283.2 K (10 °C) the determined d₀ value of 1-monopalmitoyl-rac-glycerol amounts to zero (see Table 6B). The cross-sectional area of 1-monopalmitoyl-rac-glycerol amounts to 19.7 Ų at 5 °C (equivalent to 294.2 K for 1-monostearoyl-rac-glycerol experiments). A further increase of temperature does not increase the cross-sectional area substantially (see ref. 26 and 34). Such values indicate that the packing is not as tight as in the herringbone mode (low temperatures or longer chain) explaining the small or zero d₀ values. The absolute d₀ values of 1-monostearoyl-rac-glycerol and 3-monostearoyl-sn-glycerol are very similar indicating the weak influence of chirality on the lattice distortion at low temperatures (long chain). This demonstrates that the lattice distortion is mainly determined by the packing properties (determined by the temperature) of monostearoylglycerol and not by the chirality. This statement is not valid for monopalmitoylglycerol. Here, the d₀ values of the racemic and the enantiomeric forms are quite different demonstrating a stronger influence of chirality. Plotting the d₀ values of 3-monopalmitoyl-sn-glycerol shows a completely different slope compared with 3-monostearoyl-sn-glycerol (Fig. 12). The linear fit yields a much higher temperature (311.6 K = 38.4 °C) for observing zero d₀ values in the 3-monopalmitoyl-sn-glycerol experiments. The translation of the limiting temperatures from the generic plot in Fig. 12 to the real temperatures in C16-glycerol experiments yields 9.5 °C for the racemate and 22.4 °C for the corresponding enantiomer. This shows that the lattice distortion of 3-monopalmitoyl-sn-glycerol is much more strongly influenced by the chirality. However, the clear appearance of three diffraction peaks characterizing the oblique lattice structure due to chirality is more pronounced in the homologous 3-monostearoyl-sn-glycerol monolayers with the longer alkyl chain. It is interesting to note that even for the racemate an intermediate oblique structure has been observed at low temperatures.²⁵

Fig. 12 Extrapolated d₀ values of 1-monostearoyl-rac-glycerol (●), 3-monostearoyl-sn-glycerol (▲), 1-monopalmitoyl-rac-glycerol (), and 3-monopalmitoyl-sn-glycerol () monolayers vs. temperature. Note that the temperature of the C16 experiments is shifted by 16 K (generic behavior).²⁶

Conclusions

Monoacylglycerol esters are suitable candidates for systematic studies of chiral discrimination effects between enantiomeric and racemic structures. In recent papers, studies of the phase and lattice features of the racemic 1-palmitoyl-rac-glycerol and enantiomeric 3-palmitoyl-sn-glycerol monolayers were performed using π–A isotherms, BAM, and GIXD. The lattice and phase characteristics of 1-stearoyl-rac-glycerol were thoroughly investigated to understand in more detail the influence of the alkyl chain length on the monolayer characteristics of the monoacylglycerol esters. Therefore, the present study focusses on the characterization of the corresponding chiral 3-stearoyl-sn-glycerol to obtain information about the influence of the alkyl chain length on the chiral discrimination. The results are based on the measurements of the π–A isotherms, BAM, and particularly, GIXD. The π–A isotherms of the enantiomeric 3-monostearoyl-sn-glycerol monolayers measured between 25 and 38 °C are similar to those of the racemic 1-monostearoyl-rac-glycerol monolayers suggesting small energetic differences between the enantiomeric and the racemic forms. The temperature dependence of the phase transition pressure (π_t) shows that the absolute ΔS values increase as the temperature decreases and thus, the ordering of the condensed phase increases at lower temperatures. Extrapolation to zero ΔS provides the critical temperature T_c of 42.1 °C (315.3 K), above which the monolayer cannot be compressed into the condensed state.

Similar to the racemic monoacylglycerol esters, the regular 3-monostearoyl-sn-glycerol domains are subdivided into 7 segments. However, their shape deviates already from circular, and also the inner textures show certain irregularities. In the case of 3-monostearoyl-sn-glycerol, the tendency to develop irregular deviations in the shape and inner texture of the condensed phase is high.

For obtaining reliable two-dimensional lattice structures in the accessible temperature and surface pressure ranges, GIXD measurements were performed over a large range of lateral pressures at four different temperatures (5, 10, 15 and 20 °C). The contour plots with three clearly separated diffraction signals, shifted to higher lateral pressures with increasing temperature, indicate the dominance of the chiral nature. The comparison with the contour plots of the 3-monopalmitoyl-sn-glycerol monolayers shows a larger pressure range with three separated diffraction peaks at all temperatures and indicates the stronger dominance of the chiral nature on the lattice symmetry in the homologous 3-monostearoyl-sn-glycerol monolayers (increasing alkyl chain length has a strong effect). The similarity of the lattice data obtained by fitting the contour plots with 3 or 2 peaks demonstrates the resemblance to orthorhombic structures with NN tilted molecules at low pressures and NNN tilted molecules at high pressures.

The values of the tilting transition pressure, π_t, to the non-tilted state are rather high and have not been reached experimentally, but they are slightly smaller than those of the corresponding racemic mixture. Although the π_t values of the shorter-chain C16 homolog are considerably lower, they also cannot be experimentally reached.

The comparison of the distortion at zero-tilt angle, d₀, of enantiomeric and racemic monoacylglycerols at different temperatures shows a decrease of the absolute values with increasing temperature. The d₀ values of the racemate and the enantiomer are very similar demonstrating that the lattice distortion is mainly determined by the packing properties and not by the chirality. The influence of chirality on the lattice distortion is better seen at higher temperatures by using the corresponding shorter-chain C16-homologue. The packing is now characterized by a free rotation of the chains (no contribution to the lattice distortion) so that the small influence of chirality can be seen. The difference in the limiting temperature for observing zero d₀ values between the C18 and C16 compounds demonstrates a stronger influence of chirality on the lattice distortion for the shorter-chain compound.

Acknowledgements

Open Access funding provided by the Max Planck Society.

References

1. L. Zhang, T. Wang, Z. Shen and M. Liu, Adv. Mater., 2016, 28, 1044–1059.
2. K. Ariga and J. Li, Adv. Mater., 2016, 28, 987–988.
3. K. Ariga, J. Li, J. Fei, Q. Ji and J. P. Hill, Adv. Mater., 2016, 28, 1251–1286.
4. I. Kuzmenko, H. Rapaport, K. Kjaer, J. Als-Nielsen, I. Weissbuch, M. Lahav and L. Leiserowitz, Chem. Rev., 2001, 101, 1659–1696.
5. N. Nandi and D. Vollhardt, Chem. Rev., 2003, 103, 4033–4075.
6. N. Nandi and D. Vollhardt, Acc. Chem. Res., 2007, 40, 351.
7. D. Vollhardt, N. Nandi and S. Dutta Banik, Phys. Chem. Chem. Phys., 2011, 13, 4812–4829.
8. E. Scalas, G. Brezesinski, H. Möhwald, V. M. Kaganer, W. G. Bouwman and K. Kjaer, Thin Solid Films, 1996, 285, 56–61.
9. D. Vollhardt and U. Gehlert, Prog. Colloid Polym. Sci., 1994, 97, 302–306.
10. G. Brezesinski, R. Rietz, K. Kjaer, W. G. Bouwman and H. Möhwald, Nuovo Cimento, 1994, 16, 1487–1492.
11. D. Vollhardt, U. Gehlert and S. Siegel, Colloids Surf., A, 1993, 76, 187–195.
12. U. Gehlert, G. Weidemann and D. Vollhardt, J. Colloid Interface Sci., 1995, 174, 392–399.
13. G. Weidemann, U. Gehlert and D. Vollhardt, Langmuir, 1995, 11, 864–871.
14. G. Brezesinski, E. Scalas, B. Struth, H. Möhwald, F. Bringezu, U. Gehlert, G. Weidemann and D. Vollhardt, J. Phys. Chem., 1995, 99, 8758–8762.
15. U. Gehlert, D. Vollhardt, G. Brezesinski and H. Möhwald, Langmuir, 1996, 12, 4892–4896.
16. U. Gehlert and D. Vollhardt, Langmuir, 2002, 18, 688–693.
17. D. Vollhardt and U. Gehlert, J. Phys. Chem. B, 2002, 106, 4419–4423.
18. U. Gehlert, G. Weidemann, D. Vollhardt, G. Brezesinski, R. Wagner and H. Möhwald, Langmuir, 1998, 14, 2112–2118.
19. P. E. Ebong, D. U. Owu and E. U. Isong, Plant Foods Hum. Nutr., 1999, 53, 209–222.
20. H. Moonen and H. Bas, in Emulsifiers in food technology, ed. R. J. Whitehurst, Blackwell Publishing, Ltd, Oxford, 2004, pp. 40–58.
21. F.-Q. Hu, S. P. Jiang, Y.-Z. Du, H. Yuan, Y.-Q. Ye and S. Zen, Int. J. Pharm., 2006, 314, 83–89.
22. J. M. R. Patino, C. C. Sanchez and M. R. R. Nino, Langmuir, 1999, 15, 2484–2492.
23. J. M. R. Patino, C. C. Sanchez, M. R. R. Nino, M. Cejudo and M. C. Fernandez, Langmuir, 2001, 17, 4003–4013.
24. J. M. R. Patino, C. C. Sanchez and M. R. R. Nino, J. Agric. Food Chem., 1999, 47, 4998–5008.
25. D. Vollhardt and G. Brezesinski, J. Phys. Chem. C, 2015, 119, 9934–9946.
26. D. Vollhardt and G. Brezesinski, Langmuir, 2016, 32, 7316–7325.
27. D. Vollhardt, Brewster angle microscopy: A preferential method for mesoscopic characterization of monolayers at the air/water interface, Curr. Opin. Colloid Interface Sci., 2014, 19, 183–197.
28. S. Hénon and J. Meunier, Rev. Sci. Instrum., 1991, 62, 936–939.
29. D. Hönig and D. Möbius, J. Phys. Chem., 1991, 95, 4590–4592.
30. J. Als-Nielsen, D. Jacquemain, K. Kjaer, F. Leveiller, M. Lahav and L. Leiserowitz, Phys. Rep., 1994, 246, 251–313.
31. J. Als-Nielsen and H. Möhwald, in Handbook on Synchrotron Radiation, ed. S. Ebash, M. Koch and E. Rubenstein, Elsevier, New York, 1994, vol. 4, pp. 1–53.
32. K. Kjaer, Physica B, 1994, 198, 100–109.
33. D. Vollhardt, Adv. Colloid Interface Sci., 1996, 64, 143–171.
34. D. Vollhardt and G. Brezesinski, Colloids Surf., A DOI:10.1016/j.colsurfa.2016.08.065.
35. F. Bringezu, B. Dobner and G. Brezesinski, Chem. – Eur. J., 2002, 8, 3203–3210.
36. V. M. Kaganer, H. Möhwald and P. Dutta, Rev. Mod. Phys., 1999, 71, 779–819.

---