Eu²⁺–Eu³⁺ valence transition in double, Eu-, and Na-doped PbSe from transport, magnetic, and electronic structure studies

Abstract

The Eu atoms in Pb_1−xEu_xSe have long been assumed to be divalent. We show that p-type doping of this magnetic semiconductor alloy with Na can modify the effective Eu valence: a mixed, Eu²⁺–Eu³⁺ state appears in Pb_1−x−yEu_xNa_ySe at particular values of y. Magnetization, carrier concentration, resistivity, and thermopower of Pb_1−x−yEu_xNa_ySe are reported for a number of samples with different x and y. A pronounced increase in thermopower at a given carrier concentration was identified and attributed to the presence of enhanced ionized impurity scattering. A strong decrease in the hole concentration is observed in Pb_1−yNa_ySe when Eu is added to the system, which we attribute to a Eu²⁺–Eu³⁺ self-ionization process. This is evidenced by magnetization measurements, which reveal a significant reduction of the magnetic moment of Pb_1−xEu_xSe upon alloying with Na. Further, a deviation of magnetization from a purely paramagnetic state, described by a Brillouin function, identifies antiferromagnetic interactions between the nearest-neighbor Eu atoms: a value of J_ex/k_B = −0.35 K was found for the exchange coupling parameter. The conclusion of a Eu²⁺–Eu³⁺ self-ionization process being in effect is supported further by the electronic structure calculations, which show that an instability of the 4f⁷ configuration of the Eu²⁺ ion appears with Na doping. Schematically, it was found that the Eu 4f levels form states near enough to the Fermi energy that hole doping can lower the Fermi energy and trigger a reconfiguration of a 4f electronic shell.

---

Introduction

The Pb-salt semiconductors (PbS, PbSe, and PbTe) have been the earliest practical semiconductors used in electronic devices such as crystal rectifiers, infrared sensors, diode lasers, and thermoelectric generators.¹ Recently, they also have been reported to be potential topological insulators.² This class of semiconductors hosts the materials with the highest thermoelectric ZT,^3–5 in particular in alloys in which other divalent elements such as Sr are substituted for Pb²⁺.⁶ PbSe, the binary semiconductor that is the starting point for the present study, is an excellent thermoelectric semiconductor^7,8 that avoids the use of Te, which is not abundant in the earth's crust. Another element thought to be divalent, Eu, is known to increase the band gap of PbTe⁹ and PbSe:^10,11 PbEuTe and PbEuSe have been used as the high-gap semiconductor in PbTe and PbSe double-heterojunction, quantum-well, tunable infrared diode lasers.¹¹ For these applications, the fact that Eu is divalent was one of its main advantages, as compared to other rare earth elements, since it allowed modification the band gap of the material without increasing the carrier concentration.

Magnetic studies have been performed on PbEuTe^12–15 and PbEuSe^9,16,17 alloys and superlattices. The transport properties of PbSe containing various rare-earth elements have been studied more recently.¹⁸ In these works, Eu in PbSe was found to be electrically inactive and magnetic in the Eu²⁺ state, making Pb_1−xEu_xSe one of the dilute magnetic semiconductors (DMS). None of earlier studies include a systematic variation of both the Eu content while adjusting the p-type doping level independently, as is done here with Na-doping. This approach reveals that the valence of Eu is indeed 2+ in material with low carrier concentrations but shifts from 2+ to 3+ upon p-type doping with Na. The second, electrically active impurity (Na⁺) controls the valence transition of the 4f shell into the Eu³⁺ state, leading to a mixed 4f⁶–4f⁷ valence state in the material. This changes both transport and magnetic properties. To the best of our knowledge, this is the first example of a fully controllable and tunable triggering of a valence mixing effect in a dilute magnetic semiconductor by the addition of a second, electrically active element. Moreover, the effect here appears at low doping levels, with charge carrier concentration variations orders of magnitude smaller than, for instance, in metallic CePd₃.¹⁹

Among DMS or metals in which a mixed valence or a valence fluctuation is observed, we mostly find alloys in which the concentration of the transition metal or rare-earth element has been adjusted to release the valence instability. A review of this approach for DMS based on lead chalcogenides is given in ref. 20 and references therein. One of the most studied cases of mixed-valence DMS is Fe-doped HgSe, where iron adopts Fe²⁺ configuration at low doping levels, whereas a mixed Fe²⁺–Fe³⁺ state appears^21–25 at higher Fe concentration. These two types of iron ions may form an ordered superlattice of Fe²⁺ and Fe³⁺, leading to unexpectedly high mobility of the carriers²⁶. Chromium also was reported to exist in two valence states, as Cr²⁺ and Cr³⁺ in PbTe²⁷ and PbSe²⁸. In all these materials, the transition metal (TM) impurities' valence changed with increasing TM concentration, thus there was no independent way of controlling the valence at any specific composition. Among rare-earth impurities in chalcogenides, Gd and Yb also showed a tendency to change their valence, when the carrier concentration in the samples was varied. However, for the Gd case, the 4f electronic shell configuration remained unchanged: in Sn_1−xGd_xTe,^29,30 a transition from Gd²⁺ (4f⁷5d¹) to Gd³⁺ (4f⁷5d⁰) was observed and led to modifications of the f–f exchange interactions, but in both cases 4f shell remained half-filled. The Yb behavior in Pb_1−xGe_xTe:Yb seems to be more similar to what is reported here for Eu in Pb_1−x−yNa_yEu_xSe, since the Yb valence change affected the 4f shell configuration, leading to a change in magnetic properties of Yb. It was found³¹ that as-grown samples of, e.g., Pb_0.985Ge_0.01Yb_0.005Te were p-type and paramagnetic (i.e. Yb was in Yb³⁺ [4f¹³] state), but after annealing transformed to n-type and diamagnetic (i.e. Yb was in electrically inactive and nonmagnetic Yb²⁺ [4f¹⁴] state). However, no valence mixing and no possibility to control the valence was reported in that case, unlike in Pb_1−xEu_xSe:Na, reported here. Thus, our findings in Pb_1−xEu_xSe:Na offer a new way of inducing and controlling the valence transitions in diluted magnetic semiconductors.

The manuscript is structured further as follows. Samples of Pb_1−x−yEu_xNa_ySe alloys were synthesized using a combined vacuum-melting and spark-plasma sintering (SPS) technique. The transport properties are reported next, and reveal an anomaly in the variation of the charge concentration with increasing Na content y. We show that the Pisarenko relation between the carrier concentration and the thermopower suggests an increase in ionized impurity scattering at a particular value of y, suggesting a sudden change in the valence of Eu from Eu²⁺ to Eu³⁺. Next, magnetic studies quantitatively confirm this hypothesis. A more detailed study of the deviations of the measured magnetization curves from Brillouin functions reveals the presence of antiferromagnetic interactions between Eu ions. Finally, electronic structure calculations confirm the existence of a density of Eu 4f states near the Fermi energy E_F. By changing the Na doping level one can control the E_F position independently of the Eu concentration and locate it inside the 4f states. The Eu²⁺ configuration in PbSe then can become unstable and mixed Eu²⁺–Eu³⁺ states appears.

Experimental & theoretical procedure

Elemental Pb (99.99%, American Elements), Se (99.999%, 5N Plus Inc), Na (99.95%, Aldrich), and Eu (99.9%, Chinese Rare Earth Information Center) were used for the synthesis of Pb_1−x−yEu_xNa_ySe. Ingots (20 g) with nominal compositions Pb_0.99−xEu_xNa_0.01Se (x = 0, 0.01, 0.02, 0.03, 0.04, 0.06, 0.09 and 0.12) and Pb_0.99−yEu_0.01Na_ySe (y = 0, 0.01, 0.02, 0.03, and 0.04) were prepared by mixing appropriate ratios of reagents in carbon-coated quartz tubes. The tubes were sealed under vacuum (10⁻⁴ Torr) and heated to 1423 K over a period of 12 h. The tubes then were soaked at that temperature for 5 h, and rapidly cooled to room temperature over 3 h. The obtained ingots were cleaned and ground to a powder using a mechanical grinder to reduce the particle sizes to less than 53 μm. These powders were densified at 923 K for 5 min under an axial compressive pressure of 40 MPa in an argon atmosphere in an SPS apparatus. Table 1 reports a summary of the samples studied.

Table 1 Comparison of the obtained Eu²⁺ concentration from magnetization data fitting and estimated based on carrier concentration data at 80 K and 300 K

Samples	Carrier concentration (10^19 cm^−3)		Atomic concentration of Eu^2+ (%) from magnetization fitting (in brackets: percent of the total Eu)	Atomic concentration of Eu^2+ (%) from carrier concentration (in brackets: percent of the total Eu)
	80 K	300 K
a Calculated based on carrier concentration data at 80 K.
Eu0%:Na 1%	21	17	0	0
Eu1%:Na 1%	6.0	8.2	0.24 (24%)	0.14^a (14%)
Eu2%:Na 1%	5.2	6.0	1.49 (74%)	1.1^a (55%)
Eu3%:Na 1%	2.2	3.4	2.03 (68%)	1.92^a (64%)
Eu6%:Na 1%	2.2	3.6	4.15 (69%)	4.92^a (82%)
Eu1%:Na 0%	—	0.27	0.93 (93%)	∼1 (100%)
Eu1%:Na 2%	—	19	0.15 (15%)	∼0 (0%)
Eu1%:Na 3%	—	35	0.06 (6%)	∼0 (0%)
Eu1%:Na 4%	—	41	0.017 (1.7%)	∼0 (0%)

---

Thermoelectric transport properties and galvanomagnetic properties of Pb_1−x−yEu_xNa_ySe samples were measured in a customized cryostat, either with an AC bridge, or with a static heater-and-sink method. The samples were cut into parallelepipeds with dimensions around 2 mm × 2 mm × 10 mm. To minimize heat loss, very thin copper and constantan wires were used as thermocouples. Four-probe measurements were used to measure the resistivity of the samples using 4 copper wires. Hall resistivity was obtained by applying a transverse magnetic field in the range −14 kOe ≤ H ≤ +14 kOe. All the thermoelectric and galvanomagnetic properties were measured in the temperature range 80 K ≤ T ≤ 420 K. Two experimental measurements of magnetization, M, were conducted using a superconducting quantum interference device (SQUID). The first measurement of M vs. temperature was performed by applying a magnetic field of 5 kOe and sweeping the temperature from 2 K to 300 K. From the obtained data, the magnetic susceptibility χ was calculated. The susceptibility of Eu²⁺ was then obtained by subtracting the diamagnetic susceptibility of the PbSe lattice. A second measurement of magnetization was carried out by varying the magnetic field from 0 to 60 kOe at 2 K, 4 K, and 6 K.

Electronic structure calculations were performed using the full potential linearized augmented plane wave (FP-LAPW) method, as implemented in the WIEN2k code.³² To simulate the doping, the supercell approach was used, building a 64-atom 2 × 2 × 2 supercell, starting from a cubic rock-salt PbSe unit cell (a = 6.12 Å). Spin–orbit interaction was taken into account, and the Coulomb interactions between the 4f Eu electrons were treated using the LDA + U method. We took U = 7 eV and J = 1 eV, as values of U between 7 eV and 10 eV usually are considered for Eu in the literature.^33,34 The modified Becke–Johnson semilocal exchange potential of Tran and Blaha³⁵ was used and appeared to be very efficient in its description of the 4f Eu electronic states near the band gap.

Results and discussion

A. Electronic transport properties of Pb_1−x−yEu_xNa_ySe

Transport properties (carrier concentration as measured by the Hall effect, thermopower, and resistivity) of Pb_1−x−yEu_xNa_ySe, (y = 0.01; x = 0, 0.01, 0.02, 0.03, 0.04, 0.06, 0.12) samples are shown as function of temperature in Fig. 1. The carrier concentrations in the samples (Fig. 1a) reach values between 2 and 22 × 10¹⁹ cm⁻³, and exhibit a small temperature dependence, most likely due to the temperature dependence of the Hall prefactor.³⁶ The hole concentration values at 80 K and 300 K of all samples are summarized in Table 1. We did not obtain a Hall measurement on the lowest-doped sample with the highest Eu content (x = 0.12, y = 0.01), because its resistivity was too high. We also measured a Pb_0.99Eu_0.01Se sample without any Na doping, not included in Fig. 1, and its Hall effect showed a hole concentration of about 3 × 10¹⁸ cm⁻³ at room temperature. The thermopower scales appropriately with the carrier concentration, and varies mostly linearly with temperature over the measurement range, except for the lowest-doped samples. The resistivity of most samples is quite high: the presence of Eu in the samples decreases the mobility by factors varying from 2 (x = 0.01) to over an order of magnitude (x = 0.06) when compared to similarly-doped Eu-free PbSe, as shown in Fig. 1d. The Pisarenko relation (thermopower versus the carrier concentration) of PbSe at room temperature of the samples is shown in Fig. 2a where we include data taken from the literature on other PbSe samples. The dashed lines in Fig. 2a are theoretical curves, adopted from ref. 37, and are calculated using the non-parabolic Kane model, literature values of valence band effective masses,³⁸ and assuming four different dominating scattering mechanisms, represented by appropriate scattering exponents λ (see also ref. 39 for more details). Here, the scattering exponent describes the energy dependence of the hole relaxation time τ(E), which is assumed to follow a power law , where the term , instead of pure energy E, appears due to non-parabolicity of the band structure, γ′ is its energy derivative, and E_g is the band gap. The scattering exponents take the values: λ = −1/2 for acoustic phonon scattering, λ = 0 for neutral impurity scattering, λ = 1/2 for polar optical phonon scattering, and λ = 3/2 for ionized impurity scattering.

Fig. 1 Temperature-dependent transport properties of Pb_1−x−yEu_xNa_ySe (a) carrier concentration from Hall effect measurements p(T), (b) thermopower α(T), (c) resistivity ρ(T), (d) mobility (μ) comparison at T = 300 K. The black dashed line, taken after ref. 7, represents mobility of Na-doped PbSe with differing Na doping level.

Fig. 2 (a) The Pisarenko plot (thermopower vs. carrier concentration) of PbSe with different doping elements, as described in the legend. The dotted lines are theoretical Pisarenko relations computed assuming different scattering exponents^37,39 (see, text). Experimental points are taken from ref. (Evola et al.³⁷), (Chasapsis et al.⁴⁰), (Wang et al.⁴¹); (b) comparison of the room-temperature power factor (PF) for double-doped and Na-doped PbSe.

Comparing the thermopower data in Fig. 2a to those reported in binary PbSe doped with Na, In, or Al,^37,40,41 shows that doubly-doped Eu + Na samples have considerably larger thermopower at given carrier concentration. Looking at the complete dataset in Fig. 2a and comparing to the theoretical curves, ionized impurity scattering likely is the reason for the increase in α. The resulting values of the power factors (PF = α²/ρ) in the studied samples are between 2 and 4 μW K⁻² cm⁻¹ at room temperature. This contrasts with the values between 7 and 15 (μW K⁻² cm⁻¹) that are reported⁴⁰ for solely Na-doped PbSe at similar carrier concentrations, as presented in Fig. 2b. The reduction in carrier mobility more than compensates the impact the increase in thermopower might have on the thermoelectric performance of the system.

Previous studies have reported that Eu exists as Eu²⁺ in PbSe^16,18 by analyzing its transport and magnetic properties. As a consequence, replacing Pb²⁺ with Eu²⁺ does not lead to any considerable changes in the carrier concentration (see, e.g.ref. 18). The Hall carrier concentration of the undoped Pb_0.99Eu_0.01Se sample in our studies (3 × 10¹⁸ cm⁻³) is an order of magnitude lower than one would calculate if Eu was considered an electrically active element, confirming the previous results, and results from a small number of Pb vacancies. In the next section, the magnetic properties confirm that Eu is present as Eu²⁺ in PbSe without Na-doping. This behavior changes when the PbEuSe system is doped with Na, as can be seen in Fig. 1 and 2. First, substitution of Pb with Eu in Pb_1−yNa_ySe greatly reduces the carrier concentration at the same Na concentration. The sample with (x = 0, y = 0.01), i.e. doped with 1% Na only, shows highly-degenerate semiconducting properties with approximately 2.1 × 10²⁰ cm⁻³ hole concentration at T = 80 K. This is close to the nominal carrier concentration of 1.75 × 10²⁰ cm⁻³, calculated if each monovalent Na⁺ would give a single hole to the system. After introducing 1 at% of Eu (x = 0.01, y = 0.01), the hole concentration of the sample drops to about 6.0 × 10¹⁹cm⁻³. This effect cannot be explained if Eu was still Eu²⁺ as in Pb_1−xEu_xSe, since in such a case, isovalent doping should have minimal impact on the carrier concentration. Moreover, continuous reduction in carrier concentration with higher Eu levels in (y = 0.01; x > 0.01) samples is observed, although to a lesser degree, and we reach p ∼ 2–3 × 10¹⁹ cm⁻³ (T = 80 K) for (x = 0.03 − 0.06, y = 0.01).

The proposed explanation of the order-of-magnitude reduction in the carrier concentration of Pb_0.99−xEu_xNa_0.01Se is a change of the valence of a fraction of the Eu ions from Eu²⁺ to Eu³⁺, where Eu³⁺ acts as an one-electron donor compensating the acceptor behavior of Na⁺. Since electronic configuration of neutral Eu is [Xe]4f⁷6s², Eu²⁺ has seven 4f electrons, which are not mobile. Now, the release of one electron changes Eu²⁺ to Eu³⁺, resulting in a 4f⁶ configuration of the Eu³⁺ ion with 3 mobile, valence electrons. Eu³⁺ now has one hole in the 4f shell. However, this 4f-like hole, as typical for all f-like states, is localized; thus, it does not take part in transport phenomena and cannot be detected by the Hall effect measurements. As the final effect, the presence of trivalent Eu³⁺ partly compensates the p-type doping efficiency of monovalent Na⁺, when both are substituting for divalent Pb²⁺. The effectiveness of this compensation and the ratio of the number of Eu²⁺–Eu³⁺ ions can be estimated simply by comparing the measured carrier concentrations. For the Eu-free case, Pb_0.99Na_0.01Se, the measured hole concentration is about 2.1 × 10²⁰ cm⁻³, and it drops to 6.0 × 10¹⁹ cm⁻³ in Pb_0.98Eu_0.01Na_0.01Se. Now, assuming that all the difference comes from compensation of holes by electrons delivered while forming Eu³⁺, the concentration of these electrons is 21 × 10¹⁹ cm⁻³–6.0 × 10¹⁹ cm⁻³ = 15 × 10¹⁹ cm⁻³, which means that 86% of the total number of Eu ions become Eu³⁺. Thus, addition of 1 at% of Eu to the Pb_0.99Na_0.01Se sample compensates about 86% of the holes delivered by 1 at% of Na atoms, and results in the Eu²⁺ : Eu³⁺ ratio of 14 : 86. When the Eu concentration increases, the amount of europium atoms in the Eu³⁺ donor state increases, further reducing the hole concentration in the samples. The results of the analysis performed for other samples are collected in Table 1, and, e.g., for the x = 0.02, y = 0.01 case, about 45% of Eu has to be transformed into Eu³⁺ to explain the low carrier concentration of the sample, leaving only 55% Eu as Eu²⁺.⁴² In addition to the analysis of the carrier concentration in a set of Pb_0.99−xEu_xNa_0.01Se samples, the room temperature carrier concentration in a second set of samples, Pb_0.99−yEu_0.01Na_ySe, was measured, where Eu concentration was kept at 1% and Na concentration was increased between 1% and 4%. According to Table 1, the carrier concentrations of (x = 0, y = 1) and (x = 1, y = 2) are very much similar (1.9 × 10²⁰ and 1.7 × 10²⁰ at 300 K, respectively). This also supports the idea of charge transfer between Na⁺ and Eu²⁺. 1 at% of Na⁺ in the sample of (x = 1, y = 2) takes additional electrons and transforms Eu²⁺ to Eu³⁺. Hence, only the other 1 at% of Na acts as the p-type doping agent in the sample, showing a carrier concentration that is close to that of (x = 0, y = 1). For the larger Na concentrations, most of Eu is at the Eu³⁺ configuration. This confirms that increasing the Na concentration triggers the transition from Eu²⁺ to Eu³⁺.

The Pisarenko plot in Fig. 2 is consistent with this hypothesis. As mentioned above, the PbEuSe:Na data points align well with the “ionized scattering” α(p) curve, whereas the PbSe:Na points are below, near the polar optical phonon or neutral impurity scattering curves. That means that Eu³⁺, not Na⁺, is the source of the additional scattering. This also agrees with the presence of part of Eu in the 3+ state, ionized with respect to Pb²⁺, but the scattering may be enhanced generally by the presence of Eu 4f electrons.

B. Magnetization of Pb_1−x−yEu_xNa_ySe

As the two Eu ions, Eu²⁺ and Eu³⁺, have different magnetic properties, magnetization measurements were carried out to verify the hypothesis further. According to Hund's rule, the total angular quantum number (S₀ = |L − S|) of Eu²⁺ is 7/2 (total orbital angular momentum L = 0, and spin S = 7/2), which gives the 7 μ_B magnetic moment of Eu²⁺. On the other hand, theoretical S₀ of Eu³⁺ is zero (L = 3 and S = 3 cancel each other), giving zero magnetic moment of Eu³⁺. Experimentally,⁴³ small magnetic moments were reported for Eu³⁺, but the key is that any existence of Eu³⁺ instead of Eu²⁺ always results in a significant reduction in magnetization of the system. No change in magnetization is expected with Na addition if the Eu remains in the valence state 2+. Thus, magnetization measurements are a very sensitive tool to confirm or exclude the hypothesis of Eu²⁺–Eu³⁺ transition in our samples.

The measured magnetization curves of (y = 0.01; x = 0.01, 0.02, 0.03, 0.06, 0.09, and 0.12) and (x = 0.01; y = 0, 0.01, 0.02, 0.03, and 0.04) as a function of magnetic field at 2 K are displayed in Fig. 3a and b, respectively. The weak diamagnetic contribution of PbSe matrix, with susceptibility χ_d = −3.6 × 10⁻⁷ emu (g Oe)⁻¹ was subtracted, assuming that it is temperature independent. First, in samples with fixed Na concentration (y = 0.01; x ≥ 0.01), the magnetization increases with Eu content x (Fig. 3a). This verifies that Eu gets incorporated into each sample proportionally to the amount of Eu added. In contrast to this expected behavior, the evolution of magnetic properties of Pb_1−x−yEu_xNa_ySe with y shows anomalous reduction of magnetic signal, that confirm the Eu²⁺–Eu³⁺ transition in the system independently from the anomalies in the Hall coefficient, as explained below.

Fig. 3 (a) Magnetization of Pb_1−x−yEu_xNa_ySe (y = 0.01) with varying Eu level (x) as a function of magnetic field; (b) magnetization of Pb_1−x−yEu_xNa_ySe (x = 0.01) with varying Na doping level (y) as a function of magnetic field.

The following analysis of magnetic data starts from the magnetization of the 1 at% Eu doped, Na-free sample (x = 0.01, y = 0, black top curve in Fig. 3b). M(B) at 2 K shows typical paramagnetic, Brillouin-like function shape, and the saturation magnetization value corresponds to the expected value for Eu²⁺ ion (7 μ_B, i.e. 1.27 emu g⁻¹) if the actual concentration of Eu atoms in the sample is 0.93% instead of 1%. Such a small discrepancy is consistent with a small loss of Eu during the synthesis. Thus, in agreement with previous reports^16,18 and the small carrier concentration measured in this sample, we observe that the Eu valence is 2+ in the absence of Na in PbSe.

When 1 at% of Na is added to Pb_0.99Eu_0.01Se, the magnetization of the sample drops more than three times, which is an independent signature of the transition of the majority of magnetic Eu²⁺ ions into non-magnetic Eu³⁺. Fig. 3b shows how the magnetization decreases further with increasing Na doping levels, with the sample with 4 at% Na and 1 at% Eu reaching a saturation magnetization of less than 2% of that of undoped Pb_0.99Eu_0.01Se. Here, almost all of the Eu ions are transformed into Eu³⁺. This observation is consistent quantitatively with the reduction observed for the carrier concentration (Fig. 1a), where adding Eu compensated the donor behavior of Na. The actual amount of Eu²⁺ in each sample, denoted here as x_Eu²⁺, deduced based on the saturation of experimental magnetization data and assuming 7 μ_B magnetic moment of Eu²⁺ ions, is presented in Table 1. The mixed-valence behavior, where part of the Eu is in the 2+ and the rest is in the 3+ state, is especially visible for the samples with 1 at% Na and 3–6 at% of Eu. It is worth noting, that Eu²⁺ concentrations deduced from magnetization are close to those obtained from the carrier concentration analysis. However, the Eu²⁺ concentrations deduced from magnetization measurements should be considered as more accurate, since the accuracy of Hall carrier concentration is limited by the accuracy of the formula (p = −1/eR_H, e – electron charge), and can be affected by Hall prefactors that depend on the scattering mechanism. This is the most likely reason for the differences between the two columns in Table 1.

The low-temperature field dependence of the magnetization deviates slightly but measurably from the Brillouin function that characterizes the magnetic moment of pure paramagnets. The magnetization data of the samples with (x = 0.01, y = 0) and (x = 0.03, y = 0.01) at T = 2 K, 4 K and 6 K, as a function of magnetic field, are reported in Fig. 4. The field and temperature dependence of the magnetization of the independent non-interacting (paramagnetic) Eu²⁺ ions M_BR is described by:^43,44

M_BR = M₀S₀x_Eu²⁺B_S0(ξ) (2)

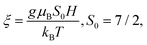where B_S0 is the Brillouin function, , M₀ = gμ_BN_A/m(x_Eu²⁺), m(x_Eu²⁺) is the molar mass of the compound, g is the g-factor of Eu²⁺ (we take g = 2), N_A is Avogadro's number, and μ_B is the Bohr magneton. Fig. 4a and c represent the field-dependent magnetization data fitted to M_BR (solid lines) at each temperature. At low field, the sample with (x = 0.01, y = 0) has slightly lower magnetization data when fitted to M_BR, suggesting the presence of antiferromagnetic (AF) interactions between Eu ions in the sample, as reported in earlier works for Eu-doped PbSe.¹⁶ The increase in Eu level in PbSe results in a larger deviation from M_BR as seen in Fig. 4c for (x = 0.03, y = 0) sample. However, with the increase in temperature, AF interactions are overcome by thermal excitations, giving better fitting of the data to M_BR; the data obtained at T = 6 K fits M_BR reasonably well.

Fig. 4 Magnetization of two Pb_1−x−yEu_xNa_ySe samples as a function of magnetic field. Solid lines in panels (a) and (c) are the curves of the calculated magnetization with Brillouin function (without corrections for the AF interaction). Solid lines in panels (b) and (d) are model (M_{AF_BR}) curves that consider AF contributions of pairs and triplets to the magnetization. The much better agreement between the measured data and models on panels (b) and (d) versus (a) and (c) is clearly visible.

To analyze the strength of AF interactions, a model, denoted here as M_{AF_BR}^16,44,45 is used. The model takes into account antiferromagnetic interactions between the nearest neighbor (NN) Eu ions. If random arrangement of magnetic ions in the crystal lattice is assumed, up to several percent Eu concentration, we have a noticeable probability of finding Eu not only in an isolated, single configuration (i.e. no other Eu as NN), but also in pairs (two Eu as NN) and triplets (three Eu as NN). For the last case we have two possibilities, open triplets (first and third Eu are not NN, like in a chain) and closed triplets (equilateral triangle, i.e. all Eu are NN). Higher order combinations can be neglected up to about 3–4% of magnetic ions⁴⁶. In this way, the total magnetization (M_{AF_BR}) can be described as M_{AF_BR} = M_S + M_p + M_OT + M_CT, where M_S, M_p, M_OT, and M_CT are the contributions to magnetization from singles, pairs, open triplets, and closed triplets, respectively. The singles' contribution (M_S) in a model (M_{AF_BR}) is the same as eqn (2), but the probability P_S of finding the singles in the sample is taken into account. Hence, the single contribution (M_S) is

M_S = M_BRP_S. (3)

The pair contribution (M_p) is^16,44,45

where S_MAX = 2S₀, J_ex is the exchange coupling parameter, and k_B is the Boltzmann constant.

The open triplet contribution (M_OT) and the closed triplet contribution (M_CT) are listed below:

where E_OT = −mgμ_BH − J_ex(S_b(S_b + 1) − S_a(S_a + 1) − S₀(S₀ + 1), E_CT = −mgμ_BH − J_ex(S_b(S_b + 1) + 3S₀(S₀ + 1))), and .

The probabilities of finding the singles (P_S), the pairs (P_P), and the triplets (P_OT and P_CT) of Eu ions in the rock salt fcc lattice are shown below:⁴⁶

P_S = (1 − x_Eu²⁺)¹²

P_P = 12x_Eu²⁺(1 − x_Eu²⁺)¹⁸ (7)

POT = 18xEu2+2(1 − xEu2+)23(5(1 − xEu2+) + 2)

PCT = 24xEu2+2(1 − xEu2+)22

These probabilities are valid under the assumption of completely random distribution of Eu ions in the samples.

The formulas above are used to fit the magnetization data in Fig. 4b and d. Note, that the procedure involves only two fitting parameters: x_Eu²⁺, fitting the saturated part of the magnetization, and the exchange interaction parameter, J_ex, describing the antiferromagnetic contribution to magnetization, seen for lower fields (J_ex was kept constant for all analyzed curves). When AF interactions between Eu ions (singles, pairs, and triplets) are considered, the best fitting curve is found with J_ex/k_B = −0.35 K; nearly all the magnetization data lies on the curve as shown in Fig. 4b and d, considerably improving the fitting against the Fig. 4a and c. This supports the notion that the exchange interaction between nearest neighbor of Eu²⁺ ions in PbSe is antiferromagnetic.

A previous study¹⁶ has also reported AF interactions of Eu²⁺ ions in Pb_1−xEu_xSe samples with J_ex/k_B = −0.24 K at T = 0.62 K from the magnetization steps analysis, whereas our obtained exchange coupling (J_ex/k_B) is slightly different, J_ex/k_B = −0.35 K from T = 2 K to 6 K. The difference may come from the different carrier concentration of the samples; however, further studies at lower temperatures would be necessary to conclude this. It should be mentioned that an increase in the Eu concentration in PbSe will also increase the probability of forming structures of NN Eu atoms that are larger than simple triangles in which the AF interactions play a role. For this reason, the magnetization fittings in the samples with (x > 0.03, y = 0.01) are not reported. For example, the total probability of the analyzed configuration, P_T = P_S + P_P + P_OT + P_CT of (x = 0.03, y = 0.01) sample is 99%, while that of (x = 0.06, y = 0.01) sample would be 92%, hence 8% of the total magnetization is delivered by the higher-order configurations (squares, etc.), and the analysis limited to triangles becomes not accurate enough and is not presented.

In Fig. 5, the inverse low field (5 kOe) susceptibility against temperature in three samples of Pb_1−x−yEu_xSe:Na_y with (x = 0.01, y = 0) (x = 0.03, y = 0.01), and (x = 0.06, y = 0.01) is reported. The data are analyzed using the Curie–Weiss law:⁴³

where T is the absolute temperature, χ_d is the diamagnetic susceptibility, C is the Curie constant, and θ is the Curie–Weiss temperature as given by⁴⁷

Fig. 5 Inverse susceptibility of three Pb_1−x−yEu_xNa_ySe samples as a function of temperature. The solid lines are obtained from the Curie–Weiss law, eqn (8).

In (9) and (10), N is z is the number of sites on the coordination sphere (z = 12), and J_ex/k_B is the exchange constant. Using the same J_ex/k_B = −0.35 K and number of magnetic Eu²⁺ ions x_Eu²⁺ as is the low-temperature magnetization analysis (Table 1), we are able to describe the susceptibility behavior, as seen in Fig. 5, where the low field magnetic (5 kOe) susceptibility data shows linear relation with temperature, following the Curie–Weiss law. This supports the conclusion of the presence of AF interactions between nearest neighboring Eu atoms (negative θ and J_ex), as well as the transformation of Eu²⁺ to Eu³⁺ with Na doping (the same x_Eu²⁺ used here).

C. Electronic structure

The experimental data analysis provides strong evidence that the Eu valence in Pb_1−x−yEu_xNa_ySe varies from 2+ to 3+. The question that remains open at this point is whether this transition may be explained by the evolution of the electronic band structure of the system, or whether it is connected to the chemistry of the material (e.g., formation of an antiferromagnetic Eu–Se secondary phases could also decrease the total magnetization of the samples, although it would not be consistent with the close correlation of the drop in magnetization with the carrier concentration change). The electronic structure calculations in this section address the question. This is a difficult task for density functional (DFT) methods, since the presence of a 4f element (Eu) requires taking into account strong Coulomb interactions on the 4f shell. Furthermore, the system under study is double-doped (Eu + Na). The Eu²⁺–Eu³⁺ transition, proposed here to explain the behavior of the Hall charge density and magnetization, would be consistent with the presence of the highest occupied Eu 4f level near the Fermi energy E_F of PbSe, so that changes in E_F with Na doping can move the Fermi energy into the Eu 4f level, leading to an instability of the 4f⁷ configuration and driving the transition to the mixed 4f⁶–4f⁷ state.

The calculated densities of states (DOS) for three concentrations of Eu and Na in PbSe are presented in Fig. 6. First, in panel (a), DOS of 64-atom PbSe supercell with a single Pb replaced with Eu (i.e. Eu₁Pb₃₁Se₃₂) is shown. This corresponds to about 3 at% of Eu in PbSe. We see full spin-polarization of the Eu 4f states, with the empty spin-down states expelled well above E_F (not shown for clarity of the figure). A semiconducting state is seen in panel (a), with Eu 4f⁷ occupied configuration and spin magnetic moment of 7 μ_B per Eu, confirming the Eu²⁺ state in PbSe. The first peak of the Eu 4f⁷ shell DOS is about 0.25 eV below the valence band edge. Panels (b) and (c) in Fig. 6 show two cases of doubly doped PbSe, Eu₁Na₃Pb₂₈Se₃₂ in panel (b) and Eu₂Na₂Pb₂₈Se₃₂ in panel (c). In these supercells, the symmetry was reduced to trigonal, to allow for different configurations of Eu and Na atoms within the same computational geometry. When Na is introduced into Pb_1−xEu_xSe (see, Fig. 6b), the Fermi level moves deep into the valence band (VB), and the 4f Eu shell DOS splits into two main parts. One, accommodating six 4f electrons, goes deeper into the VB, corresponding to a stable 4f⁶ configuration. The second, accommodating single electron, remains near the VB edge, with E_F inside the peak. The total filling of the 4f shell here is 6.7. Such a configuration, with E_F being inside the 4f peak with a large spectral weight of f-states at the Fermi level and a partial 4f shell filling, cannot be stable in the real material and should be interpreted as an “averaged” picture of the mixed 4f⁶–4f⁷ state, predicted by the static, single-electron density functional computations. The Eu²⁺(4f⁷)–Eu³⁺(4f⁶) transition avoids such energetically unfavorable electronic configuration, and the real DOS in the material will not look like the one presented in Fig. 6b, which should be treated as a signature of the valence instability. Similar results (Fig. 6c) were obtained for the third studied supercell, Eu₂Na₂Pb₂₈Se₃₂, in which the two Eu atoms were located in two inequivalent crystallographic positions with different Eu–Na distance. Also here, as the Fermi energy comes close to the Eu-4f DOS, the reconfiguration of the Eu 4f shell takes place. The Eu(1) atom, located closer to Na, exhibits larger splitting of the 4f shell and stronger reduction of the 4f⁷-th level filling (equal to 6.6), comparing to Eu(2) (filling equal to 6.8), which was placed much further from Na [the distances were: Eu(1)–Na 4.3 Å, Eu(2)–Na 7.5 Å]. This is understood, as the smaller valence electron density around Na⁺, compared to Pb²⁺, lies behind the Eu²⁺–Eu³⁺ transition, so the Eu(1) ion located closer to Na⁺, should adopt the 4f⁶ configuration more readily than Eu(2). On the other hand, this also shows that no Eu–Na clustering effects are necessary to trigger the Eu²⁺–Eu³⁺ transition; for the Eu(2) atom, the nearest Na was located as far as the 6th coordination sphere.

Fig. 6 Spin-polarized densities of states (DOS) for 64-atoms supercells of PbSe, with some of Pb atoms substituted by Eu and Na, as given in the top legend. On each of the panels, the “spin-down” DOS is plotted as negative. The left scale corresponds to the partial 4f Eu DOS (black curves) given per Eu atom and per spin, while the right scale gives the total DOS of the supercell (blue curves), divided by 32 (the number of PbSe formula units).

Note that presented results cannot determine whether the valence “mixing” is in the time domain (valence fluctuations) or in the space domain (static spatially mixed valence). Also, the calculated fraction of Eu³⁺ is a slower function of the Na concentration than that observed in the real material. The magnetization data (Table 1) show that in the samples with 1% Eu and 1% Na concentrations, 76% of Eu is in the 3+ state. In contrast, from DFT studies in Eu₂Na₂Pb₂₈Se₃₂ one sees that the average Eu 4f shell filling is 6.7, which could be interpreted as 30% of Eu in Eu³⁺ state. Nevertheless, DFT computations gave theoretical and independent support to the hypothesis of a Eu²⁺–Eu³⁺ valence transition in the studied system. Moreover, a qualitative explanation of the mechanism of transition is given, in terms of the modifications in the electronic structure of the system triggered by the unfavorable location of the Fermi energy inside the DOS of the Eu-4f electron shell.

Summary and conclusion

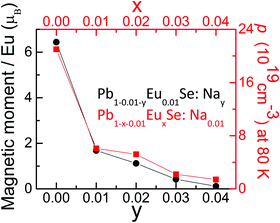
We have investigated thermoelectric, galvanomagnetic, magnetic, and electronic properties of Pb_1−x−yEu_xSe:Na_y samples. The measurement results are summarized in Fig. 7, which represents magnetization and hole concentration as a function of both Eu and Na content.

Fig. 7 Correlation between the measured magnetic moment per Eu atom, obtained from the fitting of Pb_1−x−yEu_xNa_ySe (x = 0.01; y = 0, 0.01, 0.02, 0.03, and 0.04) magnetization data (left scale, black points), and the carrier concentration at T = 80 K (y = 0, 0.01; x = 0.01, 0.02, 0.03, and 0.04) (right scale, red squares).

First, as the Eu level (x) in Pb_0.99−xEu_xNa_0.01Se is increased, the system shows a significant reduction in hole concentration. Second, when Na level (y) is increased in Pb_0.99−yEu_0.01Na_ySe, an equally significant decrease in magnetization is observed. Both phenomena can be explained by the valence transition of a fraction of the europium atoms, from magnetic and divalent Eu²⁺ to a non-magnetic and trivalent Eu³⁺, when Na is added to the system and the position of the Fermi level changes. As a result, a mixed valence state is realized in the system, and each amount of Eu in a 3+ state compensates a fraction of holes delivered by Na. When the concentrations of Eu and Na are both equal to 1%, 76% of Eu²⁺ ions are transformed into Eu³⁺. When the concentration of Na is further increased, the percentage of trivalent Eu is rising, reaching 98% for x = 1%, y = 4% case. A simplified electron-counting model for this transition would be that the Eu²⁺ concentration would change with the introduction of Na⁺, into Eu³⁺ and Na⁰. Fig. 7 then illustrates how any loss of Na⁺ causes an increase in the amount of non-magnetic Eu³⁺ and a decrease in carrier concentration. Electronic structure calculations showed that the highest energy Eu 4f level of the Eu²⁺ ion in PbSe is located about 0.25 eV below the VB edge of the system. When Na, which is an acceptor in PbSe, is added to Pb_1−xEu_xSe, E_F moves deeper into the VB, causing an instability and splitting of the Eu-4f electronic shell. This independently supports the idea of Eu²⁺–Eu³⁺ valence transition in the double-doped Pb_1−x−yEu_x Na_ySe.

Moreover, we observed and analyzed magnetic interactions between the Eu ions in the studied samples. Low-temperature magnetization data are fitted successfully to a model that takes into account the magnetic contributions of singles, pairs, and triplets of Eu²⁺ ions. Antiferromagnetic interaction between the nearest-neighbor Eu²⁺ with exchange coupling of J_ex/k_B = −0.35 K was found. This was confirmed further by the low-field susceptibility measurements, analyzed using the Curie–Weiss law and taking the same exchange constant.

The important question that remains open and should be addressed in future studies, is whether the Eu²⁺–Eu³⁺ transition will take place for acceptors other than Na in Pb_1−xEu_xSe. If the interpretation presented here is correct, the answer should be positive, since the interpretation does not involve the chemical nature of Na, but is based on a shift of the Fermi levels and a reconfiguration in Pb_1−xEu_xSe bands. In other words, the rigid band approximation applies to additions of Na, but not to additions of Eu, even if the amounts added are similar. Furthermore, a similar behavior may be possible in other rare-earth doped narrow-gap semiconductors and hints of a behavior similar to that described here might have been seen in InSb doped with Er⁴⁸ and Sm⁴⁹.

Acknowledgements

This work is supported as part of the Center for Revolutionary Materials for Solid State Energy Conversion, an EFRC funded by the U.S. DOE, Office of Science, Office of Basic Energy Sciences under Award Number DE-SC0001054. JPH is partly supported by the ARO MURI “Materials with extraordinary spin-heat coupling” under grant W911NF-14-1-0016. BH is supported by the NSF EFRI-2DARE grant number 1433467. BW was partly supported by the Polish National Science Center (project no. DEC-2011/02/A/ST3/00124).

Notes and references

1. A. F. Ioffe, Semiconductor Thermoelements and Thermoelectric Cooling, Infosearch, London, 1957.
2. K. Yang, W. Setyawan, S. Wang, M. Buongiorno Nardelli and S. Curtarolo, Nat. Mater., 2012, 11, 614.
3. J. P. Heremans, V. Jovovic, E. S. Toberer, A. Saramat, K. Kurosaki, A. Charoenphakdee, S. Yamanaka and G. J. Snyder, Science, 2008, 321, 554.
4. K. F. Hsu, S. Loo, F. Guo, W. Chen, J. S. Dyck, C. Uher, T. Hogan, E. K. Polychroniadis and M. G. Kanatzidis, Science, 2004, 303, 818.
5. P. F. P. Poudeu, J. D’Angelo, A. D. Downey, J. L. Short, T. P. Hogan and M. G. Kanatzidis, Angew. Chem., Int. Ed., 2006, 45, 3835.
6. K. Biswas, J. He, I. D. Blum, C.-I. Wu, T. P. Hogan, D. N. Seidman, V. P. Dravid and M. G. Kanatzidis, Nature, 2012, 489, 414.
7. Y. Lee, S.-H. Lo, J. Androulakis, C.-I. Wu, L.-D. Zhao, D.-Y. Chung, T. P. Hogan, V. P. Dravid and M. G. Kanatzidis, J. Am. Chem. Soc., 2013, 135, 5152.
8. J. Androulakis, Y. Lee, I. Todorov, D.-Y. Chung and M. G. Kanatzidis, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195209.
9. G. Bauer, H. Pascher and W. Zawadzki, Semicond. Sci. Technol., 1992, 7, 703.
10. H. Kanazawa, S. Adachi, T. Yamaguchi, S. Murashige and K. Murakami, J. Appl. Phys., 1999, 86, 2611.
11. A. Lambrecht, N. Herres, B. Spanger, S. Kuhn, H. Bottner, M. Tacke and J. Evers, J. Cryst. Growth, 1991, 108, 301.
12. G. Braunstein, G. Dresselhaus, J. Heremans and D. Partin, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 35, 1969.
13. J. Heremans and D. L. Partin, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 6311.
14. D. L. Partin, J. Heremans, C. M. Thrush, L. Green and C. H. Olk, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 38, 3549.
15. L. Salamanca-Young, D. L. Partin and J. Heremans, J. Appl. Phys., 1988, 63, 1504.
16. V. Bindilatti, N. F. Oliveira, Jr., Y. Shapira, G. H. McCabe, M. T. Liu, S. Isber, S. Charar, M. Averous, E. J. McNiff, Jr. and Z. Golacki, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 5472.
17. S. Isber, S. Charar, C. Fau, V. Mathet, M. Averous and Z. Golacki, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 1678.
18. V. Jovovic, S. J. Thiagarajan, J. West, J. P. Heremans, T. Story, Z. Golacki, W. Paszkowicz and V. Osinniy, J. Appl. Phys., 2007, 102, 043707.
19. V. Zlatic and R. Monnier, Modern Theory of Thermoelectricity, Oxford University Press, 2015.
20. T. Story, Semimagnetic Semiconductors Based on Lead Chalcogenides, in Lead Chalcogenides: Physics and Applications, ed. D. Khokhlov, Taylor & Francis, New York, 2003.
21. A. Lenard, T. Dietl, M. Sawicki, W. Dobrowolski, K. Dybko, T. Skośkiewicz, W. Plesiewicz, S. Miotkowska, A. Witek and A. Mycielski, J. Low Temp. Phys., 1990, 80, 15.
22. U. Zeitler, A. Wittlin, J. C. Maan, W. Dobrowolski and A. Mycielski, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 15258.
23. W. Dobrowolski, Acta Phys. Pol., A, 1996, 89, 3.
24. M. von Ortenberg, Semicond. Sci. Technol., 1993, 8, S16.
25. T. Dietl, J. Cryst. Growth, 1990, 101, 808.
26. J. Mycielski, Solid State Commun., 1986, 60, 165.
27. E. Grodzicka, W. Dobrowolski, J. Kossut, T. Story and B. Witkowska, Acta Phys. Pol., A, 1993, 84, 599.
28. T. Story, Ż. Wilamowski, E. Grodzicka, W. Dobrowolski, B. Witkowska and J. Voiron, Acta Phys. Pol., A, 1995, 87, 229.
29. T. Story, M. Górska, A. Łusakowski, M. Arciszewska, W. Dobrowolski, E. Grodzicka, Z. Gołacki and R. R. Gała̧zka, New Mechanism of f- f Exchange Interactions Controlled by Fermi Level Position, Phys. Rev. Lett., 1996, 77, 3447.
30. T. Story, Acta Phys. Pol., A, 1996, 91, 173.
31. E. Grodzicka, W. Dobrowolski, T. Story, E. I. Slynko, Yu.K. Vygranenko, M. M. H. Willekens, H. J. M. Swagten and W. J. M. de Jonge, Acta Phys. Pol., A, 1996, 90, 801.
32. P. Blaha, K. Schwarz, G. K. H. Madsen, D. Kvasnicka and J. Luitz, WIEN2K, An Augmented Plane Wave + Local Orbitals Program for Calculating Crystal Properties, Karlheinz Schwarz, Technische Universität Wien, 2001.
33. J. Kuneš and R. Laskowski, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 174415.
34. A. Rubio-Ponce, A. Conde-Gallardo and D. Olguín, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 035107.
35. F. Tran and P. Blaha, Phys. Rev. Lett., 2009, 102, 226401.
36. Y. I. Ravich, B. A. Efimova and I. A. Smirnov, Semiconducting lead chalcogenides, Plenum Press, New York, 1970.
37. E. G. Evola, M. D. Nielsen, C. M. Jaworski, H. Jin and J. P. Heremans, J. Appl. Phys., 2014, 115, 053704.
38. in Non-Tetrahedrally Bonded Elements and Binary compounds I, Lead Selenide (PbSe) Debye temperature, density, melting temperature, ed. O. Madelung, U. Rossler and M. Schulz, Springer, Berlin, 1998, vol. 41C.
39. E. Evola, High Figure of Merit Lead Selenide Doped with Indium and Aluminum for Use in Thermoelectric Waste Heat Recovery Applications at Intermediate Temperatures, Electronic thesis, Ohio State University, 2012. http://https://etd.ohiolink.edu/pg_10?0::NO:10:P10_ACCESSION_NUM:osu1338307382.
40. T. C. Chasapis, Y. Lee, E. Hatzikraniotis, K. M. Paraskevopoulos, H. Chi, C. Uher and M. G. Kanatzidis, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 085207.
41. H. Wang, Y. Pei, A. D. LaLonde and G. J. Snyder, Adv. Mater., 2011, 23, 1366.
42. Note, that if as a reference value, the nominal carrier concentration is used (1.75 × 10²⁰ cm⁻³, assuming that each Na delivers one hole to the system), instead of the measured Hall value of 2.1 × 10²⁰ cm⁻³, given Eu²⁺/Eu³⁺ concentrations are changed in about 15%.
43. N. W. Ashcroft and N. D. Mermin, Solid State Physics, Holt, Rinehart, and Winston, New York, 1976, p. 656, and references therein.
44. X. Gratens, S. Charar, M. Averous, S. Isber, J. Deportes and Z. Golacki, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 8199.
45. Y. Shapira and V. Bindilatti, J. Appl. Phys., 2002, 92, 4155.
46. M. M. Kreitman and D. L. Barnett, J. Chem. Phys., 1965, 43, 364.
47. A. Errebbahi, S. Charar, F. Terki, C. Fau, S. Isber, M. Tabbal, T. C. Christidis, D. Ravot, J. C. Tedenac and Z. Golacki, J. Magn. Magn. Mater., 2002, 247, 55.
48. J. P. Heremans, D. L. Partin, D. T. Morelli and C. M. Thrush, J. Vac. Sci. Technol., B, 1992, 10, 659.
49. D. L. Partin, J. P. Heremans, C. M. Thrush and D. T. Morelli, J. Vac. Sci. Technol., B, 1992, 10, 873.

---