Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ligand size dependence of U–N and U–O bond character in a series of uranyl hexaphyrin complexes: quantum chemical simulation and density based analysis†
Poppy
Di Pietro
 *a and
Andrew
Kerridge
*a and
Andrew
Kerridge
 *b
*b
aDepartment of Chemistry, University College London, 20 Gordon Street, London, WC1H 0AJ, UK. E-mail: poppy.pietro12@ucl.ac.uk
bDepartment of Chemistry, Lancaster University, Lancaster, LA1 4YB, UK. E-mail: a.kerridge@lancaster.ac.uk
First published on 22nd February 2017
Abstract
A series of uranyl complexes with hexaphyrin ligands are investigated at the density functional level of theory and analysed using a variety of density-based techniques. A relationship is identified between the size of the ligand and the stability of the complex, controlled by the presence of meso-carbon centres in the porphyrin ring. The complex with the smallest ligand, cyclo[6]pyrrole, is found to have enhanced covalent character in equatorial U–N bonds as defined by the quantum theory of atoms in molecules (QTAIM), as well as enhanced stability, compared to the larger complexes. QTAIM data are supported by electron density difference distributions, integrated electronic properties and analysis of the reduced density gradient (RDG), which all show unambiguous evidence of electron sharing in all U–N bonds. In all complexes, a weakening of the covalent axial U–Oyl interaction in comparison to free uranyl is found, with evidence for a separation of electronic charge resulting in a more ionic interaction. A relationship between covalent character in the U–N bonds and the magnitude of uranyl charge redistribution is identified, where the greater the covalent character of the U–N interaction, the more ionic the U–Oyl interaction appears. The complex with the largest ligand, hexaphyrin(1.1.1.1.1.1), is found to have additional interactions with the uranyl oxygen centres, perturbing the U–Oyl interaction.
Introduction
Investigations of actinide coordination are challenging from both experimental and theoretical perspectives. Radioactivity and toxicity, amongst several other factors, hamper experimental study, while strong electron correlation, weak crystal fields and significant relativistic effects mean that the modelling of these complexes is not trivial.1–6 However, developing our understanding of the bonding interactions of actinide elements is desirable from both a fundamental and practical perspective. The coordination chemistry of the actinides is a widely researched topic, with coordination by mono- and multi-dentate, as well as macrocyclic, ligands of great fundamental interest.7–20 From a practical perspective, developing an improved characterisation of bonding in actinide complexes may be useful to, for example, the nuclear industry.Worldwide, 10.9% of energy is now generated by nuclear fission,21 with a typical reactor producing 20 metric tons of spent fuel per year.22 This consists mainly of a mixture of uranium, plutonium, small amounts of the minor actinides neptunium, americium and curium, as well as fission products including lanthanides and transition metals. The amount of spent fuel generated is only likely to increase as the world becomes more reliant on fission power in order to meet growing energy demands, and how best to manage the long-lived and highly radiotoxic actinides in this spent fuel is an ongoing issue faced by the nuclear power industry. The minor actinides, whose chemistry is dominated by the trivalent oxidation state,3 present a particular challenge as current practices for their management require efficient separation from the lanthanides, which exhibit very similar chemistry. For this reason, a significant research effort is currently focussed on the identification of ligands which show actinide selectivity.
To this purpose, relatively soft N-donor ligands have been investigated with varying degrees of success.9 Several, such as ligands from the BTP, BTBP and BTPhen families, have exhibited promising selectivity,23–25 however the source of this selectivity is not fully understood, and can be destroyed, or greatly enhanced, with small modifications to the ligand,26–30 albeit not yet in a predictable way.
There is a growing body of work demonstrating that due to the actinide 5f-shell being relatively diffuse and extending beyond the 6d-shell, 5f orbitals have greater chemical availability.6,11,31–34 Actinides are therefore potentially able to form bonds with a greater degree of covalency than lanthanides,11,25,31,32,35–43 whose 4f orbitals are contracted and core-like.9,37,39,43,44 The consequence of this is enhanced covalent character in the largely ionic An–N bonds, compared to similar Ln–N bonds, with this covalency conferring additional stability upon the actinide systems. This covalency is predicted to be most pronounced for the early actinides, decreasing across the series.35–37,39,43
The minor actinides Am(III) and Cm(III) behave very similarly to the lanthanides in terms of their bonding interactions,3 hence the need for ligands which are highly selective. Covalency in complexes of the lanthanides and later actinides is weak,39,45 thus any variations in covalent character is, commensurately, very small.36–38,46–48 Uranium complexes have previously been considered as model systems26,49–52 in studies of actinide covalency due to the aforementioned magnitude of covalent character in early actinides,36,37,45–47,51 making any variation in covalency more apparent. Developing our understanding of the U–N interaction may therefore shed light on how covalency may be controlled and enhanced.
The expanded porphyrins are large, flexible, synthetic ligands capable of coordinating actinyl (di)cations in the equatorial plane53–57via pyrrolic nitrogen centres. The presence of meso-carbon centres between pyrrole units allows for modification to the size and shape of the ligand, and there are many possible substitution sites, allowing the possibility of ligands being ‘tuned’ to fit a specific cation.57–60 Additionally, expanded porphyrins follow the CHON principle, a desirable criteria of an industrially useful separation ligand, specifically that it consist only of carbon, hydrogen, nitrogen and oxygen, which can be fully combusted after use to form environmentally safe products.
Several uranyl complexes with expanded porphyrin ligands have been experimentally realised. The hexaphyrins are expanded porphyrin macrocycles comprised of six pyrrolic subunits separated by varying numbers of meso-carbon atoms. Sessler et al. reported the synthesis of a uranyl complex of the hexaphyrin ligand isoamethyrin(1.0.1.0.0.0),54 where the numbers in parentheses denote the number and position of meso-carbons (see Fig. 1), and suggested its possible use as a colorimetric actinide sensor.54,61 The Sessler group has also reported neptunyl and plutonyl complexes with isoamethyrin54,62 as well as several other expanded porphyrins and similar expanded porphyrin-like macrocycles,55 and uranyl complexes of the hexaphyrin ligands cyclo[6]pyrrole (comprising no meso-carbons) and amethyrin(1.0.0.1.0.0).53,56 Uranyl complexes of the rubyrin(1.1.0.1.1.0), rubyrin(1.1.1.1.0.0) and hexaphyrin(1.1.1.1.1.1) ligands have not been reported, however the ligands themselves have been synthesized either as free-base macrocycles or complexes of, for example, transition metals.57,60,63–74 To date, many different expanded porphyrin ligands have been synthesised.57,58,71,75–80 Due to the existence of many possible substitution sites, the basic hexapyrrolic structure of the ligands may be modified with peripheral or meso-substituents,63,71,72,81–83 or for example, replacement of a pyrrolic subunit with a different kind of ring, e.g. a furan or pyridine subunit.84 Actinide and actinyl complexes of several other expanded porphyrin-type ligands have been reported and investigated both experimentally and theoretically.85–93
 | ||
| Fig. 1 Molecular structure of isoamethyrin dianion omitting peripheral groups for clarity. Symmetry-distinct coordinating nitrogens are labelled NA, NB and NC. meso-Carbon atoms are labelled Cm. | ||
Although the equatorial bonding characteristics of uranyl, with its formally empty 5f-shell, and the trivalent minor actinides with their partially filled f-shells are expected to differ, it is intended in this instance simply to investigate the potential for expanded porphyrin ligands to coordinate a uranyl dication and to quantify the nature of the U–N bonds in such complexes with the aim being to begin to identify the characteristics of a ligand which lead to increased equatorial covalency. In this way, if the selectivity shown by ligands from the BTP/BTBP/BTPhen families is indeed covalency driven, results obtained here may be useful for informing the design of future selective ligands. Additionally, the presence of the distinctive and experimentally accessible U–Oyl stretching modes94–96 may act as probes of equatorial covalency.97 Ultimately it is intended that this work will be extended to include complexes of uranyl and plutonyl, and perhaps eventually the trivalent minor actinides.
Previously, we have performed an in-depth study on the equatorial coordination behaviour of uranyl with a range of monodentate first row ligands.97 Using density based analysis, we determined a strong correlation between covalent character in equatorial bonding and the vibrational frequencies of the U–Oyl stretching modes. Subsequently, we compared two complexes of uranyl with multidentate ligands:98 a complex with the hexadentate macrocyclic expanded porphyrin ligand isoamethyrin and a complex with two tridentate bis-triazinyl-pyridine (BTP) ligands which have been shown to act selectively for An(III) over Ln(III) in industrial separation processes. Our theoretical study concluded that the U–N bonding in these two complexes was strongly similar: largely ionic equatorial bonds with a comparable degree of covalency and a commensurate weakening of the U–O covalent interaction suggesting a redistribution of charge in the uranyl unit, with the very similar equatorial bonding in the two complexes suggesting that expanded porphyrin ligands may be interesting candidates for future investigations of actinide selectivity.98
In this contribution, we combine quantum chemical calculations at the density functional (DFT) level of theory with density-based analysis techniques to show that complexes of uranyl with hexaphyrin ligands provide an interesting set of systems for investigating covalency in the U–N interaction. We determine the effect of altering the size of the ligand core on the degree of covalent character in equatorial U–N bonds, and quantify the extent of the charge redistribution in the uranyl unit that occurs upon complexation using the experimentally accessible U–Oyl stretching frequencies.
Quantum chemical calculations have been used to investigate eight complexes in total, of which three have previously been synthetically realised: UO2-cyclo[6]pyrrole, which contains no meso-carbon atoms, as well as UO2-isoamethyrin(1.0.1.0.0.0) and UO2-amethyrin(1.0.0.1.0.0) which each contain two meso-carbon atoms. Additionally, four hypothetical complexes with synthetically realised ligands are studied: UO2-rubyrin(1.1.1.1.0.0), UO2-rubyrin(1.1.1.0.1.0), UO2-rubyrin(1.1.0.1.1.0), which each contain four meso-carbon atoms, and UO2-hexaphyrin(1.1.1.1.1.1) which contains six, one bridging each of its pyrrolic subunits. Finally, one system for which both the complex and the ligand are hypothetical, UO2-hexaphyrin(1.1.0.0.0.0), has been investigated. These ligands were selected so that the effect of increasing the size of the hexaphyrin core via meso-substitution could be directly investigated.
All complexes have been optimised at the density functional level of theory and, as a representative sample, four complexes were selected for detailed density analysis. For simplicity, the eight complexes will be referred to throughout using the labelling defined in Table 1.
| Simplified complex | Substituted complex | |
|---|---|---|
| Cyclo[6]pyrrole | C0 | C0′ |
| Hexaphyrin(1.1.0.0.0.0) | C2a | C2a′ |
| Isoamethyrin(1.0.1.0.0.0) | C2b | C2b′ |
| Amethyrin(1.0.0.1.0.0) | C2c | C2c′ |
| Rubyrin(1.1.1.1.0.0) | C4a | C4a′ |
| Rubyrin(1.1.1.0.1.0) | C4b | C4b′ |
| Rubyrin(1.1.0.1.1.0) | C4c | C4c′ |
| Hexaphyrin(1.1.1.1.1.1) | C6 | C6′ |
In order to avoid any potential ambiguities that may arise from employing orbital-based analysis techniques, we focus on electron-density based analytical approaches. Such density-based analyses have previously been successfully applied to f-element complexes14,36–39,42,47,99,100 and, in particular, allow direct comparison of results obtained using DFT with those obtained using multiconfigurational methodologies.
The quantum theory of atoms in molecules101,102 (QTAIM) has been used to assess covalent character in U–N and U–O bonds. QTAIM relies upon the partitioning of a molecule into atomic basins bound by surfaces satisfied by the condition ∇ρ(r)·n(r) = 0. n(r) is the unit vector normal to the basin surface. Points at which the gradient in the electron density vanishes, ∇ρ(r) = 0, define the critical points in ρ(r). Of particular interest in this study are “bond critical points” (BCPs), which are found where the line of maximum density defining a bond path between bonded atoms is at its minimum.103 Values of topological indicators at the BCP characterise the bonding interaction. In general, where the BCP has ρ > 0.20 a.u. and ∇2ρ < 0, a bond can be described as covalent. Broadly speaking, the higher the value of ρ, the higher the covalent character of the bond. The energy density, H, can also be used as a measure of covalency.101,102 For a covalent bond, its value is expected to be negative, with the degree of covalency indicated by the magnitude. In addition, integrated properties such as atomic populations, as well as localisation and delocalisation indices can be obtained by integrating over atomic basins and give insight into both electron sharing and charge donation.
We complement our QTAIM studies by considering regions of weak interaction,104 by investigating the reduced density gradient (RDG), defined as s(r) = |∇ρ(r)|/2(3π2)1/3ρ(r)4/3, and, finally, visualise electron density difference distributions upon complexation to qualitatively analyse the changes that are undergone upon complex formation. We compare these distributions to our quantitative data in order to develop a comprehensive description of the nature of U–N and U–O bonding in these complexes.
Computational details
Density functional theory (DFT) calculations have been performed using version 6.4 of the TURBOMOLE quantum chemistry software package.105 Ahlrichs def2-TZVP basis sets of triple-zeta quality have been used for the C, H, O and N atoms106 and the Ahlrichs def-TZVP basis set of triple-zeta quality, which incorporate a relativistic ECP comprising 60 core electrons107 has been used for the U atoms. All complexes summarised in Fig. 2 and 3 were optimised using the PBE exchange–correlation xc-functional108 which employs the generalised gradient approximation (GGA). Subsequent reoptimisation of a representative sample of complexes was also performed using the B3LYP hybrid-GGA xc-functional109,110 to approximate the exchange correlation energy. This was done in order to investigate the effects of incorporating exact exchange on properties of the electron density. Both PBE and B3LYP have previously be shown to be suitable for the accurate modelling of actinide-containing systems.3,14,97,98,111,112 Initial optimisations were carried out in the gas phase. Subsequently, the COSMO continuum solvation model,113 using a relative permittivity of εr = 8.9 was used to simulate solvation in DCM, for which there is experimental precedent.54 Vibrational analysis was performed to ensure that structures represented energetic minima.‡ Due to the closed shell nature of these systems, the effects of spin–orbit coupling were not included in the calculations.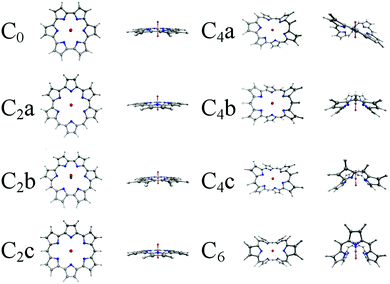 | ||
| Fig. 2 Optimised structures of the eight uranyl hexaphyrins considered in this study, optimised in the gas phase using the PBE exchange–correlation functional, without peripheral alkyl substituents. | ||
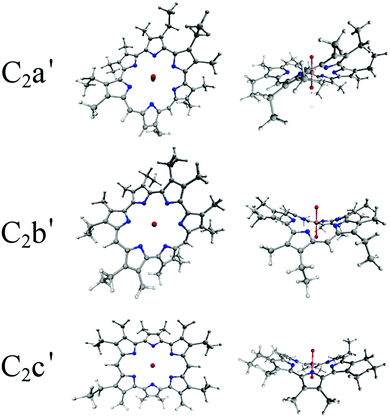 | ||
| Fig. 3 Optimised peripherally substituted C2 structures, optimised in the gas phase using the PBE exchange–correlation functional. | ||
All of the hexaphyrin macrocycles reported experimentally feature methyl substituents on the periphery of their pyrrole units (see Fig. 3). These are generally assumed to have little effect on the geometry and electronic structure of the molecule and in order to minimise computational expense, such substituents are often omitted when performing DFT simulations. However it has been shown that for UO2-isoamethyrin(1.0.1.0.0.0), this simplification leads to severely overestimated (by ∼0.1 Å) U–N bond lengths.114 Thus, as with our previous study comparing UO2-isoamethyrin(1.0.1.0.0.0) with [UO2(BTP)2]2+, optimisations have been performed with and without these substituents so that their effects on geometry could be assessed. U–N and U–O bond lengths have been compared to experimental data where available. For electron density analysis, single point energy calculations were performed at the optimised geometries using the SARC all-electron uranium basis set115 and the second-order Douglas–Kroll–Hess (DKH2) Hamiltonian to account for scalar relativistic effects.116,117 QTAIM analysis was performed using the Multiwfn118 and AIMAll119 codes in order to calculate topological and integrated properties of the electron density. RDG and density difference data were visualised using the VMD code.120
Results and discussion
Geometrical characterisation and energetic stability
Geometries of the complexes optimised using the PBE xc-functional in the gas phase are shown in Fig. 2 and 3. It is apparent (see Table S1, ESI†) that, in most cases, the inclusion of peripheral alkyl groups has a relatively small effect on the average U–N bond length, with differences of only a few hundredths of an Angstrom, and results in no significant structural variation. The exception is with the C2x complexes, in which simplified and substituted forms have differences in average bond lengths of approximately 0.1 Å, nearly an order of magnitude higher than for the C0, C4 and C6 complexes. All C2x complexes exhibit significant structural variation when peripheral substituents are included, with a degree of non-planarity introduced that acts to shorten the U–N bonds. Based on these results, C0, C4x and C6 complexes will all be considered in their simplified form for the remainder of this contribution, and substituents will only be considered in the case of the C2x complexes, with the substituted system referred to as C2x′. Table 2 summarises U–N bond lengths for the complexes C0, C2x′, C4x and C6 and U–O bond lengths can be found in Table 3.| Complex | r U–N (gas phase/DCM) | |
|---|---|---|
| C0 | 2.528–2.534/2.522–2.530 | 2.532/2.527 |
| C2a′ | 2.591–2.835/2.591–2.812 | 2.673/2.659 |
| C2b′ | 2.586–2.772/2.573–2.755 | 2.688/2.674 |
| C2c′ | 2.569–2.751/2.557–2.736 | 2.689/2.674 |
| C4a | 2.533–2.827/2.527–2.811 | 2.717/2.706 |
| C4b | 2.690–2.720/2.678–2.700 | 2.701/2.687 |
| C4c | 2.663–2.785/2.654–2.769 | 2.703/2.692 |
| C6 | 2.640–2.820/2.637–2.818 | 2.700/2.697 |
| Complex | r U–O (gas phase/DCM) |
|---|---|
| C0 | 1.799/1.812 |
| C2a′ | 1.789/1.802 |
| C2b′ | 1.787/1.799 |
| C2c′ | 1.787/1.800 |
| C4a | 1.784/1.793 |
| C4b | 1.783/1.792, 1.785/1.793 |
| C4c | 1.784/1.792 |
| C6 | 1.784/1.791, 1.789/1.796 |
| UO22+ | 1.711/1.721 |
An examination of U–N and U–O bond lengths reveals that complex C0 has the shortest average U–N bond lengths of all eight complexes, 2.532 Å (2.527 Å), when optimised in the gas phase (DCM). C0 features four longer and two slightly shorter (by ∼0.01 Å) U–N bonds. This complex also has the longest calculated U–O bond length, 1.799 Å (1.812 Å), when optimised in the gas phase (DCM), thereby exhibiting the strongest perturbation of the uranyl unit due to equatorial complexation. Additionally, a very slight degree of non-planarity is introduced upon solvation (and upon addition of peripheral substituents), although this causes no significant changes to bond lengths. When compared to experimental values, the U–N bond lengths of C0 are reproduced to within 0.01 Å (0.01 Å) in the gas phase (DCM), an excellent level of agreement, while the U–O bonds are reproduced to within 0.02 Å (0.03 Å) in the gas phase (DCM), a good level of agreement.53 It is worth mentioning that the crystal structure of C0 exhibits nearly perfect planarity, in agreement with the calculated gas phase structure.
Moving on to the complexes containing two meso-carbons, the simplified complexes C2a, C2b and C2c share several characteristics. All are perfectly or very nearly planar, with average U–N bond lengths of 2.776–2.804 Å (2.770–2.799 Å) when optimised in the gas phase (DCM) and U–O bonds of 1.777–1.778 Å (1.786–1.793 Å) when optimised in the gas phase (DCM). Our calculated U–N and U–O bond lengths for both C2b and C2b′ are in good agreement with the previous theoretical values reported by Shamov and Schreckenbach,114 and, for C2b′, structural parameters are in good agreement with experimental data.54 Shamov and Schreckenbach's work illustrated the importance of including these substituents when modelling uranyl isoamethyrin, and here we find that substituents have a similar distorting effect on both C2a′ and the hypothetical C2c′, where a presumably sterically-induced twisting of the ligand results in average U–N bond lengths of 2.673–2.689 Å (2.659–2.674 Å) when optimised in the gas phase (DCM), ∼0.1 Å shorter than their simplified analogs. Commensurately, U–O bonds in the C2x′ complexes are slightly longer than their simplified analogs, 1.787–1.789 Å (1.799–1.802 Å) when optimised in the gas phase (DCM). These differences demonstrate that careful consideration of the effects of substituents and solvation models is essential when modelling hexaphyrin complexes. It may be interesting to investigate the rigidity of these structures using perhaps MD simulations, although this has not been performed as part of this study.
Non-planarity in C4a, C4b and C4c is pronounced. Average U–N bond lengths are typically a few hundredths of an Angstrom longer than for the C2x′ complexes, 2.701–2.707 Å (2.692–2.706 Å) when optimised in the gas phase (DCM). U–O bonds are commensurately slightly shorter than those in the C2x′ complexes, 1.783–1.785 Å (1.792–1.793 Å) when optimised in the gas phase (DCM).
C6, the largest complex, is also highly non-planar, allowing equatorial U–N bonds of comparable length to the C2x′ and C4x complexes to be formed. Interestingly, in this complex the ligand is folded almost completely in half (reminiscent of a Pacman-style ligand16,89,121,122), although here the uranyl unit is coordinated at the ligands centre. This folding has the effect of bringing some ligand atoms significantly closer to the –yl oxygen ions than in any of the other complexes. Average U–N bonds are 2.700 Å (2.697 Å) when optimised in the gas phase (DCM). U–O bond lengths are 1.789 Å (1.796 Å) and 1.784 Å (1.791 Å), with an 0.005 Å elongation of one bond due to the aforementioned C–Oyl interaction.
Reoptimisations of C0, C2b′, C4a, and C6 were performed using the hybrid B3LYP functional but led to no significant structural changes. U–N bond lengths were calculated to be in the region of 0.005 Å longer and U–O bond lengths were found to be shorter by approximately the same amount. Irrespective of the functional employed, continuum solvation acts to give a slight shortening of the U–N bonds and a corresponding lengthening of U–O bonds.
Binding energies
Complex stability was investigated by calculating molecular binding energies as well as ligand deformation energies. Molecular binding energies (ΔE) were calculated as defined in eqn (1) by subtracting the energies of the optimised uranyl dication and ligand dianion fragments from that of the complex:| ΔE = EC − (EUO22+ + EL2−) | (1) |
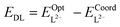 | (2) |
 | (3) |
| ΔEDA = ΔE − (EDL + EDU) | (4) |
Molecular binding energies and deformation adjusted binding energies calculated from PBE gas phase optimisations are listed in Table 4. The overall trend is for binding energies to fall as the ligands become larger, decreasing by ∼1.5 eV from C0 to the C2x′ complexes, then by another ∼1.5 eV from the C2x′ to the C4x complexes, where the effect appears to plateau. There is a decrease of only ∼0.2 eV from the C4x complexes to the C6 complex. Notably, the complexes predicted to be most stable here, C0 and C2x′, are those that have been synthetically realised, while the less stable C4x and C6 complexes have proven, so far, to be experimentally inaccessible.
| ΔE | ΔEDA | E DL | E DU | |
|---|---|---|---|---|
| C0 | −29.40 | −30.37 | 0.25 | 0.38 |
| C2a′ | −28.17 | −29.52 | 1.05 | 0.30 |
| C2b′ | −27.96 | −29.26 | 1.02 | 0.29 |
| C2c′ | −28.05 | −29.30 | 0.96 | 0.29 |
| C4a | −26.26 | −28.51 | 1.98 | 0.27 |
| C4b | −26.03 | −28.39 | 2.09 | 0.27 |
| C4c | −26.17 | −28.46 | 2.03 | 0.27 |
| C6 | −26.07 | −28.16 | 1.80 | 0.28 |
It is interesting to note that the deformation energy of the ligand increases as the core size is increased. This increase is ∼1 eV per pair of meso-carbon up to the C4x complexes, which appear to represent a maximum. Beyond this, increased flexibility in the ligand presumably reduces the deformation energy penalty. The deformation energy of the uranyl unit decreases slightly as the ligand core size increases: it is comparable, and in fact dominant, to that of the ligand in C0, whereas it is of comparable magnitude in all other complexes studied. Combined, the result is a net increase in deformation energy from C0 to C6. Whilst the deformation energy doesn't fully account for the relative stability of the smaller ligands, it does strongly correlate (R2 = 0.98) as shown in Fig. 4.
 | ||
| Fig. 4 Molecular binding energy plotted against total deformation energy for all eight complexes. Energies are taken from the structures optimised in the gas phase. | ||
When the deformation energy is subtracted from the binding energy to obtain a deformation adjusted binding energy, the relationship between binding energy and ligand size persists and there is a loss of stability for each pair of meso-carbons added, reaching a plateau at the C4x and C6 complexes.
U–O stretching frequencies
Frequencies of the U–O stretching modes calculated using the PBE functional in the gas phase and in the presence of a DCM continuum solvent are presented in Table 5. In previous studies, a degree of U–O bond weakening upon equatorial uranyl complexation has been both spectroscopically observed and theoretically calculated,42,94–97,123,124 with the magnitude of this weakening corresponding to a redshift in the distinctive uranyl stretching modes. Our previous study demonstrated strong correlations between binding energy and the frequency of the uranyl stretching modes in a series of monodentate complexes in which uranyl is coordinated by a first row species.97| ν U–Os (cm−1) | ν U–Oas (cm−1) | |
|---|---|---|
| C0 | 817.74/788.41 | 897.56/856.30 |
| C2a′ | 830.41/800.15 | 916.13/873.18 |
| C2b′ | 834.35/803.25 | 921.88/878.08 |
| C2c′ | 834.07/802.73 | 921.75/878.54 |
| C4a | 836.81/810.84 | 923.95/887.87 |
| C4b | 836.02/813.31 | 923.72/888.99 |
| C4c | 837.01/813.26 | 923.53/889.73 |
| C6 | 823.98/809.39 | 909.92/886.52 |
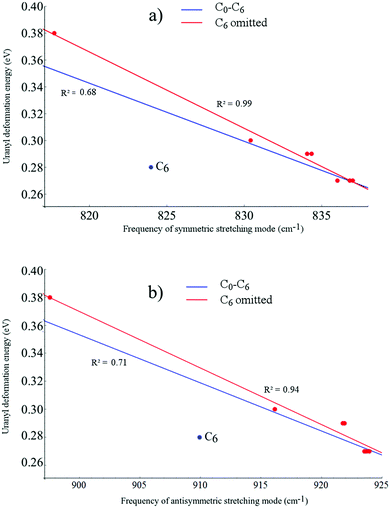
Fig. 5 shows both the symmetric and asymmetric stretching frequencies of uranyl in C0, C2a′, C2b′, C2c′, C4a, C4b, C4c and C6 plotted against the deformation adjusted binding energy. It is immediately clear that such a linear relationship is not present here, with only very weak correlation (R2 ≤ 0.3 in all cases). Plotting these frequencies against the uranyl deformation energy however, as seen in Fig. 6, results in weak correlation (R2 = 0.68 and 0.71 for the symmetric and asymmetric modes, respectively) with the C6 complex being an obvious outlier in what is otherwise an apparent linear relationship. When the C6 complex is omitted from the linear regression analysis, correlation becomes very strong (R2 = 0.99 and 0.94 for the symmetric and asymmetric modes, respectively). Returning to the relationship between the symmetric/asymmetric stretching frequencies of uranyl and the binding energy/deformation adjusted binding energy, omitting the C6 complex results in moderate correlation, with R2 values of between 0.53 and 0.83 and correlation being slightly stronger when considering the adjusted binding energy. Possible reasons for the anomalous behaviour exhibited by the C6 complex will be further explored in later sections.
For the following density based analysis, a representative set of complexes have been selected. This set comprises C0, C2b′ (which is the experimentally best characterised C2x′ complex), C4a (the most stable of the three hypothetical C4x complexes) and C6. All are simplified complexes except for C2b′ since, as discussed above, substitution was found to only impact significantly on C2x geometries. The characterisation will focus on PBE-optimised gas phase complexes, with data from B3LYP-optimised and solvated simulations given in ESI† and discussed where relevant.
Topological analysis of the electron density
Topological properties of the U–N and U–O bonds are now considered. The values of the electron density, ρ, its Laplacian, ∇2ρ, and the energy density, H, were investigated at the U–N and U–O bond critical point (BCP). Also included in this section is the delocalisation index δ(A,B), defined as the number of electrons delocalised between two atomic basins A and B. Table 6 contains average and total values of topological descriptors at the U–N BCPs. As a rule of thumb, a covalent bond is expected to have an electron density at the bond critical point of ρ ≥ 0.2 a.u., with a negative Laplacian and an energy density which is negative in sign, with its magnitude commensurate with the degree of covalency.101,102 It is immediately apparent from the data in Table 6 that, as expected, none of the U–N bonds investigated here exhibit pronounced covalency, rather each U–N bond has a small degree of covalent character which can be quantified by the values of these topological properties at the BCP. Average and total properties are given in Table 6 since it is the effect of the ligand as a whole on the uranyl unit which is of greatest interest, however there is a strong relationship between individual U–N bond lengths in C0, C2b′, C4a and C6 and ρBCP values, (see Fig. 7) where the shorter the bond, the larger the covalent component of the interaction. | ||
| Fig. 7 Values of U–N ρBCP plotted against individual U–N bond lengths for C0, C2b′, C4a and C6, for complexes optimised using the PBE xc-functional in the gas phase. | ||
When average values are considered (see Table 7), it can be seen that equatorial covalency decreases and U–N bond length increases in the order C0 > C2b′ > C6 > C4a, with C0 having by far the most U–N covalency and the other three complexes being broadly similar in their U–N character. It is worth emphasising that the U–N bonding character of C2b′, C4a and C6 is very similar in comparison to the differences between these complexes and C0. When the relationship between the frequencies of the uranyl stretching modes and the sum of ρBCP (see Table 6) for the U–N bonds is investigated, linear regression reveals only weak correlations with R2 = 0.74 and 0.61 for the antisymmetric and symmetric modes, respectively. The values of the energy density, H, at the BCPs of all U–N bonds, support conclusions drawn from the electron density, ρ, of weak covalent character. H takes negative, albeit very small, values in all complexes, with C0 having the largest magnitude, indicating the greatest degree of covalent character.
The delocalisation index (see Table 6), summed over all U–N bonds, may be considered a direct measure of electron sharing between the uranyl unit and the ligand. Supporting the assertion based on analysis of ρBCP that the U–N bonds in C0 have significantly more covalent character than any of the other complexes, C0 exhibits the greatest degree of electron delocalisation in its U–N bonds, with C2b′, C4a and C6 all exhibiting comparable values, similar to those of the [UO2(BTP)2]2+ complex we considered previously.98
In Table 8, various topological parameters of the U–O bonds are given. We find strong correlation (R2 = 0.97) between average values of ρBCP for the U–N bonds and values of ρBCP for the U–O bonds (see Fig. 8). This can be explained in terms of the effect on the uranyl unit due to the bonding in the equatorial plane, which acts to destabilise it, as we have previously reported,97,98 resulting in U–O covalency being weakest when equatorial covalency is strongest. Two things are of note when these data are considered. Firstly, C0 is again set apart from the other complexes, with significantly greater equatorial covalency and a commensurately smaller degree of covalency in the U–O interaction. Secondly, C6 again appears to differ from the other complexes in that its two U–O bonds have noticeably different values of ρBCP. This is explained by the fact that C6 has a characteristic unique amongst the complexes investigated here: QTAIM analysis reveals bond paths between two ligand meso-carbons and one of the uranyl oxygens, which is enclosed by the ligand in a manner reminiscent of a Pacman-style complex.125 Topological properties associated with this interaction are given in Table 8, showing that they are weak non-covalent interactions with ρBCP an order of magnitude lower than in the U–O bonds. When only the value of ρBCP for the unenclosed U–O bond in C6 is used, the frequencies of the uranyl stretching modes and values of ρBCP for the U–O bonds are found to have an improved linear relationship with R2 = 0.88 and 0.79 for the antisymmetric and symmetric modes, respectively. When the value of ρBCP for the enclosed U–O bond of C6 is used, linear correlations decrease to R2 = 0.70 and 0.58 for the antisymmetric and symmetric modes, respectively. Thus the uranyl stretching modes in the C6 complex are significantly perturbed by these additional interactions.
| C0 | C2b′ | C4a | C6 | ||||
|---|---|---|---|---|---|---|---|
| U–O | U–O | U–O | U–O1 | U–O2 | O1–Cm | O2–N | |
| ρ A–B | 0.290 | 0.299 | 0.301 | 0.301 | 0.299 | 0.009 | — |
| ∇2ρA–B | 0.320 | 0.315 | 0.314 | 0.323 | 0.307 | 0.037 | — |
| H A–B | −0.253 | −0.270 | −0.274 | −0.272 | −0.269 | 0.002 | — |
| δ(A,B) | 1.915 | 1.971 | 1.977 | 1.958 | 1.961 | 0.033 | 0.091 |
The effect of solvation is to slightly increase topological parameters in all U–N bonds, with a commensurate small decrease in the values of the topological parameters in the U–O bonds (see Tables S6–S9, ESI†). As in our previous work,97,98 choice of functional appears to have consistent, small, but non-negligible effects on the QTAIM parameters (see Tables S8 and S9, ESI†). For all complexes, use of the hybrid B3LYP xc-functional results in a small but appreciable increase in ρBCP for the U–O bond, and a small reduction in delocalisation. At the U–N BCPs, optimisation with B3LYP results in a small reduction in all properties measured compared to those obtained using PBE, implying that inclusion of a proportion of exact exchange results in increased electron localisation.14,48,97,98
Reduced density gradient
The reduced density gradient (RDG), s(r) = |∇ρ(r)|/2(3π2)1/3ρ(r)4/3, has very small values in regions of covalent and predominantly noncovalent interactions,104,126 tending towards zero at critical points in the electron density. In regions of covalent interactions, ρ(r) is large, and where interactions are largely noncovalent, such as the U–N bonding regions of the complexes under investigation here, ρ(r), as evidenced by our QTAIM analysis, tends to be small but non-zero. Visualising the s(r) isosurface therefore allows us to qualitatively examine the spatial regions in which these weakly covalent interactions are taking place. These isosurfaces, which are presented in Fig. 9, are colour-mapped with values of ρ(r)sgn(λ2), where sgn(x) is the signum function, returning a value of 1 where x is positive, and −1 where x is negative. λ2 is the second largest eigenvalue of the Hessian of ρ(r) and is typically negative for attractive interactions and positive for repulsive interactions.127 This allows us to discriminate between attractive and repulsive interactions.The isosurfaces, plotted at a value of s(r) = 0.35, show regions of weak attraction in each of the U–N bonding regions, with the colouring corresponding to the strength of the interaction, as can be best seen for C2b′. In all complexes, green regions may be interpreted as either weak steric repulsion or weak attraction between adjacent nitrogen atoms, although a distinction is difficult to make. As the ligands become larger and the complexes more non-planar, we find additional regions of weak interaction, between uranyl oxygen ions and nearby pyrrole units in C4a, and between the enclosed oxygen ion and interacting meso-carbons in C6. These latter interactions correspond to the bond paths identified between the uranium and meso-carbon centres in our QTAIM analysis and, as discussed above, are strong enough to noticeably perturb other molecular properties. Additionally, in C6, regions of weak interaction between two pyrrolic nitrogen centres and the uranium ion are seen to extend towards the unenclosed oxygen ion, suggesting the possible presence of further ligand-oxygen interactions, although these are not identified by bond paths in our QTAIM analysis.
Scatter plots of s(r) against ρ(r)sgn(λ2) indicating the presence of largely noncovalent interactions via spikes which occur at low densities are given in Fig. S1 (ESI†). In all complexes, s(r) falls to zero at several points, corresponding to critical points in the electron density. s(r) also falls to zero at some small positive values of ρ(r)sgn(λ2), indicating the presence of weak repulsive interactions.
Integrated properties of the electron density
Using the atomic populations, localisation and delocalisation indices associated with the uranyl unit, the accumulation and depletion of charges which occur upon complexation can be further probed. We define two additional measures, | (5) |
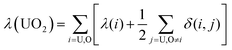 | (6) |
| UO22+ | C0 | C2b′ | C4a | C6 | |
|---|---|---|---|---|---|
| N(U) | 88.84 | 89.19 | 89.17 | 89.17 | 89.17 |
| N(O) | 8.58 | 8.86 | 8.84, 8.85 | 8.84 | 8.84 |
| λ(U) | 86.52 | 86.05 | 86.13 | 86.15 | 86.16 |
| λ(O) | 7.35 | 7.71 | 7.69 | 7.66 | 7.63, 7.61 |
| δ(U,O) | 2.32 | 1.92 | 1.97 | 1.98 | 1.96 |
| δ(O1,O2) | 0.13 | 0.10 | 0.10 | 0.10 | 0.10 |
| N(UO2) | 106.00 | 106.90 | 106.86 | 106.84 | 106.85 |
| λ(UO2) | 106.00 | 105.40 | 105.56 | 105.52 | 105.41 |
| N(UO2)–λ(UO2) | 0.00 | 1.50 | 1.30 | 1.32 | 1.44 |
These data allow us to quantify the effect of equatorial complexation by each of the ligands on the uranyl unit. This effect is broadly similar for each of the four complexes, differing only in magnitude. For all complexes N(UO2) is found to be greater than 106 and, as found in our previous comparison of C2b, C2b′ and [UO2(BTP)2]2+,98 approximately 0.8–0.9 a.u. of electronic charge is donated into the uranyl unit. This additional charge is distributed between the uranium ion and each of the oxygen ions and therefore acts to increase the electrostatic repulsion between the ions.
It might be expected that the localisation index, i.e. the amount of electronic charge density localised on an ion, may be used to estimate the strength of an ionic interaction. In all four complexes, greater electron localisation is present on the oxygen centre compared to free uranyl, alongside a decrease in localisation on the uranium centre, demonstrating that complexation results in increased ionic interaction. Additionally, for all complexes, a reduction in the delocalisation index of the U–Oyl bond, δ(U,O), which can be considered an alternative measure of bond covalency, is apparent upon complexation, indicating a reduction in the covalent interaction. This provides evidence that the ionic character of the U–Oyl bond is enhanced by equatorial complexation, and the elongation and weakening of the U–Oyl bond can thus be understood to originate from the fact that this increased ionic interaction comes at the expense of U–Oyl bond covalent interaction. The lengthening and weakening of the U–O bond compared to free uranyl seen in all four complexes investigated here can therefore be attributed to these factors. As might be expected, the effects are most pronounced for C0, with N(UO2) being 0.9 a.u. greater and λ(UO2) 0.6 a.u. less than in free uranyl. These values, combined, suggest the greatest amount of electron delocalisation between the uranyl and the ligand, commensurate with the topological data which demonstrates that C0 has the largest U–N covalent bond character.
This interpretation is in keeping with the qualitative picture given by electron density differences, which show a clear depletion of charge in the U–Oyl bonding region along with an accumulation on the Oyl centres.
In terms of charge donation onto the uranyl unit, C2b′ and C4a are similar to one another. C6 exhibits similar donation to these complexes, but less of this charge is actually localised on the uranyl unit, with C6 having a λ(UO2) value more comparable to that of C0, suggesting greater uranyl–ligand delocalisation than can be accounted for by considering the values of δ(U,N). C6 also has the smallest amount of electronic charge localised on the oxygen centres and the largest amount localised on the uranium centre. This can be explained in terms of the additional interactions between the uranyl oxygen centres and the ligand in this complex. Table 8 shows that, in total, an additional ∼0.07 a.u. of charge is delocalised in the interactions between the enclosed oxygen centre with the nearby meso-carbons, which partially accounts for the difference between C6 and C2b′/C4a. Based on the RDG isosurface of C6, further examination of the integrated properties reveals that 0.09 a.u. of charge is delocalised between the unenclosed oxygen ion and each of the two nearby nitrogen atoms, contributing to the lower than expected λ(UO2) value found in C6 and suggesting that, while ligand–uranyl interactions in planar complexes may be fairly straightforward, in larger, less planar complexes, there are potentially many other interactions which need to be considered in order to explain the charge redistribution in the uranyl unit. This O–N electron sharing also exists in the other complexes considered, but its magnitude is typically only ∼50% of that found in C6.
Solvation, irrespective of which functional is used (see Tables S11 and S13, ESI†), results in slightly higher values of N(UO2) for all four complexes, while λ(UO2) remains largely unchanged. Reoptimisation with B3LYP (see Tables S12 and S13, ESI†) results in greater localisation compared to the PBE data, as reported in the topological properties. Also apparent are lower values of N(UO2) (by ∼0.1 a.u.) and higher values of λ(UO2) (by ∼0.01 a.u.).
Density difference distributions upon complexation
Finally, we use electron density difference distributions to qualitatively examine the changes undergone by the system upon complexation. The density difference distributions in Fig. 10 are generated by subtracting the electron density of uranyl and ligand fragments held at the coordination geometry from the electron density of the complex. This leaves a map of the changes that occur when a complex is formed, with regions of electron density accumulation coloured blue and depletion coloured in green. Regions of depletion on the ligands are evidence of electron donation from the ligand, and the teardrop shaped regions of accumulation in each U–N bonding region may be interpreted as evidence of covalent interactions. It is possible, particularly in C0 and C2b′, to see that the size of these regions of accumulation varies between the different U–N bonds. The regions of accumulation in C0 are large and well-focused on the bonds whereas C2b′, exhibits smaller regions for the longest, least covalent bonds and larger regions for the shorter, more covalent interactions. Our previous study97 has shown that for more ionic uranyl–ligand interactions, these regions of charge accumulation are more diffuse.The striking changes undergone by the uranyl unit lend qualitative support to our assertion that there is a significant redistribution of charge in the uranyl unit upon complexation, based on the calculated increased U–O bond lengths, redshifted frequencies of the uranyl stretching modes, uranyl deformation energies and decreased U–O delocalisation, all compared to free UO22+. The charge accumulation on the oxygen ions and depletion in the U–O interaction region upon complexation potentially signifies the involvement of density formally associated with the uranium centre with bonding in the U–N region. The depletion in the U–O bond regions is also consistent with a reduction in the covalent character of these bonds, while accumulation on the uranyl oxygen ions and uranium ion suggests that the U–O interaction is, in accord with our other analyses, becoming more ionic upon complexation. In addition to this, charge accumulation around the uranium centre appears to have some f-like character (see Fig. S2, ESI†). The size of the regions of accumulation and depletion on the uranyl unit appear to be related to the interactions in the U–N region, i.e. as the amount of electron sharing in the U–N bonds is increased, the effects on the uranyl unit become more pronounced.
Summary and conclusions
We have investigated by means of quantum chemical calculations and a range of density based analyses the U–N and U–O interactions of several uranyl hexaphyrin complexes. It has been determined through a comparison of the geometries of simplified and peripherally substituted complexes that it is of great importance when dealing with systems such as these to ensure that the effects of common simplifications such as the removal of alkyl groups are indeed minimal. This is especially important when dealing with hypothetical complexes. It was found that in most, but not all, cases that removal of the alkyl groups had little geometrical impact.We initially established a relationship between complex stability and ligand size, as well as a weak relationship between stability and uranyl stretching mode frequencies, when a set of eight complexes were considered. This relationship was significantly weaker than that found by us in a previous study,97 but could be strengthened by omitting the anomalous data associated with the C6 complex. Subsequently, justification for considering the C6 complex as being qualitatively different from the others was found in the density based analysis.
A representative set of four complexes was selected for further analysis. We found a relationship between complex stability and the degree of covalent character as defined by the total value of ρBCP in the U–N bonds in these complexes. The magnitude of the energy density, H, is also higher for these U–N BCPs than in any other complex. Additionally, there is unambiguous evidence of electron sharing in all U–N bonds, and this is at a maximum for C0. This complex has short, strong U–N bonds and, commensurately, we see the largest effects on the uranyl unit here: complex C0 has the most significant reduction in U–O bond covalency when compared to free uranyl, the most significant U–O bond lengthening, and pays the greatest energy penalty in terms deformation of the uranyl unit. Despite this, it is the most stable complex of any we have investigated here, which may, in part, be due to covalent stabilisation from the relatively large amount of electron sharing in the U–N bonds.
Electron delocalisation and covalent character as defined by values of ρBCP and H in the U–N bonds is reduced for C2b′, C4a, and C6, although not drastically so, and these all have bond lengths which are comparable due to the flexibility of the ligands, which contort to better fit the uranyl dication in the cavity. There is an energy penalty for this, however and there is a decrease in stability in the order C0 > C2b′ > C4a > C6, a trend which appears to be replicated experimentally: the C0 and C2b′ complexes are known synthetically, while C4a and C6 are not. This energy penalty can be seen using both the molecular binding energies and the ligand deformation energies which decrease and increase, respectively, with increasing ligand size. There is also a limit as to how much this ligand distortion can act to increase the covalent character of the U–N bonds; a notable plateau is found in terms of both stability and U–N covalent bond character for C4a and C6. When the frequencies of the uranyl stretching modes are considered, the C6 data is anomalous, falling somewhere between that of the C2b′ and C4a complexes. With all complexes but C6, as in our previous study of complexes involving coordination by 1st row species,97 there is a degree of equatorial planarity. The interactions between the nitrogen ligands and the uranium ion are more or less perpendicular to the U–Oyl axis and, as such, the ligands only interact directly with the U atom and this in turn affects the U–O interaction. However in the C6 complex we see additional interactions between the uranyl oxygen ion enclosed by the ligand and two of the ligand meso-carbons, confirmed by QTAIM analysis and RDG isosurface plots, which also indicate the presence of weak interactions between two pyrrolic nitrogens with the other oxygen ion. These interactions, although weak, act to perturb the frequencies of the uranyl stretching modes as well as the topological and integrated properties of the uranyl unit.
We see dramatic and consistent changes to the uranyl unit upon complexation which are related to the covalent character of interactions in the U–N bonding region as well as the stability of the complex. This is evident in U–O bond lengths, the frequencies of the distinctive uranyl stretching modes (with the exception of C6, as discussed above), values of QTAIM descriptors and integrated charges, and can be visualised via electron density difference distributions. These add qualitative support to our assertions that electron density is redistributed in the uranyl unit upon equatorial complexation, with the magnitude of this redistribution related to the magnitude of the equatorial covalent interaction. Density difference distributions also clearly show charge accumulation in the U–N bonding regions, providing qualitative evidence of electron sharing in these interactions.
Analysis of the reduced density gradient allowed visualisation of the regions of weakly covalent interaction in all complexes, with weak attractive regions corresponding to each U–N bond found in all cases and, in the C6 complex, additional interactions between the uranyl oxygen ions and the ligand identified.
Ultimately, we conclude that hexaphyrin ligands coordinate uranyl in a broadly similar way, with the uranium atom coordinated via largely ionic interactions with small but measurable amounts of covalent character, to six pyrrolic nitrogen atoms. However, the size of the ligand core has pronounced effects on complex stability. U–N covalent character is found to correlate strongly with bond length, however ligand flexibility and its effects (shortened and thus more covalent U–N bonds, but a loss of stability) mean that no clear relationship can be identified between equatorial covalency and stability in these complexes. However, the interesting changes to the electronic structure of the uranyl unit upon complexation suggest that expanded porphyrins are useful systems for investigating the effects of complexation on the uranyl bond. The complicating factor of additional interactions caused by the proximity of the ligand in C6 suggest that investigation of complexes which have well-defined planarity may be preferable. If selectivity is indeed driven by covalency, it stands to reason that design of ligands to maximise selective behaviour ought to aim to maximise covalent character. The fact that the most stable complex with the greatest equatorial covalency, C0, is obtained using the ligand with the smallest core suggests that a fruitful avenue of future research into maximising U–N covalency may be pentapyrrolic complexes of uranyl, of which there are several experimentally realised examples including uranyl pentaphyrin7 and uranyl superphthalocyanine.128 Additionally, other actinide complexes of these ligands may be explored in order to assess whether a particular ligand has affinity for a particular actinide.
Acknowledgements
AK thanks the EPSRC for the award of a career acceleration fellowship (grant EP/J002208/2). We would like to acknowledge the use of the EPSRC UK National Service for Computational Chemistry Software (NSCCS) at Imperial College London in carrying out this work, and we also acknowledge the use of the UCL Legion and UCL Grace High Performance Computing Facilities (Legion@UCL and Grace@UCL), and associated support services, in the completion of this work.References
- M. Seth, M. Dolg, P. Fulde and P. Schwerdtfeger, J. Am. Chem. Soc., 1995, 117, 6597–6598 CrossRef CAS.
- M. Dolg, in Encyclopedia of Computational Chemistry, ed. H. F. Schaefer, Wiley, Chichester, 2002 Search PubMed.
- P. Söderlind and A. Gonis, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 1–4 CrossRef.
- G. Schreckenbach and G. A. Shamov, Acc. Chem. Res., 2010, 43, 19–29 CrossRef CAS PubMed.
- D. Wang, W. F. van Gunsteren and Z. Chai, Chem. Soc. Rev., 2012, 41, 5836 RSC.
- J. Dognon, Coord. Chem. Rev., 2014, 266–267, 110–122 CrossRef CAS.
- J. L. Sessler, A. E. Vivian, D. Seidel, A. K. Burrell, M. Hoehner, T. D. Mody, A. Gebauer, S. J. Weghorn and V. Lynch, Coord. Chem. Rev., 2001, 216–217, 411–434 CrossRef CAS.
- P. L. Arnold, J. B. Love and D. Patel, Coord. Chem. Rev., 2009, 253, 1973–1978 CrossRef CAS.
- H. H. Dam, D. N. Reinhoudt and W. Verboom, Chem. Soc. Rev., 2007, 36, 367–377 RSC.
- J. Sessler, P. Melfi and G. Pantos, Coord. Chem. Rev., 2006, 250, 816–843 CrossRef CAS.
- V. Alexander, Chem. Rev., 1995, 95, 273–342 CrossRef CAS.
- Z. Hnatejko, S. Lis, P. Starynowicz and Z. Stryła, Polyhedron, 2011, 30, 880–885 CrossRef CAS.
- J.-C. Berthet, M. Nierlich, Y. Miquel, C. Madic and M. Ephritikhine, Dalton Trans., 2005, 369–379 RSC.
- R. Beekmeyer and A. Kerridge, Inorganics, 2015, 3, 482–499 CrossRef CAS.
- Y. K. Agrawal, P. Shrivastav and S. K. Menon, Sep. Purif. Technol., 2000, 20, 177–183 CrossRef CAS.
- J. B. Love, Chem. Commun., 2009, 3154–3165 RSC.
- S. Fortier and T. W. Hayton, Coord. Chem. Rev., 2010, 254, 197–214 CrossRef CAS.
- J.-C. Berthet, P. Thuéry, J.-P. Dognon, D. Guillaneux and M. Ephritikhine, Inorg. Chem., 2008, 47, 6850–6862 CrossRef CAS PubMed.
- J.-C. Berthet, P. Thuéry and M. Ephritikhine, Chem. Commun., 2007, 604–606 RSC.
- K. Pierloot and E. van Besien, J. Chem. Phys., 2005, 123, 2043091 CrossRef PubMed.
- http://www.nei.org/Knowledge-Center/Nuclear-Statistics/World-Statistics .
- http://www.nei.org/Knowledge-Center/Nuclear-Statistics/On-Site-Storage-of-Nuclear-Waste .
- Z. Kolarik, Solvent Extr. Ion Exch., 2003, 21, 381–397 CrossRef CAS.
- M. G. B. Drew, M. R. S. J. Foreman, C. Hill, M. J. Hudson and C. Madic, Inorg. Chem. Commun., 2005, 8, 239–241 CrossRef CAS.
- F. Lewis, L. Harwood, M. J. Hudson, M. G. B. Drew, J. Desreux, G. Vidick, N. Bouslimani, G. Modolo, A. Wilden, M. Sypula, T.-H. Vu and J.-P. Simonin, J. Am. Chem. Soc., 2011, 133, 13093–13102 CrossRef CAS PubMed.
- L. Petit, C. Adamo and P. Maldivi, Inorg. Chem., 2006, 45, 8517–8522 CrossRef CAS PubMed.
- F. W. Lewis, L. M. Harwood, M. J. Hudson, M. G. B. Drew, A. Wilden, M. Sypula, G. Modolo, T. Vu, G. Vidick, N. Bouslimani and J. F. Desreux, Procedia Chem., 2012, 7, 231–238 CrossRef CAS.
- C. De Sahb, L. A. Watson, J. Nadas and B. P. Hay, Inorg. Chem., 2013, 52, 10632–10642 CrossRef CAS PubMed.
- M. Trumm and B. Schimmelpfennig, Mol. Phys., 2016, 114, 876–883 CrossRef CAS.
- J. Lan, W. Shi, L. Yuan, Y. Zhao, J. Li and Z. Chai, Inorg. Chem., 2011, 50, 9230–9237 CrossRef CAS PubMed.
- G. R. Choppin, J. Alloys Compd., 1995, 223, 174–179 CrossRef CAS.
- G. R. Choppin, J. Alloys Compd., 1995, 225, 242–245 CrossRef CAS.
- P. Söderlind, G. Kotliar, K. Haule, P. M. Oppeneer and D. Guillaumont, MRS Bull., 2010, 35, 883–888 CrossRef.
- S. O. Odoh and G. Schreckenbach, J. Phys. Chem. A, 2011, 115, 14110–14119 CrossRef CAS PubMed.
- M. L. Neidig, D. L. Clark and R. L. Martin, Coord. Chem. Rev., 2013, 257, 394–406 CrossRef CAS.
- A. Kerridge, RSC Adv., 2014, 4, 12078–12086 RSC.
- I. Kirker and N. Kaltsoyannis, Dalton Trans., 2011, 40, 124–131 RSC.
- K. I. M. Ingram, M. J. Tassell, A. J. Gaunt and N. Kaltsoyannis, Inorg. Chem., 2008, 47, 7824–7833 CrossRef CAS PubMed.
- N. Kaltsoyannis, Inorg. Chem., 2013, 52, 3407–3413 CrossRef CAS PubMed.
- F. W. Lewis, L. M. Harwood, M. J. Hudson, M. G. B. Drew, M. Sypula, G. Modolo, D. Whittaker, C. A. Sharrad, V. Videva and V. Hubscher-bruder, Dalton Trans., 2012, 41, 9209–9219 RSC.
- F. W. Lewis, M. J. Hudson and L. M. Harwood, Synlett, 2011, 2609–2632 CAS.
- V. Vallet, U. Wahlgren and I. Grenthe, J. Phys. Chem. A, 2012, 116, 12373–12380 CrossRef CAS PubMed.
- L. E. Roy, N. J. Bridges and L. R. Martin, Dalton Trans., 2013, 42, 2636–2642 RSC.
- J.-H. Lan, W.-Q. Shi, L.-Y. Yuan, J. Li, Y.-L. Zhao and Z.-F. Chai, Coord. Chem. Rev., 2012, 256, 1406–1417 CrossRef CAS.
- S. A. Kozimor, P. Yang, E. R. Batista, K. S. Boland, C. J. Burns, D. L. Clark, S. D. Conradson, R. L. Martin, M. P. Wilkerson and L. E. Wolfsberg, J. Am. Chem. Soc., 2009, 131, 12125–12136 CrossRef CAS PubMed.
- M. J. Tassell and N. Kaltsoyannis, Dalton Trans., 2010, 39, 6576–6588 RSC.
- A. Kerridge, Dalton Trans., 2013, 42, 16428–16436 RSC.
- I. Fryer-kanssen, J. Austin and A. Kerridge, Inorg. Chem., 2016, 55, 10034–10042 CrossRef CAS PubMed.
- M. Mazzanti, R. Wietzke, J. Pécaut, J.-M. Latour, P. Maldivi and M. Remy, Inorg. Chem., 2002, 41, 2389–2399 CrossRef CAS PubMed.
- D. Guillaumont, J. Phys. Chem. A, 2004, 108, 6893–6900 CrossRef CAS.
- D. Guillaumont, THEOCHEM, 2006, 771, 105–110 CrossRef CAS.
- M. A. Denecke, P. J. Panak, F. Burdet, M. Weigl, A. Geist, R. Klenze, M. Mazzanti and K. Gompper, C. R. Chim., 2007, 10, 872–882 CrossRef CAS.
- P. J. Melfi, S. K. Kim, J. T. Lee, F. Bolze, D. Seidel, V. M. Lynch, J. M. Veauthier, A. J. Gaunt, M. P. Neu, Z. Ou, K. M. Kadish, S. Fukuzumi, K. Ohkubo and J. L. Sessler, Inorg. Chem., 2007, 46, 5143–5145 CrossRef CAS PubMed.
- J. L. Sessler, P. J. Melfi, D. Seidel, A. E. V. Gorden, D. K. Ford, P. D. Palmer and C. D. Tait, Tetrahedron, 2004, 60, 11089–11097 CrossRef CAS.
- J. L. Sessler, A. E. Gorden, D. Seidel, S. Hannah, V. Lynch, P. L. Gordon, R. J. Donohoe, C. Drew Tait and D. Webster Keogh, Inorg. Chim. Acta, 2002, 341, 54–70 CrossRef CAS.
- S. Hannah, D. Seidel, J. L. Sessler and V. Lynch, Inorg. Chim. Acta, 2001, 317, 211–217 CrossRef CAS.
- J. L. Sessler and S. J. Weghorn, Expanded, Contracted & Isomeric Porphyrins, Elsevier, 1997 Search PubMed.
- J. L. Sessler and D. Seidel, Angew. Chem., Int. Ed., 2003, 42, 5134–5175 CrossRef CAS PubMed.
- J. L. Sessler and E. Tomat, Acc. Chem. Res., 2007, 40, 371–379 CrossRef CAS PubMed.
- M. R. Kumar and T. K. Chandrashekar, J. Inclusion Phenom. Macrocyclic Chem., 1999, 35, 553–582 CrossRef.
- P. J. Melfi, S. Camiolo, J. T. Lee, M. F. Ali, J. T. McDevitt, V. M. Lynch and J. L. Sessler, Dalton Trans., 2008, 1538–1540 RSC.
- J. L. Sessler, D. Seidel, A. E. Vivian, V. Lynch, B. L. Scott and D. W. Keogh, Angew. Chem., Int. Ed., 2001, 40, 591–594 CrossRef CAS PubMed.
- S. Shimizu, W. S. Cho, J. L. Sessler, H. Shinokubo and A. Osuka, Chem. – Eur. J., 2008, 14, 2668–2678 CrossRef CAS PubMed.
- S. Mori, S. Shimizu, J. Y. Shin and A. Osuka, Inorg. Chem., 2007, 46, 4374–4376 CrossRef CAS PubMed.
- J. L. Sessler, D. Seidel, C. Bucher and V. Lynch, Chem. Commun., 2000, 1473–1474 RSC.
- A. K. Gupta and T. K. Chandrashekar, Tetrahedron Lett., 2001, 42, 3391–3394 CrossRef.
- H. Rath, N. Aratani, J. M. Lim, J. S. Lee, D. Kim, H. Shinokubo and A. Osuka, Chem. Commun., 2009, 3762–3764 RSC.
- S.-Y. Kee, J. M. Lim, S.-J. Kim, J. Yoo, J.-S. Park, T. Sarma, V. M. Lynch, P. K. Panda, J. L. Sessler, D. Kim and C.-H. Lee, Chem. Commun., 2011, 47, 6813–6815 RSC.
- R. Kumar, R. Misra, T. K. Chandrashekar, A. Nag, D. Goswami, E. Suresh and C. H. Suresh, Eur. J. Org. Chem., 2007, 4552–4562 CrossRef CAS.
- Z. S. Yoon, J. H. Kwon, M.-C. Yoon, M. K. Koh, S. B. Noh, J. L. Sessler, J. T. Lee, D. Seidel, A. Aguilar, S. Shimizu, M. Suzuki, A. Osuka and D. Kim, J. Am. Chem. Soc., 2006, 128, 14128–14134 CrossRef CAS PubMed.
- R. Misra and T. K. Chandrashekar, Acc. Chem. Res., 2008, 41, 265–279 CrossRef CAS PubMed.
- S. Shimizu, V. G. Anand, R. Taniguchi, K. Furukawa, T. Kato, T. Yokoyama and A. Osuka, J. Am. Chem. Soc., 2004, 126, 12280–12281 CrossRef CAS PubMed.
- X. Zhu, S. Fu, W.-K. Wong and W.-Y. Wong, Tetrahedron Lett., 2008, 49, 1843–1846 CrossRef CAS.
- J. L. Sessler, P. J. Melfi, E. Tomat and V. M. Lynch, Dalton Trans., 2007, 629–632 RSC.
- J. L. Sessler and S. J. Weghorn, Expanded, Contracted & Isomeric Porphyrins, Pergamon, 1997 Search PubMed.
- V. V. Roznyatovskiy, C.-H. Lee and J. L. Sessler, Chem. Soc. Rev., 2013, 42, 1921–1933 RSC.
- T. K. Chandrashekar and S. Venkatraman, Acc. Chem. Res., 2003, 36, 676–691 CrossRef CAS PubMed.
- P. J. Chmielewski and L. Latos-Grażyński, Coord. Chem. Rev., 2005, 249, 2510–2533 CrossRef CAS.
- M. Stępień, N. Sprutta and L. Latos-Grażyński, Angew. Chem., Int. Ed., 2011, 50, 4288–4340 CrossRef PubMed.
- J.-Y. Shin, K. S. Kim, M.-C. Yoon, J. M. Lim, Z. S. Yoon, A. Osuka and D. Kim, Chem. Soc. Rev., 2010, 39, 2751–2767 RSC.
- S. Saito and A. Osuka, Angew. Chem., Int. Ed., 2011, 50, 4342–4373 CrossRef CAS PubMed.
- Y. Tanaka, J.-Y. Shin and A. Osuka, Eur. J. Org. Chem., 2008, 1341–1349 CrossRef CAS.
- H. Mori, Y. M. Sung, B. S. Lee, D. Kim and A. Osuka, Angew. Chem., Int. Ed., 2012, 51, 12459–12463 CrossRef CAS PubMed.
- I. T. Ho, Z. Zhang, M. Ishida, V. M. Lynch, W. Y. Cha, Y. M. Sung, D. Kim and J. L. Sessler, J. Am. Chem. Soc., 2014, 136, 4281–4286 CrossRef CAS PubMed.
- X. Cao, Q. Li, A. Moritz, Z. Xie, M. Dolg and X. Chen, Inorg. Chem., 2006, 45, 43–50 Search PubMed.
- P. L. Arnold, D. Patel, A.-F. Pécharman, C. Wilson and J. B. Love, Dalton Trans., 2010, 39, 3501–3508 RSC.
- A. Yahia, P. L. Arnold, J. B. Love and L. Maron, Chem. – Eur. J., 2010, 16, 4881–4888 CrossRef CAS PubMed.
- G. M. Jones, P. L. Arnold and J. B. Love, Chem. – Eur. J., 2013, 19, 10287–10294 CrossRef CAS PubMed.
- Q. J. Pan, G. A. Shamov and G. Schreckenbach, Chem. – Eur. J., 2010, 16, 2282–2290 CrossRef CAS PubMed.
- J. Silver, Inorg. Chim. Acta, 1988, 44, 281–288 CrossRef.
- J. H. Lan, C. Z. Wang, Q. Y. Wu, S. A. Wang, Y. X. Feng, Y. L. Zhao, Z. F. Chai and W. Q. Shi, J. Phys. Chem. A, 2015, 119(1), 9178–9188 CrossRef CAS PubMed.
- G. A. Shamov and G. Schreckenbach, J. Phys. Chem. A, 2006, 110, 9486–9499 CrossRef CAS PubMed.
- M. Yang, W. Ding and D. Wang, New J. Chem., 2017, 41, 63–74 RSC.
- F. Quilès and A. Burneau, Vib. Spectrosc., 2000, 23, 231–241 CrossRef.
- C. Nguyen-Trung, D. A. Palmer, G. M. Begun, C. Peiffert and R. E. Mesmer, J. Solution Chem., 2000, 29, 101–129 CrossRef CAS.
- F. Quilès, C. Nguyen-Trung, C. Carteret and B. Humbert, Inorg. Chem., 2011, 50, 2811–2823 CrossRef PubMed.
- P. Di Pietro and A. Kerridge, Inorg. Chem., 2016, 55, 573–583 CrossRef CAS PubMed.
- P. Di Pietro and A. Kerridge, Phys. Chem. Chem. Phys., 2016, 18, 16830–16839 RSC.
- A. E. Clark, J. L. Sonnenberg, P. J. Hay and R. L. Martin, J. Chem. Phys., 2004, 121, 2563–2570 CrossRef CAS PubMed.
- P. Miro, J. Ling, J. Qiu, P. C. Burns, L. Gagliardi and C. J. Cramer, Inorg. Chem., 2012, 51, 8784–8790 CrossRef CAS PubMed.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Oxford, 1990 Search PubMed.
- C. F. Matta and R. J. Boyd, An Introduction to the Quantum Theory of Atoms in Molecules, 2007 Search PubMed.
- R. F. W. Bader, J. Phys. Chem. A, 2009, 113, 10391–10396 CrossRef CAS PubMed.
- E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS PubMed.
- R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- W. Küchle, M. Dolg, H. Stoll and H. Preuss, J. Chem. Phys., 1994, 100, 7535 CrossRef.
- J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- P. Stephens, F. Devlin, C. Chabalowski and M. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- N. Ismail, J.-L. Heully, T. Saue, J.-P. Daudey and C. J. Marsden, Chem. Phys. Lett., 1999, 300, 296–302 CrossRef CAS.
- G. Schreckenbach, P. J. Hay and R. L. Martin, J. Comput. Chem., 1999, 20, 70–90 CrossRef CAS.
- A. Klamt and G. Schüürmann, Perkin Trans. 2, 1993, 799–805 RSC.
- G. A. Shamov and G. Schreckenbach, Inorg. Chem., 2008, 47, 805–811 CrossRef CAS PubMed.
- D. A. Pantazis and F. Neese, J. Chem. Theory Comput., 2011, 7, 677–684 CrossRef CAS.
- N. M. Kroll and M. Douglas, Ann. Phys., 1974, 83, 89–155 Search PubMed.
- B. A. Hess, Phys. Rev. A: At., Mol., Opt. Phys., 1986, 33, 3742–3748 CrossRef CAS.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- T. A. Keith, AIMAll (Version 14.11.23), TK Gristmill Software, Overl. Park KS, USA, 2014 Search PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- P. L. Arnold, D. Patel, A.-F. Pécharman, C. Wilson and J. B. Love, Dalton Trans., 2010, 39, 3501–3508 RSC.
- Q.-J. Pan, S. O. Odoh, G. Schreckenbach, P. L. Arnold and J. B. Love, Dalton Trans., 2012, 41, 8878–8885 RSC.
- S. Tsushima, Dalton Trans., 2011, 40, 6732–6737 RSC.
- D. D. Schnaars and R. E. Wilson, Inorg. Chem., 2013, 52, 14138–14147 CrossRef CAS PubMed.
- J. B. Love, Chem. Commun., 2009, 3154–3165 RSC.
- A. Zupan, K. Burke, M. Ernzerhof and J. P. Perdew, J. Chem. Phys., 1997, 106, 10184 CrossRef CAS.
- R. F. W. Bader and H. Essén, J. Chem. Phys., 1984, 80, 1943 CrossRef CAS.
- V. W. Day, T. J. Marks and W. A. Wachter, J. Am. Chem. Soc., 1975, 505, 4519–4527 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp08783c |
| ‡ Due to computational expense, vibrational frequency analysis was not performed on the C2b′ complex when optimised with the B3LYP functional. Similarly, large peripherally substituted complexes, with the exception of C2b′ which was selected for further study, were optimised using only the PBE functional. |
| This journal is © the Owner Societies 2017 |