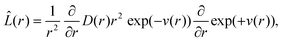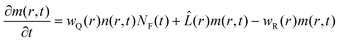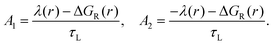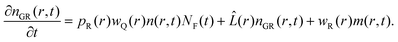Influence of the excitation light intensity on the rate of fluorescence quenching reactions: pulsed experiments
Received
15th December 2016
, Accepted 7th February 2017
First published on 7th February 2017
Abstract
The effect of multiple light excitation events on bimolecular photo-induced electron transfer reactions in liquid solution is studied experimentally. It is found that the decay of fluorescence can be up to 25% faster if a second photon is absorbed after a first cycle of quenching and recombination. A theoretical model is presented which ascribes this effect to the enrichment of the concentration of quenchers in the immediate vicinity of fluorophores that have been previously excited. Despite its simplicity, the model delivers a qualitative agreement with the observed experimental trends. The original theory by Burshtein and Igoshin (J. Chem. Phys., 2000, 112, 10930–10940) was created for continuous light excitation though. A qualitative extrapolation from the here presented pulse experiments to the continuous excitation conditions lead us to conclude that in the latter the order of magnitude of the increase of the quenching efficiency upon increasing the light intensity of excitation, must also be on the order of tens of percent. These results mean that the rate constant for photo-induced bimolecular reactions depends not only on the usual known factors, such as temperature, viscosity and other properties of the medium, but also on the intensity of the excitation light.
Introduction
Chemical reactions in solution develop at rates that depend on a number of factors: temperature, pressure, electric and magnetic fields, driving force and solvent characteristics such as the refractive index, the dielectric constant and the viscosity. However, for photo-induced reactions it has never been explored experimentally if the rate of the bimolecular reactions depends itself on the intensity of the triggering light. The present work attempts to elucidate this question.
It has been known since the seminal work of Smoluchowski1 that, in the case of bimolecular photo-induced processes, the rate coefficients are not constant but rather change with time as a result of the mutual diffusion of the reactants. This is caused by the change over time of the ensemble-averaged quencher concentration surrounding the fluorophore as the reaction proceeds. Furthermore, this time dependent distribution coupled with subsequent processes, like recombination of products in the geminate stage, can only be understood in terms of non-markovian (i.e. history-dependent) models. In the past 20 to 30 years, a number of theoretical approaches have enlightened us with a deep physical understanding of these reactions, to the point where the notion of the rate coefficient was abandoned and instead substituted by the concept of reaction kernels able to account for magnetic field effects, internal states of the reactants and reversibility.2 Experimental scrutiny of these theories is only now being performed.3–7 It has been shown how the viscosity and the magnetic field modulate reactions. For example, it has been observed that recombination efficiency depends on the viscosity of the medium non-monotonically as a combined effect of the molecular transport and the spatial characteristics of the electron transfer reactions. In the case of magnetic field effects, the observation of reversible fluorophore formation after a magneto-sensitive exciplex reaction step was addressed.8 Furthermore, the faster quenching than expected from a mere extrapolation of low viscosity measurements in high viscous media like room temperature ionic liquids has been explained by considering the interplay between non-equilibrium diffusion and distance dependence reactivity.9 Recently, the long standing problem of the disparity of the Marcus prediction for electron transfer and the experiments by Rehm and Weller could be resolved using the same concepts.10
Among the predictions of this theoretical framework, a particularly surprising one concerns the excitation intensity dependence of the rate coefficient.11 While it is plainly obvious that in a photo-induced reaction the amount of chemical transformation depends on the number of absorbed photons, it is astonishing that the rate coefficients themselves may do so as well. In other words, it is obvious that the larger the amount of photons, the larger the amount of products will be, but what is not evident is that the rate coefficient of the reaction is light intensity-dependent itself.
Using the integral version of the Encounter Theory, Burshtein and Igoshin proposed that the reaction rate coefficient of fluorescence quenching would depend on excitation light intensity.11 They described three major effects: shortage of the ground state of the fluorophore concentration, shortage of the quencher concentration – both due to a very high excited state concentration of the fluorophore – and distortion of the fluorophore–quencher distribution function. The latter effect is the most interesting of these, because it leads to an increase of the Stern–Volmer rate constant with light-intensity. The effect is due to the incident that after a cycle of excitation–quenching–recombination of products, another photon may be absorbed by the very same fluorophore molecule. If the photon flux is large, this process can occur when the original quencher is still close-by, leading to a higher quenching probability in comparison to the situation under conditions of low light. To our knowledge alternative theoretical approaches to the presented problem exist. However, at the present stage of our experiments, we will neither discuss them here, nor will we compare them among each other or to our experimental findings.12,13
Unfortunately, or fortunately for the development of photophysics, this only happens at very high photon flux levels, much greater than those delivered by the light sources usually employed in absorption or fluorescence spectrometers. On the contrary, very high excitation intensities are employed both in ultrafast spectroscopy and in various microscopic imaging techniques. High light intensities can also be reached in solar concentrators. This means that under these experimental conditions if the rate coefficients of bimolecular reactions are affected by the precise intensity of light employed, the comparison of the results obtained by different techniques must be done with care.
The major experimental problem for testing these ideas is that the needed light intensities are rather large, i.e. corresponding to excitation rates† of the order of 0.1–1 ns−1.11 A way to elegantly overcome this experimental difficulty is to perform pulsed experiments employing more than one pulse from amplified Ti:Sapphire lasers. A high continuous excitation rate can be regarded as a set of several photon absorption events separated by, on average, shorter time delays as the intensity of the excitation increases. Our experimental strategy is based on this concept: the radiation from a non-collinear parametric amplifier is split in two replicas in a Michelson like interferometer. One beam is delayed by up to 140 ps and the effect of the double-excitation is studied as a function of the inter-pulse delay. Similar experiments have been performed with longer delay times to study unimolecular processes like intersystem crossing. The approach has been demonstrated superior to conventional, i.e. single-pulse, methods in obtaining quantities such as the yields of triplet formation or the absorption coefficients of transient species.14 In the present case we have analysed the differences in the dynamics of the fluorescence decay affected by bimolecular electron transfer quenching and observed after a single pulse excitation and after two excitation pulses. As explained below, additional information about the ground state recovery or the recombination of the electron transfer products can be obtained.
The paper is organized as follows: first the experimental strategy is explained. Thereafter, the modifications to the theory of reaction–diffusion for two consecutive excitation events are presented together with the relationships defining the experimental observables. Simulations showing the predictions of the theory are discussed. Finally, the experimental results are presented, compared to the theory and explained.
Experiments and methods
All the experiments presented here were performed in acetonitrile (ACN, 99.9%, Spectroscopy grade, Uvasol, used as received). The fluorophore, the chlorine salt of Rhodamine 6G (R6G, Lambda chrome), combines the advantage of being very photo-stable, having a high absorption coefficient and showing little solvatochromism. Two quenchers with different redox potentials were used: N,N,N′N′-tetramethyl-p-phenylenediamine (TMPPD 99%, Sigma Aldrich) and N,N-dimethylaniline (DMA 99.5%, Sigma Aldrich). The relevant properties for the current experiments of these compounds are listed in Table 1. For all experiments presented here, the optical density of the sample at the excitation wavelength was between 0.1 and 0.2.
Table 1 Experimental and simulation parameters. R6G: τF, E00 and ERED are respectively the lifetime and energy of the excited singlet state and the reduction potential in ACN. Quenchers: EOX reduction potential for the oxidation of the quenchers in the same solvent. ACN: nD refractive index, ε dielectric constant, η viscosity, σS solvent diameter and τL longitudinal dielectric relaxation time. Reaction parameters (at contact distance σ): V and L are the coupling matric element and its special decay for quenching and recombination (subscripts Q and R respectively), λq and hνq are the reorganization and vibrational energy of the coupled quantum mode to the reaction and ΔG and λS are the free enthalpies and the reorganization energy for the reactions. All experimental data are taken from ref. 23 and 24
|
τ
F/ns |
4.0 |
τ
L/ps |
0.26 |
ΔGQ/eV |
TMPPD: −1.26 |
| DMA: −0.58 |
|
E
00/eV |
2.27 |
σ
S/Å |
2.6 |
ΔGR/eV |
TMPPD: −1.01 |
| DMA: −1.69 |
|
σ/A |
7.5 |
V
Q/meV |
15 |
λ
S/eV |
1.02 |
|
E
OX/V |
TMPPD: 0.13 |
L
Q/Å |
1.5 |
|
| DMA: 0.81 |
|
E
RED/V |
−0.88 |
V
R/meV |
15 |
|
n
D
|
1.3441 |
L
R/Å |
2 |
|
ε
|
37.5 |
λ
q/eV |
0.42 |
|
η/cP |
0.37 |
hν
q/eV |
0.186 |
The fluorescence time resolved measurements were performed with an up-conversion setup fed by a Ti:Sapphire oscillator centered at 795 nm, which radiation was amplified by a home built two-stage regenerative amplifier pumped with 18 W at 523 nm. The compressed amplified beam (795 nm, 4 W, 5 kHz) was used to pump two tunable non-collinear optical parametric amplifiers (NOPAs) one of which was used to excite the sample and the second to gate the fluorescence signal in a non-linear optical crystal (2 mm BBO) at different retardations to reconstruct the time evolution of the fluorescence emission by sum frequency generation. The up-converted signal is directed to an Andor spectrometer (a grating of 150 lines per mm was used) and recorded with Hamamatsu EM-CCD camera. More details related to this experimental setup can be found in ref. 15. For the two pulses experiments the excitation beam was separated in two pulses of the same energy using a Michelson interferometer, with a 1 mm thick 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 beam splitter (Thorlabs, BSW10R). The excitation wavelength was set near the maximum absorption of the fluorophore at 525 nm (FWHM of about 10 nm). The average power was varied between 0.1 to 1.3 mW at each pulse using neutral density filters. Gating beam was set to 1020 nm (10 mW, FWHM 35 nm). From cross correlation measurements the final instrument response function is circa 300 fs. Polarization of the excitation beam was set using a λ/2-plate at magic angle with respect to the gating beam. Parasitic polarizations were removed using nanoparticle polarizer (Thorlabs).
50 beam splitter (Thorlabs, BSW10R). The excitation wavelength was set near the maximum absorption of the fluorophore at 525 nm (FWHM of about 10 nm). The average power was varied between 0.1 to 1.3 mW at each pulse using neutral density filters. Gating beam was set to 1020 nm (10 mW, FWHM 35 nm). From cross correlation measurements the final instrument response function is circa 300 fs. Polarization of the excitation beam was set using a λ/2-plate at magic angle with respect to the gating beam. Parasitic polarizations were removed using nanoparticle polarizer (Thorlabs).
Solutions were placed in cuvettes with 0.2 mm optical path length using a flow system (peristaltic pump with flow rate 7.5 ml min−1) in order to prevent decomposition. The fluorescence was recorded in a narrow range of wavelengths (ca. 60 nm) and it was spectrally filtered in such a way that the intensity of fluorescence was still relatively high but avoiding any parasitic signals coming from excitation beam or some residual white light coming from the NOPA or produced in the sample, recording usually from 550 nm to longer wavelengths.
For the experiment to succeed, it is essential that both consecutive pulses excite the same volume of the solution. As a consequence, the alignment of the two beams needs to be precise. First the path of the two beams was aligned at 3 referencing points. Secondly the cross correlation was measured for the two pulses separated by 1 and 100 ps delays such that the two optimized cross correlation signals had very similar intensity (with ratio at least 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.95). A final test was performed by recording the emission of fluorophore sample without quencher: the intensity of the second fluorescence signal is reduced as much as the ground state is depopulated indicating that the beams are impinging the same volume. A scheme of the set-up is shown in the Scheme 1.
0.95). A final test was performed by recording the emission of fluorophore sample without quencher: the intensity of the second fluorescence signal is reduced as much as the ground state is depopulated indicating that the beams are impinging the same volume. A scheme of the set-up is shown in the Scheme 1.
 |
| | Scheme 1 Key elements in the fluorescence up-conversion set-up for two consecutive pulsed excitation. Green dotted lines denote the excitation beams. Red dotted lines the gating beam. Yellow shadowed surfaces the fluorescence from the sample focused in the non-linear BBO crystal by a Schwarzschild objective. The up-converted fluorescence signal is depicted as a violet dotted line. BS stands for the beam splitter in the Michelson interferometer. Black double arrows are associated with time delays. | |
The effect showed to be very sensitive to the position of the foci of the exciting beams. This is confirmed by measuring the size of the focused beams with a camera placed at different positions along the path. We conclude that a variation of 1.5 mm increases the size of the beam by a factor of 10 from a diameter of 12 μm at the focal point of a BK-7 lens of one inch diameter and a focal length of 75 mm. The output beam of the NOPA had a size of about 5 mm in diameter.
Measurements of fluorescence decay were obtained for a series of different delays from 0 to 140 ps. The measurements for 0 ps delay were done with just one beam (one of the mirrors in Michelson interferometer was blocked). To extract the kinetics of fluorescence decay after the second pulse the kinetics recorded for 0 ps delay was subtracted from the measurement with two pulses. Often pre-pulses produced in the beam splitter of the Michelson interferometer were observed and their effect was taken into account.
The transient absorption setup16 consisted of femtosecond pulse source (Pharos from Light Conversion) with output beam of 0.44 W 1030 nm and repetition rate 1 kHz, which was used to pump a two-stage NOPA to produce an excitation beam at wavelengths similar to those used in the fluorescence measurements. A white light continuum generated in a sapphire plate was used for probing. The excitation pulse energy before the sample was set at 0.5 μJ. The time resolution of the experiment was of about 50 fs. The polarization between excitation beam and probe beam was set to magic angle. The transient absorption signal was recorded by comparing consecutive single probe pulses with and without excitation pulse impinging on the sample. On average a set of 500 spectra per time step were recorded. Each kinetic trace was recorded 5 times and the results were averaged. In none of the cases presented a decrease in the fluorescence intensity was observed from measurement to measurement of a given series, indicating no substantial degradation of the sample.
Chirp correction was performed with an Optical Kerr Effect signal recorded from a 1 mm thick fused silica plate. Samples were flowed through a 0.5 mm thick cell.
Theoretical model
In order to model the transient excited state concentration of the fluorophore, which is proportional to the observed fluorescence signal, we require a theory able to assess the time dependence of the diffusion influenced bimolecular reaction responsible for its depletion. As all the reactions in the scheme are irreversible, such a model can be found in the so called Unified Encounter Theory.2 A simplified reaction scheme is depicted in Scheme 2.
 |
| | Scheme 2
N
G, NF and NP stand for the three possible states of the fluorophore: ground and excited electronic states and quenching product state, respectively. Q and QP are the two equivalent states of the quencher. For the ground state of the fluorophore produced by recombination of the quenching products NGR has been introduced to ease the discussion. | |
In order to model the quenching reaction after a single pulse it is sufficient to consider the irreversible reaction of the fluorophore with the quencher in terms of a reaction–diffusion model provided by the Different Encounter Theory.2 This model has been used on several occasions in the past and generally demonstrated a reasonable capability to explain quenching reactions. The time evolution of the excited state concentration is given by:
| |  | (1) |
where
τF is the natural decay time of the fluorophore in absence of any quenching reaction,
c is the concentration of the quencher and
kQ(
t) is the time-dependent quenching rate coefficient. It is assumed that the quencher concentration is much larger than that of the excited state of the fluorophore. This rate constant is time-dependent due to the influence of diffusion, and it is given by:
| |  | (2) |
which is the integral over space of the product of the reaction rate of the quenching reaction and the pair correlation function of quenchers with respect to the fluorophore. The necessity of including the reaction rate in the integral is motivated by the fact that many chemical reactions, most notably ET reactions, occur not only at contact but with a distant-dependent probability. In the cases we have studied here, the reaction is an electron transfer with an intrinsic rate described by the extended Marcus expression given below. This expression is slightly unusual in the “pre-exponential”-factor. According to Newton
17 and Gould,
18 the expression has two advantages over the simpler version of the theory. Firstly, it can be used for electron coupling elements larger than the thermal energy,
i.e. it expands the applicability to slightly adiabatic reactions. Secondly, as the dependence of the rate constant on the coupling are different in the normal (NMR) and inverted (MIR) Marcus regions, the jump probabilities are different. This is mandated by the fact that in the NMR the transition takes place within one adiabatic potential energy surface (PES) while in the MIR the system jumps from one PES to another. We also include in the expression the multichannel character of the reaction (with a single vibrational mode coupled to the electron transfer
19) and the dielectric relaxation of the solvent. The expression reduces to the usual single channel Marcus expression without solvent control and with the usual Levich–Dogonadze pre-exponential factor (
U(
r)) for small free enthalpies and small couplings.
| |  | (3) |
The free enthalpy for the quenching reaction is defined by the Weller equation:
| |  | (4) |
in which the first term is the singlet excited state energy with respect to the ground state, the redox potentials are defined in the solvent of interest and the last term stands for the attractive Coulombic potential between the ions. It is important to note that the larger the dielectric constant of the medium the smaller the Onsager radius, making it closer to the contact distance and negligible the distance dependence of this quantity.
The remaining quantities in the expression above, eqn (3), are defined as follows:
The Huang–Rhys factor is the ratio between the reorganization energy of the inner quantum high frequency vibrational mode coupled to the electron transfer reaction, and the energy of the mode. This quantity is specific of the reactants and in principle independent of the solvent.
| |  | (5) |
Following the continuum model for the solvent as follows and assuming a small difference of the radii of the reactants, the distance dependent reorganization energy can be written:
| |  | (6) |
| |  | (7) |
The distance dependence of the reorganization energy is quite importantly modulating the shape of the reactivity in consonance with that of the free enthalpy. Such is the influence that for the lower channels of the reaction in the MIR, the maximum of the reactivity is shifted away from contact creating a layer of strong recombination probability few Angstroms away from the contact distance
σ.
2 This effect has been shown experimentally.
3,4
The solvent relaxation time expression is as follows:
| |  | (8) |
The Levich–Dogonadze pre-exponential factor contains the most distance-dependent factor of all, the coupling between the reactants state and the products state,
V(
r):
| |  | (9) |
In first approximation, the distance-dependent coupling matrix element decays exponentially (this is absolutely correct for perfectly spherical reactants, and alternative dependences including angular functions have been needed in the past to explain experimental results
20):
| |  | (10) |
The pair correlation function in
eqn (2), can be obtained by solving the reaction–diffusion equation:
| |  | (11) |
which is a partial differential equation with a sink term for the chemical reaction, and a diffusional term with the Smoluchowski–Debye operator:
| | 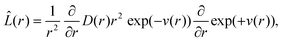 | (12) |
which contains the potential
v(
r) (in units of
kBT) and a distance dependent diffusion coefficient. The former is introduced to take into account the structure of the solvent (
g(
r) is the pair correlation function for the solvent and is obtained from the Perkus–Yevich approximation) and the Coulombic potential created by the charges of the reactants:
5–7| | | v(r) = −ln(g(r)) + rC/r, | (13) |
where the coulombic potential is described by the Onsager radius:
| |  | (14) |
The latter is introduced to account for the fact that the closer the reactants the larger the hydrodynamic hindrance to their additional approach:
21| |  | (15) |
We have shown in the past that both components are needed in the description of bimolecular quenching reactions.
5–7
The previous reaction–diffusion eqn (11), is solved with a reflective boundary condition at the contact distance (excluding the volume of the reactants from the available space) and an initial condition in agreement with the structure of the solvent
As we will see,
n(
r,0) is the quantity that experiences the major change after the second pulsed excitation: the initial conditions for the re-excited fluorophores are altered by the story of the reaction. In order to calculate this new initial distribution for the second pulse of quenchers around this particular subpopulation of fluorophores, we need to calculate the rest of the reaction scheme. In other words, we need to calculate the time evolution of the products of the reaction and how they recombine back to the ground state. Unified Encounter Theory provides us with a recipe to make this estimation.
2 In a similar manner as for the quenching, a partial differential equation can be written for the evolution of the pair distribution function of the products created by the quenching reaction:
| | 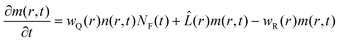 | (17) |
This approach just takes into account the geminate process, this is, the reaction that takes place between correlated fluorophore–quencher pairs and not with reaction partners produced in other quenching events (those other events are part of the so called bulk reactions and at times short enough can be neglected for low fluorophore concentrations). There are now three terms in the equation: the first stands for the creation of the quenching products, the second for the diffusion of the products, with the same operator as before and the third stands for the recombination to the ground state. Now the recombination reaction probability,
eqn (3), changes respect to the quenching or ionization due to a change in the free enthalpy of the reaction. The corresponding Weller equation can be written as:
| |  | (18) |
Also the coupling and its decay length can change with respect to the first reaction step as the orbitals involved in both steps are different: excited state of the fluorophore and ground state of the quencher leads to the charge separated or charge shifted state (products) in the quenching, and these lead to the ground states of fluorophore and quencher in the recombination.
Again, the inner boundary condition is reflective; the initial condition is zero everywhere. However, it has been shown by Ivanov and Potovi that the reaction scheme is not as simple as depicted: whenever the products state is energetically close enough to the ground state, it is possible that the reaction of quenching leads directly to the ground state as it crosses the products state and the dielectric friction increases the passage time over this crossing, in the manner depicted in the Scheme 3.22
 |
| | Scheme 3 PES for the ground state (black) excited state (green) and quenching products (red) as a function of the reaction coordinate (solvent polarization for electron transfer). The quantities shown are defined in the text. The blue arrows depict the Ivanov–Potovi effect,22eqn (19)–(21). | |
Thus the reaction–diffusion equation for the geminate ions is re-written in the following way:
| |  | (19) |
where the probability to cross to the ground state before reaching the minimum of the products is given by:
| |  | (20) |
with
| | 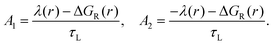 | (21) |
The time evolution of the concentration of the products can be calculated from the former pair distribution function:
| |  | (22) |
Finally, the pair distribution function of the recovered ground state by recombination of the former products is the solution to the next partial differential equation with reflective boundary condition at contact again and zero initial condition, as we are only interested in the distribution of the ground state that is created anew after the first cycle of quenching and recombination:
| | 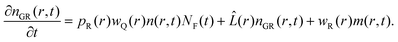 | (23) |
This closes the cycle of quenching and recombination after the first pulse.
After a given time Δt, part of the population of the fluorophore is in one of three possible states: the excited state, product form (reduced or oxidized by the electron transfer reaction), or in the ground state. The latter is composed of two populations: one which was never excited and a second that has undergone the full cycle of excitation, quenching and recombination. The former sees a pair distribution function of quenchers like the initial one, g(r). The latter has an altered population due to the quenching and recombination. In fact, the latter has an increased probability of having a quencher nearby, at least as long as diffusion does not separate the recombination products. This means that this altered pair distribution function evolves with time and finally vanishes at times long after the first pulse. If at this moment a second pulse of light illuminates the pre-excited sample with the same intensity, an equal fraction of both populations in the ground state are excited. Now, the kinetics of the quenching process will be different from those observed after the first pulse, because of the difference in the initial distribution of quenchers around the fluorophore. It can be interpreted as an increase in the static quenching regime through the alteration of the quencher distribution. In order to calculate this new initial distribution we have to sum the probabilities of finding a quencher–fluorophore pair in a given volume that has not reacted before, and that has reacted before. The probability of finding one that did not react is given by:
| |  | (24) |
On the other hand a pair in which the fluorophore has been excited, quenched and recombined has the following probability:
| |  | (25) |
Counting the number of pairs that in total have recombined, those that are still in the excited state and in the products state, one can get to the following new probability of finding a pair when the second pulse arrives exciting a fraction
fex of fluorophores in the ground state:
| |  | (26) |
In this expression
φR(Δ
t) is the probability that an excited fluorophore, which has formed a radical ion pair, has recombined at the time of arrival of the second pulse, or the quantum yield of recombination at this instance:
| |  | (27) |
Δ
Q is the number of ground-state quenchers,
i.e. the total number of quencher molecules that is not in the products state:
| |  | (28) |
In deriving
eqn (26), we have partitioned the total number of fluorophores in two populations: fluorophores that had undergone a complete excitation and recombination cycle and fluorophores that had not been excited. For the first group, the recombination reaction leads to a spatial correlation of the fluorophore and the reaction partner. As a consequence, for these fluorophores the initial pair correlation function is given by
| |  | (29) |
which is the weighted average of (Δ
Q − 1) uncorrelated quenchers contributing
P1 and one contributing
P2 as a result of the recombination reaction. For the second group of fluorophores, no correlation has been generated and, thus, the initial condition is still simply given by
| |  | (30) |
In
eqn (26),
n′ was weighted by the probability that the fluorophore had been excited, reacted, and recombined,
fexφR(Δ
t), and
n′′ by the probability that fluorophore had remained unexcited by the first light pulse, (1 −
fex). On account of the fact the fluorophores that were excited by the first light pulse but did not react until Δ
t do not contribute to the second fluorescence decay (but to the background emanating from the first cycle), the resulting expression has to be renormalized by dividing by
fexφR(Δ
t) + (1 −
fex) to eventually obtain
eqn (26). Due to the recombination of quencher radical that already existed prior to the second laser pulse, the pair correlation function in principle acquires an additional time-dependence. As our estimates suggest that this contribution is negligible this effect has not been included here.
Substituting the defined quantities in eqn (26), and assuming the thermodynamic limit (the total volume of the sample, V is much larger than any of the volume integrals appearing in the expression) we find that the new initial distribution for the fluorophores excited by the second pulse is:
| |  | (31) |
So it differs from the initial distribution after the first pulse by the second term. This term increases with the fraction of excited molecules, which cannot exceed 0.5, and exhibits a non-trivial dependence on the amount of products recombined. What is evident is that if the distribution of recombined products is close to the quenching reaction zone, where
wQ(
r) is not zero, the quenching will be enhanced respect to the quenching after the first pulse and the fluorophore decay will be accelerated. An example of the dependence of
nGR with Δ
t is given in
Fig. 1.
 |
| | Fig. 1 Initial distributions of quenchers respect to the fluorophore for the usual conditions of excitation with a single pulse (black line) and after a second pulse arriving at Δt. The calculations have been performed with eqn (31). Parameters are to be found in Table 1 (TMPPD, fex = 0.5). R in the legend is defined in eqn (34). | |
It is interesting to note that the denominator of the second term in the former expression, eqn (31), is related to the relative height of the initial value of the fluorescence at the time of arrival of each of the pulses:
| | | S1P(0) ∝ NG(0)S2P(Δt) − S1P(Δt) ∝ NG(Δt) | (32) |
Here, the first expression means that the signal of fluorescence observed immediately after the first pulse is proportional to the ground state fluorophore population (which at
t = 0 equals the total fluorophore population). The second means that the increase of the signal observed due to the arrival of the second pulse is proportional to the remaining ground state concentration at the time of arrival of that pulse.
At the moment of arrival of the second pulse, this population is the sum of what actually remained non-excited plus what has recombined up to that moment:
| |  | (33) |
Thus, dividing one signal by the other we get:
| |  | (34) |
This suggests that, in principle, the two-pulse experiment allows evaluating the yield of recombination to the ground state at any given moment from the fraction of emission intensities. The more separated in time the excitation pulses are, the smaller the intensity ratio in
eqn (34) will be as a consequence of higher recombination yields. This is expected to apply up to a time limit at which the geminate recombination is inefficient and the products escape by diffusion. The expression also serves to evaluate the fraction of excited state produced by the pulse. If the quantity is close to 1 for all delay times it is a clear indication of a low excitation rate as a result of either a low photon flux or a small absorption coefficient of the fluorophore or both.
Finally to characterize the amount of the effect of the second pulse it is useful to define the relative quantity:
| |  | (35) |
from the kinetics of the excited state recorded from the fluorescence after one pulse (
N1p(
t)) and after the second one (
N2P(
t,Δ
t)) clean of the former (the kinetics of the fluorescence decay after the second pulse contain both kinetics otherwise). In
Fig. 2 there is an exemplary calculation.
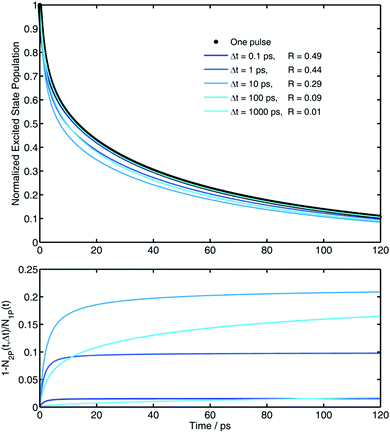 |
| | Fig. 2 Upper panel: Simulations of the decay of the excited state in presence of 0.4 M of quencher after one pulse and after a second pulse arriving at different Δt. Bottom panel: Relative extent of the effect of the enhancement of quenching for the decay after a second pulse (SPE(t), eqn (35)). In both panels the color code represents the same delays between pulses. fex = 0.5 for all cases. Simulation parameters: see Table 1. R in the legend is defined in eqn (34). | |
Results
The possibility of observing an effect of a second pulse in the kinetics of fluorescence quenching depends strongly on the efficiency and rate of the recombination. A too small quantum yield of recombination or a too slow recombination rate preclude an enhancement of the initial distribution after the second pulse and would thus not lead to a difference in the fluorescence emission after the two pulses. Additionally, we require a fluorophore stable enough to not suffer from significant photo-degradation, with a large extinction coefficient to increase the probability of saturating the transition during the excitation pulse (i.e. increase fex) and a large radiative rate constant to increase the signal to noise ratio in the fluorescence up-conversion experiment. Laser dyes provide all these characteristics. Rhodamine 6G has been used in the past to study photo-induced electron transfer reactions as it is not too difficult to reduce to the neutral radical (see Table 1). In order to demonstrate the effect of the recombination rate we have employed reductants with different potentials: TMPPD and DMA, of which the former is a much stronger reducing agent than the latter (Table 1). Both are aromatic tertiary amines. TMPPD has the additional advantage of producing a deeply coloured radical cation which in principle can serve to monitor the reaction by means of transient absorption. The concentration of the quencher has been kept high to warranty high quenching yields and fast kinetics. At low quencher concentrations the effect is unlikely to be observable as most of the reaction would take longer than the diffusion motion of the products, thereby fading out the effect on the pair correlation function.
We have first tested if the intensity of the excitation pulses was high enough to create a large excited state concentration. To this end measurements of the fluorophore in absence of quencher have been performed at different inter-pulse delays and excitation intensities. We have observed that the intensity of the second fluorescence peak in the region between 550 and 610 nm decreases respect to that of the first pulse as the intensity of the excitation increases, in accordance to eqn (34) for φR(Δt) = 0. In this way we can get a qualitative understanding of the excitation efficiency and its relation to the employed laser power. However, one has to bear in mind that the experimental conditions vary from day to day due to the tuning of the laser system: a small change in the conditions of the amplifier or the NOPA can lead to marked changes in the size and shape of the beam, which precludes a quantitative calibration of fex.
As can be seen in Fig. 3, the second signal is markedly reduced with respect to the first, what leads us to conclude that saturation of the transition can be easily achieved under the employed conditions of our set-up.
 |
| | Fig. 3 Example of the double pulse measurement with R6G in ACN. The sample had an optical density of 0.1 at the excitation wavelength, 524 nm. The excitation average power was 0.3 mW at each pulse. The ratio R (eqn (34)) from the two fluorescence maxima delayed by 60 ps is about 0.46. | |
Adding TMPPD to the R6G ACN solution to a concentration of 0.4 M leads to substantial quenching of the fluorescence. The excited state population disappears almost completely after 200 ps, having R6G a fluorescence lifetime of around 4 ns. In order to find the best experimental conditions to observe a difference between the kinetics after one and two pulses, we first performed measurements with different delays between pulses at a moderate excitation rate (see Fig. 4). Similar measurements have also been performed with DMA as a quencher.
 |
| | Fig. 4 R6G fluorescence after one (blue) and two pulses (black) in presence of 0.4 M of TMPPD dissolved in ACN at different delays. The difference between the two kinetic traces (and shifted Δt) is depicted in red. The insets show the relative effect (SPE(t), eqn (35)). The excitation power was approximately of 0.3 mW. The ratio R, eqn (34), between the two fluorescence peaks at increasing delays are: 0.24, 0.23, 0.16 and 0.08 for 20, 40, 60 and 100 ps respectively. | |
While for the quenching by DMA no differences between the decays recorded after both pulses can be observed, in most of the cases measured with TMPPD there is a clear difference between the kinetics after one or two pulses. This means that the recombination in the former case is not fast enough for the ground state to recover after the first quenching event, while for the latter is. This is in agreement with the energetics of the reactions as collected in Table 1. In fact measurements of transient absorption for the system R6G-TMPPD (see Fig. 5) indicate that the ions live for an extremely short time. In fact the signal of TMPPD radical cation (positive signal above 600 nm) is barely observable making the extraction of the kinetics from these measurements very difficult despite the high quality of the data. What is mostly observed is that the stimulated emission signal disappears (550–600 nm) in a time range similar to the decay of the fluorescence in the up-conversion measurements (right panel), and that the ground state bleaching (below 550 nm) signal fills up and then remains constant at long times. The time-invariant signal for the latter is related to the escaped ions from the geminate recombination. In case of having a recombination process faster than the quenching, the kinetics that would be recovered from the transient signal of the products would reflect their formation and not the recombination (inverted kinetics) making the extraction of the recombination parameters very difficult, if not impossible.
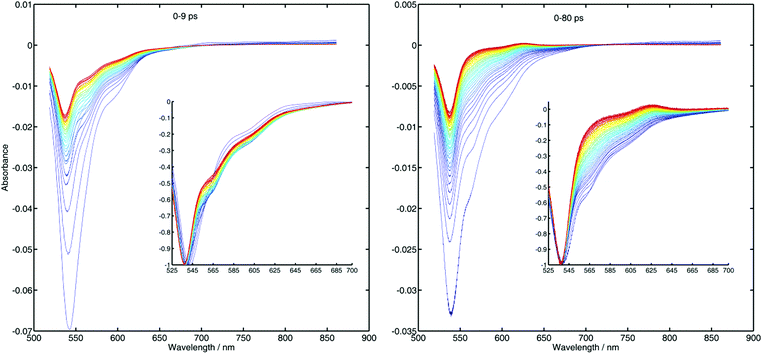 |
| | Fig. 5 Transient absorption spectra after excitation with 524 nm of a sample of R6G with 0.6 M of TMPPD in ACN. The left panel shows the spectra at different delay times from time zero to 9 ps. The right panel shows the same for a longer time scale up to 80 ps. The insets show the same spectra but normalized at their minima. With increasing time delay the color of the lines goes from blue to red. | |
According to the eqn (34), it is in principle possible to retrieve the evolution of the recombination from the measurements of the effect of the second pulse on the kinetics and height of the signal of fluorescence as a function of the delay time. As expected from the simulations either too short or too long delays decrease the amount of the effect, which has an optimum value around 30–60 ps, in qualitative agreement with the simulations shown in the theoretical section above (Fig. 4).
For these two delays between pulses, 30 and 60 ps, we have performed measurements increasing the intensity of the excitation (Fig. 6). In agreement with the prediction, the difference between the kinetics increases with the excitation power.
 |
| | Fig. 6 R6G fluorescence after one (blue) and two pulses (black) in presence of 0.4 M of TMPPD dissolved in ACN at excitation powers. The difference between the two kinetic traces (and shifted Δt) is depicted in red. The insets show the relative effect (SPE(t), eqn (35)). The delay between pulses was 60 ps. The quantity R, defined in eqn (34), extracted from the ratio of the two fluorescence peaks is: 0, 0.15, 0.17, 0.20, 0.22 and 0.27 for 0.1, 0.3, 0.5, 0.7, 1.0 and 1.3 mW respectively. | |
A more detailed analysis can be done by integrating the relative effect over the first 200 ps (Fig. 7). The delay of 60 ps shows a larger effect than that of 30 ps, meaning that the recombination is not complete after 30 ps, and at 60 ps the diffusion has not yet washed out the excess of quenchers nearby fluorophores with which they have previously recombined. For both delays studied the effect saturates in the range of excitation power used. The model exposed above predicts a linear dependence for the integrated effect with the fraction of excited state. As at a given delay the amount of recombined pairs of the quenching products per excited molecule is independent of the excitation intensity, the only plausible explanation for the shape of the curves in Fig. 7 is the saturation of the transition, which starts before reaching the population inversion.
 |
| | Fig. 7 Integrated over 200 ps relative effect (SPE(t), eqn (35)) for two different delays (red dots: 30 ps, blue dots: 60 ps) as a function of the excitation power for R6G quenched by 0.4 M of TMPPD in ACN. | |
Despite qualitatively correct, the model is not able to reproduce quantitatively all the experimental results. A comparison between the experiment and the model for the highest used power assuming a perfect population inversion is shown in Fig. 8. Not only in the present set of measurements, is the effect predicted smaller than that observed experimentally. The parameters used for the simulations and collected in Table 1, are those which led to the maximum effect taking into account the properties of R6G and TMPPD. Increasing further the recombination rate at contact, by for example increasing the coupling matrix element for the electron transfer, does not increase the effect with a delay of 60 ps. So at the current state of the theory the most that can be assessed is that the recombination rate is larger than the quenching rate, and that the coupling matrix element associated is of at least the order collected in Table 1. Furthermore, this finding is in agreement with the very low signal of the radical cation of TMPPD in the transient absorption experiment. On the other hand, increasing the recombination rate has a negative effect on the agreement between simulations and experiments for the quantity R, eqn (34), from the peaks ratio: increasing too much the recombination rate decreases to zero the quantity R, while the measured value is quite different. This indicates that despite the disagreement, the recombination cannot be much larger than the minimum estimated to achieve the largest simulated effect.
 |
| | Fig. 8 Upper panel: R6G fluorescence decay in presence of 0.4 M TMPPD in ACN kinetics after one (blue) and two pulses (red). Simulation curves performed with the model presented in the theoretical section for the kinetics after each of the pulses (first: cyan, second: yellow). Lower panel: Relative effect (SPE(t), eqn (35)) from the experimental data in red and from the simulations in green. The delay between pulses was 60 ps and the excitation power 1.3 mW. The quantity R, eqn (34), extracted from the ratio between the two fluorescence peaks is 0.27 for the experimental data and 0.14 for the theoretical simulations. | |
Conclusions
A clear effect of multi-pulse excitation on the kinetics of bimolecular photo-induced reactions has been observed. The main reason for this is the transient enhancement of the local concentration of the quencher around fluorophores excited twice within a short time. Despite in qualitative agreement with the measurements and the observed trends with delay pulses and pulse intensity, the theoretical prediction gives a smaller amount of the effect due to yet unknown reasons.
The recombination efficiency can be estimated from the described two-pulse fluorescence measurements. In the case of quenching by TMPPD, this information is not readily available from the transient absorption data as the ground state recovery kinetics is governed by the kinetics of appearance of the quenching products. This opens the possibility for using this method to study consecutive reaction in the case of inverse kinetics.
A direct quantitative comparison between the measurements with consecutive pulses and with intense stationary excitation, which are the conditions studied theoretically by Igoshin and Burshtein,11 is rather complicated. The probability for two consecutive photon absorption events under continuous illumination should be calculated with the presented model, and evaluate if further absorption events are to be considered, in which case the model here is insufficient. But in view of the fact that experimentally, and according to the model, the effect decreases with the delay between two absorption events for the same fluorophore, it is relatively safe to assume for the sake of a qualitative discussion that no more than two consecutive cycles of excitation quenching and recombination need to be considered. Under such conditions, the maximum expectable effect in the stationary conditions can be evaluated from the effect observed at a delay of 30 to 60 ps. This different kinetics would lead to an increase of the Stern–Volmer quenching rate constant by about 25% for the highest possible pump rates. This is of the same order of magnitude as predicted by Igoshin and Burshtein.11
Acknowledgements
G. A. acknowledges financial support from the Narodowe Centrum Nauki within the “Harmonia 3” program, grant number 2012/06/M/ST4/00037. Helpful discussions with Dr Arnulf Rosspeintner from the University of Geneva and Professors Konstantin Ivanov and Nikita Lukzen from the International Tomography Center of the Russian Academy of Sciences in Novosibirsk are also cherished.
References
- M. v. Smoluchowski, Z. Phys. Chem., 1917, 92, 129–168 Search PubMed.
- A. I. Burshtein, Adv. Chem. Phys., 2000, 114, 419–587 CrossRef CAS; A. I. Burshtein, Adv. Chem. Phys., 2004, 129, 105–418 Search PubMed.
- G. Angulo, G. Grampp, A. A. Neufeld and A. I. Burshtein, J. Phys. Chem. A, 2003, 107, 6913–6919 CrossRef CAS.
- A. A. Neufeld, A. I. Burshtein, G. Angulo and G. Grampp, J. Chem. Phys., 2002, 116, 2472–2479 CrossRef CAS.
- A. Rosspeintner, D. R. Kattnig, G. Angulo, S. Landgraf, G. Grampp and A. Cuetos, Chem. – Eur. J., 2007, 13, 6474–6483 CrossRef CAS PubMed.
- A. Rosspeintner, D. R. Kattnig, G. Angulo, S. Landgraf and G. Grampp, Chem. – Eur. J., 2008, 14, 6213–6221 CrossRef CAS PubMed.
- G. Angulo, D. R. Kattnig, A. Rosspeintner, G. Grampp and E. Vauthey, Chem. – Eur. J., 2010, 16, 2291–2299 CrossRef CAS PubMed.
- D. R. Kattnig, A. Rosspeintner and G. Grampp, Angew. Chem., Int. Ed., 2008, 47, 960–962 CrossRef CAS PubMed.
- M. Koch, A. Rosspeintner, G. Angulo and E. Vauthey, J. Am. Chem. Soc., 2012, 134, 3729–3736 CrossRef CAS PubMed.
- A. Rosspeintner, G. Angulo and E. Vauthey, J. Am. Chem. Soc., 2014, 136, 2026–2032 CrossRef CAS PubMed.
- O. A. Igoshin and A. I. Burshtein, J. Chem. Phys., 2000, 112, 10930–10940 CrossRef CAS.
- M. Yang, S. Lee, K. J. Shin and K. Y. Choo, Bull. Korean Chem. Soc., 1991, 12, 414–423 CAS.
- W. Naumann and A. Szabo, J. Chem. Phys., 1997, 107, 402–407 CrossRef CAS.
- D. Peceli, S. Webster, D. A. Fishman, C. M. Cirloganu, H. Hu, O. V. Przhonska, V. V. Kurdyukov, Y. L. Slominsky, A. I. Tolmachev, A. D. Kachkovski, R. R. Dasari, S. Barlow, S. R. Marder, D. J. Hagan and E. W. Van Stryland, J. Phys. Chem. A, 2012, 116, 4833–4841 CrossRef CAS PubMed.
- B. Białkowski, Y. Stepanenko, M. Nejbauer, C. Radzewicz and J. Waluk, J. Photochem. Photobiol., A, 2012, 234, 100–106 CrossRef CAS; P. Wnuk, G. Burdziński, M. Sliwa, M. Kijak, A. Grabowska, J. Sepioł and J. Kubicki, Phys. Chem. Chem. Phys., 2014, 16, 2542–2552 RSC.
-
M. Nejbauer, PhD thesis, Warsaw, 2015.
- M. D. Newton and N. Sutin, Annu. Rev. Phys. Chem., 1984, 35, 437–480 CrossRef CAS.
- I. R. Gould, R. H. Young, R. E. Moody and S. Farid, J. Phys. Chem., 1991, 95, 2068–2080 CrossRef CAS.
- S. Efrima and M. Bixon, Chem. Phys. Lett., 1974, 25, 34–37 CrossRef CAS.
- G. Angulo, A. Cuetos, A. Rosspeintner and E. Vauthey, J. Phys. Chem. A, 2013, 117, 8814–8825 CrossRef CAS PubMed.
- S. H. Northrup and J. T. Hynes, J. Chem. Phys., 1979, 71, 871–883 CrossRef CAS.
- A. I. Ivanov and V. V. Potovoi, Chem. Phys., 1999, 247, 245–259 CrossRef CAS.
-
M. Montalti, A. Credi, L. Prodi and M. T. Gandolfi, Handbook of Photochemistry, CRC Press, Boca Raton, USA, 3rd edn, 2006 Search PubMed.
-
Y. Marcus, The Properties of Solvents, Wiley Series in Solution Chemistry, Wiley, 1998 Search PubMed.
Footnote |
| † Excitation rate and the light intensity of the source are related by kEX = σPλ/hc where σ is the absorption cross section of the chromophore, P is the power of the light source, λ its wavelength and h and c the Planck's constant and the speed of light. |
|
| This journal is © the Owner Societies 2017 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Jadwiga
Milkiewicz
a,
Daniel
Kattnig
b,
Michał
Nejbauer
a,
Yuriy
Stepanenko
a,
Jan
Szczepanek
ac,
Czesław
Radzewicz
ac,
Paweł
Wnuk
acde and
Günter
Grampp
f
*a,
Jadwiga
Milkiewicz
a,
Daniel
Kattnig
b,
Michał
Nejbauer
a,
Yuriy
Stepanenko
a,
Jan
Szczepanek
ac,
Czesław
Radzewicz
ac,
Paweł
Wnuk
acde and
Günter
Grampp
f
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 beam splitter (Thorlabs, BSW10R). The excitation wavelength was set near the maximum absorption of the fluorophore at 525 nm (FWHM of about 10 nm). The average power was varied between 0.1 to 1.3 mW at each pulse using neutral density filters. Gating beam was set to 1020 nm (10 mW, FWHM 35 nm). From cross correlation measurements the final instrument response function is circa 300 fs. Polarization of the excitation beam was set using a λ/2-plate at magic angle with respect to the gating beam. Parasitic polarizations were removed using nanoparticle polarizer (Thorlabs).
50 beam splitter (Thorlabs, BSW10R). The excitation wavelength was set near the maximum absorption of the fluorophore at 525 nm (FWHM of about 10 nm). The average power was varied between 0.1 to 1.3 mW at each pulse using neutral density filters. Gating beam was set to 1020 nm (10 mW, FWHM 35 nm). From cross correlation measurements the final instrument response function is circa 300 fs. Polarization of the excitation beam was set using a λ/2-plate at magic angle with respect to the gating beam. Parasitic polarizations were removed using nanoparticle polarizer (Thorlabs).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.95). A final test was performed by recording the emission of fluorophore sample without quencher: the intensity of the second fluorescence signal is reduced as much as the ground state is depopulated indicating that the beams are impinging the same volume. A scheme of the set-up is shown in the Scheme 1.
0.95). A final test was performed by recording the emission of fluorophore sample without quencher: the intensity of the second fluorescence signal is reduced as much as the ground state is depopulated indicating that the beams are impinging the same volume. A scheme of the set-up is shown in the Scheme 1.