Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Polarization loss in the organic ferroelectric trialkylbenzene-1,3,5-tricarboxamide (BTA)†
A. V.
Gorbunov
a,
X.
Meng
b,
I.
Urbanaviciute
c,
T.
Putzeys
d,
M.
Wübbenhorst
 d,
R. P.
Sijbesma
d,
R. P.
Sijbesma
 b and
M.
Kemerink
b and
M.
Kemerink
 *ac
*ac
aDepartment of Applied Physics, Eindhoven University of Technology, PO Box 513, 5600 MB Eindhoven, The Netherlands
bLaboratory of Macromolecular and Organic Chemistry, Eindhoven University of Technology, P.O. Box 513, 5600 MB Eindhoven, The Netherlands
cComplex Materials and Devices, Department of Physics, Chemistry and Biology (IFM), Linköping University, 58183 Linköping, Sweden. E-mail: martijn.kemerink@liu.se
dDepartment of Physics and Astronomy, Laboratory for Soft Matter and Biophysics, KU Leuven, Celestijnenlaan 200D, B-3001 Heverlee, Belgium
First published on 23rd December 2016
Abstract
We investigate the polarization loss in the archetypical molecular organic ferroelectric trialkylbenzene-1,3,5-tricarboxamide (BTA). We prove that the polarization loss is due to thermally activated R-relaxation, which is a collective reversal of the amide dipole moments in ferroelectric domains. By applying a weak electrostatic field both the polarization loss and the R-relaxation are suppressed, leading to an enhancement of the retention time by at least several orders of magnitude. Alternative loss mechanisms are discussed and ruled out. By operating the thin-film devices slightly above the crystalline to liquid crystalline phase transition temperature the retention time of one compound becomes more than 12 hours even in absence of supportive bias, which is among the longest reported so far for organic ferroelectric materials.
1 Introduction
Organic ferroelectric materials are starting to gain increasing attention, although they still form a largely unexplored ‘terra incognito’ in comparison to their inorganic counterparts.1–8 The advantages organic ferroelectrics may have are no different from those of e.g. organic semiconductors. While in the latter the relatively easy processing on conformal and flexible substrates and the nearly infinite freedom to modify and tailor properties through chemical design have already lead to actual applications in displays, solar cells and electronic circuitry, organic ferroelectrics are still in an explorative stage – the exception to this observation being the polymer ferroelectric PVDF and its copolymers with TrFE.9,10A crucial characteristic of any ferroelectric material is the retention time of the polarization.11 From the lack of reported results of experiments on retention one could possibly conclude that, for organic crystalline and liquid crystalline ferroelectrics, polarization retention remains a problem. Although many papers introduce new molecular materials and concepts leading to ferroelectric activity, the polarization retention part is typically not addressed.1–8,12–18 Some works evaluate polarization relaxation from temporal measurements of the second harmonic generation (SHG) intensity. Measurements on a liquid crystalline urea-based compound showed fast decay of SHG intensity in millisecond range.19 On the other hand, in self-assembled umbrella-shaped liquid crystals with flipping cyano groups, only around one fourth of the SHG intensity was lost in 1000 minutes.4 However, the retention mechanism was not analysed. Intriguingly, none of the mentioned reports apply direct electrical measurement of polarization retention, which is broadly used for the characterization of inorganic systems.20,21
Poling of a ferroelectric is a temperature- and field-driven process.22 Besides thermal impact, the polarization loss in thin films of highly insulating materials is commonly understood as being caused by depolarization fields, usually arising from the presence of non-switching “dead” layers at the metal/ferroelectric interfaces, assuming that metal electrodes supply sufficient compensation charges.23–25 However, the underlying processes are not yet well understood.11 We will study possible intrinsic depolarization processes in the context of extrinsic, device related effects, such as depolarization fields.
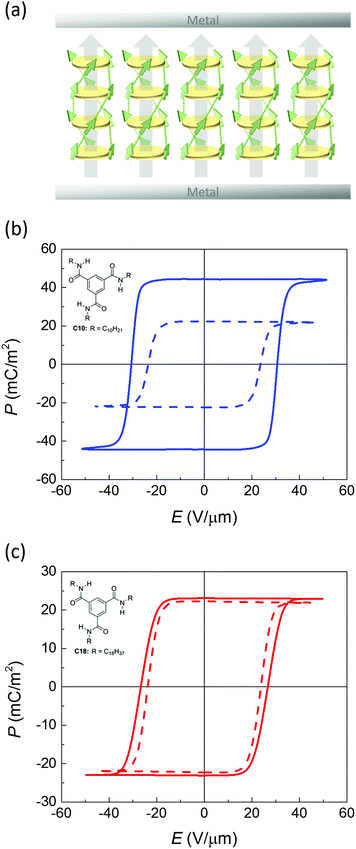
In this work we will investigate the polarization loss mechanism of an archetypical molecular ferroelectric material, trialkylbenzene-1,3,5-tricarboxamide (BTA). Its structure is shown in the inset to Fig. 1. Slightly above room temperature this material enters a columnar hexagonal liquid crystalline mesophase that can be aligned by an external electric field.6 Upon field reversal a dipolar switching signal is observed that can be associated with the collective reversal of the amide groups that surround the benzene core. Although this switching was recently shown to be truly ferroelectric, with a Curie–Weiss temperature of ∼200 °C at which the dielectric susceptibility reaches a maximum,26 the poor retention of the polarization remains a problem for actual applications. At the temperatures required for easy dipolar switching, typically between 80 °C and 150 °C, the polarization is lost in several minutes.27 As this loss is not accompanied by a reduction in the hexagonal columnar packing order it must be attributed to a randomization of the orientation of the amide dipoles only. The mechanism with which this happens is largely unknown, although we previously suggested it to be connected with R-relaxation that we associated with the collective polarization reversal in a defect domain.27
In the present work we perform a detailed investigation of the polarization loss mechanism in BTA and ways to mitigate it. We demonstrate that application of an electric field that is significantly below the coercive field suppresses both R-relaxation and polarization loss, leading to an increase in retention time by at least several orders of magnitude. Moreover, by operating close to room temperature, the retention time in absence of supporting bias can be extended to over 12 hours.
2 Results and discussion
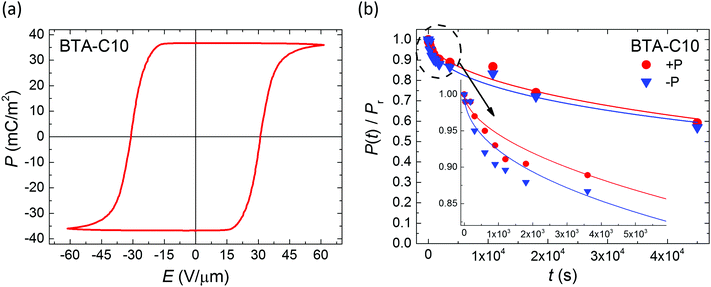
Thin-film metal–ferroelectric–metal capacitor devices were fabricated and measured as described before.26 In brief, electrodes were formed by thermally evaporating Au through a shadow mask, defining a device area around 0.04–1 mm2. The active layer was formed by spin coating of the symmetrically substituted benzene-1,3,5-tricarboxamide derivatives BTA-C10 or BTA-C18, where C10 and C18 refer to the number of C-atoms in the solubilizing alkyl chains.6 Upon solvent evaporation BTA forms hydrogen bonded columns that lay in-plane after fabrication. The desired out-of-plane alignment (Fig. 1a) is achieved by heating the samples to typically 100–110 °C, where the material is in a columnar hexagonal liquid crystalline phase of relatively low viscosity,27 while applying a slowly alternating electric field. Subsequently the devices are cooled down to the desired measurement temperature.The saturated polarization curves of both BTA-C10 and BTA-C18 as measured under quasi steady state conditions are displayed in Fig. 1. The measurement details can be found in the Experimental section. Both materials show excellent saturation of the remnant polarization Pr. The frequency dependence of the coercive field and other transient characteristics are addressed in our previous work ref. 26 in which it is also shown that the dipolar switching is of truly ferroelectric nature.
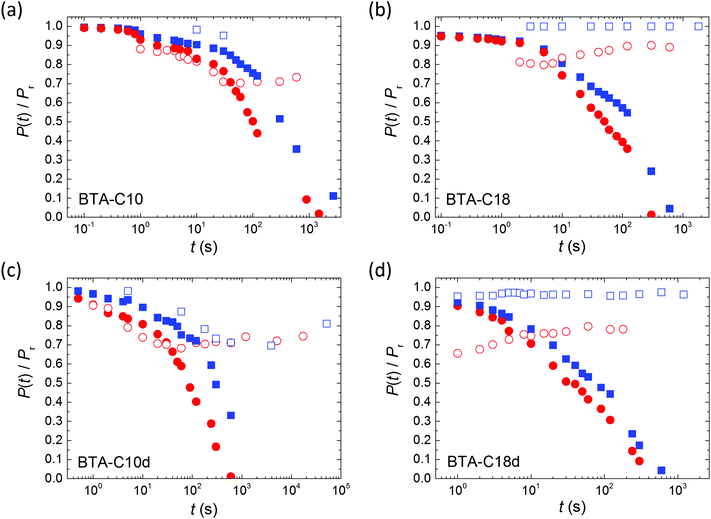
Despite the well-developed ferroelectric behavior, both materials exhibit a rapid loss of polarization, ranging from several seconds to several minutes, depending mostly on temperature. Fig. 2 shows the normalized remaining polarization after a waiting time t after full poling, as defined in panel a. It was checked that the response to the + and − probe pulses add up to 2Pr. The data can be well described by a stretched exponential function,
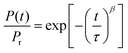 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Ea/kBT) with kB the Boltzmann constant, as in Fig. 3. In the analysis of the temperature dependence of the polarization loss, it is important that the saturation value for the remnant polarization Pr is essentially independent of temperature, as confirmed in Fig. S2 of the ESI.†
exp(−Ea/kBT) with kB the Boltzmann constant, as in Fig. 3. In the analysis of the temperature dependence of the polarization loss, it is important that the saturation value for the remnant polarization Pr is essentially independent of temperature, as confirmed in Fig. S2 of the ESI.†
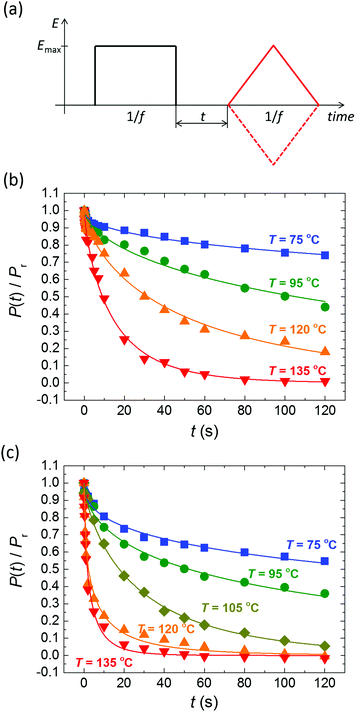 | ||
| Fig. 2 (a) Pulse sequence used for polarization retention measurements; a variable delay t separates poling (black) and probing (red) pulses. Emax > Ec, f = 1–5 Hz. (b and c) Normalized polarization vs. delay time for BTA-C10 (b) and BTA-C18 (c) thin-film capacitors at various temperatures. Symbols are experiments, solid lines are fits to eqn (1) with β = 0.5–0.75. Experiments are performed without supportive bias, i.e. the sample is grounded during the delay time. Each data point is obtained after full repolarization. | ||
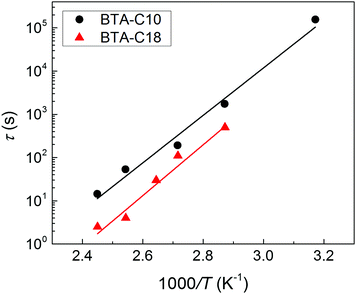 | ||
| Fig. 3 Thermal activation of the depolarization process in BTA-C10 (black circles) and BTA-C18 (red triangles) thin-film capacitor devices. Data points are obtained by the fits in Fig. 2, lines indicate Arrhenius behavior with an activation energy of 105 kJ mol−1 = 1.1 eV for BTA-C10 and 113 kJ mol−1 = 1.2 eV for BTA-C18. | ||
The activation energies of 105 kJ mol−1 for BTA-C10 and 113 kJ mol−1 for BTA-C18 extracted from Fig. 3 are similar to the 108 kJ mol−1 and 87 kJ mol−1 found in our earlier work.27 The minor differences are attributed to better alignment in the present thin film devices than in the liquid crystal (LC) cells used before. Interestingly, these energies are very similar to Wb = 0.9–1.2 eV calculated for P(VDF:TrFE).28
Qualitatively, the short retention time and modest activation energy of depolarization both indicate that the energy barrier between up and down polarization states is also quite modest, as explained by Landau–Devonshire theory. This would be consistent with the coercive field and remnant polarization that are substantially lower compared to e.g. Ec ≈ 50 V μm−1 and Pr ≈ 85 mC m−2 found for P(VDF:TrFE) at room temperature,29 for which thin film polarization retention times in the order of several hours have been reported,30–32 and compared to inorganics like BFO and PZT where Ec ≈ 50 V μm−1, Pr ≈ 1000 mC m−2 and retention times in thin film can be over 104 s with an energy barrier Wb = 1.25 eV.33,34
To further interpret the data in Fig. 3, we use the model by Vopsaroiu et al. for the depolarization switching time tsw.22
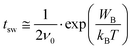 | (2) |
As noted before, the activation energies mentioned above are quite similar to the activation energies for R-relaxation as probed by dielectric relaxation spectroscopy (DRS) of 147 ± 10 kJ mol−1 and 124 ± 10 kJ mol−1 for C10 and C18, respectively. This similarity and the fact that R-relaxation is a loss channel for polarization hints at the relevance of this process for the polarization loss in BTA-based thin-film capacitor devices. In the following sections, we shall therefore inspect this, and a number of other potential depolarization mechanisms in more detail. Apart from the R-relaxation, we shall consider loss of the homeotropic alignment, ionic motion, and proton-tunneling.
Of these, polarization loss due to a loss of the homeotropic alignment of columnar hexagonal phase can readily be ruled out on basis of polarization optical microscopy (POM) performed on LC cells, in which no change in the (black) texture upon depolarization is observed (not shown). Moreover, depolarized devices can immediately be repolarized, whereas (re)establishing structural order is a comparatively slow process. In Section S7 of the ESI† it is shown that only insignificant distortions of the repolarization current transients occur at high temperatures, even after extensive delay times. Moreover, the integrated remnant polarization value does not change in the whole time range of the measurement, indicating intact homeotropic alignment.
Alternatively, one can imagine that slow ionic motion may lead to partial or complete screening of the polarization surface charges in the active layer. In this case, ‘repolarization’ would imply a redistribution of the screening ions which would give rise to a transient switching current that has different kinetics than a true polarization reversal. This is not the case. Apart from having a different magnitude, repolarization transients have the same characteristics and shape as those corresponding to a normal polarization reversal, as seen in Fig. S7-2 of the ESI.†
Polarization loss through proton transfer from nitrogen N–H to the neighboring carbonyl group results in the iminol tautomeric form of the amide, as concisely illustrated in Fig. 4a and in detail in Fig. S8 of the ESI.† This mechanism has recently been proposed to underlay ferroelectric behavior of hydrogen bonding compounds.36,37 Concerted proton transfer has been studied theoretically in formamide dimers, and in those dimers in the gas phase, the proton transfer has a high activation energy of around 42 kJ mol−1 and a low barrier for reversal (6.5 kJ mol−1).38
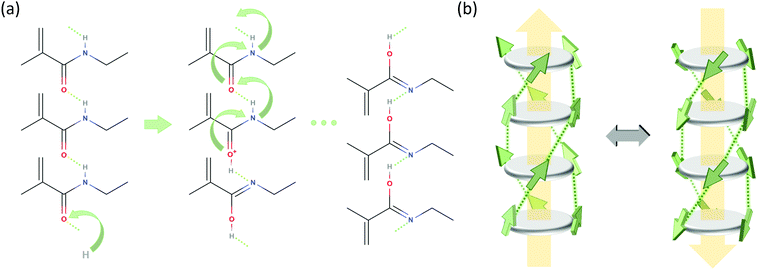 | ||
| Fig. 4 Possible polarization loss mechanisms. (a) Proton transfer mechanism, only showing the relevant part of stacked BTA molecules. Step 1 (left): proton uptake and tautomerization; step 2 (middle): intermolecular proton transfer by tunneling along the molecular stack; step 3: rotation of amide groups. (b) R-relaxation process in BTAs proposed in ref. 27. The BTA core is depicted as a dark gray disk and the amide groups as green arrows indicating the orientation of the dipole moment (side chains are omitted for clarity). Hydrogen bonds between the amide groups are shown as dotted lines and the macrodipole direction is indicated by large yellow arrows. | ||
To investigate the relevance of the proton tunneling scenario outlined above, we prepared deuterated BTA-C10d and BTA-C18d as described in the ESI,† Sections S4–S6. In terms of structural properties and phase behavior the deuterated materials are very similar to the normal protonated materials as is shown in Sections S1 and S3 of the ESI.† Also the P–E curves of deuterated BTAs are very similar to those of normal BTA as is visible in Fig. 1.
In Fig. 5 the retention behavior of all materials are compared. Focusing on the measurements without bias support – the ones with bias support will be discussed below – it is clear that deuteration has only a minor influence on the depolarization, possibly causing a minor speed-up of depolarization. As tunneling processes depend, in lowest order, exponentially on the mass of the tunneling particle, a much stronger and opposite effect would be observed in case proton tunneling was responsible for the depolarization. Hence, proton tunneling can be ruled out.
Also in case R-relaxation is responsible for the polarization loss, an effect of exchanging H with D would be expected. However, the effect of isotopic substitution on R-relaxation, which is related to hydrogen bond strength, is much smaller than the effect on a proton transfer mechanism. Due to the lower zero point energy of the N–D bond, it is slightly shorter than the N–H bond, but donor–H⋯acceptor bond lengths of deuterated hydrogen bonds tend to be longer and slightly weaker than their protonated counterparts.39 Experimental evidence of bond weakening upon deuteration will be given below.
Inspired by the strong positive effect the application of a supportive bias was found to have on the retention of blended ferroelectric–semiconductor resistive memory diodes,40 we repeated the retention experiments while applying a supportive bias of 10 V μm−1 (≪Ec) to the device during the waiting time between poling and readout. For all materials the retention is heavily affected by the supportive field, even though this field is significantly lower than the coercive field, see the open symbols in Fig. 5. Qualitatively similar effects were previously observed for both organic31 and inorganic ferroelectrics.41 For all measured materials the application of a supportive field stabilizes the polarization at longer times. This behavior is in marked contrast to that observed on the phase separated memory diodes mentioned above where the depolarization under supportive bias continues to occur, albeit at a lower rate than when the device is grounded.40 We attribute this difference to the very different depolarization mechanism in both systems: minimization of the energy associated with the stray field in non-ferroelectric domains versus R-relaxation.
The applied supportive electric field in our experiment (Fig. 5) is much larger than the depolarization field Emetald that would arise due to the finite screening length of the metal electrode.24
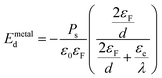 | (3) |
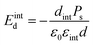 | (4) |
We also evaluate the dipole moment M* = PSV* of the typical domain, cf.eqn (2), for BTA-C10 from the fact that under a supportive field of Eapp ≈ 10 V μm−1 the equilibrium polarization is ∼70% of Pr (Fig. 5a and c). Hence, 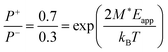 , giving M* ≈ 66 D. This corresponds to roughly 7 BTA molecules, as the dipole moment induced by three amide groups in a single BTA molecule is around 10 D.6 Moreover, using the known remnant polarization value, the typical domain volume V* ≈ 9 × 10−27 m3 was estimated, which is a reasonable estimate for a stack of ∼7 BTA molecules.
, giving M* ≈ 66 D. This corresponds to roughly 7 BTA molecules, as the dipole moment induced by three amide groups in a single BTA molecule is around 10 D.6 Moreover, using the known remnant polarization value, the typical domain volume V* ≈ 9 × 10−27 m3 was estimated, which is a reasonable estimate for a stack of ∼7 BTA molecules.
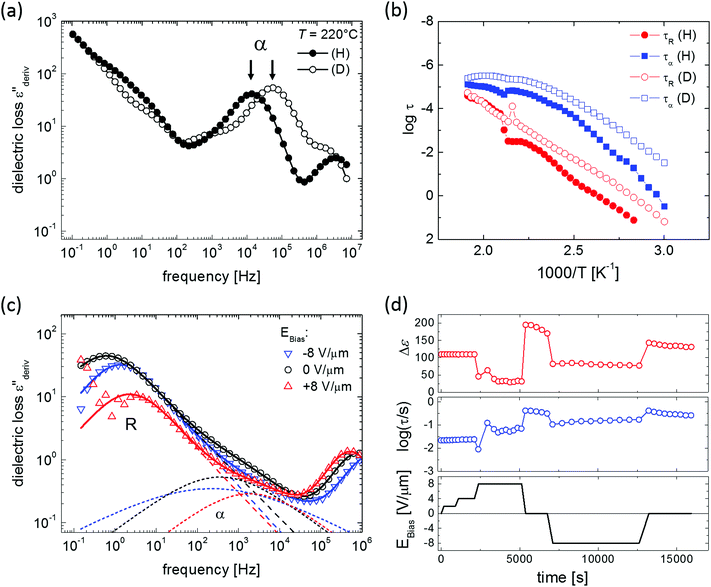
To substantiate the assignment of R-relaxation as the main culprit for polarization loss and to further rationalize the effect of supportive bias, we have investigated the effect of deuteration and a DC-bias field on the dielectric relaxations. The main results are summarized in Fig. 6.
In previous work26,27 we have discussed the α-relaxation in general terms as orientation fluctuations of short BTA stacks in an isotropic environment, which give rise to orientation polarization based on the macrodipole being collinear to the long columnar axis. In the paraelectric, i.e. isotropic phase, this process is the dominant relaxation process, the strength of which can reach remarkable values Δε ≈ 60 for BTA-C18 indicating a dipole–dipole (Kirkwood) correlation factor far above unity.42 Consequently, Δε depends on the effective normal dipole moment of the BTA unit (≈10 D, see above) as well as on the number of stacked BTA molecules. Under equilibrium conditions, the mean stack length should represent the minimum free energy state balancing the molecular interaction energy (maximizing H-bonds and other energetic contributions) with the loss in entropy as the result of column formation. Hence, by altering the strength of the H-bonds via deuteration as discussed above, we would expect a shift of the chemical equilibrium towards shorter stacks resulting in a speed-up of the rotational diffusion of the BTA stacks as manifested by the α-relaxation time.
Inspecting Fig. 6a we indeed notice a substantial shift of τα for deuterated BTA-C18 over its protonated counterpart. Considering a BTA stack as a Brownian rigid rod, we can predict a relation between the (stack) length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and its rotational diffusion time τ according to τ ∝
and its rotational diffusion time τ according to τ ∝ ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 3.43,44 Inserting τα(C18h) ≈ 4 × τα(C18d) in this relation we obtain a ratio between the columnar length of deuterated BTA-C18 over BTA-C18h in the order of
3.43,44 Inserting τα(C18h) ≈ 4 × τα(C18d) in this relation we obtain a ratio between the columnar length of deuterated BTA-C18 over BTA-C18h in the order of 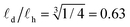 , implying that deuterated stacks are in average 1/3rd shorter than their hydrogenated counterparts. This general speed-up of the α-process persists in the whole temperature range investigated as shown in Fig. 6b.
, implying that deuterated stacks are in average 1/3rd shorter than their hydrogenated counterparts. This general speed-up of the α-process persists in the whole temperature range investigated as shown in Fig. 6b.
Interestingly, Fig. 6b also reveals an isotope effect on the R-relaxation though this effect is restricted to the ferroelectric state. In analogy to the α-relaxation, the deuterated BTA-C18 is characterized by an R-process being up to 1 decade faster. Moreover, the activation energy of BTA-C18d at about 100 kJ mol−1 is markedly lower compared to a maximum Ea ≈ 140 kJ mol−1 for BTA-C18h.
In ref. 26 we have discussed the R-relaxation as a time-dependent macro-dipole fluctuation that involves nucleation and one-dimensional diffusion of inversion defects within long columnar stacks. The elementary step for such inversion is the rotation of three amide groups of a particular BTA molecule involving the breakage and subsequent reformation of 3 or (more likely) 6 H-bonds. While under high (poling) field conditions this mechanism ultimately results in a full inversion of an entire macrodipole and thus the build-up of a macroscopic polarization, these fluctuations are present all the time and lead to thermally driven spontaneous columnar inversions and thus randomization of the initial polar order of the columnar stacks on a longer time scale.
The observed effects on the R-relaxation in BTA-C18d seem to support our physical picture. Deuteration obviously lowers the activation barrier for the elementary BTA-inversions by weakening the strength of the H-bonds. Hence both the apparent activation energy is lowered while the characteristic time-scale for column inversion is shortened. We would thus expect that the deuterated versions of the BTAs would show inferior retention properties. The results in Fig. 5 might indeed point in this direction, at least what concerns the initial part of the polarization decay.
While, as seen from Fig. 5, deuteration might have some small effect on the retention behavior, the application of a DC bias field in the order of 10 V μm−1 appears to be an effective measure to stabilize the remnant polarization to about 70–90% of its initial value. This finding is more remarkable since the supporting field is well below the coercive field strength of ∼25 V μm−1. Having just confirmed a link between the R-relaxation and the microscopic switching mechanism during poling and depolarization, we would expect a strong sensitivity of the R-relaxation to a DC bias as well.
To contest this idea, we have performed DRS-measurements using a low amplitude AC field (0.2 V μm−1) superimposed by a variable DC bias of up to 8 V μm−1 (=40 V over a sample thickness of 5 μm). The results are displayed in Fig. 6c and d showing three selected loss spectra (panel c) at 0 V μm−1, +8 V μm−1 and −8 V μm−1, as well as the time dependence bias field along with the strength Δε and the relaxation time of the R-process (panel d). The following observations can be made from Fig. 6d:
(i) While a bias field as low as 4 V μm−1 has no significant effect on the relaxation spectrum of the initially “virgin” sample, a field of 8 V μm−1 causes a dramatic decrease in the strength ΔεR of the R-process.
(ii) The reduction in ΔεR goes along with a speed-up of the R-relaxation for both positive and negative bias fields, which can be described by the approximate relation −log(τR) ∝ log(εR). The slow-down at both polarities is most clearly seen from the sign of the steps in log(τR) upon returning to zero bias.
(iii) After turning off the bias, the R-relaxation recovers its former strength and longer relaxation time, though there is a clear underlying trend towards longer relaxation times upon prolonged field-exposure.
It is particularly the correlation between the strength and the relaxation time of the R-process, which supports our physical picture about the R-process. In this view, 1D-diffusion of an inversion defect is thought responsible for the fluctuation of the macrodipole of an individual BTA-column. Here, the length of an individual BTA-stack, consisting of n BTA units, determines the maximum dipole moment that causes an approximately linear dependence of ΔεR(n) according to ΔεR ∝ nμ with μ being the dipole moment of a single BTA molecule. On the other hand, the characteristic time for inversion of such a stack should be given by the diffusion time tD over the length n × Δz, where Δz denotes the mean stacking distance. Hence we expect τR ≈ tD ∝ (nΔz)2, a relation that leads us to −log(τR) ∝ 2log(ΔεR) confirming our empirical expression above.
The effect of a strong DC field on the R-relaxation remains counterintuitive on the first sight: does the speed-up and partial suppression of the R-process mean that the average stack length shortens? This implication is highly unlikely to occur since strong DC fields are known to rather improve the columnar order as e.g. witnessed by POM. An alternative interpretation can be found by re-inspecting Fig. 6c. For all three spectra, referring to different bias conditions, we notice a clear broadening of the R-process over the “Debye” limit (=slope of unity in log–log-presentation of the dielectric loss) indicating that the R-relaxation comprises a distribution of relaxation times instead of a single-relaxation time process,45 which is consistent with the dispersive switching kinetics observed earlier.26 We think that the application of a DC bias selectively suppresses the slowest modes corresponding to the longest BTA-stack fraction by virtue of defect pinning due to the DC bias field. In other words, the defect diffusion in long BTA-stacks is modified by a field-induced asymmetric barrier that causes defect drift and defect trapping/annihilation. Consequently, the apparently up-shifted R-peak is just the remainder of the former distribution in relaxation times predominantly representing the fastest fraction of the inversion fluctuations originating from the shortest columnar fraction. As such, the size of roughly 7 BTA molecules that was found in the discussion of eqn (3) and (4) above should be regarded as a typical size of the domains that are stabilized by the field; smaller (larger) domains are less (more) stabilized and will therefore contribute more (less) to the depolarization.
Having established the mechanism underlying polarization loss and its activated nature, an evident pathway to improve retention is to operate the devices at as low temperatures as possible. In the case of BTA-C10 and BTA-C18 that would mean to operate at the lower end of the switching-friendly columnar hexagonal LC phase, i.e. around 5–15 °C and 55–75 °C, respectively, just before the crystalline phase is formed, see ESI† Section S3. In this range, any limited switchability at lower T is expected to be kinetic in nature. However, most likely due to the increasing viscosity with decreasing temperature it is generally hard to obtain any switching response below the temperatures shown in Fig. 2.26 As this article puts emphasis on elucidating the depolarization mechanism, we chose a non-extreme, but therefore still workable measurement temperature of 40–45° to prove the retention enhancement at lower temperatures. For BTA-C10 we obtained the saturated P–E-curves as shown in Fig. 7a. Note that the values for Pr (37 mC m−2) and Ec (32 V μm−1) do not deviate significantly from those in Fig. 1 and Fig. S2 (ESI†), whereas Ec is higher at lower T as it is expected for ferroelectric materials. Panel b shows the corresponding retention measurements. After 4.5 × 104 seconds, i.e. ∼12 hours still more than 50% of the polarization remains. The associated time constant τ (eqn (1)) is plotted as the rightmost point of BTA-C10 data (black circles) in Fig. 3 and fits well in the trend obtained from higher temperatures, suggesting the dominant polarization loss mechanism remains unchanged. This finding is important as it shows that the polarization retention of liquid crystalline ferroelectrics is not fundamentally limited to minutes but likely can be extended to time scales that are relevant to actual applications. The number found here is in the same ballpark range as the values for P(VDF:TrFe) and BFO and PZT thin films as discussed above.
 | ||
| Fig. 7 (a) Saturated ferroelectric polarization vs. applied field measured on BTA-C10 under quasi-static conditions (f = 1 Hz) at T = 40–45 °C. (b) Corresponding polarization retention for both polarization directions measured without supportive bias. Inset: Zoom-in on short time scale. Symbols and lines are experiments and fits to eqn (1), respectively. | ||
3 Conclusions
We have investigated the physical processes responsible for the polarization loss in the archetypical molecular ferroelectric trialkylbenzene-1,3,5-tricarboxamide (BTA). R-relaxation, which is a time-dependent macro-dipole fluctuation that involves nucleation and one-dimensional diffusion of inversion defects within long columnar stacks, was found to be the dominant mechanism. At large electric field strengths, around and above the coercive field, the R-process results in a full inversion of an entire macrodipole and thus the build-up of a macroscopic polarization; at small or zero field it leads to randomization of the polarization direction, i.e. depolarization. We have demonstrated that application of DC fields that are significantly below the coercive field suppresses the R-relaxation of the slowest modes corresponding to the longest BTA-stacks in the active layer. Concomitantly, the polarization retention time is enhanced by several orders of magnitude. The strongly activated nature of the R-relaxation process makes that the retention time (in absence of supportive bias) of the BTA-C10 compound can be increased from minutes to ∼12 hours by operating the thin-film device slightly above the crystalline to liquid crystalline phase transition temperature.4 Experimental information
BTA molecules with C10H21 and C18H37 alkyl chains (BTA-C10 and BTA-C18, respectively) were synthesized according to the procedure reported before.6,26,27Metal/ferroelectric/metal capacitor devices were prepared by spin-coating (500 rpm) of 40 mg ml−1 chloroform solution on a chemically cleaned glass substrate with patterned chromium/gold (5/70 nm) electrodes resulting in 500–700 nm thick films, as tested by a Dektak XT profilometer, followed by the deposition of the top (70 nm thick gold) electrode through a shadow mask under high vacuum conditions.26
Electrical characterization was performed by direct measurement of the switching current using a Keithley 6485 picoammeter, visualized and saved via an Agilent DSO7104A oscilloscope. An Agilent 33120a arbitrary waveform generator and a Falco WMA-300 or TReK Model PZD350A high voltage amplifier was used for input signal generation.26
Dielectric relaxation spectra were obtained using a high precision dielectric analyzer (ALPHA analyzer, Novocontrol Technologies) in combination with a Novocontrol Quatro temperature system providing control of the sample temperature with high stability of 0.05 K. BTA-filled Linkam ITO-cells with a 5 μm gap were used as samples in a parallel plate geometry. After measurement, the high frequency parasitic cell peak was partially corrected using a lumped circuit approach.26
Acknowledgements
The work of A. V. G. and X. M. was supported by the NWO Nano program. I. U. acknowledges funding by Vetenskapsrådet. The authors thank G. M. Bögels of the Eindhoven University of Technology for assistance with the GIWAXS measurements and interpretation.References
- K. Kishikawa, S. Nakahara, Y. Nishikawa, S. Kohmoto and M. Yamamoto, J. Am. Chem. Soc., 2005, 127, 2565–2571 CrossRef CAS PubMed.
- S. Horiuchi and Y. Tokura, Nat. Mater., 2008, 7, 357–366 CrossRef CAS PubMed.
- S. Horiuchi, Y. Tokunaga, G. Giovannetti, S. Picozzi, H. Itoh, R. Shimano, R. Kumai and Y. Tokura, Nature, 2010, 463, 789–792 CrossRef CAS PubMed.
- D. Miyajima, F. Araoka, H. Takezoe, J. Kim, K. Kato, M. Takata and T. Aida, Science, 2012, 336, 209–213 CrossRef CAS PubMed.
- A. S. Tayi, A. K. Shveyd, A. C.-H. Sue, J. M. Szarko, B. S. Rolczynski, D. Cao, T. J. Kennedy, A. A. Sarjeant, C. L. Stern, W. F. Paxton, W. Wu, S. K. Dey, A. C. Fahrenbach, J. R. Guest, H. Mohseni, L. X. Chen, K. L. Wang, J. F. Stoddart and S. I. Stupp, Nature, 2012, 488, 485–489 CrossRef CAS PubMed.
- C. F. C. Fitié, W. S. C. Roelofs, M. Kemerink and R. P. Sijbesma, J. Am. Chem. Soc., 2010, 132, 6892–6893 CrossRef PubMed.
- A. S. Tayi, A. Kaeser, M. Matsumoto, T. Aida and S. I. Stupp, Nat. Chem., 2015, 7, 281–294 CrossRef CAS PubMed.
- J. Guilleme, E. Cavero, T. Sierra, J. Ortega, C. L. Folcia, J. Etxebarria, T. Torres and D. González-Rodríguez, Adv. Mater., 2015, 27, 4280–4284 CrossRef CAS PubMed.
- I. Katsouras, K. Asadi, M. Li, T. B. van Driel, K. S. Kjær, D. Zhao, T. Lenz, Y. Gu, P. W. M. Blom, D. Damjanovic, M. M. Nielsen and D. M. de Leeuw, Nat. Mater., 2016, 15, 78–84 CrossRef CAS PubMed.
- M. Li, H. J. Wondergem, M.-J. Spijkman, K. Asadi, I. Katsouras, P. W. M. Blom and D. M. de Leeuw, Nat. Mater., 2013, 12, 433–438 CrossRef CAS PubMed.
- X. J. Lou, J. Appl. Phys., 2009, 105, 94107 CrossRef.
- T. Akutagawa, H. Koshinaka, D. Sato, S. Takeda, S.-I. Noro, H. Takahashi, R. Kumai, Y. Tokura and T. Nakamura, Nat. Mater., 2009, 8, 342–347 CrossRef CAS PubMed.
- S. Kang, X. Li, S. Kawauchi, M. Tokita and J. Watanabe, Mol. Cryst. Liq. Cryst., 2011, 549, 184–193 CrossRef CAS.
- G. Dantlgraber, A. Eremin, S. Diele, A. Hauser, H. Kresse, G. Pelzl and C. Tschierske, Angew. Chem., Int. Ed., 2002, 41, 2408–2412 CrossRef CAS PubMed.
- D. Krüerke, P. Rudquist, S. T. Lagerwall, H. Sawade and G. Heppke, Ferroelectrics, 2000, 243, 207–220 CrossRef.
- S. Horiuchi, F. Ishii, R. Kumai, Y. Okimoto, H. Tachibana, N. Nagaosa and Y. Tokura, Nat. Mater., 2005, 4, 163–166 CrossRef CAS PubMed.
- F. Kagawa, S. Horiuchi, N. Minami, S. Ishibashi, K. Kobayashi, R. Kumai, Y. Murakami and Y. Tokura, Nano Lett., 2014, 14, 239–243 CrossRef CAS PubMed.
- D.-W. Fu, W. Zhang, H.-L. Cai, Y. Zhang, J.-Z. Ge, R.-G. Xiong and S. D. Huang, J. Am. Chem. Soc., 2011, 133, 12780–12786 CrossRef CAS PubMed.
- Y. Okada, S. Matsumoto, Y. Takanishi, K. Ishikawa, S. Nakahara, K. Kishikawa and H. Takezoe, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 20701 CrossRef PubMed.
- I. G. Jenkins, T. K. Song, S. Madhukar, A. S. Prakash, S. Aggarwal and R. Ramesh, Appl. Phys. Lett., 1998, 72, 3300–3302 CrossRef CAS.
- Z. G. Zhang, Y. N. Wang, J. S. Zhu, F. Yan, X. M. Lu, H. M. Shen and J. S. Liu, Appl. Phys. Lett., 1998, 73, 3674–3676 CrossRef CAS.
- M. Vopsaroiu, J. Blackburn, M. G. Cain and P. M. Weaver, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 24109 CrossRef.
- J. M. Benedetto, R. A. Moore and F. B. McLean, J. Appl. Phys., 1994, 75, 460–466 CrossRef CAS.
- R. R. Mehta, B. D. Silverman and J. T. Jacobs, J. Appl. Phys., 1973, 44, 3379–3385 CrossRef CAS.
- C. T. Black, C. Farrell and T. J. Licata, Appl. Phys. Lett., 1997, 71, 2041–2043 CrossRef CAS.
- A. V. Gorbunov, T. Putzeys, I. Urbanavičiūtė, R. A. J. Janssen, M. Wübbenhorst, R. P. Sijbesma and M. Kemerink, Phys. Chem. Chem. Phys., 2016, 18, 23663–23672 RSC.
- C. F. C. Fitié, W. S. C. Roelofs, P. C. M. M. Magusin, M. Wübbenhorst, M. Kemerink and R. P. Sijbesma, J. Phys. Chem. B, 2012, 116, 3928–3937 CrossRef PubMed.
- Y.-J. Yu and A. J. H. McGaughey, J. Chem. Phys., 2016, 144, 14901 CrossRef PubMed.
- T. Furukawa, T. Nakajima and Y. Takahashi, IEEE Trans. Dielectr. Electr. Insul., 2006, 13, 1120–1131 CAS.
- M. Mai, B. Martin and H. Kliem, J. Appl. Phys., 2011, 110, 64101 CrossRef.
- R. C. G. Naber, B. de Boer, P. W. M. Blom and D. M. de Leeuw, Appl. Phys. Lett., 2005, 87, 203509 CrossRef.
- G. H. Gelinck, A. W. Marsman, F. J. Touwslager, S. Setayesh, D. M. de Leeuw, R. C. G. Naber and P. W. M. Blom, Appl. Phys. Lett., 2005, 87, 92903 CrossRef.
- Y. Nomura, K. Nomura, K. Kinoshita, T. Kawae and A. Morimoto, Phys. Status Solidi RRL, 2014, 8, 536–539 CrossRef CAS.
- Y. Nomura, T. Tachi, T. Kawae and A. Morimoto, Phys. Status Solidi B, 2015, 252, 833–838 CrossRef CAS.
- D. Prevosto, S. Capaccioli, M. Lucchesi, S. Sharifi, K. Kessairi and K. L. Ngai, Philos. Mag., 2008, 88, 4063–4069 CrossRef CAS.
- S. Horiuchi, R. Kumai and Y. Tokura, Angew. Chem., Int. Ed., 2007, 46, 3497–3501 CrossRef CAS PubMed.
- Z. Gan, X. Wu, X. Zhu and J. Shen, Angew. Chem., Int. Ed., 2013, 52, 2055–2059 CrossRef CAS PubMed.
- J. C. Hargis, E. Vöhringer-Martinez, H. L. Woodcock, A. Toro-Labbé and H. F. Schaefer, J. Phys. Chem. A, 2011, 115, 2650–2657 CrossRef CAS PubMed.
- L. Sobczyk, M. Obrzud and A. Filarowski, Molecules, 2013, 18, 4467–4476 CrossRef CAS PubMed.
- V. Khikhlovskyi, A. J. J. M. van Breemen, R. A. J. Janssen, G. H. Gelinck and M. Kemerink, Org. Electron., 2016, 31, 56–62 CrossRef CAS.
- A. Q. Jiang, C. Wang, K. J. Jin, X. B. Liu, J. F. Scott, C. S. Hwang, T. A. Tang, H. B. Lu and G. Z. Yang, Adv. Mater., 2011, 23, 1277–1281 CrossRef CAS PubMed.
- J. G. Kirkwood, J. Chem. Phys., 1939, 7, 911–919 CrossRef CAS.
- S. Broersma, J. Chem. Phys., 1960, 32, 1626 CrossRef CAS.
- O. van den Berg, M. Wübbenhorst, S. J. Picken and W. F. Jager, J. Non-Cryst. Solids, 2005, 351, 2694–2702 CrossRef CAS.
- M. Wübbenhorst and J. van Turnhout, J. Non-Cryst. Solids, 2002, 305, 40–49 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp08015d |
| This journal is © the Owner Societies 2017 |