Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Polarization independence of laser-induced nucleation in supersaturated aqueous urea solutions†
Yao
Liu
,
Martin R.
Ward
and
Andrew J.
Alexander
 *
*
School of Chemistry, University of Edinburgh, David Brewster Road, Edinburgh, Scotland EH9 3FJ, UK. E-mail: andrew.alexander@ed.ac.uk
First published on 10th January 2017
Abstract
In a seminal report on laser-induced nucleation in aqueous supersaturated solutions (Phys. Rev. Lett., 1996, 77, 3475) it was noted that needle-shaped crystals of urea were aligned with the direction of the electric field of the linearly polarized laser pulse. The results gave rise to a new mechanism for control of crystal nucleation involving alignment of solute molecules (optical Kerr effect) now commonly known as non-photochemical laser-induced nucleation (NPLIN). Recent theoretical and experimental work has cast doubts on the optical Kerr effect mechanism. In the present letter we present results from digital imaging of urea-crystal growth immediately following laser-induced nucleation. Analysis of the data shows no statistically significant correlation between crystal angle and direction of linear polarization. The results overturn a long-held result that has shaped theoretical and experimental studies of NPLIN.
Introduction
Nucleation is of fundamental scientific interest and has significant economic value. It occurs throughout nature, e.g., in biomineralization, and is used in the production of high-value solid materials, such as pharmaceuticals. A number of methods for inducing nucleation by external perturbations have been employed, for example, electric fields, mechanical shock and ultrasound.1–3 Laser-induced nucleation is a relatively unexplored technique that offers advantages to localizing—temporally and spatially—the point of nucleation.4,5 Such control opens up avenues, e.g., to study of the dynamics of nucleation or to control product homogeneity during manufacture of solids.The discovery of non-photochemical laser-induced nucleation (NPLIN) happened by chance, while Garetz et al. had been looking for second-harmonic generation in aqueous solutions of urea.6 They observed nucleation of needle-shaped crystals in supersaturated solutions exposed to pulses of unfocussed, near-infrared laser light (1064 nm, ∼20 ns pulse-width, ∼2 mm2 beam profile, 100–200 pulses at energies of ∼100 mJ pulse−1). There are no absorption bands for urea at this wavelength, and multiphoton absorption was discounted due to the relatively low power densities used. Heating of the water (by absorption through weak vibrational overtones) was also considered to be negligible, and if anything, ought to inhibit nucleation by reducing supersaturation. The term non-photochemical was introduced to distinguish the effect from nucleation arising from condensation or aggregation due to photochemistry.7–9
Possibly the most significant observation on NPLIN was the correlation between the plane of linear polarization of the light and the direction of the initial urea crystals. To quote Garetz et al.: “When the laser was vertically polarized, the initial crystallite was observed to be oriented approximately vertically (to within ∼5°). When the laser was horizontally polarized, the initial crystallite was oriented approximately horizontally. These correlations were consistently observed for 12.0, 12.5, and 13.0 M solutions” (the concentration of saturated solution was 10.5 M).6 The correlation between crystal axis and polarization of light was strong evidence that NPLIN was a new nucleation phenomenon. The mechanism proposed for NPLIN was based on the optical Kerr effect (OKE), where the most-polarizable axis of the molecule tends to align with the direction of the oscillating electric field of the light. In urea, the direction of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond is the most-polarizable axis; in the crystal these bonds lie along the [001] direction, which is parallel to the needle axis. In a follow-up study on aqueous supersaturated glycine it was found that the product polymorph could be controlled, with circularly polarized light producing α-glycine and linearly polarized light producing γ-glycine.10 It was later noted that complete binary control between the two polymorphs occurred only within a small window of supersaturation (146–155%).11 The influence of the polarization of light on product crystal polymorph through NPLIN has been observed for glycine,10L-histidine,12 carbamazepine,13 and sulfathiazole.14
O bond is the most-polarizable axis; in the crystal these bonds lie along the [001] direction, which is parallel to the needle axis. In a follow-up study on aqueous supersaturated glycine it was found that the product polymorph could be controlled, with circularly polarized light producing α-glycine and linearly polarized light producing γ-glycine.10 It was later noted that complete binary control between the two polymorphs occurred only within a small window of supersaturation (146–155%).11 The influence of the polarization of light on product crystal polymorph through NPLIN has been observed for glycine,10L-histidine,12 carbamazepine,13 and sulfathiazole.14
Several reports have questioned the feasibility of the OKE mechanism for NPLIN. Theoretical considerations indicate that the field strengths involved are too small to align solute molecules sufficiently, even including co-operative effects in solute clusters.15,16 Alternative mechanisms have been put forward.17 Recent experimental results have pointed towards a mechanism based on heating of trace impurity nanoparticles.18,19 Since the observation of alignment of urea needles along the electric field of the light is central to understanding the mechanism, we have carried out digital imaging of crystal growth during NPLIN of urea.
Experimental methods
Urea was obtained from Sigma Aldrich (Sigma Aldrich U5128, 99.0–100.5%) and used without further purification. The solubility of urea (molality) in water at 25 °C is Csat = 20.1 mol kg−1.20 Garetz et al. used sample concentrations 11.5–13.0 M (molarity), but it should be noted that molarity depends on the density of the final solution. From tabulated data we estimate that C = 30.2 mol kg−1 (S = C/Csat = 1.5) corresponds to the 12.5 M solutions.21 Supersaturated (S = 1.5) aqueous solutions were prepared by dissolving solid urea in ultrapure water (18.2 MΩ cm). Screw-cap glass sample vials (11.7 mm diameter) were cleaned with detergent and rinsed several times, the final rising with filtered water [0.22 μm, Millex GP, poly(ether sulfone) membrane]. To ensure equal treatment, all sample vials were prepared and then recrystallized by transferring to a fridge for one day to induce spontaneous nucleation. Supersaturated samples were regenerated by heating in an oven at 50 °C for two days, and the dissolved samples were transferred to another oven with temperature of 25 °C for two day before use.The laser setup is similar to that described previously.4 The light used was obtained from a Q-switched Nd3+:YAG laser: either the second harmonic (532 nm, Continuum Surelite II-10, 5.0 ns pulses) or the fundamental (1064 nm, Quantel Brilliant, 5.6 ns pulses). The pulse repetition rate was 10 Hz. The beam was passed through a Glan-laser polarizer to control the transmitted power and to ensure purity of the linear polarization. The beam was passed through a half-wave plate to set the angle of laser polarization with respect to the vertical direction. A Galilean telescope was used to reduce the beam width, giving final diameters of 4.8 mm (532 nm) or 2.5 mm (1064 nm). The formation of crystals was recorded using a camera (AVT, Stingray F033B) protected by a glass filter (Comar Optics, OG570 or BG39 glass). Each vial was exposed to laser pulses for up to 30 s to induce nucleation; the laser pulses were blocked immediately following nucleation. The vial acts as a cylindrical lens, loosely focusing the beam in the horizontal plane. The refractive index of the solution was estimated to be 1.43.21 The peak power density (jpeak) was calculated using the area of the beam at the exit of vial. The mean incident laser powers were 0.75 W (532 nm) or 0.31 W (1064 nm), giving peak power densities at the exit of the vials of 200 MW cm−2 or 270 MW cm−2, respectively: comparable to those employed by Garetz et al.6,22
Results and discussion
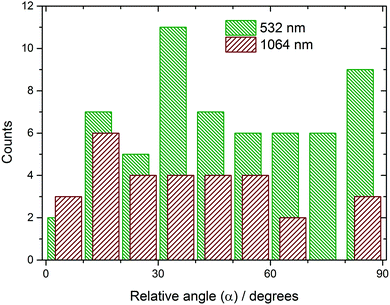
Samples that nucleated showed the quick growth of at least one needle-shaped crystallite (Fig. 1), which eventually became a network of needles. The angle (α) between the direction of the electric field of the light and the projection of the initial needle-shaped crystal on the plane of the image (as observed looking along the direction of the beam) was measured from video frames using ImageJ software.23 It should be noted that α is not the angle between the electric field and the crystal needle axis, but is sufficient to test the correlation noted by Garetz et al. The total number of samples nucleated was 59 at 532 nm and 36 at 1064 nm, respectively. A histogram showing the distribution of the projected angle of the crystal relative to the direction of polarization is shown in Fig. 2 (a scatter plot is given in the ESI†). The mean relative angle and standard deviation are given in Table 1. The correlation between the directions appears to be quite random, at both wavelengths.| Wavelength/nm | Number of samples (n) | Mean relative angle (![[small alpha, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c2.gif) )/deg. )/deg. |
Standard deviation of angle (s)/deg. | KS-test statistic (D) | KS-test critical value (D*) |
|---|---|---|---|---|---|
| 532 | 59 | 48.6 | 24.2 | 0.119 | 0.174 |
| 1064 | 30 | 37.8 | 24.1 | 0.176 | 0.242 |
To determine if there was a statistically significant correlation in the data, a Kolmogorov–Smirnov (KS) test was performed.24 The data are first arranged in a sequence in increasing numerical order. The KS test compares the cumulative distribution function Fo(α) of the measurements to a continuous model distribution Fe(α). For a sequence of uniformly random angles, we would expect a straight-line model distribution, Fe(α) = α/(90°). The null hypothesis (H0) was that there was no correlation between laser polarization and crystal direction, i.e., H0: Fo(α) = Fe(α) for all angles. The alternative hypothesis H1: Fo(α) ≠ Fe(α) for some angles. In order to decide whether the difference between Fo(α) and Fe(α) was significant, we calculated the D statistic, which is the maximum deviation between the distributions:
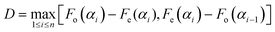 | (1) |
There is no simple explanation for the discrepancy between the original report on urea and the present work. The measurements presented in the original report were quasi-quantitative, with only two polarizations (vertical and horizontal) mentioned. Since the observations were apparently made by eye, it is possible that some delay between nucleation and observation of a sufficiently large needle gave the impression of alignment. Rotation of a growing crystal may be influenced by sedimentation or by convection of the surrounding fluid, which tends to flow toward the crystal.
Apart from NPLIN of urea, Sun et al. reported on alignment of a liquid crystal during cooling through a phase transition.25 It is difficult to draw comparisons to the present experiments, because of significant differences in the experimental setup. Differences include the use of shorter laser pulses (45 ps), exposure to thousands of pulses over an hour of cooling, and the presence of directing polymer surfaces. For some other small-molecule systems, the ellipticity of polarization appears to influence the polymorph obtained.11–14 In the case of glycine, we note that results from different groups do not agree on the fraction of γ-glycine obtained at different supersaturations.11,26,27 However, this may be due to different experimental conditions. In the work of Clair et al. the beam passed through both glass–solution and air–solution interface,26 whereas in other studies the beam passed only glass–solution interfaces.11,27
Studies on NPLIN of carbon dioxide bubbles and on filtration of solutions have suggested that transient heating of an impurity nanoparticle can cause rapid expansion and collapse of a vapor bubble, which triggers nucleation.18,19,27,28 The heating mechanism satisfies several observations that the OKE mechanism does not, including the existence of a distinct laser-power threshold, and the fact that some substances do not exhibit NPLIN despite being likely candidates.19 Absorption and heating would be expected to show little effect of polarization on direction of product nucleation, although further experiments are required to study this systematically.
In summary, the present work has demonstrated that nascent needle-shaped crystals of urea are not aligned with the direction of the electric field as a result of NPLIN. Further experimental and theoretical effort is required to understand the mechanisms underlying laser-induced nucleation.
Acknowledgements
Data employed in this study are available via the Edinburgh DataShare repository (DOI: 10.7488/ds/1692). We acknowledge funding from the Engineering and Physical Sciences Research Council (EP/I033459/1 and EP/L022397/1) and the EPSRC Center for Innovative Manufacturing in Continuous Manufacturing and Crystallisation (http://www.cmac.ac.uk).References
- J. W. Mullin, Crystallization, Butterworth-Heinemann, Oxford, 4th edn, 2001 Search PubMed.
- G. Ruecroft, D. Hipkiss, T. Ly, N. Maxted and P. W. Cains, Org. Process Res. Dev., 2005, 9, 923–932 CrossRef CAS.
- E. Revalor, Z. Hammadi, J.-P. Astier, R. Grossier, E. Garcia, C. Hoff, K. Furuta, T. Okustu, R. Morin and S. Veesler, J. Cryst. Growth, 2010, 312, 939–946 CrossRef CAS.
- A. J. Alexander and P. J. Camp, Cryst. Growth Des., 2009, 9, 958–963 CAS.
- C. Duffus, P. J. Camp and A. J. Alexander, J. Am. Chem. Soc., 2009, 131, 11676–11677 CrossRef CAS PubMed.
- B. A. Garetz, J. E. Aber, N. L. Goddard, R. G. Young and A. S. Myerson, Phys. Rev. Lett., 1996, 77, 3475–3476 CrossRef CAS PubMed.
- H. Adachi, K. Takano, Y. Hosokawa, T. Inoue, Y. Mori, H. Matsumura, M. Yoshimura, Y. Tsunaka, M. Morikawa, S. Kanaya, H. Masuhara, Y. Kai and T. Sasaki, Jpn. J. Appl. Phys., 2003, 42, L798–L800 CrossRef CAS.
- N. Nakashima, H. Inoue, M. Sumitani and K. Yoshihara, J. Chem. Phys., 1980, 73, 4693–4694 CrossRef CAS.
- T. Okutsu, K. Furuta, M. Terao, H. Hiratsuka, A. Yamano, N. Ferté and S. Veesler, Cryst. Growth Des., 2005, 5, 1393–1398 CAS.
- B. A. Garetz, J. Matic and A. S. Myerson, Phys. Rev. Lett., 2002, 89, 177501 CrossRef PubMed.
- X. Y. Sun, B. A. Garetz and A. S. Myerson, Cryst. Growth Des., 2006, 6, 684–689 CAS.
- X. Sun, B. A. Garetz and A. S. Myerson, Cryst. Growth Des., 2008, 8, 1720–1722 CAS.
- A. Ikni, B. Clair, P. Scouflaire, S. Veesler, J. M. Gillet, N. El Hassan, F. Dumas and A. Spasojević-deBiré, Cryst. Growth Des., 2014, 14, 3286–3299 CAS.
- W. Li, A. Ikni, P. Scouflaire, X. Shi, N. El Hassan, P. Gémeiner, J.-M. Gillet and A. Spasojević-deBiré, Cryst. Growth Des., 2016, 16, 2514–2526 CAS.
- V. Agarwal and B. Peters, Adv. Chem. Phys., 2014, 155, 97–160 CrossRef CAS.
- B. C. Knott, M. F. Doherty and B. Peters, J. Chem. Phys., 2011, 134, 154501 CrossRef PubMed.
- M. Nardone and V. G. Karpov, Phys. Chem. Chem. Phys., 2012, 14, 13601–13611 RSC.
- M. R. Ward, W. J. Jamieson, C. A. Leckey and A. J. Alexander, J. Chem. Phys., 2015, 142, 144501 CrossRef PubMed.
- M. R. Ward, A. M. Mackenzie and A. J. Alexander, Cryst. Growth Des., 2016, 16, 6790–6796 CAS.
- A. Seidell, Solubilities of Organic Compounds, D. Van Nostrand Company, Inc., New York, 3rd edn, 1941 Search PubMed.
- CRC Handbook of Chemistry and Physics, ed. D. Lide, 86th edn, CRC Press, Boca Raton, FL, 2005 Search PubMed.
- J. Matic, X. Sun, B. A. Garetz and A. S. Myerson, Cryst. Growth Des., 2005, 5, 1565–1567 CAS.
- C. A. Schneider, W. S. Rasband and K. W. Eliceiri, Nat. Methods, 2012, 9, 671–675 CrossRef CAS PubMed.
- D. J. Sheskin, Handbook of Parametric and Nonparametric Statistical Procedures, CRC Press, Boca Raton, FL, 5th edn, 2011 Search PubMed.
- X. Y. Sun, B. A. Garetz, M. F. Moreira and P. Palffy-Muhoray, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 021710 Search PubMed.
- B. Clair, A. Ikni, W. Li, P. Scouflaire, V. Quemener and A. Spasojević-de Biré, J. Appl. Crystallogr., 2014, 47, 1252–1260 CAS.
- N. Javid, T. Kendall, I. S. Burns and J. Sefcik, Cryst. Growth Des., 2016, 16, 4196–4202 CAS.
- B. C. Knott, J. L. LaRue, A. M. Wodtke, M. F. Doherty and B. Peters, J. Chem. Phys., 2011, 134, 171102 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp07997k |
| This journal is © the Owner Societies 2017 |