Solvent effects on ligand binding to a serine protease

Abstract

Solvation plays an important role in virtually all biomolecular recognition and binding processes. However, the consequences of changes in solvation conditions often remain elusive. In this work, we combined isothermal titration calorimetry (ITC) and molecular dynamics (MD) simulations to investigate the effect of solvent composition on the thermodynamics of protein–ligand binding. We studied the binding of p-aminobenzamidine (PAB) to trypsin in various water/methanol mixtures as a model system for a biomolecular complex. Our ITC experiments show that the free energy of binding changes only very modestly with methanol concentration, and that this small change is due to strong enthalpy–entropy compensation. The MD and free energy simulations not only reproduce the experimental binding free energies, but also provide atomic-level insights into the mechanisms behind the thermodynamic observations. The more favorable binding enthalpy at increased methanol concentrations (when compared to pure water) is attributed to stronger protein–ligand and intramolecular protein–protein interactions. The stronger protein–ligand interaction is linked to a small-scale conformational rearrangement of the L2 binding pocket loop, which senses the solvent environment. Remarkably, the stronger interactions do not substantially reduce the configurational entropy of the protein. Instead, the more disfavorable entropy contribution to the binding free energy at increased methanol concentrations is due to the desolvation of the ligand from the bulk, which is more favorable in pure aqueous solution than in the presence of methanol. Our work thus underpins the importance of including conformational flexibility, even for an overall rather rigid complex, since even small-amplitude motions can significantly alter the binding energetics. Furthermore, the ability of our combined ITC/MD approach to assign different thermodynamic contributions to distinct conformational states might contribute to an enhanced understanding of biomolecular binding processes in general.

---

1 Introduction

Molecular recognition events take place in aqueous solution and are thus susceptible to be affected by changes of solvation conditions.^1–3 Water is an important participant in virtually all biomolecular processes and plays a crucial role in hydrophobic association^4,5 and in mediating specific interactions between the binding partners;^6–10 the latter often involves positionally ordered water molecules that form hydrogen bonds. In any case, there can be sizable solvent contributions to the thermodynamics of the binding process. However, despite this importance, the thermodynamic implications of solvation effects remain elusive in many cases, not only in terms of the overall free energy but especially also in terms of the decomposition into enthalpy and entropy. For example, while the conventional view of hydrophobic association is that it is entropy-driven, Baron and co-workers recently found that binding of a spherical model hydrophobe to a concave hydrophobic cavity in water is driven by enthalpy and opposed by entropy.^11,12 This mechanism has been controversially discussed, though.^13,14 Along the same lines, Englert and co-workers¹⁵ reported that displacing a few disordered water molecules from a hydrophobic pocket in the protein thermolysin upon phosphonamidate binding is dominated by enthalpy. Snyder and co-workers¹⁶ reported an enthalpy-driven signal with growing hydrophobic surface of heterocyclic sulfonamides that bind to carbonic anhydrase. Another recent study¹⁷ showed how variations in the shape and polarity of a model hydrophobic pocket influence the magnitude of enthalpy and entropy changes upon water displacement. Confinement of localized, structured water molecules that are forming hydrogen bonds is expected to have an entropically unfavorable contribution,¹⁸ and binding free energy should thus benefit from an entropy gain upon release of such bound water molecules.^19–21 However, it has also been reported that such displacement can reduce binding affinity.^22–24 These examples illustrate that the current picture is rather heterogeneous and that the actual thermodynamic signatures can be very system specific. Detailed interpretations of the underlying driving forces are thus highly non-trivial, underlining the importance of developing theoretical methods to describe solvation effects.^25–40

In many experiments, some form of enthalpy–entropy (H/S) compensation has been reported and used to explain the observed partitioning of the free energy into enthalpic and entropic components.^16,41–53H/S compensation has even been invoked as a general principle,⁴¹ as it seems to play a role for many different processes, ranging from partitioning of small molecules between polar and apolar phases to protein folding/unfolding and protein–protein as well as protein–ligand binding.⁵⁴ However, the existence of this phenomenon has also been controversially discussed.^54–56 Since it can frustrate lead optimization,^57,58H/S compensation has been widely discussed in the context of protein–ligand binding, with some recent studies focusing on the implications of displacing localized water molecules.^59–61 In essentially all cases, unraveling the atomic-level mechanisms behind the observed thermodynamic signatures remains a formidable challenge.

To our knowledge, the effect of solvent composition on protein–ligand binding, and in particular on putative H/S compensation, remains largely unexplored. We hypothesize that solvent composition could have a pronounced influence on binding thermodynamics. In principle, changes in solvation can affect both the bound state (i.e., the protein–ligand complex) as well as the unbound state (i.e., the state in which protein and ligand are dissociated and individually solvated). However, in particular for rigid complexes in which neither of the binding partners undergoes large structural changes, the unbound state is presumably even more susceptible to changes in solvation conditions, because both the solvation of the empty binding pocket of the apo protein and the solvation of the unbound ligand could be affected, and both need to be – at least partially – desolvated upon binding.

To test these ideas, we combined isothermal titration calorimetry (ITC) and molecular dynamics (MD) simulations to study binding of the p-aminobenzamidine (PAB) cation to trypsin in various water/methanol mixtures, ranging from pure aqueous solution up to 30% (v/v) methanol. The trypsin–PAB complex was chosen as a model system for a rather rigid protein–ligand complex. Trypsin and other serine proteases, such as thrombin, plasmin, and factor Xa, can be efficiently inhibited by high affinity benzamidine-based ligands, and several high-resolution X-ray crystal structures are available.^62,63 Consequently, they were widely used as model systems for studying binding with different computational methods.^64–73 Our ITC experiments of trypsin–PAB binding show that the free energy of binding changes only very modestly with methanol concentration, and that this small change is indeed due to strong H/S compensation: a more negative (favorable) binding enthalpy at higher methanol concentration is almost completely offset by counteracting changes in entropy. Extensive MD and free energy simulations not only reproduce the experimental binding free energies, but also provide the missing atomic scale insights into the molecular driving forces and mechanisms behind the thermodynamic signatures.

The article is organized as follows. After describing the experimental and computational methods, we report the thermodynamics of PAB binding to trypsin obtained from experiments, including the dissection of the binding free energy into its enthalpic and entropic contributions. Then, we discuss the binding free energies obtained from our MD simulations. Subsequently, we present a detailed analysis of the simulations in terms of the atomic-level details behind the observed thermodynamic signatures with a special emphasis on H/S compensation. We conclude with a brief Summary and conclusions section.

2 Methods

2.1 Experiments

Materials. Bovine pancreatic trypsin, p-aminobenzamidine (PAB) and methanol were purchased from Sigma. The ligand and methanol were of the highest purity available. All other chemicals used were of reagent grade. For every experiment the buffer was freshly prepared and degassed before adding methanol. The experiments were carried out in two different buffers; either 50 mmol l⁻¹ Hepes pH 8.0, or 50 mmol l⁻¹ Tris pH 8.0, and 150 mmol l⁻¹ NaCl, 10 mmol l⁻¹ CaCl₂, and different fractions of methanol, ranging from 0% to 30% v/v. The ligand was directly dissolved in the buffer and the concentrations were determined by UV-spectroscopy at 294 nm using a molar absorption coefficient⁷⁴ of 17 010 mol l⁻¹ cm⁻¹. Trypsin was dissolved in buffer without methanol and purified by size exclusion chromatography with a Superdex 75 26/60 (GE Healthcare). By buffer exchange with a Zeba Spin Desalting Column (Thermo Scientific) trypsin was transferred into the appropriate buffer for the titration experiments. Concentration of the trypsin solution was determined by UV spectroscopy at 280 nm using a molar absorption coefficient of 37 000 mol l⁻¹ cm⁻¹ and a molecular weight of 23.8 kDa.^75,76

Isothermal titration calorimetry. The thermodynamic parameters of the complex formation of trypsin and p-aminobenzamidine (PAB) in different water/methanol mixtures were determined by isothermal titration calorimetry (ITC). Titration experiments were performed using a MicroCal Auto-ITC₂₀₀ (GE Healthcare). The syringe was loaded with a 2.5 mmol l⁻¹ solution of the ligand and the sample cell was loaded with 200 μl of a 250 μmol l⁻¹ trypsin solution or with pure buffer for a reference measurement. The titration experiments were performed at 25 °C and started with an initial injection of 0.5 μl, followed by 25 injections of 1.5 μl into the stirred cell. Blank titration of ligand into buffer was subtracted from the trypsin–ligand titrations to correct dilution and mixing effects. Data were analyzed using Origin software (Microcal Inc.). By fitting a single-site binding model the binding enthalpy ΔH_bind and the binding constant K_a (and the according free energy of binding, ΔG_bind = −k_BT ln K_a) were determined.⁷⁷ From these, the entropy of binding was calculated, −TΔS_bind = ΔG_bind − ΔH_bind. Every measurement was repeated at least three times (Fig. S1, ESI†). K_a and ΔH_bind were reproducible to within 3% and the errors in ΔS_bind were within 10%.

Fluorescence titration. As an independent check for our ITC results, we determined ΔG_bind by fluorescence titration using PAB as a fluorescent probe.⁷⁸ Trypsin and PAB stock solutions and buffers were prepared as described in the ITC section. The titration experiments were carried out in a fluorescence spectrometer (Perkin Elmer) at an excitation wavelength of 320 nm. PAB concentration was kept constant (1 μM) and the emission between 340 nm and 400 nm (maximum at 360 nm) was detected at different trypsin concentrations. For the intrinsic fluorescence of trypsin, the measurements were repeated without PAB. The binding free energy was calculated from the dissociation constant, K_d = 1/K_a, obtained from a hyperbolic fit to the fluorescence intensities at various trypsin concentrations (Fig. S2, ESI†).

2.2 Computations

Molecular dynamics simulations. The starting structure for the simulations was based on an X-ray crystal structure of the trypsin–benzamidine complex (PDB:3PTB).⁶² The p-aminobenzamidine (PAB) ligand was placed into the binding site by replacing the p-hydrogen with an NH₂ group. The protonation states of titratable groups were assigned with the PROPKA program.^79,80 For the catalytic triad residue His57, the N_δ1 tautomer was chosen to enable the formation of hydrogen bonds with Asp102 and Ser195. All crystallographic waters were retained in the starting structure used for MD simulations.

For PAB, the generalized amber force field (GAFF)⁸¹ was used. The atomic partial charges were determined with the RESP method⁸² from a fit to the electrostatic potential of PAB in vacuum, which was obtained from a B3LYP/6-31+G(d) calculation with the Merz–Singh–Kollman scheme. The Lennard-Jones (6,12) parameters were assigned based on the corresponding atom types in the GAFF force field. The non-bonded parameters of PAB are shown in Fig. S3 of the ESI.†

All simulations were carried out with GROMACS, version 5.0.6.⁸³ The Amber99sb-ILDN force field was used for the protein.^84,85 Water was represented using the TIP3P model.⁸⁶ For methanol, a GAFF-based generic organic solvents force field⁸⁷ was used. The density and static dielectric constant of binary water/methanol mixtures at room temperature reproduce the experimental trends (Fig. S4, ESI†). All MD simulations were carried out in cubic boxes using periodic boundary conditions. NaCl counter-ions were added at a concentration of ca. 150 mM to neutralize the net charge of the simulation box. All systems were simulated in the NpT ensemble at a temperature of 298 K and 1 bar pressure, using a leap-frog integrator to integrate the equations of motion with a 2 fs time step. Temperature was controlled with a velocity rescaling thermostat (τ_T = 0.1 ps),⁸⁸ and pressure with a Berendsen barostat (τ_p = 0.5 ps, compressibility 4.5 × 10⁻⁵ bar⁻¹).⁸⁹ Short-range Lennard-Jones and electrostatic interactions were calculated within a 1.0 nm cutoff. The Verlet buffered pair list scheme⁹⁰ was used. Analytical corrections to the pressure and potential energy were applied to compensate for the truncation of the Lennard-Jones interactions. Long-range electrostatic interactions were treated with the smooth particle-mesh Ewald (PME) method⁹¹ using cubic spline interpolation and a grid spacing of 0.12 nm. The SETTLE algorithm⁹² was used to constrain the bonds and angles of the water molecules, and LINCS⁹³ for all other bonds, applying four iterations to correct for rotational bond lengthening. All systems were equilibrated with a protocol consisting of an initial energy minimization (1000 steps steepest descent), 200 ps NVT runs with harmonic position restraints (force constant 1000 kJ mol⁻¹ nm⁻²) on all protein heavy atoms at 200 K and 298 K, respectively, followed by a 200 ps NpT simulation at 298 K during which the position restraints were still applied. Finally, the position restraints were switched off, and production MD simulations were carried out for the trypsin–PAB complex, apo trypsin, and free PAB in solution. Simulations were carried out at different solvation conditions, varying from pure water to 10%, 20%, and 30% (v/v) methanol (Table S1, ESI†). The total accumulated sampling time of these equilibrium MD simulations amounts to 6.1 μs.

Free energy of ligand binding. The free energy simulations were performed under the same conditions as the above standard MD simulations, with the exception that temperature was kept constant at 298 K using mild Langevin coupling (stochastic dynamics (SD) leap-frog integrator⁹⁴ in GROMACS) with a friction coefficient of 1 ps⁻¹. The absolute binding free energy was calculated using a thermodynamic cycle illustrated in Fig. S5 of the ESI.†⁹⁵ This cycle involves two separate sets of simulations, one where the inter-molecular non-bonded interactions between the ligand and the surrounding are turned off (non-interacting ligand in vacuum), and the other involving the calculation of the free energy change of introducing the ligand from vacuum to the bulk solvent. To enhance the sampling of the bound state during the first step, the ligand is restrained to the binding pocket by using a set of restraining potentials; the associated free energy contribution for the non-interacting (decoupled) state was calculated analytically, see Fig. S6 and Table S2 of the ESI.† The transition from state A (interacting ligand) to B (non-interacting ligand) was accomplished using a coupling parameter approach,^96–98 where a combined potential energy function (1 − λ)U_A + λU_B smoothly shifts the system from state A (λ = 0) to B (λ = 1) as a function of the coupling parameter λ. The electrostatic and Lennard-Jones interactions were decoupled separately, and soft-core potentials were used during the decoupling of Lennard-Jones interactions. For decoupling the ligand from the protein, a spacing of Δλ = 0.05 was used for both electrostatic and Lennard-Jones interactions; additional λ-points were used for perturbing the restraining potentials in the fully interacting state. At each of the total of 55 λ-points, 10 ns of MD sampling was carried out. Thus, for every individual set of free energy simulations, the sampling time amounts to 0.55 μs. For each solvent mixture (pure water, 10%, 20%, 30% methanol), three independent sets of simulations were performed, with different initial velocities. The average of these three runs is reported unless otherwise noted. Thus, the total sampling time for decoupling the ligand from the protein is 6.6 μs. For decoupling the ligand from bulk solvent, a similar approach to the one just outlined for the protein–ligand complex was used. The differences are that (i) no restraining potentials were necessary, (ii) for decoupling the Lennard-Jones interactions, 25 λ-points (instead of 21 for the complex) were used, with a closer spacing of Δλ = 0.02 close to the end states (λ = 0 and λ = 1, respectively), and (iii) sampling at each λ-point was 5 ns (instead of 10 ns for the complex). Two independent sets of free energy simulations were also carried out for every solvent mixture in this case, and the total sampling time for decoupling the ligand from bulk solution is thus 2.0 μs.

In all cases, prior to the production runs, the systems were equilibrated at each λ-point with a short equilibration protocol consisting of minimization (1000 steps steepest descent) and position restrained NVT and NpT runs (250 ps each). The first 500 ps of the final production simulations were disregarded in the final analysis. The free energy difference between states A and B was obtained with the Bennett acceptance ratio (BAR) method.⁹⁹ The convergence of the free energy calculations was verified by comparing the forward and backward (time-reversed trajectory) estimates (Fig. S7, ESI†), as suggested by Klimovich and co-workers.¹⁰⁰ The values obtained with BAR were also compared with those obtained from multistate BAR (MBAR)¹⁰¹ and simple trapezoidal integration (TI) of the 〈∂U(λ)/∂λ〉 over λ curves (Tables S3–S5, ESI†).

The ligand (PAB) has a net positive charge of +1, which in the decoupled state leads to a net charge of the system. To correct for the finite-size effects of the charging component of the free energy, which arise under periodic boundary conditions with lattice-sum electrostatics, we used the approach described by Rocklin and co-workers.¹⁰² The results are summarized in Tables S6–S12, ESI.†

Free energy of water binding. The free energy change associated with tying up a water molecule in the binding site (WAT in Fig. 1), ΔG_WATbind, is estimated using the thermodynamic cycle which is conceptually very similar to the one used for ligand binding (see ESI†). The set-up of the free energy simulations, including the number of λ-points, sampling at each λ-point, etc., was identical to the those used for decoupling the ligand from bulk solution (see above), with the exception that for decoupling the electrostatic interactions between WAT and the surrounding, a λ-spacing of 0.1 (instead of 0.05) was used. In addition, the small size of the water molecule allowed for sampling of both forward (removing water) and backward (introducing water) reactions. The free energies reported in the text are the average of these two independent sets of simulations. The total accumulated sampling used for obtaining the free energy of WAT binding amounts to 2.0 μs. To improve sampling of the bound state, WAT was immobilized in the binding pocket by applying a harmonic position restraint potential on its oxygen atom. The corresponding contribution to the free energy, ΔG^res, was calculated analytically.¹⁰³ Weak harmonic position restraints (force constant 10 kJ mol⁻¹ nm⁻²) were also applied to protein C_α-atoms that are at least 1 nm away from the center of mass of the binding site, as was done previously.¹⁰⁴ One possible pitfall of the WAT binding simulations is that in the completely decoupled state, another water molecule from the bulk might enter the binding site region and occupy the same position as the decoupled WAT molecule, thereby leading to another bound state instead of the desired unbound state. We carefully analyzed all λ-points and found that this undesired replacement does not occur on the time scale of the simulations, presumably due to a kinetic barrier associated with WAT binding. For further details of the free energy simulations, we refer to the ESI.†

Fig. 1 Structure of the trypsin–PAB complex. The ligand (PAB) and important residues in the binding site (dashed box) are shown as sticks. The residues in the S1 region (188–196, 214–220, and 226–230), and loops L1, L2 (185–188, 221–224) are shown in orange and blue, respectively. A bound crystal water (WAT) that adopts a bridging position between PAB and Val227 is also shown.

Since WAT stays bound in the binding pocket, the enthalpy of binding can be obtained using the following relation

ΔH_WATbind ≈ E_{complex–WAT} − E_bulk (1a)

E_{complex–WAT} = E_Prot–WAT + E_PAB–WAT + E_W–WAT + E_M–WAT (1b)

where E_Prot–WAT, E_PAB–WAT, E_W–WAT, and E_M–WAT are the average interaction energies of the bound water with the protein, PAB, water, and methanol, respectively. E_bulk is the average interaction energy of a water molecule in the bulk. These energies were obtained from additional 100 ns equilibrium MD simulations that were carried out under similar conditions as used in the free energy simulations, i.e., including the position restraints on the WAT molecule and protein C_α-atoms that are further than 1 nm away from the binding site. The entropic contribution is obtained as −TΔS_WATbind = ΔG_WATbind − (ΔH_WATbind − ΔG^res).

3 Results and discussion

3.1 Binding thermodynamics

The thermodynamics of p-aminobenzamidine (PAB) binding to trypsin in different water/methanol mixtures were investigated with ITC. Fig. 2A shows the data of typical binding titration experiments, and Fig. 2B the corresponding enthalpograms. As described in Methods, a single-site binding model was used to fit a binding isotherm to the data to determine the binding constant K_a and binding enthalpy ΔH_bind.⁷⁷ From these, ΔG_bind and TΔS_bind can be calculated using ΔG_bind = −k_BT ln K_a = ΔH_bind − TΔS_bind. In our experiments the stoichiometry value (N-value) obtained is in the range of 0.7 rather than 1 as would be expected for a 1 : 1 complex. Within a limit of less than 5%, the ligand concentration (as determined by the weight of PAB dissolved in buffer) agrees with the value measured by optical absorption at 294 nm. Further purification of commercial trypsin by size exclusion chromatography did not improve the N-value by more than 10%. Thus, the trypsin purchased with the highest available quality may not be active to 100%. Nevertheless, this potential error in active trypsin concentration and the resulting N-value of 0.7 does not lead to erroneous results of the thermodynamic values we report. Due to the setup of our experiments with PAB as the titrant in the syringe, the heat evolving at each titration step is referred to the PAB concentration, which is most accurate.

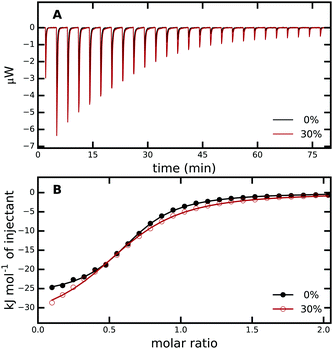Fig. 2 (A) ITC raw data for titration of PAB into trypsin in 0% (black) and 30% (red) aqueous methanol solution. (B) Enthalpograms retrieved from (A). The solid lines represent fits to a single-site binding model. The average from three independent ITC runs was used. For every measurement, all PAB solutions were freshly prepared and different trypsin stock solutions were used, see Methods and Fig. S1 in the ESI† for more details.

The experiments were carried out at different methanol concentrations to analyze the influence of the solvent on trypsin–ligand binding, ranging from 0% (i.e., pure aqueous buffer) to 30% (v/v) methanol/water. Trypsin aggregation impeded exploration of higher methanol concentrations. Given an equilibrium dissociation constant of the PAB/trypsin complex in the range of 5–8 μM in aqueous buffer and the concentration of trypsin of 250 μM in the cell, an optimal ratio of concentration and equilibrium dissociation constant of 35–50 is achieved (in the context of ITC measurements usually termed C-value). This allows one to obtain the equilibrium constant with high accuracy. A very good C-value of 5–10 is also achieved at 30% methanol.

For the binding of the ligand to trypsin in pure aqueous buffer (without methanol), we obtained values for ΔG_bind, ΔH_bind, and −TΔS_bind of −28.8, −27.0, and −1.8 kJ mol⁻¹, respectively, in excellent agreement with the values reported by Talhout and co-workers.¹⁰⁵ In Tris buffer (instead of Hepes), these values are −29.5, −28.5 and −1.0 kJ mol⁻¹, respectively (Table S13, ESI†). In light of the different ionization enthalpies of Tris and Hepes buffers (47.5 vs. 20.4 kJ mol⁻¹), we conclude that no net protonation/deprotonation occurs upon complex formation.

Table 1 shows that binding affinity drops only marginally with increasing methanol concentration, with a difference ΔΔG_bind of only 2.7 kJ mol⁻¹ between 30% and 0% methanol. These ITC results were confirmed by our fluorescence titrations, which yielded ΔG_bind of −29.4 and −26.9 kJ mol⁻¹ for pure aqueous solution and 30% methanol, respectively (Fig. S2, ESI†). Remarkably, the almost unchanged binding free energies at the different methanol concentrations result from substantial, compensating changes in enthalpy and entropy of binding (Table 1, last two columns). With increasing methanol concentration, the binding process becomes more exothermic (ΔH_bind becomes more negative) but, at the same time, entropically more unfavorable (−TΔS_bind becomes more positive). The effect seems to level off towards 30% methanol, in the sense that the relative changes between 0–10% and 10–20% are more pronounced than between 20–30%.

Table 1 Thermodynamics of PAB binding to trypsin obtained from ITC experiments. The results shown are for Hepes buffer; similar results were obtained in Tris buffer (see Table S13, ESI). Uncertainties (from differences between several independent ITC runs) are indicated in brackets. Units are kJ mol⁻¹

System (%)	ΔGbind	ΔHbind	−TΔSbind	ΔΔGbind	ΔΔHbind	−TΔΔSbind
0	−28.8 (0.1)	−27.0 (0.3)	−1.8 (0.3)	—	—	—
10	−28.0 (0.1)	−30.0 (0.2)	+2.0 (0.1)	+0.8	−3.0	+3.8
20	−27.3 (0.1)	−34.1 (0.5)	+6.8 (0.4)	+1.5	−7.1	+8.6
30	−26.1 (0.2)	−34.5 (0.3)	+8.4 (0.4)	+2.7	−7.5	+10.2

---

The results in Table 1 strongly suggest that enthalpy–entropy compensation is at play. For ITC, Chodera and Mobley⁵⁴ pointed out that large, under-reported uncertainties in ΔH and TΔS can lead to apparent compensation due to correlated errors. Uncertainty in the concentration of the titrant is the major source of uncertainty in ITC measurements and leads to corresponding errors in ΔH_bind, ΔG_bind, and TΔS_bind.⁵⁴ We therefore repeated every measurement at least three times, each time with a freshly prepared stock solution (Fig. S1, ESI†). The differences in ΔG_bind and ΔH_bind between the individual ITC runs are less than 0.5 kJ mol⁻¹. This reproducibility, together with the agreement with the values obtained by Talhout and co-workers¹⁰⁵ for pure aqueous solution, strongly supports our results.

Next, to answer the intriguing question of what the molecular mechanism behind the observed strong enthalpy–entropy compensation is, we carried out all-atom molecular dynamics simulations. The binding free energies obtained from our simulations (see Methods and the ESI† for details) are shown in Fig. 3 and compare very favorably with the ITC values, both concerning the magnitude and, importantly, also the trend of largely unchanged ΔG_bind with increasing methanol concentration. The simulations slightly overestimate the binding affinity, as expected from a force field with fixed point charges because mutual polarization weakens binding.⁶⁷ The effect is very modest, though, with ΔG_bind being too negative by only 1–2 kJ mol⁻¹. To confirm the results of our free energy simulations and the applied corrections due to a net-charged periodic system, we carried out additional sets of simulations in which an alternative thermodynamic cycle for ΔG_bind was used (Fig. S8 and Table S14 of the ESI†). Within the statistical uncertainty, the results are indistinguishable (Fig. 3).

Fig. 3 Comparison of binding free energies from ITC and MD-based free energy simulations for various methanol concentrations. The error bars for the MD values are the standard errors of the mean from three independent sets of simulations. The red data points were obtained from additional, independent sets of free energy simulations that employ an alternative thermodynamic cycle (see ESI†).

The agreement between ITC and MD simulations is reassuring, especially in light of the fact that in contrast to computations of relative differences of binding free energies, absolute binding free energy calculations do not profit from systematic error cancellation. However, the data in Fig. 3 does not (yet) provide insights into the underlying mechanisms in terms of structure, dynamics, and molecular driving forces. MD simulations can provide these missing atomic-level interpretations, which will be described in the following.

3.2 Protein structure

The overall protein structure is very stable during our MD simulations and does not change significantly due to the presence of methanol (Fig. S9, ESI†). Likewise, the RMS fluctuations of the protein residues are also not affected by an increase in methanol concentration (Fig. S10, ESI†). A closer look at the ligand binding pocket (Fig. 4 and Fig. S11, ESI†) reveals that not only the global protein structure, but also the binding pose of PAB as well as the S1 binding pocket region are structurally very stable, although subtle changes are observed for 10% (trypsin–PAB complex) and 30% methanol (apo). The additional maxima observed for these two systems can be attributed to a conformational switch of Trp215 (Fig. S12, ESI†). In the majority of our simulations, Trp215 adopts the open conformation that is also seen in the X-ray crystal structure. However, at the two indicated concentrations, Trp215 undergoes a conformational transition to a closed state in our simulations, which has been observed also in other serine protease structures.^106,107 Based on MD simulations, Plattner and co-workers suggested that the closed form is one of the meta-stable states that can contribute to the binding process as it is more stable than the open form in the absence of the ligand.⁷³ Interconversions between closed and open forms occur on the μs time scale, which is longer than the time scale of our simulations. However, the presence of methanol might speed up the transition by lowering the barrier and, in addition, it might change the free energy difference between the open and closed states of Trp215. The limited sampling of our current simulations does not enable us to fully address this issue, which will be subject of future work.

Fig. 4 Comparison of the RMSD of the S1 pocket relative to the X-ray crystal structure, as obtained from equilibrium MD simulations at different methanol concentrations of (A) the trypsin–PAB complex, and (B) apo trypsin. The RMSD was calculated for all heavy atoms of the residues belonging to the S1 pocket, which in the numbering of the original PDB file is defined as residues 188–196, 214–220, and 226–230.

Next, we analyzed the hydrogen bonds between PAB and residues in the binding site as well as between PAB and solvent molecules (Table S15, ESI†). Irrespective of methanol concentration, PAB forms on average ca. 3 hydrogen bonds with protein residues, especially Asp189, Ser190, Ser195 and Gly219 (Table S16, ESI†). In addition, PAB also forms hydrogen bonds with solvent molecules, including a very persistent one with a bound crystal water molecule that adopts a bridging position between the ligand and Val227 (see below). Overall, the number of hydrogen bonds with solvent molecules does not change with methanol concentration, since less hydrogen bonds with water are compensated by additional hydrogen bonds with methanol molecules. A similar pattern is also observed for the hydrogen bonds between PAB and solvent molecules for the free ligand in solution (Table S15, ESI†).

Our above analysis shows that there are no pronounced changes with increasing methanol concentration of the protein structure as well as protein–ligand hydrogen bonds. At first sight, this seems to be consistent with our observation that the binding free energy is only very weakly affected by methanol concentration. However, this interpretation is somewhat superficial, since it largely neglects changes in solvation, of both the ligand and the protein, which accompany the transition from the unbound to the bound state. Association of PAB with trypsin requires at least partial desolvation of the ligand and the binding pocket, and the rearrangement of solvent molecules in the vicinity. These processes and their thermodynamic signatures might depend on the composition of the solvent. Hence, understanding binding requires to take both the bound and unbound states into account, and to explicitly investigate how solvation patterns change as a function of methanol concentration.

3.3 Solvation

Before discussing the solvation of the binding site, we first focus on the solvation of the unbound ligand, i.e., free PAB in solution. To that end, we counted the number of solvent molecules in the vicinity of the ligand. Table 2 compares the ratio of water to methanol molecules in the vicinity of free PAB (last column) to the corresponding ratio in the bulk solution (second column). There is a local enrichment of methanol (relative to the bulk) around free PAB in solution, as the ratios are smaller than in bulk for all investigated methanol concentrations. Thus, PAB itself slightly prefers methanol over water, a conclusion that is supported by our solvation free energy calculations, see below. Interestingly, this trend is reversed in the trypsin–PAB complex (Table 2, third column). When confined in the binding pocket, PAB is preferentially solvated by water. This change in solvation pattern is due to the lack of space in the binding pocket, which can host water but not sterically more demanding methanol molecules when occupied with PAB. As seen for free PAB in solution, the general trend does not change with increasing methanol concentration. The only trend that qualitatively changes with methanol concentration is the solvation of the empty binding pocket, i.e., in the apo form (Table 2, fourth column). The binding pocket is actually not empty, but occupied by solvent molecules. For 10% methanol, it is preferentially occupied by methanol (relative to the bulk ratio), whereas for 30% methanol it is preferentially hydrated. Close inspection revealed that at 10% methanol, in apo trypsin, a single methanol molecule repeatedly and reversibly occupies the position of the aromatic ring of PAB in the binding pocket. Thus, upon binding, the ligand not only needs to strip off its solvation shell, which is slightly enriched with methanol, but also needs to displace a varying number and nature (water or methanol) of solvent molecules from the binding pocket, which might have implications for the thermodynamics of binding.

Table 2 Average number of water molecules per methanol molecule in the binding pocket for the bound and apo form, and in the vicinity of free PAB in solution. The bulk ratios are also listed for reference. The binding pocket is defined with respect to the center of mass (COM) of PAB. For the apo state, a group of atoms whose COM is very close to that of PAB was used as reference point. A solvent molecule was counted if its COM was within a distance of 0.8 nm from the reference point. This cutoff radius of 0.8 nm includes the first solvation peak (see radial distribution functions in Fig. S13 of the ESI); qualitatively similar ratios were obtained with other cutoffs

System (%)	Bulk	Binding pocket
		Bound	Apo	Free
10	9.8	13.0	4.8	7.0
20	4.3	6.1	4.3	3.2
30	2.7	5.6	4.5	2.1

---

To further analyze and obtain a spatially resolved picture of the solvation pattern, we calculated the spatial distribution of solvent molecules in the binding pocket. A cubic region of 8 nm³ which encloses the S1 pocket and the L1 and L2 loops was chosen for analysis. Fig. 5 shows the density maps at 0% and 30% methanol concentration. In line with the data in Table 2, the binding pocket of the trypsin–PAB complex is preferentially hydrated (as compared to the bulk) at 30% methanol concentration. A noticeable feature is the cluster of water densities that appears at the same place for both systems. Some of these regions correspond to positions occupied by crystal waters near the ligand in the X-ray structure (marked by black/red arrows in Fig. 5). In particular, the red arrow indicates the position of a tightly bound crystal water that interacts strongly with the backbone of Val227 as well as the ligand. This water molecule (WAT) stays tightly bound during all our simulations of the trypsin–PAB complex and is found to contribute favorably to the binding of the ligand (see below). Another notable feature is the enhanced hydration near the loops L1 and L2, whose dynamics was suggested to correlate with that of the S1 binding pocket, thus contributing to enzyme specificity.^108,109 For the apo state, similar to the complex, a preferential clustering of water molecules in the binding pocket is observed, but only at higher methanol concentrations (Fig. S15, ESI†).

Fig. 5 Spatial density map of water in the S1 pocket region for 0% (A) and 30% (B) methanol. Only those regions where the number density of water molecules are either equal to or greater than in bulk are shown. The arrows mark the location of crystal water molecules near the ligand. The density map was calculated by averaging over the entire trajectories on a grid of bin size 0.05 nm³ using the VolMap plugin of VMD.¹¹⁰ Qualitatively similar results were obtained for 10% and 20% methanol, see Fig. S14 in the ESI.†

Our above results show that (i) at the structural level, there are no pronounced changes with changing solvent composition, and (ii) the solvation pattern does change in a distinct manner, depending on the water/methanol mixture. However, the thermodynamic implications are not obvious, in particular concerning the enthalpy–entropy compensation observed in our ITC experiments. Thus, in the following, we set out to investigate the molecular determinants of the thermodynamic signatures, including a dissection into the enthalpic and entropic contributions due to protein–ligand, protein–protein, ligand–solvent, and protein–solvent interactions.

3.4 Thermodynamic signatures and molecular driving forces

In the following, we concentrate on the comparison of PAB binding to trypsin in pure aqueous solution and in 30% methanol, since (i) the entropic/enthalpic differences are most strongly pronounced in this case, and (ii) the effects are found to level off between 20% and 30% methanol concentrations (Table 1). We start with the contribution due to desolvation of the ligand from the bulk, which constitutes one half of the thermodynamic cycle of binding (Fig. S5, ESI†). Table 3 shows that the solvation free energy of PAB is more negative in 30% methanol than in pure water, with a difference of ΔΔG_solv(30–0%) = −7.3 kJ mol⁻¹. Since formally, the ligand is first desolvated from bulk solution and then resolvated in the binding pocket upon binding, this more negative solvation free energy needs to be overcompensated by the protein in the second step, see below. In addition to the free energy, the small size of the ligand/solvent system allows a rigorous decomposition of ΔG_solv into the enthalpic and entropic contributions (Table 3). The solvation enthalpy was calculated from the differences in potential energy¹¹² according to ΔH_solv ≈ 〈U_system〉 − (〈U_solvent〉 + 〈U_PAB〉), where 〈U_system〉, 〈U_solvent〉, and 〈U_PAB〉 are the average potential energies of the system (PAB in solvent), pure solvent, and PAB in vacuum, respectively. The missing pΔV contribution is very small in condensed liquid phases at ambient pressure and can therefore be neglected.¹¹² The entropic contribution is obtained from the difference, −TΔS_solv = ΔG_solv − ΔH_solv. The H/S decomposition reveals that the more negative ΔG_solv at 30% methanol is almost entirely due to a less unfavorable solvation entropy (ΔΔH_solv = −0.3 kJ mol⁻¹, −TΔΔS_solv = −7.0 kJ mol⁻¹). This result is interesting, since our ITC experiments show that for the overall binding process, the enthalpy of binding is more negative in 30% methanol than in pure water, by ΔΔH_bind = −7.5 kJ mol⁻¹ (Table 1). Thus, PAB seems to more favorably interact with the protein binding pocket at 30% methanol. How this can be achieved is not obvious in light of the highly similar structures and binding modes in pure water and 30% methanol, and we will focus on this intriguing aspect below. From the entropic viewpoint, solvating the ligand in pure water is more unfavorable than in 30% methanol. Since the ligand is almost completely desolvated upon binding,§ a large part of the entropy difference of −TΔΔS_desolv(30–0%) = +7.0 kJ mol⁻¹ will contribute to the overall binding entropy difference of +10.2 kJ mol⁻¹ (Table 1).

Table 3 Thermodynamics of solvation of PAB at two methanol concentrations. The internal energy of PAB in vacuum, 〈U_PAB〉, is −471.5 kJ mol⁻¹. Energies are averages from 250 ns (system) or 150 ns (solvent, PAB in vacuum) equilibrium MD simulations. Statistical uncertainties, as obtained from block averaging,¹¹¹ are indicated in brackets. Units are kJ mol⁻¹

System (%)	ΔGsolv	〈Usystem〉	〈Usolvent〉	ΔHsolv	−TΔSsolv
0	−269.3 (0.1)	−505632.4 (1.7)	−504832.1 (2.2)	−328.8 (2.8)	59.5 (2.8)
30	−276.6 (0.3)	−338549.9 (2.3)	−337749.3 (3.1)	−329.1 (3.9)	52.5 (3.9)

---

Next, we turn to the energetic (enthalpic) changes associated with the binding of the ligand to trypsin, which constitutes the other half of the thermodynamic cycle (Fig. S5, ESI†). To that end, we analyzed the interactions of the ligand in the protein binding pocket, and how these differ between 30% and 0% methanol. In addition to the interactions between the ligand and the protein, there might also be intramolecular changes within the protein itself upon ligand binding, which are in principle possible in our simulations since we do not apply restraints that limit the conformational flexibility. Such changes, if present, could be reflected in changes of the internal energy of the protein. Since PAB is a rigid molecule, intramolecular changes within the ligand are negligible. However, there might be sizable contributions due to the solvent, which can include both changes in protein-solvent and also solvent–solvent interactions.

First, to obtain a spatially resolved picture in terms of the contributions of the individual protein residues, we analyzed the interaction energies between PAB and all residues in the binding pocket, both for the complex in pure water and in 30% methanol; all energies are listed in Tables S17 and S18 of the ESI.† Summed over all protein residues, PAB interacts more strongly with the trypsin binding pocket in 30% methanol than in pure water, by an energy difference of ΔE_PAB–Prot(30–0%) = −13.2 kJ mol⁻¹ (Table 4). Fig. 6 shows that Gly219 contributes most to the more favorable trypsin–PAB interaction in 30% methanol than in pure aqueous solution. In particular, the backbone oxygen of Gly219 interacts more favorably with the amidine group of PAB in 30% methanol. Fig. 7 shows that Gly219 can switch between two distinct states, which are populated differently at 30% and 0% methanol. In the state in which Gly219 interacts more favorably with PAB (average interaction energy ca. −40 kJ mol⁻¹), the PAB amidine group forms a close contact with the backbone oxygen atom, whereas in the other state, this distance is significantly larger and the interaction energy is only about −5 kJ mol⁻¹ (Fig. 7A and B). Closer analysis revealed that the transition between these two states is related to the flipping of the backbone dihedral angle ϕ_Gly219 (Fig. S16, ESI†), concomitant with a small displacement of the entire L2 loop, which is in contact with the solvent surrounding (Fig. 7C and D). In pure aqueous solution, the dominant state is the more weakly interacting state with ϕ_Gly219 ≈ −160°. In contrast, in 30% methanol, the state with ϕ_Gly219 ≈ 70°, in which Gly219 more favorably interacts with PAB, is the major state. Thus, the more favorable interaction energy between PAB and the protein in 30% methanol of −13.2 kJ mol⁻¹ can be assigned to a population shift between these two conformational states. In summary, our simulations reveal that even a modest degree of protein plasticity, such as the observed small-amplitude motion of the L2 loop, can play an important role for the interaction energy between the protein and the ligand, and hence modulate binding energetics.

Table 4 Average interaction energies from MD simulations. For the protein–protein and protein–solvent contributions, the difference in interaction energies between the PAB-bound and apo states are listed; the value in the last column is the difference of these, ΔΔE. The protein–PAB interaction energy is considered to be zero in the apo state. See Tables S17–S20 of the ESI for all raw data. Statistical uncertainties (standard error of the mean) are estimated from three independent sets of simulations. Units are kJ mol⁻¹

Interactions	ΔE0%	ΔE30%	ΔΔE(30–0%)
Protein–PAB	−233.6 (5.8)	−246.8 (3.3)	−13.2 (6.7)
Protein–protein	−21.7 (13.8)	−64.0 (28.7)	−42.3 (31.8)
Protein–solvent	159.7 (14.7)	195.3 (14.0)	35.6 (20.3)

---

Fig. 6 (A) Interaction energies between PAB and trypsin residues at 0% and 30% methanol concentration. (B) Interaction energy differences between 30% methanol and pure water, ΔΔE_PAB–Prot(30–0%), are mapped onto the structure. Residues are colored by the strength of their contributions. See Tables S17 and S18 of the ESI† for all individual values.

Fig. 7 Comparison of PAB–Gly219 interactions. (A) Interaction energy. (B) N1_PAB–O_Gly219 distance. (C) Backbone ϕ dihedral angle of Gly219. (D) Overlay of the two conformations of the L2 loop. The strongly and weakly interacting states are colored magenta and green, respectively.

As discussed above, there might not only be differences between the protein–ligand interactions in 30% and 0% methanol, but also contributions due to changes within the protein itself. For this analysis, we proceeded in two steps. First, we calculated the difference in intramolecular protein–protein interactions between the ligand-bound and apo states, both for pure aqueous solution and for 30% methanol. Then, to compare the two different solvent compositions, the difference ΔΔE between these two was calculated. As shown in Table 4, protein–protein interaction energies are also more favorable in 30% methanol than in pure aqueous solution, by ΔΔE_Prot–Prot(30–0%) = −42.3 kJ mol⁻¹. This analysis is restricted to a local region, in the sense that it includes the interactions of the binding pocket residues with themselves and with the rest of the protein (Table S19, ESI†), because the effect is otherwise masked by the very large fluctuations of the total potential energy of the entire protein (see discussion below).

Finally, in addition to the protein–protein contribution, we also analyzed protein–solvent interactions, and how they differ between 30% and 0% methanol. For this analysis, we again focused on the residues that constitute the binding pocket. The difference in protein–solvent interaction energy between the ligand-bound and apo states was computed, both for pure aqueous solution and for 30% methanol to yield ΔΔE(30–0%), as was done for the protein–protein interaction energy (Table S20, ESI†). The rationale behind this approach is that upon binding to the protein, the ligand needs to displace solvent molecules that occupy the binding pocket in the apo state (Table 2), the energetics of which might depend on the methanol concentration. Indeed, as shown in Table 4 (bottom row), desolvation of the binding pocket upon PAB binding is energetically more unfavorable in 30% methanol than in pure aqueous solution. The corresponding energy difference of ΔΔE(30–0%) = +35.6 kJ mol⁻¹, which also contributes to the overall binding energy difference, thus counteracts the previous two contributions. Nevertheless, taken together, our simulations reveal that the binding of PAB to trypsin is energetically (enthalpically) significantly more favorable in 30% methanol than in pure aqueous solution by −13.2–42.3 + 35.6 = −19.9 kJ mol⁻¹. Considering the difference in ligand desolvation enthalpy of +0.3 kJ mol⁻¹ (Table 3), we obtain a final estimate for ΔΔH_bind(30–0%) of −19.6 kJ mol⁻¹. Although this value is a rather rough estimate (see discussion below), it is at least in qualitative agreement with the −7.5 kJ mol⁻¹ obtained from ITC.

Our above analysis showed that the more favorable enthalpy of binding in 30% methanol can be assigned to more favorable protein–ligand and protein–protein interaction energies. This might suggest that the corresponding more unfavorable entropy of binding could be due to a reduced configurational entropy of the protein as a result of these tighter interactions. However, neither the root-mean-squared fluctuations of the individual trypsin residues (Fig. S10, ESI†) nor configurational entropies (Fig. S17, ESI†) differ significantly between 30% and 0% methanol. Instead, our H/S decomposition of the ligand solvation free energies (see above) revealed that a remarkably large part of the binding entropy difference of −TΔΔS_bind(30–0%) = +10.2 kJ mol⁻¹, as obtained from ITC (Table 1), is linked to differential entropy of desolvation of PAB from the bulk, −TΔΔS_desolv(30–0%) = +7.0 kJ mol⁻¹. We did not attempt to analyze the entropy of the solvent around the protein, since established methods, such as grid cell theory,³⁵ inhomogeneous fluid solvation theory,^25,26 or grid inhomogeneous solvation theory,^33,34 have not (yet) been extended to solvent mixtures. We expect this missing entropic contribution to be small anyway, because the largest entropy change is likely linked to solvent rearrangement upon ligand desolvation from the bulk, which is included in our calculations.

In the following, we shall briefly discuss the limitations our approach used to decompose ΔG into ΔH and TΔS, and compare it to other methods in the literature. Why did we, for the protein–ligand complex, use pairwise interaction energies as a proxy for enthalpy and not perform a rigorous decomposition, as done for the solvation free energy of the ligand? To answer this question, one needs to consider (i) the large size of the system, and (ii) the conformational flexibility, which is fully included in our approach. Despite the rather extensive MD sampling carried out in this work, the large fluctuations did not allow us to extract statistically meaningful total potential energy differences, which would have enabled us to straightforwardly compute the binding energy from the ensemble averages, ΔU_bind = 〈U〉_Prot–Lig − (〈U〉_Prot + 〈U〉_Lig). For fully flexible systems, the decomposition of ΔG_bind by computing enthalpy directly requires extensive sampling, and was thus, to our knowledge, successfully done only for small host–guest systems.¹¹³ Likewise, the direct estimation of entropy from the temperature dependence of the free energy is only possible for small systems.^114,115 We attempted both these approaches for our system, but did not succeed in obtaining statistically precise results due to the large fluctuations and slow decorrelation times. Methods that directly estimate enthalpies and entropies for large protein systems have been reported,^34,39 but to facilitate convergence they require (i) strong restraints to suppress conformational flexibility of the protein, and (ii) the use of unrealistic ionization states of solvent-exposed amino acids to maintain an overall neutral charge of the system without counterions. Especially the first approximation is rather drastic. In fact, our results show that even for the investigated trypsin–PAB complex, which might be considered a prototype for a rigid protein–ligand complex, conformational flexibility plays an important role. Binding energy is modulated to an unexpectedly large extent by even a small-amplitude motion of the L2 loop bearing the Gly219 residue that switches between two distinct states. Thus, instead of applying a spatial energy decomposition on a Cartesian 3D grid, which requires strong restraints, we resorted to analyzing residue–residue interactions. Furthermore, as mentioned above, changes in solvent entropy and solvent–solvent interaction energies around the protein are neglected in our approach. For aqueous systems, it has been suggested that the change in water–water interaction energy, ΔE_W−W, can be estimated from solute–water interaction energy, E_solute–W, by introducing a simple scaling factor,³⁸ ΔE_W–W = −c·E_solute–W, with c = −0.5. We refrain from using a similar scaling here, because we are interested in differences between pure aqueous solution and 30% methanol, and it is not clear whether the same scaling factor applies under these conditions. We conclude this discussion by emphasizing that, unlike for the free energy, we do not aim to obtain accurate enthalpies and entropies that are quantitatively comparable to the experimental values, but rather to provide qualitative but detailed insights (at the level of the individual residues) into the molecular mechanisms behind the thermodynamic signatures.

3.5 Contribution of a localized water molecule

Water molecules are commonly found to mediate protein–ligand interactions in many systems, including serine proteases (see Table S21, ESI†).^116–118 In our simulations, we found that a single crystal water molecule (WAT in Fig. 1) stays bound next to PAB at all investigated methanol concentrations, suggesting that it plays an important role. A thorough understanding of the binding process thus requires to also explicitly investigate the contributions of this localized water molecule. The free energy of binding of WAT, ΔG_WATbind, is not directly experimentally accessible. However, it is implicitly contained in the overall ligand binding free energy (both experimentally, but also in ΔG_bind obtained from our simulations, see above). To single out the contributions of WAT, we carried out additional free energy simulations, following the approach suggested by Hamelberg and co-workers.¹⁰³ In addition to the free energy of tying up the water molecule in the binding pocket, we also decomposed ΔG_WATbind into the entropic and enthalpic contributions.

The computation of ΔG_WATbind involves two sets of simulations (Fig. S18, ESI†). First, the free energy of introducing a water molecule in the bulk (ΔG₁), and second the free energy of decoupling WAT from the binding pocket (ΔG₂). For the first step, we obtained ΔG₁ = −26.4 kJ mol⁻¹, in agreement with previous computational¹⁰³ and experimental values.¹¹⁹ ΔG₁ remains largely unaffected by methanol concentration (Table 5).

Table 5 Thermodynamics of tying up a water molecule in the binding pocket. ΔG_WATbind, from the thermodynamic cycle (Fig. S18, ESI) is equal to −(ΔG₁ + ΔG₂ + ΔG^res). The enthalpies are estimated from 100 ns simulations that were carried out under identical conditions as the free energy simulations (Table S24, ESI). The entropic component is estimated using the relation: ΔG_WATbind − (ΔH_WATbind − ΔG^res). Statistical uncertainties for ΔG₂ and ΔH_WATbind are estimated from the difference of the forward and backward transformations and from block averaging, respectively. Units are kJ mol⁻¹

System (%)	ΔG2			ΔG1	ΔG^res	ΔGWATbind	ΔHWATbind	−TΔSWATbind
	Forward	Backward	Average
0	53.0	50.0	51.5 (1.5)	−26.4 (0.1)	−9.5	−15.6 (1.5)	−33.2 (0.9)	8.1 (1.7)
10	48.7	48.0	48.3 (0.4)	−26.1 (0.1)	−10.1	−12.1 (0.4)	−29.7 (0.5)	7.5 (0.6)
20	41.4	41.8	41.6 (0.2)	−25.7 (0.1)	−10.2	−5.7 (0.2)	−18.8 (0.2)	2.9 (0.3)
30	40.9	40.8	40.9 (0.1)	−25.2 (0.1)	−11.2	−4.5 (0.1)	−16.1 (0.5)	0.4 (0.5)

---

To obtain ΔG₂, the water molecule was restrained in the binding pocket during our simulations using a harmonic restraint potential whose force constant was determined from the positional fluctuations observed in the equilibrium MD simulations (Table S22, ESI†). The small size of the perturbed molecule enabled us to sample both the forward (decoupling WAT from the binding site) and backward (introducing WAT in the binding site) processes. The average from these two sets of simulations is shown in Table 5. After applying the correction for the restraining potential, the free energy of binding the water molecule next to PAB is found be −15.6 kJ mol⁻¹. This value agrees with previous studies of similar systems,^9,103 considering that we refer to a standard volume that corresponds to a concentration of 55 mol l⁻¹ for pure water (Table S23, ESI†). For a standard concentration of 1 mol l⁻¹ (standard volume of 1.660 nm³), ΔG_WATbind reduces from −15.6 to −5.6 kJ mol⁻¹.

Table 5 shows that ΔG_WATbind is favorable at all investigated methanol concentrations, but becomes less favorable with increasing methanol concentration. To further analyze this effect, we decomposed ΔG_WATbind into the enthalpic and entropic contributions (Table 5). The interaction energy of WAT with the protein (E_Prot–WAT) and with the solvent (E_{Solvent–WAT}) remain approximately the same at all methanol concentrations, but the favorable interactions with the ligand (E_PAB–WAT) gradually decrease with increasing methanol concentration (Table S24, ESI†). The presence of a stronger hydrogen bond between the amidine group of PAB and WAT in pure water (97.5% of simulation time) vs. in 30% methanol (68% of simulation time) accounts for the observed behavior. As opposed to binding enthalpy, which becomes less favorable, the entropy contribution −TΔS_WATbind gets less unfavorable with increasing methanol concentration. Thus, similar to the overall ligand binding process (which includes binding of the localized water molecule), the differences in ΔG_WATbind between 30% and 0% methanol result from H/S compensation. The value of −TΔS_WATbind = 8.1 kJ mol⁻¹ in pure water agrees with entropies estimated from anhydrous inorganic salts and their hydrates,¹⁸ as well as other simulation studies of a set of proteins.^21,38

4 Summary and conclusions

We combined MD simulations and ITC experiments to investigate the effect of solvent composition on the thermodynamics of binding of p-aminobenzamidine to trypsin. Different water/methanol mixtures were used, varying between 0% methanol (i.e., pure aqueous solution) to 30% (v/v) methanol. ITC revealed (i) that the binding free energy, ΔG_bind, changes only very modestly with solvent composition, and (ii) that this small change in ΔG_bind is due to strong enthalpy–entropy compensation. To provide atomic-scale insights into the mechanisms underlying the thermodynamic signatures, extensive multi-μs MD simulations were carried out. The overall binding free energies obtained from our simulations agree with the experimental values. Furthermore, approximate decomposition of the free energy into its enthalpy and entropy contributions reveals that the more negative ΔH_bind at higher alcohol concentration is due to stronger protein–ligand and intramolecular protein–protein interactions when compared to pure aqueous solution. This more favorable binding enthalpy can be attributed to a distinct, small-scale conformational transition of the L2 binding pocket loop, which senses the solvent surrounding. Upon rearrangement of the L2 loop, a flexible glycine residue (Gly219) is brought into closer, energetically more favorable contact with the ligand, hence explaining the more negative ΔH_bind. Interestingly, these stronger interactions do not lead to a substantial reduction of the conformational entropy of the protein at higher methanol concentrations. Instead, the observed entropy change is due to different entropies of desolvation of the unbound ligand from the bulk: ligand desolvation is entropically less favorable in 30% methanol than in pure water, thus explaining the more disfavorable entropy contribution to the binding free energy, −TΔS_bind, at higher methanol concentrations. Our simulations thus provide a detailed picture of the molecular mechanisms underlying the observed H/S compensation. They highlight the importance of taking conformational flexibility into account, even for overall rather rigid complexes, since even local, small-amplitude motions can significantly alter binding energetics. Furthermore, our results reinforce the idea that it is essential to take both the bound and unbound states into account for understanding binding processes. From a more general perspective, the ability of the presented combined ITC/MD approach to assign, at the atomic level, different thermodynamic contributions to the population of distinct conformational states can contribute to an enhanced understanding of solvation effects in molecular recognition.

Acknowledgements

The German Research Foundation supported this work (Cluster of Excellence RESOLV (EXC 1069), Emmy Noether grant to L. S.).

References

1. Y. Levy and J. N. Onuchic, Annu. Rev. Biophys. Biomol. Struct., 2006, 35, 389–415.
2. P. Ball, Chem. Rev., 2008, 108, 74–108.
3. G. Hummer, Nat. Chem., 2010, 2, 906–907.
4. N. T. Southall, K. A. Dill and A. D. J. Haymet, J. Phys. Chem. B, 2002, 106, 521–533.
5. D. Chandler, Nature, 2005, 437, 640–647.
6. C. S. Poornima and P. M. Dean, J. Comput.-Aided Mol. Des., 1995, 9, 500–512.
7. J. E. Ladbury, Chem. Biol., 1996, 3, 973–980.
8. Y. Lu, R. Wang, C.-Y. Yang and S. Wang, J. Chem. Inf. Model., 2007, 47, 668–675.
9. C. Barillari, J. Taylor, R. Viner and J. W. Essex, J. Am. Chem. Soc., 2007, 129, 2577–2587.
10. M. S. Bodnarchuk, Drug Discovery Today, 2016, 21, 1139–1146.
11. P. Setny, R. Baron and J. A. McCammon, J. Chem. Theory Comput., 2010, 6, 2866–2871.
12. R. Baron, P. Setny and J. A. McCammon, J. Am. Chem. Soc., 2010, 132, 12091–12097.
13. G. Graziano, Chem. Phys. Lett., 2012, 533, 95–99.
14. P. Setny, R. Baron and J. A. McCammon, Chem. Phys. Lett., 2013, 555, 306–309.
15. L. Englert, A. Biela, M. Zayed, A. Heine, D. Hangauer and G. Klebe, Biochim. Biophys. Acta, 2010, 1800, 1192–1202.
16. P. W. Snyder, J. Mecinović, D. T. Moustakas, S. W. Thomas, M. Harder, E. T. Mack, M. R. Lockett, A. Héroux, W. Sherman and G. M. Whitesides, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 17889–17894.
17. J. Michel, R. H. Henchman, G. Gerogiokas, M. W. Y. Southey, M. P. Mazanetz and R. J. Law, J. Chem. Theory Comput., 2014, 10, 4055–4068.
18. J. D. Dunitz, Science, 1994, 264, 670.
19. P. Y. Lam, P. K. Jadhav, C. J. Eyermann, C. N. Hodge, Y. Ru, L. T. Bacheler, J. L. Meek, M. J. Otto, M. M. Rayner, Y. N. Wong, C.-H. Chang, P. C. Weber, D. A. Jackson, T. R. Sharpe and S. Erickson-Viitanen, Science, 1994, 263, 380–384.
20. J. M. Chen, S. L. Xu, Z. Wawrzak, G. S. Basarab and D. B. Jordan, Biochemistry, 1998, 37, 17735–17744.
21. Z. Li and T. Lazaridis, J. Am. Chem. Soc., 2003, 125, 6636–6637.
22. V. Mikol, C. Papageorgiou and X. Borer, J. Med. Chem., 1995, 38, 3361–3367.
23. A. Wissner, D. M. Berger, D. H. Boschelli, M. B. Floyd, L. M. Greenberger, B. C. Gruber, B. D. Johnson, N. Mamuya, R. Nilakantan, M. F. Reich, R. Shen, H. R. Tsou, E. Upeslacis, Y. F. Wang, B. Wu, F. Ye and N. Zhang, J. Med. Chem., 2000, 43, 3244–3256.
24. A. Biela, M. Khayat, H. Tan, J. Kong, A. Heine, D. Hangauer and G. Klebe, J. Mol. Biol., 2012, 418, 350–366.
25. T. Lazaridis, J. Phys. Chem. B, 1998, 102, 3531–3541.
26. T. Lazaridis, J. Phys. Chem. B, 1998, 102, 3542–3550.
27. T. Young, R. Abel, B. Kim, B. J. Berne and R. A. Friesner, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 808–813.
28. R. Abel, T. Young, R. Farid, B. J. Berne and R. A. Friesner, J. Am. Chem. Soc., 2008, 130, 2817–2831.
29. J. C. Rasaiah, S. Garde and G. Hummer, Annu. Rev. Phys. Chem., 2008, 59, 713–740.
30. J. Michel, J. Tirado-Rives and W. L. Jorgensen, J. Am. Chem. Soc., 2009, 131, 15403–15411.
31. J. Michel, J. Tirado-Rives and W. L. Jorgensen, J. Phys. Chem. B, 2009, 113, 13337–13346.
32. Z. Li and T. Lazaridis, Methods Mol. Biol., 2012, 819, 393–404.
33. C. N. Nguyen, T. K. Young and M. K. Gilson, J. Chem. Phys., 2012, 137, 044101.
34. C. N. Nguyen, A. Cruz, M. K. Gilson and T. Kurtzman, J. Chem. Theory Comput., 2014, 10, 2769–2780.
35. G. Gerogiokas, G. Calabro, R. H. Henchman, M. W. Y. Southey, R. J. Law and J. Michel, J. Chem. Theory Comput., 2014, 10, 35–48.
36. G. Gerogiokas, M. W. Y. Southey, M. P. Mazanetz, A. Hefeitz, M. Bodkin, R. J. Law and J. Michel, Phys. Chem. Chem. Phys., 2015, 17, 8416–8426.
37. D. J. Huggins, J. Chem. Theory Comput., 2014, 10, 3617–3625.
38. D. J. Huggins, Biophys. J., 2015, 108, 928–936.
39. E. P. Raman and A. D. MacKerell, J. Am. Chem. Soc., 2015, 137, 2608–2621.
40. S. Ramsey, C. Nguyen, R. Salomon-Ferrer, R. C. Walker, M. K. Gilson and T. Kurtzman, J. Comput. Chem., 2016, 37, 2029–2037.
41. J. D. Dunitz, Chem. Biol., 1995, 2, 709–712.
42. H. A. Yu and M. Karplus, J. Chem. Phys., 1988, 89, 2366–2379.
43. V. M. Krishnamurthy, B. R. Bohall, V. Semetey and G. M. Whitesides, J. Am. Chem. Soc., 2006, 128, 5802–5812.
44. V. Lafont, A. A. Armstrong, H. Ohtaka, Y. Kiso, L. Mario Amzel and E. Freire, Chem. Biol. Drug Des., 2007, 69, 413–422.
45. B. Baum, L. Muley, M. Smolinski, A. Heine, D. Hangauer and G. Klebe, J. Mol. Biol., 2010, 397, 1042–1054.
46. T. S. G. Olsson, J. E. Ladbury, W. R. Pitt and M. A. Williams, Protein Sci., 2011, 20, 1607–1618.
47. C. H. Reynolds and M. K. Holloway, ACS Med. Chem. Lett., 2011, 2, 433–437.
48. T. Brandt, N. Holzmann, L. Muley, M. Khayat, C. Wegscheid-Gerlach, B. Baum, A. Heine, D. Hangauer and G. Klebe, J. Mol. Biol., 2011, 405, 1170–1187.
49. A. Ferrante and J. Gorski, J. Mol. Biol., 2012, 417, 454–467.
50. N. M. King, M. Prabu-Jeyabalan, R. M. Bandaranayake, M. N. Nalam, E. A. Nalivaika, A. Özen, T. Haliloglu, N. K. Yilmaz and C. A. Schiffer, ACS Chem. Biol., 2012, 7, 1536–1546.
51. S.-R. Tzeng and C. G. Kalodimos, Nature, 2012, 488, 236–240.
52. A. Ben-Naim, J. Chem. Phys., 2013, 139, 165105.
53. M. Ahmad, V. Helms, T. Lengauer and O. V. Kalinina, J. Chem. Theory Comput., 2015, 11, 1410–1418.
54. J. D. Chodera and D. L. Mobley, Annu. Rev. Biophys., 2013, 42, 121–142.
55. K. Sharp, Protein Sci., 2001, 10, 661–667.
56. A. Cornish-Bowden, J. Biosci., 2002, 27, 121–126.
57. E. Freire, Drug Discovery Today, 2008, 13, 869–874.
58. J. E. Ladbury, G. Klebe and E. Freire, Nat. Rev. Drug Discovery, 2010, 9, 23–27.
59. A. Biela, F. Sielaff, F. Terwesten, A. Heine, T. Steinmetzer and G. Klebe, J. Med. Chem., 2012, 55, 6094–6110.
60. B. Breiten, M. R. Lockett, W. Sherman, S. Fujita, M. Al-Sayah, H. Lange, C. M. Bowers, A. Heroux, G. Krilov and G. M. Whitesides, J. Am. Chem. Soc., 2013, 135, 15579–15584.
61. M. R. Lockett, H. Lange, B. Breiten, A. Heroux, W. Sherman, D. Rappoport, P. O. Yau, P. W. Snyder and G. M. Whitesides, Angew. Chem., Int. Ed., 2013, 52, 7714–7717.
62. M. Marquart, J. Walter, J. Deisenhofer, W. Bode and R. Huber, Acta Crystallogr., Sect. B: Struct. Sci., 1983, 39, 480–490.
63. M. Böhm, J. Stürzebecher and G. Klebe, J. Med. Chem., 1999, 42, 458–477.
64. J. W. Essex, D. L. Severance, J. Tirado-Rives and W. L. Jorgensen, J. Phys. Chem. B, 1997, 101, 9663–9669.
65. R. Talhout, A. Villa, A. E. Mark and J. B. F. N. Engberts, J. Am. Chem. Soc., 2003, 125, 10570–10579.
66. S. Doudou, N. A. Burton and R. H. Henchman, J. Chem. Theory Comput., 2009, 5, 909–918.
67. D. Jiao, P. A. Golubkov, T. A. Darden and P. Ren, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 6290–6295.
68. D. Jiao, J. Zhang, R. E. Duke, G. Li, M. J. Schnieders and P. Ren, J. Comput. Chem., 2009, 30, 1701–1711.
69. I. Buch, T. Giorgino and G. De Fabritiis, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 10184–10189.
70. A. de Ruiter and C. Oostenbrink, J. Chem. Theory Comput., 2012, 8, 3686–3695.
71. V. Limongelli, M. Bonomi and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 6358–6363.
72. P. Tiwary, V. Limongelli, M. Salvalaglio and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, E386–E391.
73. N. Plattner and F. Noé, Nat. Commun., 2015, 6, 7653.
74. N. J. Alves and J. A. Kline, Biochem. Biophys. Res. Commun., 2015, 457, 358–362.
75. L. W. Cunningham, J. Biol. Chem., 1954, 211, 13–19.
76. E. Shaw, M. Mares-Guia and W. Cohen, Biochemistry, 1965, 4, 2219–2224.
77. T. Wiseman, S. Williston, J. F. Brandts and L.-N. Lin, Anal. Biochem., 1989, 179, 131–137.
78. S. A. Evans, S. Olson and J. Shore, J. Biol. Chem., 1982, 257, 3014–3017.
79. C. R. Søndergaard, M. H. Olsson, M. Rostkowski and J. H. Jensen, J. Chem. Theory Comput., 2011, 7, 2284–2295.
80. M. H. Olsson, C. R. Søndergaard, M. Rostkowski and J. H. Jensen, J. Chem. Theory Comput., 2011, 7, 525–537.
81. J. M. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174.
82. C. I. Bayly, P. Cieplak, W. Cornell and P. A. Kollman, J. Phys. Chem., 1993, 97, 10269–10280.
83. M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25.
84. V. Hornak, R. Abel, A. Okur, B. Strockbine, A. Roitberg and C. Simmerling, Proteins, 2006, 65, 712–725.
85. K. Lindorff-Larsen, S. Piana, K. Palmo, P. Maragakis, J. L. Klepeis, R. O. Dror and D. E. Shaw, Proteins, 2010, 78, 1950–1958.
86. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935.
87. C. Caleman, P. J. van Maaren, M. Hong, J. S. Hub, L. T. Costa and D. van der Spoel, J. Chem. Theory Comput., 2012, 8, 61–74.
88. G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101.
89. H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690.
90. S. Páll and B. Hess, Comput. Phys. Commun., 2013, 184, 2641–2650.
91. U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593.
92. S. Miyamoto and P. A. Kollman, J. Comput. Chem., 1992, 13, 952–962.
93. B. Hess, J. Chem. Theory Comput., 2008, 4, 116–122.
94. W. F. van Gunsteren and H. J. C. Berendsen, Mol. Simul., 1988, 1, 173–185.
95. D. L. Mobley, J. D. Chodera and K. A. Dill, J. Chem. Phys., 2006, 125, 084902.
96. M. K. Gilson, J. A. Given, B. L. Bush and J. A. McCammon, Biophys. J., 1997, 72, 1047–1069.
97. Y. Deng and B. Roux, J. Phys. Chem. B, 1997, 113, 2234–2246.
98. C. Chipot, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 71–89.
99. C. Bennett, J. Comput. Phys., 1976, 22, 245–268.
100. P. V. Klimovich, M. R. Shirts and D. L. Mobley, J. Comput.-Aided Mol. Des., 2015, 29, 397–411.
101. M. R. Shirts and J. D. Chodera, J. Chem. Phys., 2008, 129, 124105.
102. G. J. Rocklin, D. L. Mobley, K. A. Dill and P. H. Hünenberger, J. Chem. Phys., 2013, 139, 184103.
103. D. Hamelberg and J. A. McCammon, J. Am. Chem. Soc., 2004, 126, 7683–7689.
104. Y. Lu, C.-Y. Yang and S. Wang, J. Am. Chem. Soc., 2006, 128, 11830–11839.
105. R. Talhout and J. B. Engberts, Eur. J. Biochem., 2001, 268, 1554–1560.
106. D. W. Gohara and E. Di Cera, Trends Biotechnol., 2011, 29, 577–585.
107. N. Pozzi, A. D. Vogt, D. W. Gohara and E. Di Cera, Curr. Opin. Struct. Biol., 2012, 22, 421–431.
108. W. Ma, C. Tang and L. Lai, Biophys. J., 2005, 89, 1183–1193.
109. J. J. Perona, L. Hedstrom, W. J. Rutter and R. J. Fletterick, Biochemistry, 2005, 89, 1183–1193.
110. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
111. B. Hess, J. Chem. Phys., 2002, 116, 209–217.
112. B. Hess and N. F. A. van der Vegt, J. Phys. Chem. B, 2006, 110, 17616–17626.
113. A. Fenley, N. M. Henriksen, H. S. Muddana and M. K. Gilson, J. Chem. Theory Comput., 2014, 10, 4069–4078.
114. K. Sharp, J. Chem. Theory Comput., 2013, 9, 1164–1172.
115. T. Hajari and N. F. A. van der Vegt, J. Chem. Phys., 2015, 142, 144502.
116. P. C. Sanschagrin and L. A. Kuhn, Protein Sci., 1998, 7, 2054–2064.
117. R. L. Mackman, B. A. Katz, J. G. Breitenbucher, H. C. Hui, C. Luong, L. Liu and P. A. Sprengeler, J. Med. Chem., 2001, 44, 3856–3871.
118. C. A. Bottoms, T. A. White and J. J. Tanner, Proteins, 2006, 64, 404–421.
119. A. Ben-Naim and Y. Marcus, J. Chem. Phys., 1984, 81, 2016–2027.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp07899k

‡ Equal contribution to this work.

§ E.g., for pure water, the average number of solvent molecules within 0.8 nm of the COM of PAB drops from 64.8 to 17.1 upon binding.

---