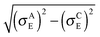Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Modelling of the charge carrier mobility in disordered linear polymer materials†
Petr
Toman
 *a,
Miroslav
Menšík
a,
Wojciech
Bartkowiak
b and
Jiří
Pfleger
a
*a,
Miroslav
Menšík
a,
Wojciech
Bartkowiak
b and
Jiří
Pfleger
a
aInstitute of Macromolecular Chemistry, Academy of Sciences of the Czech Republic, v.v.i., Heyrovský Sq. 2, 162 06 Prague 6, Czech Republic. E-mail: toman@imc.cas.cz
bDepartment of Physical and Quantum Chemistry, Faculty of Chemistry, Wrocław University of Science and Technology, Wyb. Wyspiańskiego 27, 50-370 Wrocław, Poland
First published on 20th February 2017
Abstract
We introduced a molecular-scale description of disordered on-chain charge carrier states into a theoretical model of the charge carrier transport in polymer semiconductors. The presented model combines the quantum mechanical approach with a semi-classical solution of the inter-chain charge hopping. Our model takes into account the significant local anisotropy of the charge carrier mobility present in linear conjugated polymers. Contrary to the models based on the effective medium approximation, our approach allowed avoiding artefacts in the calculated concentration dependence of the mobility originated in its problematic configurational averaging. Monte Carlo numerical calculations show that, depending on the degree of the energetic and structural disorder, the charge carrier mobility increases significantly with increasing charge concentration due to trap filling. At high charge carrier concentrations, the effect of the energetic disorder disappears and the mobility decreases slightly due to the lower density of unoccupied states available for the hopping transport. It could explain the experimentally observed mobility degradation in organic field-effect transistors at high gate voltage.
Introduction
Improvement in the performance of organic field-effect transistors (OFETs) is a critical research issue required for increasing their applicability in printable organic devices, particularly in thin flexible displays, wearable electronics and radio-frequency identification (RFID) tags.1–3 Contrary to inorganic semiconductors there are several drawbacks that limit the performance of OFETs, such as low charge carrier mobility and limited lifetime of free charge carriers. Understanding physical processes, which influence the charge carrier transport in organic materials, is hence an important prerequisite for the optimization of the chemical structure and morphology of materials for the OFET active channel and for the optimization of the device geometry.Several papers have appeared recently, which deal with the sensitivity of the charge carrier mobility in semiconducting polymers or low molecular weight semiconductors to their molecular structure, charge carrier concentration, presence of traps, etc.4–6 The increase of the charge carrier mobility with increasing gate voltage was assigned to trap filling7 and the decrease of mobility at higher voltages to the reduced mobility of charges at the boundary between the semiconductor and insulator due to the presence of various scattering agents.8
Unlike crystalline inorganic semiconductors, polymers are mostly disordered materials, which has a significant impact on their charge carrier mobility. Poly(3-hexylthiophene-2,5-diyl) (P3HT) deposited from solutions forms a complex structure with locally well-ordered crystalline domains of size from tens to several hundreds of nanometres depending on the preparation conditions, in which P3HT is packed in a lamellar arrangement. These crystalline domains are separated by disordered amorphous regions (see e.g.ref. 9 and references therein). Even optimizing the preparation procedure or employing a postprocessing treatment leads to polymer layers with amorphous regions, which play a significant role as a bottleneck deteriorating the long-distance charge carrier transport. Even in crystalline domains the polymer is subjected to thermal disorder, which has an impact on the localization of electronic states and, hence, on the charge carrier transport.10
The structural disorder is predominantly given by the disorder in torsion angles between adjacent repeat units of individual π-conjugated polymer chains. This structural disorder can be described using either an approximation of rod-like polymer segments or a continuous disorder model. While the former model assumes a polymer chain composed of rather short ideally ordered rod-like chain segments mutually separated by structural defects, the latter assumes a long polymer chain possessing random structural perturbations between any adjacent repeat units. The model based on rod-like segments is more suitable for the description of well-ordered crystalline domains. For an amorphous phase the continuous disorder model seems to be more relevant.
Despite the above mentioned structural disorder, it should be noted that conformations of the conjugated thiophene repeat units are rather rigid and mutual interactions of frontier orbitals of adjacent units in a polymer chain are relatively strong amounting to several tenths of eV, depending on their mutual torsion. Consequently, the charge carriers may be significantly delocalized. Furthermore, thiophene rings of neighbouring polymer chains in the crystalline domain exhibit a strong π–π interaction, which supports ordering of polymer backbones into the π-stack structure perpendicular to the chain direction (see Fig. 1).4,5,11 Finally, the alkyl side-chains are packed by van der Waals interactions in the third dimension. Chain folding together with a rather small width of nanofibers (ca. 20 nm) limits the on-chain charge carrier transport. Thus, the P3HT crystal structure shows significant structural and, consequently, electrical anisotropy with the preferential charge carrier transport in the stack direction and poor charge transport in the side-chain direction. Hence, a suitable model for the charge carrier transport should reflect both the quantum mechanical nature of the on-chain charge carrier state delocalization and the inter-chain hopping mechanism, which can be described in a semi-classical way.
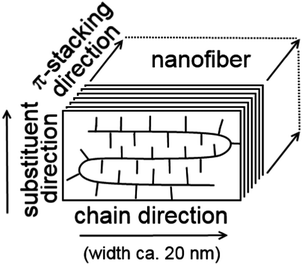 | ||
| Fig. 1 Schematic depiction of the P3HT chains packed in a lamellar arrangement forming a nanofiber in the π-stacking direction. | ||
Our approach presented in this work was inspired by the Gaussian disorder model (GDM) introduced by Bässler12 for disordered organic photoconductors. His model considers a 3D lattice of single-state sites possessing Gaussian energetic disorder. The jump rates among these sites are described by means of the Miller–Abrahams relation.13 This relation is appropriate for systems in which polaronic effects can be neglected and, simultaneously, the electron–phonon coupling is strong enough to allow for the charge carrier thermalization between the subsequent jumps. The inter-site coupling parameters are decomposed into site-specific randomized ones. Consequently, the model considers also a Gaussian geometric (off-diagonal) disorder. A similar GDM based approach was also used by Fishchuk et al.14–18 for their analytic solution of the charge carrier transport. Several authors19–21 studied the charge carrier concentration dependent mobility in PPV-based polymers. Using the GDM approach they provided a unified description of the charge carrier transport at both the low charge carrier concentration and field-effect transistor (FET) accumulation regimes. Their theoretical models were successfully used for the description of current–voltage characteristics of polymer-based diodes.
Arkhipov et al.22 used the concept of the effective transport energy in order to formulate an analytic model to describe the effects of traps and high carrier densities on the equilibrium weak-field carrier hopping in disordered organic materials. Although their method should be applicable also to other analytic forms of the density of states (DOS), they considered only the Gaussian one. Schmechel23,24 used a GDM with the “transport energy concept” for description of high carrier densities in p-doped zinc-phthalocyanine (ZnPc) and compared his results with experimental data published by Maenning et al.25 Since ZnPc is a small molecule with inter-molecular transfer integrals smaller than the value of the energetic disorder, the use of a GDM is fully appropriate. As an alternative to the GDM, an exponential DOS distribution was used by some authors for the modelling of OFET characteristics.26,27
Among theoretical methods starting from an analytic form of the DOS the most successful one so far is the percolation approach.28,29 Using percolation theory and the concept of hopping in an exponential tail DOS Vissenberg and Matters30 derived an analytic expression for the field-effect mobility in a thin-film transistor of an amorphous organic semiconductor. Although exponential tail DOS is relevant rather for amorphous inorganic semiconductors, they claim a good agreement of the calculated temperature and gate voltage dependence with those observed in pentacene and poly(thienylene vinylene) thin films. Baranovskii et al. showed that the percolation approach gives results that are in an excellent agreement with those obtained by using a more transparent, though less rigorous, approach based on the concept of transport energy.31,32
The percolation theory provides a very strong analytic tool and in many cases it can very successfully explain experimental charge carrier transport in polymers composed of stacked π-conjugated segments and containing both crystalline and amorphous domains with additional dipolar traps. However, it can lead to problems in the interpretation of the microscopic origin of the energy disorder in DOS and mobility dependence on charge concentration. This comes from the approximations on which the percolation theory is based, namely neglecting the dependence of the transfer integral (preexponential factor in the Marcus or Miller–Abrahams transfer rate equation) on the disorder, neglecting the delocalization of the percolation sites, and presence of the manifold of hopping energy levels (i.e. several hopping rates between two percolation sites).
Shaked et al.33 published a study of the effect of the molecular weight of poly[2-methoxy-5-(2-ethylhexyloxy)-1,4-phenylenevinylene] (MEH-PPV) on its charge transport properties in field-effect transistors, which uses a GDM extended by Roichman and Tessler.34,35 Although they claimed qualitative agreement with the experimental data for both the light emitting diodes and FETs, they also stated that as more material information becomes available (such as the DOS), exact modeling and data fitting may become a valid task.
In common organic materials the thermal energy kT at room temperature is smaller than the value of the energetic disorder and, hence, the shape of the DOS spectrum plays a crucial role in the charge transport and it should be determined.36 Although some authors claim30 that there is no principal difference in the concentration dependence of the mobility for various steep DOS functions, Nenashev et al.36 showed that for the Gaussian DOS there is a threshold concentration nc below which the mobility saturates, while it always increases for the exponential DOS. Furthermore, Oelerich et al.37 showed that the threshold concentration nc drastically depends on the shape of DOS.
While various GDMs or other approaches based on analytic forms of the DOS have been successful as satisfactory phenomenological models with just a few empirical parameters, they are obviously incorrect at the molecular-scale level, namely due to their failure to properly describe delocalized on-chain charge carrier states in conjugated polymers and corresponding density of states. An interesting step forward is a molecular-scale extension of the GDM, designed recently by Kordt et al.38,39 for low-molecular-weight materials. Their approach is based on a hierarchical set of models, starting with the calculation of the chemical structure and ending with the prediction of macroscopic properties of devices. An alternative approach was used by Zhao et al.40 and Hu et al.41 in their theoretical investigations of pentacene and 5,6,7-trithiapentacene-13-one (TTPO) derivatives, respectively. Their incoherent hopping model takes into account local anisotropy of molecular crystals, but it completely neglects structural and energetic disorder. Another recent example of the molecular-scale extension of the GDM applied on low-molecular-weight materials is a detailed calculation procedure suggested by Deng et al. in Nature Protocols,42 or the work published by Yavuz et al.,43,44 in which the parameters of Gaussian DOS were obtained for the crystal structures calculated using molecular dynamics.
In the models described above all molecules are represented by a single energy level. This is, however, not appropriate for linear conjugated systems, in which the DOS function is composed of delocalized states. In reality, the charge transfer between nearest polymer chains should include the charge transfer between sets of all delocalized eigenstates on both polymer chains. As the Marcus formula is sensitive to both eigenenergy and eigenstate functions (determining inter-chain transfer integral) and the occupation of states in both chains depends on the hole concentration, inclusion of both DOS functions can introduce a relevant sensitivity of the mobility to the hole concentration. Next, the standard Marcus (or Miller–Abrahams) approach neglects the adiabatic coupling of electronic eigenstates to nuclear degrees of freedom along the charge transfer pathway and sets the transfer integral between initial and final configurations independent of nuclear coordinates. In our approach, we will introduce a correction to the Marcus theory by considering an adiabatic coupling of electronic eigenstates to torsional angles in the amorphous phase of the polymer chain.
It follows from the paragraphs above that knowing the suitable DOS is crucial for the correct description of the charge transport. Key factors influencing the DOS shape are disorder in site energies, average values and disorder in transfer integrals among sites, periodicity and the general topology of the system. Hence, the following steps are necessary for DOS determination: (i) careful analysis of the system to select a suitable type of the transport (band model, hopping model, etc., see e.g.ref. 45 for details) and to select suitable model sites, among which the charge carriers move, (ii) quantum chemical calculations or molecular dynamics simulations to obtain molecular parameters of the transport sites, and (iii) construction of a molecular-scale model of the transport. Parameters of such models are clearly connected with particular microscopic properties of the molecules.
It should be noted that disorder in site energies and disorder in transfer integrals usually depend not only on the chemical structure of the material, but also on the particular preparation procedure and further processing and storage of the sample. On the other hand, if models designed for small molecules are directly applied to the conjugated polymers, they can in some cases sufficiently mimic many experimental data, but the connection between the model parameters and the microscopic molecular properties remains obscure.
To the best of our knowledge, there has not been reported yet any molecular-scale model for linear conjugated polymers that could yield the charge carrier concentration-dependent mobility. In our work we extend our previous model46 by seeking a more realistic description of the charge carrier on-chain states calculated by means of the eigensolution of the electronic delocalized states of the Hamiltonian explicitly reformulated in the monomer site orbital representation for the following reasons: (a) it enables a direct estimate of the influence of additives on the electronic DOS at given geometry due to the explicitly controlled shift of the local site energies. (b) Inclusion of adiabatically coupled torsional angles influencing on-chain transfer integrals and DOS. (c) Correct inclusion of transfer integrals between polymer chains for explicitly specified mutual arrangement. In contrast to the previous fully phenomenological GDMs, our model includes ab initio description of the molecular-scale (chemical) structure of the material. On the other hand, the description of the meso-scale structure of crystal grains and amorphous grain boundaries stays on a phenomenological level, since it is significantly influenced by the sample preparation procedure (e.g. annealing). Although the numerical calculations are shown only for P3HT, this approach can be adopted also for modelling the charge carrier mobility in other linear conjugated polymers.
Description of the model
Charge carrier on-chain states
The oligothiophene main chain is modelled as a sequence of N interacting sites (thiophene repeat units), which can be occupied by a charge carrier. Since P3HT is a hole-transporting material, only holes will be taken into account. For simplicity, the charge carrier on-chain states can be described within the tight-binding approximation by Hamiltonian (although it can be extended by an inclusion of adiabatic coupling to relevant nuclear modes and Coulombic repulsion and exchange corrections for high hole densities)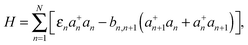 | (1) |
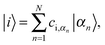 | (2) |
Site energies
In the first approximation, the local site energy of the hole located at a repeat unit is equal to the ionization potential of this repeat unit, and its interactions with the neighbour sites of the polymer can be neglected. Since the zero-energy level in the Schrödinger equation is not a priori fixed and all P3HT repeat units are identical from the chemical point of view, we put the energy reference level in the position of the ionization potential of the isolated thiophene unit. In a real polymer, the local site energies are modified by the Coulomb interaction of the hole with all charges present in the neighbourhood. Assuming frozen orbital approximation by analogy to the Koopmans' theorem derivation, it can be easily found that the perturbation Δε of the site energy caused by the presence of neighbouring charged species is equal to the electrostatic potential energy VCol of the hole averaged over the highest occupied molecular orbital |HOMO〉| Δε = 〈HOMO|VCol|HOMO〉. | (3) |
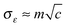 characterizing the width of the Gaussian distribution of Δε. The value of the parameter σε should be chosen also with respect to the possible presence of some other accidental impurities.
characterizing the width of the Gaussian distribution of Δε. The value of the parameter σε should be chosen also with respect to the possible presence of some other accidental impurities.
In order to properly include the above mentioned site-to-site correlation into our on-chain state model, the distribution of Δε was calculated as follows. Randomly oriented point dipoles were randomly placed in the vicinity of the polymer chain. Taking into account the size of the substituents, no dipole was placed at a distance shorter than 10 Å from the polymer backbone. The influence of dipoles located at a distance longer than 50 Å from the polymer chain was neglected. Dipoles were also placed far enough beyond the chain ends in order to ensure the homogeneity of the Δε distribution along the whole chain. Then, local energies εn of a hole residing at single repeat units of the chain were calculated as the sum of potentials from all dipoles. The values of the dipole moment m and the concentration c of the dipoles were adjusted to get values of the model parameter σε (Gaussian width) from zero to 0.2 eV with a step of 0.05 eV.
We are aware of the fact that this model of the local energetic disorder is rather approximate. However, as explained above, energetic disorder in a particular sample depends on many factors, which cannot be analysed within the scope of this paper. Besides the charge–dipole interactions it may also include relatively strong charge–ion interactions in doped polymers. On the other hand, our model presented below is applicable to any arbitrary local energetic disorder and it at least attempts to correlate the model parameters to the molecular structure.
On-chain charge transfer integrals
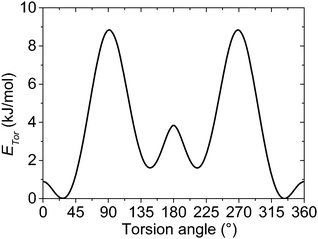
Similar to the on-site energy the on-chain transfer integrals are also subjected to a distribution, which substantially differs for the crystalline and amorphous phases of P3HT. For the crystalline phase, our rod-like model is based on the lowest-energy structure I(LL) calculated by Xie et al.49 The parameters of this orthorhombic lattice model show a good agreement with X-ray diffraction and electron diffraction measurements.50,51 Such ideal crystal structure assumes no torsion between adjacent repeat units within the rod-like chain segment, which is a consequence of the stabilization of the chain by relatively strong π–π stacking interaction and a regular packing of the alkyl substituents.For the amorphous phase, the torsion angle distribution similar to that in a solution is considered. In this case the on-chain torsional disorder is governed mainly by the mutual interaction of the adjacent repeat units. Disordered alkyl side chains are assumed to act rather as spacers among neighbouring polymer chains preventing them from the π–π stacking interactions. Our idealized model does not take into account the possible presence of an intermediate phase with a partially ordered structure on the crystal grain boundaries. For these reasons, the inter-unit torsion angles between repeat units in the amorphous phase are sampled by the Boltzmann distribution using the rotational potential energy profiles of the unsubstituted polythiophene, similarly to what was suggested by Grozema for P3HT in solutions.52 We are aware of the fact that neglecting the influence of the side chain interactions on the potential energy profiles can yield more significant errors in the amorphous phase than in the solution. On the other hand, neglecting dynamic fluctuations of the polymer chain in this static disorder model is acceptable for the solid state. The molecular geometries of the unsubstituted bithiophene as a model of the most simplified P3HT chain were calculated using the second order Møller–Plesset perturbation theory (MP2) and Dunning's cc-pVDZ basis set.53 A fully relaxed potential energy surface scan was done for the inter-unit torsion angle with a step of 1°. A single point energy calculation was done for each torsion angle at the MP2/aug-cc-pVTZ level (see Fig. 2).
The values of the effective charge-transfer integrals bn,n+1 corresponding to different torsion angles were calculated by means of the fragment orbital approach.54,55 The BPW91 density functional combining the Becke's exchange56 and the Perdew–Wang's correlation part57–61 was used together with the aug-cc-pVTZ basis set and previously optimized geometries. This functional or its variations, like BP86, are often chosen for the charge-transfer integral calculations, see e.g.ref. 54, 62 and 63. The fragment orbital calculation of the transfer integrals is superior to the alternative energy level splitting-in-dimer method because it does not rely on the zero spatial overlap between initial and final states. Although the fragment orbital method is implemented in the Amsterdam Density Functional (ADF) theory program,64–66 its implementation is intended exclusively for the studies of separated closed-shell molecules. For this reason, the effective transfer integrals between the thiophene units in bithiophene were calculated within Gaussian 0967 using the procedure described in the ESI.† The resulting dependence of the hole transfer integral on the inter-unit torsion angle is shown in Fig. 3.
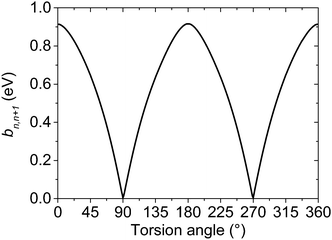 | ||
| Fig. 3 Effective on-chain hole charge transfer integral bn,n+1 between thiophene repeat units as a function of the inter-unit torsion angle calculated at the BPW91/aug-cc-pVTZ//MP2/cc-pVDZ level. | ||
Density of valence band states
The calculated densities of the valence band energy states of the crystalline phase are shown in Fig. 4 for different values of the local energetic disorder. Without an energetic disorder the valence band consists of a discrete spectrum of hole energy levels, which follow the well-known relation for eigenenergies of linear polyenes.68 With the increasing value of the local energetic disorder, these discrete levels are broadened and, finally, interconnected into one continuum band with a local minimum in the centre of the band.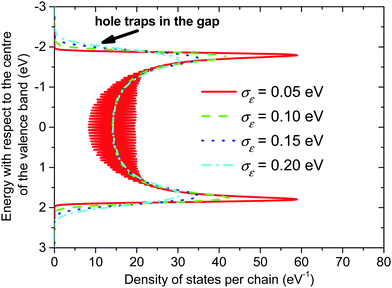 | ||
| Fig. 4 Valence band of the crystalline phase of P3HT. The length of the conjugated chain segment was N = 80. | ||
On the other hand, presence of a significant torsional disorder in the amorphous phase gives rise to a continuum valence band even without introducing a local energetic disorder (see Fig. 5, σε = 0 eV). Additionally, the torsional disorder leads to the creation of a distinct peak in the centre of the valence band, which is almost isoenergetic for σε = 0 eV but it broadens and decreases with the increasing value of the local energetic disorder.
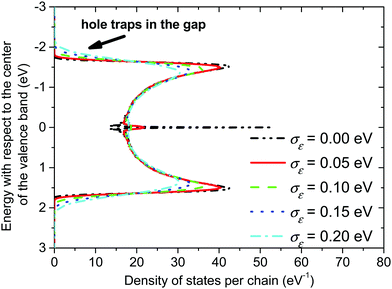 | ||
| Fig. 5 Valence band in the amorphous phase of P3HT. The length of the conjugated chain segment was N = 80. | ||
In both crystalline and amorphous phases, the overall shape of the valence band significantly differs from the Gaussian one. However, the valence band edge slope may be quite well approximated by a Gaussian distribution function. Consequently, using the Gaussian disorder approximation may be acceptable for the description of the charge carrier transport at low charge carrier concentrations,12,14–17,19–21 but it becomes questionable under the conditions in FETs, where the charge carrier concentrations may reach values higher than 10−2 of the charge carrier per repeat unit (i.e. 10−1 nm−3). The critical value of the charge concentration, where GDM fails, is closely correlated with the maximum of DOS of delocalized states without structural disorder. The fitted Gaussian widths (standard deviations) σE for different values of the local energetic disorder σε in the crystalline and amorphous phases are shown in Table 1. For the crystalline phase the values of widths of the energetic disorder σCE are superlinear with respect to the values of σε, which are directly obtained from the microscopic modelling. For the amorphous phase the widths σAE are higher due to the presence of the torsional disorder, but the difference σAE − σε is quite random. Moreover, neither σAE − σCE nor 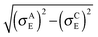 provides an additive term to the crystalline disorder influenced by the torsional angles. Note that in the GDM12 the values of the local energetic disorder σε are identical to the Gaussian widths σE of the valence band. Hence, even if experimentally determined DOSs are phenomenologically well fitted by the GDM the origin of the width with respect to the influence of additives or torsional angles is practically unclear.
provides an additive term to the crystalline disorder influenced by the torsional angles. Note that in the GDM12 the values of the local energetic disorder σε are identical to the Gaussian widths σE of the valence band. Hence, even if experimentally determined DOSs are phenomenologically well fitted by the GDM the origin of the width with respect to the influence of additives or torsional angles is practically unclear.
| σ ε | σ CE | σ AE | σ AE − σε | σ AE − σCE | |
|---|---|---|---|---|---|
| Crystalline | Amorphous | ||||
| a Energy levels in the crystalline model without energetic disorder are discrete lines. The band edge slope is in this case sharp and can be fitted by a degenerate Gaussian function with a zero width. | |||||
| 0.00 | 0.000a | 0.067 | 0.067 | 0.067 | 0.067 |
| 0.05 | 0.051 | 0.094 | 0.044 | 0.043 | 0.078 |
| 0.10 | 0.105 | 0.139 | 0.039 | 0.034 | 0.099 |
| 0.15 | 0.162 | 0.189 | 0.039 | 0.027 | 0.097 |
| 0.20 | 0.224 | 0.247 | 0.047 | 0.023 | 0.104 |
Polymer chain alignment
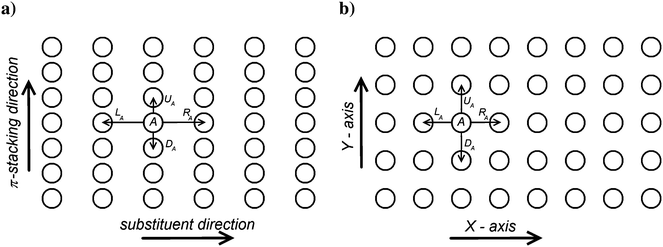
Each polymer chain segment in P3HT crystals adjoins four other chains4,5,10 as schematically depicted in Fig. 6a. This simplified three-dimensional polymer structure can be described as an array of parallel polymer chain segments of a given length N, regularly placed with a shorter inter-chain distance of 3.85 Å in the π-stacking direction and a distance of 17.24 Å in the substituent direction, respectively.It should be noted that within the crystalline phase rod-like model the length N corresponds to the effective conjugation length of the polymer and not to the distance between the chain chemical defects. Each polymer chain is characterized by a set of its eigenstates |i〉 (see eqn (2)), in which a charge carrier can be found. Only the transitions between four nearest neighbour chains are taken into account. In Fig. 6 the corresponding transfer hopping rates from chain A are denoted as LA, RA, DA, and UA, respectively. The crystal is considered as infinite in the two dimensions perpendicular to the chains, with 20 × 20 independent chains in an “elementary cell”. Mutual positions of the chains in our calculations are taken according to the model I(LL) proposed by Xie et al.49
In the amorphous phase we assume a random distribution of the on-chain torsion angles (vide supra). Consequently, the positions of adjacent chains are disordered, too. The disordered bulky aliphatic substituents prevent closer contacts of thiophene repeat units of adjacent chains. For this reason, for the inter-chain hopping our model assumes randomly oriented repeat units of neighbouring chains placed at an average distance ddens calculated from the polymer density ρ = 1.1 g cm−3 and molar weight of the repeat unit Mm = 168.3 g mol−1. Similarly to the crystalline phase four nearest neighbouring chains are considered for each polymer chain. Then,
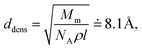 | (4) |
Inter-chain charge transfer integrals
Transfer integrals Jαβ between the repeat units α and β of neighbouring chains were calculated by means of the fragment orbital approach with the same density functional BPW91 used for the calculation of the intra-chain transfer integrals (vide supra). These two repeat units were treated as isolated closed-shell molecules. This assumption made it possible to use the Amsterdam Density Functional (ADF) theory program64–66 and directly calculate the transfer integrals. ADF uses Slater-Type Orbitals (STOs) as atomic basis functions. Slater basis functions resemble the true atomic orbitals more closely than Gaussian basis functions used by majority of quantum chemistry programs. STOs can display the correct nuclear cusp and asymptotic decay. This leads to a more accurate and more intuitive description of the molecular orbitals at the same size of the basis set. While the correct description of the asymptotic decay of molecular orbitals has no significant meaning for intra-chain transfer integrals, it is very important for the calculation of the relatively small overlap and transfer integrals of separated molecules. ADF calculations were done using the AUG/ATZ2P basis set, good quality Becke grid for numerical integration and good quality density-fitting scheme (so-called Zlm Fit). For the exchange–correlation potential the true density was used instead of the fitted one (default setting in ADF) in order to get more accurate and stable results.Then, inter-chain transfer integrals Jij between the charge carrier delocalized states i and j located on adjacent chains can be calculated from the expansion coefficients ci,α and cj,β of the states i and j, respectively, and from the transfer integrals Jαβ between the repeat units α and β of the chains A and B, respectively:
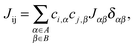 | (5) |
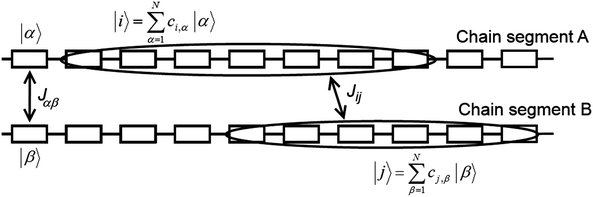 | ||
| Fig. 7 Details of two neighbouring polymer chains A and B. Letters α and β denote repeat units of chains A and B, respectively, and i and j are the on-chain hole states. | ||
Inter-chain hopping in crystalline or amorphous phase
The extent of the charge carrier localization plays a major role in the selection of a suitable model of charge carrier transport. In the case of delocalized charges it is usually possible to neglect the charge carrier interactions with the nuclear lattice in the first approximation. However, in the case of localized charges it is important to take the charge carrier thermalization into account. On a molecular scale, these two cases differ by the relative values of the transfer integrals between neighbouring sites and their energetic disorder: the delocalization is observed for bigger transfer integrals whereas energetic disorder is responsible for more pronounced localization. While the motion of the delocalized charges should be generally treated by means of quantum mechanical methods, localized charges lose their quantum coherence due to thermalization and thus the semi-classical methods are more appropriate. The band model is usually not suitable for polymers, unless the polymer is really perfectly ordered like, for example, in the case of planar ladder-type conjugated polymers exhibiting an extra-high intra-chain charge carrier mobility of several hundreds of cm2 V−1 s−1.69Since the inter-chain transfer is slower than the charge carrier thermalization, which occurs typically on a time scale of several picoseconds, charge carriers thermalize to the Fermi–Dirac distribution over all delocalized states of the given chain segment between two subsequent inter-chain hops. Since we address here also the charge transport under rather high charge carrier densities, as e.g. in the FET channel, the simplified Boltzmann statistics adopted in our previous model46 cannot be applied.
Hence, we can describe the charge carrier transport as consisting of the following steps: (i) hole moving to any possible state on the chain segment A, (ii) thermalization of the hole over all its possible states on the chain segment A, and (iii) hop of the hole to any possible state on one of the nearest neighbouring chain segments B. Longer hops can be safely neglected due to the corresponding negligible transfer integrals. Thus, the occupation probability pi(Ei) of the state i with energy Ei of the chain segment A follows just a simple Fermi–Dirac distribution with EFA being the local Fermi energy at that particular chain segment A.
A conjugated polymer chain conformation is relatively soft and undergoes significant deformation in the case of an excess of charge, which leads to a polaron formation. The polaron hopping rate νi→j between an initial state i with the energy Ei on chain A and a final state j with the energy Ej on an adjacent chain B can be calculated using a semi-classical Marcus approach:70
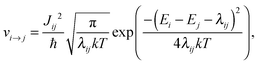 | (6) |
From the charge transfer rates νi→j between two states and the thermalized occupation probabilities pi and pj of the initial and final state the charge hopping probability TA→B between two adjacent chains A and B can be easily calculated:
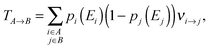 | (7) |
Determining the TA→B values makes it possible to construct the master equation describing the inter-chain charge carrier motion
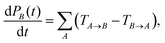 | (8) |
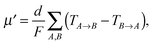 | (9) |
Results and discussion
Concentration dependent hole mobility
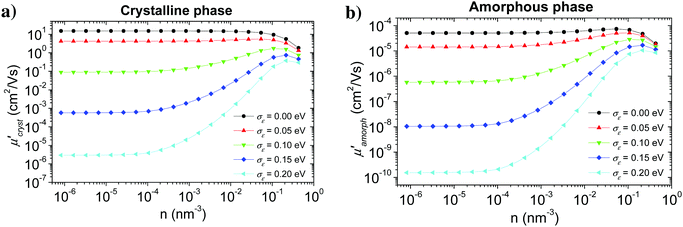
The calculation started with a very small hole concentration, for which the Boltzmann distribution can be used, and proceeded with gradually increasing (doubling) the hole concentration using the results of the previous step as an initial estimate of hopping probabilities TA→B and the distribution of charge carriers PA(t).Fig. 8 shows the calculated hole mobility as a function of the hole concentration for various values of the energetic disorder in crystalline (a) and amorphous (b) phase. Calculation was done for an external electric field 107 V m−1 oriented in the π-stacking direction in the crystalline phase and along one of the axes in the amorphous phase (see Fig. 6). Our numerical modelling proved that the hole mobility in the substituent direction in the crystalline phase can be neglected, because of very small inter-segment transfer integrals.
While shapes of the calculated dependence are similar for both the crystalline and amorphous phases, the values of the mobility in the crystal are about five orders of magnitude higher than in the amorphous material. It is in agreement with many experimental findings that an improved molecular ordering, achieved e.g. by solution ageing before layer deposition, or using a solvent mixture, significantly increases the charge carrier mobility.73,74 In the case of no energetic disorder, there is almost no concentration dependence of the mobility up to about n ∼ 10−2 nm−3 for both phases. For higher concentrations the mobility slightly decreases due to the lower density of unoccupied states with the energy suitable for the hopping transport. An increase in the value of the energetic disorder leads to a decrease in the hole mobility by several orders of magnitude due to the charge carrier trapping. Charge carrier concentration dependence shows that this effect is strongly reduced at hole concentrations higher than 10−4 nm−3, which can be explained by the charge carrier trap filling.
Orientation of crystalline domains in real polymer films is usually highly disordered. For the crystalline phase the mobility in the π-stacking direction is much higher than the mobility in the two perpendicular directions. Thus, for crystalline domains randomly oriented with respect to the external electric field, the mean projection of the length of the hopping vector d (identical with the lattice vector in the π-stacking direction) to the direction of the electric field can be calculated by integration over the whole sphere Ω resulting in the hole mobility μcryst through the randomly oriented crystalline domains
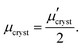 | (10) |
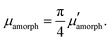 | (11) |
Charge carrier transport in polycrystalline materials
Charge carrier transport in polycrystalline materials proceeds predominantly through the randomly oriented crystalline domains connected by the amorphous phase with much lower conductivity. Then, the charge carrier mobility can be calculated as a weighted harmonic mean value of mobilities μcryst and μamorph obtained for the amorphous and crystalline phases, respectively,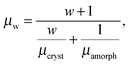 | (12) |
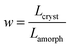 corresponds to the ratio of the total lengths Lcryst and Lamorph of the paths travelled by the charge in the crystalline and amorphous phase, respectively.
corresponds to the ratio of the total lengths Lcryst and Lamorph of the paths travelled by the charge in the crystalline and amorphous phase, respectively.
Concentration dependence of the hole mobility in a polycrystalline material with the local energetic disorder σε = 0.1 eV (typical value for conjugated polymers without admixed polar additives75,76) for different weight factors w of the crystalline phase is shown in Fig. 9. While the absolute values of the mobility μw depend on the parameter w, the shapes of all curves (except for a pure crystalline material) are almost the same, given by the concentration dependence of the mobility in the amorphous phase. This fact comes from the harmonic averaging of two very different numbers. Note that the parameter w depends not only on the volume ratio of both phases, but also on the shape of the crystalline domains and their percolation. Because the detailed structure of a real material is usually unknown, this parameter can be hardly determined. For these reasons, we suggest estimating w from the low charge carrier concentration limit of the mobility of the particular sample.
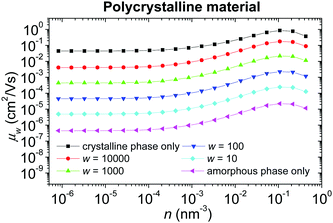 | ||
| Fig. 9 Concentration dependence of the hole mobility in the polycrystalline material with local energetic disorder σε = 0.1 eV for different weight factors w of the crystalline phase. | ||
Limitations of the model
The suggested model is based on several simplifications, namely on the structural simplifications in the inter-chain hopping description and on neglecting the possible inter-chain delocalization of hopping states. Taking a constant inter-chain distance ddens (see eqn (4)) in the amorphous phase model can be seen as inappropriate. We have also tested the dependence of the mobility on the distribution of inter-chain transfer integrals and we have found that the hopping mobility depends on the average magnitude of the inter-unit transfer integrals Jαβ in the electric field direction, but it is almost independent of the shape of the Jαβ distribution. This finding can be explained by “averaging” the inter-unit transfer integrals Jαβ in the calculation of the inter-chain transfer integrals Jij according to eqn (5).Neglecting the possible inter-chain delocalization of the hopping states is definitely correct for the amorphous phase, but it may be questionable for the crystalline phase due to the relatively strong π-stacking interaction. However, according to the recent study of the effect of the wave function localization in π-stacked P3HT chains published by Mladenović et al.10 the thermal disorder in the main chains is present also in the crystalline phase, which leads to the localization of hole states usually only on two neighbouring chains. For this reason, we do not expect a significant influence of the possible inter-chain delocalization of the hole states. Moreover, the bottleneck of the charge carrier transport in real (polycrystalline) samples is in the amorphous phase located in the space between nanofibers. Further simplifications include neglecting dynamic fluctuations and mutual interaction between charge carriers caused by a quasi-inhomogeneity of the charge carrier density, and assuming full charge carrier thermalization when calculating the on-chain energy states. It should be noted that similar imperfections are commonly observed also in most models based on the Gaussian disorder.
Outlook for the model
Our model represents a general frame for the mobility calculation, which can be further modified by(a) Calculating on-chain charge kinetics beyond the tight-binding model. Polaron dressing and Coulomb interaction for high charge concentration could be included under particular kinetic theories with defined relations to monomer site-representation.
(b) Replacing the Marcus approach, which describes the inter-chain kinetic transfer, either by the Miller–Abrahams model or by more advanced perturbative or non-perturbative treatments.
(c) Optimization of the mutual positions of adjacent chains by various quantum-chemistry or molecular dynamics methods with well-defined inter-chain transfer integrals between the adjacent monomer units.
(d) Introduction of chemical doping. For polymers highly doped with polar species, the concentration of dopants will control both the on-chain charge concentration and the value of the local site energy disorder σε. The presented model (contrary to GDM) enables a direct correlation of both quantities with the concentration of chemical dopants.
Conclusions
Combining the quantum mechanical approach with a semi-classical solution of the inter-chain charge hopping enabled us to improve the Gaussian disorder models of the charge carrier mobility designed previously for disordered organic solids by taking into account significant local anisotropy of the charge carrier mobility, and to properly involve both the on-chain charge carrier delocalization in conjugated polymers and the inter-chain hopping among states, which markedly differ in the magnitude of the related transfer integrals. We found that the on-chain delocalization of the charge carrier states results in a non-Gaussian distribution of the state energies (see Fig. 4 and 5). Unlike models based on the effective medium approximation, our approach does not require problematic configurational averaging of the mobility, which was found to have a profound effect on the concentration dependent mobility.17,28 The unification of the models for crystalline and amorphous phases made it possible to describe the dependence of the hole mobility on the charge carrier concentration and on the energetic disorder parameter in real (polycrystalline) materials such as P3HT.The proposed model contains only two free empirical parameters, namely the local energetic disorder σε, connected with the presence of impurities (incl. oxygen), and the weight factor w, given by the extent and percolation within the amorphous and crystalline phases. The values of these parameters are sensitive to particular experimental conditions during the sample preparation procedure and they cannot be effectively calculated even using e.g. some time-consuming molecular dynamics simulations.
For low values of the charge carrier concentration, the mobility is strongly deteriorated by on-chain traps for holes formed due to the energetic disorder. It leads to a significant increase of the mobility with increasing charge carrier concentration starting at some critical concentration (ca. 10−3 nm−3) due to the charge carrier trap filling. The value of the critical concentration slightly decreases with the magnitude of the energetic disorder. For higher values of the charge carrier concentration, however, the effect of the energetic disorder disappears and the mobility slightly decreases due to the lower density of unoccupied states with the energy suitable for the hopping transport.
The obtained concentration dependence of the mobility significantly differs from previously published19–21 dependence calculated using the GDM approach. Unlike concentration dependence calculated by Meisel et al.,21 it shows a low-concentration saturation also for high values of the energetic disorder (cf.Fig. 8). The tendencies of our concentration dependent mobility resembles the gate voltage dependent mobility curves obtained for OFET by different authors (see e.g.ref. 8). There is no doubt that the initial increase in mobility with increasing gate voltage is connected with trap filling. The decrease in mobility, however, sometimes observed at high gate voltages (so called mobility degradation) and ascribed to the lower charge mobility at the semiconductor–insulator interface (see e.g. Mottaghi et al.77 and Kim et al.8), could be explained within our model as due to the deficiency of available hopping states at higher charge concentrations. This new model could be useful for the description and better understanding of electrical characteristics of OFETs, diodes, and other devices based on conjugated polymers. It could be easily modified for the description of many other linear conjugated polymers like e.g. poly(p-phenylene vinylene).
Acknowledgements
This work was funded by the Czech Science Foundation (Project no. 15-05095S) and by the Academy of Sciences of the Czech Republic (Project no. M200501204). The access to the CERIT-SC computing and storage facilities provided under the program Projects of Large Research, Development, and Innovations Infrastructures (CERIT Scientific Cloud LM2015085), and to the Wroclaw Centre for Networking and Supercomputing (WCSS) is gratefully acknowledged.References
- F. So, Organic Electronics: Materials, Processing, Devices and Applications, CRC Press, Boca Raton, 2009 Search PubMed.
- I. Frac, M. Kucinska, P. Gawrys, M. Zagorska, W. Maniukiewicz, A. Nosal, J. Ulanski and M. Gazicki-Lipman, Synth. Met., 2016, 220, 194–201 CrossRef CAS.
- I. Tszydel, T. Marszalek, J. Ulanski, A. Nosal and M. Gazicki-Lipman, Surf. Coat. Technol., 2016, 290, 21–27 CrossRef CAS.
- S. Holliday, J. E. Donaghey and I. McCulloch, Chem. Mater., 2014, 26, 647–663 CrossRef CAS.
- J. Mei and Z. Bao, Chem. Mater., 2014, 26, 604–615 CrossRef CAS.
- P. A. Bobbert, A. Sharma, S. G. J. Mathijssen, M. Kemerink and D. M. de Leeuw, Adv. Mater., 2012, 24, 1146–1158 CrossRef CAS PubMed.
- G. Horowitz, M. E. Hajlaoui and R. Hajlaoui, J. Appl. Phys., 2000, 87, 4456–4463 CrossRef CAS.
- C. H. Kim, Y. Bonnassieux and G. Horowitz, IEEE Trans. Electron Devices, 2013, 60, 280–287 CrossRef CAS.
- S. Joshi, P. Pingel, S. Grigorian, T. Panzner, U. Pietsch, D. Neher, M. Forster and U. Scherf, Macromolecules, 2009, 42, 4651–4660 CrossRef CAS.
- M. Mladenović and N. Vukmirović, Phys. Chem. Chem. Phys., 2014, 16, 25950–25958 RSC.
- Y. Han, Y. Guo, Y. Chang, Y. Geng and Z. Su, Macromolecules, 2014, 47, 3708–3712 CrossRef CAS.
- H. Bässler, Phys. Status Solidi, 1993, 175, 15–56 CrossRef.
- A. Miller and E. Abrahams, Phys. Rev., 1960, 120, 745–755 CrossRef CAS.
- I. I. Fishchuk, A. Kadashchuk, H. Bässler and S. Nešpůrek, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 224303 CrossRef.
- I. I. Fishchuk, V. I. Arkhipov, A. Kadashchuk, P. Heremans and H. Bässler, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 45210 CrossRef.
- I. I. Fishchuk, A. Kadashchuk, V. N. Poroshin and H. Bässler, Philos. Mag., 2010, 90, 1229–1244 CrossRef CAS.
- I. I. Fishchuk, A. Kadashchuk, S. T. Hoffmann, S. Athanasopoulos, J. Genoe, H. Bässler and A. Köhler, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 125202 CrossRef.
- I. I. Fishchuk, A. Kadashchuk, S. T. Hoffmann, S. Athanasopoulos, J. Genoe, H. Bässler and A. Köhler, AIP Conference Proceedings, American Institute of Physics Inc., 2014, vol. 1610, pp. 47–52 Search PubMed.
- W. F. Pasveer, J. Cottaar, C. Tanase, R. Coehoorn, P. A. Bobbert, P. W. M. Blom, D. M. de Leeuw and M. A. J. Michels, Phys. Rev. Lett., 2005, 94, 206601 CrossRef CAS PubMed.
- R. Coehoorn, W. F. Pasveer, P. A. Bobbert and M. A. J. Michels, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 155206 CrossRef.
- K. D. Meisel, W. F. Pasveer, J. Cottaar, C. Tanase, R. Coehoorn, P. A. Bobbert, P. W. M. Blom, D. M. de Leeuw and M. A. J. Michels, Phys. Status Solidi, 2006, 3, 267–270 CrossRef CAS.
- V. I. Arkhipov, P. Heremans, E. V Emelianova, G. J. Adriaenssens and H. Bässler, J. Phys.: Condens. Matter, 2002, 14, 9899–9911 CrossRef CAS.
- R. Schmechel, J. Appl. Phys., 2003, 93, 4653–4660 CrossRef CAS.
- R. Schmechel, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 235206 CrossRef.
- B. Maennig, M. Pfeiffer, A. Nollau, X. Zhou, K. Leo and P. Simon, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 195208 CrossRef.
- A. Castro-Carranza, J. C. Nolasco, M. Estrada, R. Gwoziecki, M. Benwadih, Y. Xu, A. Cerdeira, L. F. Marsal, G. Ghibaudo, B. Iniguez and J. Pallares, IEEE Electron Device Lett., 2012, 33, 1201–1203 CrossRef CAS.
- M. Estrada, I. Mejía, A. Cerdeira, J. Pallares, L. F. Marsal and B. Iñiguez, Solid. State. Electron., 2008, 52, 787–794 CrossRef CAS.
- S. Baranovski, Charge transport in disordered solids with applications in electronics, Wiley, Chichester, 2006 Search PubMed.
- S. D. Baranovskii, Phys. Status Solidi, 2014, 251, 487–525 CrossRef CAS.
- M. C. J. M. Vissenberg and M. Matters, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 12964 CrossRef CAS.
- S. D. Baranovskii, I. P. Zvyagin, H. Cordes, S. Yamasaki and P. Thomas, Phys. Status Solidi B, 2002, 230, 281–287 CrossRef CAS.
- S. D. Baranovskii, I. P. Zvyagin, H. Cordes, S. Yamasaki and P. Thomas, J. Non-Cryst. Solids, 2002, 299, 416–419 CrossRef.
- S. Shaked, S. Tal, Y. Roichman, A. Razin, S. Xiao, Y. Eichen and N. Tessler, Adv. Mater., 2003, 15, 913–916 CrossRef CAS.
- Y. Roichman and N. Tessler, Appl. Phys. Lett., 2002, 80, 1948–1950 CrossRef CAS.
- Y. Roichman and N. Tessler, Synth. Met., 2003, 135–136, 443–444 CrossRef CAS.
- A. V Nenashev, J. O. Oelerich and S. D. Baranovskii, J. Phys.: Condens. Matter, 2015, 27, 93201 CrossRef PubMed.
- J. O. Oelerich, D. Huemmer and S. D. Baranovskii, Phys. Rev. Lett., 2012, 108, 226403 CrossRef CAS PubMed.
- P. Kordt, O. Stenzel, B. Baumeier, V. Schmidt and D. Andrienko, J. Chem. Theory Comput., 2014, 10, 2508–2513 CrossRef CAS PubMed.
- P. Kordt, J. J. M. van der Holst, M. Al Helwi, W. Kowalsky, F. May, A. Badinski, C. Lennartz and D. Andrienko, Adv. Funct. Mater., 2015, 25, 1955–1971 CrossRef CAS.
- C. Zhao, H. Ge, S. Yin and W. Wang, J. Mol. Model., 2014, 20, 2158 CrossRef PubMed.
- Y. Hu, K. Chaitanya, J. Yin and X.-H. Ju, J. Mater. Sci., 2016, 51, 6235–6248 CrossRef CAS.
- W.-Q. Deng, L. Sun, J.-D. Huang, S. Chai, S.-H. Wen and K.-L. Han, Nat. Protoc., 2015, 10, 632–642 CrossRef CAS PubMed.
- I. Yavuz, B. N. Martin, J. Park and K. N. Houk, J. Am. Chem. Soc., 2015, 137, 2856–2866 CrossRef CAS PubMed.
- I. Yavuz, S. A. Lopez, J. B. Lin and K. N. Houk, J. Mater. Chem. C, 2016, 4, 11238–11243 RSC.
- F. C. Grozema and L. D. A. Siebbeles, Int. Rev. Phys. Chem., 2008, 27, 87–138 CrossRef CAS.
- P. Toman, S. Nešpůrek, M. Weiter, M. Vala, J. Sworakowski, W. Bartkowiak and M. Menšík, Polym. Adv. Technol., 2009, 20, 263–267 CrossRef CAS.
- M. S. A. Abdou, F. P. Orfino, Y. Son and S. Holdcroft, J. Am. Chem. Soc., 1997, 119, 4518–4524 CrossRef CAS.
- O. V. Kozlov and S. A. Zapunidi, Synth. Met., 2013, 169, 48–54 CrossRef CAS.
- W. Xie, Y. Y. Sun, S. B. Zhang and J. E. Northrup, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 184117 CrossRef.
- T. J. Prosa, M. J. Winokur, J. Moulton, P. Smith and A. J. Heeger, Macromolecules, 1992, 25, 4364–4372 CrossRef CAS.
- N. Kayunkid, S. Uttiya and M. Brinkmann, Macromolecules, 2010, 43, 4961–4967 CrossRef CAS.
- F. C. Grozema, P. T. van Duijnen, Y. A. Berlin, M. A. Ratner and L. D. A. Siebbeles, J. Phys. Chem. B, 2002, 106, 7791–7795 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- K. Senthilkumar, F. C. Grozema, F. M. Bickelhaupt and L. D. A. Siebbeles, J. Chem. Phys., 2003, 119, 9809–9817 CrossRef CAS.
- K. Senthilkumar, F. C. Grozema, C. F. Guerra, F. M. Bickelhaupt, F. D. Lewis, Y. A. Berlin, M. A. Ratner and L. D. A. Siebbeles, J. Am. Chem. Soc., 2005, 127, 14894–14903 CrossRef CAS PubMed.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS.
- J. Perdew, Electronic Structure of Solids, Akademie Verlag GmbH, Berlin, 1991, vol. 91, pp. 11–20 Search PubMed.
- J. P. Perdew, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687 CrossRef CAS.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 4978 CrossRef CAS.
- J. P. Perdew, K. Burke and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16533–16539 CrossRef CAS.
- K. Burke, J. P. Perdew and Y. Wang, in Electronic Density Functional Theory: Recent Progress and New Directions, ed. J. F. Dobson, G. Vignale and M. P. Das, Plenum, 1998 Search PubMed.
- P. Prins, F. C. Grozema, F. Galbrecht, U. Scherf and L. D. A. Siebbeles, J. Phys. Chem. C, 2007, 111, 11104–11112 CAS.
- S. Fratiloiu, K. Senthilkumar, F. C. Grozema, H. Christian-Pandya, Z. I. Niazimbetova, Y. J. Bhandari, M. E. Galvin and L. D. A. Siebbeles, Chem. Mater., 2006, 18, 2118–2129 CrossRef CAS.
- E. J. Baerends, T. Ziegler, J. Autschbach, D. Bashford, A. Bérces, F. M. Bickelhaupt, C. Bo, P. M. Boerrigter, L. Cavallo, D. P. Chong, L. Deng, R. M. Dickson, D. E. Ellis, M. van Faassen, L. Fan, T. H. Fischer, C. Fonseca Guerra, M. Franchini, A. Ghysels, A. Giammona, S. J. A. van Gisbergen, A. W. Götz, J. A. Groeneveld, O. V. Gritsenko, M. Grüning, S. Gusarov, F. E. Harris, P. van den Hoek, C. R. Jacob, H. Jacobsen, L. Jensen, J. W. Kaminski, G. van Kessel, F. Kootstra, A. Kovalenko, M. V. Krykunov, E. van Lenthe, D. A. McCormack, A. Michalak, M. Mitoraj, S. M. Morton, J. Neugebauer, V. P. Nicu, L. Noodleman, V. P. Osinga, S. Patchkovskii, M. Pavanello, P. H. T. Philipsen, D. Post, C. C. Pye, W. Ravenek, J. I. Rodríguez, P. Ros, P. R. T. Schipper, G. Schreckenbach, J. S. Seldenthuis, M. Seth, J. G. Snijders, M. Solà, M. Swart, D. Swerhone, G. te Velde, P. Vernooijs, L. Versluis, L. Visscher, O. Visser, F. Wang, T. A. Wesolowski, E. M. van Wezenbeek, G. Wiesenekker, S. K. Wolff, T. K. Woo and A. L. Yakovlev, Computer program ADF 2013, 2013 Search PubMed.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- C. Fonseca Guerra, J. G. Snijders, G. te Velde and E. J. Baerends, Theor. Chem. Acc., 1998, 99, 391–403 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Computer program Gaussian 09, Revision C.01, Gaussian, Inc., Wallingford CT, 2010 Search PubMed.
- P. Atkins and J. De Paula, Physical Chemistry, W. H. Freeman, New York, 8th edn, 2006 Search PubMed.
- P. Prins, F. C. Grozema, J. M. Schins, S. Patil, U. Scherf and L. D. A. Siebbeles, Phys. Rev. Lett., 2006, 96, 146601 CrossRef CAS PubMed.
- V. May and O. Kühn, Charge and energy transfer dynamics in molecular systems, Wiley-VCH Verlag Berlin GmbH, Berlin, 1st edn, 2008 Search PubMed.
- H. L. Tavernier and M. D. Fayer, J. Chem. Phys., 2001, 114, 4552 CrossRef CAS.
- G. R. Hutchison, M. A. Ratner and T. J. Marks, J. Am. Chem. Soc., 2005, 127, 2339–2350 CrossRef CAS PubMed.
- U. Bielecka, P. Lutsyk, K. Janus, J. Sworakowski and W. Bartkowiak, Org. Electron., 2011, 12, 1768–1776 CrossRef CAS.
- D. Choi, M. Chang and E. Reichmanis, Adv. Funct. Mater., 2015, 25, 920–927 CrossRef CAS.
- G. Garcia-Belmonte, Solid-State Electron., 2013, 79, 201–205 CrossRef.
- A. R. Inigo, H.-C. Chiu, W. Fann, Y.-S. Huang, U. S. Jeng, C. H. Hsu, K.-Y. Peng and S.-A. Chen, Synth. Met., 2003, 139, 581–584 CrossRef CAS.
- M. Mottaghi and G. Horowitz, Org. Electron., 2006, 7, 528–536 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Fragment orbital approach calculation of hole transfer integrals between covalently bound monomer units in a dimer using Gaussian 09 program. See DOI: 10.1039/c6cp07789g |
| This journal is © the Owner Societies 2017 |