Open Access Article
Open Access ArticleWater aggregation and dissociation on the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/h2_char_0031_0304.gif) 0) surface†
0) surface†
Stephane
Kenmoe‡
 * and
P. Ulrich
Biedermann
* and
P. Ulrich
Biedermann
Max-Planck-Institut für Eisenforschung GmbH, Max-Planck-Str. 1, 40237 Düsseldorf, Germany. E-mail: stephane.kenmoe@uni-due.de; Fax: +49 201 183 2656; Tel: +49 201 183 2497
First published on 7th December 2016
Abstract
A comprehensive search for stable structures in the low coverage regime (0–1 ML) and at 2 ML and 3 ML using DFT revealed several new aggregation states of water on the non-polar ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface. Ladder-like structures consisting of half-dissociated dimers, arranged side-by-side along the polar axis, constitute the most stable aggregate at low coverages (≤1 ML) with a binding energy exceeding that of the monolayer. At coverages beyond the monolayer – a regime that has hardly been studied previously – a novel type of structure with a continuous honeycomb-like 2D network of hydrogen bonds was discovered, where each surface oxygen atom is coordinated by additional H-bonding water molecules. This flat double-monolayer has a relatively high adsorption energy, every zinc and oxygen atom is 4-fold coordinated and every hydrogen atom is engaged in a hydrogen bond. Hence this honeycomb double monolayer offers no H-bond donor or acceptor sites for further growth of the water film. At 3 ML coverage, the interface restructures forming a contact layer of half-dissociated water dimers and a liquid-like overlayer of water attached by hydrogen bonds. The structures and their adsorption energies are analysed to understand the driving forces for aggregation and dissociation of water on the surface. We apply a decomposition scheme based on a Born–Haber cycle, discussing difficulties that may occur in applying such an analysis to the adsorption of dissociated molecules and point out alternatives to circumvent the bias against severely stretched bonds. Water aggregation on the ZnO surface is favoured by direct water–water interactions including H-bonds and dipole–dipole interactions and surface- or adsorption-mediated interactions including enhanced water–surface interactions and reduced relaxations of the water molecules and surface. While dissociation of isolated adsorbed molecules is unfavourable, partial or even full dissociation is preferred for aggregates. Nevertheless, direct water–water interactions change very little in the dissociation reaction. Dissociation is governed by a subtle balance between strongly enhanced water–surface interactions and the large energies required for the geometric changes of the water molecule(s) and the surface. Our conclusions are discussed on the background of the current knowledge on water adsorption at metals and non-metallic surfaces.
0) surface. Ladder-like structures consisting of half-dissociated dimers, arranged side-by-side along the polar axis, constitute the most stable aggregate at low coverages (≤1 ML) with a binding energy exceeding that of the monolayer. At coverages beyond the monolayer – a regime that has hardly been studied previously – a novel type of structure with a continuous honeycomb-like 2D network of hydrogen bonds was discovered, where each surface oxygen atom is coordinated by additional H-bonding water molecules. This flat double-monolayer has a relatively high adsorption energy, every zinc and oxygen atom is 4-fold coordinated and every hydrogen atom is engaged in a hydrogen bond. Hence this honeycomb double monolayer offers no H-bond donor or acceptor sites for further growth of the water film. At 3 ML coverage, the interface restructures forming a contact layer of half-dissociated water dimers and a liquid-like overlayer of water attached by hydrogen bonds. The structures and their adsorption energies are analysed to understand the driving forces for aggregation and dissociation of water on the surface. We apply a decomposition scheme based on a Born–Haber cycle, discussing difficulties that may occur in applying such an analysis to the adsorption of dissociated molecules and point out alternatives to circumvent the bias against severely stretched bonds. Water aggregation on the ZnO surface is favoured by direct water–water interactions including H-bonds and dipole–dipole interactions and surface- or adsorption-mediated interactions including enhanced water–surface interactions and reduced relaxations of the water molecules and surface. While dissociation of isolated adsorbed molecules is unfavourable, partial or even full dissociation is preferred for aggregates. Nevertheless, direct water–water interactions change very little in the dissociation reaction. Dissociation is governed by a subtle balance between strongly enhanced water–surface interactions and the large energies required for the geometric changes of the water molecule(s) and the surface. Our conclusions are discussed on the background of the current knowledge on water adsorption at metals and non-metallic surfaces.
1. Introduction
The interactions of water with zinc oxide play an important role in many applications including medical and cosmetic formulations, gas sensors, transparent conducting oxides, e.g., in dye-sensitized solar cells, and heterogeneous catalysts for industrially important processes like the water gas shift reaction and methanol synthesis.1–7 Furthermore, zinc oxide is developed as active material for water splitting and photocatalysis.8,9Under ambient conditions water is present on most surfaces forming a thin film of 4–10 Å or 1–3 monolayers.10–12 However water adsorption, aggregation and wetting is strongly dependent on the subtle interplay of water–substrate and water–water interactions and the availability of dangling OH-groups.11,13 The presence of water strongly modifies the surface properties depending on the substrate and coverage. For example, it may passivate dangling bonds and stabilize or destabilize reconstructions. Furthermore, adsorbed water can catalyse heterogeneous reactions and corrosion by proton transfer and solvating products and transition states. On the other hand water can also block active sites.10,12 The adsorbed water itself may have distinct properties differing substantially from bulk ice or water in structure, diffusivity, freezing point, dissociation degree and solvating properties due to the confinement in a thin layer, interactions with the substrate and the often epitaxially templated arrangement.10,11,14,15 Dissociation of adsorbed water is of particular interest for catalysis, as this may be the first step in the activation of water molecules for chemical reactions.
The water binding mechanism on solid surfaces has been reviewed previously, analysing different types of interactions including electrostatic ion–dipole and dipole–dipole interactions, dispersion interactions, and more specific chemical interactions.10,11,16 It is commonly agreed that the main interaction of water molecules with surfaces is due to the doubly occupied 3a1 and 1b1 water orbitals (lone pairs) hybridizing/interacting with empty orbitals on metal atoms and cations,11,14,16–22 with partial charge transfer to the surface.16,19,20,23 In particular on non-metallic surfaces these interactions can be very strong resulting in a Lewis acid–base type chemical bond.16 The directional properties of the orbitals involved result in a preferred adsorption position slightly displaced from exactly on top the metal atom and an orientation of the molecule nearly parallel to the surface.19,20 In addition to this interaction with electron deficient centres, water molecules form hydrogen bonds between the OH groups and anions or other water molecules.
A lot of experimental surface science studies and theoretical work has focused on metals, in particular on well-defined single-crystal surfaces.17,18,23 The adsorption energy for water molecules on metals is in the range of 0.1 to 0.4 eV, increasing in the series Au < Ag < Cu < Pd < Pt < Ru < Rh.14,15,18–20 The Variation is due to the metal–water interaction,24 which is weaker than the nearly constant water–water interaction or of comparable strength.15 Furthermore, cooperative effects were observed: the metal–water oxygen interaction enhances the H-bond donor strength of the molecule, while it weakens the H-bond acceptor strength.17–19,21 Both is due to the electron withdrawing effect of the water–metal interaction.
Isolated water molecules easily diffuse on metal surfaces, even at low temperatures, facilitating aggregation and a special “waltzing” mechanism promotes diffusion of dimers.14,15,19,25 At very low temperatures and low coverage initially isolated molecules and small clusters are observed.15,21,23 However, with increasing temperature diffusion sets in, leading to water aggregates of various size stabilized by H-bonds.17,23 On the (111) surfaces of Pd, Cu, and Ag, water aggregation leads to 6-rings and heptamers to nonamers based on a 6-ring core.17–19,21 One-dimensional (1D), chain-like aggregates have been observed on the Cu(110) surface.26 Density functional theory (DFT) calculations revealed that they are based on edge-sharing water pentagons adsorbed on top of Cu atoms, which are also predicted for Ni(110), while edge-sharing hexagons are more stable on the (110) surfaces of Pd and Ag.26,27 On Pd(111) at 100 K and coverages of ∼0.5 ML complex rosette or lace like structures are observed that are built from hexagons interconnected by additional H-bonded water molecules.14,18,28
Early studies of saturated water monolayers on metals suggested a buckled hexagonal bilayer structure similar to the basal plane of ice Ih, based on the (√3 × √3)R30° low energy electron diffraction (LEED) pattern and a saturation coverage of 2/3 ML.17,18,23,29 The bilayer consists of an epitaxial hexagonal 2D-network of water molecules. Every second molecule is bound on top of a metal atom with a slightly upward tilted orientation as described above. The remaining molecules are not in direct contact with the metal and adsorbed by H-bonds with the lower layer. DFT calculations supported this structure and showed that such hexagonal networks of H-bonded water can adapt to a wide range of substrate lattice constants with relatively low strain energies.24 However, more recently high resolution scanning tunnelling microscopy (STM) revealed a more complex behaviour of adsorbed water layers and a rich variety of structures, which comprise also 5- and 7-rings and other defects.17 On Pt(111) 2D-layers of water with (√39 × √39)R16.1° and (√37 × √37)R25.3° have been observed, while the (√3 × √3)R30° bilayer structure is stable only in small domains at 85 K and becomes stable in multilayers at coverages >2 bilayers.19 On Ni a (2√7 × 2√7)R19° monolayer has been observed, which reorders into an incommensurate ice film for multilayers.18 These complex structures are due to a subtle competition of water–water H-bonding (number of H-bonds, optimum distances, angles) and water metal bonding (epitaxial on top position, parallel orientation), which leads to the stunning manifold of structures.17 Recently a unified model has been proposed that accounts for the relative stability of the different patterns on close-packed hexagonal surfaces.30 The adsorption energy was decomposed into water–water and water–metal interactions and expressed as parametric function of the lattice deformation. This approach allows predicting the most stable structure for Pd, Pt, Ag, Au, Ir, and Rh, Ru close packed surfaces. Besides layers of intact water molecules also mixed OH/H2O layers with (√3 × √3)R30° were observed, which are flat in contrast to the buckled bilayer of intact water molecules.18,20,31 Water dissociation is controlled by the metal–OH bond strength.24
In the high coverage regime at low temperatures, where diffusion is too slow, metastable amorphous water films are formed.17,18 At higher temperature two limiting behaviours are observed. On the (111) surfaces of Ni and Pt, for example, incommensurate bulk ice films are observed, indicating that the interface has restructured with preferred orientation along metal rows. On the other hand Ru(0001) has a tightly bound (√3 × √3)R30° first wetting layer, which does not restructure upon further water adsorption. Therefore, de-wetting occurs and 3D ice clusters form on the persistent monolayer. There are two prerequisites for wetting and growth of multilayers: strong H-bonding of multilayer ice due to the presence of free OH groups (or via easy restructuring) and a suitable lateral registry to match the 3D-structure of ice.13,17,18,29
In the case of non-metallic substrates, the information is much more scarce and scattered. For ionic compounds, the trends in water monomer adsorption and dissociation on flat (100) surfaces of a broad range of alkaline earth oxides and sulphides, as well as alkali fluorides and chlorides with rocksalt structures has been studied with DFT.32 On the surfaces of these mostly ionic compounds, the anions and cations, which are octahedrally 6-fold coordinated in the bulk, are arranged in a checkboard pattern and have 5 nearest neighbours. Adsorption of intact isolated water molecules is favoured on most substrates including all alkali halides, the alkali earth sulphides and MgO, while dissociation is preferred only on the heavier oxides CaO, SrO and BaO. In the dissociated structures, one hydrogen is transferred to a surface oxygen and the hydroxyl group adsorbs above an adjacent metal ion with the OH-bond directed towards the vacuum. The adsorption energies increase from −0.9 eV for CaO to −1.5 eV for BaO. For molecular adsorption different types of structures have been found. On MgO, MgS, CaS, LiF, LiCl, and NaCl, the water oxygen is above a metal ion with a slight lateral displacement and the molecular plane is almost parallel to the surface, as described in the beginning. On the other hand, the water molecule is on a hollow site with the hydrogens facing downward and forming two H-bonds for SrS, BaS, NaF, KF, RbF, KCl, and RbCl, and one H-bond for CsF and RbF. The adsorption energy of intact water molecules on cations decreases with the size of the metal ion, while the strength of the H-bond to the surface anion increases with the size of the cation. The opposing trends lead to the observed cross over from metal–water oxygen binding to H-bonding at the anions.
For the covalently bound semiconductors with tetrahedral coordination and diamond, zinc-blende or wurtzite structure, passivation of the partially filled dangling bonds at the surface is critical. The principles determining the stability of semiconductor surface structures have been developed in the 1980-ties and often summarized as “electron counting rules”.33–37 They allow to understand the complex reconstructions of Silicon as well as the stoichiometry of surface vacancies, adatoms and adsorbates on polar surfaces of III–V, II–VI and I–VII compound semiconductors. For the non-polar surfaces of compound semiconductors an auto compensation mechanism leads to a buckling of the surface dimers or chains. Charge transfer from the cation dangling bonds to the anion dangling bonds leads to fully occupied and completely empty orbitals. The outward relaxation of the anions increases the s-character of the completely filled dangling bond lowering its energy, while the inward relaxation of the cations, which approach an almost planar 3-fold coordination increases the p-character of its empty dangling bond orbital pushing it higher into the conduction band. This opens a band gap in the surface states. Intact water molecules interact only weakly (−0.5 eV) with the buckled dimers of the Si(100)-2 × 1 surface, however, easily dissociate via a small barrier forming a much more stable surface (−2.5 eV) with mixed OH/H termination on the now tetrahedrally coordinated and no longer buckled surface dimers.38–42 The interaction energies for molecular adsorption increases to −0.7 eV on GaN (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) and −1.0 eV on ZnO (10
0) and −1.0 eV on ZnO (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0), while for dissociated water they decrease to −1.7 eV and −0.9 eV, respectively.43–45 At 1 ML, a structure with half-dissociated water dimers is favoured on ZnO in contrast to GaN.44 The trend of decreasing dissociation of the contact layer is also observed at the interface with bulk water. For GaN(10
0), while for dissociated water they decrease to −1.7 eV and −0.9 eV, respectively.43–45 At 1 ML, a structure with half-dissociated water dimers is favoured on ZnO in contrast to GaN.44 The trend of decreasing dissociation of the contact layer is also observed at the interface with bulk water. For GaN(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) 80–100% dissociation was calculated,8,46,47 while for ZnO(10
0) 80–100% dissociation was calculated,8,46,47 while for ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) a dissociation degree slightly larger than 50% was predicted based on DFT-molecular dynamics.8,48
0) a dissociation degree slightly larger than 50% was predicted based on DFT-molecular dynamics.8,48
Aggregation of water was also reported on the surfaces of ionic and semiconducting materials. On NaCl(100) tetrameric water clusters have been reported recently as basic building blocks by cryogenic STM and DFT.49 The water molecules are bound on top Na+ ions oriented parallel to the surface and H-bonded in a cyclic fashion. These tetramers can form chain- or flake-shaped larger clusters and a 2D layer via additional linking water molecules that are accepting H-bonds from two neighbouring tetramers and donate one H-bond to a chloride anion. In addition 1 × 1 bilayers with 2 ML coverage and c(4 × 2) overlayers with 1.5 ML coverage have been observed on NaCl(100).15,50 On MgO(100) water clustering and wetting layers can coexist.15 At low coverage a c(4 × 2) structure with 1.25 ML coverage was observed, which transforms at 185 K into a monolayer with p(3 × 2) structure that is stable up to 235 K.15,51 At 1 ML coverage 2 of the 6 water molecules are dissociated and the water molecules and OH groups are bound to Mg cations, while in the c(4 × 2) structure the dissociated OH groups have a larger distance from the surface and are H-bonded by four water molecules occupying the Mg-sites. Apart from isolated molecules, small clusters and 2D-layers,11,15,16 also some examples of 1D-aggregates have been reported. On TiO2 surfaces water aggregation follows the anisotropic row-structure of the surface.52,53 On the other hand, on CaO(100) a thermodynamically stable phase of extended 1D-clusters was reported that breaks the 4-fold symmetry of the surface.54 Symmetry-broken half-dissociated tetramers direct the linear growth and the larger lattice constant of CaO destabilizes a 2D-layer as on MgO, hence a 1D-structure is preferred.
ZnO crystallizes in the polar wurtzite structure with hexagonal symmetry and has four low Miller index cleavage surfaces: cleavage perpendicular to the polar c axis leads to two distinct surfaces, the Zn-terminated (0001) surface and the O-terminated (000![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) surface, while cleavage along the c axis results in the non-polar surfaces (10
) surface, while cleavage along the c axis results in the non-polar surfaces (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) and (11
0) and (11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0) with a stoichiometric surface termination.7 The macroscopic dipole and electrostatic instability of the polar surfaces has been reviewed.7,55–57 Various stabilization mechanisms by electron transfer, reconstructions and adsorbates have been proposed.7,58–68 In ZnO powders, the non-polar facets contribute 80% of the surface.7 The clean, low index, non-polar (10
0) with a stoichiometric surface termination.7 The macroscopic dipole and electrostatic instability of the polar surfaces has been reviewed.7,55–57 Various stabilization mechanisms by electron transfer, reconstructions and adsorbates have been proposed.7,58–68 In ZnO powders, the non-polar facets contribute 80% of the surface.7 The clean, low index, non-polar (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) and (11
0) and (11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0) facets have been subject of many experimental and theoretical investigations. Different surface science experimental techniques including LEED,58,69 high resolution transmission electron microscopy (HRTEM),70 X-ray photoelectron spectroscopy (XPS),71 as well as electronic structure calculations9,72–74 have revealed that these stoichiometric surface terminations are auto passivating. Upon cleaving the crystal, an empty dangling bond at the Zn cation and a fully occupied dangling bond at the O anion are created.73 To lower the surface energy, the cation rehybridizes from sp3 towards sp2 and moves downward by about 0.34 Å until it lies nearly in the plane of its three anion neighbours. The anion, on the other hand, almost stays in a bulk-like position while its bond angles decrease leading to an increased s-character of the lone pair. The result is a tilt of the ZnO surface dimers by about 12° and a dimer bond length contraction of roughly 7%, in good agreement between experimental observation69,70 and theoretical prediction.73
0) facets have been subject of many experimental and theoretical investigations. Different surface science experimental techniques including LEED,58,69 high resolution transmission electron microscopy (HRTEM),70 X-ray photoelectron spectroscopy (XPS),71 as well as electronic structure calculations9,72–74 have revealed that these stoichiometric surface terminations are auto passivating. Upon cleaving the crystal, an empty dangling bond at the Zn cation and a fully occupied dangling bond at the O anion are created.73 To lower the surface energy, the cation rehybridizes from sp3 towards sp2 and moves downward by about 0.34 Å until it lies nearly in the plane of its three anion neighbours. The anion, on the other hand, almost stays in a bulk-like position while its bond angles decrease leading to an increased s-character of the lone pair. The result is a tilt of the ZnO surface dimers by about 12° and a dimer bond length contraction of roughly 7%, in good agreement between experimental observation69,70 and theoretical prediction.73
The adsorption of water on ZnO has captured attention for many years due to the relevance for important catalytic processes including the water gas shift reaction and methanol synthesis.7 Zwicker and Jacobi used thermal desorption spectroscopy (TDS) and XPS to study the adsorption and condensation of water on ZnO single crystal surfaces.75,76 Their studies identified several adsorption states of water with different desorption energies on the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface depending on the exposure. Based on the atomic and electronic structure of the clean ZnO(10
0) surface depending on the exposure. Based on the atomic and electronic structure of the clean ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface discussed above, favourable interactions of water molecules with this surface were predicted as either a molecular adsorption with the water oxygen atoms coordinated to surface Zn atoms and hydrogen bonds between the water molecules and surface O atoms, or a dissociative adsorption with H atoms and OH groups saturating the dangling bonds of the O and Zn atoms at the surface, respectively.44 Using DFT, the adsorption of single isolated molecules has been analysed in several works and molecular adsorption has been found to be more stable than dissociative adsorption.43–45,77–79 Intact isolated molecules bind to the surface via a strong Zn–O covalent bond between the Zn cation and one of the water lone pairs and donate one H bond to the surface oxygen across the trench.
0) surface discussed above, favourable interactions of water molecules with this surface were predicted as either a molecular adsorption with the water oxygen atoms coordinated to surface Zn atoms and hydrogen bonds between the water molecules and surface O atoms, or a dissociative adsorption with H atoms and OH groups saturating the dangling bonds of the O and Zn atoms at the surface, respectively.44 Using DFT, the adsorption of single isolated molecules has been analysed in several works and molecular adsorption has been found to be more stable than dissociative adsorption.43–45,77–79 Intact isolated molecules bind to the surface via a strong Zn–O covalent bond between the Zn cation and one of the water lone pairs and donate one H bond to the surface oxygen across the trench.
Formation of a water monolayer on the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface has been reported in many studies. Experimental observations based on He-atom scattering (HAS), low-energy electron diffraction (LEED), STM images77,80 and high resolution electron energy loss spectroscopy (HREELS)81 have agreed with the formation of a 2D water superstructure with (2 × 1) periodicity, having a long-range order and existing up to 340 K in ultra-high vacuum conditions. In the STM images,80 domains with half-dissociated (2 × 1) and fully molecular (1 × 1) periodicity of water molecules coexist, together with a third domain with (2 × 1) periodicity, but less corrugated than the half-dissociated one. Though this last domain could not be assigned from the DFT calculations, several studies using DFT,43–45,77–80,82–84 and REAXFF78 have confirmed the prevalence of the half-dissociated (2 × 1) domain over the (1 × 1) molecular structure and in some cases predicted the existence of a monolayer of fully dissociated water molecules with (1 × 1) periodicity binding to the surface as strong as the (1 × 1) molecular monolayer. Half-dissociative adsorption may occur as a compromise between the steric repulsion and covalent and hydrogen bond formation with both the substrate and the impinging molecules.82 The driving force for dissociation was attributed to the hydrogen bond interactions, which gain in strength for increasing coverage, leading to almost degenerate molecular and dissociative adsorption modes at monolayer.84 The presence of these water–water hydrogen bonds is the key issue that drives the stabilization of the adlayer and the dissociation process that occurs at high coverages.82 The calculated energy barrier per water molecule to go from a molecular to a dissociated monolayer is 0.02 eV, while there is no barrier to go from a molecular to a half-dissociated monolayer.44,78,84 Furthermore, the possibility of domains with mixed (2 × 1) and c(2 × 2) structures of half-dissociated molecules was also predicted.44,79
0) surface has been reported in many studies. Experimental observations based on He-atom scattering (HAS), low-energy electron diffraction (LEED), STM images77,80 and high resolution electron energy loss spectroscopy (HREELS)81 have agreed with the formation of a 2D water superstructure with (2 × 1) periodicity, having a long-range order and existing up to 340 K in ultra-high vacuum conditions. In the STM images,80 domains with half-dissociated (2 × 1) and fully molecular (1 × 1) periodicity of water molecules coexist, together with a third domain with (2 × 1) periodicity, but less corrugated than the half-dissociated one. Though this last domain could not be assigned from the DFT calculations, several studies using DFT,43–45,77–80,82–84 and REAXFF78 have confirmed the prevalence of the half-dissociated (2 × 1) domain over the (1 × 1) molecular structure and in some cases predicted the existence of a monolayer of fully dissociated water molecules with (1 × 1) periodicity binding to the surface as strong as the (1 × 1) molecular monolayer. Half-dissociative adsorption may occur as a compromise between the steric repulsion and covalent and hydrogen bond formation with both the substrate and the impinging molecules.82 The driving force for dissociation was attributed to the hydrogen bond interactions, which gain in strength for increasing coverage, leading to almost degenerate molecular and dissociative adsorption modes at monolayer.84 The presence of these water–water hydrogen bonds is the key issue that drives the stabilization of the adlayer and the dissociation process that occurs at high coverages.82 The calculated energy barrier per water molecule to go from a molecular to a dissociated monolayer is 0.02 eV, while there is no barrier to go from a molecular to a half-dissociated monolayer.44,78,84 Furthermore, the possibility of domains with mixed (2 × 1) and c(2 × 2) structures of half-dissociated molecules was also predicted.44,79
In the high coverage regime, water films have been addressed using ReaxFF calculations.85 High dissociation degrees (80%) and proton transfer reactions between water molecules and hydroxyl via a Grotthuss-like mechanism in the contact layer have been reported. Very recently, important contributions to the microscopic understanding of the liquid water/ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) interface were made8,48 by comparing the interface structure and proton dynamics of a water monolayer and thick water layer. Using ab initio MD, 50% dissociation was found in the contact layer of a liquid water film as well as in the monolayer. Due to H-bond fluctuations that lower the proton transfer barrier, a higher rate of dissociation and recombination was found in the contact layer of the liquid film compared to the monolayer.
0) interface were made8,48 by comparing the interface structure and proton dynamics of a water monolayer and thick water layer. Using ab initio MD, 50% dissociation was found in the contact layer of a liquid water film as well as in the monolayer. Due to H-bond fluctuations that lower the proton transfer barrier, a higher rate of dissociation and recombination was found in the contact layer of the liquid film compared to the monolayer.
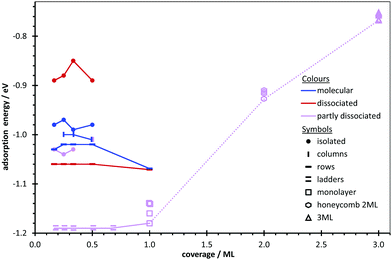
Though the adsorption of water on the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface has been studied for isolated single molecules, monolayers, and to some extent for the interface with bulk liquid water, no information is available about the aggregates that may form in between these three coverage regimes, as well as on the coverage dependence of their binding energies. Therefore, we investigate the questions of water aggregates at low coverage and of multilayer formation. Furthermore, we analyse the mechanisms stabilizing such aggregates as well as the trends in the binding energy and dissociation degree with respect to coverage. We present a comprehensive and systematic search of all possible aggregates by successively increasing the coverage of water molecules up to 1 ML, using density functional theory (DFT). Molecular, dissociative and partial dissociative adsorption modes are considered. For all aggregates, we perform a thorough search of energy minima and investigate the coverage dependence of their adsorption energy up to the limit of formation of higher aggregates. The coverage regime between monolayer and thick films representing the interface with bulk water has not been studied with DFT previously, although TDS spectra clearly show distinct desorption peaks between those assigned to bulk ice and the monolayer.75 We present first results on interfaces with 2 ML and 3 ML water coverage based on small unit cells, which was motivated by the observation of (2 × 1) periodicity at 1 ML77,80,81 as well at the contact layer with bulk water.8,48 In order to gain insight into the driving forces for aggregation and dissociation, the strength of surface–water and water–water interactions, as well as the modification of water molecule and ZnO surface geometries and corresponding energies are quantified using a thermodynamic cycle to decompose the adsorption energies. The impact of water adsorption on the passivation of dangling bonds, surface states and the band gap are also analysed.
0) surface has been studied for isolated single molecules, monolayers, and to some extent for the interface with bulk liquid water, no information is available about the aggregates that may form in between these three coverage regimes, as well as on the coverage dependence of their binding energies. Therefore, we investigate the questions of water aggregates at low coverage and of multilayer formation. Furthermore, we analyse the mechanisms stabilizing such aggregates as well as the trends in the binding energy and dissociation degree with respect to coverage. We present a comprehensive and systematic search of all possible aggregates by successively increasing the coverage of water molecules up to 1 ML, using density functional theory (DFT). Molecular, dissociative and partial dissociative adsorption modes are considered. For all aggregates, we perform a thorough search of energy minima and investigate the coverage dependence of their adsorption energy up to the limit of formation of higher aggregates. The coverage regime between monolayer and thick films representing the interface with bulk water has not been studied with DFT previously, although TDS spectra clearly show distinct desorption peaks between those assigned to bulk ice and the monolayer.75 We present first results on interfaces with 2 ML and 3 ML water coverage based on small unit cells, which was motivated by the observation of (2 × 1) periodicity at 1 ML77,80,81 as well at the contact layer with bulk water.8,48 In order to gain insight into the driving forces for aggregation and dissociation, the strength of surface–water and water–water interactions, as well as the modification of water molecule and ZnO surface geometries and corresponding energies are quantified using a thermodynamic cycle to decompose the adsorption energies. The impact of water adsorption on the passivation of dangling bonds, surface states and the band gap are also analysed.
2. Methods
At low coverage, up to 1 ML, all possible structures of water aggregates were generated by systematically constructing low-energy structures. This was guided by the principles summarized as electron counting rules as explained in the Introduction.33,44 3-Coordinated zinc surface-sites of the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface have an empty dangling bond that may form a strong Lewis acid–base type bond with the lone pairs of water molecules. As each water molecule has two lone pairs, also adsorption in bridging positions forming two Zn–O bonds was considered. In addition, the completely filled dangling bonds at 3-coordinated surface oxygens may serve as acceptors for hydrogen bonds or form OH-groups due to proton transfer. Molecular adsorption of intact water molecules, as well as, dissociation into an OH-group bound at zinc sites and a hydrogen adsorbed at an oxygen site was considered. In addition, partial dissociative adsorption forming aggregates consisting of a mixture of intact and dissociated molecules were included. Furthermore, double dissociation of water into a Zn-bound oxygen and two adsorbed hydrogen atoms was tested. Formation of aggregates along the polar axis (rows) and along the trenches (columns) was studied. The latter arrangement offers the possibility of intermolecular hydrogen bonds.44 At 2 ML and 3 ML coverage, the number of possible structures and the complexity of the H-bonding networks preclude such an approach to rationally construct all possible arrangements. Therefore, MD runs were used to sample the configuration space of low-energy structures. This also avoids the limitation by preconceived structural concepts inherent in manually generated structures. The MD trajectories§ were calculated for a total simulated time of 70 ps and 60 ps at 2 ML and 3 ML, respectively. Snapshots were taken at regular intervals (ca. 1000 fs) and the corresponding structures optimized with VASP. In the high coverage regime, a relatively small supercell (2 × 1) was chosen to generate small periodic model structures suitable for accurate electronic structure calculations. The (2 × 1) periodicity was also found at the interface with bulk water.8,48 The MD was not meant to simulate a multilayer and its dynamic behaviour at room temperature, since a realistic interface would probably be much more disordered and require a significantly larger supercell. However, the small model structures should be sufficient to give a first insight into the energetics of water multilayers and the main structural features.
0) surface have an empty dangling bond that may form a strong Lewis acid–base type bond with the lone pairs of water molecules. As each water molecule has two lone pairs, also adsorption in bridging positions forming two Zn–O bonds was considered. In addition, the completely filled dangling bonds at 3-coordinated surface oxygens may serve as acceptors for hydrogen bonds or form OH-groups due to proton transfer. Molecular adsorption of intact water molecules, as well as, dissociation into an OH-group bound at zinc sites and a hydrogen adsorbed at an oxygen site was considered. In addition, partial dissociative adsorption forming aggregates consisting of a mixture of intact and dissociated molecules were included. Furthermore, double dissociation of water into a Zn-bound oxygen and two adsorbed hydrogen atoms was tested. Formation of aggregates along the polar axis (rows) and along the trenches (columns) was studied. The latter arrangement offers the possibility of intermolecular hydrogen bonds.44 At 2 ML and 3 ML coverage, the number of possible structures and the complexity of the H-bonding networks preclude such an approach to rationally construct all possible arrangements. Therefore, MD runs were used to sample the configuration space of low-energy structures. This also avoids the limitation by preconceived structural concepts inherent in manually generated structures. The MD trajectories§ were calculated for a total simulated time of 70 ps and 60 ps at 2 ML and 3 ML, respectively. Snapshots were taken at regular intervals (ca. 1000 fs) and the corresponding structures optimized with VASP. In the high coverage regime, a relatively small supercell (2 × 1) was chosen to generate small periodic model structures suitable for accurate electronic structure calculations. The (2 × 1) periodicity was also found at the interface with bulk water.8,48 The MD was not meant to simulate a multilayer and its dynamic behaviour at room temperature, since a realistic interface would probably be much more disordered and require a significantly larger supercell. However, the small model structures should be sufficient to give a first insight into the energetics of water multilayers and the main structural features.
The DFT calculations employed the generalized gradient approximation (GGA) exchange correlation functional of Perdew, Burke, and Ernzerhof (PBE)86 because of its established good accuracy in predicting equilibrium structures and binding energies of adsorbates on ZnO surfaces,44,77 as well as for hydrogen bonded systems.87 GGA functionals underestimate the band gap of ZnO, which is 0.73 eV for PBE, compared to an experimental band gap of 3.37 eV.5 The impact of this deficiency on adsorption energies and structures was tested using the hybrid DFT functional SHE06,88 which improves the description of the electronic structure by inclusion of exact exchange into Kohn–Sham DFT and calculates a band gap of 2.48 eV for ZnO. Test calculations showed that the adsorption energies slightly increase in a systematic way by 8–13% (see ESI,† Table S1). However, the general trend in the relative stability of undissociated, partially dissociated and dissociated structures remains unchanged. Thus more advanced methods are required for an accurate description of the band structure, however, PBE is sufficient for adsorption structures and energies. This observation agrees with recent results for water adsorption on CeO2 and H2S adsorption on ZnO calculated using GGA+U or hybrid DFTs.89,90 PBE calculates structures and adsorption energies for water on ZnO in good agreement with experiment44,77 and these properties are not significantly affected by the underestimated band gap. In particular, the trends in relative stability are preserved. In view of the large computational effort necessary for hybrid DFT calculations, the present study involving many large structures was performed with the computationally more efficient PBE functional. The Vienna ab initio Simulation Package (VASP)91 was used with the PAW92,93 method to treat the electron–nuclei interactions. The expansion of the electronic wave functions was truncated at a kinetic energy cutoff of 550 eV. For integration inside the Brillouin zone, the tetrahedron approach with Blöchl corrections was used with a Monkhorst–Pack scheme sampling based on a 1 × 6 × 4 mesh for the (1 × 1) unit cell and corresponding smaller grids for supercells according to the band folding. This assures that adsorption energies calculated for different unit cells are directly comparable. For density of states (DOS) analysis, the k-point mesh was refined to 1 × 16 × 10 and the back side of the slab was passivated with pseudo hydrogens to achieve a flat electrostatic potential in the bulk region. The energy scales were aligned according to this bulk electrostatic potential with the bulk valence band maximum at 0 eV.
The ZnO surface was modelled using slabs of 8 layers (16 atoms in the primitive unit cell) separated by 17.2 Å vacuum. The bottom half of the slab was kept frozen in bulk configuration, while the top half was fully relaxed together with the adsorbates. The quasi-Newton minimization algorithm (after initial conjugate gradient) was employed for structure optimization with a convergence criterion of 0.2 × 10−3 eV Å−1 for the Hellmann–Feynman forces. The asymmetry due to freezing the bottom half of the slab and water adsorption on only one side lead to a dipole moment, which was compensated by a dipole correction to annihilate the electric field gradient in the vacuum. The estimated deviation of binding energies from a fully converged result is ≤0.01 eV for this slab and computational setup. For all important adsorbate structures phonons were calculated to confirm them as true minima and not artefacts of an imposed translational symmetry.
The small displacement method as implemented in the PHON code94 was utilized to calculate the OH stretching frequencies. In each case, at least a (2 × 2) supercell was used with a 1 × 10 × 10 q-point mesh. Atoms in the relaxed part of the slab were displaced by 0.01 Å and the acoustic sum rule was applied to insure the translational invariance of the supercell. The root mean square deviations (RMSD) of the frequencies with respect to the displacement amplitude, the k-point grid and the cut-off value for a (2 × 2) supercell are <1 cm−1 and the RMSD with respect to the supercell size is <18 cm−1.
The adsorption energy per water molecule was calculated using eqn (1).
| Eads = (E(ZnO+nH2O) − E(ZnO) − nH2OE(H2O))/nH2O | (1) |
An insight into the different contributions to the adsorption energy may be gained from the following decomposition based on a Born–Haber thermodynamic cycle. The desorption process may be divided into four steps:
(1) Separation of the adsorbate layer from the surface without any geometrical changes. This step estimates the water–surface interaction energy without other contributions (eqn (2)).
 | (2) |
(2) Separation of the layer of n water molecules into isolated molecules, still frozen in the adsorbed geometry. This defines the water–water interaction energy (eqn (3)).
 | (3) |
(3) Relaxation of the isolated water molecule(s) from the adsorbed structure to that of a molecule isolated in vacuum. This quantifies the energies required for the geometry changes of the water molecule(s) (eqn (4)); the average water relaxation energy enters the binding energy.
 | (4) |
(4) Relaxation of the surface from the structure optimized with adsorbates to the clean surface, quantifying the energy required to modify the structure of the ZnO substrate (eqn (5)).
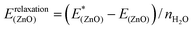 | (5) |
 and
and  are the total energies of the separated substrate and adsorbate layer calculated in the supercell with their atoms frozen in their adsorbed configurations.
are the total energies of the separated substrate and adsorbate layer calculated in the supercell with their atoms frozen in their adsorbed configurations. 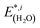 is the total energy of a water molecule frozen in the adsorbed geometry but calculated in the big unit cell.
is the total energy of a water molecule frozen in the adsorbed geometry but calculated in the big unit cell.
As the decomposition is based on a thermodynamic cycle, the sum of the four terms corresponds to the adsorption energy Eads as shown in eqn (6):
| Eads = Einteraction(ZnO/W) + Einteraction(W/W) + Erelaxation(W) + Erelaxation(ZnO) | (6) |
This decomposition scheme has been previously applied for molecular adsorption of water on the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface.44 In this study, the scheme is extended to full and partial dissociative adsorption. For water molecules with O–H distances >1.6 Å spin polarization was taken into account. With this provision, PBE calculates a bond dissociation energy of 5.51 eV in good agreement with high-level calculations and the experimental value (5.29 eV and 5.46 eV, respectively) and reproduces the bond dissociation curve well over the whole range (see ESI,† Fig. S1).95 The surface relaxation has been discussed in the context of water dissociation on GaN(10
0) surface.44 In this study, the scheme is extended to full and partial dissociative adsorption. For water molecules with O–H distances >1.6 Å spin polarization was taken into account. With this provision, PBE calculates a bond dissociation energy of 5.51 eV in good agreement with high-level calculations and the experimental value (5.29 eV and 5.46 eV, respectively) and reproduces the bond dissociation curve well over the whole range (see ESI,† Fig. S1).95 The surface relaxation has been discussed in the context of water dissociation on GaN(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0).45 In the case of dissociatively adsorbed water molecules, the water–surface interaction energy and the water relaxation energy should be analysed with caution, because the underlying assumption that the adsorbed state can be separated into two parts without substantially changing their properties may break down in some cases. The electronic structure of an OH group and a hydrogen atom bound to the ZnO surface may be quite different from the “dissociated” water molecule held in the same frozen geometry in vacuum. The latter is probably best described by a very long covalent bond between OH and H, while the dissociated hydrogen atom on the surface is bound to a surface oxygen and the OH-group to a Zinc atom with little electron density in the region between H and OH. The severely stretched covalent O–H bond results in high DFT energies for the frozen water layer
0).45 In the case of dissociatively adsorbed water molecules, the water–surface interaction energy and the water relaxation energy should be analysed with caution, because the underlying assumption that the adsorbed state can be separated into two parts without substantially changing their properties may break down in some cases. The electronic structure of an OH group and a hydrogen atom bound to the ZnO surface may be quite different from the “dissociated” water molecule held in the same frozen geometry in vacuum. The latter is probably best described by a very long covalent bond between OH and H, while the dissociated hydrogen atom on the surface is bound to a surface oxygen and the OH-group to a Zinc atom with little electron density in the region between H and OH. The severely stretched covalent O–H bond results in high DFT energies for the frozen water layer  and frozen isolated molecule
and frozen isolated molecule 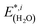 , leading to a very negative water–surface interaction energy Einteraction(ZnO/W) and a very high relaxation energy Erelaxation(W). Problematic cases will be pointed out in the discussion and the differences in electron density will be analysed.
, leading to a very negative water–surface interaction energy Einteraction(ZnO/W) and a very high relaxation energy Erelaxation(W). Problematic cases will be pointed out in the discussion and the differences in electron density will be analysed.
3. Results and discussions
3.1 Isolated single molecules adsorption
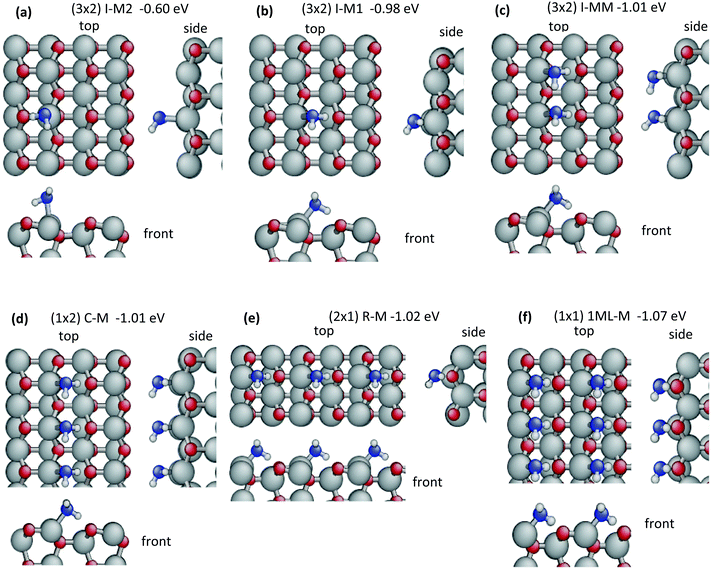
In order to investigate the driving forces for water aggregation on the surface, the adsorption of an isolated single molecule may be taken as reference, as water–water interactions may be neglected in this situation and binding is governed only by interactions with the surface. More than 25 starting configurations have been constructed. These included undissociated, dissociated and doubly dissociated water molecules, adsorbed on top surface zinc-sites, bridging two zinc-sites and/or H-bonding to surface oxygen sites. Full optimization resulted in two molecular (Fig. 1a and b) and three dissociative (Fig. 2a–c) adsorption configurations with exothermic (negative) adsorption energies. Structures with doubly dissociated water molecules are higher in energy than a gas-phase water molecule and the relaxed clean surface (see ESI,† Fig. S2) and are not further discussed.For molecular adsorption, the best adsorption configuration is I-M1 (I = isolated, M = molecular, −0.98 eV, Fig. 1b) in which the water molecule binds via a strong covalent bond (Zn–OW = 2.076 Å, Table 1) between its oxygen and a surface Zn atom. The bond length is comparable to bulk zinc oxide (2.012 Å) and restores a 4-fold, nearly tetrahedral coordination at the Zn atom. Furthermore, an H-bond (HW⋯OS = 1.517 Å) to a surface oxygen located on the nearest ZnO dimer across the trench is formed, coordinating the doubly occupied dangling bond orbital. This adsorption energy of the water molecule is very similar to the relaxed surface energy (0.93 eV per unit cell), which corresponds to the formation of one pair of dangling bonds. Thus the strength of the bonds formed by water adsorption is comparable to the bonds in bulk ZnO, illustrating the high degree of passivation of the surface dangling bonds upon water adsorption. In the second molecular adsorption structure, I-M2, the water molecule is flipped with respect to I-M1 and forms an H-bond with the surface oxygen of the same ZnO dimer. The Zn–OW bond and HW⋯OS H-bond are longer (2.180 Å and 1.814 Å) than in I-M1 and hence expected to be weaker according to the empirical bond-length bond-strength relationships.96 Moreover, the OW–HW⋯OS angle ϕ of the H-bond deviates more from linearity in I-M2 (132.3°) compared to the angle in I-M1 (161.8°). This less favourable geometry corresponds to a weaker adsorption energy (−0.60 eV) and a weaker water–surface interaction energy Einteraction(ZnO/W) = −0.73 eV in I-M2 (−1.39 eV in I-M1). The water–water interaction energies are negligible for both structures, confirming that a (3 × 2) supercell measuring 9.9 Å × 10.6 Å is sufficient to avoid interactions of periodic images. The O–H bond involved in hydrogen bonding stretches considerably in I-M1 (OW–HW = 1.049 Å vs. 0.972 Å in gas phase) due to the stronger H-bond compared to I-M2 (1.006 Å) in agreement with the higher water relaxation energy Erelaxation(W) = 0.14 eV versus 0.04 eV. Also the relaxation energy of the ZnO substrate is larger in I-M1 (0.27 eV), showing that the surface and the water molecule undergo considerable changes in their geometries to optimize their interaction in contrast to the weaker effects in I-M2 (0.10 eV).
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surfacea
0) surfacea
| Structures | I-M2 | I-M1 | I-MM | R-M | C-M | 1ML-M |
|---|---|---|---|---|---|---|
| a Energies in (eV) distances in (Å), angles in (°). b Bond length of the surface Zn–O dimer (2.012 Å in bulk and 1.872 Å in the clean surface). c Bond length between zinc atom and the water oxygen. d Length of H-bond between water and surface oxygen. e Length of water O–H bond forming a hydrogen bond to the surface. f H-bond between water molecules. g Length of free water O–H bond (0.972 Å in gas phase). h Height difference between top surface layer and corresponding bulk layer centre of mass (−0.274 Å in the clean surface). i Angle of hydrogen bond OW–HW⋯OS. | ||||||
| Figure # | 1a | 1b | 1c | 1e | 1d | 1f |
| Supercell | (3 × 2) | (3 × 2) | (3 × 2) | (2 × 1) | (1 × 2) | (1 × 1) |
| # H2O | 1 | 1 | 2 | 1 | 1 | 1 |
| Coverage (ML) | 1/6 | 1/6 | 1/3 | 1/2 | 1/2 | 1 |
| Energies | ||||||
| E interaction(ZnO/W) | −0.73 | −1.39 | −1.35 | −1.51 | −1.24 | −1.39 |
| E interaction(W/W) | −0.004 | −0.004 | −0.09 | −0.03 | −0.12 | −0.15 |
| E relaxation(ZnO) | 0.10 | 0.27 | 0.26 | 0.27 | 0.23 | 0.24 |
| E relaxation(W) | 0.04 | 0.14 | 0.16 | 0.26 | 0.11 | 0.23 |
| E ads | −0.60 | −0.98 | −1.01 | −1.02 | −1.01 | −1.07 |
| Geometry | ||||||
| Zn–OSb | 1.959 | 1.901 | 1.904 | 1.946 | 1.908 | 1.959 |
| 1.907 | ||||||
| Zn–OWc | 2.180 | 2.076 | 2.086 | 2.068 | 2.141 | 2.114 |
| 2.145 | ||||||
| HW⋯OSd | 1.814 | 1.517 | 1.622 | 1.441 | 1.546 | 1.459 |
| 1.996 | ||||||
| OW–HWe | 1.006 | 1.049 | 1.084 | 1.084 | 1.043 | 1.079 |
| 1.025 | ||||||
| HW1⋯OW2f | n/a | n/a | 1.492 | n/a | 2.429 | 2.484 |
| OW–HWg | 0.973 | 0.972 | 0.973 | 0.972 | 0.978 | 0.978 |
| 0.986 | ||||||
| δ h(L1)h | −0.257 | −0.232 | −0.190 | −0.141 | −0.153 | −0.022 |
| ϕ | 132.3 | 161.8 | 161.5 | 165.1 | 164.2 | 166.7 |
| 163.8 | ||||||
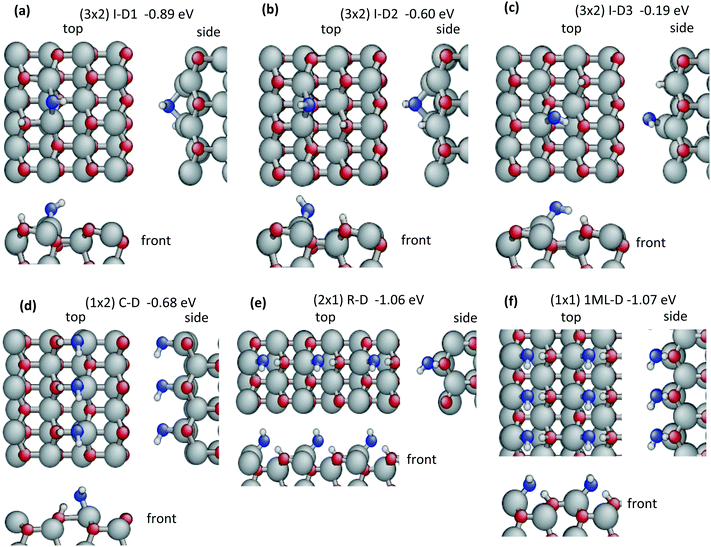
In the case of dissociative adsorption, the most stable configuration is I-D1 (D = dissociated, Eads = −0.89 eV, Fig. 2a). The OH-group sits in a bridging position between two neighbouring ZnO surface dimers and makes two covalent bonds with the surface Zn atoms (Zn–OOH = 2.012 Å and 1.999 Å). One H atom is transferred to a surface oxygen of one of the bridged dimers. When dissociation occurs across the trench, as in the second configuration I-D2 (Fig. 2b), these bonds lengthen (Zn–OOH = 2.072 Å and 2.042 Å) and the binding energy is reduced to −0.60 eV. In the third configuration I-D3 (Fig. 2c, Eads = −0.19 eV), the OH group binds via only one strong covalent bond to a surface Zn (Zn–OOH = 1.873 Å) and a strong H-bond (HW⋯OS = 1.517 Å and ϕ = 141.5°) with the nearest surface oxygen across the trench. The distances between the dissociated hydrogen atom and the OH-group are quite large with 2.861 Å in I-D1, 3.125 Å in I-D2 and 3.146 Å in I-D3. This results in very high water relaxation energies: Erelaxation(W) = 5.48 eV, 5.38 eV and 5.35 eV, respectively. As discussed in the Methods section, the high energies of the frozen water molecules due to the stretched bonds also contribute to the water–surface interaction energies calculated viaeqn (2) with Einteraction(ZnO/W) ranging from −7.13 to 7.94 eV (Table 2). Formally, this consequence of calculating Einteraction(ZnO/W) from frozen geometries may be accounted for by combining Einteraction(ZnO/W) + Erelaxation(W), which approximately corresponds to adsorbing and dissociating a relaxed gas-phase water molecule on the frozen ZnO surface (neglecting water–water interactions). The resulting value of −2.47 eV for I-D1 emphasizes the high strength of this adsorbate–surface interaction via two Zn–OOH bonds and one HS–OS bond. The corresponding value for undissociated water is −1.25 eV for I-M1, which is adsorbed via one Zn–OW bond and one H-bond. The very strong interaction with the surface requires large modifications in the substrate geometry reflected by the high relaxation energy Erelaxation(ZnO) = 1.58 eV for I-D1 compared to 0.27 eV for I-M1. Thus, the gain in water–surface interaction energy due to dissociation is less than the increase in relaxation energies required to form the dissociated structure and therefore the dissociation of an isolated water molecule is not favourable on ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0).
0).
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surfacea
0) surfacea
| Structures | I-D3 | I-D2 | I-D1 | C-D | R-D | 1ML-D |
|---|---|---|---|---|---|---|
| a Energies in (eV) distances in (Å), angles in (°). b Bond length of the surface Zn–O dimer (2.012 Å in bulk and 1.872 Å in the clean surface). c Length of the bond between zinc and the OH group oxygen. d Distance between the dissociated hydrogen atom and the OH group oxygen. e Bond length between dissociated hydrogen and surface oxygen. f Bond length of OH-group (0.972 Å in gas phase). g Height difference between top surface layer and corresponding bulk layer centre of mass (−0.274 Å in the clean surface). h Angle OOH⋯HS–OS of the H-bond. | ||||||
| Figure # | 2c | 2b | 2a | 2d | 2e | 2f |
| Supercell | (3 × 2) | (3 × 2) | (3 × 2) | (1 × 2) | (2 × 1) | (1 × 1) |
| # H2O | 1 | 1 | 1 | 1 | 1 | 1 |
| Coverage (ML) | 1/6 | 1/6 | 1/6 | 1/2 | 1/2 | 1 |
| Energies | ||||||
| E interaction(ZnO/W) | −7.13 | −7.69 | −7.94 | −5.18 | −4.70 | −4.11 |
| E interaction(W/W) | −0.003 | −0.003 | −0.00 | −0.11 | −0.04 | −0.15 |
| E relaxation(ZnO) | 1.59 | 1.71 | 1.58 | 1.20 | 0.68 | 0.67 |
| E relaxation(W) | 5.35 | 5.38 | 5.48 | 3.41 | 3.00 | 2.52 |
| E ads | −0.19 | −0.60 | −0.89 | −0.68 | −1.06 | −1.07 |
| Geometry | ||||||
| Zn–OSb | 1.909 | 1.933 | 1.934 | 2.391OH | 2.011OH,H | 2.038 |
| 1.937 | 2.126 | 1.874H | 1.887 | |||
| Zn–OOHc | 1.873 | 2.072 | 2.012 | 1.898 | 1.926 | 1.953 |
| 2.042 | 1.999 | |||||
| OOH⋯HSd | 3.146 | 3.125 | 2.861 | 1.661 | 1.555 | 1.497 |
| HS–OSe | 0.977 | 0.976 | 0.976 | 1.020 | 1.045 | 1.069 |
| OOH–HOHf | 0.978 | 0.973 | 0.974 | 0.978 | 0.970 | 0.977 |
| δ h(L1)g | −0.182 | −0.168 | −0.172 | −0.102 | −0.076 | 0.103 |
| ϕ | 141.5 | 78.6 | 105.7 | 145.7 | 157.2 | 161.2 |
Our results for structures I-M1, I-M2 and I-D1 agree with those reported previously,43,44,79,82 however, configurations I-D2 and I-D3 are new. Meyer et al.,44 have studied the adsorption of isolated water molecules on ZnO in great detail considering also many high-symmetry configurations. They reported 9 different configurations including 2 dissociated and 7 molecular absorption structures. Hellström, et al.,43 found only four minima and noted that the higher energy adsorption configurations of Meyer, et al.,44 converged to one of their four configurations after optimization.
3.2 Aggregation
While the adsorption of isolated water molecules on ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) has been reported in several works,43,44,79,82 formation of water clusters and further aggregation has not been studied, although this is an important process observed on many surfaces, including metals and oxides.11,15,16,21 In the following, the direct and substrate-mediated interactions of water molecules driving aggregation will be analysed as well as the driving forces for dissociation.
0) has been reported in several works,43,44,79,82 formation of water clusters and further aggregation has not been studied, although this is an important process observed on many surfaces, including metals and oxides.11,15,16,21 In the following, the direct and substrate-mediated interactions of water molecules driving aggregation will be analysed as well as the driving forces for dissociation.
The water molecule accepting the H-bond is further polarized elongating the O–H bond that forms a H-bond to the surface to 1.084 Å (1.049 Å in the isolated molecule) and now easily transfers one proton to the surface oxygen. The resulting structure of a half-dissociated dimer is shown in Fig. 3a. Its binding energy is −1.03 eV. Thus for dimers, dissociation of the acceptor molecule is exothermic by 0.02 eV, in contrast to the strongly endothermic dissociation of isolated molecules. According to the energy decomposition (Table 3), the water–water interaction energy is −0.10 eV and comparable to the molecular dimer. Therefore, the driving force for dissociation of the dimer is not due to direct water–water interactions. Actually the intermolecular H-bond between the intact water molecule and the OH group is 1.677 Å, longer than in the molecular dimer. On the other hand, the bonds to the surface Zn atoms are shorter with 2.059 Å for the water molecule and 1.997 Å for the OH-group. The interaction energy with the surface, based on the decomposition scheme with frozen structures, is −3.15 eV per molecule, more than twice as large as for the molecular dimer. However, this is affected by the high relaxation energy of the dissociated molecule (+3.30 eV). Combining the surface interaction with the average water relaxation energy gives Einteraction(ZnO/W) + Erelaxation(W) = −1.47 eV for the half-dissociated dimer compared to −1.19 eV for the molecular dimer. According to both analyses, the surface-interactions strongly favour dissociation. On the other hand, the surface relaxation energies counteract dissociation with Erelaxation(ZnO) = 0.53 eV for the half-dissociated dimer versus 0.26 eV for the molecular dimer. Therefore, partial dissociation of the adsorbed water dimer is favourable because the enhancement of the surface-interactions is larger than the increase of the relaxation energies. A fully dissociated dimer could not be found. All starting structures converged to a half-dissociated dimer after optimization.
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface as isolated water dimer (I-MD), half-dissociated column (C-MD), ladder-like row of dimers (R-MD), half-dissociated monolayer (1ML-MD), and the most stable structures with 2 ML and 3 ML of watera
0) surface as isolated water dimer (I-MD), half-dissociated column (C-MD), ladder-like row of dimers (R-MD), half-dissociated monolayer (1ML-MD), and the most stable structures with 2 ML and 3 ML of watera
| Structures | I-MD | C-MD | R-MD | 1ML-MD | 2ML1b | 3ML1b |
|---|---|---|---|---|---|---|
| a Energies in (eV) distances in (Å), angles in (°). b One undissociated and one dissociated molecule adsorbed on the surface Zn-sites, the additional water molecules are undissociated (see Fig. 3h and i, respectively). c W1 is the dissociated water molecule and W2 the undissociated water molecule. The average of the relaxation energies contributes to the binding energy Eads. d E relax(W) of the two water molecules not bound to surface Zn-sites are 0.05 eV and 0.11 eV. e E relax(W) of the four water molecules not bound to surface Zn-sites are 0.08 eV, 0.06 eV, 0.04 eV and 0.02 eV. f Bond length of surface dimer(s) (2.012 Å in bulk and 1.872 Å in the clean surface). The dimers carrying an undissociated or dissociated water molecule are indicated by M or D, respectively. g Bond length Zn–Ow for the undissociated water molecule. h Bond length Zn–OOH of the dissociated water molecule. i H-bond of the undissociated water molecule to the surface oxygen across trench. j H-bond between dissociated hydrogen and OH-group. k H-bond between adsorbed water and OH-group. l Bond length between dissociated hydrogen and surface oxygen. m Bond length of water O–H making H-bond to the surface (0.972 Å in gas phase). n Bond length of water O–H making a H-bond with the OH group. o Bond length of OH-group. p Height difference between top surface layer and corresponding bulk layer centre of mass (−0.274 Å in the clean surface). | ||||||
| Figure # | 3a | 3d | 3b | 3e | 3h | 3i |
| Supercell | (3 × 2) | (2 × 2) | (4 × 1) | (2 × 1) | (2 × 1) | (2 × 1) |
| # H2O | 2 | 2 | 2 | 2 | 4 | 6 |
| Cov. (ML) | 1/3 | 1/2 | 1/2 | 1 | 2 | 3 |
| Energies | ||||||
| E interaction(ZnO/W) | −3.15 | −2.99 | −3.67 | −3.58 | −1.91 | −1.39 |
| E interaction(W/W) | −0.10 | −0.12 | −0.14 | −0.16 | −0.66 | −0.54 |
| E relaxation(ZnO) | 0.53 | 0.52 | 0.50 | 0.48 | 0.22 | 0.18 |

|
3.30 | 3.10 | 4.15 | 4.07 | 5.38 | 5.51 |

|
0.07 | 0.07 | 0.08 | 0.09 | 0.16d | 0.24e |
| E ads | −1.03 | −1.01 | −1.19 | −1.18 | −0.93 | −0.77 |
| Geometry | ||||||
| Zn–OSf | 1.910M | 1.915M | 1.938M | 1.947M | 1.973M | 1.942M |
| 1.952D | 1.957D | 2.038D | 2.052D | 2.064D | 2.061D | |
| Zn–OWg | 2.059 | 2.079 | 2.049 | 2.060 | 2.037 | 2.003 |
| Zn–OOHh | 1.997 | 2.008 | 1.960 | 1.965 | 1.967 | 1.983 |
| HW⋯OSi | 1.728 | 1.739 | 1.691 | 1.702 | — | — |
| OOH⋯HSj | 1.615 | 1.582 | 1.794 | 1.793 | — | — |
| HW⋯OOHk | 1.677 | 1.685 | 1.679 | 1.663 | 1.475 | 1.471 |
| HS–OSl | 1.031 | 1.039 | 1.005 | 1.006 | 1.027 | 0.982 |
| OW–HWm | 1.016 | 1.015 | 1.014 | 1.018 | 1.003 | 1.008 |
| OW–HWn | 1.008 | 1.006 | 1.017 | 1.016 | 1.055 | 1.067 |
| OOH–HOHo | 0.972 | 0.972 | 0.971 | 0.972 | 0.981 | 0.997 |
| δ h(L1)p | −0.161 | −0.107 | −0.146 | 0.039 | 0.007 | 0.038 |
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface. Two different types of 1D aggregates may form due to the surface anisotropy: columns along the trenches and rows along the polar axis. Therefore, comparing water aggregation along the rows and columns may allow deeper insight into the subtle interplay of direct interactions between water molecules and indirect water–water interactions mediated by adsorption on different surface structures.
0) surface. Two different types of 1D aggregates may form due to the surface anisotropy: columns along the trenches and rows along the polar axis. Therefore, comparing water aggregation along the rows and columns may allow deeper insight into the subtle interplay of direct interactions between water molecules and indirect water–water interactions mediated by adsorption on different surface structures.
When water molecules arrange in a column along the trench, they may form an extended H-bonded chain as illustrated in Fig. 1d, where every molecule donates and accepts one intermolecular H-bond. This results in a similar binding energy (−1.01 eV) as for the isolated molecular dimer and corresponds to a stabilization of 0.03 eV relative to isolated molecules. However, the underlying ZnO substrate imposes a very long intermolecular H-bond of 2.429 Å in the column, compared to 1.492 Å in the dimer, where bending of bond-angles allows to optimize the intermolecular distance. Nevertheless, the energy decomposition reveals a strong water–water interaction of −0.12 eV in the column, compared to −0.09 eV per molecule in the dimer. Bearing in mind that the dimer has only one H-bond per two molecules, its bond strength is −0.18 eV, which is 50% more than that of the long H-bond of the column. The water–ZnO interaction is weaker in the column with −1.24 eV, compared to −1.35 eV per molecule in the dimer and −1.39 eV in the isolated molecules. This reduces the stabilizing effect of the direct water–water interaction. On the other hand, reduced relaxation energies of the water and zinc oxide stabilize the column relative to adsorption as dimer or isolated molecule (Table 1).
As an alternative structure, every second molecule in the column of water molecules may dissociate resulting in a column of half-dissociated dimers as shown in Fig. 3d. The binding energy is −1.01 eV as for the undissociated column. This contrasts with the isolated dimers, where half-dissociation was favourable. A completely dissociated column of water molecules (Fig. 2d) is considerably less stable with a binding energy of only −0.68 eV. The energy decomposition and structure is given in Table 2, but will not be further discussed. The arrangement of half-dissociated dimers in a column leads to a weak effective repulsion (Eads = −1.01 eV for the column, compared to −1.03 eV for the isolated dimer) in spite of an enhanced water–water interaction of Einteraction(W/W) = −0.12 eV in the column, compared to −0.10 eV in the dimer. However, the H-bond donated by the water molecule to the OH-group is 1.685 Å, slightly longer in the column than in the isolated dimer (1.677 Å) and thus not enhanced. Furthermore, the H-bond donated by the OH-group to the water molecule of the neighbouring dimer is 3.409 Å, even longer than in the undissociated column. The bonds with the surface, Zn–OW = 2.079 Å, Zn–OOH = 2.008 Å, HS–OS = 1.039 Å and the H-bond HW⋯OS = 1.739 Å are all longer in the half-dissociated column than in the isolated dimer. This agrees with the weaker water–surface interaction Einteraction(ZnO/W) = −2.99 eV in the column, compared to −3.15 eV in the dimer resulting in a significant surface-mediated repulsion. On the other hand, the reduced relaxation energies for the surface and water molecules (Erelaxation(ZnO) = 0.52 eV and average Erelaxation(W) = 1.58 eV in the column, versus 0.53 eV and 1.68 eV in the isolated dimer) contribute an indirect attraction. Thus the weak repulsive interaction between half-dissociated dimers aligned in a column is due to the weaker interaction with the surface, which more than compensates the attractive contributions of direct water–water interactions and relaxations.
When water molecules occupy every Zn-site along the polar axis forming a row as shown in Fig. 1e, they cannot form hydrogen bonds among each other due to the larger distance imposed by the substrate and the orientation imposed by the H-bond across the trench. Nevertheless, the binding energy is −1.02 eV, slightly stronger than in the column (−1.01 eV) and isolated molecules (−0.98 eV). This effective attraction of −0.04 eV relative to isolated molecules corresponds to a direct water–water interaction of −0.03 eV according to the energy decomposition, which may be due to dipole–dipole interactions. The Zn–OW bond of 2.068 Å and the hydrogen bond HW⋯OS = 1.441 Å with the surface are shorter than in the isolated molecule (2.076 Å and 1.517 Å, respectively) and indicate an enhanced interaction with the surface in agreement with an increased Einteraction(ZnO/W) = −1.51 eV, compared to −1.39 eV. This −0.12 eV indirect attraction is, however, compensated by an increase in the water relaxation (0.26 eV in the row, compared to 0.14 eV for the isolated molecule), which has the same magnitude. The relaxation energy of the surface does not change.
Dissociation of the above row of molecules is very favourable resulting in a high binding energy of −1.06 eV. This contrasts with the unfavourable dissociation of isolated molecules and columns and illustrates the sensitivity of water dissociation to the detailed interactions with the surface and neighbouring water molecules – including indirect surface-mediated interactions. The molecules in the row dissociate by transferring the hydrogen, which is polarized (OW–HW = 1.084 Å) by the H-bond to the surface, onto the oxygen across the trench forming a new bond HS–OS = 1.045 Å and a strong H-bond OOH⋯HS = 1.555 Å (Fig. 2e). The OH-group is bound via a single Zn–OOH bond of 1.926 Å in contrast to the two Zn–OOH bonds of the most stable isolated dissociated water molecule (I-D1), which is in a bridging position. Furthermore, the dissociated hydrogen is adsorbed in a different position in the isolated dissociated water molecules (Fig. 2a–c). These differences in the adsorbed structures should be born in mind when comparing the corresponding energy decomposition results. Alternatively, one can compare to the undissociated row of water molecules. The water–water interactions have similar magnitudes with Einteraction(W/W) −0.04 eV for the dissociated row, compared to −0.03 eV for the undissociated row. Thus direct water–water interactions contribute very little to the favourable dissociation. The water–surface interaction is very large for the dissociated row: Einteraction(ZnO/W) = −4.70 eV. However, this value may be biased by the high energy due to the very long O–H bond in the frozen geometry of the water molecule. The relaxation energy of the dissociated water molecule is 3.00 eV. Combining the water–surface interaction with the water relaxation gives −1.70 eV. The corresponding value for the row of undissociated molecules is −1.25 eV. Thus the water–surface interactions strongly favour dissociation, even when the water relaxation energies are included. On the other hand, the surface relaxation is much larger for the dissociated row with 0.68 eV, compared to 0.27 eV for the undissociated row, counteracting dissociation. However, in contrast to dissociation of an isolated molecule, the energy gain by the enhanced surface interaction is larger than the increase in relaxation energies and dissociation of a row of water molecules is favourable.
Ladders formed from larger water clusters, e.g., timers (Fig. 3c), are less favourable and have a weaker binding energy (−1.14 eV). Furthermore, the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 or 1
1 or 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 dissociation ratio in trimers with the MMD, MDD and MDM structures (ESI,† Fig. S3) show that the (1
2 dissociation ratio in trimers with the MMD, MDD and MDM structures (ESI,† Fig. S3) show that the (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) dissociative ratio in half-dissociated water dimers is the optimum on ZnO.
1) dissociative ratio in half-dissociated water dimers is the optimum on ZnO.
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0). Experimental studies have found a (2 × 1) periodicity using LEED, STM, He-atom scattering and HREELS.77,80,81 Many theoretical studies43–45,78,79,82–85 have described the lowest energy structure shown in Fig. 3e that is composed of half-dissociated dimers. It may be understood as the next level in the hierarchy of aggregation, where ladders densely cover the surface such that each zinc atom at the surface is coordinated by an adsorbed water molecule or OH-group, leaving no free sites between the ladders. The adsorption energy is −1.18 eV, slightly less than for the ladder structure (−1.19 eV), indicating a weak effective repulsion between adjacent ladders. Thus the formation of the dense monolayer is driven by maximizing the number of strong Zn–OW bonds by saturating all zinc surface sites, rather than by attractive interactions between ladders. On the other hand, the energy decomposition reveals a slight increase in the water–water interaction energies from Einteraction(W/W) = −0.14 eV in ladders to −0.16 eV in the monolayer. This is analogous to the situation in the columns of half-dissociated dimers, where an effective repulsion between adjacent dimers was found in spite of an apparently attractive water–water interaction.
0). Experimental studies have found a (2 × 1) periodicity using LEED, STM, He-atom scattering and HREELS.77,80,81 Many theoretical studies43–45,78,79,82–85 have described the lowest energy structure shown in Fig. 3e that is composed of half-dissociated dimers. It may be understood as the next level in the hierarchy of aggregation, where ladders densely cover the surface such that each zinc atom at the surface is coordinated by an adsorbed water molecule or OH-group, leaving no free sites between the ladders. The adsorption energy is −1.18 eV, slightly less than for the ladder structure (−1.19 eV), indicating a weak effective repulsion between adjacent ladders. Thus the formation of the dense monolayer is driven by maximizing the number of strong Zn–OW bonds by saturating all zinc surface sites, rather than by attractive interactions between ladders. On the other hand, the energy decomposition reveals a slight increase in the water–water interaction energies from Einteraction(W/W) = −0.14 eV in ladders to −0.16 eV in the monolayer. This is analogous to the situation in the columns of half-dissociated dimers, where an effective repulsion between adjacent dimers was found in spite of an apparently attractive water–water interaction.
Besides this half-dissociated monolayer, previous theoretical studies also reported molecular (non-dissociated, Fig. 1f) and fully dissociated monolayers (Fig. 2f) with a (1 × 1) periodicity and weaker binding energies of −1.07 eV.43–45,78,79,82,83 These tree different monolayer structures can easily interconvert with a barrier of 0.02 eV for going from the molecular the to the fully dissociated (1 × 1) structure and no barrier for going from the molecular (1 × 1) to the half-dissociated (2 × 1) structure.44,78,84 According to our phonon calculations, the (1 × 1) structures have imaginary frequencies and hence are not minima. When the unit cell of the molecular or fully dissociated monolayers is doubled, the structures optimize to the half-dissociated monolayer with (2 × 1) periodicity. Comparing the energy decompositions for the monolayer structures shows that the water–water interactions are very similar with Einteraction(W/W) = −0.15 eV for the molecular and fully dissociated structures and −0.16 eV for the half-dissociated monolayer. This corresponds to only 10% of the preference for the half-dissociated monolayer. Dissociation is strongly favoured by the dramatic increase in water–surface interactions from Einteraction(ZnO/W) = −1.39 eV in the molecular monolayer to −3.58 eV in the half-dissociated and −4.11 eV in the fully dissociated monolayer. On the other hand, the water relaxation energies also strongly increase from Erelaxation(W) = 0.23 eV to 2.08 eV and 2.52 eV, respectively. Likewise, the surface relaxation disfavours dissociation with Erelaxation(ZnO) = 0.24 eV, 0.48 eV and 0.67 eV for 0%, 50%, and 100% dissociation, respectively. Thus the half-dissociated monolayer is preferred because it has the best balance between the increase of water–surface interactions, which strongly favour dissociation and the relaxation energies that hinder dissociation. Up to half-dissociation the water–surface interaction dominates, while for full dissociation, the relaxation energies dominate. Fig. 4 shows the adsorption energies of monolayer structures as function of the dissociation degree. It also includes the results for (3 × 1) structures with 1/3 and 2/3 dissociated molecules (see ESI,† Fig. S4 for details). The symmetric shape suggests that 50% dissociation indeed is the optimum.
In the monolayers, all surface Zn- and O-sites are 4-fold coordinated leading to strongly reduced buckling of the top layer (0.022 Å for molecular, 0.103 Å for dissociated and 0.039 Å for half-dissociated monolayers) in contrast to the clean surface (−0.274 Å) and lower aggregates where higher corrugation amplitudes are found.
In view of the little prior knowledge about the principles governing the structures of water multilayers and the large number of arrangements for multiple water molecules on the surface, we have used an MD to sample the low-energy structures and optimized snapshots resulting in a total of 21 distinct structures with 4 molecules adsorbed on a (2 × 1) supercell corresponding to a coverage of 2 ML. The 10 lowest energy configurations are shown in Fig. 3h (2ML1) and in the ESI,† Fig. S6. The most stable structure 2ML1 has a binding energy of −0.93 eV per water molecule and shows a honeycomb like continuous 2D network of hydrogen-bonded 6-rings of water molecules in the relatively flat overlayer. In contrast to the monolayer, the half-dissociated dimer bound on the surface Zn-sites forms H-bonds to the additional water molecules rather than to the surface. The additional water molecules cannot form a Zn–OW bond, since all Zn-sites are already occupied at 1 ML, but H-bond to the surface: the water molecule oriented parallel to the surface plane is H-bound to the dissociated H, while the water molecule oriented perpendicular to the surface plane makes an H-bond to the surface oxygen. Additional H-bonds between the water molecules form the 2D honeycomb network. Flipping rows of H-bonds within this network results in structures with very similar binding energies (within ∼10–20 meV, see ESI,† Fig. S6). This indicates proton disorder in the honey-comb like H-bonding network of the 2D adsorbate layer. This is analogous to the phenomenon first described by Bernal and Fowler for the 3D structure of ice Ih97 and also observed in many other 3D-crystalline water phases including most ice phases and clathrates. The configurational entropy due to this proton disorder98 will contribute to the stability of this adsorbate phase at finite temperatures. As for the monolayer, all ZnO surface atoms are saturated with a nearly tetrahedral 4-fold coordination: Zn surface atoms are forming a bond to either an OH-group or a water molecule (1.967 Å and 2.037 Å, respectively), while the surface oxygens either bind the dissociated hydrogen atom (HS–OS = 1.027 Å) or accept an H-bond from a water molecule. The water–surface interaction energy is −3.82 eV per surface unit cell¶ and hence stronger than in the monolayer (−3.58 eV). On the other hand, the relaxation energies of the surfaces are comparable with −0.44 eV per surface unit cell¶ for the honeycomb double monolayer and −0.48 eV for the monolayer. The H-bonds in the honeycomb network range from 1.661 Å to 2.261 Å and the water–water interactions are strong, −0.66 eV per water molecule (Einteraction(W/W) and 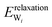 should be taken with care as the separation into isolated molecules is not unique for 2 ML). In the honeycomb double monolayer structures all water molecules and OH-groups are 4-fold coordinated counting surface Zn-sites and surface OH-groups as additional donors and the lone pairs of surface oxygens as acceptor sites. The 4-fold coordination of the additional water molecules may be compared to the Bernal Fowler ice rules.97,98 In contrast to the 2D ice rules of Salmeron13 that limit the growth of water clusters on noble metals, an infinitely large 2D layer can exist on ZnO because the surface also offers acceptor sites. However, the lack of dangling OH-bonds and lone pairs in the honeycomb double monolayer precludes the further growth of the water film by simply attaching more water molecules. Further growth, forming multilayers, requires restructuring of the 2 ML film to expose the necessary binding sites. Similar restructuring has been observed for water films grown on close-packed hexagonal metal surfaces.17–19 In case water molecules are arranged on ZnO(10
should be taken with care as the separation into isolated molecules is not unique for 2 ML). In the honeycomb double monolayer structures all water molecules and OH-groups are 4-fold coordinated counting surface Zn-sites and surface OH-groups as additional donors and the lone pairs of surface oxygens as acceptor sites. The 4-fold coordination of the additional water molecules may be compared to the Bernal Fowler ice rules.97,98 In contrast to the 2D ice rules of Salmeron13 that limit the growth of water clusters on noble metals, an infinitely large 2D layer can exist on ZnO because the surface also offers acceptor sites. However, the lack of dangling OH-bonds and lone pairs in the honeycomb double monolayer precludes the further growth of the water film by simply attaching more water molecules. Further growth, forming multilayers, requires restructuring of the 2 ML film to expose the necessary binding sites. Similar restructuring has been observed for water films grown on close-packed hexagonal metal surfaces.17–19 In case water molecules are arranged on ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) in such a way that square 4-rings of H-bonded water are formed in the overlayers (see ESI,† Fig. S6), the binding energy decreases by 40 meV compared to the most stable structure (2ML1) due to increased angle strain. Breaking the connectivity in the rings of the water overlayer decreases the binding energy further (∼50 meV) compared to the most stable structure, since the 4-fold coordination is lost and dangling donor and acceptor sites are formed.
0) in such a way that square 4-rings of H-bonded water are formed in the overlayers (see ESI,† Fig. S6), the binding energy decreases by 40 meV compared to the most stable structure (2ML1) due to increased angle strain. Breaking the connectivity in the rings of the water overlayer decreases the binding energy further (∼50 meV) compared to the most stable structure, since the 4-fold coordination is lost and dangling donor and acceptor sites are formed.
In contrast to the ice-like buckled bilayer or flat mixed OH/H2O layers with (√3 × √3)R30° lattice observed on many close-packed hexagonal metal substrates,17,18,20,24,31 the water molecules that cannot bind to Zn-sites form H-bonds to surface oxygens. The ice-like buckled bilayer has a much weaker interaction with the substrate of 0.1–0.4 eV,14,15,18–20 a coverage of only 2/3 ML, and exposes dangling OH bonds that may allow continuous growth of a multilayer.17,18,29 Furthermore, the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) substrate is not hexagonal and half of the Zn-bound water molecules are dissociated.
0) substrate is not hexagonal and half of the Zn-bound water molecules are dissociated.
| Structure | 3ML1 | 3ML2 | 3ML3 | 3ML4 | 3ML5 | 3ML6 | 3ML7 | 3ML8 | 3ML9 | 3ML10 |
|---|---|---|---|---|---|---|---|---|---|---|
a Binding motif in the contact layer.
b Ring size(s) of the H-bond network.
c W1 (W2) is the dissociated (undissociated) water molecule adsorbed on a surface Zn-site.
d Additional water molecules in the second layer not bound to a surface Zn-site.
e Additional water molecules in the third layer not bound to a surface Zn-site.
f The average of the water relaxation energies 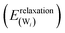 contributes to Eads. contributes to Eads.
|
||||||||||
| Motifa | a | b | a | a | c | c | c | c | b | c |
| H-bond topologyb | 4-5-8 | 6 | 4-5-8 | 4-5-8 | 8-10 | 8-10 | 5-8-10 | 6 | 5-6-8-10 | 6-7 |
| E interaction(ZnO/W) | −1.39 | −1.26 | −1.33 | −1.40 | −1.15 | −1.13 | −1.13 | −1.14 | −1.27 | −1.14 |
| E interaction(W/W) | −0.54 | −0.51 | −0.59 | −0.52 | −0.45 | −0.45 | −0.47 | −0.45 | −0.59 | −0.45 |
| E relaxation(ZnO) | 0.18 | 0.17 | 0.17 | 0.18 | 0.16 | 0.16 | 0.16 | 0.16 | 0.14 | 0.16 |

|
5.51 | 4.55 | 5.51 | 5.51 | 3.79 | 3.69 | 3.76 | 3.78 | 5.51 | 3.77 |
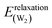
|
0.24 | 0.27 | 0.23 | 0.24 | 0.14 | 0.14 | 0.14 | 0.12 | 0.12 | 0.12 |

|
0.08 | 0.03 | 0.09 | 0.07 | 0.10 | 0.09 | 0.08 | 0.12 | 0.11 | 0.12 |

|
0.06 | 0.06 | 0.04 | 0.04 | 0.03 | 0.03 | 0.01 | 0.01 | 0.02 | 0.02 |

|
0.04 | 0.06 | 0.01 | 0.02 | 0.03 | 0.02 | 0.10 | 0.01 | 0.01 | 0.01 |

|
0.02 | 0.02 | 0.02 | 0.04 | 0.02 | 0.03 | 0.03 | 0.02 | 0.02 | 0.02 |
| E ads | −0.77 | −0.77 | −0.77 | −0.76 | −0.76 | −0.75 | −0.75 | −0.75 | −0.75 | −0.75 |
 | ||
Fig. 5 Binding motifs in the contact layer at the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)/3 ML interface. The additional water molecules have been removed for clarity. 0)/3 ML interface. The additional water molecules have been removed for clarity. | ||
In few structures an additional water molecule takes part in the H-bonding between the contact layer dimer and the surface (see, e.g., structure 3ML9 in the ESI,† Fig. S7h). However, in general the additional water molecules are attached to H-bond donor and acceptor sites on top of the half-dissociated contact layer and the water molecules are interconnected via a 3D H-bond network. Many different H-bond topologies are observed and consist of H-bonding water molecules forming 4-, 5-, 6-, 7-, 8- and 10-membered rings. While most of the water molecules are 4-fold coordinated in agreement with the Bernal–Fowler ice rules, the highest water molecules are 3-fold coordinated exposing dangling H-bond donor and acceptor sites that can bind additional water layers, allowing a continuous growth of thick multilayers or bulk water on the surface. Indeed, similar interface structures composed of a contact layer with partially dissociated dimers and an H-bonded network of undissociated molecules on top was reported for thicker water layers on the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface. Two recent DFT-MD studies reported a dissociation degree of ca. 55 ± 5%8,48 in good agreement with our results, while a higher dissociation around 80% was found using the more approximate ReaXX force field.85 A detailed analysis of structures in the contact layer revealed dynamic proton transfers between binding motifs (a) and (b) as well as (b) and (c) with free energy barriers of ∼100 meV and ∼70 meV, respectively.48 Furthermore, a ∼16% increased water density at the contact layer was noted due to excess water molecules H-bonding to surface oxygen atoms,48 similar to the situation in one of our 3 ML structures (3ML9).
0) surface. Two recent DFT-MD studies reported a dissociation degree of ca. 55 ± 5%8,48 in good agreement with our results, while a higher dissociation around 80% was found using the more approximate ReaXX force field.85 A detailed analysis of structures in the contact layer revealed dynamic proton transfers between binding motifs (a) and (b) as well as (b) and (c) with free energy barriers of ∼100 meV and ∼70 meV, respectively.48 Furthermore, a ∼16% increased water density at the contact layer was noted due to excess water molecules H-bonding to surface oxygen atoms,48 similar to the situation in one of our 3 ML structures (3ML9).
As shown in Table 4, the strongest interaction energies with the surface (−1.33 eV to −1.40 eV) are observed in structures 3ML1, 3ML3 and 3ML4 in which binding motif (a) is present. When the water binds via the binding motif (b), the water/surface interaction energy is lowered (−1.26 eV to −1.27 eV) as observed in structures 3ML2 and 3ML9. In structures 3ML5, 3ML6, 3ML7, 3ML8 and 3ML10 in which the water dimer in the contact layer binds via motif (c), the interaction energy is weaker (−1.13 eV to −1.15 eV). This may be related to the water relaxation energies and the distances between the OH-group and dissociated hydrogen, which are large for motif (a) and small for motif (c). The strength of the average water–water interaction energy does not depend on the amount of H-bond rings nor on the size n of the rings formed, but rather depends considerably on the binding motif in the contact layer. The strongest water–water interaction energies (−0.51 eV to −0.59 eV) are found in structures with binding motifs (a) and (b), while configurations with binding motif (c) in the contact layer have lower values (−0.45 eV to −0.47 eV). On the other hand, the relaxation energy of the ZnO substrate has roughly the same value for all structures with 0.16 eV per water molecule or 0.49 eV per surface unit cell, which is similar to the half-dissociated monolayer (0.48 eV).
3.3 Binding energy trends
The previous section has shown that several classes of aggregates can be stable on the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface. In all structures, the strong interaction of water with the surface Zn-sites enforces an epitactic arrangement of the water molecules in the contact layers. In the low coverage regime (0–1 ML) the adsorption energy of each class of aggregates shows little dependence on the coverage (Fig. 6). Formation of the monolayer may be envisioned as a stepwise process passing through a hierarchy of aggregates from isolated molecules, via dimers that partially dissociate and ladders that have the highest binding energy, −1.19 eV per water molecule. Comparing the adsorption energies of isolated molecules with columns, rows and monolayers reveals a near additivity of the lateral interactions in the two directions. For molecular adsorption the increase in the binding energy relative to an isolated molecule is −0.03 eV for columns, −0.04 eV for rows and −0.09 eV for the monolayer (Table 1). Likewise, for half-dissociated adsorption the increments in binding energy relative to the isolated dimer are +0.02 eV for columns, −0.16 eV for the rows and −0.15 eV for the monolayer (Table 3). The direct water–water interactions based on the energy decomposition show an exact additivity of the interactions in rows and columns. The additivity may be related to structural similarities. For fully dissociated water the adsorption structure of the isolated molecule is unique with a bridging OH-group in contrast to single Zn–OOH bonds in the columns, rows and monolayer and the additivity of the adsorption energy increments does not hold.
0) surface. In all structures, the strong interaction of water with the surface Zn-sites enforces an epitactic arrangement of the water molecules in the contact layers. In the low coverage regime (0–1 ML) the adsorption energy of each class of aggregates shows little dependence on the coverage (Fig. 6). Formation of the monolayer may be envisioned as a stepwise process passing through a hierarchy of aggregates from isolated molecules, via dimers that partially dissociate and ladders that have the highest binding energy, −1.19 eV per water molecule. Comparing the adsorption energies of isolated molecules with columns, rows and monolayers reveals a near additivity of the lateral interactions in the two directions. For molecular adsorption the increase in the binding energy relative to an isolated molecule is −0.03 eV for columns, −0.04 eV for rows and −0.09 eV for the monolayer (Table 1). Likewise, for half-dissociated adsorption the increments in binding energy relative to the isolated dimer are +0.02 eV for columns, −0.16 eV for the rows and −0.15 eV for the monolayer (Table 3). The direct water–water interactions based on the energy decomposition show an exact additivity of the interactions in rows and columns. The additivity may be related to structural similarities. For fully dissociated water the adsorption structure of the isolated molecule is unique with a bridging OH-group in contrast to single Zn–OOH bonds in the columns, rows and monolayer and the additivity of the adsorption energy increments does not hold.
Increasing the coverage beyond 1 ML decreases the binding energy because all under coordinated surface zinc sites are occupied and the additional water molecules can only bind via hydrogen bonds. At 2 ML, the most stable adsorption configuration has a binding energy of −0.93 eV. All water molecules are tightly bound with no dangling O–H that could bind more water molecules. At 3 ML, the additional water molecules do not H-bond to the surface oxygens but are H-bonding to the contact layer. The water forms distinct H-bonded overlayers and many structures with very similar binding energies (−0.77 to −0.75 eV for the ten best adsorption configurations). For higher coverages, the binding energy is expected to approach the cohesive energy of ice (−0.55 eV), the limiting value for very thick layers of adsorbed water molecules at 0 K. These trends in the calculated binding energies agree at least qualitatively with the TDS data reported for the condensation of water on the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface.75,76 At low exposure a desorption peak at 340 K was reported that saturated and was assigned to binding on the Zn-site. The fact that this peak does not shift with coverage agrees with our finding that ladders and the half-dissociated monolayer have nearly identical adsorption energies. At higher exposures several peaks with lower desorption temperatures (220–152 K) were observed and assigned to H-bonded molecules in clusters, on oxygen sites, 2D ice and 3D ice. A water binding energy of 1.02 eV corresponding to a desorption peak at 367 K observed with He-scattering was estimated using Redhead analysis.77 This agrees reasonably well with our adsorption energy for the monolayer (−1.18 eV).
0) surface.75,76 At low exposure a desorption peak at 340 K was reported that saturated and was assigned to binding on the Zn-site. The fact that this peak does not shift with coverage agrees with our finding that ladders and the half-dissociated monolayer have nearly identical adsorption energies. At higher exposures several peaks with lower desorption temperatures (220–152 K) were observed and assigned to H-bonded molecules in clusters, on oxygen sites, 2D ice and 3D ice. A water binding energy of 1.02 eV corresponding to a desorption peak at 367 K observed with He-scattering was estimated using Redhead analysis.77 This agrees reasonably well with our adsorption energy for the monolayer (−1.18 eV).
The driving forces for water aggregation may be derived by comparing structures with identical dissociation degree and similar structures to avoid superposition by other effects. An overview of the energetic changes in such aggregation processes (ESI,† Fig. S8) reveals that direct water–water interactions (Einteraction(W/W)) are always in favour of forming larger aggregates. Likewise, the surface relaxation (Erelaxation(ZnO)) generally is smaller for larger aggregates and hence favours aggregation. This contrasts with the very recent report that on the rutile TiO2(110) surface relaxations due to adsorbed methanol or water reduce the adsorption energy on neighbouring sites and hence have a repulsive effect.99 The changes in water–surface interaction energy (Einteraction(ZnO/W)) and water relaxation (Erelaxation(W)) depend on the size and type of aggregate. In several cases weakening of the water–surface interactions is more important than the gain due to the other contributions, rendering aggregation unfavourable in this specific case. Thus, the driving force for aggregation of water molecules on the surface is due to a subtle interplay of direct water–water interactions and interactions mediated by surface-adsorption and due to geometry changes.
The driving forces for water dissociation may be analysed by comparing the changes in the energy decomposition terms in similar aggregates (ESI,† Fig. S9). As dissociation or partial dissociation is favourable only for certain aggregates, such as rows, the dimer and the monolayer, it was surprising to find that direct water–water interactions hardly contribute to water dissociation. Einteraction(W/W) changes by less than ±0.02 eV. The driving force for dissociation is due to a very strong increase in water–surface interactions (Einteraction(ZnO/W)), which can reach several eV. On the other hand, the relaxation energies of water and the surface strongly oppose dissociation. In most cases, the combined water and surface relaxation energies required for dissociation are larger than the gain due to enhanced surface interactions. Dissociation is favourable only if the energy gain due to increased water–surface interactions is larger than the energy required for the geometrical changes.
3.4 Electronic structure and binding mechanisms
Fig. 7a compares the density of states (DOS) distributions of bulk ZnO, the clean surface and two water covered ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surfaces considering both molecular and dissociative adsorption modes. For simplicity (1 × 1) supercells are used to represent the two adsorption modes of water (Fig. 1f and 2f). Hybridization of the Zn 3d and O 2p bands in the valence band (which is overestimated in GGA-DFT) constitute the main signature of the bulk density of states in the range 0.0 to −5.8 eV, besides a sharp peak for the O 2s band at −16.9 eV. The Zn 3d and O 2p bands are slightly more broadened in the projected density of states (PDOS) of the top Zn and O atoms of the clean surface as compared to the bulk PDOS. Near the valence band maximum there is a strong double peak of the oxygen PDOS, which probably corresponds to the dangling bond and has a tail reaching +0.2 eV. Furthermore, the O 2s peak is shifted 0.5 eV higher due to the cleaved Zn–O bond. On the other hand, the PDOS of the surface zinc now has strong contributions near −6 eV. After absorption of molecular water, the PDOS of the surface zinc and oxygen atoms look very similar to the bulk DOS in agreement with the bulk-like tetrahedral coordination and geometry (Section 3.2.4). This shows that water adsorption efficiently passivates the dangling bonds and thus reverses the shifts characteristic for the clean surface. The O 2s band is back at 16.9 eV and the band due to hybridization of Zn 3d and O 2p has the same dispersion and very similar profile as in the bulk. The water orbitals corresponding to the O–H bonds (at −19.4 eV and −7.2 eV in gas-phase water) are shifted to −20.0 eV and −7.9 eV due to adsorption on ZnO, while the water lone pairs (at −3.4 eV and −1.3 eV in gas phase water) hybridize with Zn 3d orbitals resulting in a wide band at −5.9 to −0.1 eV (exaggerated due to the high Zn 3d states). Due to the proton transfer that leads to dissociative adsorption, the O 2s bands of water and ZnO shift in opposite directions by +2.5 eV and −1.7 eV, respectively. The surface O 2p states contribute to binding of the transferred proton with a new band at −6.7 eV in the PDOS of the surface oxygen, while the water O 2p states are now included in the broad binding state at −5.8 to −0.1 eV. The opposite directions (and comparable magnitudes) of the shifts in the PDOS of the surface and water oxygen atoms due to the proton transfer agree with the fact that both adsorption modes have comparable binding energies.
0) surfaces considering both molecular and dissociative adsorption modes. For simplicity (1 × 1) supercells are used to represent the two adsorption modes of water (Fig. 1f and 2f). Hybridization of the Zn 3d and O 2p bands in the valence band (which is overestimated in GGA-DFT) constitute the main signature of the bulk density of states in the range 0.0 to −5.8 eV, besides a sharp peak for the O 2s band at −16.9 eV. The Zn 3d and O 2p bands are slightly more broadened in the projected density of states (PDOS) of the top Zn and O atoms of the clean surface as compared to the bulk PDOS. Near the valence band maximum there is a strong double peak of the oxygen PDOS, which probably corresponds to the dangling bond and has a tail reaching +0.2 eV. Furthermore, the O 2s peak is shifted 0.5 eV higher due to the cleaved Zn–O bond. On the other hand, the PDOS of the surface zinc now has strong contributions near −6 eV. After absorption of molecular water, the PDOS of the surface zinc and oxygen atoms look very similar to the bulk DOS in agreement with the bulk-like tetrahedral coordination and geometry (Section 3.2.4). This shows that water adsorption efficiently passivates the dangling bonds and thus reverses the shifts characteristic for the clean surface. The O 2s band is back at 16.9 eV and the band due to hybridization of Zn 3d and O 2p has the same dispersion and very similar profile as in the bulk. The water orbitals corresponding to the O–H bonds (at −19.4 eV and −7.2 eV in gas-phase water) are shifted to −20.0 eV and −7.9 eV due to adsorption on ZnO, while the water lone pairs (at −3.4 eV and −1.3 eV in gas phase water) hybridize with Zn 3d orbitals resulting in a wide band at −5.9 to −0.1 eV (exaggerated due to the high Zn 3d states). Due to the proton transfer that leads to dissociative adsorption, the O 2s bands of water and ZnO shift in opposite directions by +2.5 eV and −1.7 eV, respectively. The surface O 2p states contribute to binding of the transferred proton with a new band at −6.7 eV in the PDOS of the surface oxygen, while the water O 2p states are now included in the broad binding state at −5.8 to −0.1 eV. The opposite directions (and comparable magnitudes) of the shifts in the PDOS of the surface and water oxygen atoms due to the proton transfer agree with the fact that both adsorption modes have comparable binding energies.
Fig. 7b and c show difference electron densities for molecular and dissociative adsorption, respectively. They were calculated by subtracting the electron density of the slab and adsorbate, calculated separately in the frozen geometry, from the electron density of the optimized structures. Molecular adsorption (Fig. 7b) leads to polarization of the water molecule shifting electron density from the O–H bond forming the H-bond and the top of the molecule toward the centre of the H-bond, the centre of the Zn–O bond forming, and to the region of the remaining lone-pair of the water molecule. Polarization of the surface zinc and oxygen atoms also contributes to the charge build-up in the new bonds formed. Dissociative adsorption (Fig. 7c) results in even stronger polarization of the strongly distorted water molecule, shifting electrons from the centre of the OW⋯HS H-bond (in the calculation of the frozen water molecule this is a long O–H bond) towards the new OS–HS and Zn–OW bonds and the region of lone pairs of the OH-group. The surface (and to lesser extent the sub-surface) zinc and oxygen atoms are also polarized shifting electron density towards the bonds formed. In spite of the stronger electron redistribution in the dissociated structure, the order of magnitude of the difference densities seem to be comparable, which indicates that the electron densities of the frozen water layers are not too different from those in the corresponding complete structures. This suggests that the assumptions underlying the energy decomposition are valid for the monolayer structures.
3.5 OH stretching modes
In Table 5, the OH stretching frequencies are reported for gas phase water, various structures at different coverages and bulk ice comparing DFT with high-level theory and experimental data. The vibrational frequencies of the free water molecule are underestimated by ∼100 cm−1 compared to the high level CCSD(T) calculations and experimental harmonic frequencies,100 due to the systematic errors in DFT. On the other hand, the harmonic DFT frequencies are ∼50 cm−1 higher than the experimental anharmonic frequencies.101 In each of the adsorbate structures, only one frequency is not shifted to below 3700 cm−1. This is probably the dangling OH-bond or a weakly H-bonding OH group. The frequencies shifted to lower values indicate the presence of H-bonds among the water molecules and between the water molecules and the surface. We note the strong similarity of the calculated IR frequencies of the half-dissociated dimer, the ladder and the monolayer, which all contain same the dimer binding motif. They all have one frequency around 3750 cm−1, which corresponds to the dissociated OH-group that does not form an H-bond. Furthermore, there are two frequencies at ca. 3000 and 3100 cm−1 and one very strongly shifted frequency that shifts from 2523 cm−1 in the isolated dimer to ca. 2930 cm−1 in the ladders and monolayer. Our calculated frequencies for the monolayer are in agreement with previous calculations102 and agree reasonably well with HREELS data determined for monolayer coverage,81 with the highest frequency overestimated by ∼50 cm−1 as expected. The values reported for 2 ML and 3 ML are predictions that may help to experimentally identify the honeycomb 2 ML structure and thicker multilayers. The number of shifted frequencies, as well as the magnitude of the shift to lower wavenumbers, considerably increases with the coverage. Based on the correlation of frequency shift and H-bond strength described in,103 this illustrates the strengthening of the H-bond network. At 2 ML and 3 ML, nearly all OH frequencies are included within the calculated range of OH frequencies in ice (2709–3789), which indicates an extended H-bonded network.| Aggregate | Coverage | Supercell | n H2O | Dissociation | Frequencies (cm−1) | |||
|---|---|---|---|---|---|---|---|---|
| a For the periodic structures, calculated frequencies at the Γ-point are given. b CCSD(T)-F12, agrees with experimental harmonic frequencies within 0.5 cm−1.100 c IR.101 d PBE.102 e HREELS.81 f FTIR of ice Ih.104 | ||||||||
| H2O | Gas phase | (19 Å)3 | 1 | M | 3703 | 3820 | ||
| H2Ob | Gas phase | 1 | M | 3832 | 3942 | |||
| H2Oc | Gas phase | M | 3657 | 3756 | ||||
| Isolated | 1/6 | (3 × 2) | 1 | M | 2537 | 3639 | ||
| Dimer | 1/6 | (4 × 3) | 2 | MD | 2523 | 3041 | 3125 | 3751 |
| Ladder | 1/2 | (4 × 1) | 2 | MD | 2932 | 3017 | 3107 | 3759 |
| 2D | 1 | (1 × 1) | 1 | M | 1918 | 3719 | ||
| 2D | 1 | (1 × 1) | 1 | D | 2122 | 3703 | ||
| 2D | 1 | (2 × 1) | 2 | MD | 2926 | 2981 | 3088 | 3757 |
| 2Dd | 1 | (2 × 1) | 2 | MD | 2864 | 2994 | 3155 | 3765 |
| 2De | 1 | (2 × 1) | 2 | MD | 3193 | 3677 | 3709 | |
| Honeycomb layer | 2 | (2 × 1) | 4 | MD | 2259 | 2473 | 2840 | 3166 |
| MM | 3225 | 3262 | 3606 | 3727 | ||||
| Multilayer | 3 | (2 × 1) | 6 | MD | 1969 | 2745 | 2841 | 2911 |
| MM | 3199 | 3261 | 3332 | 3364 | ||||
| MM | 3405 | 3427 | 3475 | 3740 | ||||
| Ice | Bulk | 12 | 2709–3789 | |||||
| Icef | Bulk | 3100–3420 | ||||||
4. Conclusions
Our systematic investigation of water adsorption on the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface from low coverage to 3 ML revealed several important new structures including ladder-like rows of half-dissociated dimers that hold the record in adsorption energy with −1.19 eV per water molecule and at 2 ML an novel honeycomb double monolayer. The latter structure is composed of Zn-bound half-dissociated dimers and additional water molecules H-bonded to surface oxygens and surface OH-groups. The water molecules form a H-bonded network of 6-memberd rings, which is proton disordered – a 2D analogon of the disorder in the 3D structures of ice phases and clathrates. The configurational entropy due to this proton disorder will contribute to the stability of this adsorbate phase at finite temperatures. All water molecules and the OH group are 4-fold coordinated. Due to the absence of free OH-groups and lone-pairs, further growth of the water layer requires a major restructuring of the interface. This is illustrated by the 3 ML structures that are attached to the ZnO surface via a contact layer composed of three different binding motifs of Zn-bound half-dissociated dimers. The additional water molecules form an H-bonded network of 4- to 10-membered rings that is H-bonding to the contact layer and only in few exceptions to surface-oxygens. The large number of rather different structures with very similar energies suggests an amorphous or liquid phase and significant configurational entropy. The availability of dangling H-bond donor and acceptor sites allows further growth of this layer. In the present study small (2 × 1) unit cells have been used to gain a first insight into possible structures and their stability at this intermediate coverage regime, which had not been studied with DFT previously, although TDS experiments indicate such adsorbate phases. In spite of the small unit cells, the similarity of our results for the 3 ML film with the main features at the interface of thicker water layers with the ZnO(10
0) surface from low coverage to 3 ML revealed several important new structures including ladder-like rows of half-dissociated dimers that hold the record in adsorption energy with −1.19 eV per water molecule and at 2 ML an novel honeycomb double monolayer. The latter structure is composed of Zn-bound half-dissociated dimers and additional water molecules H-bonded to surface oxygens and surface OH-groups. The water molecules form a H-bonded network of 6-memberd rings, which is proton disordered – a 2D analogon of the disorder in the 3D structures of ice phases and clathrates. The configurational entropy due to this proton disorder will contribute to the stability of this adsorbate phase at finite temperatures. All water molecules and the OH group are 4-fold coordinated. Due to the absence of free OH-groups and lone-pairs, further growth of the water layer requires a major restructuring of the interface. This is illustrated by the 3 ML structures that are attached to the ZnO surface via a contact layer composed of three different binding motifs of Zn-bound half-dissociated dimers. The additional water molecules form an H-bonded network of 4- to 10-membered rings that is H-bonding to the contact layer and only in few exceptions to surface-oxygens. The large number of rather different structures with very similar energies suggests an amorphous or liquid phase and significant configurational entropy. The availability of dangling H-bond donor and acceptor sites allows further growth of this layer. In the present study small (2 × 1) unit cells have been used to gain a first insight into possible structures and their stability at this intermediate coverage regime, which had not been studied with DFT previously, although TDS experiments indicate such adsorbate phases. In spite of the small unit cells, the similarity of our results for the 3 ML film with the main features at the interface of thicker water layers with the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface described in the literature8,48 indicates that a minimal model with a (2 × 1) supercell and 6 water molecules already captures the key features of the interface of ZnO with bulk water. The water reorientation dynamics, proton hopping dynamics, diffusivity and the entropic stabilization of water films with 2 ML and 3 ML coverage will be subject of a future larger-scale MD study.
0) surface described in the literature8,48 indicates that a minimal model with a (2 × 1) supercell and 6 water molecules already captures the key features of the interface of ZnO with bulk water. The water reorientation dynamics, proton hopping dynamics, diffusivity and the entropic stabilization of water films with 2 ML and 3 ML coverage will be subject of a future larger-scale MD study.
At low coverage, a hierarchy of aggregation states was revealed. Two adsorbed molecules may form a dimer with an intermolecular H-bond. This dimerization activates the dissociation of the H-bond acceptor molecule, which is exothermic by −0.02 eV in contrast to dissociation of an isolated adsorbed molecule that is endothermic by 0.09 eV. The half-dissociated dimers may further aggregate forming ladder-like rows that have a higher adsorption energy than the monolayer, which is also composed of half-dissociated dimers. This indicates a weak lateral repulsion between ladders. Therefore, water monolayers form on the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface because this allows maximizing the number of strong Zn–OW bonds by saturating all surface Zn atoms and completing their 4-fold coordination, not because of attractive lateral interactions. At coverages below 1 ML, ladders separated by one or more empty rows are predicted to be slightly more stable than domains with full monolayer coverage and large empty areas.
0) surface because this allows maximizing the number of strong Zn–OW bonds by saturating all surface Zn atoms and completing their 4-fold coordination, not because of attractive lateral interactions. At coverages below 1 ML, ladders separated by one or more empty rows are predicted to be slightly more stable than domains with full monolayer coverage and large empty areas.
Water aggregation on ZnO is controlled by a subtle interplay of direct water–water interactions including H-bonds and dipole–dipole interactions versus surface- or adsorption-mediated interactions including enhanced (or reduced) water–surface interactions and relaxation energies required to optimize the geometry of the water molecules and ZnO surface for adsorption. For all cases studied, the direct water–water interaction energies, Einteraction(W/W), favour formation of larger aggregates and the contributions in column and row directions add up in the monolayer. The surface relaxation energies, Erelaxation(ZnO), also generally contribute towards aggregation or do not change. On the other hand, the sign and magnitude of the changes in water–surface interaction energies, Einteraction(ZnO/W), and water relaxation energies, Erelaxation(W), depend on the type of aggregates formed. For example, the sign of these two contributions may change from rows to columns for molecular adsorption. Furthermore, their magnitudes are much higher for dissociated water molecules. The final outcome, whether aggregation is favourable or not, depends on a subtle balance in the changes of all four terms.
Water dissociation on the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface also sensitively depends on the type of aggregate. While dissociation is unfavourable for isolated molecules, 100% dissociation is favourable for rows and 50% dissociation is preferred for dimers, ladders and the monolayer. Columns are a border line case, where molecular adsorption and half-dissociation leads to very similar energies. Furthermore, at 2 ML and 3 ML coverage every second water molecule bound to a surface Zn-site is dissociated. The preference for 50% dissociation of water molecules adsorbed on Zn-atoms is due to half-dissociated dimers, which appear as common motif in the corresponding structures. While the degree of water dissociation clearly depends on the type of aggregates, the binding energy decomposition reveals that direct water–water interactions (Einteraction(W/W)) change by only ±0.02 eV or less when similar aggregates with different dissociation degree are compared. The changes in water–surface interactions are about two orders of magnitude larger and always strongly favour dissociation. On the other hand, the relaxation energies of the water molecules and the surface strongly increase upon dissociation and hence counteract dissociation with a contribution of similar magnitude. Therefore, the energetics of water dissociation on ZnO is determined by a subtle balance of strongly enhanced water–surface interactions versus increased relaxation energies. Thus the different behaviour of the various aggregates results from indirect, surface-mediated interactions.
0) surface also sensitively depends on the type of aggregate. While dissociation is unfavourable for isolated molecules, 100% dissociation is favourable for rows and 50% dissociation is preferred for dimers, ladders and the monolayer. Columns are a border line case, where molecular adsorption and half-dissociation leads to very similar energies. Furthermore, at 2 ML and 3 ML coverage every second water molecule bound to a surface Zn-site is dissociated. The preference for 50% dissociation of water molecules adsorbed on Zn-atoms is due to half-dissociated dimers, which appear as common motif in the corresponding structures. While the degree of water dissociation clearly depends on the type of aggregates, the binding energy decomposition reveals that direct water–water interactions (Einteraction(W/W)) change by only ±0.02 eV or less when similar aggregates with different dissociation degree are compared. The changes in water–surface interactions are about two orders of magnitude larger and always strongly favour dissociation. On the other hand, the relaxation energies of the water molecules and the surface strongly increase upon dissociation and hence counteract dissociation with a contribution of similar magnitude. Therefore, the energetics of water dissociation on ZnO is determined by a subtle balance of strongly enhanced water–surface interactions versus increased relaxation energies. Thus the different behaviour of the various aggregates results from indirect, surface-mediated interactions.
For many substrates a relation of water dissociation and water–surface interaction strength has been pointed out. On the structurally related GaN(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface higher dissociation degrees have been reported than on ZnO.8,46,47 The increased dissociation is also reported for the GaN/ZnO alloy surface.8 On silicon(100) water molecules rapidly dissociate with a very small barrier for proton transfer.38–42 Parallel to the increase in dissociation in the series ZnO, GaN, Si, the adsorption energies for molecular adsorption decrease from −1.07 eV to −0.74 eV and −0.36 eV, while they increase for dissociative adsorption: −1.07 eV, −2.18 eV, −2.47 eV, respectively.41,46 This agrees with our conclusion that enhanced water–surface interactions are the driving force for water dissociation. Analogous trends in the adsorption energies for molecular versus dissociative adsorption were observed for isolated water molecules on the more ionic alkaline earth oxides MgO, CaO, SrO and BaO.32 The stability of the dissociated state increases with the lattice constant and the flexibility of the substrate towards relaxation. The latter factor reduces the surface relaxation energy required to bind dissociated water, which opposes dissociation. On metal surfaces, the stability of mixed OH/H2O layers depends mainly on the OH–metal bonding and not on H-bonding.24
0) surface higher dissociation degrees have been reported than on ZnO.8,46,47 The increased dissociation is also reported for the GaN/ZnO alloy surface.8 On silicon(100) water molecules rapidly dissociate with a very small barrier for proton transfer.38–42 Parallel to the increase in dissociation in the series ZnO, GaN, Si, the adsorption energies for molecular adsorption decrease from −1.07 eV to −0.74 eV and −0.36 eV, while they increase for dissociative adsorption: −1.07 eV, −2.18 eV, −2.47 eV, respectively.41,46 This agrees with our conclusion that enhanced water–surface interactions are the driving force for water dissociation. Analogous trends in the adsorption energies for molecular versus dissociative adsorption were observed for isolated water molecules on the more ionic alkaline earth oxides MgO, CaO, SrO and BaO.32 The stability of the dissociated state increases with the lattice constant and the flexibility of the substrate towards relaxation. The latter factor reduces the surface relaxation energy required to bind dissociated water, which opposes dissociation. On metal surfaces, the stability of mixed OH/H2O layers depends mainly on the OH–metal bonding and not on H-bonding.24
Acknowledgements
S. K. thanks the International Max Planck Research School for Surface and Interface Engineering in Advanced Materials (IMPRS-SurMat) for a scholarship.References
- M. Bowker, H. Houghton and K. C. Waugh, J. Chem. Soc., Faraday Trans. 1, 1981, 77, 3023–3036 RSC.
- D. C. Look, Mater. Sci. Eng., B, 2001, 80, 383–387 CrossRef.
- C. V. Ovesen, B. S. Clausen, B. S. Hammershøj, G. Steffensen, T. Askgaard, I. Chorkendorff, J. K. Nørskov, P. B. Rasmussen, P. Stoltze and P. Taylor, J. Catal., 1996, 158, 170–180 CrossRef CAS.
- C. V. Ovesen, B. S. Clausen, J. Schiøtz, P. Stoltze, H. Topsøe and J. K. Nørskov, J. Catal., 1997, 168, 133–142 CrossRef CAS.
- Ü. Özgür, Y. I. Alivov, C. Liu, A. Teke, M. A. Reshchikov, S. Doğan, V. Avrutin, S. J. Cho and H. Morkoç, J. Appl. Phys., 2005, 98, 041301 CrossRef.
- P. J. A. Tijm, F. J. Waller and D. M. Brown, Appl. Catal., A, 2001, 221, 275–282 CrossRef CAS.
- C. Wöll, Prog. Surf. Sci., 2007, 82, 55–120 CrossRef.
- N. Kharche, M. S. Hybertsen and J. T. Muckerman, Phys. Chem. Chem. Phys., 2014, 16, 12057–12066 RSC.
- H. F. Zhang, S. X. Lu, W. G. Xu and F. Yuan, J. Appl. Phys., 2013, 113, 034903 CrossRef.
- G. E. Ewing, Chem. Rev., 2006, 106, 1511–1526 CrossRef CAS PubMed.
- M. A. Henderson, Surf. Sci. Rep., 2002, 46, 1–308 CrossRef CAS.
- G. Rubasinghege and V. H. Grassian, Chem. Commun., 2013, 49, 3071–3094 RSC.
- M. Salmeron, H. Bluhm, N. Tatarkhanov, G. Ketteler, T. K. Shimizu, A. Mugarza, X. Y. Deng, T. Herranz, S. Yamamoto and A. Nilsson, Faraday Discuss., 2009, 141, 221–229 RSC.
- A. Michaelides, Appl. Phys. A: Mater. Sci. Process., 2006, 85, 415–425 CrossRef CAS.
- A. Verdaguer, G. M. Sacha, H. Bluhm and M. Salmeron, Chem. Rev., 2006, 106, 1478–1510 CrossRef CAS PubMed.
- P. A. Thiel and T. E. Madey, Surf. Sci. Rep., 1987, 7, 211–385 CrossRef CAS.
- J. Carrasco, A. Hodgson and A. Michaelides, Nat. Mater., 2012, 11, 667–674 CrossRef CAS PubMed.
- A. Hodgson and S. Haq, Surf. Sci. Rep., 2009, 64, 381–451 CrossRef CAS.
- S. Meng, E. G. Wang and S. W. Gao, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 195404 CrossRef.
- A. Michaelides, A. Alavi and D. A. King, J. Am. Chem. Soc., 2003, 125, 2746–2755 CrossRef CAS PubMed.
- A. Michaelides and K. Morgenstern, Nat. Mater., 2007, 6, 597–601 CrossRef CAS PubMed.
- A. Poissier, S. Ganeshan and M. V. Fernández-Serra, Phys. Chem. Chem. Phys., 2011, 13, 3375–3384 RSC.
- G. Pirug and M. Morgenstern, H2O on metals, in Landolt-Börnstein, numerical data and functional relationships in science and technology, ed. H. P. Bonzel, New Series III, Springer-Verlag, Berlin, 2006, ch. 3.8.1, vol. 42A5, pp. 133–168 Search PubMed.
- A. Michaelides, A. Alavi and D. A. King, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 113404 CrossRef.
- V. A. Ranea, A. Michaelides, R. Ramirez, P. L. de Andres, J. A. Verges and D. A. King, Phys. Rev. Lett., 2004, 92, 136104 CrossRef CAS PubMed.
- J. Carrasco, A. Michaelides and M. Scheffler, J. Chem. Phys., 2009, 130, 184707 CrossRef PubMed.
- A. Baghbanpourasl, K. Hingerl, S. Wippermann and W. G. Schmidt, Surf. Sci., 2013, 612, 82–89 CrossRef CAS.
- J. Cerda, A. Michaelides, M. L. Bocquet, P. J. Feibelman, T. Mitsui, M. Rose, E. Fomin and M. Salmeron, Phys. Rev. Lett., 2004, 93, 116101 CrossRef CAS PubMed.
- S. Nie, P. J. Feibelman, N. C. Bartelt and K. Thürmer, Phys. Rev. Lett., 2010, 105, 026102 CrossRef CAS PubMed.
- G. Revilla-Lopez and N. Lopez, Phys. Chem. Chem. Phys., 2014, 16, 18933–18940 RSC.
- M. Forster, R. Raval, J. Carrasco, A. Michaelides and A. Hodgson, Chem. Sci., 2012, 3, 93–102 RSC.
- X. L. Hu, J. Carrasco, J. Klimes and A. Michaelides, Phys. Chem. Chem. Phys., 2011, 13, 12447–12453 RSC.
- C. B. Duke, Chem. Rev., 1996, 96, 1237–1259 CrossRef CAS PubMed.
- H. H. Farrell, J. P. Harbison and L. D. Peterson, J. Vac. Sci. Technol., B: Microelectron. Nanometer Struct. – Process., Meas., Phenom., 1987, 5, 1482–1489 CrossRef CAS.
- W. A. Harrison, J. Vac. Sci. Technol., 1979, 16, 1492–1496 CrossRef CAS.
- M. D. Pashley, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 10481–10487 CrossRef CAS.
- G. P. Srivastava, Appl. Surf. Sci., 2006, 252, 7600–7607 CrossRef CAS.
- J. H. Cho, K. S. Kim, S. H. Lee and M. H. Kang, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 4503–4506 CrossRef CAS.
- R. Konecny and D. J. Doren, J. Chem. Phys., 1997, 106, 2426–2435 CrossRef CAS.
- Y. Okamoto, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 10632–10635 CrossRef CAS.
- R. D. Smardon and G. P. Srivastava, Surf. Sci., 2005, 584, 161–168 CrossRef CAS.
- M. K. Weldon, B. B. Stefanov, K. Raghavachari and Y. J. Chabal, Phys. Rev. Lett., 1997, 79, 2851–2854 CrossRef CAS.
- M. Hellström, K. Jorner, M. Bryngelsson, S. E. Huber, J. Kullgren, T. Frauenheim and P. Broqvist, J. Phys. Chem. C, 2013, 117, 17004–17015 Search PubMed.
- B. Meyer, H. Rabaa and D. Marx, Phys. Chem. Chem. Phys., 2006, 8, 1513–1520 RSC.
- X. Shen, P. B. Allen, M. S. Hybertsen and J. T. Muckerman, J. Phys. Chem. C, 2009, 113, 3365–3368 CAS.
- X. Shen, Y. A. Small, J. Wang, P. B. Allen, M. V. Fernandez-Serra, M. S. Hybertsen and J. T. Muckerman, J. Phys. Chem. C, 2010, 114, 13695–13704 CAS.
- J. Wang, L. S. Pedroza, A. Poissier and M. V. Fernandez-Serra, J. Phys. Chem. C, 2012, 116, 14382–14389 CAS.
- G. Tocci and A. Michaelides, J. Phys. Chem. Lett., 2014, 5, 474–480 CrossRef CAS PubMed.
- J. Chen, J. Guo, X. Z. Meng, J. B. Peng, J. M. Sheng, L. M. Xu, Y. Jiang, X. Z. Li and E. G. Wang, Nat. Commun., 2014, 5, 4056 CAS.
- P. Cabrera-Sanfelix, A. Arnau, G. R. Darling and D. Sanchez-Portal, J. Chem. Phys., 2007, 126, 214707 CrossRef PubMed.
- R. Wlodarczyk, M. Sierka, K. Kwapien, J. Sauer, E. Carrasco, A. Aumer, J. F. Gomes, M. Sterrer and H. J. Freund, J. Phys. Chem. C, 2011, 115, 6764–6774 CAS.
- Y. B. He, W. K. Li, X. Q. Gong, O. Dulub, A. Selloni and U. Diebold, J. Phys. Chem. C, 2009, 113, 10329–10332 CAS.
- J. Lee, D. C. Sorescu, X. Y. Deng and K. D. Jordan, J. Phys. Chem. Lett., 2013, 4, 53–57 CrossRef CAS PubMed.
- X. H. Zhao, X. Shao, Y. Fujimori, S. Bhattacharya, L. M. Ghiringhelli, H. J. Freund, M. Sterrer, N. Nilius and S. V. Levchenko, J. Phys. Chem. Lett., 2015, 6, 1204–1208 CrossRef CAS PubMed.
- J. Goniakowski, F. Finocchi and C. Noguera, Rep. Prog. Phys., 2008, 71, 016501 CrossRef.
- C. Noguera, J. Phys.: Condens. Matter, 2000, 12, R367–R410 CrossRef CAS.
- R. W. Nosker, P. Mark and J. D. Levine, Surf. Sci., 1970, 19, 291–317 CrossRef CAS.
- O. Dulub, L. A. Boatner and U. Diebold, Surf. Sci., 2002, 519, 201–217 CrossRef CAS.
- O. Dulub, U. Diebold and G. Kresse, Phys. Rev. Lett., 2003, 90, 016102 CrossRef PubMed.
- G. Kresse, O. Dulub and U. Diebold, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 245409 CrossRef.
- M. Kunat, S. G. Girol, U. Burghaus and C. Wöll, J. Phys. Chem. B, 2003, 107, 14350–14356 CrossRef CAS.
- B. Meyer, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 045416 CrossRef.
- A. Önsten, D. Stoltz, P. Palmgren, S. Yu, M. Göthelid and U. O. Karlsson, J. Phys. Chem. C, 2010, 114, 11157–11161 Search PubMed.
- M. Schiek, K. Al-Shamery, M. Kunat, F. Traeger and C. Wöll, Phys. Chem. Chem. Phys., 2006, 8, 1505–1512 RSC.
- S. Torbrügge, F. Ostendorf and M. Reichling, J. Phys. Chem. C, 2009, 113, 4909–4914 Search PubMed.
- M. Valtiner, M. Todorova, G. Grundmeier and J. Neugebauer, Phys. Rev. Lett., 2009, 103, 065502 CrossRef PubMed.
- M. Valtiner, M. Todorova and J. Neugebauer, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 165418 CrossRef.
- C. J. Zhou and J. Y. Kang, J. Mater. Sci.: Mater. Electron., 2008, 19, S229–S233 CrossRef CAS.
- C. B. Duke, A. R. Lubinsky, S. C. Chang, B. W. Lee and P. Mark, Phys. Rev. B: Condens. Matter Mater. Phys., 1977, 15, 4865–4873 CrossRef CAS.
- M. R. He, R. Yu and J. Zhu, Nano Lett., 2012, 12, 704–708 CrossRef CAS PubMed.
- K. Ozawa, K. Sawada, Y. Shirotori, K. Edamoto and M. Nakatake, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 125417 CrossRef.
- N. L. Marana, V. M. Longo, E. Longo, J. B. L. Martins and J. R. Sambrano, J. Phys. Chem. A, 2008, 112, 8958–8963 CrossRef CAS PubMed.
- B. Meyer and D. Marx, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 035403 CrossRef.
- A. Wander and N. M. Harrison, Surf. Sci., 2000, 457, L342–L346 CrossRef CAS.
- G. Zwicker and K. Jacobi, Surf. Sci., 1983, 131, 179–194 CrossRef CAS.
- G. Zwicker, K. Jacobi and J. Cunningham, Int. J. Mass Spectrom., 1984, 60, 213–223 CrossRef CAS.
- B. Meyer, D. Marx, O. Dulub, U. Diebold, M. Kunat, D. Langenberg and C. Wöll, Angew. Chem., Int. Ed., 2004, 43, 6642–6645 CrossRef PubMed.
- D. Raymand, A. C. T. van Duin, D. Spangberg, W. A. Goddard and K. Hermansson, Surf. Sci., 2010, 604, 741–752 CrossRef CAS.
- Y. Yan and M. M. Al-Jassim, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 235406 CrossRef.
- O. Dulub, B. Meyer and U. Diebold, Phys. Rev. Lett., 2005, 95, 136101 CrossRef PubMed.
- Y. Wang, M. Muhler and C. Wöll, Phys. Chem. Chem. Phys., 2006, 8, 1521–1524 RSC.
- A. Calzolari and A. Catellani, J. Phys. Chem. C, 2009, 113, 2896–2902 CAS.
- D. J. Cooke, A. Marmier and S. C. Parker, J. Phys. Chem. B, 2006, 110, 7985–7991 CrossRef CAS PubMed.
- H. Xu, R. Q. Zhang and S. Y. Tong, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 155326 CrossRef.
- D. Raymand, A. C. T. van Duin, W. A. Goddard, K. Hermansson and D. Spangberg, J. Phys. Chem. C, 2011, 115, 8573–8579 CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- B. Santra, A. Michaelides and M. Scheffler, J. Chem. Phys., 2007, 127, 184104 CrossRef PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- D. Fernández-Torre, K. Kośmider, J. Carrasco, M. V. Ganduglia-Pirovano and R. Pérez, J. Phys. Chem. C, 2012, 116, 13584–13593 Search PubMed.
- J. Goclon and B. Meyer, Phys. Chem. Chem. Phys., 2013, 15, 8373–8382 RSC.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- G. Kresse and J. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- D. Alfè, Comput. Phys. Commun., 2009, 180, 2622–2633 CrossRef.
- F. Jensen, in Introduction to Computational Chemistry, John Wiley and Sons Ltd, Chichester, 1999, ch. 11.5, pp. 274–284 Search PubMed.
- I. D. Brown and R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1973, A29, 266–282 CrossRef.
- J. D. Bernal and R. H. Fowler, J. Chem. Phys., 1933, 1, 515–548 CrossRef CAS.
- L. Pauling, J. Am. Chem. Soc., 1935, 57, 2680–2684 CrossRef CAS.
- D. Silber, P. M. Kowalski, F. Traeger, M. Buchholz, F. Bebensee, B. Meyer and C. Wöll, Nat. Commun., 2016, 7, 12888 CrossRef CAS PubMed.
- G. Rauhut, G. Knizia and H. J. Werner, J. Chem. Phys., 2009, 130, 054105 CrossRef PubMed.
- W. S. Benedict, N. Gailar and K. E. Plyler, J. Chem. Phys., 1956, 24, 1139–1165 CrossRef CAS.
- F. Vines, A. Iglesias-Juez, F. Illas and M. Fernandez-Garcia, J. Phys. Chem. C, 2014, 118, 1492–1505 CAS.
- M. Rozenberg, A. Loewenschuss and Y. Marcus, Phys. Chem. Chem. Phys., 2000, 2, 2699–2702 RSC.
- F. Perakis and P. Hamm, Phys. Chem. Chem. Phys., 2012, 14, 6250–6256 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp07516a |
| ‡ Current address: Department of Theoretical Chemistry, University of Duisburg-Essen, Universitätsstr. 2, 45141 Essen, Germany. |
| § For computational speed a more approximate setup was chosen using the Siesta Program, norm-conserving pseudopotentials, a DZP atomic orbital basis and 100 Ry cutoff. The Nose thermostat was used for the Born Oppenheimer MD with 1 fs time steps. The temperature of the MD was kept high (400–500 K) to overcome barriers and sample many different structures, and lowered in case of desorption. |
| ¶ The values Einteraction(ZnO/W) = −1.91 eV and Erelaxation(ZnO) = −0.22 eV in Table 3 are normalized per water molecule, see eqn (2) and (5). |
| This journal is © the Owner Societies 2017 |