Quantum ergodicity breaking in semi-classical electron transfer dynamics
Received
20th October 2016
, Accepted 15th December 2016
First published on 20th December 2016
Abstract
Can the statistical properties of single-electron transfer events be correctly predicted within a common equilibrium ensemble description? This fundamental in nanoworld question of ergodic behavior is scrutinized within a very basic semi-classical curve-crossing problem. It is shown that in the limit of non-adiabatic electron transfer (weak tunneling) well-described by the Marcus–Levich–Dogonadze (MLD) rate the answer is yes. However, in the limit of the so-called solvent-controlled adiabatic electron transfer, a profound breaking of ergodicity occurs. Namely, a common description based on the ensemble reduced density matrix with an initial equilibrium distribution of the reaction coordinate is not able to reproduce the statistics of single-trajectory events in this seemingly classical regime. For sufficiently large activation barriers, the ensemble survival probability in a state remains nearly exponential with the inverse rate given by the sum of the adiabatic curve crossing (Kramers) time and the inverse MLD rate. In contrast, near to the adiabatic regime, the single-electron survival probability is clearly non-exponential, even though it possesses an exponential tail which agrees well with the ensemble description. Initially, it is well described by a Mittag-Leffler distribution with a fractional rate. Paradoxically, the mean transfer time in this classical on the ensemble level regime is well described by the inverse of the nonadiabatic quantum tunneling rate on a single particle level. An analytical theory is developed which perfectly agrees with stochastic simulations and explains our findings.
1 Introduction
Statistical physics and physical chemistry normally deal with large ensembles of physical entities.1 With the advance of single-molecular research on the nanoscale the statistical properties of single separated objects become even more important. In macroscopic systems, fluctuations play an additional subordinated role, away from phase transitions, on top of deterministic mean-field dynamics. In contrast, the dynamics of single elements is fundamentally stochastic, always. Consider a simple two-level system mimicking e.g. electron transfer (ET) between two sites of localization in a molecule,2–5 as shown in Fig. 1. Within the picture of two diabatic spatially localized electronic quantum states |1〉 and |2〉 with energies E1 and E2, an electron can make transitions between these two states due to the tunnel coupling Vtun, which provides corrections beyond the adiabatic Born–Oppenheimer approximation (BOP).2–5 The electron energies E1(x) and E2(x) depend on a collective nuclear reaction coordinate x and provide potential curves for the dynamics of this latter one within BOP. Within such a one-dimensional reaction coordinate picture, the rest of the molecular nuclear degrees of freedom and environment act as friction and noise in the dynamics of the reaction coordinate.2–5 These friction and noise are related by the fluctuation-dissipation theorem (FDT) at thermal equilibrium.2,3 The potential minima correspond to the equilibrium nuclei positions in the corresponding electronic states. Note that the spatial localizations of the electronic wave functions ψ1,2(r) = 〈r|1,2〉 have nothing in common with the nuclear x.2,3 The electronic transitions 1 → 2 or 2 → 1 are accompanied by a spatial jump of the electron, which occurs instantly.2 This is the so-called curve crossing problem, which provides a basic model for the quantum transport in condensed matter.2,3,5 Importantly, it applies not only to electron transfer in various molecular systems,2,6,7 but also to electronic transitions in colloidal semiconductor quantum dots.8–13
 |
| | Fig. 1 Curve crossing problem in the case of two equal potential curvatures κ (i.e. no nuclear frequency change occurs at electronic transitions). Diabatic electron energy levels E1,2(x) provide harmonic potentials for the dynamics of nuclear or molecular reaction coordinate x. x0 is the nuclear equilibrium shift for different electronic terms, and ε0 is the corresponding electron energy difference. λ = κx02/2 is nuclear (molecular) reorganization energy. | |
Within this model at a single-molecular level, the electron stochastically fluctuates between two sites of localization, say r1 and r2, exhibiting a two-state or dichotomous jumping process in space r. The probability density of the electron is given by |ψi(r)|2, depending on its quantum state “i”. On the ensemble level, a standard approach is to derive a kinetic equation for the reduced density matrix ρij(x,v,t) of the “electron + reaction coordinate” (v = ẋ), and one for the electronic subsystem only,  .2–5 In the simplest, ultimately reduced case the electronic populations pi(t) = Pii(t) just follow a Pauli master or balance equation, which corresponds to a classical Markovian two-state process of electron jumps with some quantum rates. Such and similar Markovian kinetic equations describe quantum relaxation dynamics of an ensemble of many identical systems.2,3
.2–5 In the simplest, ultimately reduced case the electronic populations pi(t) = Pii(t) just follow a Pauli master or balance equation, which corresponds to a classical Markovian two-state process of electron jumps with some quantum rates. Such and similar Markovian kinetic equations describe quantum relaxation dynamics of an ensemble of many identical systems.2,3
A very profound question is: can such kinetic equations describe the statistics of single-trajectory events? Contrary to a popular belief, which currently dominates the literature, the general answer is surprisingly NO, which is the focus of this paper. It affects a large body of current research on nanophysics and nanochemistry. It will be shown below that within a seemingly classical (on the ensemble level) solvent-controlled ET regime the genuine statistics of single-electron transfer events is very different from the one given by the master equation for electronic populations. This is because ET retains its quantum nature and is intrinsically non-Markovian. The conflict between the ensemble and trajectory descriptions means that ergodicity is fundamentally broken in this regime. These results are very important e.g. for the research on blinking statistics in single colloidal quantum dots11–13 because the discussed kinetics equations are central to the theory approaches based on continuous spectral diffusion.8–10 Basically, our main conclusion is that the standard kinetics equations may not be suitable to describe the statistics of single trajectories in a solvent- or diffusion-controlled regime, even though they can nicely describe the ensemble kinetics at the same time. Here we reveal a profound ergodicity breaking, a deep conflict between single-trajectory and ensemble level descriptions.
The important observation that trajectory and density descriptions of stochastic and kinetic processes can be very different has been made in ref. 14. Subsequently, it has been realized15–22 that this is a general feature of continuous time random walk (CTRW) dynamics featured by divergent mean residence times (MRTs) in the traps,23–26 and the related descriptions such as the fractional Fokker–Planck equation (FFPE).26 Such FFPEs may fail to describe the statistical properties of single trajectories.20 For example, subdiffusive FFPEs can be used to derive a general expression for fractional velocity (subvelocity) of biased subdiffusion in tilted periodic potentials.27–29 However, the FFPE is useless to find the mean subvelocity of a single particle, no matter how long its trajectory is. The latter quantity remains always random and exhibits some universal fluctuations.16,20,29 Averaging over these fluctuations gives the ensemble value of fractional velocity, which can be found from the FFPE.20
Ergodicity can be understood in various senses. The primary definition is that the time and ensemble averages of a stationary physical observable, say x(t), coincide in the limit of infinitely long trajectories and infinitely large ensembles, correspondingly.30 This is ergodicity in mean.30 Clearly, for any finite system both averages are different. They are also trivially different for any nonstationary dynamics.30 Clearly, if the phase space of a dynamical system is separated into some unconnected domains, the corresponding dynamics cannot be ergodic in principle if the statistical averaging is done on the whole phase space. The reason for ergodicity breaking of CTRW dynamics with divergent MRTs is very different. It is rooted in the absence of stationarity of the increments22δx(t|t′) = x(t + t′) − x(t′) with respect to the sliding time point t′, which is used for computing a time-average. For such processes, the increments are never stationary, even in the limit t′ → ∞. Hence, the time average of [δx(t|t′)]2 with respect to t′ can never coincide with the ensemble average 〈[δx(t|t′)]2〉, which depends on t′ because of the absence of stationarity, for any finite t′.† This was named as weak ergodicity breaking.16,31 The relation of weak ergodicity breaking to aging was first realized by Bouchaud.31 The corresponding systems age for infinite time and never reach a stationary limit. In the real world, this can be of course mostly a transient phenomenon. However, even some standard normal-diffusion models like diffusion in Gaussian disordered potentials with short-range correlations32,33 can be mesoscopically anomalous34–36 and non-ergodic,36 even if they are truly ergodic in the limit t′ → ∞. In the current literature, the ergodicity of diffusion processes is mostly understood namely in the sense of mean-squared increments.37 Nevertheless, ergodicity can also be understood in the sense of higher moments, autocorrelation functions, and distribution densities.30 In the latter case, the question is:30 can we deduce the probability density of an observable from its single infinitely long trajectory? If yes, the process is ergodic in the probability density sense.
The ergodicity violation which we describe in this paper occurs in the sense of a fundamental conflict between the single trajectory and equilibrium ensemble descriptions. Namely, we ask the question: are the statistics of electronic transitions the same when derived from single electron trajectories (as in single-molecular experiments38) and, alternatively, from a common density description with initial equilibrium distribution of the reaction coordinate (as in the majority of pertinent theories developed thus far and macroscopic experiments)? We show that they are very different in the solvent-controlled ET regime, even if the reaction coordinate x(t) dynamics is fully ergodic. This is because ET remains fundamentally quantum-mechanical and non-Markovian even within this seemingly classical Markovian regime. Hence, standard master or kinetics equations may fail completely in describing the statistics of single trajectories in such and similar regimes. This is a real surprise overlooked thus far, except for a paper by Tang and Marcus,9 which does not address, however, the issue of ergodicity. We develop both an analytical theory and stochastic numerics, which remarkably agree, confirming our major results and conclusions.
2 Theory
2.1 Landau–Zener tunneling, semi-classical curve crossing problem, and Zusman equations
Consider a curve-crossing problem in Fig. 1 for two parabolas, Ei(x) = κ(x − x0δ2,i)2/2 − ε0δ2,i, of equal curvature κ (i.e. no nuclear frequency change occurs at electronic transition, for simplicity). x0 is the reaction coordinate shift, ε0 is the equilibrium difference of electron energies, and δ2,i is the Kronecker symbol. The quantum system is characterized by the Hamiltonian Ĥ(x) = E1(x)|1〉〈1| + E2(x)|2〉〈2| + Vtun(|1〉〈2| + |2〉〈1|), and the reaction coordinate x(t) is treated classically. Tunnel coupling Vtun is assumed to be coordinate independent, as in most ET theories, which is known as Condon approximation.2,3 This, of course, does not exhaust all the possibilities. Non-Condon effects in general and, in particular, for conical intersections, where Vtun ∝ x − x*, have attracted increasing attention.39,40 They are beyond the scope of this work, where we focus on the simplest possible minimal model. What is the probability of electronic transition between two localized quantum states |1〉 and |2〉 depending on the reaction coordinate velocity v? Within the Landau–Zener–Stückelberg theory (LZS)41–43 applied to this problem the answer is2| | | PLZ(v) = 1 − exp[−f(v)]. | (1) |
This result presents a milestone in the theory of quantum transport. Here,| | 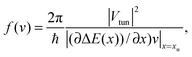 | (2) |
is the lowest second order approximation in the tunnel coupling Vtun, and ΔE(x) = E1(x) − E2(x) is the difference of electron energies. The latter result follows immediately from Fermi's Golden Rule quantum transition rate| |  | (3) |
applied at the level crossing point x*, ΔE(x*) = 0. Here, δ(x) is Dirac's delta-function. In the present case, ΔE(x) = ε0 − λ + 2λx/x0, where λ = κx02/2 is the nuclear reorganization energy. Once again, the electron tunnel distance has nothing in common with x0. Electrons tunnel in space once a transition |1〉 → |2〉, or |2〉 → |1〉 takes place. Very importantly: while electronic transitions always show a discontinuous jump-like quantum character, the reaction coordinate dynamics remain continuous. This is the ultimate reason for the quantum breaking of ergodicity, see below. Likewise, blinking of a quantum dot occurs from a light emitting quantum state upon a radiative quantum transition.8 Depending on the coupling strength Vtun and the velocity v = ẋ at the crossing point PLZ(v) can vary from PLZ(v) ≈ f(v) ∝ |Vtun|2/|v| (nonadiabatic transition) to one (adiabatic transition).
Within a classical treatment of the reaction coordinate x, one considers it as a particle of mass M subjected to viscous frictional force ηv, with a friction coefficient η, and zero-mean white Gaussian thermal noise of the environment ξ(t) at temperature T. Friction and noise are related by the fluctuation-dissipation relation 〈ξ(t)ξ(t′)〉 = 2kBTηδ(t − t′), where 〈⋯〉 denotes the ensemble averaging. Stochastic dynamics of x(t) follows the Langevin equation:
| |  | (4) |
which depends on the quantum state |
i〉. The electron-reaction coordinate dynamics can be described in a semi-classical approximation by mixed quantum-classical dynamics of the reduced density matrix
ρij(
x,
v,
t), where the quantum degree follows quantum dynamics while the dynamics in (
x,
v) phase space for a fixed quantum state
i is classical. Generally, the phase-space dynamics is described by the Kramers–Fokker–Planck equation (KFPE). In the overdamped case,

, the reaction coordinate velocity is thermally distributed,

,

, all the time. In a singular limit of
M → 0, the KFPE for a fixed state
i reduces to the Smoluchowski–Fokker–Planck dynamics,
ṗi(
x,
t) =
![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) ipi
ipi(
x,
t) characterized by the Smoluchowski operator
![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) i
i =
D(∂/∂
x){exp[−
βEi(
x)](∂/∂
x)exp[
βEi(
x)]}. Here,
β = 1/
kBT is inverse temperature, and
D =
kBT/
η is the diffusion coefficient. The corresponding semi-classical description is well known under the label of Zusman equations.
4,44 Within it, the reduced dynamics of population densities

is described by
ṗ1(x,t) = −Γ(x)[p1(x,t) − p2(x,t)] + ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) 1p1(x,t), 1p1(x,t), |
| | ṗ2(x,t) = Γ(x)[p1(x,t) − p2(x,t)] + ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) 2p2(x,t), 2p2(x,t), | (5) |
where
Γ(
x) is the Golden Rule expression in
eqn (3). This equation is obtained from a full reduced density matrix equation description after excluding (projecting out) the dynamics of quantum coherences, and within the so-called contact approximation.
44 One must stress that no rigorous second order approximation in the tunnel coupling
Vtun is done in
eqn (5), but rather nonlocality and memory effects are neglected.
45 The appearance of
Γ(
x) ∝ |
Vtun|
2 in
eqn (5) is due to a singular limit of overdamped dynamics. Indeed, since
vT → ∞ in this limit, one can safely approximate
PLZ(
v) ≈
f(
v), and also the contact approximation (locality in
x) is well justified from the quantum uncertainty relation.
4 We confirm below this very important remark while doing stochastic simulations of electron trajectories. In these simulations, we use generically
PLZ(
v), instead of
f(
v), which, however, does not change the results for overdamped dynamics. For a strong electron-nuclear coupling (
λ ≫
Vtun), in the absence of inertial effects, and in the limit where the quantum effects in the reaction coordinate dynamics are entirely neglected, this contact approximation is well justified.
4,44 It presents a very important reference point, which allows also for further generalizations toward anomalous subdiffusive dynamics of the reaction coordinate.
10
Indeed, within this approximation one obtains very elegant and important analytical results. Consider first very small Vtun, with the reaction coordinate being thermally equilibrated, 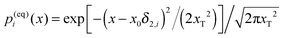 , where
, where 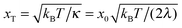 is a thermal width. Then, the nonadiabatic quantum transition rate is
is a thermal width. Then, the nonadiabatic quantum transition rate is
| |  | (6) |
with activation energies
E(a)1,2 = (
ε0 ∓
λ)
2/(4
λ). This is the celebrated Marcus–Levich–Dogonadze rate expression.
1,2,46–49 Parabolic dependence of
E(a)i on
ε0 is famously known as a Marcus parabola. Note that in this respect the so-called inverted regime of electron transfer for
ε0 >
λ is entirely a quantum-mechanical feature which is physically impossible within an adiabatic classical treatment.
With the increase of Vtun the reaction coordinate dynamics become even more important and can limit the overall rate. Assuming that the reaction coordinate is thermally equilibrated in the initial electronic state, the following master equation
| ṗ1(t) = −k1p1(t) + k2p2(t), |
| | | ṗ2(t) = k1p1(t) − k2p2(t) | (7) |
has been derived
4,44,45,50–52 from
eqn (5) with the rates
| |  | (8) |
In
eqn (8)| |  | (9) |
is the mean escape time in the parabolic potential with cusp,
45 and
τ =
η/
κ is the reaction coordinate relaxation time, or the Debye solvent correlation time. Here,
2F2(
a,
b;
c,
d;
z) is a generalized hypergeometric series.
53 It is worth noting that this theory is restricted by the parameter domain
Vtun ≪
kBT,
λ. The relaxation of populations is single-exponential
| | | p1,2(t) = p1,2(∞) + [p1,2(0) − p1,2(∞)]e−kt | (10) |
with
p1,2(∞) = 1/[1 + exp(±
ε0/
kBT)], and
k =
k1 +
k2. Physically, this requires sufficiently large activation barriers. For
E(a)i ≫
kBT,

.
44 Hence, for such large activation barriers,
eqn (8) takes the form
| |  | (11) |
which is known as the Zusman rate,
44 where
| | 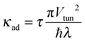 | (12) |
is an adiabaticity factor. Moreover, for
κad ≫ 1 and
ε0 <
λ| | 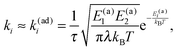 | (13) |
which is the adiabatic Marcus rate. For a particular case
ε0 = 0, where
E(a)1 =
E(a)2 =
λ/4,
k(ad)1,2 coincides with the Kramers rate for the adiabatic transitions in the cusp potential
33 consisting of two pieces of diabatic curves in
Fig. 1, and
| | 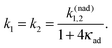 | (14) |
Hence, for a sufficiently large
Vtun or sufficiently large
τ (solvent control), so that
κad ≫ 1, ET becomes purely classical and adiabatic within this ensemble description. This is the so-called solvent-controlled adiabatic ET. The rate expressions
(6), (11), (12) and (14) are traditionally used to interpret and analyze the experimental data.
7 The fact that a change of the solvent relaxation time
τ can control the rate of intramolecular ET has been shown
e.g. in
ref. 54. Long-range electron transfer occurs typically in the non-adiabatic regime, while intramolecular electron self-exchange processes in molecular compounds and mixed-valence systems can occur adiabatically.
1,2,6
3 Results and discussion
3.1 Trajectory description
In this work we focus our attention on a stochastic trajectory counterpart of this well-known ensemble theory. It can be obtained as follows, quite in the spirit of a surface hopping approach.39,55 We propagate overdamped (with M = 0) Langevin dynamics (4) on one potential surface. Once the threshold x* is reached quantum hopping onto another surface occurs with the LZS probability (1), where v = δx/δt, δt is the time integration step, and δx is the x displacement by crossing the threshold. After a quantum jump, Langevin dynamics are continuously propagated on another surface, until the next jump occurs. Note that even if for δt → 0 the formal limit of δx/δt does not exist in a mean-square sense for the strictly overdamped dynamics, at any finite δt, v is finite. The overdamped dynamics of the reaction coordinate lead, however, to effective linearization of eqn (1) in f(v), PLZ(v) ≈ f(v), i.e. the results do not depend on whether we use eqn (1), or (2) in simulations of the overdamped dynamics. This is our first remarkable result which is completely confirmed by numerics and agrees with the Zusman equation theory. We consider the symmetric case ε0 = 0 further in this work.
Numerical simulations of eqn (4) in a nondimensionalized form‡ for a fixed electronic state were performed using the stochastic Heun method56 with a fixed time integration step δt, which has been varied to achieve the convergency of numerical results. In most simulations, δt = 10−5. For the strictly overdamped (M → 0) dynamics and PLZ(v) ≈ f(v), the dynamics of an ensemble of particles based on single-trajectory simulations corresponds precisely to the density dynamics in eqn (7). By propagating many (104) particles simultaneously starting from the quantum state “1” and distributing initial x(0) in accordance with P(eq)1(x), we can keep track of the state populations. The corresponding results in Fig. 2 for a sufficiently high activation barrier λ/4 of 2.5kBT, which is typical for many molecular systems, e.g., for ET in the azurin dimer,57 agree remarkably well with the theoretical result in eqn (6)–(10). In other words, the result of ensemble-averaged trajectories nicely agrees with the analytical solution of Zusman equations. The ensemble kinetics is practically single-exponential. For a very small Vtun, ET is non-adiabatic and characterized by the MLD rate. Upon the increase of Vtun, the adiabatic transport regime is gradually established. It is almost achieved for Vtun = 0.03, as shown in Fig. 2.
 |
| | Fig. 2 Numerical relaxation of p1(t) (symbols) vs. the analytical results in eqn (8)–(10) (lines) for ε0 = 0, λ = 800, T = 0.1 and various values of Vtun shown in the plot. For Vtun = 0.001, ET is nearly non-adiabatic, while for Vtun = 0.03 it is already close to adiabatic ET with k(ad) = 0.066, from the ensemble perspective. The numerically fitted values of knum (not shown) agree with the theoretical results shown in the plot with the accuracy better than 0.5% except for Vtun = 0.001 (about 4%). N = 104 particles are used in simulations. | |
3.2 Statistics of single trajectories from a master equation perspective
Single-trajectory electron transition statistics is commonly characterized by residence time distributions (RTDs) in the electronic states. Such a RTD at the ensemble level can be obtained by preparing all the particles in one state, with the reaction coordinate initially thermally equilibrated and taking out particles once they jump to another state, until no particles remain in the initial state. This is how one standardly proceeds within a master equation theory. For the considered high activation barrier, the corresponding survival probability F1(τ) decays single-exponentially, see Fig. 3, however, with the rate Γ1, which is different from the above k1. Indeed, by repeating straightforwardly an analytical derivation in ref. 45 modified for the stated absorbing boundary conditions one obtains| | 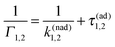 | (15) |
in place of eqn (8). Another derivation of this result is given in Appendix A. This result has a very simple interpretation. Namely, the average time to make a transition is the sum of the average time to reach the threshold x* and the inverse of the nonadiabatic tunneling rate. Indeed, numerics remarkably agree with this simple and insightful result based on the density description, see Fig. 3.
 |
| | Fig. 3 Survival probability in one electronic state at the ensemble level. Parameters are the same as in Fig. 2. Numerical results are depicted by symbols, whereas an exponential decay with the rate in eqn (15) is shown by lines. | |
3.2.1 Non-Markovian yet exponential kinetics.
Trajectory simulations contain, however, in principle much more information than a density description can deliver. In particular, we can study the residence time distributions (RTDs) in the electronic states directly by observing a very long single trajectory. We proceed further by noticing that for Markovian dynamics it must be Γ1,2 = k1,2. This is indeed the case in the nonadiabatic ET regime. However, the dynamics of single-electron transitions become increasingly non-Markovian upon taking adiabatic corrections into account with the increase of Vtun. This is in spite of a single-exponential character of the ET kinetics at the ensemble level! Ref. 58 already pointed out that in a similar very paradoxical situation: a highly non-Markovian bursting process can have a nearly exponentially decaying autocorrelation function. Indeed, for most researchers the exponential decay of survival probability in Fig. 3 would imply that electronic state populations undergo a two-state Markovian stochastic process with two equal rates Γ1 = Γ2. If so, then on average there would occur only one electronic transition within a mean residence time interval 1/Γ1. However, a short inspection of a single trajectory realization of electronic transitions in a near to adiabatic regime depicted in Fig. 4 reveals immediately that this is not the case. Many transitions can occur on the time scale 1/Γ1. This reveals clearly a non-Markovian character of electronic transitions, which remains hidden in the traditional ensemble theories operating using Markovian master equations for the electronic populations, like eqn (7). Bursting provides such a visual proof.58 Hence, the actual statistics of electronic transitions are expected to be very different from those implied by the ensemble kinetics measurements. This implies that ergodicity is broken. Note that a popular statement that in an adiabatic ET regime an electron just follows nuclear rearrangement is in fact rather misleading on the level of single electron trajectories. This is so because electrons jump immediately at the level crossing (in the contact approximation) and not after nuclei complete their rearrangement. ET remains quantum even within this adiabatic seemingly fully classical regime! And namely this causes the quantum breaking of ergodicity described next.
 |
| | Fig. 4 Quantum state trajectory realization in the non-Markovian regime with broken ergodicity. ε0 = 0, λ = 800, T = 0.1, and Vtun = 0.01. Judging from the survival probability in Fig. 3 one might deduce that the electronic state undergoes two-state Markovian fluctuations with the mean residence time (MRT) 1/Γ1,2 ≈ 42.37 in both states. Hence, only one switch between two electronic states should occur typically on this time scale. However, quite on the contrary, many transitions can occur within a MRT interval in the form of bursting activity separated by time intervals of the order of 1/Γ1,2 and larger. | |
3.3 Actual statistics of single trajectories
Indeed, the study of survival probabilities based on very long single trajectories surprisingly indicates that ergodicity is broken in this profoundly non-Markovian regime. The corresponding survival probability in a state is depicted in Fig. 5(a). It is profoundly non-exponential, very different from the corresponding ensemble result in Fig. 3. The rate Γ1 describes only the tail of distribution, which is the initially stretched exponential. It can possess also an intermediate power law regime for a larger Vtun, see part (b) in Fig. 5, where the exponential tail has a weight of less than 10%. Very surprisingly, the mean residence time is well described by the inverse of the Marcus–Levich–Dogonadze rate, 〈τi〉 = 1/k(nad)i, at the level of single trajectories. This result must be contrasted with the prediction of the equilibrium ensemble theory, 〈τi〉ens = 1/Γi, extended ad hoc onto single trajectories. The latter one is in fact completely wrong because the electron jump process is profoundly non-Markovian. Indeed, to derive the correct distribution of single-electron residence times from Zusman eqn (5) one must solve a very different initial-value boundary problem.8 Indeed, after each jump the electron starts its evolution at a very non-equilibrium value of the reaction coordinate x ≈ x*. For example, in state “1”, p1(x,0) = δ(x − x* + ε), with ε → 0, and a radiative boundary condition is placed exactly at x = x*. An analytical solution of this problem in the Laplace space is given in Appendix A. The corresponding theoretical result in eqn (A18), which is different from the one attempted by Tang and Marcus,8 nicely agrees with the numerics in Fig. 5. Moreover, a simple and nice analytical approximation follows from eqn (A13), in the adiabatic limit k(nad)iτ(ad)i ≫ 1:| |  | (16) |
where  is the Mittag-Leffler function of the fractional order 1/2 and argument
is the Mittag-Leffler function of the fractional order 1/2 and argument  , and
, and| |  | (17) |
is a fractional transfer rate, see Appendix A for details. For high activation energies, E(a)i ≫ kBT,| | 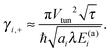 | (18) |
 |
| | Fig. 5 Survival probability in one electronic state at a single trajectory level. The parameters are the same as in Fig. 2, and (a) Vtun = 0.01 (as in Fig. 4), (b) Vtun = 0.04. Numerical results are depicted by symbols and the exponential tails by broken black lines. The initial Mittag-Leffler distribution regime in eqn (16) with the fractional rate in eqn (17) is depicted by full red lines. Theoretical results given by eqn (A18) are depicted by dash-dotted blue lines. It is not easy to distinguish them in the plot because they practically coincide with the results of the corresponding stochastic simulations. The theory and stochastic numerics agree perfectly. | |
This approximation excellently describes the non-exponential transport regime in Fig. 5, with ai ≈ 1, which covers about 90% of the probability transfer in Fig. 5(b). In accordance with it, the initial decay of the survival probability is always a stretched-exponential,  . Here we introduced a characteristic time
. Here we introduced a characteristic time
| |  | (19) |
The corresponding residence time density is
| | 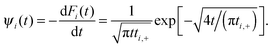 | (20) |
Note that even though
ψi(
t) does contain a

scaling part, our result is very different from the one by Tang and Marcus.
8,9 First, it describes a stretched-exponential and not a power law distribution. Second, our
ti,+ in
(19) is also different from the corresponding critical time in
ref. 8 and 9, which marks transition from one power law regime to another one therein. Namely, we have
aiE(a)i in
(19) instead of 2
kBT in the expression for this critical time in
ref. 8 and 9. Note that numerically for
E(a)i in the range [2.5
kBT,10
kBT],
ai ≈
E(a)i/(2.5
kBT), whereas
ai ≈ 1 for
E(a)i in the range [0.5
kBT,2.5
kBT]. Hence, our result and the one in
ref. 8 and 9 have very different temperature dependences. Furthermore, for
t ≫
ti,+ an intermediate power law regime follows,

and
ψi(
t) ∝
t−3/2, which ends with an exponential tail, which is described by the rate
Γi in
eqn (15). This power law regime and an exponential tail were obtained in
ref. 8. However, the exponential tails here and in
ref. 8 and 9 have different rates.
All in all, the corresponding statistics are generally very different from the one following from the custom equilibrium ensemble description of adiabatic electron transfer. Strikingly enough, while the ensemble kinetics is strictly exponential, the single-electron transfer statistics is described by the Mittag-Leffler relaxation kinetics in the strictly adiabatic ET regime. Therefore, one can speak about profound ergodicity breaking in this context. The observed striking result, namely that the mean residence time is always given by the inverse MLD rate, is explained within our analytical expression (A9) for the survival probability derived in Appendix A. Moreover, our analytical result, which corrects the earlier one by Tang and Marcus,8 explains also why the tail of distribution is always given by the Zusman type rate Γi in eqn (15), which becomes the Marcus adiabatic rate in the strict adiabatic limit. Most of these remarkable features are missed in the previous analysis by Tang and Marcus.8,9
Moreover, the result that the mean residence time is always the inverse of a non-adiabatic MLD rate can also be explained within a modification of the classical level-crossing theory.30 For this, let us take formally into account small inertial effects (keeping M finite). Then, the velocity process v(t) is not singular anymore. Consider dynamics in the state i. Assuming stationarity of x(t), the averaged number of level crossings ni(![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) ) within a very long time interval
) within a very long time interval ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) is according to ref. 30ni(
is according to ref. 30ni(![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) ) =
) = ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) P(eq)i(x*) 〈|v(t)|〉x(t)=x*, and hence,
P(eq)i(x*) 〈|v(t)|〉x(t)=x*, and hence,  . By the same token and taking into account probability (1) to make a quantum jump to another state at each level crossing, we obtain
. By the same token and taking into account probability (1) to make a quantum jump to another state at each level crossing, we obtain
| | | 〈τi〉−1 = P(eq)i(x*)〈|v|PLZ(v)〉x(t)=x*. | (21) |
Indeed, consider an auxiliary variable
φ(
t) =
x(
t) −
x*. The crossings occur at random times
ti, and

, where we used
![[small phi (variant), Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a4.gif)
(
t) =
v(
t). From this, it follows that
| |  | (22) |
Note that if the transitions occur at each crossing, the integral of l.h.s. of
eqn (22) within a time-interval
![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif)
would give the number of transitions to another electronic surface within this time interval. Since the probability of such transitions is merely
PLZ(
v(
ti)), one should consider
| |  | (23) |
instead of
eqn (22). Then, the time-average of
ζ(
t) in the case of infinitely long
![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif)
yields the inverse mean time between the switching events, or the mean transition rate. Assuming ergodicity of the point process
ti, the time-average can be replaced with the ensemble average using
P(
x,
v) =
P(eq)(
x)
PM(
v), which yields
(21). Note a very paradoxical situation: even if
ζ(
t) is an ergodic process, the process of electron fluctuations between two localization sites is generally nonergodic, whenever its equilibrium ensemble and single trajectory statistics are in conflict.
Averaging in (21) with Maxwellian equilibrium PM(v) yields an important result
| | | 〈τi〉−1 = k(nad)iR(z = v0/vT), | (24) |
where
| | 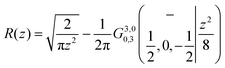 | (25) |
is a renormalization function taking inertial effects into account. It is expressed
via a Meijer G-function,
53 and
v0 = π|
Vtun|
2x0/(ℏ
λ) is a characteristic tunnel velocity. Numerically,
R(
z) ≈ exp(−1.57
z0.9) for 0 <
z < 0.1 with the accuracy of about 10%. In the formal overdamped limit,

, and we obtain 〈
τ1〉
−1 =
k(nad)1, in agreement with numerics. Moreover, we also did numerics which include the inertial effects in
eqn (4), within the contact approximation, and confirm the analytical result in
(24) and (25), see
Fig. 6. The numerical results for the renormalization function
R(
z) (symbols) are compared therein with the analytical result in
eqn (25). The agreement is remarkable indeed, and a detailed treatment of the inertial case will be presented elsewhere. The observed ergodicity breaking is thus not an artifact of the overdamped singular approximation. It expresses the profoundly quantum nature of electron transfer even in the adiabatic regime as manifested at the level of single-trajectory dynamics.
 |
| | Fig. 6 Renormalization factor R as a function of  , where , where  is angular frequency of the reaction coordinate. The theoretical result (full line) in eqn (25) is compared with the numerical results (symbols) obtained for Vtun = 0.04, λ = 800, and T = 0.1, and varying z through ω0. is angular frequency of the reaction coordinate. The theoretical result (full line) in eqn (25) is compared with the numerical results (symbols) obtained for Vtun = 0.04, λ = 800, and T = 0.1, and varying z through ω0. | |
4 Conclusions and outlook
As a major result of this work, equations like Zusman equations and other semi-classical and even fully quantum-mechanical ensemble descriptions should be used with great care to describe the properties of single electron trajectories in a profoundly non-Markovian ET regime, which can mistakenly be identified as a Markovian one (due to single-exponential kinetics) on the ensemble level. The kinetics equations involving the reaction coordinated dynamics must be used for this with a very nonequilibrium initial preparation of the reaction coordinate, which reflects the quantum nature of electron transfer, always, even within a seemingly purely classical adiabatic regime. Tang and Marcus earlier observed this striking feature.9 However, their attention was not drawn to it as a manifestation of profound non-ergodic effects, which are currently in the limelight, and they missed several very important features we discussed.
Single-trajectory events can display a stretched exponential and power law statistics in the case of strictly exponential ensemble kinetics. This effect can be relevant e.g. for adiabatic ET in mixed-valence systems and molecular compounds.1,6 Even long-range ET in proteins, with Vtun exponentially decaying with the tunneling distance, can enter the corresponding transfer regime when the reaction coordinate relaxation time is in the nano- and millisecond range as e.g. in cytochrome c, where τ ∼ 200 ns.7 Another class of important experimental systems is provided by colloidal quantum dots such as CdSe–CdS nanocrystals,12,13 and quantum dot-molecule complexes.59 It is very important that already a simplest ET model of textbook character and standard use1–3 studied in this work reveals the effect. Of course, many important issues remain to be addressed and clarified in the future. These are, in particular: (1) will the effect persist also for crossing multi-dimensional electron energy surfaces? (2) What is the role of non-Condon effects, e.g. for conical intersections? (3) What is the role of long-range memory effects in the reaction coordinate dynamics? The latter ones were revealed e.g. experimentally for ET in protein systems.38 The answer for question (1) seems to be intuitively clear: YES, the effect should persist whenever diffusion of the reaction coordinate on the electron energy surface limits the overall ET rate within the ensemble description. However, additional research is nevertheless welcome. Many more questions can, of course, be raised and addressed in follow-up research.
Beyond doubt, such a nonergodic behavior is pertinent also for diffusion-controlled dynamics in the case of low activation barriers, where power law features emerge already on the ensemble level. This can also be relevant e.g. for the blinking statistics in quantum dots in non-exponential regimes, whenever the reaction coordinate dynamics is very essential.10 In this case, the predictions based on equilibrium density dynamics are generally inappropriate to describe the actual statistics of single trajectory events. This is especially true for anomalously slow subdiffusive dynamics with memory, which is the subject of a separate follow-up work. In the case of normal reaction coordinate diffusion, a non-equilibrium ensemble perspective does deliver the correct result for single trajectories, as we showed in this work. Will it be also true for anomalously slow stochastic dynamics with long-range memory? There exist profound doubts that it is so. The intrigue remains because the formal solution of the corresponding non-Markovian Fokker–Planck equation of viscoelastic subdiffusion10,60 can be very different from a more physical treatment of the underlying stochastic dynamics with memory, which properly takes the slow modes of the environment into account, as explained in detail in ref. 60. This problem will be addressed in a follow-up work. The discovered non-ergodic features in a simple and well-known model of normal-diffusion charge transport dynamics are expected to influence a large body of current research on nanoscale transport phenomena. The author is confident that many other ensemble transport models should be reexamined from a trajectory point of view with focus on possible non-ergodic features.
A Appendix
Let us consider first electrons starting in an electronic state “i” at t = 0 with the initial equilibrium nuclei distribution p(eq)(x). The subindex “i” is dropped for a while for simplicity of notations. Given a singular sink term S(x) = v0δ(x − x*), with v0 = π|Vtun|2x0/(ℏλ), the probability density p(x,t) develops in time as follows:61| |  | (A1) |
where| |  | (A2) |
is the Green function of normal diffusion in a parabolic potential. In (A2), it is written for electronic term “1”. For term “2”, the Green function is modified by the replacement, x → x − x0 and x → x′ − x0. Integrating the solution of eqn (A1) yields the survival probability 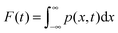 , and its negative derivative, ψ(t) = −dF(t)/dt, is the residence time distribution (RTD) in the electronic state. We solve the problem in the Laplace space,
, and its negative derivative, ψ(t) = −dF(t)/dt, is the residence time distribution (RTD) in the electronic state. We solve the problem in the Laplace space,  , where eqn (A1) takes on the form
, where eqn (A1) takes on the form| | ![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) (x,s) = p(eq)(x)/s − v0 (x,s) = p(eq)(x)/s − v0![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) (x,s|x*)p(x*,s). (x,s|x*)p(x*,s). | (A3) |
From it,| |  | (A4) |
Next, by integrating eqn (A3) using the normalization of probability, we obtain| |  | (A5) |
The first line in eqn (A5) says that the RTD is ψ(t) = v0p(x*,t) because, quite generally, ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) (s) = [1 −
(s) = [1 − ![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) (s)]/s. Next, we note that in the limit s → 0,
(s)]/s. Next, we note that in the limit s → 0,| |  | (A6) |
i.e. G(x*,s|x*) has a singularity at s = 0, which is quite obvious because  . Here lies the major difference of our treatment with the one in ref. 8, which we correct thereby. Subsequently, we use the decomposition
. Here lies the major difference of our treatment with the one in ref. 8, which we correct thereby. Subsequently, we use the decomposition ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) (x*,s|x*) − p(eq)(x*)/s = τ(s), where
(x*,s|x*) − p(eq)(x*)/s = τ(s), where| |  | (A7) |
and note that ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) (0) = τ(ad), see ref. 45, which yields eqn (9). Furthermore, because v0p(eq)(x*) = k(nad), we finally have
(0) = τ(ad), see ref. 45, which yields eqn (9). Furthermore, because v0p(eq)(x*) = k(nad), we finally have| |  | (A8) |
where we restored the subindex of the electronic state. Since ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) i(0) = 〈τi〉 is the mean residence time in the state “i” and Γi = 1/〈τi〉 is the corresponding rate in the exponential regime of high barriers, we obtain immediately from eqn (A8) our result in eqn (15).
i(0) = 〈τi〉 is the mean residence time in the state “i” and Γi = 1/〈τi〉 is the corresponding rate in the exponential regime of high barriers, we obtain immediately from eqn (A8) our result in eqn (15).
Next, let us consider the particles starting at some x′ for t = 0. Then, in eqn (A1) one must replace p(eq)(x) with G(x,t|x′). Repeating the above derivation for x′ = x*, we obtain
| |  | (A9) |
From it, two of our central results follow immediately. First, in this case 〈
τi〉 = 1/
k(nad)i,
i.e. the inverse of mean time is always the quantum non-adiabatic rate. Second, by replacing
![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) i
i(
s) with
τ(ad)i in
(A9), we deduce that asymptotically the distribution is exponential and characterized by the rate
Γi. Showing that initially the distribution is always stretched exponential (another point of difference with
ref. 8 and 9), and an intermediate power law emerges in a close to adiabatic transport regime even for high activation barriers, requires a bit more work.
Unfortunately, it is difficult to find a compact analytical expression for ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) (s). The corresponding integral can be evaluated exactly as an infinite sum of generalized hypergeometric functions. Our subsequent numerical evaluations of
(s). The corresponding integral can be evaluated exactly as an infinite sum of generalized hypergeometric functions. Our subsequent numerical evaluations of ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) (s) show that it is very well approximated for a high activation barrier (exceeding kBT/2) by
(s) show that it is very well approximated for a high activation barrier (exceeding kBT/2) by
| |  | (A10) |
where
ai is some constant. For the activation barriers
E(a)i in the range [2.5,10] in units of
kBT, an excellent numerical fit is given by
ai ≈
E(a)i/(2.5
kBT), while for
E(a)i in the range [0.5,2.5],
ai ≈ 1. For the parameters used in the numerics in this work
a ≈ 1, with a very good accuracy (within the line width for the results presented). Using
(A10) in
eqn (A9), we have
| |  | (A11) |
approximately. Note that this result is very different from the one by Tang and Marcus.
8 It allows us to find the initial stretched-exponential and intermediate power-law behaviors. Indeed, on the timescale
t ≪
aiτ, which corresponds to
aiτs ≫ 1,
eqn (A11) can be approximated as
| |  | (A12) |
and inverted to the time-domain in the form
| |  | (A13) |
where

is expressed
via the Mittag-Leffler function,
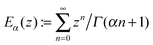
, of the fractional order 1/2. Furthermore, erfc(
z) is the complementary error function, and
| |  | (A14) |
are two fractional rates. For small arguments
z ≪ 1,
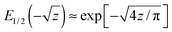
, and, therefore,
Fi(
t) displays initially stretched-exponential kinetics, always. For
z ≫ 1,

. Our theory nicely explains all the striking features observed in stochastic simulations.
Moreover, expression (A11) can be inverted exactly to the time domain, without any further approximation. Indeed, it can be decomposed as
| |  | (A15) |
where
rm,i are roots of the cubic algebraic equation
| | | r3 − bi,2r2 + bi,1r + bi,2 = 0 | (A16) |
with
and the coefficients
ci,m are:
| ci,1 = 1/[(ri,3 − ri,1)(ri,1 − ri,2)], |
| ci,2 = 1/[(ri,2 − ri,3)(ri,1 − ri,2)], |
| ci,3 = 1/[(ri,1 − ri,3)(ri,2 − ri,3)]. |
Note that

. The roots of
(A16) are found as
62| |  | (A17) |
where
Qi = (
bi,2/3)
2 −
bi,1/3,
ηi = arccos(
Ri/
Qi3/2), and
R = (
bi,2/3)
3 −
bi,2bi,1/6 −
bi,2/2. Expression
(A15) yields, in the time domain,
| |  | (A18) |
This nontrivial analytical result practically coincides with the results of stochastic simulations in
Fig. 5.
Acknowledgements
Funding of this research by the Deutsche Forschungsgemeinschaft (German Research Foundation), Grants GO 2052/1-2 and GO 2052/3-1 is gratefully acknowledged.
References
-
P. Atkins and J. de Paula, Atkins' Physical Chemistry, Oxford University Press, Oxford, 8th edn, 2006 Search PubMed.
-
A. Nitzan, Chemical Dynamics in Condensed Phases: Relaxation, Transfer and Reactions in Condensed Molecular Systems, Oxford University Press, Oxford, 2007 Search PubMed.
-
V. May and O. Kuhn, Charge and Energy Transfer Dynamics in Molecular Systems, Willey-VCH, Weinheim, 3rd edn, 2011 Search PubMed.
- A. Garg, J. N. Onuchic and V. Ambegaokar, J. Chem. Phys., 1985, 83, 4491–4503 CrossRef CAS.
- P. Wolynes, J. Chem. Phys., 1987, 86, 1957 CrossRef CAS.
- P. F. Barbara, T. J. Meyer and M. A. Ratner, J. Phys. Chem., 1996, 100, 13148–13168 CrossRef CAS.
- H. B. Gray and J. R. Winkler, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 3534–3539 CrossRef CAS PubMed.
- J. Tang and R. A. Marcus, J. Chem. Phys., 2005, 123, 054704 CrossRef PubMed.
- J. Tang and R. A. Marcus, J. Chem. Phys., 2005, 123, 204511 CrossRef PubMed.
- J. Tang and R. A. Marcus, Phys. Rev. Lett., 2005, 95, 107401 CrossRef PubMed.
- P. Frantsuzov, M. Kuno, B. Janko and R. A. Marcus, Nat. Phys., 2008, 4, 519–522 CrossRef.
- A. L. Efros and D. J. Nesbitt, Nat. Nanotechnol., 2016, 11, 661 CrossRef CAS PubMed.
- M. Pelton, G. Smith, N. F. Scherer and R. A. Marcus, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 14249–14254 CrossRef CAS PubMed.
- M. Bologna, P. Grigolini and B. West, Chem. Phys., 2002, 284, 115–128 CrossRef CAS.
- G. Margolin and E. Barkai, J. Chem. Phys., 2004, 121, 1566 CrossRef CAS PubMed.
- G. Bel and E. Barkai, Phys. Rev. Lett., 2005, 94, 240602 CrossRef.
- G. Margolin and E. Barkai, Phys. Rev. Lett., 2005, 94, 080601 CrossRef CAS PubMed.
- A. Lubelski, I. M. Sokolov and J. Klafter, Phys. Rev. Lett., 2008, 100, 250602 CrossRef PubMed.
- Y. He, S. Burov, R. Metzler and E. Barkai, Phys. Rev. Lett., 2008, 101, 058101 CrossRef CAS PubMed.
- I. Sokolov, E. Heinsalu, P. Hänggi and I. Goychuk, Europhys. Lett., 2009, 86, 30009 CrossRef.
- F. D. Stefani, J. P. Hoogenboom and E. Barkai, Phys. Today, 2009, 62, 34–39 CrossRef CAS.
- E. Barkai, Y. Garini and R. Metzler, Phys. Today, 2012, 65, 29–35 CrossRef CAS.
- M. F. Schlesinger, J. Stat. Phys., 1974, 10, 421–434 CrossRef.
- H. Scher and E. Montroll, Phys. Rev. B: Solid State, 1975, 12, 2455–2477 CrossRef CAS.
-
B. D. Hughes, Random walks and Random Environments, Clarendon Press, Oxford, vol. 1 and 2, 1995 Search PubMed.
- R. Metzler and J. Klafter, Phys. Rep., 2000, 339, 1–77 CrossRef CAS.
- I. Goychuk, E. Heinsalu, M. Patriarca, G. Schmid and P. Hänggi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 020101 CrossRef CAS PubMed.
- E. Heinsalu, M. Patriarca, I. Goychuk, G. Schmid and P. Hänggi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 046133 CrossRef CAS PubMed.
-
I. Goychuk and P. Hänggi, in Fractional Dynamics: Recent Advances, ed. J. Klafter, S. C. Lim and R. Metzler, World Scientific, Singapore, 2011, ch. 13, pp. 307–329 Search PubMed.
-
A. Papoulis, Probability, Random Variables, and Stochastic Processes, McGraw-Hill Book Company, New York, 3rd edn, 1991 Search PubMed.
- J. P. Bouchaud, J. Phys. I, 1992, 2, 1705–1713 CrossRef.
- R. Zwanzig, Proc. Natl. Acad. Sci. U. S. A., 1988, 85, 2029–2030 CrossRef CAS.
- P. Hänggi, P. Talkner and M. Borkovec, Rev. Mod. Phys., 1990, 62, 251–341 CrossRef.
- A. H. Romero and J. M. Sancho, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 58, 2833–2837 CrossRef CAS.
- M. Khoury, A. M. Lacasta, J. M. Sancho and K. Lindenberg, Phys. Rev. Lett., 2011, 106, 090602 CrossRef CAS PubMed.
- I. Goychuk and V. O. Kharchenko, Phys. Rev. Lett., 2014, 113, 100601 CrossRef PubMed.
- R. Metzler, J.-H. Jeon, A. G. Cherstvy and E. Barkai, Phys. Chem. Chem. Phys., 2014, 16, 24128–24164 RSC.
- H. Yang, G. Luo, P. Karnchanaphanurach, T.-M. Louie, I. Rech, S. Cova, L. Xun and X. S. Xie, Science, 2003, 302, 262–266 CrossRef CAS PubMed.
- U. Müller and G. Stock, J. Chem. Phys., 1997, 107, 6230–6245 CrossRef.
- A. L. Sobolewski, W. Domcke, C. Dedonder-Lardeux and C. Jouvet, Phys. Chem. Chem. Phys., 2002, 4, 1093–1100 RSC.
- L. D. Landau, Phys. Z. Sowjetunion, 1932, 2, 46–51 CAS.
- C. Zener, Proc. R. Soc. London, Ser. A, 1932, 137, 696–702 CrossRef.
- E. C. G. Stueckelberg, Helv. Phys. Acta, 1932, 5, 369–422 Search PubMed.
- L. D. Zusman, Chem. Phys., 1980, 49, 295–304 CrossRef CAS.
- L. Hartmann, I. Goychuk and P. Hänggi, J. Chem. Phys., 2000, 113, 11159–11175 CrossRef CAS.
- R. A. Marcus, J. Chem. Phys., 1956, 24, 966–978 CrossRef CAS.
- R. A. Marcus, J. Chem. Phys., 1957, 26, 867–871 CrossRef CAS.
- R. A. Marcus, Discuss. Faraday Soc., 1960, 26, 872–877 Search PubMed.
- V. G. Levich and R. R. Dogonadze, Dokl. Akad. Nauk SSSR, 1959, 124, 123–126 CAS.
- D. Y. Yang and R. I. Cukier, J. Chem. Phys., 1989, 91, 281 CrossRef CAS.
- J. Casado-Pasqual, I. Goychuk, M. Morillo and P. Hänggi, Chem. Phys. Lett., 2002, 360, 333–339 CrossRef.
- J. Casado-Pasqual, M. Morillo, I. Goychuk and P. Hänggi, J. Chem. Phys., 2003, 118, 291–303 CrossRef.
-
I. S. Gradstein and I. M. Ryzhik, Table of Integrals, Series, and Products, Academic Press, New York, 1965 Search PubMed.
- E. M. Kosower and D. Huppert, Chem. Phys. Lett., 1983, 96, 433–435 CrossRef CAS.
- J. C. Tully and R. K. Preston, J. Chem. Phys., 1971, 55, 562–572 CrossRef CAS.
-
T. C. Gard, Introduction to Stochastic Differential Equations, Marcel Dekker, New York, 1988 Search PubMed.
- K. V. Mikkelsen, L. K. Skov, H. Nart and O. Farveru, Proc. Natl. Acad. Sci. U. S. A., 1990, 93, 5443–5445 Search PubMed.
- I. Goychuk, J. Chem. Phys., 2005, 122, 164506 CrossRef PubMed.
- R. D. Harris, S. B. Homan, M. Kodaimati, C. He, A. B. Nepomnyashchii, N. K. Swenson, S. Lian, R. Calzada and E. A. Weiss, Chem. Rev., 2016, 116, 12865–12919 CrossRef CAS PubMed.
-
I. Goychuk, in Adv. Chem. Phys., ed. S. A. Rice and A. R. Dinner, John Willey & Sons, Hoboken, NJ, 2012, ch. 5, vol. 150, pp. 187–253 Search PubMed.
- G. Wilemski and M. Fixman, J. Chem. Phys., 1973, 58, 4009–4019 CrossRef CAS.
-
G. A. Korn and T. M. Korn, Mathematical Handbook for Scientists and Engineers, Dover, New York, 2000 Search PubMed.
Footnotes |
| † Some earlier studies failed to notice this because they focused on a very particular case t′ = 0. However, the limit t′ → ∞ is relevant to find the stationary ensemble averages. |
| ‡ Time is scaled in units of τ = η/κ, λ in the units of λτ/ℏ, kBT and other energy parameters in the units of λ. For a typical τ ∼ 2 ps, ℏ/τ ∼ 2.5 cm−1 (in spectroscopic units), and λ = 800 corresponds to 2000 cm−1 or 0.25 eV, whereas T = 0.1 to 200 cm−1 or room temperatures. |
|
| This journal is © the Owner Societies 2017 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article
 .2–5 In the simplest, ultimately reduced case the electronic populations pi(t) = Pii(t) just follow a Pauli master or balance equation, which corresponds to a classical Markovian two-state process of electron jumps with some quantum rates. Such and similar Markovian kinetic equations describe quantum relaxation dynamics of an ensemble of many identical systems.2,3
.2–5 In the simplest, ultimately reduced case the electronic populations pi(t) = Pii(t) just follow a Pauli master or balance equation, which corresponds to a classical Markovian two-state process of electron jumps with some quantum rates. Such and similar Markovian kinetic equations describe quantum relaxation dynamics of an ensemble of many identical systems.2,3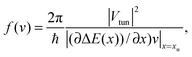


 , the reaction coordinate velocity is thermally distributed,
, the reaction coordinate velocity is thermally distributed,  ,
,  , all the time. In a singular limit of M → 0, the KFPE for a fixed state i reduces to the Smoluchowski–Fokker–Planck dynamics, ṗi(x,t) =
, all the time. In a singular limit of M → 0, the KFPE for a fixed state i reduces to the Smoluchowski–Fokker–Planck dynamics, ṗi(x,t) = ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) ipi(x,t) characterized by the Smoluchowski operator
ipi(x,t) characterized by the Smoluchowski operator ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) i = D(∂/∂x){exp[−βEi(x)](∂/∂x)exp[βEi(x)]}. Here, β = 1/kBT is inverse temperature, and D = kBT/η is the diffusion coefficient. The corresponding semi-classical description is well known under the label of Zusman equations.4,44 Within it, the reduced dynamics of population densities
i = D(∂/∂x){exp[−βEi(x)](∂/∂x)exp[βEi(x)]}. Here, β = 1/kBT is inverse temperature, and D = kBT/η is the diffusion coefficient. The corresponding semi-classical description is well known under the label of Zusman equations.4,44 Within it, the reduced dynamics of population densities  is described by
is described by![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) 1p1(x,t),
1p1(x,t),![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) 2p2(x,t),
2p2(x,t),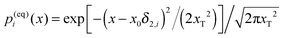 , where
, where 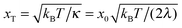 is a thermal width. Then, the nonadiabatic quantum transition rate is
is a thermal width. Then, the nonadiabatic quantum transition rate is


 .44 Hence, for such large activation barriers, eqn (8) takes the form
.44 Hence, for such large activation barriers, eqn (8) takes the form
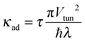
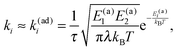
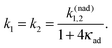

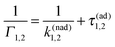



 is the Mittag-Leffler function of the fractional order 1/2 and argument
is the Mittag-Leffler function of the fractional order 1/2 and argument  , and
, and
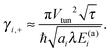

 . Here we introduced a characteristic time
. Here we introduced a characteristic time
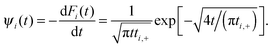
 scaling part, our result is very different from the one by Tang and Marcus.8,9 First, it describes a stretched-exponential and not a power law distribution. Second, our ti,+ in (19) is also different from the corresponding critical time in ref. 8 and 9, which marks transition from one power law regime to another one therein. Namely, we have aiE(a)i in (19) instead of 2kBT in the expression for this critical time in ref. 8 and 9. Note that numerically for E(a)i in the range [2.5kBT,10kBT], ai ≈ E(a)i/(2.5kBT), whereas ai ≈ 1 for E(a)i in the range [0.5kBT,2.5kBT]. Hence, our result and the one in ref. 8 and 9 have very different temperature dependences. Furthermore, for t ≫ ti,+ an intermediate power law regime follows,
scaling part, our result is very different from the one by Tang and Marcus.8,9 First, it describes a stretched-exponential and not a power law distribution. Second, our ti,+ in (19) is also different from the corresponding critical time in ref. 8 and 9, which marks transition from one power law regime to another one therein. Namely, we have aiE(a)i in (19) instead of 2kBT in the expression for this critical time in ref. 8 and 9. Note that numerically for E(a)i in the range [2.5kBT,10kBT], ai ≈ E(a)i/(2.5kBT), whereas ai ≈ 1 for E(a)i in the range [0.5kBT,2.5kBT]. Hence, our result and the one in ref. 8 and 9 have very different temperature dependences. Furthermore, for t ≫ ti,+ an intermediate power law regime follows,  and ψi(t) ∝ t−3/2, which ends with an exponential tail, which is described by the rate Γi in eqn (15). This power law regime and an exponential tail were obtained in ref. 8. However, the exponential tails here and in ref. 8 and 9 have different rates.
and ψi(t) ∝ t−3/2, which ends with an exponential tail, which is described by the rate Γi in eqn (15). This power law regime and an exponential tail were obtained in ref. 8. However, the exponential tails here and in ref. 8 and 9 have different rates.
![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) ) within a very long time interval
) within a very long time interval ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) is according to ref. 30ni(
is according to ref. 30ni(![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) ) =
) = ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) P(eq)i(x*) 〈|v(t)|〉x(t)=x*, and hence,
P(eq)i(x*) 〈|v(t)|〉x(t)=x*, and hence,  . By the same token and taking into account probability (1) to make a quantum jump to another state at each level crossing, we obtain
. By the same token and taking into account probability (1) to make a quantum jump to another state at each level crossing, we obtain , where we used
, where we used ![[small phi (variant), Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a4.gif) (t) = v(t). From this, it follows that
(t) = v(t). From this, it follows that
![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) would give the number of transitions to another electronic surface within this time interval. Since the probability of such transitions is merely PLZ(v(ti)), one should consider
would give the number of transitions to another electronic surface within this time interval. Since the probability of such transitions is merely PLZ(v(ti)), one should consider
![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) yields the inverse mean time between the switching events, or the mean transition rate. Assuming ergodicity of the point process ti, the time-average can be replaced with the ensemble average using P(x,v) = P(eq)(x)PM(v), which yields (21). Note a very paradoxical situation: even if ζ(t) is an ergodic process, the process of electron fluctuations between two localization sites is generally nonergodic, whenever its equilibrium ensemble and single trajectory statistics are in conflict.
yields the inverse mean time between the switching events, or the mean transition rate. Assuming ergodicity of the point process ti, the time-average can be replaced with the ensemble average using P(x,v) = P(eq)(x)PM(v), which yields (21). Note a very paradoxical situation: even if ζ(t) is an ergodic process, the process of electron fluctuations between two localization sites is generally nonergodic, whenever its equilibrium ensemble and single trajectory statistics are in conflict.
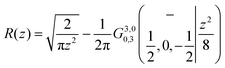
 , and we obtain 〈τ1〉−1 = k(nad)1, in agreement with numerics. Moreover, we also did numerics which include the inertial effects in eqn (4), within the contact approximation, and confirm the analytical result in (24) and (25), see Fig. 6. The numerical results for the renormalization function R(z) (symbols) are compared therein with the analytical result in eqn (25). The agreement is remarkable indeed, and a detailed treatment of the inertial case will be presented elsewhere. The observed ergodicity breaking is thus not an artifact of the overdamped singular approximation. It expresses the profoundly quantum nature of electron transfer even in the adiabatic regime as manifested at the level of single-trajectory dynamics.
, and we obtain 〈τ1〉−1 = k(nad)1, in agreement with numerics. Moreover, we also did numerics which include the inertial effects in eqn (4), within the contact approximation, and confirm the analytical result in (24) and (25), see Fig. 6. The numerical results for the renormalization function R(z) (symbols) are compared therein with the analytical result in eqn (25). The agreement is remarkable indeed, and a detailed treatment of the inertial case will be presented elsewhere. The observed ergodicity breaking is thus not an artifact of the overdamped singular approximation. It expresses the profoundly quantum nature of electron transfer even in the adiabatic regime as manifested at the level of single-trajectory dynamics.

 , where
, where  is angular frequency of the reaction coordinate. The theoretical result (full line) in eqn (25) is compared with the numerical results (symbols) obtained for Vtun = 0.04, λ = 800, and T = 0.1, and varying z through ω0.
is angular frequency of the reaction coordinate. The theoretical result (full line) in eqn (25) is compared with the numerical results (symbols) obtained for Vtun = 0.04, λ = 800, and T = 0.1, and varying z through ω0.

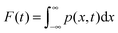 , and its negative derivative, ψ(t) = −dF(t)/dt, is the residence time distribution (RTD) in the electronic state. We solve the problem in the Laplace space,
, and its negative derivative, ψ(t) = −dF(t)/dt, is the residence time distribution (RTD) in the electronic state. We solve the problem in the Laplace space,  , where eqn (A1) takes on the form
, where eqn (A1) takes on the form![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) (x,s) = p(eq)(x)/s − v0
(x,s) = p(eq)(x)/s − v0![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) (x,s|x*)p(x*,s).
(x,s|x*)p(x*,s).

![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) (s) = [1 −
(s) = [1 − ![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) (s)]/s. Next, we note that in the limit s → 0,
(s)]/s. Next, we note that in the limit s → 0,
 . Here lies the major difference of our treatment with the one in ref. 8, which we correct thereby. Subsequently, we use the decomposition
. Here lies the major difference of our treatment with the one in ref. 8, which we correct thereby. Subsequently, we use the decomposition ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) (x*,s|x*) − p(eq)(x*)/s = τ(s), where
(x*,s|x*) − p(eq)(x*)/s = τ(s), where
![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) (0) = τ(ad), see ref. 45, which yields eqn (9). Furthermore, because v0p(eq)(x*) = k(nad), we finally have
(0) = τ(ad), see ref. 45, which yields eqn (9). Furthermore, because v0p(eq)(x*) = k(nad), we finally have
![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) i(0) = 〈τi〉 is the mean residence time in the state “i” and Γi = 1/〈τi〉 is the corresponding rate in the exponential regime of high barriers, we obtain immediately from eqn (A8) our result in eqn (15).
i(0) = 〈τi〉 is the mean residence time in the state “i” and Γi = 1/〈τi〉 is the corresponding rate in the exponential regime of high barriers, we obtain immediately from eqn (A8) our result in eqn (15).

![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) i(s) with τ(ad)i in (A9), we deduce that asymptotically the distribution is exponential and characterized by the rate Γi. Showing that initially the distribution is always stretched exponential (another point of difference with ref. 8 and 9), and an intermediate power law emerges in a close to adiabatic transport regime even for high activation barriers, requires a bit more work.
i(s) with τ(ad)i in (A9), we deduce that asymptotically the distribution is exponential and characterized by the rate Γi. Showing that initially the distribution is always stretched exponential (another point of difference with ref. 8 and 9), and an intermediate power law emerges in a close to adiabatic transport regime even for high activation barriers, requires a bit more work.
![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) (s). The corresponding integral can be evaluated exactly as an infinite sum of generalized hypergeometric functions. Our subsequent numerical evaluations of
(s). The corresponding integral can be evaluated exactly as an infinite sum of generalized hypergeometric functions. Our subsequent numerical evaluations of ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) (s) show that it is very well approximated for a high activation barrier (exceeding kBT/2) by
(s) show that it is very well approximated for a high activation barrier (exceeding kBT/2) by



 is expressed via the Mittag-Leffler function,
is expressed via the Mittag-Leffler function, 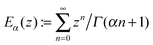 , of the fractional order 1/2. Furthermore, erfc(z) is the complementary error function, and
, of the fractional order 1/2. Furthermore, erfc(z) is the complementary error function, and
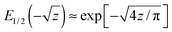 , and, therefore, Fi(t) displays initially stretched-exponential kinetics, always. For z ≫ 1,
, and, therefore, Fi(t) displays initially stretched-exponential kinetics, always. For z ≫ 1,  . Our theory nicely explains all the striking features observed in stochastic simulations.
. Our theory nicely explains all the striking features observed in stochastic simulations.

 . The roots of (A16) are found as62
. The roots of (A16) are found as62


