Low intensity, continuous wave photodoping of ZnO quantum dots – photon energy and particle size effects

Abstract

The unique properties of semiconductor quantum dots (QDs) have found application in the conversion of solar to chemical energy. How the relative rates of the redox processes that control QD photon efficiencies depend on the particle radius (r) and photon energy (E_λ), however, is not fully understood. Here, we address these issues and report the quantum yields (Φs) of interfacial charge transfer and electron doping in ZnO QDs capped with ethylene glycol (EG) as a function of r and E_λ in the presence and absence of methyl viologen (MV²⁺) as an electron acceptor, respectively. We found that Φs for the oxidation of EG are independent of E_λ and photon fluence (φ_λ), but markedly increase with r. The independence of Φs on φ_λ ensures that QDs are never populated by more than one electron–hole pair, thereby excluding Auger-type terminations. We show that these findings are consistent with the operation of an interfacial redox process that involves thermalized carriers in the Marcus inverted region. In the absence of MV²⁺, QDs accumulate electrons up to limiting volumetric densities ρ_e,∞ that depend sigmoidally on excess photon energy E* = E_λ − E_BG(r), where E_BG(r) is the r-dependent bandgap energy. The maximum electron densities: ρ_ev,∞ ∼ 4 × 10²⁰ cm⁻³, are reached at E* > 0.5 eV, independent of the particle radius.

---

Introduction

The readily tunable optical and electrical properties of semiconductor QDs have found extensive applications in optoelectronics, light harvesting, solar energy conversion and photocatalysis.^1–9 A key advantage is that QD properties can be tailored by modifying their chemical composition, size and shape.¹⁰ The distinctive feature that impacts the QD properties is the discreteness of the lower rungs of their electronic band manifolds.¹¹ Thus, the excess electronic energy: E* = E_λ − E_BG, carried by the electron–hole pairs (e⁻–h⁺) generated by photons of wavelengths shorter than bandgap thresholds: λ < λ_BG, was expected to be slowed in QDs due to the larger mismatch of electronic vs. vibrational manifolds.¹² The failure of such expectations,^13,14 was ascribed to Auger-type processes that bypass the putative phonon bottlenecks.^15–17 QDs can also become overcharged¹⁸ upon irradiation in the absence of suitable electron acceptors. The progressive filling of discrete conduction band levels leads to the occupation of upper levels by electrons that convert QDs in powerful reductants.^19,20

Since the utilization of photoinduced carriers in QDs is determined by the competition between energy dissipation, electron accumulation and interfacial electron transfer, it is essential to understand how the relative rates of these processes depend on excitation energy and QD properties.^21–25

Here, we address these issues in a quantitative experimental investigation of the photochemistry of ZnO QDs of various sizes driven by low intensity, continuous monochromatic beams under well-defined experimental conditions. Low intensity irradiation with monochromatic light in the presence of methyl viologen (MV²⁺) allows us to exclude Auger-type carrier terminations and investigate the effect of photon energy on the efficiency of interfacial electron transfer. Similar experiments in the absence of MV²⁺ let us probe the impact of r and E_λ on electron accumulation.

Experimental section

Materials

Methyl viologen dichloride hydrate, MV²⁺ (98%, Aldrich); zinc acetate dehydrate, Zn(CH₃COO)₂·2H₂O (Fluka); lithium hydroxide, LiOH (Sigma-Aldrich); tetra-methyl-ammonium hydroxide, (Me)₄NOH (Sigma) were of the highest available purity and used as received. Ethanol, EtOH (Sintorgan); ethylene glycol, EG (Biopack); ethyl acetate (Sintorgan); heptane (Sintorgan) and dimethyl-sulfoxide, DMSO (chromatographic grade, Sintorgan) were used without further purification.

Preparation of EG-capped ZnO QD sols

EG-capped ZnO nanoparticle sols were prepared by two different procedures. In one of them, colloidal ZnO nanoparticles were synthesized via alkaline hydrolysis/condensation reaction by slowly adding 6.25 mL of 0.55 M (Me)₄NOH in EtOH to 20 mL of 0.1 M Zn(CH₃COO)₂ in DMSO at room temperature.^26,27 The reaction was stopped by precipitating the resulting ZnO nanoparticles with ethyl acetate. Nanoparticles were then suspended in neat EG and purified twice by a cycle involving precipitation with heptane and resuspension in EG. Alternatively, ZnO nanoparticles were prepared by the arrested alkaline hydrolysis of alcoholic solutions of Zn(CH₃COO)₂ in EtOH according to Meulenkamp et al.²⁸ 2.5 mmol of Zn(CH₃COO)₂·2H₂O were dissolved in 25 ml EtOH at 50 °C and then thermalized at variable reaction temperatures T_R. To this solution, 10 ml of 0.35 M LiOH in EtOH at T_R were quickly added and maintained at T_R for two hours under vigorous stirring, followed by ripening the resulting ZnO nanoparticles for least 48 hours. Ripening, which leads to particle size homogenization, was completed within the first 24 hours, as reported by the UV spectra of the evolving sols. ZnO particle size distributions obtained by this procedure were essentially determined by T_R, if sols were stored at T_S ≤ T_R, and by T_S otherwise. As a rule, particles with larger mean sizes were produced at higher T_R/T_S.²⁹ We found that the particle size distributions reached after 24 hours at T_R were stabilized by diluting the sol (1 : 20) in neat EG. Photochemical experiments were performed on the optically clear, indefinitely stable EG-capped ZnO QD sols obtained by this procedure (Fig. 1). See the ESI-1† for further details. The mean particle sizes and size distributions of the EG-capped ZnO sols produced at 0, 25 and 60 °C were derived from the UV absorption spectra of Fig. 1 following the method reported by Pesika et al.,³⁰ see ESI-2.†

Fig. 1 UV absorption spectra of EG-capped ZnO QD sols produced at (a) 0, (b) 25 and (c) 60 °C as a function of wavelength. Inset: Tauc plots of (αhν)²vs. hν. Linear extrapolation yields band gap energies.

Φ-Measurements

EG-capped ZnO QD sols in [MV²⁺] = 10.6 μM within 3.0 mL, 1 cm optical path fused silica cuvettes were thoroughly deaerated by sparging with argon for 1 h, and then sealed to ensure anaerobic conditions throughout. They were irradiated with monochromatic light at λ = 303 ± 5, 315 ± 10, 330 ± 10 and 350 ± 10 nm, at <1 × 10⁻³ W cm⁻² fluences,¹ from a 1 kW high-pressure Hg-Xe/Kratos-Schoeffel monochromator source. The initial rates of MV⁺˙ formation, R_λ, from the reduction of MV²⁺ by photogenerated electrons were determined by absorption spectrophotometry at 397 nm (ε_MV,397nm⁺˙ = 37 500 M⁻¹ cm⁻¹, ε_MV,602nm⁺˙ = 12 800 M⁻¹ cm⁻¹).³¹ At each wavelength, the rates of light absorption by EG-capped ZnO QD sols, I_a,λ were calculated from: I_a,λ = I_0,λ × (1 − 10^−A_λ), where A_λ are the sol absorbances, and I_0,λ the incident light intensities (in M s⁻¹) determined via chemical actinometry using phenylglyoxylic acid.²⁰ From this information, Φs was calculated, at each λ, by means of eqn (E1). Independent experiments confirmed that MV⁺˙ formation requires both EG-capped ZnO nanoparticles and light. For further experimental details, see the ESI-3.†

Excess electron measurements

Similar experiments were performed in the absence of added MV²⁺. In this case, the progress of photolysis was followed by monitoring the blue shift in the absorption spectra of the EG-capped ZnO QD sols as a function of time. We found that shifts reached limiting values after irradiation times, τ_∞, which increased at lower I_0,λ. Samples were further irradiated for 15 min to ensure doping completion. Excess electron concentrations [N_e] were determined by titration with MV²⁺ under strict anaerobic conditions.²⁷ From this information, the average number of excess electrons per ZnO particle, n_e, was evaluated by means of eqn (E2):where [N_p] is the concentration of ZnO particles.

Results and discussion

MV⁺˙ formation requires the presence of EG, we infer that the process controlling Φs is the oxidation of EG to glycol aldehyde, GA, reaction (R1):

HOCH₂–CH₂OH + 2h⁺ = HOCH₂–CHO + 2H⁺ (R1)

which proceeds in two steps via current doubling.³² The first step, reaction (R2), is deemed to yield strongly reducing α-hydroxyalkyl radicals, HOCH₂–C(˙)HOH, which subsequently inject an electron into the ZnO conduction band, e_CB⁻, to produce GA, reaction (R3).

HOCH₂–CH₂OH + h⁺ = HOCH₂–C(˙)HOH + H⁺ (R2)

HOCH₂–C(˙)HOH = HOCH₂–CHO + H⁺ + e_CB⁻ (R3)

We have shown that the kinetics of the evolution of the few electron–hole pairs generated under weak illumination falls in the stochastic regime and cannot be described by conventional kinetic laws involving continuum concentrations.² Under such conditions, Φs are controlled by the faster charge transfer process, in this case the oxidation of EG.

Φs as a function of particle radius, photon fluence and excess photon energy

E _BG(r) band gap energies as a function of r were evaluated from the onsets of light absorption as a function of photon energy (Fig. 1, inset). The energies of conduction band E_CB(r) and valence band E_VB(r) edges were calculated using Brus's effective mass approximation,^33–35 see ESI-4.† The resulting parameters are summarized in Table 1.

Table 1 Band gap energies, and energy shifts of the conduction and valence bands of the EG-capped ZnO nanoparticles derived from the UV-absorption spectra of Fig. 1. Samples A, B, and C

Sample	E BG (eV)	r (nm)	[E^CB(r) − E^CB(∞)]^c (eV)	[E^VB(r) − E^VB(∞)]^c (eV)
a Derived from Fig. 1. b Derived according to the method reported by Pesika,^30 see ESI-2. c Calculated using Brus's effective mass approximation,^33 see ESI-4.
A	3.85	1.70	−0.43	0.23
B	3.60	2.10	−0.26	0.14
C	3.45	2.65	−0.13	0.08

---

Irradiation with photons of energies E_λ > E_BG generates correlated e⁻–h⁺ pairs possessing excess energies: E* = E_λ − E_BG(r). Fig. 2 shows experimental Φs (from eqn (E1)) as a function of E* and r. It is apparent that Φs: (1) are independent of E* within experimental error, implying that the hot carriers produced by above-bandgap irradiation are thermalized before they engage in interfacial electron transfer, and (2) perhaps unexpectedly, increase dramatically with r from Φ (1.70 nm) = 3.2% to Φ (2.65 nm) = 25%.

Fig. 2 Φs for MV²⁺ reduction in irradiated EG-capped ZnO QD sols at different irradiation wavelengths: 315 ± 10 nm (magenta), 303 ± 5 nm (cyan) 330 ± 10 nm (magenta), and 315 ± 10 nm (dark brown) as a function of particle radius, r, and excess photon energy, E*.

We infer that relaxation rates of hot carriers are faster than the electron transfer processes that determine Φs under the present conditions.

The strict linear dependence of initial rates R_λ on I_a,λ (Fig. 3) implies that hole transfer competes with a pseudo first-order bimolecular e⁻–h⁺ recombination process.² A pseudo first-order bimolecular carrier recombination process in turn is only possible if QDs contain at most a single electron–hole pair. Since Auger-type termination mechanisms require bi-excitons, i.e., the simultaneous presence of two or more carrier pairs, our experiments exclude Auger-type recombination.³⁶

Fig. 3 MV²⁺ reduction rates and (inset) Φs as a function of the frequency of photon absorption, I_ap = photon s⁻¹. See ESI-3.† Irradiation wavelength: 303 nm. Sample A, r = 1.70 nm.

Thus, the strong direct dependence of Φs on r reflects the competition between electron transfer and e⁻–h⁺ first-order recombination under quantum confinement. Our interpretation of this finding is based on the dependence of transfer rates on free energy predicted by Marcus's theory from the E_VB shifts (to less positive values vs. vacuum), and a plausible dependence of e⁻–h⁺ recombination rates on r.

Φ-Dependence on free energy

As pointed out above, in our experiments quantum yields represent the fraction of photogenerated holes that accept an electron from EG with a pseudo first-order rate constant k_et(r) in competition with a pseudo first-order (see above) e⁻–h⁺ recombination with a rate constant k_r(r) (eqn (E3)). Anodic (EG oxidation) and cathodic (MV²⁺ reduction) processes, of course, are not necessarily synchronous. We had shown that in the stochastic kinetic regime that applies to the evolution of a single e⁻–h⁺ pair it is the faster (rather than the slower) interfacial electron transfer process that determines Φs.³⁷ This is so because in this case once the more reactive carrier exits the particle, the remaining carrier must react before the arrival of another photon. By rearranging eqn (E3) we obtain eqn (E4), in which the ratio k_et(r)/k_r(r) is expressed as an implicit function of r via experimental Φ(r)s.Eqn (E4) is, of course, independent of any mechanistic considerations. The dependence of k_et on r arises from the E_VB shifts due to quantum effects (shown in the inset of Fig. 4B). Under the approximations implicit in classical Marcus's theory, k_et is given by eqn (E5):In the above expression, A is a frequency factor, ΔG⁰(r) is the free energy change and λ_RE the reorganization energy associated with hole transfer.³⁸ We assume that k_r is an inverse function of r, i.e.: k_r = Br⁻ⁿ, with 1 ≤ n ≤ 3. Stronger, n > 3 r-dependence is deemed to be unrealistic. Thus, f(r) is given by eqn (E6).E⁰(D) is the reduction potential for the one-electron oxidation of EG into its radical cation, E_VB(r) is the energy of the valence band edge of ZnO nanoparticles, λ_RE = 0.5 eV the reorganization energy, and C is a constant C = A/B. Fig. 4B shows fits to the experimental results using C and E⁰(D) as adjustable parameters for plausible 1 ≤ n ≤ 3 values.

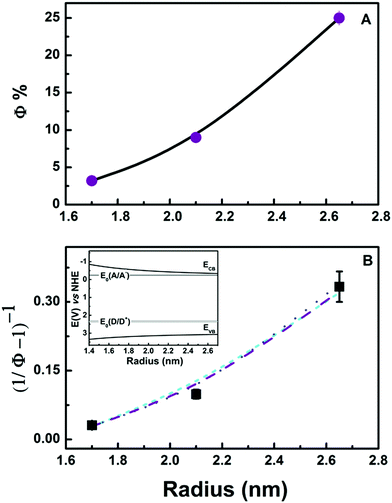Fig. 4 (A) Φs as a function of QD radius r. Lines are putative quadratic regressions to the data. (B) Symbols: experimental data. Lines are calculated values from eqn (E6) with n = 1 (light blue, short dashed line); n = 2, (purple, dashed line); n = 3 (blue, dotted line). See text. Inset: Energy diagram showing the dependence of band edge positions on r.

We found that experimental data could be fitted by using the following {C, E⁰(D), n} parameter sets: {0.485, 2.30 V, 1}, {0.095, 2.37 V, 2}, and {0.024, 2.40 V, 3}. The main conclusion is that EG oxidation occurs in the Marcus inverted region. This conclusion is robust because hole transfer in the Marcus direct region would require a physically untenable strong inverse dependence of recombination rates on r, i.e.: n ≫ 3.

Electron photodoping

The irradiation of EG-capped ZnO QD sols in the absence of the MV²⁺ electron acceptor leads to perceptible changes. The UV spectra of ZnO QD sols shift to the blue region as expected from the progressive filling (bleaching) of low conduction band energy states.²⁸ We quantified the spectral shifts by tracking the displacement of the wavelength corresponding to 50% absorption, λ_1/2.²⁸Fig. 5 shows how λ_1/2 evolves as a function of irradiation time for EG-capped ZnO QDs r = 2.10 nm sols. λ_1/2 closely follows a λ_1/2,∞(1 − exp(−βt)) saturation-type kinetics, where λ_1/2,∞ is the limiting asymptotic value of λ_1/2, which is independent of photon fluence φ_λ, and β is a first order rate constant that is an increasing function of φ_λ, i.e., saturation under larger photon fluences is reached in shorter illumination times τ_∞.

Fig. 5 Evolution λ_1/2 (the wavelength at 50% absorption) as a function of the irradiation time for EG-capped ZnO QDs. r = 2.10 nm, [ZnO] = 0.78 mM, λ = 303 ± 10 nm, I₀ = 2.27 × 10⁻⁶ M s⁻¹.

The observed saturation-type kinetics corresponds to the filling of a fixed number of conduction band states that are available at the irradiation wavelength/photon energy in each experiment (see below). The electrons accumulated in the ZnO QD sols were titrated with MV²⁺ as described in the Experimental section. The results are shown in Table 2, where we present the limiting average number of electrons per particle, n_e,∞, and the volumetric, ρ_ev,∞, and surficial, ρ_es,∞, electron densities as a function of excess photon energy E* for various particle radii.

Table 2 Maximum excess electron densities ρ_e,∞ as a function of particle size and excitation wavelength

λ (nm)	r (nm)	E* (eV) = Eλ − EBG	n e,∞	ρ ev,∞ (10^20 cm^−3)	ρ es,∞ (10^13 cm^−2)
a Number of stored excess electrons per particle. b Volumetric electron density per particle. c Surficial electron density per particle.
330	2.10	0.15	6	0.9	1.9
	2.65	0.40	17	1.3	3.4
303	1.70	0.24	2.3	0.7	1.2
	2.10	0.49	30	4.6	9.7
	2.65	0.79	51	3.9	10.3

---

For a given r, the dependence of ρ_ev,∞ and ρ_es,∞ on E* is consistent with the filling of r-dependent discrete conduction band levels which become quasi continuous above a ∼E_CB + 0.4 eV threshold, as observed for particle radii above 2 nm.^39–41Fig. 6 shows a schematic representation of the levels that become accessible upon excitation at two selected irradiation wavelengths (303 and 330 nm) for different particle sizes.

Fig. 6 E _CB, E_VB, and schematic representation of the discrete CB energy levels vs. NHE as a function of nanoparticle radius r. The green and pink arrows correspond to 330 and 303 nm excitations, respectively.

On the other hand, Fig. 7 shows that both volumetric and surficial electron densities display a sigmoid dependence on E*, with inflection points near E* = 0.43 eV, reaching maximum values above E* ∼ 0.5 eV.

Fig. 7 Volumetric ρ_ev (blue) and surficial ρ_es electron densities (red) as a function of excess energies E* for various rs: circles 1.7 nm, squares 2.1 nm, triangles 2.65 nm.

The sigmoid dependence on E* is consistent with a titration process in which conduction band levels are progressively filled by higher energy photons. It is apparent that electron–hole recombination is the dominant process above excess electron energies E* ∼ 0.5 eV, probably reflecting that the number of available states at these excess energies is no longer the limiting factor.

Conclusions

Photochemical experiments involving low intensity, continuous wave, monochromatic irradiation of ethylene glycol-capped ZnO quantum dots of controlled size show that: (1) the quantum yields of interfacial redox processes increase with particle radius, a finding that can be accounted by the classical Marcus theory of electron transfer in the inverted region, and (2) in the absence of electron acceptors, ZnO quantum dots are charged with electron densities that depend sigmoidally on E* and reach a maximum at E* > 0.5 eV. At smaller excess energies, the accumulated electron densities are determined by the number of discrete energy levels accessible to photons with energies exceeding the band gap.

Acknowledgements

This work was financially supported by ANPCyT (ARGENTINA) under project 1456, MEA thanks CONICET for a postdoctoral fellowship.

References

1. D. A. Hines and P. V. Kamat, J. Phys. Chem. C, 2014, 117, 14418.
2. P. V. Kamat, J. Phys. Chem. C, 2008, 112, 18737.
3. W. R. Algar, D. Wegner, A. L. Huston, J. B. Blanco-Canosa, M. H. Stewart, A. Armstrong, P. E. Dawson, N. Hildebrandt and I. L. Medintz, J. Am. Chem. Soc., 2012, 134, 1876.
4. M. C. Beard, J. Phys. Chem. Lett., 2011, 2, 1282.
5. A. B. Madrid, K. Hyeon-Deuk, B. F. Habenicht and O. V. Prezhdo, ACS Nano, 2009, 3, 2487.
6. W. Yu, D. Noureldine, T. Isimjan, B. Lin, S. Del Gobbo, M. Abulikemu, M. N. Hedhili, D. H. Anjum and K. Takanabe, Phys. Chem. Chem. Phys., 2014, 17, 1001.
7. Y. Dong, J. Choi, H.-K. Jeong and D. H. Son, J. Am. Chem. Soc., 2015, 137, 5549.
8. R. T. Ross and A. J. Nozik, J. Appl. Phys., 1982, 53, 3813.
9. K. Tvrdy, P. A. Frantsuzov and P. V. Kamat, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 29.
10. K. E. Knowles, M. T. Frederick, D. B. Tice, A. J Morris-Cohen and E. A. Weiss, J. Phys. Chem. Lett., 2012, 3, 18.
11. A. P. Alivisatos, Science, 1996, 271, 933.
12. A. J. Nozik, Annu. Rev. Phys. Chem., 2001, 52, 193.
13. S. V. Kilina, A. J. Neukirch, B. F. Habenicht, D. S. Kilin and O. V. Prezhdo, Phys. Rev. Lett., 2013, 110, 180404.
14. A. Pandey and P. Guyot-Sionnest, Science, 2008, 322, 929.
15. J. M. An, M. Califano, A. Franceschetti and A. Zunger, J. Chem. Phys., 2008, 128, 164720.
16. K. Zheng, K. Karki, K. Sidek and T. N. Pullerits, Nano Res., 2015, 8, 2125.
17. F. C. M. Spoor, L. T. Kunneman, W. H. Evers, N. Renaud, F. C. Grozema, A. J. Houtepen and L. D. A. Siebbeles, ACS Nano, 2016, 10, 695.
18. A. M. Schimpf, C. E. Gunthardt, J. D. Rinehart, J. M. Mayer and D. R. Gamelin, J. Am. Chem. Soc., 2013, 135, 16569.
19. I. K. Levy, M. A. Brusa, M. E. Aguirre, G. Custo, E. San Roman, M. I. Litter and M. A. Grela, Phys. Chem. Chem. Phys., 2013, 15, 10335.
20. Y. Di Iorio, M. E. Aguirre, M. A. Brusa and M. A. Grela, J. Phys. Chem. C, 2012, 116, 9646.
21. D. J. Trivedi, L. Wang and O. V. Prezhdo, Nano Lett., 2015, 15, 2086.
22. M. D. Peterson, L. C. Cass, R. D. Harris, K. Edme, K. Sung and E. A. Weiss, Annu. Rev. Phys. Chem., 2014, 65, 317.
23. S. Kilina, K. A. Velizhanin, S. Ivanov, O. V. Prezhdo and S. Tretiak, ACS Nano, 2012, 6, 6515.
24. F. C. M. Spoor, L. T. Kunneman, W. H. Evers, N. Renaud, F. C. Grozema, A. J. Houtepen and L. D. A. Siebbeles, ACS Nano, 2016, 10, 695.
25. R. R. Cooney, S. L. Sewall, E. A. Dias, D. M. Sagar, K. E. H. Anderson and P. Kambhampati, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 245311.
26. D. A. Schwartz, N. S. Norberg, Q. P. Nguyen, J. M. Parker and D. R. Gamelin, J. Am. Chem. Soc., 2003, 125, 13205.
27. M. E. Aguirre, G. Perelstein, A. Feldhoff, A. Condo, A. J. Tolley and M. A. Grela, New J. Chem., 2015, 39, 909.
28. E. A. Meulenkamp, J. Phys. Chem. B, 1998, 102, 5566.
29. A. Wood, M. Giersig, M. Hilgendorff, A. Vilas-Campos, L. M. Liz-Marzán and P. Mulvaney, Aust. J. Chem., 2003, 56, 1051.
30. N. S. Pesika, K. J. Stebe and P. C. Searson, J. Phys. Chem. B, 2003, 107, 10412.
31. M. D. Ward, J. R. White and A. J. Bard, J. Am. Chem. Soc., 1983, 105, 27.
32. N. Hykaway, W. M. Sears, H. Morisaki and S. R. Morrison, J. Phys. Chem., 1986, 90, 6663–6667.
33. L. Brus, J. Phys. Chem., 1986, 90, 2555.
34. T. J. Jacobsson and T. Edvinsson, Inorg. Chem., 2011, 50, 9578.
35. L. Zhang, L. Yin, C. Wang, N. lun, Y. Qi and D. Xiang, J. Phys. Chem. C, 2010, 114, 9651.
36. M. Grundmann, The Physics of Semiconductors: An Introduction Including Nanophysics and Applications, Springer Berlin Heidelberg, Germany, 2010.
37. M. A. Grela and A. J. Colussi, J. Phys. Chem., 1996, 100, 18214.
38. M. A. Grela, M. A. Brusa and A. J. Colussi, J. Phys. Chem. B, 1999, 103, 6400.
39. S. Verma, A. Das and H. N. Ghosh, J. Phys. Chem. C, 2014, 118, 28898.
40. L. Dallali, S. Jaziri, J. El Haskouri and P. Amorós, Superlattices Microstruct., 2009, 46, 907.
41. A. Germeau, A. L. Roest, D. Vanmaekelbergh, G. Allan, C. Delerue and E. A. Meulenkamp, Phys. Rev. Lett., 2003, 90, 097401.

---

Footnote

† Electronic supplementary information (ESI) available: Size distribution, details of the photochemical experiments and data treatment. See DOI: 10.1039/c6cp06829d

---