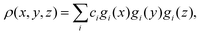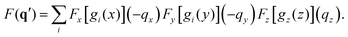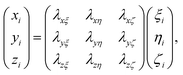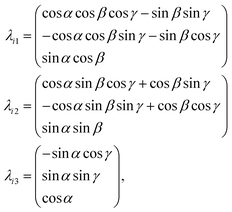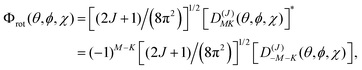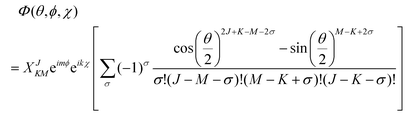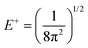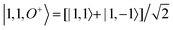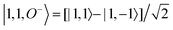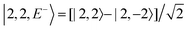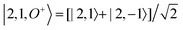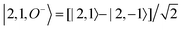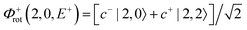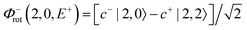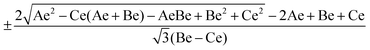Imaging rotations and vibrations in polyatomic molecules with X-ray scattering
Received
4th October 2016
, Accepted 24th February 2017
First published on 24th February 2017
Abstract
An approach for calculating elastic X-ray scattering from polyatomic molecules in specific electronic, vibrational, and rotational states is presented, and is used to consider the characterization of specific states in polyatomic molecules using elastic X-ray scattering. Instead of the standard independent atom model (IAM) method, the X-ray scattering is calculated directly from ab initio wavefunctions. The role of molecular symmetry and Friedel's law is examined, with the molecules BF3, C5H5−, NF3, and 1,3-cyclohexadiene used as specific examples. The contributions to the elastic X-ray scattering from the electronic, vibrational, and rotational portions of the molecular wavefunction are examined in CS2. In particular, it is observed that the rotational states give rise to distinct signatures in the scattering signal.
1 Introduction
X-ray Free-Electron Lasers (XFELs) have higher intensity and shorter pulse durations than synchrotrons, and have been adopted for many experiments including X-ray spectroscopy,1,2 Coulomb explosion imaging,3 and ultrafast scattering.4,5 Elastic scattering of X-rays, in particular, provides valuable insight into molecular structure and function. An attractive feature of XFELs is that the high intensity of the radiation reduces the need for crystals to amplify the scattered signal, with important implications for e.g. the diffractive imaging of biomolecules.6–8 In the absence of a crystal, the Bragg peaks disappear and the scattering image becomes continuous. Furthermore, the short pulse duration of XFELs limits the effect of radiation damage on the scattering signal.7,8
Gas-phase X-ray scattering9–13 is currently undergoing a revival.4,14–17 The main reason for this is that the high intensity of XFELs can compensate for small X-ray scattering cross sections, albeit gas-phase scattering is also possible at synchrotrons.18–21 An important aspect is that rapid development of alignment and orientation techniques22 and experimental methods to prepare molecules in specific quantum states23–27 makes it possible to generate highly anisotropic samples with a large fraction of identical molecules. As a consequence, the degree of thermal averaging in the data becomes small, invalidating the incoherent thermal averaging of the signal originally proposed by Debye.28 All these factors, i.e. continuous scattering, limited accumulation of radiation damage, non-thermal or even state-selected samples will contribute to more complete and detailed data sets, that will require more sophisticated analysis.
Standard analysis of diffraction data relies on the independent atom model (IAM), which uses tabulated atomic form factors calculated for single atoms at the Hartree–Fock (HF) level29–31 to assemble an approximate representation of the scattering. In thermal samples, this is generally sufficient,32–34 although well-known examples exist35,36 where the failure of IAM to account for changes in electron density due to e.g. chemical bonding renders IAM inadequate. Given the advances in electronic structure calculations, an interesting improvement on IAM is to calculate molecular scattering form factors directly from the molecular wavefunctions. Potentially this could provide the most flexible, general, and accurate approach to calculating X-ray scattering.37–41 Our recently developed AIXRD code42 does exactly this.
In the following, we consider the effect of rotational and vibrational motion on the scattering pattern of polyatomic molecules, and show that these can be incorporated into our AIXRD treatment. We explore the properties of state-specific scattering patterns from polyatomic molecules, and assess the impact of vibrational, rotational and electronic states on the scattering signal in CS2, an important molecule in gas-phase spectroscopy and dynamics.43–48 We also examine the convergence of AIXRD calculations compared to IAM, with the molecules NH3 and BF3 used as specific examples, and the computational requirements with regards to the basis set used. The consequences of Friedel's law and molecular symmetry on the scattering patterns are also examined, with the molecules BF3, C5H5−, NF3, and 1,3-cyclohexadiene used as examples.
2 Theory
2.1 X-ray scattering
For static X-ray scattering, the total differential cross section is given by Fermi's golden rule,49| | 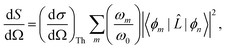 | (1) |
where ϕm and ϕn are the final and initial states, and correspondingly ωm and ω0 are the angular frequencies of the scattered and incident X-rays. The pre-factor (dσ/dΩ)Th = (e2/mec2)K is the Thomson cross section of a free electron, with me and e the mass and charge of an electron, c the velocity of light, and K the polarization factor. Ignoring the weak interaction between the electromagnetic field and the nuclei, the scattering operator ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) is defined as,
is defined as,| | 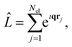 | (2) |
where the sum runs over the Nel electrons in the molecule, with rj the electron coordinate and q = k0 − k the momentum transfer vector. In this article, we focus on the elastic scattering contribution as a means to characterise molecular states. The elastic scattering is proportional to the matrix element Lnn in eqn (1), i.e.| | Ĩn(q) = |Lnn|2 = |〈ϕn|![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |ϕn〉|2, |ϕn〉|2, | (3) |
which is also known as the structure factor, and which we denote as Ĩn(q). For elastic scattering, the incident (k0) and scattered (k) wave vectors have the same length, |k| = |k0|.
2.2 Scattering from molecular wavefunctions
In order to calculate the structure factor Ĩn(q) in eqn (3), we require a representation of the molecular state |ϕn〉. Using the Born–Oppenheimer ansatz and assuming that the rotational–vibrational coupling is small, and that electronic states are sufficiently well separated that non-adiabatic couplings can be ignored, the state n can be written as a direct product of rotational, vibrational and electronic wavefunctions,| | |ϕn〉 = ΨrotJKM(Ω)Ψvibν(![[R with combining macron]](https://www.rsc.org/images/entities/b_char_0052_0304.gif) )Ψelecα( )Ψelecα(![[r with combining macron]](https://www.rsc.org/images/entities/b_char_0072_0304.gif) ; ;![[R with combining macron]](https://www.rsc.org/images/entities/b_char_0052_0304.gif) ,Ω), ,Ω), | (4) |
where the electronic wavefunction, Ψelecα(![[r with combining macron]](https://www.rsc.org/images/entities/b_char_0072_0304.gif) ;
;![[R with combining macron]](https://www.rsc.org/images/entities/b_char_0052_0304.gif) ,Ω), depends parametrically on the nuclear coordinates
,Ω), depends parametrically on the nuclear coordinates ![[R with combining macron]](https://www.rsc.org/images/entities/b_char_0052_0304.gif) and on the orientation of the molecular frame specified by the rotational Euler angles Ω = (α,β,γ) (see Appendix). The rotational wavefunction ΨrotJKM(Ω) is characterized by the three rotational quantum numbers J, K, and M, and the vibrational wavefunction Ψvibν(
and on the orientation of the molecular frame specified by the rotational Euler angles Ω = (α,β,γ) (see Appendix). The rotational wavefunction ΨrotJKM(Ω) is characterized by the three rotational quantum numbers J, K, and M, and the vibrational wavefunction Ψvibν(![[R with combining macron]](https://www.rsc.org/images/entities/b_char_0052_0304.gif) ) by the full set of vibrational quantum numbers ν. Since the scattering operator in eqn (2) acts on the electrons, it is convenient to first evaluate the scattering in terms of the form factor for the electronic wavefunction,
) by the full set of vibrational quantum numbers ν. Since the scattering operator in eqn (2) acts on the electrons, it is convenient to first evaluate the scattering in terms of the form factor for the electronic wavefunction,| | f0α(q;![[R with combining macron]](https://www.rsc.org/images/entities/b_char_0052_0304.gif) ,Ω) = 〈Ψelecα| ,Ω) = 〈Ψelecα|![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |Ψelecα〉. |Ψelecα〉. | (5) |
The form factor f0α(q;![[R with combining macron]](https://www.rsc.org/images/entities/b_char_0052_0304.gif) ,Ω) can be calculated directly from the ab initio electronic wavefunction.39,42,50 For ab initio wavefunctions constructed from Gaussian primitives, the calculation of f0α(q;
,Ω) can be calculated directly from the ab initio electronic wavefunction.39,42,50 For ab initio wavefunctions constructed from Gaussian primitives, the calculation of f0α(q;![[R with combining macron]](https://www.rsc.org/images/entities/b_char_0052_0304.gif) ,Ω) can be done semi-analytically,42 although numerical Fourier transforms of the electron density represented on a grid are also possible.42
,Ω) can be done semi-analytically,42 although numerical Fourier transforms of the electron density represented on a grid are also possible.42
The structure factor, Ĩn(q), can thus be calculated as a convolution of f0α(q;![[R with combining macron]](https://www.rsc.org/images/entities/b_char_0052_0304.gif) ,Ω) by the vibrational and rotational probability distributions,
,Ω) by the vibrational and rotational probability distributions,
| | 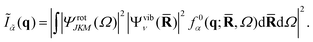 | (6) |
It is worth pointing out that the rotational averaging undertaken in
eqn (6) is different from the isotropic and incoherent rotational averaging normally used for thermal samples, first derived by Debye,
28 whereby |
f0α(
q;
![[R with combining macron]](https://www.rsc.org/images/entities/b_char_0052_0304.gif)
,
Ω)|
2 is uniformly integrated over all directions of
q.
51
The multiconfigurational electronic wavefunctions used to calculate the form factor in eqn (5) have been discussed at length in ref. 42, but we consider here in some further detail the vibrational and rotational wavefunctions that enter eqn (6) since these were not accounted for in the previous treatment. The vibrational wavefunctions are represented as harmonic oscillators, with normal modes and associated frequencies obtained from the Hessian of the ab initio molecular wavefunction at optimised energy minima. Since only small values of the vibrational quantum numbers ν are considered here, anharmonic regions of the potential energy surface are avoided. In terms of the rotational wavefunctions, we do not include rotational coupling, and can therefore fully determine the wavefunctions from the rotational constants and associated quantum numbers. Further details on the rotational wave functions used are given in the Appendix.
One important point regarding the rotational convolution in eqn (6) relates to the fact that the form factor f0α(q;![[R with combining macron]](https://www.rsc.org/images/entities/b_char_0052_0304.gif) ,Ω) depends on the orientation of the molecular frame in the laboratory (scattering) frame. When the electronic wavefunction rotates through the Euler angles Ω = (α,β,γ), the wavefunction expansion coefficients change. The rotated coefficients can be determined by re-calculating the electronic wavefunction in the rotated molecular frame, but this is inefficient. A slightly better approach is to rotate the electronic wavefunction directly, but this requires that the coefficients for all Gaussian primitives with l > 0 are transformed. Ultimately, the simplest and computationally most efficient approach is to rotate q rather than the molecule. This amounts to applying the inverse (i.e. transpose) of the rotation matrix to the vector q for each set of rotation angles (α,β,γ), while leaving the electronic wavefunction fixed in the original molecular frame used in the ab initio calculation. An attempt to illustrate the equivalence of these two scenarios, i.e. rotating the molecule versus rotating q, is shown in Fig. 1.
,Ω) depends on the orientation of the molecular frame in the laboratory (scattering) frame. When the electronic wavefunction rotates through the Euler angles Ω = (α,β,γ), the wavefunction expansion coefficients change. The rotated coefficients can be determined by re-calculating the electronic wavefunction in the rotated molecular frame, but this is inefficient. A slightly better approach is to rotate the electronic wavefunction directly, but this requires that the coefficients for all Gaussian primitives with l > 0 are transformed. Ultimately, the simplest and computationally most efficient approach is to rotate q rather than the molecule. This amounts to applying the inverse (i.e. transpose) of the rotation matrix to the vector q for each set of rotation angles (α,β,γ), while leaving the electronic wavefunction fixed in the original molecular frame used in the ab initio calculation. An attempt to illustrate the equivalence of these two scenarios, i.e. rotating the molecule versus rotating q, is shown in Fig. 1.
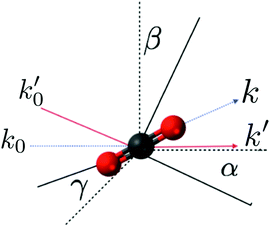 |
| | Fig. 1 Schematic illustration of how the rotation of the molecule through Euler angles (α,β,γ) can be substituted by the inverse rotation of the momentum transfer vector q = k0 − k. The components k0 and k are transformed into k0′ and k′ by the inverse rotation matrix. In the figure the molecular and laboratory frames are rotated to show the equivalence of both rotations. The dashed lines represent the original axis and vectors, and the solid lines the final positions. | |
2.3 Effective electron density and IAM
One of the main reasons why elastic X-ray scattering is such an important tool for structure determination32 is that the form factor corresponds to a Fourier transform of the electron density, ρα(r;![[R with combining macron]](https://www.rsc.org/images/entities/b_char_0052_0304.gif) ,Ω),
,Ω),| | 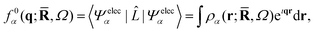 | (7) |
thus giving direct access to the “shape” of a molecule. In the independent atom model (IAM)32 the electron density is approximated by a sum of spherical single-atom densities, which yield the form factor as a sum of atomic form factors pre-fixed by a phase factor that depends on the relative positions of the atomic nuclei. The convenience of IAM stems from the fact that the atomic form factors have been calculated and tabulated for all future use,33 but the drawback is that distortions in the electron distribution, for instance due to molecular bonding or electronic excitations, are not included. This situation can to some extent be alleviated by the use of generalized form factors fitted to the distorted charge distributions for the bonded atoms,33,35,36 for instance to describe hydrogen atoms in organic molecular crystals.
An interesting point is that the electron density observed in a gas-phase experiment corresponds to the total molecular wavefunction and hence the structure factor Ĩn(q) in eqn (3) and (6). This structure factor is the Fourier transform of the total (effective) electron density,
| | 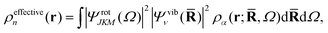 | (8) |
rather than the molecular electron density
ρα(
r;
![[R with combining macron]](https://www.rsc.org/images/entities/b_char_0052_0304.gif)
,
Ω) in
eqn (7). This changes the meaning of the “shape” of the molecule, with the rotational and vibrational wavefunctions beginning to play an important role. For instance, a homonuclear diatomic in the ground rotational and vibrational state appears as a hollow spherical shell, while the same molecule in the first excited vibrational state appears as two spherical shells, one inside the other. This clearly differs from the picture of an ensemble of “ball-and-stick” diatomic molecules, each in a random orientation, leading to an incoherent thermal averaging of |
f0α|.
28,51
3 Computational
The ab initio electronic structure calculations have been carried out using Molpro.52 The wavefunctions for ground state molecules have been calculated using Hartree–Fock (HF) theory, except for the CS2 molecule, where multiconfigurational self-consistent field theory (CAS-SCF) with an active space of (10,8), i.e. 8 electrons in 10 active orbitals, was used in combination with a 6-311G* basis for the rotational and 3-211G* for vibrational calculations. The smaller basis for the vibrational calculations is precipitated by the large numbers of displacements necessary to integrate all vibrational degrees of freedom numerically. The frequency calculations required for determining the harmonic vibrational wavefunctions have been carried out by solving for the Hessian for all degrees of freedom using CAS-SCF(10,8)/6-311G* in Molpro.52 Integration over rotational and vibrational wavefunctions has been carried out numerically using quadrature, with the wavefunctions determined using the rigid rotor and harmonic approximations respectively. Finally, the elastic scattering has been calculated using the AIXRD code.42
4 Results
4.1 Effect of basis size and comparison to IAM
We begin by examining the dependence of the calculated scattering signal on the ab initio basis set for non-relativistic ground state Hartree–Fock (HF) wavefunctions. We also include in the comparison the scattering signal calculated by the independent atom model (IAM) using tabulated atomic form factors.33 These are calculated from relativistic HF (RHF) wavefunctions,29,31,33 but the difference is negligible for the light elements under consideration here. In each case, we evaluate the absolute percent difference (relative error), |%ΔĨ(q)|, for rotationally averaged scattering,| | 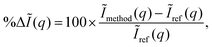 | (9) |
with the reference, Ĩref(q), defined as scattering from the HF/aug-cc-pVQZ wavefunction. The trigonal planar BF3 and the trigonal pyramidal NH3 molecules are used for the comparison, with their geometry optimised at the HF/aug-cc-pVQZ level using Molpro52 (RBF = 2.444a0 and RNH = 1.886a0). The absolute percent difference (relative error) is shown in Fig. 2 as a function of the momentum transfer q. Notably, the errors remain significant at large q, corresponding to high-resolution data, meaning that the resolution attainable from diffraction is adversely affected. It is also worth noting that the errors shown are rotationally averaged, meaning that for anisotropic samples such as molecular crystals or aligned gas-phase molecules the errors can be even greater for specific orientations of the vector q.
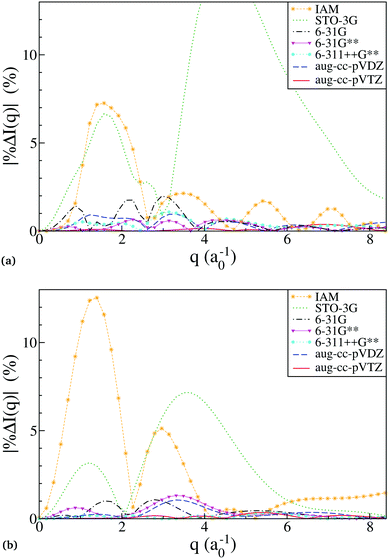 |
| | Fig. 2 The relative error in calculated scattering as a function of the basis used for the ab initio electronic wavefunction, shown as percent error, eqn (9), for molecules (a) BF3, and (b) NH3. The nuclei are frozen at the HF/aug-cc-pVQZ ground-state energy-optimised geometry, and the scattering signal is rotationally averaged. (a) The relative error in scattering calculations for the molecule BF3. The truncated STO-3G curve peaks at 15% at around q = 4.4. (b) The relative error in scattering calculations for the molecule NH3. | |
A striking feature in Fig. 2 is the poor performance by HF/STO-3G. This becomes less surprising if one considers that STO-3G reproduces the tabulated atomic form factors used in the IAM calculation poorly, while all the other basis sets, including 6-31G, converge to the tabulated form factors.53 Essentially, the STO-3G wavefunctions are insufficiently accurate even for single atoms. For all other basis sets, the discrepancy between the ab initio scattering and the IAM relates to the failure of the latter to account for the redistribution of valence electrons due to chemical bonding. The smaller discrepancy between IAM and ab initio scattering in BF3 compared to NH3 brings to light that IAM performs better the larger the fraction of core electrons compared to valence electrons.
Table 1 shows the maximum and mean errors in the scattering, with the mean calculated as,
| | 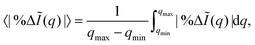 | (10) |
with the integration interval [
qmin,
qmax] = [0,8.3]
a0−1, while the error itself is calculated using
eqn (9) above. The average ratio of maximum to mean for the HF calculations is 3.1, while the ratio for IAM is 4.3, indicating that IAM is prone to greater systematic errors. The energy difference, Δ
E = |
E −
Eref|, of each
ab initio calculation relative the HF/aug-cc-pVTZ reference is also provided in
Table 1. If we use Δ
E as a proxy for the convergence of the
ab initio calculations, we see a clear correlation between Δ
E and the accuracy of the scattering. In BF
3 it correctly identifies the best and the poorest performers, with a slight outperformance by the 6-31G** calculation. In NH
3, Δ
E, correctly ranks the mean scattering error except for a swapping around of 6-31G and 6-31G**, which rank sixth and fifth in terms of energy, but fifth and sixth in terms of mean scattering convergence.
Table 1 Convergence and computational requirements for scattering from HF electronic wavefunctions calculated using various basis sets in molecules BF3 (top half) and NH3 (bottom half). Note that the ** and ++ basis sets are equivalent to * and + for molecules without hydrogen atoms, such as BF3. The ΔE for NH3 is given in units of 10−1 x Eh
| Method |
Error (%) |
ΔE |
N
g
|
N
gp
|
Speed up |
| Mean |
Max |
(Eh) |
(×103) |
| BF3 |
| IAM |
1.75 |
7.3 |
— |
— |
41k |
| STO-3G |
6.36 |
15 |
4.69 |
1.0 |
10 |
68 |
| 6-31G |
0.54 |
2.0 |
0.27 |
1.4 |
21 |
31 |
| 6-31G** |
0.26 |
0.7 |
0.16 |
1.8 |
32 |
20 |
| 6-311++G** |
0.39 |
1.1 |
0.07 |
2.3 |
51 |
13 |
| aug-cc-pVDZ |
0.41 |
1.0 |
0.13 |
4.3 |
105 |
6 |
| aug-cc-pVTZ |
0.11 |
0.4 |
0.02 |
8.1 |
259 |
3 |
| aug-cc-pVQZ |
0 |
0 |
0 |
14 |
655 |
1 |
|
|
| NH3 |
| IAM |
2.94 |
13 |
— |
— |
16k |
| STO-3G |
2.54 |
7.2 |
7.73 |
0.1 |
1.5 |
173 |
| 6-31G |
0.35 |
1.1 |
0.62 |
0.2 |
3 |
87 |
| 6-31G** |
0.38 |
1.3 |
0.29 |
0.2 |
6 |
43 |
| 6-311++G** |
0.12 |
0.3 |
0.10 |
0.3 |
10 |
26 |
| aug-cc-pVDZ |
0.31 |
1.1 |
0.20 |
0.6 |
19 |
14 |
| aug-cc-pVTZ |
0.11 |
0.4 |
0.04 |
1.2 |
74 |
4 |
| aug-cc-pVQZ |
0 |
0 |
0 |
2.2 |
260 |
1 |
4.2 Scaling of AIXRD calculations
The ab initio scattering calculations essentially scale as the number of terms that have to be evaluated, which in turn depend on the size of the basis used to represent the electronic wavefunction. Table 1 shows the number of primitive Gaussian functions per calculation, Ng, and more importantly, the number of non-zero unique Gaussian products, Ngp. The computational effort to calculate the scattering scales linearly with the number of unique non-zero Gaussian products, Ngp, rather than the actual number of Gaussian primitives, Ng. For BF3, Ngp ≈ Ng1.38, and for NH3Ngp ≈ Ng1.58.
Table 1 also shows the speed-up, i.e. the time required for each scattering calculation relative the reference aug-cc-pVTZ wavefunction (the time for the ab initio calculation itself is not included in the comparison). It is readily apparent that the IAM is several orders of magnitude faster than calculation of the scattering directly from the ab initio wavefunction, and more than 104 times faster than the reference calculation. However, this comparison verges on the meaningless, since IAM is based on tabulated values and thus does not require a scattering calculation at all, but merely interpolation and summation of tabulated values.
Pragmatically, it is worth noticing that in both molecules all the basis sets except STO-3G have a mean error of less than 0.6%, showing that unless supreme accuracy is required, any medium-sized basis set is a reasonable choice. The 6-31G** appears to lie in a sweet spot of low percent error and high computational efficiency, but the 6-31G basis set could also be used if an even larger speed-up is required. For higher accuracy, one would have to resort to post-HF methods (e.g. CASSCF or CASPT2) that better account for electron correlation. Examples where this becomes important include ground states with biradical character or excited electronic states (as in Section 4.3.4). Notably, post-HF methods follow the same scaling with basis size as discussed above, but with a larger prefactor. However, we emphasize that HF already delivers a significant improvement on IAM, at least for ground-state molecules containing light elements.
4.3 Molecular scattering images
The discussion in the following sections hinges around calculated X-ray scattering images that are 2D projections of the detector image presuming that the entire Ewald sphere is covered by the detector. The images are thus shown as polar plots in terms of the polar angle (0 ≤ ϕ < 2π) and the radial angle (0 ≤ θ ≤ π) that specify the deflection of the scattered wavevector k relative the incident wavevector k0. The center of the image thus corresponds to θ = 0 (forward-scattering) and the outer rim to θ = π (back-scattering). Since q = 2k0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/2, we have that qmax = 2k0 at θ = π. All images are shown without the outer absolute square in eqn (6) to make it easier to discern features at large values of q in the figures. In several instances, difference images are shown to emphasize the changes in the scattering pattern upon excitation to a specific state. These difference images are calculated by subtracting a reference image from the excited state scattering image, with the subtraction done between images sans the absolute square. In the following, we first examine the effect of molecular symmetry on the scattering images (Section 4.3.1), and then move on to examine the different partial contributions to the scattering in the CS2 molecule (Sections 4.3.2–4.3.4).
θ/2, we have that qmax = 2k0 at θ = π. All images are shown without the outer absolute square in eqn (6) to make it easier to discern features at large values of q in the figures. In several instances, difference images are shown to emphasize the changes in the scattering pattern upon excitation to a specific state. These difference images are calculated by subtracting a reference image from the excited state scattering image, with the subtraction done between images sans the absolute square. In the following, we first examine the effect of molecular symmetry on the scattering images (Section 4.3.1), and then move on to examine the different partial contributions to the scattering in the CS2 molecule (Sections 4.3.2–4.3.4).
4.3.1 Symmetry and centrosymmetry.
The symmetry of a molecule relative the X-ray beam is reflected in the scattering image. For instance, if the molecule has a rotational symmetry axis parallel to the incoming X-rays, this axis is replicated in the scattering.42 An interesting feature present in many of the scattering images shown here is centrosymmetry, i.e. the scattering signal for (ϕ,θ) and (ϕ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
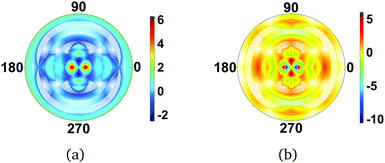
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) π,θ) is identical. A curious consequence of the centrosymmetry is that any odd-numbered rotational axis is doubled, as can be seen in the scattering patterns for BF3 (D3h point group) and the cyclopentadienyl anion, C5H5− (D5h point group) in Fig. 3. The 3-fold axis for BF3 and the 5-fold axis for C5H5− become 6- and 10-fold axes. In contrast, an even-numbered rotational axis, e.g. C4, will result in the same rotational C4 axis in the scattering image, with no apparent doubling since the images are already centrosymmetric. The mathematical background to this phenomenon is elaborated in the Appendix.
π,θ) is identical. A curious consequence of the centrosymmetry is that any odd-numbered rotational axis is doubled, as can be seen in the scattering patterns for BF3 (D3h point group) and the cyclopentadienyl anion, C5H5− (D5h point group) in Fig. 3. The 3-fold axis for BF3 and the 5-fold axis for C5H5− become 6- and 10-fold axes. In contrast, an even-numbered rotational axis, e.g. C4, will result in the same rotational C4 axis in the scattering image, with no apparent doubling since the images are already centrosymmetric. The mathematical background to this phenomenon is elaborated in the Appendix.
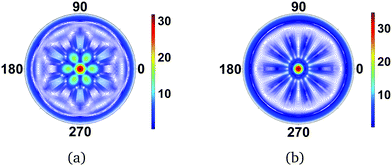 |
| | Fig. 3 Scattering images for (a) BF3 (D3h point group) and (b) C5H5− (D5h point group). The planar molecules are perpendicular to the incoming X-ray and the resulting diffraction image thus doubles the molecular rotational symmetry axis due to centrosymmetry. The value of qmax is 15.8 Å−1. | |
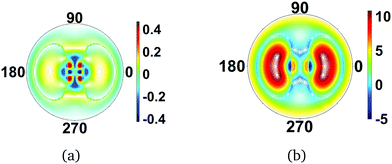
A necessary condition for the centrosymmetry is that the molecule contains a mirror plane orthogonal to the incoming X-ray beam, as for instance is the case for the planar molecules in the two examples above. In contrast, Fig. 4 shows the scattering image for NF3, a strongly-scattering ammonia analogue with C3v point group symmetry. The additional interference due to the out-of-plane nitrogen atom diminishes the centrosymmetry in the image, but the fundamental C3 axis remains. Proceeding to a molecule with no discernable symmetry, 1,3-cyclohexadiene (C1 point group), there is a corresponding absence of symmetry in the scattering image. Note, however, that some remnant of ‘not-quite’ centrosymmetry remains even in this image. This simply reflects the approximate degree of mirror symmetry perpendical to the incoming X-ray.
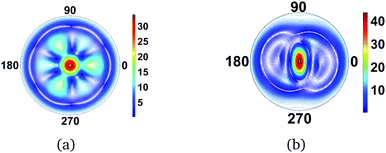 |
| | Fig. 4 Scattering images for (a) NF3 (C3v point group) and (b) 1,3-cyclohexadiene (C1 point group). The main plane of the molecules is aligned perpendicular to the incoming X-ray. The absence of a mirror plane orthogonal to the incoming X-rays removes or diminishes centrosymmetry in the images. The value of qmax is 15.8 Å−1. | |
4.3.2 CS2 vibrations.
We now examine the effect of vibrational states on the scattering pattern of CS2. The rotational states are not included at this stage, in order to keep the comparison as simple as possible. The modulations of the static scattering patterns will come from the changes in the distribution of relative atomic positions in the excited vibrational states, with scope from interferences due to the nodes in the vibrational wavefunctions. We consider the molecule CS2. In the ground state CS2 is linear with a C–S bond distance of 1.584 Å. The vibrational wavefunctions are calculated in the harmonic approximation. The normal mode frequencies are calculated at the CAS(10,8)-SCF/6-311G* level of theory, and compare favourably with experimental values from the NIST database (see Table 2), with the differences less than 3%.
Table 2 Comparison between experimental and calculated frequencies for CS2 in the electronic ground state. The frequencies have been calculated using the analytical Hessian at the CAS(10,8)-SCF/6-311G* level of theory
| Exp. (cm−1) |
Calc. (cm−1) |
Δ (%) |
Mode |
|
Note that the bending mode is doubly degenerate.
|
| 1535 |
1491 |
2.9 |
Symmetric |
| 658 |
652 |
1.0 |
Asymmetric |
| 397 |
399 |
0.6 |
Bendinga |
The difference scattering images for CS2 shown in Fig. 5 are calculated from the full CAS-SCF electronic wavefunction and the vibrational wavefunctions. In each image, the vibrational wavefunction has one quantum of excitation in a different vibrational mode. The symmetric, Fig. 5(a), and asymmetric, Fig. 5(b), stretches give rise to overall similar changes in the scattering pattern, but the asymmetric stretch has additional interferences rings due to the broken symmetry in the C–S bond distances. Likewise, the two bending modes generate very similar scattering patterns. The differences here are due to the bending mode in Fig. 5(c) being oriented perpendicular to the incoming X-ray (in-plane), while it is directed toward the incoming X-ray (out-of-plane) in Fig. 5(d). Whether these two modes can be distinguished is therefore dependent on the degree of orientation of the molecule. It is worth pointing out that since the S atoms are comparatively heavy, the vibrations in CS2 have small amplitudes. In terms of the asymmetric stretch and the bending modes, one can essentially consider these vibrations as small displacements of the central C atom relative two stationary S atoms. The changes in the scattering pattern due to vibrational state are therefore only on the order of 1% or less.
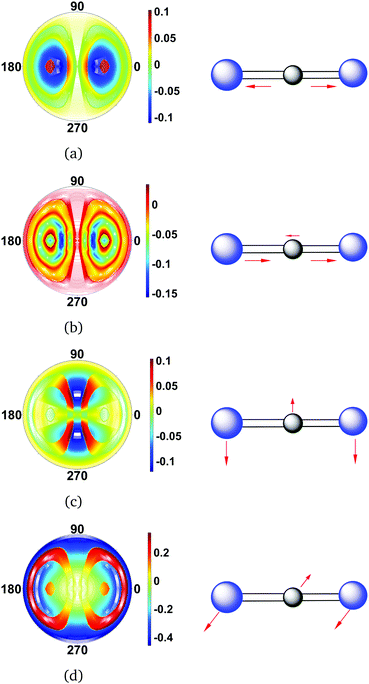 |
| | Fig. 5 Difference scattering images for each of the normal vibrational modes of CS2. The vibrational states are specified as |ν1ν2ν3ν4〉vib, with the order of vibrational quantum numbers corresponding to descending energy (see Table 2). The following vibrational states are considered: (a) symmetric stretch |1000〉vib, (b) asymmetric stretch |0100〉vib, (c) first bending mode |0010〉vib, and (d) second bending mode |0001〉vib. The vibrational ground state |0000〉vib is taken as reference, and the value of qmax is 5.3 Å−1 in each image. Note that the molecules are perfectly aligned with the vibration orthogonal to the direction of the incoming X-ray in (c) and parallel in (d). | |
4.3.3 CS2 rotations.
Next, we examine the effect of different rotational states calculated in the rigid rotor approximation on the scattering images. We continue to consider the CS2 molecule. Since this symmetric top molecule is linear, the K quantum number is zero. Effectively, this reduces the rotational wavefunctions to spherical harmonics. The different values of J and M produce a various types of precession around the laboratory frame z-axis, leading to probability distributions that correspond to the spherical harmonics.
The calculated difference images are shown in Fig. 6. The first overall observation is that the effect of changes in rotational quantum state has a strong impact on the scattering image, with the signal changing more than an order of magnitude in specific scattering directions. Examining the individual images in Fig. 6, we see that the images fall into several categories. Fig. 6(a), (d), and (e), are quite similar. They correspond to scattering from dumb-bell or p-orbital type shapes of the rotational wavefunction, with Fig. 6(d) the most elongated in real space and Fig. 6(a) the least. The scattering images in Fig. 6(b), (c) and (f), on the other hand, correspond to doughnut-like shapes, with Fig. 6(f) the flattest in real space and Fig. 6(b) and (c) identical since the difference between them is a phase-factor in the wavefunction which does not affect the scattering. Looking at the overall effect of the rotational states on the scattering, it is greater than that of vibrations.
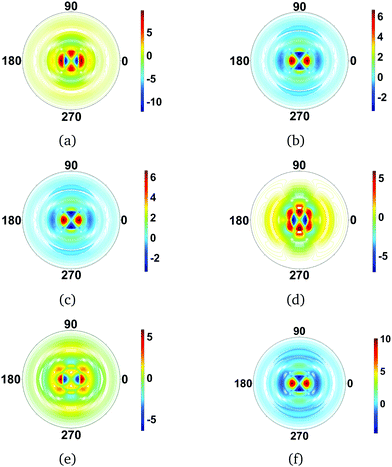 |
| | Fig. 6 Difference scattering images for rotational states in CS2, with the ground rotational state |000〉rot taken as reference. The following rotational states |JKM〉rot are considered: (a) |100〉rot, (b) |101〉rot, (c) |10−1〉rot, (d) |200〉rot, (e) |201〉rot and (f) |202〉rot. For the linear CS2 molecule, with K = 0 by definition, the images essentially reflect the shape of the spherical harmonics, with each of the rotational states leaving a strong signature in the scattering. The value of qmax is 5.3 Å−1 throughout. | |
4.3.4 CS2 rotational, vibrational, and electronic states.
We move on to simultaneously considering both rotational and vibrational states. Fig. 7 shows difference images for the |101〉rot|1111〉vib and |100〉rot|1111〉vib states. The trends observed when considering each type of motion separately, as in previous sections, are preserved. The rotational states lead to strong, order of magnitude, changes in specific scattering directions (translating into specific pixels on the detector), while the vibrational states leave much weaker signatures on the order of <1%, which is unsurprising given that only small harmonic oscillations around the equilibrium geometry are considered. If larger amplitude motion were included, the changes in molecular geometry would indeed leave a very strong signature in the scattering and eventually dominate all other contributions.
 |
| | Fig. 7 Difference scattering images for CS2 in the electronic ground state for combined rotational–vibrational molecular states (a) |101〉rot|1111〉vib, and (b) |100〉rot|1111〉vib. The reference scattering image corresponds to the overall ground state (|000〉rot|0000〉vib). The shape of the scattering pattern is similar in the two examples, but with inverted intensity. The value of qmax = 5.3 Å−1. | |
As the total molecular wavefunction is discussed in this section, we also consider changes in the electronic state of the molecule. In Fig. 8(a) the changes in scattering pattern due to a vertical excitation from the CS2 ground X state to the bright excited B state are shown. The redistribution of the electrons in the molecule leads to a distinct change in the scattering pattern, not quite on the same order as the effect of rotations, but significantly stronger than the effect of small equilibrium vibrations. It is important to point out, however, that since the equilibrium geometry of the electronic B state is different from the ground X state, nuclear motion necessarily ensues upon excitation, and these large-amplitude vibrations have a strong effect on the diffraction pattern. It is therefore non-trivial in general to separate the contributions from electronic redistribution and nuclear motion. As an illustration, Fig. 8(b) shows the scattering from the molecule in the electronic B state at the B-state equilibrium geometry, rather than the ground state geometry. The change in geometry gives a very large change in the scattering, and overwhelms the effect of rotation and equilibrium vibrations.
 |
| | Fig. 8 Difference scattering images for CS2 in the optically bright excited electronic |B〉 state and the electronic ground state |X〉 in (a) the ground state geometry, i.e. vertical excitation, and (b) the B state equilibrium geometry. The image (b) emphasizes the effect of molecular geometry on the scattering images. The value of qmax = 5.3 Å−1, and the incoming X-ray is perpendicular to the plane of the molecule in both cases. | |
5 Conclusions
We have examined X-ray diffraction images from molecules in specific electronic, vibrational, and rotational states, and find that the scattering images carry distinct fingerprints of the total molecular wavefunction. The differences in intensity between different rotational states are an order of magnitude in specific directions of scattering (i.e. towards particular positions on the detector). In contrast, the changes due to different vibrational states are modest, about 1% or less. This is a consequence of the fact that low-lying vibrational states are considered, implying small and local nuclear displacements around equilibrium positions and hence no net change in molecular geometry. A technical point is that the integration over the multidimensional vibrational wavefunction is time-consuming, and given the small nuclear displacements considered in the harmonic approximation one could, in the future, examine the possibility of interpolating the electronic wavefunction coefficients. Electronic states also affect the scattering,42,54,55 with effects comparable to those of rotations in the presence of significant orientation or alignment. However, in most situations electronic excitation leads to changes in the nuclear geometry,56,57 since the potential energy surfaces associated with different electronic states are rarely parallel. This leads to very strong changes in the scattering, associated with the change in molecular geometry. An interesting point is that the greater the redistribution of electrons during vertical excitation of the molecule, and hence stronger signature of the electronic state, the greater is the likely effect on the nuclear motion, which itself bears an even stronger signature. Overall, it is apparent that disentangling different contributions, especially the vibrational and the electronic, to the scattering is not trivial.
The AIXRD calculations, which yield the elastic X-ray scattering directly from the ab initio wavefunction, convincingly show the shortcomings of the simple but widely used independent atom model (IAM). The discrepancy between IAM and the more accurate AIXRD calculations persists even if full rotational averaging is considered. Although fitted generalized form factors can be used to address the deficiencies inherent in IAM, advances in computing and modern electronic structure codes make AIXRD calculations feasible, with large potential gains in accuracy and generality. It is particularly encouraging that the description of the scattering improves significantly already at quite modest levels of theory. This suggests that ab initio HF calculations with reasonable basis sets or even density functional theory (DFT) could be used to determine molecular form factors for ground state molecules. A practical point is that the energy convergence of ab initio electronic structure calculations serves as an adequate proxy for the quality of the wavefunction and thus the calculated scattering. Future work will examine if X-ray scattering may resolve more subtle aspects of fully coupled rovibronic states using higher-level spectroscopic-accuracy theory.58–60 Finally, given recent advances in ultrafast X-ray scattering,4,61,62 the greatest value of the current study is that it demonstrates that AIXRD can be effectively combined with calculations that include nuclear degrees of freedom, thus opening the door for calculating the signals from ultrafast dynamics.4,61,63
Appendix
Image symmetry and Friedel's law
The centrosymmetry or near-centrosymmetry observed in many of the scattering images relates to the mirror symmetry of the molecule relative the direction of the incoming X-ray. Assuming that X-rays enter along the z-axis, k0 = (0,0,k0), a pair of momentum transfer vectors corresponding to two points on the opposite sides of the detector are given by q = (qx,qy,qz) and q′ = (−qx,−qy,qz). Centrosymmetry requires that |F(q′)|2 = |F(q)|2.
If we express the electron density as a sum over Gaussian functions, each a product of x, y, and z components,42
| | 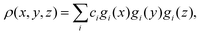 | (11) |
the Fourier transform of the density for the
q′ vector becomes,
| | 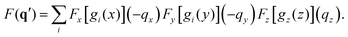 | (12) |
Friedel's law for Fourier transforms,
F(
q) =
F*(−
q), is valid for real-valued functions such as the electron density. It applies to the
x and
y components in
eqn (12), but not the
z-component. However, if the overall electron density is symmetric with regards to the
z-axis, the net Fourier transform along the
z-axis must be real-valued (in practice this occurs by collecting symmetry-related pairs in the sum in
eqn (12) with identical
x and
y components and complex conjugate
z components). In that situation the Fourier transform of the
z-component does not invalidate Friedel's law for the overall expression and we obtain
F*(
q′) =
F(
q), which in turn implies |
F(
q′)|
2 = |
F(
q)|
2 as required for centrosymmetry.
It is worth noting that Friedel's law always applies to the x and y components (since the electron density is real), and that the degree of centrosymmetry only relates to the degree of symmetry along the z-axis, with strict centrosymmetry requiring a mirror plane orthogonal to the incoming X-ray. In fact, a quicker and more elegant way to arrive at this result is to consider that the mirror symmetry operation, when present in the molecule, can be applied to the q′ vector such that (−qx,−qy,qz) → (−qx,−qy,−qz), at which point the three-dimensional version of Friedel's law, F(q) = F*(−q), applies.
Rotational matrix
Rotations correspond to changes in the frame (coordinate system) given by the Euler angles (α,β,γ) show in Fig. 9. Coordinates in (ξ,η,ζ) axis systems can be related to the (x,y,z) system by the standard rotation matrix (see eqn (10-5) and (10-7) in ref. 64 or Table I-1 in ref. 65),| | 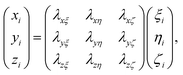 | (13) |
with the column vectors of the rotation matrix λ defined as,| | 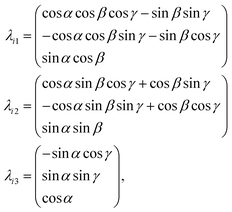 | (14) |
where (α,β,γ) are the Euler angles specified in Fig. 9. Since the rotation matrix λ is unitary, inverse rotations are given by the transpose of the matrix.
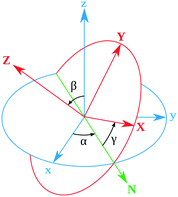 |
| | Fig. 9 Definition of the rotational Euler angles (α,β,γ). The two frames are related by the rotation matrix (see Appendix). | |
Classification of rigid rotor wavefunctions
The general form of this mathematical expression can be obtained calculating the rotational Hamiltonian,| | | Ĥrot = ℏ2(AeJa2 + BeJb2 + CeJc2), | (15) |
where Ae, Be and Ce are the rotational constants of the molecule and Jα are the principal inertial axes of the equilibrium configuration. The classification of molecules according to their moments of inertia is given in Fig. 10. Depending on the moments of inertia around the three axes of rotation, the molecules are classified as either spherical, symmetric and asymmetric tops. Each of these classes behaves differently under rotation and thus have different rotational wavefunctions.
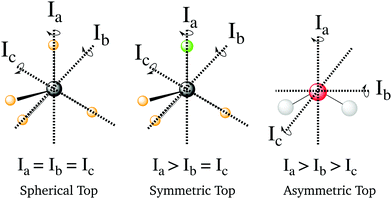 |
| | Fig. 10 Representation of the different types of molecules depending on their rotational symmetry. The relative size of the different moments of inertia, In, determines the rotational symmetry of a molecule. The spherical tops are characterized by Ia = Ib = Ic, the symmetric tops by two identical moments of inertia, subdivided into oblate symmetric tops (disc-shaped), Ia = Ib > Ic, and prolate symmetric tops (cylindrical), Ia > Ib = Ic, and finally asymmetric tops have Ia > Ib > Ic. | |
Rotational wavefunctions for spherical and symmetric tops
These two classes of molecules share the same wavefunctions to describe their rotational states and can be expressed as a combination of spherical harmonics multiplied by a phase. The Schrödinger equation for a prolate symmetric top is,| | | ℏ−2[AeJa2 + Be(Jb2 + Jc2)]Φrot(θ,ϕ,χ) = ErotΦrot(θ,ϕ,χ). | (16) |
The angular momentum operators Ĵ2, Ĵχ, and Ĵz commute with each other and their eigenfunctions are the so-called rotation matrices. If we select the principal axis of rotation as z (known as the Ir convention), we can rewrite the equation in terms of angular momentum operators,| | | ℏ2[BeĴ2 + (Ae − Be)Ĵz2]Φrot(θ,ϕ,χ) = ErotΦrot(θ,ϕ,χ). | (17) |
Using the rotation matrices and eigenvalues of the operators we can obtain the representation of the wavefunction for a prolate symmetric top,| | 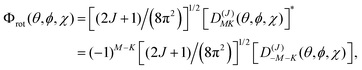 | (18) |
where D(J)MK are the rotation matrices and J, K and M the rotational quantum numbers, with |K| and |M| having allowed values ≤J. The equation can be rewritten as a function of the Euler angles (θ,ϕ,χ),| | 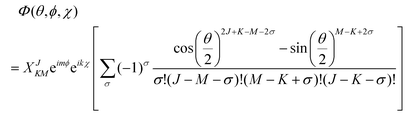 | (19) |
where XJKM is a normalization constant with the form,| | | XJKM = [(J + M)!(J − M)!(J + K)!(J − K)!(2J + 1)/(8π2)]1/2. | (20) |
It is important to note that this wavefunction is only valid if our molecule has its origin of coordinates in the center of mass and the principal axis of symmetry is oriented along the z-axis. Other conventions can be used and they depend on the orientation of the coordinate system and the molecular symmetry (IIIr).
The Hamiltonian form will change depending on the type of molecule we choose but the wavefunction will be the same as for prolate symmetric top if the system has at least two axis of inertia with the same value (spherical, prolate and oblate symmetric top molecules).
Rotational wavefunctions for asymmetric top molecules
Asymmetric top molecules, such as water, are the most common. In this class, all three axes of inertia are different. To evaluate the wavefunction of an asymmetric molecule we need a linear combination of symmetric top wavefunctions (|JKM〉),| | | Φ(θ,ϕ,χ) = a|JKM〉 + b|J′K′M′〉. | (21) |
To obtain these basis and their coefficients we need to diagonalize the rotational Hamiltonian expressed in the |JKM〉 basis,| | | Ĥrot = ℏ−2[[(Be + Ce)/2]Ĵ2 + [Ae − (Be + Ce)/2]Ĵz2 + [(Be − Ce)/4][(Ĵ+M)2 + (Ĵ−M)2]]. | (22) |
For each J we will have (2J + 1) states in K and M, the basis need to be build as ±K linear combinations to be eigenfunctions of the operators presented in Hrot. We can classify them by the symbols O+, O−, E+ and E− depending on the value of K (even or odd) and the sign of the linear combination (+ or −). The resultant basis functions can be directly diagonal elements of the Hamiltonian and therefore eigenvectors of it. In case we have off-diagonal elements we need to proceed with the diagonalisation of the system, obtaining linear combination of basis as rotational wavefunctions (see Table 3).
Table 3 Asymmetric top wavefunctions for the three first J values and all K. The nomenclature excludes M, since the equations are independent of M. E, O, + and − depend on whether K is odd or even and the positive or negative linear combination of |J,K,M〉. The J = 0 and J = 1 cases are nearly trivial, but calculation of J = 2 requires diagonalization of the rotational Hamiltonian matrix
|
J
|
Wavefunction |
| 0 |
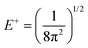
|
|
|
| 1 |
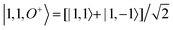
|
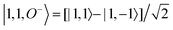
|
| |1, 0, E+〉 = |1, 0〉 |
|
|
| 2 |
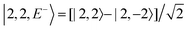
|
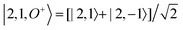
|
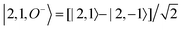
|
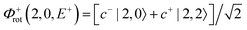
|
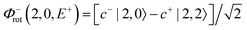
|
|
|
|
c± |
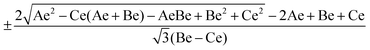
|
Acknowledgements
AK and AMC acknowledge funding from the European Union (FP7-PEOPLE-2013-CIG-NEWLIGHT) and the hospitality of Prof. Roland Lindh (Uppsala University). AK further acknowledges the Leverhulme Trust (RPG-2013-365) and sabbatical support from Magnus Bergvalls Stiftelse (Sweden).
References
- M. Dell'Angela, T. Anniyev, M. Beye, R. Coffee, A. Fohlisch, J. Gladh, T. Katayama, S. Kaya, O. Krupin, J. LaRue, A. Mogelhoj, D. Nordlund, J. K. Norskov, H. Oberg, H. Ogasawara, H. Ostrom, L. G. M. Pettersson, W. F. Schlotter, J. A. Sellberg, F. Sorgenfrei, J. J. Turner, M. Wolf, W. Wurth and A. Nilsson, Science, 2013, 339, 1302 CrossRef PubMed.
- M. Beye, H. Öberg, H. Xin, G. L. Dakovski, M. Dell'Angela, A. Föhlisch, J. Gladh, M. Hantschmann, F. Hieke, S. Kaya, D. Kühn, J. LaRue, G. Mercurio, M. P. Minitti, A. Mitra, S. P. Moeller, M. L. Ng, A. Nilsson, D. Nordlund, J. Norskov, H. Öström, H. Ogasawara, M. Persson, W. F. Schlotter, J. A. Sellberg, M. Wolf, F. Abild-Pedersen, L. G. M. Pettersson and W. Wurth, J. Phys. Chem. Lett., 2016, 7, 3647–3651 CrossRef CAS PubMed.
- V. S. Petrović, M. Siano, J. L. White, N. Berrah, C. Bostedt, J. D. Bozek, D. Broege, M. Chalfin, R. N. Coffee, J. Cryan, L. Fang, J. P. Farrell, L. J. Frasinski, J. M. Glownia, M. Gühr, M. Hoener, D. M. P. Holland, J. Kim, J. P. Marangos, T. Martinez, B. K. McFarland, R. S. Minns, S. Miyabe, S. Schorb, R. J. Sension, L. S. Spector, R. Squibb, H. Tao, J. G. Underwood and P. H. Bucksbaum, Phys. Rev. Lett., 2012, 108, 253006 CrossRef PubMed.
- M. P. Minitti, J. M. Budarz, A. Kirrander, J. S. Robinson, D. Ratner, T. J. Lane, D. Zhu, J. M. Glownia, M. Kozina, H. T. Lemke, M. Sikorski, Y. Feng, S. Nelson, K. Saita, B. Stankus, T. Northey, J. B. Hastings and P. M. Weber, Phys. Rev. Lett., 2015, 114, 255501 CrossRef CAS PubMed.
- K. H. Kim, J. G. Kim, S. Nozawa, T. Sato, K. Y. Oang, T. W. Kim, H. Ki, J. Jo, S. Park, C. Song, T. Sato, K. Ogawa, T. Togashi, K. Tono, M. Yabashi, T. Ishikawa, J. Kim, R. Ryoo, J. Kim, H. Ihee and S. i. Adachi, Nature, 2015, 518, 385 CrossRef CAS PubMed.
- R. Neutze, R. Wouts, D. van der Spoel, E. Weckert and J. Hajdu, Nature, 2000, 406, 752 CrossRef CAS PubMed.
- J. R. Helliwell, Science, 2013, 339, 146 CrossRef CAS PubMed.
- E. F. Garman, Science, 2014, 343, 1102 CrossRef CAS PubMed.
- C. S. Barrett, Phys. Rev., 1928, 32, 22 CrossRef CAS.
- P. Debye, L. Bewilogua and F. Ehrhardt, Phys. Z., 1929, 30, 84 CAS.
- E. O. Wollan, Phys. Rev., 1931, 37, 862 CrossRef CAS.
-
M. H. Pirenne, The Diffraction of X-Rays and Electrons by Free Molecules, Cambridge University Press, London, 1946 Search PubMed.
- D. R. Chipman and L. D. Jennings, Phys. Rev., 1963, 132, 728 CrossRef CAS.
- M. P. Minitti, J. M. Budarz, A. Kirrander, J. Robinson, T. J. Lane, D. Ratner, K. Saita, T. Northey, B. Stankus, V. Cofer-Shabica, J. Hastings and P. M. Weber, Faraday Discuss., 2014, 171, 81 RSC.
- J. M. Budarz, M. P. Minitti, D. V. Cofer-Shabica, B. Stankus, A. Kirrander, J. B. Hastings and P. M. Weber, J. Phys. B, 2016, 49, 034001 CrossRef.
- B. Stankus, J. M. Budarz, A. Kirrander, D. Rogers, J. Robinson, T. J. Lane, D. Ratner, J. Hastings, M. P. Minitti and P. M. Weber, Faraday Discuss., 2016, 194, 525–536 RSC.
- J. Küpper, S. Stern, L. Holmegaard, F. Filsinger, A. Rouzée, A. Rudenko, P. Johnsson, A. V. Martin, M. Adolph, A. Aquila, S. Bajt, A. Barty, C. Bostedt, J. Bozek, C. Caleman, R. Coffee, N. Coppola, T. Delmas, S. Epp, B. Erk, L. Foucar, T. Gorkhover, L. Gumprecht, A. Hartmann, R. Hartmann, G. Hauser, P. Holl, A. Hömke, N. Kimmel, F. Krasniqi, K.-U. Kühnel, J. Maurer, M. Messerschmidt, R. Moshammer, C. Reich, B. Rudek, R. Santra, I. Schlichting, C. Schmidt, S. Schorb, J. Schulz, H. Soltau, J. C. H. Spence, D. Starodub, L. Strüder, J. Thøgersen, M. J. J. Vrakking, G. Weidenspointner, T. A. White, C. Wunderer, G. Meijer, J. Ullrich, H. Stapelfeldt, D. Rolles and H. N. Chapman, Phys. Rev. Lett., 2014, 112, 083002 CrossRef.
- B. Xie, L. Zhu, K. Yang, B. Zhou, N. Hiraoka, Y. Cai, Y. Yao, C. Wu, E. Wang and D. Feng, Phys. Rev. A: At., Mol., Opt. Phys., 2010, 82, 032501 CrossRef.
- Y.-W. Liu, X.-X. Mei, X. Kang, K. Yang, W.-Q. Xu, Y.-G. Peng, N. Hiraoka, K.-D. Tsuei, P.-F. Zhang and L.-F. Zhu, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 89, 014502 CrossRef.
- L. Zhu, L. Wang, B. Xie, K. Yang, N. Hiraoka, Y. Cai and D. Feng, J. Phys. B, 2011, 44, 025203 CrossRef.
- Y.-G. Peng, X. Kang, K. Yang, X.-L. Zhao, Y.-W. Liu, X.-X. Mei, W.-Q. Xu, N. Hiraoka, K.-D. Tsuei and L.-F. Zhu, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 89, 032512 CrossRef.
- C. Vallance, Phys. Chem. Chem. Phys., 2011, 13, 14427 RSC.
- G. Sitz and R. L. Farrow, J. Chem. Phys., 1994, 101, 4682–4687 CrossRef CAS.
- A. D. Rudert, J. Martin, W.-B. Gao, J. B. Halpern and H. Zacharias, J. Chem. Phys., 1999, 111, 9549 CrossRef CAS.
- N. C. M. Bartlett, D. J. Miller, R. N. Zare, D. Sofikitis, P. T. Rakitzis and A. J. Alexander, J. Chem. Phys., 2008, 129, 084312 CrossRef PubMed.
- N. Mukherjee and R. N. Zare, J. Chem. Phys., 2011, 135, 024201 CrossRef PubMed.
- N. Mukherjee, W. Dong, J. Harrison and R. Zare, J. Chem. Phys., 2013, 138, 051101 CrossRef PubMed.
- P. Debye, Ann. Phys., 1915, 46, 809 CrossRef CAS.
- P. A. Doyle and P. S. Turner, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1968, 24, 390–397 CrossRef CAS.
- J. H. Hubbell, W. J. Veigele, E. A. Briggs, R. T. Brown, D. T. Cromer and R. J. Howerton, J. Phys. Chem. Ref. Data, 1975, 4, 471 CrossRef CAS.
- A. G. Fox, M. A. O'Keefe and M. A. Tabbernor, Acta Crystallogr., Sect. A: Found. Crystallogr., 1989, 45, 786–793 CrossRef.
-
D. McMorrow and J. Als-Nielsen, Elements of Modern X-Ray Physics, Wiley-Blackwell, 2nd edn, 2011 Search PubMed.
-
International Tables for Crystallography Volume C: Mathematical, Physical and Chemical Tables, ed. E. Prince, Wiley, 3rd edn, 2006 Search PubMed.
- A. O. Dohn, E. Biasin, K. Haldrup, M. M. Nielsen, N. E. Henriksen and K. B. Møller, J. Phys. B, 2015, 48, 244010 CrossRef.
- R. F. Stewart, J. Bentley and B. Goodman, J. Chem. Phys., 1975, 63, 3786 CrossRef CAS.
- J. Bentley and R. F. Stewart, J. Chem. Phys., 1975, 63, 3794 CrossRef CAS.
- R. F. Stewart, E. R. Davidson and W. T. Simpson, J. Chem. Phys., 1965, 42, 3175 CrossRef CAS.
- J. Epstein and R. F. Stewart, J. Chem. Phys., 1977, 66, 4057 CrossRef CAS.
- A. Debnarova and S. Techert, J. Chem. Phys., 2006, 125, 224101 CrossRef PubMed.
- A. Debnarova, S. Techert and S. Schmatz, J. Chem. Phys., 2010, 133, 124309 CrossRef PubMed.
- A. Debnarova, S. Techert and S. Schmatz, J. Chem. Phys., 2011, 134, 054302 CrossRef PubMed.
- T. Northey, N. Zotev and A. Kirrander, J. Chem. Theory Comput., 2014, 10, 4911 CrossRef CAS PubMed.
- J. Yang, J. Beck, C. J. Uiterwaal and M. Centurion, Nat. Commun., 2015, 6, 8172 CrossRef PubMed.
- K. Wang, V. McKoy, P. Hockett and M. S. Schuurman, Phys. Rev. Lett., 2014, 112, 113007 CrossRef PubMed.
- P. Hockett, C. Z. Bisgaard, O. J. Clarkin and A. Stolow, Nat. Phys., 2011, 7, 612–615 CrossRef CAS.
- T. Fuji, Y.-I. Suzuki, T. Horio and T. Suzuki, Chem. – Asian J., 2011, 6, 3028–3034 CrossRef CAS PubMed.
- C. Z. Bisgaard, O. J. Clarkin, G. Wu, A. M. D. Lee, O. Gessner, C. C. Hayden and A. Stolow, Science, 2009, 323, 1464–1468 CrossRef CAS PubMed.
- D. Townsend, H. Satzger, T. Ejdrup, A. M. D. Lee, H. Stapelfeldt and A. Stolow, J. Chem. Phys., 2006, 125, 234302 CrossRef PubMed.
-
W. Schülke, Electron Dynamics by Inelastic X-Ray Scattering, Oxford Science Publications, 1st edn, 2007 Search PubMed.
- J. Bentley and R. F. Stewart, J. Comput. Phys., 1973, 11, 127 CrossRef.
-
I. Hargittai and M. Hargittai, Stereochemical applications of gas-phase electron diffraction: part A the electron diffraction technique, VCH, 1st edn, 1988 Search PubMed.
-
H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, et al., MOLPRO, version 2012.1, a package of ab initio programs, 2012 Search PubMed.
-
T. Northey, PhD thesis, The University of Edinburgh, 2016.
- A. Kirrander, J. Chem. Phys., 2012, 137, 154310 CrossRef PubMed.
- H. J. Suominen and A. Kirrander, Phys. Rev. Lett., 2014, 112, 043002 CrossRef PubMed.
- M. R. Pressprich, M. A. White and P. Coppens, J. Am. Chem. Soc., 1993, 115, 6444 CrossRef CAS.
- M. R. Pressprich, M. A. White, Y. Vekhter and P. Coppens, J. Am. Chem. Soc., 1994, 116, 5233 CrossRef CAS.
- A. Kirrander, C. Jungen and H. H. Fielding, Phys. Chem. Chem. Phys., 2010, 12, 8948 RSC.
- A. Kirrander, J. Chem. Phys., 2010, 133, 121103 CrossRef PubMed.
- A. Kirrander and C. Jungen, Phys. Rev. A: At., Mol., Opt. Phys., 2011, 84, 052512 CrossRef.
- A. Kirrander, K. Saita and D. V. Shalashilin, J. Chem. Theory Comput., 2016, 12, 957–967 CrossRef CAS PubMed.
- C. C. Pemberton, Y. Zhang, K. Saita, A. Kirrander and P. M. Weber, J. Phys. Chem. A, 2015, 119, 8832 CrossRef CAS PubMed.
- R. Neutze, R. Wouts, S. Techert, J. Davidsson, M. Kocsis, A. Kirrander, F. Schotte and M. Wulff, Phys. Rev. Lett., 2001, 87, 195508 CrossRef CAS PubMed.
-
P. R. Bunker and P. Jensen, Molecular Symmetry and Spectroscopy, NRC Research Press, 2nd edn, 1998 Search PubMed.
-
J. E. Bright Wilson, J. C. Decius and P. C. Cross, Molecular Vibrations: The Theory of Infrared and Raman Vibrational Spectra, Dover, 1st edn, 1955 Search PubMed.
|
| This journal is © the Owner Societies 2017 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *
*
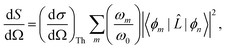
![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) is defined as,
is defined as,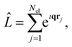
![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |ϕn〉|2,
|ϕn〉|2,![[R with combining macron]](https://www.rsc.org/images/entities/b_char_0052_0304.gif) )Ψelecα(
)Ψelecα(![[r with combining macron]](https://www.rsc.org/images/entities/b_char_0072_0304.gif) ;
;![[R with combining macron]](https://www.rsc.org/images/entities/b_char_0052_0304.gif) ,Ω),
,Ω),![[r with combining macron]](https://www.rsc.org/images/entities/b_char_0072_0304.gif) ;
;![[R with combining macron]](https://www.rsc.org/images/entities/b_char_0052_0304.gif) ,Ω), depends parametrically on the nuclear coordinates
,Ω), depends parametrically on the nuclear coordinates ![[R with combining macron]](https://www.rsc.org/images/entities/b_char_0052_0304.gif) and on the orientation of the molecular frame specified by the rotational Euler angles Ω = (α,β,γ) (see Appendix). The rotational wavefunction ΨrotJKM(Ω) is characterized by the three rotational quantum numbers J, K, and M, and the vibrational wavefunction Ψvibν(
and on the orientation of the molecular frame specified by the rotational Euler angles Ω = (α,β,γ) (see Appendix). The rotational wavefunction ΨrotJKM(Ω) is characterized by the three rotational quantum numbers J, K, and M, and the vibrational wavefunction Ψvibν(![[R with combining macron]](https://www.rsc.org/images/entities/b_char_0052_0304.gif) ) by the full set of vibrational quantum numbers ν. Since the scattering operator in eqn (2) acts on the electrons, it is convenient to first evaluate the scattering in terms of the form factor for the electronic wavefunction,
) by the full set of vibrational quantum numbers ν. Since the scattering operator in eqn (2) acts on the electrons, it is convenient to first evaluate the scattering in terms of the form factor for the electronic wavefunction,![[R with combining macron]](https://www.rsc.org/images/entities/b_char_0052_0304.gif) ,Ω) = 〈Ψelecα|
,Ω) = 〈Ψelecα|![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |Ψelecα〉.
|Ψelecα〉.![[R with combining macron]](https://www.rsc.org/images/entities/b_char_0052_0304.gif) ,Ω) can be calculated directly from the ab initio electronic wavefunction.39,42,50 For ab initio wavefunctions constructed from Gaussian primitives, the calculation of f0α(q;
,Ω) can be calculated directly from the ab initio electronic wavefunction.39,42,50 For ab initio wavefunctions constructed from Gaussian primitives, the calculation of f0α(q;![[R with combining macron]](https://www.rsc.org/images/entities/b_char_0052_0304.gif) ,Ω) can be done semi-analytically,42 although numerical Fourier transforms of the electron density represented on a grid are also possible.42
,Ω) can be done semi-analytically,42 although numerical Fourier transforms of the electron density represented on a grid are also possible.42
![[R with combining macron]](https://www.rsc.org/images/entities/b_char_0052_0304.gif) ,Ω) by the vibrational and rotational probability distributions,
,Ω) by the vibrational and rotational probability distributions,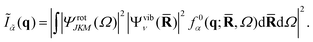
![[R with combining macron]](https://www.rsc.org/images/entities/b_char_0052_0304.gif) ,Ω)|2 is uniformly integrated over all directions of q.51
,Ω)|2 is uniformly integrated over all directions of q.51
![[R with combining macron]](https://www.rsc.org/images/entities/b_char_0052_0304.gif) ,Ω) depends on the orientation of the molecular frame in the laboratory (scattering) frame. When the electronic wavefunction rotates through the Euler angles Ω = (α,β,γ), the wavefunction expansion coefficients change. The rotated coefficients can be determined by re-calculating the electronic wavefunction in the rotated molecular frame, but this is inefficient. A slightly better approach is to rotate the electronic wavefunction directly, but this requires that the coefficients for all Gaussian primitives with l > 0 are transformed. Ultimately, the simplest and computationally most efficient approach is to rotate q rather than the molecule. This amounts to applying the inverse (i.e. transpose) of the rotation matrix to the vector q for each set of rotation angles (α,β,γ), while leaving the electronic wavefunction fixed in the original molecular frame used in the ab initio calculation. An attempt to illustrate the equivalence of these two scenarios, i.e. rotating the molecule versus rotating q, is shown in Fig. 1.
,Ω) depends on the orientation of the molecular frame in the laboratory (scattering) frame. When the electronic wavefunction rotates through the Euler angles Ω = (α,β,γ), the wavefunction expansion coefficients change. The rotated coefficients can be determined by re-calculating the electronic wavefunction in the rotated molecular frame, but this is inefficient. A slightly better approach is to rotate the electronic wavefunction directly, but this requires that the coefficients for all Gaussian primitives with l > 0 are transformed. Ultimately, the simplest and computationally most efficient approach is to rotate q rather than the molecule. This amounts to applying the inverse (i.e. transpose) of the rotation matrix to the vector q for each set of rotation angles (α,β,γ), while leaving the electronic wavefunction fixed in the original molecular frame used in the ab initio calculation. An attempt to illustrate the equivalence of these two scenarios, i.e. rotating the molecule versus rotating q, is shown in Fig. 1.![[R with combining macron]](https://www.rsc.org/images/entities/b_char_0052_0304.gif) ,Ω),
,Ω),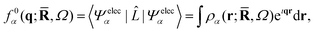
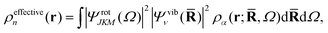
![[R with combining macron]](https://www.rsc.org/images/entities/b_char_0052_0304.gif) ,Ω) in eqn (7). This changes the meaning of the “shape” of the molecule, with the rotational and vibrational wavefunctions beginning to play an important role. For instance, a homonuclear diatomic in the ground rotational and vibrational state appears as a hollow spherical shell, while the same molecule in the first excited vibrational state appears as two spherical shells, one inside the other. This clearly differs from the picture of an ensemble of “ball-and-stick” diatomic molecules, each in a random orientation, leading to an incoherent thermal averaging of |f0α|.28,51
,Ω) in eqn (7). This changes the meaning of the “shape” of the molecule, with the rotational and vibrational wavefunctions beginning to play an important role. For instance, a homonuclear diatomic in the ground rotational and vibrational state appears as a hollow spherical shell, while the same molecule in the first excited vibrational state appears as two spherical shells, one inside the other. This clearly differs from the picture of an ensemble of “ball-and-stick” diatomic molecules, each in a random orientation, leading to an incoherent thermal averaging of |f0α|.28,51
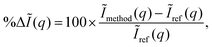

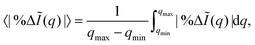
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/2, we have that qmax = 2k0 at θ = π. All images are shown without the outer absolute square in eqn (6) to make it easier to discern features at large values of q in the figures. In several instances, difference images are shown to emphasize the changes in the scattering pattern upon excitation to a specific state. These difference images are calculated by subtracting a reference image from the excited state scattering image, with the subtraction done between images sans the absolute square. In the following, we first examine the effect of molecular symmetry on the scattering images (Section 4.3.1), and then move on to examine the different partial contributions to the scattering in the CS2 molecule (Sections 4.3.2–4.3.4).
θ/2, we have that qmax = 2k0 at θ = π. All images are shown without the outer absolute square in eqn (6) to make it easier to discern features at large values of q in the figures. In several instances, difference images are shown to emphasize the changes in the scattering pattern upon excitation to a specific state. These difference images are calculated by subtracting a reference image from the excited state scattering image, with the subtraction done between images sans the absolute square. In the following, we first examine the effect of molecular symmetry on the scattering images (Section 4.3.1), and then move on to examine the different partial contributions to the scattering in the CS2 molecule (Sections 4.3.2–4.3.4).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) π,θ) is identical. A curious consequence of the centrosymmetry is that any odd-numbered rotational axis is doubled, as can be seen in the scattering patterns for BF3 (D3h point group) and the cyclopentadienyl anion, C5H5− (D5h point group) in Fig. 3. The 3-fold axis for BF3 and the 5-fold axis for C5H5− become 6- and 10-fold axes. In contrast, an even-numbered rotational axis, e.g. C4, will result in the same rotational C4 axis in the scattering image, with no apparent doubling since the images are already centrosymmetric. The mathematical background to this phenomenon is elaborated in the Appendix.
π,θ) is identical. A curious consequence of the centrosymmetry is that any odd-numbered rotational axis is doubled, as can be seen in the scattering patterns for BF3 (D3h point group) and the cyclopentadienyl anion, C5H5− (D5h point group) in Fig. 3. The 3-fold axis for BF3 and the 5-fold axis for C5H5− become 6- and 10-fold axes. In contrast, an even-numbered rotational axis, e.g. C4, will result in the same rotational C4 axis in the scattering image, with no apparent doubling since the images are already centrosymmetric. The mathematical background to this phenomenon is elaborated in the Appendix.