 Open Access Article
Open Access ArticleCorrelated/non-correlated ion dynamics of charge-neutral ion couples: the origin of ionicity in ionic liquids
G. W.
Driver
*,
Y.
Huang
,
A.
Laaksonen†
,
T.
Sparrman
 ,
Y.-L.
Wang‡
,
Y.-L.
Wang‡
 and
P.-O.
Westlund
and
P.-O.
Westlund
 *
*
Department of Chemistry, Umea University, SE 90187 Umea, Sweden. E-mail: Per-Olof.Westlund@umu.se; Gordon.Driver@umu.se
First published on 8th December 2016
Abstract
Proton/fluoride spin–lattice (T1) nuclear magnetic relaxation dispersion (NMRD) measurements of 1-butyl-3-methyl-1H-imidazolium hexafluorophosphate, [C4mim][PF6], have been carried out using high field spectrometers and a fast-field-cycling instrument at proton Larmor frequencies ranging from 10 kHz to 40 MHz, at different temperatures. The NMRD profiles are interpreted by means of a simple relaxation model based on the inter- and intra-ionic dipole–dipole relaxation mechanism. Using an atomic molecular-ion dynamic simulation at 323 K the relevant spin dipole–dipole (DD) correlation functions are calculated. The results indicate that the NMRD profiles can be rationalized using intra- and inter-ionic spin DD interactions, however, anions are mainly modulated by ionic reorientation because of temporary correlations with cations, where modulation by translational diffusion plays a minor role. Reorientational dynamics of charge-neutral ion couples (i.e. [C4mim]⋯[PF6]) and [C4mim]+ ions are in the nano-second (ns) time range whereas the reorientation of [PF6]− is characterized by a reorientational correlation time in the pico-second (ps) regime. Based on the NMRD profiles we conclude that the main relaxation mechanism for [PF6]− is due to fast internal reorientational motion, a partially averaged F–F intra- and F–H inter-ionic DD coupling as the anion resides in close proximity to its temporary oppositely charged cation partner. The F-T1-NMRD data display a ns dispersion which is interpreted as being due to correlated reorientational modulations resulting from the H-containing charge-neutral ion couple [C4mim]⋯[PF6]. The analysis of ionicity is based on the free anion fraction, f, and it increases with temperature with f → 1 at the highest temperatures investigated. The fraction is obtained from the H–F NMRD profiles as correlated–non-correlated dynamics of the ions. The analysis of T1 relaxation rates of C, H, F and P at high fields cannot generally give the fraction of ions but is consistent with the interpretation based on the NMRD profiles with relaxation contributions due to DD-intra and -inter, CSA-intra (and -inter for C), including spin rotation for P. The investigation has led to a description of the mechanics governing ion transport in the title ionic liquid via identification of transient correlated/non-correlated ion dynamics.
1 Introduction
Liquid salts, or, “ionic liquids” (ILs), studied since the 1800s,1–3 have become popular materials for scientific investigation in efforts to identify replacement solvents (and additives) with enhanced utility towards known and developing chemical processes.4–6 The shear quantity of cation and anion combinations available, which yield salts exhibiting stable liquid compositions at temperatures of interest, has inspired a situation where new solvents are formulated, produced and put into use faster than their physical properties are being investigated, detailed and understood.Fundamental knowledge concerning available solvent–solute interactions (i.e. active solvation modes, and liquid state dynamics) is highly sought after in order to reduce scientific efforts required to identify appropriately tuned materials. In this way, designs anchored to a specific chemical task will provide liquids that enable solution control through maximisation/minimisation of favourable/unfavourable ion–ion and ion–solute contact interactions. Of equal importance are native ion–ion contact encounters, provided by the pure liquid, where the possibility for correlated/non-correlated ionic motion becomes an important factor in any fundamental understanding of the origins of ion transport mechanics, upon which the physico-chemical fluid properties depend (e.g. conductivity, fluidity, density and saturation vapour pressure). As such, the desire to elucidate and define the liquid structure provided by these complex materials has attracted much attention in recent decades and continues to be an area of intense focus in the literature.7
Nuclear magnetic resonance spectroscopy (NMR) is a powerful, highly developed, tool capable of recording dynamics expressed by such intra- and inter-ionic (and/or molecular) ion–ion and ion–solute contact interactions via liquid state encounters. Most commonly the NMR approach utilises static high-field spectrometers (e.g.1H Larmor frequencies of 200–900 MHz) that can produce magnetic fields of 4.7–21 T to selectively discriminate varieties of reorientational motion, through spin-relaxation methods that probe the various spin-active nuclei. Cycled low-field NMR dispersion spectroscopy (NMRD),8 capable of alternating the field strength in a single experiment (e.g.1H Larmor frequencies of 0.01–40 MHz, producing magnetic fields <1 T), is also available, but such spectrometers are much less commonly employed in a given NMR platform. As the time-scale of the reorientational dynamics recorded is inversely proportional to the magnitude of the observed frequency, the NMRD approach is capable of probing motional characteristics in μs to ns that result from much slower dynamics relative to those observed using high-fields.
The title salt, 3-butyl-1-methyl-1H-imidazolium hexafluorophosphate, [C4mim][PF6] (see Fig. 1), has to date received much attention in the arena of molecular dynamics (MD), usually employing static high field approaches that probe fast motions.9–11 Our interest in this particular salt, which possesses limited stability under certain conditions,12 arises solely from the ionic symmetries provided, which are otherwise unavailable with other salts. The protic cation provides a bulky planar asymmetric geometry (anisotropic) for study with various accessible spin-active nuclei (i.e.14N, 15N, 13C and 1H) in contrast to the (isotropic) anion, which possesses a high degree of sphericity (Φ = 0.93), a low charge to volume ratio and distinct spin-active nuclei not available from the cation (i.e.31P and 19F). Anionic contributions to available dynamics were, therefore, expected to be distinguishable from those due to cations, in the NMRD experiments, thus permitting the disentanglement of “inter”-relaxation interactions between each ion of the oppositely charged ion set, in efforts to rationalise overall ion-dynamics of the liquid system.
 | ||
| Fig. 1 3-Butyl-1-methyl-1H-imidazolium hexafluorophosphate, [C4mim][PF6], green = C, white = H, blue = N, red = F, yellow = P. | ||
Herein, we report on the MD behaviour recorded using both low- and high-field experimental NMR methods that probe various nuclei, and include complementary MD simulations for qualitative guidance. We report on the molecular-ion dynamic behaviour of [C4mim][PF6] (at several temperatures) through a combined analysis employing experimentally recorded spin lattice relaxation of 1H and 19F determined by low-field fast field cycling (FFC) NMRD, 13C, 31P, 19F and 1H determined by high-field NMR with MD simulations and spin relaxation theory.13–15 The analysis aims to describe ionic reorientational motion responsible for proton and fluoride spin–lattice NMRD relaxation profiles and 31P, 13C, 1H and 19F T1 relaxation at high fields, with complementary MD simulations providing qualitative guidance in the experimental data evaluations. The NMRD field dependence of the longitudinal spin relaxation is displayed using relaxation profiles (Fig. 2) where spin–lattice relaxation rates are measured as a function of the proton Larmor frequency ranging from 10 kHz to 40 MHz. A model was developed to interpret relaxation data in terms of inter- and intra-ionic spin dipole–dipole correlation functions obtained from a full atom molecular dynamics simulation model.16 The time correlation functions (see Fig. 7–9) are mainly modulated by short and long correlation times characterising ionic reorientation and an order parameter (S).
 | ||
| Fig. 2 R 1-NMRD profiles of R1,H,EXP(ω) (a) and R1,F,EXP(ω) (b) at temperatures ranging from 278 K to 323 K. Best fit parameters obtained from the NMRD analysis are given in Tables 2 and 3. | ||
Spin–lattice NMR dispersion experiments are used extensively for studies of molecular dynamics (mainly water) in different solutions and more recently also for ionic liquids.17–21 NMR relaxation theory provides a connection between experimental T1 NMRD profiles and relevant molecular/ionic reorientational/translational dynamics, which is studied using the MD simulations and which determines the spectral densities of the relaxation model describing the spin relaxation rates and the shape of the R1-NMRD profiles.
NMR dispersion experiments were performed by Seyedlar et al.22 in their analysis of the dynamics of the ionic liquid [C4mim][NTf2]. They assume more simplified relaxation expressions for the relevant NMR relaxation mechanisms that are the intra- and inter-ionic dipole–dipole interactions as induced by ionic translational and rotational diffusion of the molecular-ions. They also focus on super cooled states where ionic reorientation and translation are (strongly) correlated and much more complex than at higher temperatures. Kruk et al.23 presented an H and F T1-NMRD study of [C4mim][PF6] covering the proton frequency range from 10 kHz to 20 MHz. The paper focused on extraction of translational diffusion coefficients from dispersion profiles obtained by FFC-NMRD measurements. In contrast to our approach, however, they assume that translational diffusion is relevant as the only time modulation of the dominant H–H inter-ionic dipole–dipole contribution, obtaining good fits to the low field part of the measured 1H spin–lattice relaxation rates. They concluded that 19F relaxation is dominated by inter-ionic dipole–dipole coupling where F–H and F–F contributions are comparable. While we agree that the main relaxation pathway is inter-ionic F–H dipole–dipole coupling, we instead assume that it is mainly modulated by cationic reorientational motion, and that 19F relaxation of [PF6]− has a relatively small intra-ionic contribution because of fast (ps) rotation.
Our approach is also a simplification, although it is partly supported by the experimental results indicating that self-diffusion of the ions [C4mim]+ and [PF6]− is very slow; experimentally determined diffusion coefficients are Dcation = 6.7 × 10−7 cm2 s−1 and Danion = 5.7 × 10−7 cm2 s−1 at 353 K.24 While molecular-ion dynamic simulations give approximately an order of magnitude faster translational diffusion coefficients they indicate that both ions have similar diffusion coefficients and a similar temperature dependence. These findings thus support translational motion of the oppositely charged ion couples as being slow and strongly correlated.39 The crucial observation (Fig. 2) is the ns-dispersion displayed in the NMRD profiles for both the bulky cation and the small anion. That the small symmetric anion [PF6]− would display a T1-dispersion at the same frequencies as for the much larger cation was unexpected. One would have rather expected dispersion of the anion to be absent or instead appear at considerably higher frequencies, with its reorientation being much faster than for the cation. The 19F T1-NMRD profiles at T < 298 K, however, strongly indicate that the spin relaxation of anions is the same as for the cations. How the observation of such dynamics can be rationalized is the main focus of this work. The solution is obtained by developing a relaxation model describing that of both anions and cations. The model developed, and the analysis using it, indicate correlated motions between ions of opposite charge, at low temperatures. This correlated motion (all but) disappears at higher temperatures. We rationalised this as the consequence of the main anionic relaxation mechanism being resultant from inter-ionic F–H dipole–dipole-interactions with cations. At low temperatures, ions move predominantly as transient charge-neutral ion couples. The model explains the unexpected correlation by introducing a fraction (f) in eqn (4) of ion couples which is temperature dependent. The presence of charge-neutral ion couples is thus captured by the temperature dependent fraction f which provides new insights into ILs not previously achieved by NMR relaxation analysis or any other experimental method. The gradual disappearance of the ns dispersion thus reflects the temperature dependence of the fraction f and the decrease of charge-neutral ion couple populations. The NMRD profiles display a somewhat stretched behaviour and are fitted using 2 fractions of charge-neutral ion couples, to account for the 2 types of [C4mim]⋯[PF6] that possess 2 different life-times. The effective correlation times are thus defined as: 1/τc,i = 1/τR + 1/τres where the rotational correlation time (τR) is combined with the residence life time (τres) of the ion couple. In Tables 2 and 3 the fraction of one of the charge neutral couple species has been normalized to the low temperature NMRD profile showing the increase of f, the fraction of free anions, with temperature (see Fig. 4). The same qualitative behaviour is obtained for both types of charge-neutral species.
| T/K, B0/MHz | R 1 (s−1) | Δσ (ppm) | R CSA1,intra (s−1) | τ CSAintra | R CSA1,inter (s−1) | τ CSAinter (ps) |
|---|---|---|---|---|---|---|
| Cation | C4 | |||||
| 278, 500/600 | 2.439/1.852 | 121.3 | 0.011/0.010 | 11.39/7.32 | 1.950/1.534 | 199/109 |
| 328, 500/600 | 1.961/1.786 | 121.3 | 0.025/0.033 | 24.35/22.17 | 0.872/0.784 | 854/534 |
| T/K, B0/MHz | R 1 (s−1) | Δσ (ppm) | R DD1,intra | τ DDintra (ps) | R DD1,inter (s−1) | R SR1 (s−1) |
|---|---|---|---|---|---|---|
| Cation | C4 | |||||
| 278, 500/600 | 2.439/1.852 | 121.3 | 0.478/0.307 | 11.39/7.32 | — | — |
| 328, 500/600 | 1.961/1.786 | 121.3 | 1.06/0.969 | 24.35/22.17 | — | — |
| Cation | H4 | |||||
| 278, 500/600 | 0.952/0.977 | — | 0.059/0.0380 | 11.39/7.32 | 0.893/0.939 | — |
| 328, 500/600 | 0.730/0.689 | — | 0.132/0.120 | 24.34/22.17 | 0.598/0.569 | — |
| Anion | P | |||||
| 278, 500/600 | 0.230/0.238 | −2.845 | 0.0912/0.0943 | 3.35/3.47 | — | 0.139/0.144 |
| 328, 500/600 | 0.256/0.253 | −2.845 | 0.0419/0.0414 | 1.48/1.46 | — | 0.215/0.212 |
| F | ||||||
| 278, 500/600 | 0.789/1.082 | −99.99 | 0.134/0.139 | 3.35/3.47 | 0.565/0.810 | — |
| 328, 500/600 | 0.583/0.758 | −99.99 | 0.062/0.061 | 1.48/1.46 | 0.480/0.638 | — |
| T/K | τ c,1 (ns) | τ c,2 (ns) | α (s−1) | R 1(max) (s−1) | f 2 R 1(τc,2) (s−1) | 1 − f2/f2(268) ± 0.3 | cred |
|---|---|---|---|---|---|---|---|
| 268 | 202 ± 23 | 15.0 ± 0.7 | 9.8 ± 0.6 | 164.7 ± 1.4 | 94.0 ± 3.4 | 0 | 0.41 |
| 278 | 150 ± 18 | 10.5 ± 0.6 | 11.0 ± 0.8 | 88.7 ± 0.7 | 48.3 ± 1.7 | 0.22 | 0.67 |
| 283 | 153 ± 21 | 9.0 ± 0.6 | 11.0 ± 0.8 | 64.8 ± 0.5 | 36.3 ± 1.0 | 0.36 | 0.85 |
| 288 | 129 ± 20 | 7.5 ± 0.6 | 10.7 ± 0.8 | 48.1 ± 0.3 | 26.0 ± 0.9 | 0.45 | 0.94 |
| 293 | 134 ± 22 | 7.5 ± 0.8 | 11.1 ± 0.8 | 36.5 ± 0.2 | 17.9 ± 0.7 | 0.62 | 0.97 |
| 298 | 130 ± 21 | 7.4 ± 0.9 | 10.4 ± 0.6 | 26.0 ± 0.1 | 10.8 ± 0.5 | 0.77 | 0.98 |
| 303 | 149 ± 27 | 8.3 ± 1.0 | 10.2 ± 0.4 | 19.9 ± 0.1 | 6.7 ± 0.4 | 0.89 | 0.99 |
| 308 | 117 ± 25 | 7.9 ± 1.4 | 8.9 ± 0.3 | 15.2 ± 0.1 | 4.5 ± 0.3 | 0.91 | 0.99 |
| 313 | 253 ± 53 | 11.6 ± 1.8 | 8.0 ± 0.2 | 12.2 ± 0.1 | 2.8 ± 0.2 | 0.94 | 0.99 |
| 318 | 138 ± 33 | 8.8 ± 1.7 | 6.7 ± 0.2 | 9.95 ± 0.05 | 2.2 ± 0.2 | 0.95 | 0.99 |
| 323 | 153 ± 39 | 9.0 ± 2.0 | 5.9 ± 0.2 | 8.13 ± 0.03 | 1.51 ± 0.14 | 0.97 | 1.0 |
| T/K | τ c,1 (ns) | τ c,2 (ns) | α (s−1) | R 1(max) (s−1) | f 2 R 1(τc,2) (s−1) | 1 − f2/f2(268) ± 0.3 | cred |
|---|---|---|---|---|---|---|---|
| 268 | 194 ± 20 | 21.5 ± 1.4 | 4.4 ± 0.4 | 131 ± 1.5 | 52.2 ± 3.5 | 0 | 0.30 |
| 278 | 157 ± 22 | 17.3 ± 1.2 | 4.5 ± 0.3 | 80.7 ± 1.0 | 37.7 ± 2.7 | 0.11 | 0.93 |
| 283 | 156 ± 23 | 15.3 ± 1.0 | 4.2 ± 0.3 | 61.9 ± 0.8 | 32.3 ± 1.9 | 0.13 | 0.93 |
| 288 | 226 ± 30 | 13.25 ± 0.7 | 4.0 ± 0.2 | 49.5 ± 0.6 | 25.1 ± 0.9 | 0.22 | 0.71 |
| 293 | 206 ± 27 | 11.3 ± 0.7 | 3.7 ± 0.2 | 38.6 ± 0.5 | 19.6 ± 0.7 | 0.29 | 0.89 |
| 298 | 140 ± 34 | 9.8 ± 1.0 | 3.5 ± 0.3 | 21.9 ± 0.3 | 12.9 ± 0.6 | 0.46 | 1.0 |
| 303 | 127 ± 38 | 9.0 ± 1.2 | 3.5 ± 0.3 | 16.7 ± 0.2 | 9.5 ± 0.5 | 0.57 | 1.0 |
| 308 | 111 ± 30 | 8.0 ± 1.2 | 3.3 ± 0.3 | 13.0 ± 0.2 | 7.0 ± 0.4 | 0.64 | 1.0 |
| 313 | 108 ± 44 | 7.8 ± 1.4 | 3.2 ± 0.3 | 10.4 ± 0.1 | 5.2 ± 0.4 | 0.72 | 1.0 |
| 318 | 120 ± 58 | 7.5 ± 1.4 | 2.9 ± 0.4 | 8.2 ± 0.1 | 4.0 ± 0.3 | 0.78 | 1.0 |
| 323 | 114 ± 76 | 7.1 ± 1.7 | 2.6 ± 0.4 | 6.7 ± 0.1 | 3.1 ± 0.3 | 0.82 | 1.0 |
 | ||
| Fig. 3 The temperature dependence of the relaxation rates in Tables 2 and 3 of H(R1(max) (a)) and F(R1(max) (b)) versus the 100/T, are displayed. H and F R1-NMRD profiles have the same temperature dependence. Also the temperature dependence of the correlation time (Tau_c2) = τc,2 and R1(slow) = R1(τc2) of Tables 2 and 3 is displayed. | ||
 | ||
| Fig. 4 (a) Free ion fractions of [C4mim]+ and [PF6]− ions, in the range T = 268–323 K. (b) Corresponding Walden plot, (c) corresponding N–E plot. | ||
Multi-exponential reorientational dynamics may be expected due to the low symmetry of the [C4mim]⋯[PF6] and [C4mim]+ entities, however, the relevant time correlation functions obtained from the full atomic MD simulations display a slow decay which is approximately singly exponential for the long time tail for both inter- and intra-ionic dipole–dipole correlation functions.
The consequences of these findings are of relevance to long standing interest in liquid salts' literature concerning general aspects of ion transport and more specifically the ongoing debate entertaining the question of the existence of “classical” long-lived contact ion-pairs in the neat liquids. We briefly address here the generally preferred assumption for the dominance of translational diffusion that has been almost exclusively relied upon with regard to given rationalisations of ion transport and ion dynamics:
(1) Previously, almost all theoretical efforts describing “inter”-relaxation effects have been based on the assumption that such interactions are entirely controlled by translational diffusion. This began especially with numerous and monumental works of Ayant/Belorszky/Fries25,26 which assume from the start that τinter ∝ 1/D, where D ≡ self-diffusion coefficient. Kruk's work23 also operates on this assumption. In the present work one important distinction is that remote-spin interactions are not governed exclusively by translational diffusion but rather via molecular-ion reorientation.
(2) The field independent relaxation contribution at low field, denoted α, reveals at high fields an “inter-ionic” chemical shift anisotropy (CSA) interaction, which we denote CSA-inter, that is modulated by the on-and-off exchange motion of anions where F atoms form “hydrogen” bonds to cation H thus generating a chemical shift. This relaxation mechanism can thus operate at higher fields. This observation was unexpected since in the typical case, the amplitude of the CSA mechanism is directed by intra-ionic reorientational motion and dispersed at high fields. Further details are presented in the section featuring the α term analysis, where the effect of the anion on the cation is detailed.
(3) Empirical quantification of liquid salt ionicity, in the spirit of the Nernst–Einstein (N–E) ratio, Λexp't/ΛN–E, (with Λexp't the experimentally determined molar conductivity, and ΛN–E that estimated using the Nernst–Einstein relation, long known to be an over-estimation), also relies on the strict assumption that ionic conductivity is solely determined by translational diffusion. Deviations from Λexp't/ΛN–E = 1 are exclusively rationalised in terms of long-lived ion-pair formation to account for “missing” ion-transport contributions. As a result, the possibility of Λexp't/ΛN–E < 1 being effectively the combined result of the ionic friction (kinetic energy losses due to electrophoretic effects), an asymmetric dipole density, and fleetingly correlated charge-neutral ion couples, have largely been ignored. In the present work, fractions f describing ionicity of [C4mim][PF6] are obtained directly from the model (i.e. without any need for detailed assumptions) which display an anticipated temperature dependence, and that far exceed those obtained using the typical empirical approaches. This temperature dependent fraction thus indicates correlated/non-correlated ion dynamics, and becomes an important quantity in any rationalisation of the origins of ion transport in ionic liquids.
2 Materials and methods and the experimental results
The ionic liquid 1-butyl-3-methyl-1H-imidazolium hexafluorophosphate, [C4mim][PF6], purchased from Fluka (98.5%), was introduced to the NMR tube without any other preparations. The 10 mm NMR tube for NMRD was sealed to prevent water ingress into the ionic liquid sample and at high field 5 mm tubes with a DMSO capillary.2.1 Molecular dynamics simulations of [C4mim][PF6]
2.2 Proton 1H and 19F spin relaxation measurements
(1) Low field: the proton and fluoride longitudinal relaxation rate, REXP1(ω), was measured on a 1T Stelar FFC2000 fast-field-cycling instrument with polarization at 25 MHz and detection at 16.29 MHz (17.32 for F, the field is expressed in proton Larmor frequency). The relaxation takes place at different proton Larmor frequencies ranging from 0.01 to 40 MHz. The switching time is 3 ms with a 90° pulse length of 8.1 μs. The polarization and recovery time was set to 4 T1 and the number of accumulated transients was 4 for all samples. The sample temperatures are 268–323 K, determined within ±1 degree but maintained within ±0.1 degree using the temperature unit of the Stelar spectrometer.(2) High field: the NMR spectra were recorded using Bruker Avance III HD 600 MHz and Bruker Avance III 500 MHz spectrometers equipped with a 5 mm broad band observe cryo probe, and a 5 mm inverse broad band probe, respectively. 1H, 19F and 31P spectra were recorded using direct polarization without decoupling and corresponding T1-relaxation was measured using the inversion recovery method. 13C spectra and inversion recoveries were recorded using 1H WALTZ-16 decoupling at 2500 Hz field strength during acquisition. The heteronuclear Overhauser effect was measured according to the Berger method28 with continuous wave 1H presaturation on compared to off resonance for 20 s at 2500 Hz field strength followed by a 13C 90 excitation pulse and on resonance CW decoupling during acquisition. The hetero NOEs were run for the three direct 1H–13C bond pairs of the [C4mim]+ imidazolium ring and the 31P–19F bond pairs of [PF6]−.
2.3 Experimental results
In Fig. 2 the 1H and 19F spin–lattice relaxation profiles are displayed for temperatures ranging from T = 268 K to 323 K. Both 1H and 19F NMRD profiles at low temperatures (268–303 K) display pronounced and similar dispersions with low field relaxation rates that decrease at higher temperatures. The NMRD profiles at 323 K seem to be almost constant with field, however, the relaxation rate has decreased an order of magnitude and the relatively small dispersion shifts towards a higher field but is still connected to a correlation time in the ns regime. The somewhat stretched dispersion indicates at least 2 effective correlation times, referring to some similar dynamics for both protons and fluoride.In Fig. 3 the temperature dependence of the low field limit values, R1,H,EXP(ωmin) (=R1(max)) and R1,F,EXP(ωmin), (=R1(max)) versus 100/T is shown. One should note that the slopes of H and F relaxation rates are the same which supports the same physical process being involved in the changes observed for the relaxation rates of both F and H. That is, we assume that the dominant modulation is due to cationic reorientation. Also shown in Fig. 3 is the temperature dependence of the relaxation contribution (R1(τc2)) from one of the [C4mim]⋯[PF6] species with effective correlation time τc2 (Tau_c2, ns). These two quantities are obtained from the relaxation model and the analysis summarized in Tables 2 and 3. The relaxation rate R1(τc2) displays the same temperature dependence as for the unprocessed relaxation data R1(max). The temperature dependence of τc,2 is very small because it is dominated by the residence time (τres) rather than the reorientational correlation time (τR). Thus the temperature dependence of these results is consistent with the temperature dependence of the unprocessed relaxation rates.
3 Relaxation theory and the IL relaxation model
In a simple picture of the ionic liquid the equilibrium is:[C4mim]⋯[PF6] ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) [C4mim]+ + [PF6]− [C4mim]+ + [PF6]− | (1) |
 whereas its fluoride relaxation rate is given by
whereas its fluoride relaxation rate is given by  . The corresponding relaxation rates for the ions are
. The corresponding relaxation rates for the ions are  and
and  , respectively. This simple picture thus ignores more complex equilibrium such as:
, respectively. This simple picture thus ignores more complex equilibrium such as:[C4mim]⋯[PF6]N ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) [C4mim]⋯[PF6]N−1 + [C4mim]+ + [PF6]− [C4mim]⋯[PF6]N−1 + [C4mim]+ + [PF6]− | (2) |
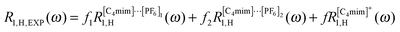 | (3) |
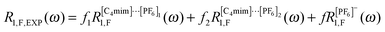 | (4) |
We first consider eqn (3) and the 15 protons of [C4mim]+ and [C4mim]⋯[PF6]. These protons are not individually resolved in the relaxation measurement of the FFC spectrometer which means that proton relaxation is due to spin dipole–dipole coupling to all other nuclear spins which are most conveniently divided into homo- and hetero-nuclear intra- and inter-ionic dipole–dipole interactions.15 The first relaxation contribution of eqn (3) reads for fk, k = 1, 2:
 | (5) |
 is due to homo-nuclear intra-ionic dipole–dipole coupling of the protons of the cation and is assumed to be the same as the intra-homo nuclear relaxation contribution of eqn (5) thus assuming that the reorientation of the cation and the charge-neutral ion couple is very much the same. Here, we thus ignore the inter-ionic dipole–dipole interactions between protons of different [C4mim]+ ions or [C4mim]⋯[PF6] couples. Consequently, eqn (3) can be rewritten as:
is due to homo-nuclear intra-ionic dipole–dipole coupling of the protons of the cation and is assumed to be the same as the intra-homo nuclear relaxation contribution of eqn (5) thus assuming that the reorientation of the cation and the charge-neutral ion couple is very much the same. Here, we thus ignore the inter-ionic dipole–dipole interactions between protons of different [C4mim]+ ions or [C4mim]⋯[PF6] couples. Consequently, eqn (3) can be rewritten as:| R1,H,EXP(ω) = f1RInter,hetero1,H–F1(ω) + f2RInter,hetero1,H–F2(ω) + RIntra,homo1,H(ω) | (6) |
 | (7) |
| R1,F,EXP(ω) = f1(〈RIntra,homo1,F(ω)〉 + 〈RInter,hetero1,H–F1(ω)〉) + f2(〈RIntra,homo1,F(ω)〉 + 〈RInter,hetero1,H–F2(ω)〉) + α. | (8) |
4 Results: the analysis of the NMRD profiles
The measured proton and fluoride spin–lattice relaxation profiles are analyzed using eqn (3)–(8) and (15), with the relaxation contributions in eqn (6) reading:15 | (9) |
 | (10) |
 | (11) |
 | (12) |
 | (13) |
The proton R1,H,EXP(ω) and fluoride R1,F,EXP(ω) -NMRD profiles are displayed in Fig. 2 at temperatures ranging from T = 268 K to 323 K. They are slightly stretched with a dispersion which gradually disappears at higher temperatures. The four fitting parameters of the relaxation model are: [f2R1(τc,2)], α, τc,1 and τc,2 and we obtain the dependent relaxation rate parameter [f1R1(τc,1)] from R1(max) − α − f2R1(τc,2) where R1(max) is the experimental low field value of the NMRD profile. The best fit parameters using the Levenberg–Marquardt-fitting procedure are summarised in Tables 2 and 3.
If the fraction f(T) of free [PF6]− ions is very small, as may be expected at low temperatures, the relative change of f(T) with temperature can be estimated from the variation of the relaxation rates. In Tables 2 and 3 we relate the fraction to f2(268) and calculate the relative change of the fractions with temperatures using [f2R1(τc,2)] with the shortest effective correlation time τc2.
 | (14) |
4.1 The field independent relaxation contribution α at 278 and 328 K
Static field NMR differs from NMRD in that it enables selective investigation of individual spin-active nuclei and provides a discriminating analysis involving multiple relaxation mechanisms. At low field, NMRD probes slower ionic motion in the dispersive regime, while high field approaches are more often employed to probe fast motion (α term). In the following analysis, all rates were processed using the following order parameters: S = 0.63 at T = 278 K and S = 0.61 at T = 328 K. Data detailed here are presented in Table 1 below.At low temperatures, anions form temporary charge-neutral ion couples with the cation, where internal rotations are expected to contribute to the α term. The relevant correlation functions from the MD simulations are displayed in Fig. 7–9. All display an initial fast decay (ps) followed by a slow single exponential decay in the ns time regime. In the effective correlation function, the initial decay is described by τf and is given in the range of 10–20 ps according to the simulation, which compare well with those determined experimentally at high field (e.g. 1–3 ps). The α terms thus have contributions expressed in eqn (20) and (21).
Observation of this initial fast decay led us to probe the IL using higher static fields of 500 and 600 MHz (based on the proton Larmor frequency), with optimal relaxation recorded at the respective observe frequencies, exhibiting correlation times C/ω0(500MHz) and C/ω0(600MHz), where C is a spectral density dependent constant. Experimental data recorded at these increased field strengths (11–14 T), at 278 and 328 K, indicate that the IL exhibits frequency independent T1 relaxation, having fulfilled the condition of motional narrowing (ω0τ ≪ 1) for 19F and 31P, giving rise to the reorientational motion regime corresponding to the α term.
The 31P nucleus of [PF6]−, residing on the interior of a symmetrical octahedron comprised of 19F vertices, is found to relax via dipole–dipole (DD), chemical shift anisotropy (CSA) and spin-rotation (SR), at high field. Overall 31P rates on each static field exhibit a reverse temperature dependence (i.e. increasing with temperature and extreme narrowing), the signature of SR, which opposes that of all other known relaxation mechanisms. This assignment is strictly intuitive and should be considered with caution; SR relaxation theory was developed for homogenous solution and may not be relevant for the more complex micro-heterogeneous ILs. While CSA is active for 31P nuclei, with Δσ = −2.85 ppm, it contributes negligibly to the overall relaxation (<0.003%), and is found to decrease with increasing temperature.
31P–19F NOEs were recorded (ηNOE = 0.46 and 0.19 for low and high temperatures respectively) enabling the disentanglement of intra-ionic DD from the overall rate; inter-ionic DD is not active for 31P. Intra-ionic DD relaxation was found to account for 40 and 16% of R1 at temperatures 278 and 328 K, respectively, with the residual rate accounted for by the SR mechanism, with associated contributions of 60 and 84%, on both fields. 19F nuclei are found to relax predominantly via inter-ionic DD coupling by other 19F and 31P (70 and 80% of R1 at 278 and 328 K), directed by F–H hydrogen bond formation with cations (intra-ionic DD provides a 17 and 10% contribution at 278 and 328 K). In this way, DD relaxation rates scale proportionally to those found from the NMRD experiments. Δσ = −99.99 ppm is of a sizeable magnitude for 19F in [PF6]−, however, the CSA mechanism contributes only 11 and 7% at the low and high temperature, respectively, and is governed by internal reorientational anionic motion.
In terms of the cation, a small intra-ionic contribution to α for the DD proton relaxation, as well as a dominating inter-ionic DD contribution indicate a dense packing (with as small as possible rij distances) as might be expected for a highly concentrated liquid salt (4.89 M, or, ≈10 M for the binary system, at T = 278 K). Inter-ionic DD relaxation accounts for as much as 95 and 86% of R1 at temperatures of 278 and 328 K respectively, in complete accord with NMRD data. Intra-ionic DD correlation times are on the order of 10–30 ps across both fields, with the highest values observed at high temperatures.
Analysis of the ring carbons C2, C4 and C5 (alkyl group C were not analysed) provided NOEs on the order of ηNOE = 0.30 and 1.00 for low and high temperatures respectively, with DD rates found to decrease at high temperature. Intra-ionic DD relaxation was found to account for 20 and 60% of R1 at temperatures 278 and 328 K, respectively, with the residual rate accounted for by the CSA mechanism. 13C nuclei were found to relax predominantly by CSA at a low temperature (Δσ ≈ 120 ppm), with magnitudes observed to fall at a high temperature, and required fits that revealed both intra- and inter-ionic contributions. CSA-intra relaxation, modulated strictly by internal reorientational cationic motion, exhibited the expected field dependence, and was found to increase 2-fold from the low to high temperature, across both fields. Fast internal motion, with its associated correlation time (on the order of 10–20 ps), however, could not completely account for the entire 13C CSA rate, with large magnitude residual rates remaining at both temperatures and fields.
The relaxation analysis reveals a correlation time, τCSAinter = 2–0.8 ns, which is in accord with the formation and break-up of charge-neutral ion couples, as F–H hydrogen bonds are formed and broken. This formation is, however, shorter than the residence time (10–20 ns) of the anion at the cation surface since the anion is locally rotating whereby its various F atoms form and break hydrogen bonds which are thereby responsible for the chemical shift and thus modulation of the CSA. In this way, the high field relaxation analysis is actually capable of revealing the formation and break-up, via CSA-inter modulation, of charge-neutral ion couples, as identified through the NMRD analysis.
It is noteworthy that the CSA-inter rates are halved at a high temperature, at the same time that CSA-intra rates double. This reveals the impact of increasing kT, with respect to the charge-neutral ion couple populations. At low temperatures, where such couples predominate, the influence of the anion partner, as well as the radial distribution of anions in the first cationic solvation shell, are shown with CSA-inter rates on the order of 1.27 s−1 (with correlation times on the order of 1.2 ns) which comprise 80% of the total 13C relaxation rate (as compared to 0.5–0.6% due to CSA-intra at the same temperature). CSA-inter rates reduce in magnitude by up to 50% at a high temperature, dropping overall contributions to total CSA relaxation accordingly, as the fraction f of free oppositely charged ions increases to > 90% and charge-neutral ion couple populations are almost entirely depleted. This behaviour is very much in agreement with the low field analysis, with fast cationic motion recorded at high field found to increase with temperature, and where CSA-inter contributions reduce (correlation times drop to values of ≈0.5 ns) in accordance with the drop in density due to bulk volume expansion.
Overall the α term analysis indicates a dominance of fast motion, increasing from the low temperature and becoming quite pronounced at the highest temperature investigated. This signals the continuous break-up of the charge-neutral ion couples as the magnitude of kT increases, concordant with the NMRD analysis.
4.2 Ionicity
Methods designed to determine the extent to which liquid salt ions are dissociated have been of scientific interest since at least the 1960s.29 The most accessible approach for the determination of ionic liquid ionicity tends to employ the ion transport properties (molar conductivity Λ, self-diffusivity D and viscosity η) and oversimplified empirical functions based on Stokes' Law (i.e. Walden's viscosity rule) and the Nernst–Einstein (N–E) relation.30,31In essence, the magnitude of the experimentally measured properties never achieves the empirically estimated reference level, with so-called “missing” ion transport subsequently rationalised in terms of the existence of “classical” contact ion-pairs and/or an outright lack of ion formation.32,33 The mathematical simplicity of the N–E relation ΛN–E = F2DIL/RT (in units of S cm2 mol−1), leading to the N–E ratio, Λexp't/ΛN–E, is also projected into the result, which ignores electrophoretic effects, asymmetric distributions of dipole density and inter-ionic frictional forces. Such physical properties were previously shown to provide predicted deviations from the N–E relation, even for theoretically ideal liquid salts (i.e. 100% dissociated), with assumptions of contact ion-pairing being completely unnecessary.34 The Walden viscosity rule is equally ineffective because it fails to account for the strong influence of hydrogen bonding on the various transport properties. Additionally, Walden's viscosity rule requires static equilibrium conditions.35 This is of course not possible in ionic liquids, as has been demonstrated in this work, where the transient correlated/non-correlated anionic dynamics, akin to chemical exchange of ions, (i.e. a dynamic equilibrium), renders the Walden viscosity rule inapplicable.
At the lowest temperatures investigated in this work, the liquid is heavily (almost exclusively) populated with transient charge-neutral ion couples, with dynamics subsequently guided by slow motions of the bulky asymmetrical cation. As temperatures increase, these species break-up, and the liquid increasingly populates with the free ions, as can be seen in Fig. 4, presenting the free ion fraction evolution as a function of temperature (a Walden plot and results from the N–E analysis are included for comparison). Such a result might be anticipated as any increase in magnitude of kT would be expected to increasingly oppose available Coulomb forces, as the Onsager radii, R+/−, reduces accordingly (with R+/− on the order of 40 Å). Additionally, an Arrhenius plot employing favg implies a ≈4-fold drop in Ea across the temperature range investigated. It is noted that the Walden plot indicates the strongest divergence from ideality (i.e. from 100% dissociation) at the highest temperatures, while the N–E plot simply indicates the extent by which ΛN–E over-estimates the expected molar conductivity of [C4mim][PF6], with Λexp't/ΛN–E providing a (temperature independent) constant value of 0.66.
Free ion fractions f obtained for [C4mim][PF6] are observed to have increased, tending towards the maximum value, by T = 328 K, in contrast to the notions of “missing” ion transport inferred by both the N–E and Walden approaches. We note that investigations concluding liquid salts possess large free ion fractions, mixed with temperature dependent transiently correlated/associated oppositely charged ion populations (i.e. in contrast to notions of “classical” contact ion-pairs), are rare, with reports existing for a series of Cl− salts using experimental spectroscopic methods, and for [C4mim]I and [C4mim][PF6] by high quality MD simulation analyses.20,36,37
5 Conclusions
The aim of this work was to investigate the [C4mim][PF6] ionic liquid using NMRD-T1 analysis in order to provide a detailed description of the liquid state based on the ion-dynamics that govern it. The unexpected similarity of the dispersion profiles recorded for each ion type, over the temperature range explored, indicated the dynamics to be the result of transient charge-neutral ion couples, which populate the liquid predominantly at the lower temperatures. The loss of recorded dispersion, as temperatures were increased, signalled a continuous break-up of the transient charge-neutral ion couples and an ever increasing dynamical contribution from the increasing free ion populations. The model developed herein, guided qualitatively by the accompanying MD analysis, assumed that the main modulation of the spin dipole–dipole interaction was governed not by translational diffusion, but rather via molecular-ion reorientation of transient charge-neutral ion couples. That is to say, the inter-ionic H–F dipole–dipole interaction was the main source of relaxation as a result of correlated [C4mim]⋯[PF6] reorientation. This approach was directed by the similarity of the NMRD dispersion profiles acquired for H (cation) and F (anion) across several temperatures, and was subsequently required in order to build a consistent picture of the available ion-dynamics. Interestingly, it was noted that both F and H NMRD profiles may be characterized by the same correlation times and the activation energy term, when the temperature dependence is described, a feature that was also supported by the MD simulations.The α term analysis revealed an inter-ionic modulation by CSA interactions which followed the temperature dependence of the break-up of the transient charge-neutral ion couples identified in the NMRD analysis. The resultant fraction f of [PF6]−, characterising free ion populations, provided a direct measure of salt ionicity that clearly revealed the temperature dependent correlated/non-correlated dynamics or break-up of charge-neutral ion couples with an increase of kT over the temperature range investigated, in accord with increased magnitudes of the associated transport properties. Overall, this NMRD investigation has provided detailed insights into the fundamental origins of the ion transport mechanics, where the dynamics recorded reveal the transient correlated/non-correlated rotational nature of the oppositely charged ions comprising the liquid.
Appendix A: molecular dynamics simulations and relaxation theory
A.1 Atomistic simulations
Atomistic simulations of the [C4mim][PF6] ionic liquid (IL) system consisting of 160 ion pairs were performed using the M.Dynamix package38 with standard three-dimensional periodic boundary conditions. The equations of motion were integrated using the Tuckerman–Berne double time step algorithm with short and long time steps of 0.2 and 2.0 fs, respectively. A short time step was used for integrating fast intra-ionic vibrations and non-bonded interactions within 0.5 nm, while a long time step was used for integrating van der Waals and electrostatic forces, as well as dihedral angle motions, within a cutoff distance of 1.5 nm. Electrostatic interactions between atom-centered point charges were treated with the standard Ewald summation method. Atomistic simulations were equilibrated for 15 ns in the isothermal/isobaric (NPT) ensemble maintained using the Nose–Hoover thermostat at 323 K and a barostat under 1 atm with time coupling constants of 1000 and 100 fs, respectively. Another 20 ns atomistic simulations were further performed and the simulation trajectories were recorded at an interval of 100 fs for further analysis. The center-of-mass radial distribution functions (RDFs) for cation–cation, cation–anion, and anion–anion are calculated and displayed in Fig. 5. It is shown that the first and the second solvation shells for cation–anion couples form at about 0.5 nm and 1.06 nm, respectively. Additionally, it is noticed that a weak ordering persists beyond 1.8 nm due to strong and long-range Columbic interactions. The first pronounced peak in the cation–cation RDF occurs at 0.79 nm, and the anion–anion RDF shows a bifurcated feature with two peaks registered at approximately 0.66 and 0.92 nm, respectively. This observation is attributed to the sequential ordering distribution of ionic groups induced by distinct cation–anion couples. The RDF displayed in Fig. 5 is very similar to the RDF presented as Fig. 5 in ref. 39.A.2 MD-simulation results
The liquid structures are depicted by the SDF displayed in Fig. 6 which give the probability of finding an atom around a center molecule in three-dimensional space, in contrast to the average values given by RDFs.(1) The first one is the SDF of the P atoms in the [PF6]− anions around [C4mim]+ cations. There are mainly three high probability regions where the P atoms are found, which contribute to the first shell in the corresponding cation–anion RDF. The three distinct regions are around the C2 and the CW atoms (C2 is the C atom bonded to two N atoms in the imidazolium ring, and CW is the other two C atoms in the imidazolium ring, respectively), both above and below the plane of the imidazolium ring, since these regions are highly positively charged. With two [PF6]− anions in each region, there are six counter-ions which can be found in the first shell. In addition, a minor region exists along the N–C methyl bond vector representing the second solvation shell in the corresponding cation–anion RDF.
(2) The second one is the SDF of the C2 atoms and two N atoms in the [C4mim]+ cations around the [PF6]− anion. A well-ordered distribution of the C2 and N atoms in the [C4mim]+ cation around the [PF6]− anion is observed. There are eight high probability regions, corresponding to the octahedron formed by the six F atoms in the [PF6]− anion.
When the spin dipole–dipole correlation functions are calculated the spin contributions are divided into intra-ionic and inter-ionic dipole couplings. The total dipole–dipole Hamiltonian was thus divided into Hintra(t) + Hinter(t) which is often an excellent approximation in simple liquids. The relaxation contributions in the ionic liquid, however, with strong Coulomb interactions motivated us to check this approximation. In Fig. 7 and 8 the cross correlation functions are displayed, referring to 〈Hintra(0)Hinter(t)〉 denoted as CDDcross(t). We noticed that no cross correlation is observed. The correlation functions are introduced in eqn (17) and (18) and determined using the MD-simulation trajectories of 9 ns length.
In Fig. 7 the normalized proton dipole–dipole correlation functions CDD0,Intra(t)/CDD0,Intra(0), CDD0,Inter(t)/CDD0,Intra(0), and the cross correlation function are displayed. The normalized Intra dipole–dipole correlation function displays a fast initial decay in the time interval 30–40 ps whereas the partially averaged correlation function with an order parameter S ≈ 0.6, (S2 = 0.4), is characterised by a correlation time (for a long time tail) τc of about 50 ns. CDD0,Inter(red) has an order parameter S ≈ 0.7, (S2 = 0.5) with a similar a decay of about 50 ns. The cross term is approximately zero over the whole time interval.
In Fig. 8 the corresponding correlation functions relevant for describing fluoride relaxation are displayed. The free anion correlation function CDD0,Intra(t)/CDD0,Intra(0) is displayed in black and decays with an integral correlation time of 10 ps and a long time tail with τc of about 25 ns. The inter-ionic F–H correlation function, CDD0,Inter(t)/CDD0,Inter(0), displays a fast initial decay of about 10 ps because of local fast rotations of the anion and the slow decay from S2 = 0.4 with a characteristic correlation time, τc = 25 ns. The lower part of Fig. 7 and 8 shows the logarithm of the normalized correlation functions.
In Fig. 9 the normalised inter-ionic 19F–H dipole–dipole correlation function is displayed showing a initial fast decay in the ps regime and a slow long time decay which is approximately single exponential and characterized by a effective correlation time of about 40 ns. The initial fast decay indicates that the symmetric [PF6]− ion relaxes due to local anisotropic reorientation, whereas the partially averaged inter-ionic H–F spin dipole–dipole interaction decays in the ns time regime. It was also clear from the MD-simulations that the translational diffusion of charge-neutral ion couples and the ions is very slow. Considering a charge-neutral ion couple in the beginning of the simulation, the counter ion changes its mother ion approximately once during the 9 ns simulation which indicates that the residence correlation time is in the ns time regime. The loss of correlation for the inter-ionic dipole–dipole correlation function is thus characterised by the effective correlation time τc defined in eqn (13) with a residence time τres in the ns regime. The time correlation functions have the functional form which is approximately given by:
| C(t) = (1 − S2)e−t/τf + S2e−t/τc | (15) |
A.3 1H and 19F spin–lattice relaxation and dipole–dipole correlation functions from MD simulations
The spin–dipole interaction Hamiltonian describing the spin interaction between a pair of spins (i,j) is: | (16) |
 which describes the dipole–dipole interaction of spin i to all possible j-spins.13 The dipole–dipole correlation functions that determine the relaxation contribution are given by:
which describes the dipole–dipole interaction of spin i to all possible j-spins.13 The dipole–dipole correlation functions that determine the relaxation contribution are given by:| CDDn,i(t) = 〈hDDn,i(t)hDDn,i(0)〉 | (17) |
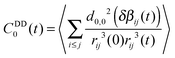 | (18) |
| CDD0(t)/CDD0(0) ≈ (1 − S2)e−t/τf + S2e−t/τs | (19) |
 | (20) |
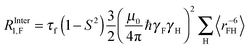 | (21) |
 the intra spin distance. The relaxation contributions due to inter ionic F–F dipole coupling and P–F are negligible.
the intra spin distance. The relaxation contributions due to inter ionic F–F dipole coupling and P–F are negligible.
In the charge-neutral ion couple [C4mim]⋯[PF6] the fluoride containing anion probably has a hydrogen-bond directed residence time where the partially averaged F–H dipole–dipole coupling is modulated by the reorientation of the entire ion couple and the chemical exchange process characterised by a residence time τres. When the fraction f(T) of free anions is small (at low temperature) the inter H–F relaxation contribution of F in [C4mim][PF6]− becomes dominant. The low field relaxation value is thus τc times the partially averaged dipole–dipole coupling given by:
 | (22) |
| 1/τc = 1/τR + 1/τres | (23) |
Author contributions
The author order is alphabetic: G. W. Driver: NMR analysis of the α term. Y. H.: numerical analysis of MD-data. T. S.: NMRD and Highfield NMR experiments. POW: designed the project, relaxation theory, NMRD experiments and analysis. A. L.: MD simulations. Y.-L. W.: MD simulations and analysis of MD-data. All authors contributed in writing the paper.Acknowledgements
This work is financed by the Swedish research council (VR).References
- M. Faraday, Philos. Trans. R. Soc. London, 1833, 123, 675–710 CrossRef.
- W. Hittorf, Ann. Phys., 1847, 148, 481–485 CrossRef.
- J. J. Berzelius, Lehrbuch der Chemie, Friedrich Vieweg und Sohn, Braunschweig, vol. 3, 1856 Search PubMed.
- M. J. Earle, M. Noe, A. Perosa and K. R. Seddon, RSC Adv., 2014, 4(3), 1204–1211 RSC.
- P. G. Jessop, Green Chem., 2011, 13(6), 1391–1398 RSC.
- J. P. Hallett and T. Welton, Chem. Rev., 2011, 111(5), 3508–3576 CrossRef CAS PubMed.
- R. Hayes, G. G. Warr and R. Atkin, Chem. Rev., 2015, 115, 6357–6426 CrossRef CAS PubMed.
- R. Kimmich and E. Anoardo, Prog. Nucl. Magn. Reson. Spectrosc., 2004, 44, 257–320 CrossRef CAS.
- W. R. Carper, P. G. Wahlbeck and A. Dölle, J. Phys. Chem. A, 2004, 108, 6096–6099 CrossRef CAS.
- V. V. Matveev, D. A. Markelov, E. A. Brui, V. I. Chizhik, P. Ingman and E. Lähderanta, Phys. Chem. Chem. Phys., 2014, 16, 10480–10484 RSC.
- D. Roy, N. Patel, S. Conte and M. Maroncelli, J. Phys. Chem. B, 2010, 114, 8410–8424 CrossRef CAS PubMed.
- R. P. Swatloski, J. D. Holbrey and R. D. Rogers, Green Chem., 2003, 5(4), 361–363 RSC.
- A. Abragam, Principles of Nuclear Magnetism, Clarendon Press, Oxford, 1961 Search PubMed.
- C. P. Slichter, Principles of Magnetic Resonance, Springer Verlag, 3rd edn, 1992, ch. 3 Search PubMed.
- J. McConnell, The theory of nuclear magnetic relaxation in liquids, Cambridge Univ. Press, 1987 Search PubMed.
- F. Mocci, A. Laaksonen, Y. Wang, G. Saba, A. Lai and F. Cesare Marincola, The Structure of Ionic Liquids, Springer, 2014, ch. 4, pp. 94–126 Search PubMed.
- J. H. Antony, A. Dölle, D. Mertens, P. Wasserscheid, W. R. Carper and P. G. Wahlbeck, J. Phys. Chem. A, 2005, 109, 6676–6682 CrossRef CAS PubMed.
- Y. Yasaka, M. L. Klein, M. Nakahara and N. Matubayasi, J. Chem. Phys., 2011, 134, 191101 CrossRef PubMed.
- Y. Yasaka, M. L. Klein, M. Nakahara and N. Matubayasi, J. Chem. Phys., 2012, 136, 074508 CrossRef PubMed.
- P. Ingman and G. W. Driver, Phys. Chem. Chem. Phys., 2012, 14, 13053–13057 RSC.
- K. Hayamizu, S. Tsuzuki, S. Seki and Y. Umebayashi, J. Phys. Chem. B, 2012, 116, 11284–11291 CrossRef CAS PubMed.
- A. O. Seyedlar, S. Stapf and C. Mattea, Phys. Chem. Chem. Phys., 2015, 17, 1653–1659 RSC.
- D. Kruk, R. Meier, A. Rachocki, A. Korpała, R. K. Singh and E. A. Rössler, J. Chem. Phys., 2014, 140, 244509 CrossRef CAS PubMed.
- S. Tsuzuki, ChemPhysChem, 2012, 13, 1664–1670 CrossRef CAS PubMed.
- Y. Ayant, E. Belorizky, J. Alizon and J. Gallice, Le Journal de Physique, 1975, 36(10), 991–1004 CrossRef CAS.
- Y. Ayant, E. Belorizky, P. Fries and J. Rosset, Le Journal de Physique, 1977, 38(3), 325–337 CrossRef CAS.
- Z. Liu, S. Huang and W. Wang, J. Phys. Chem. B, 2004, 108(34), 12978–12989 CrossRef CAS.
- S. Berger and S. Braun, 200 and More NMR Experiments: A Practical Course, Wiley-VCH, Weinheim, 2004, p. 137 Search PubMed.
- C. T. Moynihan, in Ionic Interactions: From Dilute Solutions to Fused Salts, ed. S. Petrucci, Academic, New York, 1971, vol. 1, pp. 261–384 Search PubMed.
- R. A. Robinson and R. H. Stokes, Electrolyte Solutions, Dover, 2nd edn, 2002 Search PubMed.
- (a) K. R. Harris, J. Phys. Chem. B, 2010, 114, 9572–9577 CrossRef CAS PubMed; (b) K. R. Harris and M. Kanakubo, Faraday Discuss., 2012, 154, 425–438 RSC.
- H. Weingärtner, Angew. Chem., Int. Ed., 2008, 47, 654–670 CrossRef PubMed.
- (a) D. R. MacFarlane and K. R. Seddon, Aust. J. Chem., 2007, 60, 3–5 CrossRef CAS; (b) H. A. Every, A. G. Bishop, D. R. MacFarlane, G. Orädd and M. Forsyth, Phys. Chem. Chem. Phys., 2004, 6, 1758–1765 RSC; (c) S. K. Davidowski, F. Thompson, W. Huang, M. Hasani, S. A. Amin, C. Austen Angell and J. L. Yarger, J. Phys. Chem. B, 2016, 120, 4279–4285 CrossRef CAS PubMed; (d) D. R. MacFarlane, M. Forsyth, E. I. Izgorodina, A. P. Abbott, G. Annat and K. Fraser, Phys. Chem. Chem. Phys., 2009, 11, 4962–4967 RSC.
- B. Berne and S. A. Rice, J. Chem. Phys., 1964, 40, 1347–1362 CrossRef CAS . (see section V. Discussion).
- F. Klanberg, in The Chemistry of Non-Aqueous Solvents: Acidic and Basic Solvents, ed. J. J. Lagowski, Academic Press, 1967, vol. II Search PubMed.
- M. Sha, Z. Tang, G. Zhu and W. Guozhong, J. Phys. Chem. Lett., 2015, 6, 3713–3720 CrossRef CAS PubMed.
- W. Zhao, F. Leroy, B. Heggen, S. Zahn, B. Kirchner, S. Balasubramanian and F. Müller-Plathe, J. Am. Chem. Soc., 2009, 131, 15825–15833 CrossRef CAS PubMed.
- A. P. Lyubartsev and A. Laaksonen, Comput. Phys. Commun., 2000, 128(3), 565–589 CrossRef CAS.
- T. I. Morrow and E. J. Maginn, J. Phys. Chem. B, 2002, 106, 12807–12813 CrossRef CAS.
- D. M. Brink and G. R. Satchler, Angular Momentum, Oxford Univ. Press, 3rd edn, 1993 Search PubMed.
- P.-O. Westlund and R. M. Lynden-Bell, J. Magn. Reson., 1987, 72, 522–531 CAS.
- B. Halle and H. Wennerström, J. Chem. Phys., 1981, 75, 1928–1943 CrossRef CAS.
- G. Lipari and A. Szabo, J. Am. Chem. Soc., 1982, 104, 4546–4559 CrossRef CAS.
- B. Halle, J. Chem. Phys., 2009, 131, 224507 CrossRef PubMed.
Footnotes |
| † Department of Materials and Environmental Chemistry, Arrhenius Laboratory, Stockholm University, Stockholm SE 106 91, Sweden. |
| ‡ Department of Chemistry, KTH Royal Institute of Technology, 114 28 Stockholm, Sweden. |
| This journal is © the Owner Societies 2017 |





