Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Collective proton transfer in ordinary ice: local environments, temperature dependence and deuteration effects
Christof
Drechsel-Grau
 * and
Dominik
Marx
*
* and
Dominik
Marx
*
Lehrstuhl für Theoretische Chemie, Ruhr-Universität Bochum, 44780 Bochum, Germany. E-mail: Christof.Drechsel-Grau@rub.de; Dominik.Marx@rub.de; Fax: +49 234 321 4045; Tel: +49 234 322 6485
First published on 7th November 2016
Abstract
The transfer of multiple protons in hydrogen-bonded networks usually occurs one proton at a time. At sufficiently high temperatures, each proton transfers via thermally activated hopping along its hydrogen bond, thereby moving a charge defect through the network. At low temperatures, quantum-mechanical tunnelling might set in instead, thus avoiding hopping over the energy barriers. In the case of several transferring protons, independent thermal hopping or quantum tunnelling of the individual protons becomes less favourable because of a significant creation of charge defects. In individual molecules or hydrogen-bonded molecular complexes, for instance, double proton transfer is often found to be concerted. Multiple proton transfer that avoids charge defects can occur in cyclic topologies built from several hydrogen bonds that allow for directional chains of proton transfer. This requires perfect proton order within these rings, which imposes handedness and thus chirality, and changes parity upon transfer of all protons. Ordinary ice, which is hexagonal ice Ih, is the most stable form of crystalline ice obtained upon freezing liquid water at ambient pressure and consists of interconnected six rings of oxygen atoms that host six protons each. These hexagonal rings remain proton disordered even down to low temperatures, as heralded by the residual entropy of ice Ih. However, owing to combinatorics, a certain number of these six rings is proton ordered in macroscopic crystals. These chiral hexameric rings might support coherent tunnelling of the hosted protons. Indeed, there is some evidence in the recent literature, both experimental and simulational, that correlated tunnelling of all six protons might be possible in proton-ordered six rings in ice Ih if temperatures are low enough. In this Perspective, the key ideas and previous findings will be reviewed in the light of relevant experiments with a focus on available ab initio path integral simulation work supplemented with additional data provided herein.
1 Background: nuclear quantum effects and multiple proton transfer
Proton tunnelling belongs to the hallmarks of quantum mechanics. It represents the classically forbidden motion of a proton through the potential energy barrier that separates the final from the initial state – instead of the classically allowed thermally activated process of hopping over the top of that barrier. Although this intriguing phenomenon has attracted attention since the beginning of quantum mechanics, it is the exception rather than the rule in standard condensed phase chemical reactions at not too low temperatures. Much more common quantum effects in chemical kinetics are quantum delocalisation and zero-point motion. Proton tunnelling gets strongly suppressed upon increasing the height and/or the width of potential energy barriers and typically requires unusually favourable circumstances (such as short hydrogen bonds and stiff molecular skeletons) to contribute appreciably to chemical dynamics.Liquid water and aqueous solutions first come to mind when looking for quantum effects in hydrogen-bonded networks, and in particular for proton tunnelling.1 Despite these expectations, molecular simulations that explicitly include nuclear quantum effects in terms of path integrals disclosed that both proton and hydroxide transfers in water under ambient conditions are mainly driven by specific hydrogen-bond fluctuations around these charge defects and, therefore, are essentially thermally activated processes.1–5 These fluctuations dramatically lower the energy barrier, which is unacceptably high at the typical hydrogen-bond distances in such systems of ∼2.8 Å but is greatly reduced if the donor–acceptor distance for proton transfer is decreased, for instance as a result of thermal motion or extreme compression.1 Therefore, the reduction of the intermolecular O⋯O distance in conjunction with proton transfer is often observed for aqueous systems and goes hand in hand with an essentially thermally activated transfer process.1 If at all, proton tunnelling during proton transfer under ambient conditions might occur near the barrier top and only modulate the thermal activation dominating chemical kinetics. When it comes to the hosting liquid, i.e. water, nuclear quantum effects on its structure have also been shown to be effectively rather moderate,6–8 which has been traced back later to so-called “competing quantum effects”, as recently comprehensively reviewed.9 Overall, nuclear quantum effects in liquid water and aqueous solutions mostly lead to broadened distributions and quantum delocalisation, but they rarely change the qualitative picture of the underlying physical process with reference to the classical, i.e. thermally activated process.
The strength of hydrogen bonds is a key feature influencing the possibility of proton tunnelling and depends sensitively on the potential energy surface.10 Given the complexity of hydrogen bonding interactions already at the level of an individual water dimer,11,12 it is unsurprising that the wetting behaviour of various surfaces13 and a variety of nanostructures on metals14 indicate a vast richness of hydrogen-bond strengths. Proton transfer to and from water molecules on a metal oxide surface, for example, has been identified as the pathway for hydrogen migration.15 Although double proton transfer is a coherent tunnelling process in the formic-acid dimer at low temperatures, as evidenced by the measured tunnelling splitting in the gas phase,16 the transfer of the two protons via zero-point motion is quantum mechanically uncorrelated at higher temperatures.17 In contrast, double proton transfer is stepwise in hydroporphyrins.18 In biologically relevant systems, hydrogen-bonded chains create pathways for proton transfer,19 and proton-ordered, hydrogen-bonded, cyclic topologies might contribute to glycine formation in the interstellar medium.20 These examples illustrate the delicate balance of the strength of hydrogen bonds in a network between the limits of a sufficient coupling for strong donor–acceptor interactions and sufficient flexibility for donor–acceptor fluctuations.
Hexagonal ice, dubbed ice Ih, provides a rich playground for the study of nuclear quantum effects owing to its peculiar arrangement governed by the ice rules,21,22 giving rise to its residual entropy.23,24 Nuclear quantum effects affect the molecular dipole-moment distribution in hexagonal ice25 and explain the anomalous lattice expansion upon H → D substitution.26 Ice Ih is the most stable pure phase of water at low temperature and ambient pressure.22 Cubic ice I, denoted as Ic, is its metastable variant but never transforms to ice Ih upon cooling.22 A fully proton-ordered form of ice Ih, called ice XI, only exists in the presence of dopants such as KOH and is thus not a pure phase of solid H2O.22 Hexagonal ice is, therefore, the most natural phase of solid water to study nuclear quantum effects at low temperature and ambient pressure. Nuclear quantum effects also underlie the low-temperature dynamics of non-crystalline water near the glass transition temperature.27 Overall, nuclear quantum effects in solid water seem more important compared to the role they play in liquid water.
Beyond hydrogen-bonded complexes in the gas phase, tunnelling of individual protons is already quite rare and requires short donor–acceptor distances as in the case of an enzyme with a short hydrogen bond,28 low temperatures as in hydrogen-bonded ferroelectric materials,29–31 or high pressure as in ice VII/VIII,32,33 but the tunnelling of multiple protons is even scarcer. In the condensed phase at low temperature, tunnelling of multiple protons is known since long to occur in hydrogen-bonded molecular crystals34–37 or within individual molecules embedded in crystals.38,39 More recently, STM experiments have paved the way for controlling correlated proton tunnelling in a water tetramer.40,41 Most interestingly, quasi-elastic neutron scattering (QENS) experiments provided evidence for concerted proton tunnelling involving several protons in hexagonal ice Ih at low temperature.42 As a result of detailed analyses and partial deuteration of ice, it has been suggested that the tunnelling contribution to the total signal stems from the concerted movement of all six protons in proton-ordered water hexamers. The latter occur also in macroscopically proton-disordered ice Ih crystals owing to statistical reasons. Stimulated by these experimental suggestions (ab initio path integral) simulations43,44 of atomistic ice as well as (quantum U(1) lattice gauge) theory45 of lattice ice investigated the possibility of collective multiple proton tunnelling in ice.
In this Perspective, we extend our previous work on collective proton transfer in hexagonal ice,43,44 identifying the temperature region in which the crossover occurs from the low-temperature quantum behaviour to the high-temperature classical behaviour; it is important to note that the notion “classical simulation” refers here exclusively to the representation of the nuclei in terms of classical statistical mechanics (versus quantum statistical mechanics in the case of “quantum simulations”) while the interactions between the nuclei are always obtained from concurrent electronic structure calculations as these ab initio simulations proceed (see Section 6 for background, technical details, and accuracy). We also elucidate the role of the local environment in the proton-ordered six ring embedded in the proton-disordered crystal, and we investigate the influence of the deuteration fraction on the correlated transfer of six protons. In the light of these analyses and conclusions, we also review the recent experimental and theoretical evidence for collective proton tunnelling in hydrogen-bonded networks at low temperature in the subsequent discussion Section 3.
2 Collective proton transfer in ice Ih as seen by ab initio path integrals
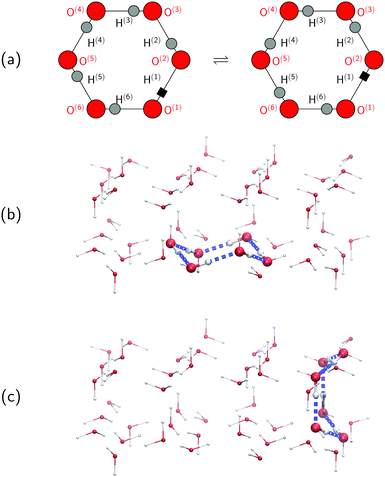
To set the stage for this study, let us first concisely summarise the results of our simulations on collective proton transfer in hexagonal ice.43,44 As in the present work, we used previously also (ab initio path integral46–48) quantum simulations (see Section 6 for background and details) to investigate the nature of the transfer of six protons within a proton-ordered six ring (water hexamer) embedded in proton-disordered hexagonal ice (see Fig. 1a and b). Qualitative differences in the mechanism of collective proton transfer prevail as a function of temperature.43 At high temperature, the thermally activated transfer (hopping) of individual protons creates charge defects associated with a high free energy barrier. At low temperature, the six protons tunnel in a perfectly correlated (and concerted) manner like a delocalised quasi-particle that essentially prevents charge defects; the corresponding effective free energy barrier is greatly reduced compared to the high-temperature (classical) regime. To go beyond the temperature dependence, we studied the effect of partial deuteration on collective proton transfer at 50 K,44 which leads experimentally to the suppression of the signal in the QENS study.42 Compared to the system containing only protons, the partially deuterated system exhibits a higher free energy barrier and higher occurrence of charge defects in the transition state. Whereas all six hydrogen bonds of the proton-ordered six ring in the fully protonated system are equivalent, partial deuteration renders the hydrogen bonds inequivalent. Charge defects localise in a symmetric Zundel-like complex,44i.e. [HO⋯D⋯OH], around the deuteron in the proton-ordered six ring, thus destroying perfectly correlated collective proton tunnelling and the delocalised quasi-particle consisting of six protons. In summary, we can safely conclude in this state that the results of the above temperature- and isotope-dependent simulational work43,44 do not contradict collective proton tunnelling of six protons in hexagonal ice at low temperature.Despite the published evidence in favour of collective proton transfer within proton-ordered six rings in overall proton-disordered ice Ih, several questions persist. Ordinary (hexagonal) ice consists of both chair-like and boat-like six rings, which constitute the basal planes or interconnect these basal planes, respectively (see Fig. 1b and c). The impact of the six-ring conformation on the concerted (versus sequential) nature of proton transfer is unknown. We also ignore the exact temperature dependence of proton transfer and, in particular, in what temperature range the change in scenario from perfectly concerted many-body quasi-particle tunnelling to the sequential hopping of the individual protons occurs, which is not expected to be a sharp transition but a smooth crossover.49 Finally, we ask if even a single deuteron impurity in the system might perturb the concerted nature of the transfer process within the ordered six ring or if additional deuterons in the environment are required, as experimentally realised in the QENS study (vide infra).42 We address all these effects, and combinations thereof, in what follows as the basis for a general discussion.
2.1 Influence of six-ring conformation
Every oxygen in hexagonal ice is tetrahedrally surrounded by four nearest oxygen neighbours. The oxygen tetrahedra are connected in such a way that six oxygens form cyclic rings, as illustrated in Fig. 1. The cyclic six rings either lie in the basal plane and adopt a chair-like conformation (Fig. 1b) or connect adjacent basal planes and adopt a boat-like conformation (Fig. 1c), see e.g.ref. 22 for comprehensive background on ice polymorphs. The chair-like and boat-like conformations constitute, in principle, different local environments, and we investigate below how the six-ring conformation influences collective proton transfer.To elucidate the effect of the local environment on this phenomenon, we induced collective proton transfer at 50 K both in chair-like (filled blue squares in all figures; see also Table 1) and boat-like (empty red circles in Fig. 2) proton-ordered six rings without any D impurities. The process showed no qualitative differences in the two six-ring conformations, as evidenced by the respective data in Fig. 2, which exhibits essentially superimposed filled blue squares and empty red circles for all quantities that characterise collective proton tunnelling. Thus, to improve clarity and readability, only data for chair-like proton-ordered six-ring conformations are presented in Fig. 3–10 because the data for boat-like conformations hardly differ.
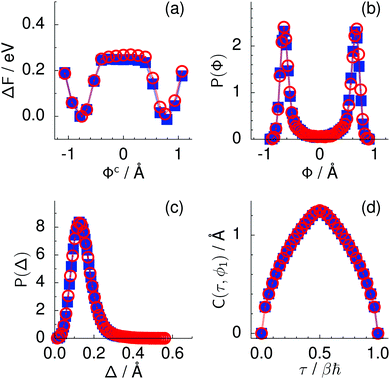 | ||
Fig. 2 Comparison of collective proton transfer in chair-like (filled blue squares) and boat-like (empty red circles) proton-ordered six rings in proton-disordered hexagonal ice (see Fig. 1) for key observables: (a) free energy profile along the constrained collective proton transfer coordinate Φc; (b) distribution of the collective proton transfer coordinate 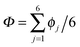 ; (c) distribution of ; (c) distribution of 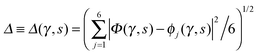 ; and (d) representative imaginary time correlation function C(τ,ϕ1) = 〈|ϕ1(τ) − ϕ1(0)|2〉1/2. See Table 1 for symbol definitions and the text for detailed variable definitions. ; and (d) representative imaginary time correlation function C(τ,ϕ1) = 〈|ϕ1(τ) − ϕ1(0)|2〉1/2. See Table 1 for symbol definitions and the text for detailed variable definitions. | ||
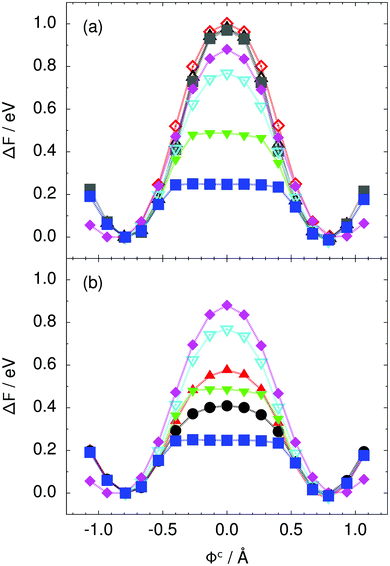 | ||
| Fig. 3 Free energy profile along the constrained collective proton transfer coordinate Φc in proton-ordered six rings (see Fig. 1) for (a) the pure H2O systems and for (b) all quantum systems. Simulations that treat all nuclei classically are shown in (a) for 50 (filled grey squares), 100 (empty black up triangles), and 300 K (empty red diamonds). Simulations that treat all or most nuclei quantum mechanically are shown in (b) for non-deuterated (filled blue squares: 50 K; filled green down triangles: 100 K; empty cyan down triangles: 200 K; filled pink diamonds: 320 K) and partially deuterated (filled black circles: 50 K and one deuteron; filled red up triangles: 50 K and one deuteron per six ring) systems. See Table 1 for symbol definitions. | ||
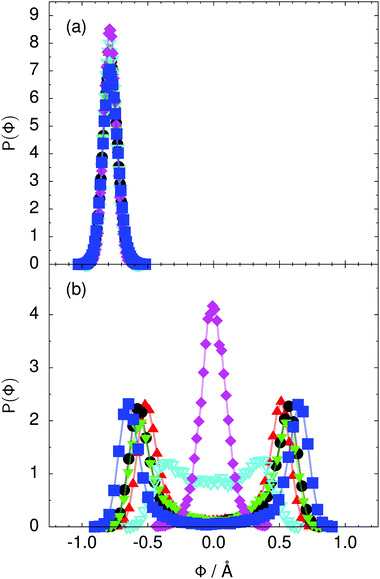 | ||
Fig. 4 Distribution of the collective proton transfer coordinate (see the text), 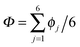 , (a) in the initial state and (b) in the transition state for collective proton transfer in a proton-ordered six ring (see Table 1 for symbol definitions). , (a) in the initial state and (b) in the transition state for collective proton transfer in a proton-ordered six ring (see Table 1 for symbol definitions). | ||
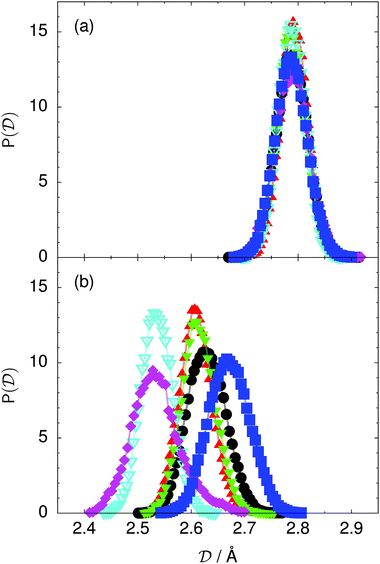 | ||
| Fig. 5 Distribution of the average donor–acceptor distance within the chair-like proton-ordered six ring (a) in the initial state and (b) in the transition state for collective proton transfer (see Table 1 for symbol definitions). | ||
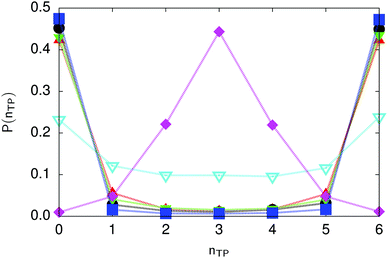 | ||
| Fig. 6 Distribution of the number of transferred protons in the transition state for collective proton transfer (see Table 1 for symbol definitions). Data points at 50 K overlap on the scale of this figure for P(nTP) ∼ 0. | ||
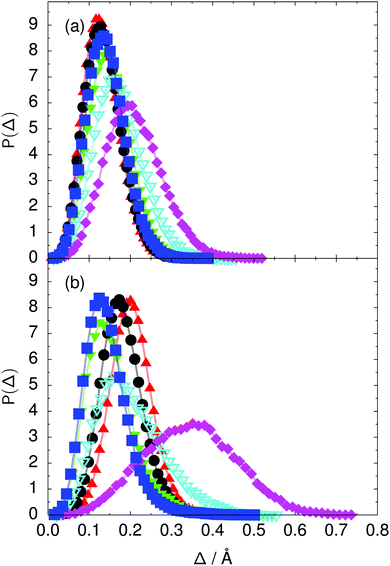 | ||
Fig. 7 Distribution of the deviation 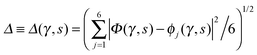 of the local proton transfer coordinates ϕj from the collective proton transfer coordinate Φ for each computed configuration γ and at all imaginary times τ ∈ [0,ℏβ] as represented by the discrete Trotter bead index s = 1,…,P (a) in the initial state and (b) in the transition state for collective proton transfer (see Table 1 for symbol definitions). Note that Δ = 0 indicates perfect correlation among the global coordinate Φ and all local proton transfer coordinates ϕj at that particular configuration and Trotter slice. of the local proton transfer coordinates ϕj from the collective proton transfer coordinate Φ for each computed configuration γ and at all imaginary times τ ∈ [0,ℏβ] as represented by the discrete Trotter bead index s = 1,…,P (a) in the initial state and (b) in the transition state for collective proton transfer (see Table 1 for symbol definitions). Note that Δ = 0 indicates perfect correlation among the global coordinate Φ and all local proton transfer coordinates ϕj at that particular configuration and Trotter slice. | ||
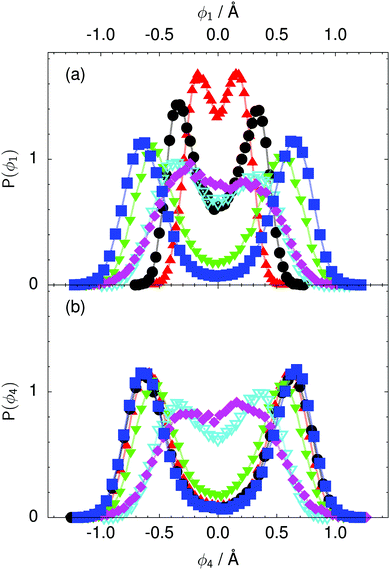 | ||
| Fig. 8 Distribution of the local proton transfer coordinate (a) ϕ1 and (b) ϕ4 in the transition state for collective proton transfer (see Fig. 1 for the numbering of the hydrogen bonds and Table 1 for symbol definitions). Black circles, red up triangles, and blue squares in (b) overlap on the scale of this figure. | ||
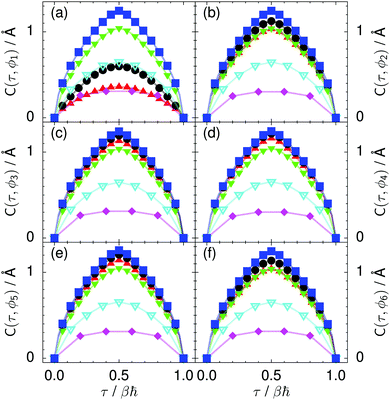 | ||
| Fig. 9 Imaginary time correlation function of all local proton transfer coordinates ϕ1, ϕ2,…, ϕ6, defined as C(τ,ϕj) = 〈|ϕj(τ) − ϕj(0)|2〉1/2, in (a) to (f) in the transition state for collective proton transfer (see Fig. 1 for the numbering of the hydrogen bonds and Table 1 for symbol definitions). Filled red up and green down triangles overlap in (b) and (f); filled black circles and blue squares overlap in (c)–(e). | ||
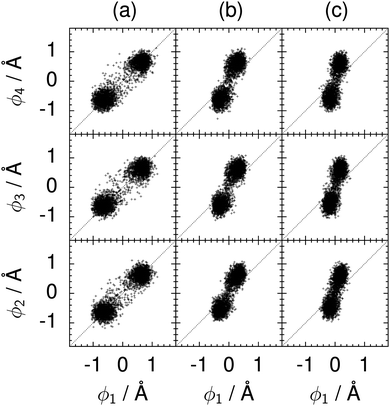 | ||
| Fig. 10 Correlation between the local proton transfer coordinates ϕ1 and ϕj with j = 2, 3, 4 in the transition state for collective proton transfer in a chair-like proton-ordered six ring at 50 K (see Fig. 1 for the numbering of the hydrogen bonds). Panel (a) represents pure H2O. Panels (b) and (c) represent systems with one deuteron and with one deuteron per six ring, respectively. For clarity, only every hundredth data point is displayed. | ||
According to the full quantum simulations at 50 K, collective proton tunnelling43,44 exhibits strong correlations between the collective (or global) proton transfer coordinate, 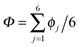 , and all six individual proton transfer coordinates ϕj = d(O(j)H(j)) − d(H(j)O(j+1)) in the six ring. Above, d(XY) is the distance between sites X and Y, where O(j), H(j), and O(j+1) denote the donor, the proton, and the acceptor of hydrogen bond j in the initially proton-ordered six ring (see Fig. 1a for our labelling of the hydrogen bonds). This concerted proton motion within the six ring results in essentially identical distributions P(ϕj) of the six individual proton transfer coordinates in the transition state (shown for j = 1 and 4 in Fig. 8 for chair-like conformations) and large quantum delocalisation in the transition state, as seen from Fig. 2d.
, and all six individual proton transfer coordinates ϕj = d(O(j)H(j)) − d(H(j)O(j+1)) in the six ring. Above, d(XY) is the distance between sites X and Y, where O(j), H(j), and O(j+1) denote the donor, the proton, and the acceptor of hydrogen bond j in the initially proton-ordered six ring (see Fig. 1a for our labelling of the hydrogen bonds). This concerted proton motion within the six ring results in essentially identical distributions P(ϕj) of the six individual proton transfer coordinates in the transition state (shown for j = 1 and 4 in Fig. 8 for chair-like conformations) and large quantum delocalisation in the transition state, as seen from Fig. 2d.
Key analysis underlying the previous conclusion43 that all six protons tunnel in a perfectly concerted manner in the sense of a delocalised quasi-particle is provided by the data in Fig. 2c; the interested reader is referred to additional so-called world-line analysis of individual tunnelling paths in Fig. 3 of ref. 43 and to the representative videos present in its ESI. The many-body concerted nature of the tunnelling process at low temperature is disclosed by comparing in a statistical sense the imaginary time evolution of the individual six local proton transfer coordinates ϕj (as depicted in Fig. 2d for ϕ1 in terms of its correlation function) to the one of the collective proton transfer coordinate Φ. This is established by computing the average difference 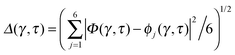 between the collective and all six local proton transfer coordinates, i.e. deviations between Φ(τ) and all ϕj(τ) at each sampled configuration γ and all imaginary times τ ∈ [0,ℏβ] as represented by the discretised Trotter beads s given in the caption of Fig. 7 (see Section 6 for background). Thus, 〈Δ〉 ≡ 0 Å if all local proton transfer coordinates ϕj(τ) always exactly follow the global Φ(τ) for all imaginary times τ. For the initial state depicted in panel (a) of Fig. 7, the distribution P(Δ) at 50 K is sharply peaked at a small value Δmax that quantifies ordinary quantum broadening at low temperatures due to zero-point motion. Importantly, its shape in the transition state at 50 K is statistically identical to that in the initial state, see panel (b), thereby unveiling that all six protons must move collectively as a quasi-particle at 50 K.
between the collective and all six local proton transfer coordinates, i.e. deviations between Φ(τ) and all ϕj(τ) at each sampled configuration γ and all imaginary times τ ∈ [0,ℏβ] as represented by the discretised Trotter beads s given in the caption of Fig. 7 (see Section 6 for background). Thus, 〈Δ〉 ≡ 0 Å if all local proton transfer coordinates ϕj(τ) always exactly follow the global Φ(τ) for all imaginary times τ. For the initial state depicted in panel (a) of Fig. 7, the distribution P(Δ) at 50 K is sharply peaked at a small value Δmax that quantifies ordinary quantum broadening at low temperatures due to zero-point motion. Importantly, its shape in the transition state at 50 K is statistically identical to that in the initial state, see panel (b), thereby unveiling that all six protons must move collectively as a quasi-particle at 50 K.
The concerted proton motion at 50 K also leads to a negligible number of formal charge defects in the transition state, as evidenced by the bimodal distribution of the number of transferred protons peaked at 0 and 6 in Fig. 6, and to a negligible probability of observing Φ = 0 (Fig. 2b). All protons are statistically identical within the sampling error, as seen from Fig. 8 and 10, which shows the distribution of and the correlation between representative local proton transfer coordinates. Hydrogen bond 4 is located opposite of hydrogen bond 1 in the six ring, and hydrogen bonds 2 and 3 are symmetrically equivalent to hydrogen bonds 6 and 5, as illustrated in Fig. 1. The strong correlation among protons in the transition state is also essentially identical for collective proton transfer in chair-like and boat-like six rings (see Fig. 2c). The rather small contraction of the six-ring skeleton for the boat-like conformation resembles that for the chair-like conformation, as seen from the distribution of the mean donor–acceptor distance in Fig. 5, and results in a similarly low free energy barrier, displayed in Fig. 2a.
The strong similarity between the full quantum simulation results for collective proton transfer in chair-like and boat-like six rings at 50 K shows that the conformation of proton-ordered six rings within hexagonal ice, and thus the local environment, has no effect on the computed observables. What matters most for collective proton transfer at sufficiently low temperatures in non-deuterated hexagonal ice is the cyclic arrangement of the six water molecules within the crystal and the local proton order within the six ring.
Having disclosed the negligible influence of the local six-ring conformation on collective proton transfer above, we focus on chair-like proton-ordered six rings throughout the remainder of this Perspective.
2.2 Influence of temperature
Prior work on hexagonal ice43,44 has only established two limiting cases, namely concerted quantum tunnelling at 50 K (filled squares in all figures) and sequential classical proton transfer at 320 K (diamonds in all figures). Importantly, the high-temperature quantum simulations were found to share all qualitative features of classical simulations at 300 K. The shapes of the free energy profiles as well as the resulting barrier heights are seen to be essentially identical at 300, 100, and 50 K provided that the protons are treated as classical particles (see Fig. 3). Thus, the free energy barrier for quantum simulations at 320 K approaches that of these classical simulations, which demonstrates that thermal fluctuations do not influence the system if nuclear motion is treated classically in this temperature window. This implies that the proton transfer barrier is very high at the scale of the thermal energy; note that 1 kBT ≈ 0.026 eV or ≈0.6 kcal mol−1 at 300 K. We thus consider herein the temperature dependence of collective proton transfer for quantum systems only over the entire temperature range from 50 to 320 K by including results for 100 (filled down triangles) and 200 K (empty down triangles).Fig. 3–10 show the substantial qualitative similarity between quantum simulations at 50 and 100 K. Both at 50 and 100 K, the bimodal transition state distributions of the collective proton transfer coordinate Φ (Fig. 4) and of the number of transferred protons (Fig. 6) show no significant probability of observing either configurations with Φ = 0 or one to five transferred protons, respectively. Small quantitative differences prevail, suggesting that thermal fluctuations increasingly perturb quantum fluctuations at higher temperatures. In particular, the simulations at 100 K exhibit smaller quantum delocalisation (Fig. 9) and a smaller average donor–acceptor distance (Fig. 5) in the six ring than the simulations at 50 K, resulting in a larger free energy barrier at 100 K (Fig. 3).
In contrast to the concerted proton transfer at 50 and 100 K, collective proton transfer exhibits charge defects in a high fraction of sampled transition state configurations at 320 K, resulting in a large free energy barrier (see Fig. 3) and in a unimodal distribution of the number of transferred protons in Fig. 6, according to the full quantum simulations at 320 K, similar to the classical 300 K case. Most transition state configurations exhibit a collective proton transfer coordinate close to zero (see Fig. 4), which also implies the presence of formal charge defects. Quantum delocalisation and correlation between the collective and local proton transfer coordinates reach their minimum at 320 K, as shown in Fig. 7 and 9.
The limiting scenarios of concerted tunnelling at low temperature and uncorrelated sequential proton transfer at high temperature raise the question of where the temperature of transition between the two scenarios lies. Although we cannot provide a precise transition temperature, which is anyway expected to occur in the sense of a smooth crossover,49 our simulation results indicate a crossover regime somewhere above 100 and below 200 K, where the system's behaviour resembles neither the typical low-temperature quantum regime nor the high-temperature classical limit. The mean donor–acceptor distance in the transition state at 200 K (see Fig. 5) is closer to that at 320 K (∼2.5 Å) than to that at 50 K (∼2.7 Å). The distributions of the individual proton transfer coordinates in Fig. 8 also resemble those at 320 K more than those at 50 K. In contrast, the peak positions of P(Δ) in Fig. 7 show no significant difference when going from the initial to the transition state, similar to the low-temperature quantum scenario. Fig. 9 indicates a quantum delocalisation in between the quantum and classical limits. Its magnitude of ∼0.5 Å is a bit shorter than the jump distance extracted from experiment.42Fig. 4 and 6 show characteristics of both the quantum and the classical scenario at 200 K. On the one hand, the transition state distributions are bimodal, as in the quantum regime. On the other hand, the same distributions show substantial non-zero probabilities for Φ = 0 and P(nTP) = 1–5, as in the classical regime. These observations support not only a crossover from quantum to classical behaviour somewhere between 100 and 200 K but also the experimental observation of a signal up to unexpectedly high temperatures; the experimental data up to 100 K were considered consistent with non-classical proton jumps.42 The present work thus provides specific characteristics of the transition temperature region and its relation to the limiting high- and low-temperature scenarios.
2.3 Influence of the deuteration fraction
Quantum behaviour not only depends on temperature but also on the nuclear mass of the particles involved. Although zero-point vibrations of hydrogen nuclei bonded to heavier atoms such as carbon, nitrogen, and oxygen constitute the most common quantum effect, tunnelling depends sensitively on the mass of the tunnelling particle and, in turn, provides a means to detect quantum behaviour.Replacing, on average, one proton per six ring by a deuteron (corresponding to a deuteration fraction of about 20%) has been shown to lead to the breakdown of collective proton tunnelling at low temperature both in the QENS measurements42 and in the ab initio path integral simulations.44 This deuteration represents a significant perturbation because it not only replaces about one fifth of all protons in the system but also destroys on average the symmetry in the proton-ordered six rings. At variance with experiment, computer experiments allow us to replace protons by deuterons in a controlled manner. Here, we study the extreme case of replacing only one proton by a deuteron in the proton-ordered six ring to investigate the effect of this much milder perturbation of the entire system.
We found that even a single deuteron in the entire system, located in the proton-ordered six ring (filled black circles), strongly perturbs the collective proton tunnelling process. The free energy barrier almost doubles compared to the fully protonated system (filled blue squares), as seen from Fig. 3. One deuteron in the six ring also leads to significant deviations from the all-proton system in the distributions P(Δ), P(ϕ1), and C(τ,ϕ1), and in the correlation between local proton transfer coordinates in the transition state, see Fig. 7–10, respectively. Although deuteration hardly affects the distributions of other collective variables, these deviations suggest that the replacement of a single proton by a deuteron in the entire system, if taking place in the proton-ordered six ring, induces localisation around this impurity very similar to the case of one deuteron per six ring.44
The effect of deuterating a single proton site in the entire system appears substantially weaker than deuterating one proton in each six ring (filled red up triangles), but the qualitative effect on the fully protonated system is the same. Fig. 10(b) and (c) show that partial deuteration destroys the perfect correlation among hydrogen bonds within the proton-ordered six ring, whereas Fig. 8 and 9 reveal the influence of deuterons on the environment outside the proton-ordered six ring. Adding deuterons to the environment increases the free energy barrier and the amount of localisation of the protons within the proton-ordered six ring.
Having discussed the effects of temperature and deuteration separately, we compare them in the following section.
2.4 Estimating the quantum-to-classical crossover temperature
The free energy profiles in Fig. 3b show that the activation free energy of the fully protonated system at 100 K is higher than that of the system with a single deuteron and lower than that of the system with one deuteron per six ring at 50 K. A similar bracketing is observed for the distributions of the collective proton transfer coordinate and the mean donor–acceptor distance in Fig. 4b and 5b. In contrast, the distributions P(Δ) and P(ϕ1) of the deuterated systems resemble their protonated counterparts at 200 K more closely than those at 100 K, as seen from Fig. 7b and 8a.The subtle effects of temperature and deuteration on correlated proton transfer raise the question at what point the collective proton tunnelling breaks down. Careful analysis of Fig. 3–10 suggests that collective proton tunnelling exists when the following three criteria are met. First, the free energy profile exhibits a plateau in the transition state region. Second, the peak of the transition state distribution P(Δ) lies below 0.15 Å. Third, the imaginary time correlation functions of all local proton transfer coordinates must exhibit a delocalisation of at least the proton transfer distance, i.e. 0.8 Å.
According to the above criteria extracted from our simulation data, yet being of a purely phenomenological nature, multiple proton transfer in hexagonal ice occurs for fully protonated systems at temperatures up to about 100 K as a concerted many-body tunnelling process that involves all protons within proton-ordered hydrogen-bonded cyclic hexamers in the spirit of a quasi-particle. In contrast, temperatures above 100 K or one deuteron impurity in locally proton-ordered six rings at 50 K already induce a clear breakdown of this peculiar collective proton tunnelling process. This assessment is consistent with our earlier finding from Section 2.2 of a broad crossover regime from quantum to classical behaviour somewhere between 100 and 200 K.
3 Discussion
The simulations presented herein predict that the mechanism of the transfer of six protons in a locally proton-ordered six ring in hexagonal ice depends on temperature and isotopic composition as discussed in the previous section. This greatly extends the previous findings that, at 50 K, all six protons in proton-ordered six rings tunnel collectively in a perfectly concerted manner akin to a quasi-particle, which is destroyed by either partial deuteration or heating the system up to room temperature.43,44 These conclusions hinge on a set of approximations in order to make the underlying large-scale quantum simulations computationally practical. First of all, the simulations assume proton transfer along hydrogen bonds exclusively within the proton-ordered six rings by explicitly preventing proton transfer of the ordered six ring with its environment via hydrogen bonds (see Section 6 for details). They also induce the collective proton transfer within the proton-ordered hexamer by means of a constraint, as explained in Section 6 (which, however, does not impose the collective nature of the transfer but allows for defect formation as indeed produced in the high-temperature limit). Another approximation is the use of the classical limit of nuclei to assess the effect of (partial) deuteration by representing their paths by points in space. This approach more clearly brings out the consequences of deuteration given limited statistical sampling at the expense of not providing quantitative insights, which would be available by replacing the proton mass by that of the deuteron in the framework of quantum simulations. Moreover, these thermal path integral simulations are strictly time independent (despite using molecular dynamics to sample the path integrals) and, therefore, provide exclusively thermal averages of time-independent observables, i.e. no insights whatsoever into the quantum dynamics and thus into the timescale of the process. Unfortunately, the free energy barrier obtained in the deep tunnelling limit can also not be straightforwardly used in a (quantum) transition state theory framework to estimate the rate of the associated dynamical process without considering involved corrections.50–52 All these caveats obviously imply that the present quantum simulations cannot tell us how important the correlated tunnelling process is compared to alternative proton dynamics in low temperature ice owing to fundamental reasons. They also yield no quantitative observable signal such as structure factors, rate constants, kinetic isotope effects or tunnelling splittings. Overall, these simulations strongly support the possibility of concerted many-body quasi-particle tunnelling processes at low temperatures within the proton-ordered six rings of hexagonal ice, but only experiments and possibly refined many-body quantum dynamics simulations can yield conclusive evidence for this intriguing phenomenon.Recent experiments probed collective proton motion in locally ordered water rings: a study using incoherent quasi-elastic neutron scattering (QENS) investigated bulk hexagonal ice42 and a scanning tunnelling microscopy (STM) study manipulated a hydrogen-bonded water tetramer adsorbed on a sodium chloride film supported on gold.40 The QENS study discovered proton motion in proton-disordered hexagonal ice down to 5 K. The quasi-elastic signal disappeared both in fully proton-ordered ice VIII and in partially deuterated hexagonal ice, suggesting that the signal arises only in macroscopically proton-disordered phases of ice and involves the correlated quantum motion of more than one proton. The QENS study suggested a picture of six collectively tunnelling protons in locally proton-ordered water hexamers as they occur naturally in bulk hexagonal ice at thermal equilibrium. Open questions include the high rate constant of the collective proton motion, the transition temperature to the classical limit, the reason for the complete vanishing of the signal upon partial deuteration, and the role of the model and its implied temperature dependence in interpreting the raw data.
The STM study investigated four cyclically arranged water molecules with proton-ordered hydrogen bonds.40 The proton-ordered water tetramer exists in two chiral arrangements: clockwise and anti-clockwise hydrogen bonds within the ring by close analogy with the proton-ordered cyclic hexamers in ice.41 The tunnelling current changed between two values for a given distance of the STM tip and the water tetramer, suggesting the collective proton transfer of all four protons in the four-ring to go from one chiral state of the tetramer to the other. The switching rates between the chiral states are virtually independent of temperature, tunnelling current, and bias potential, but they depend both on the distance of the STM tip from the water tetramer and on the position of the tip relative to the centre of the water tetramer. Whereas nearly symmetric tip positions recorded collective proton motion, both asymmetric tip positions and deuteration lead to much lower switching rates, thus indicating the quasi-particle nature of the process. The complex interaction of the STM tip with the water tetramer and the substrate might allow for control of collective proton motion in the future. However, further research is needed to understand the difference between the clockwise and anti-clockwise chiral states in terms of barriers and switching rates as well as possible experimental artifacts in this utmost sophisticated STM experiment.
In addition to the obvious differences between the two systems in the QENS and STM studies, the vast differences of many orders of magnitude in the inferred timescales of the collective proton motion call for far more data and analyses from future experiment.
A recent study combining quantum U(1) lattice gauge theory and associated numerical studies characterised proton-disordered hexagonal ice.45 This study45 put forward the “… possibility that the protons in ice Ih could form a quantum liquid at low temperatures, in which protons are not merely disordered, but continually fluctuate between different configurations obeying the ice rules”. This quantum proton liquid is a coherent superposition of an exponentially large number of proton configurations obeying the ice rules and provides a unique quantum ground state with vanishing entropy. Thus, this scenario assumes both the absence of a proton-ordering transition and collective proton transfer in all proton-ordered loops in the entire crystal, therefore representing a zero-entropy state at T = 0 K. But how can this entropy be lost? Above temperatures of 0.5 K, no anomaly exists in the heat capacity of hexagonal ice,53–55 and the residual entropy of hexagonal ice is already close to its Pauling value,45 suggesting that thermal fluctuations cause the breakdown of the quantum ground state in the proton-disordered phase. The predictions developed in ref. 45 can be compared best to coherent scattering experiments. In particular, a direct comparison to the incoherent QENS study42 remains inconclusive because the parameters entering the theory require independent determination and because incoherent scattering probes local proton motion. Yet, appealing predictions are made as to explain the “wings” greatly extending beyond the width of the elastic line that have been observed in the QENS experiments.42
Despite a wealth of stimulating insights obtained so far from simulations and theory, refined and extended studies are required that probe more directly the consequences of the different scenarios in terms of experimental observables. Of prime interest would be the full dynamical (quantum) structure factor, thus including both the coherent and incoherent contributions, as a function of both temperature and deuteration fraction as well as the associated timescales of all underlying processes.
4 Conclusions and outlook
We have presented simulations of the correlated transfer of six protons within proton-ordered six rings, i.e. chiral hydrogen-bonded cyclic hexamers, in hexagonal ice as a function of conformational structure, temperature and isotopic substitution. Our simulations included thermal and quantum fluctuations to reveal the influence of the local environment, thermal activation and nuclear mass, respectively, on the nature of collective proton transfer. We provided evidence that the local environment in terms of chair-like or boat-like conformational arrangements of the proton-ordered six ring embedded in the crystal influences neither the barrier nor the mechanism of the transition. Our results suggest moreover a temperature of the order of 200 K for the transition from the low-temperature concerted many-body quasi-particle tunnelling to the high-temperature thermally activated sequential hopping regime, which appears to be surprisingly high. Even more unexpected might be the finding that upon variation of the degree of deuteration a single deuteron impurity in the proton-ordered six ring sufficed to prevent collective tunnelling at low temperature, 50 K. Additional or complete deuteration at 50 K enhanced this effect and corresponded to undeuterated systems of at least 200 K. Collective proton tunnelling in locally proton-ordered six rings in hexagonal ice occurred for proton delocalisations of about 0.8 Å and strong correlations between all local proton transfer coordinates and the global proton transfer coordinate describing the quasi-particle. Our detailed investigation is subject to a set of approximations and limitations, all of which are difficult to circumvent as exposed in the Discussion section, but it contradicts no current experimental data.To date, the most direct evidence for collective proton tunnelling stems from a QENS study of hexagonal ice as a function of temperature compared to proton-ordered ice VIII and to partially deuterated samples.42 Further supporting evidence for the concept of collective proton tunnelling in cyclic hydrogen-bonded topologies comes from an STM study that attributed the chirality switching of a water tetramer on a substrate to collective tunnelling.40 Indeed, path integral simulations disclosed the possibility that all protons in proton-ordered water six rings occurring in ordinary ice can tunnel in a perfectly concerted manner like a delocalised quasi-particle at low temperatures, whereas both increasing thermal fluctuations and deuteration fraction destroy this phenomenon and lead to the usual activated sequential hopping of the six individual protons instead.43,44 Recent lattice gauge theoretical investigations, on the other hand, propose a quantum proton liquid ground state with vanishing entropy for hexagonal ice, being a coherent superposition of an exponentially large number of proton configurations obeying the usual ice rules.45 All these studies contribute to our understanding of the collective transfer of multiple protons in hydrogen-bonded systems in the low-temperature quantum regime. However, despite this growing yet partially contradicting evidence in favour of some sort of collective quantum proton transfer in condensed systems at low temperature, possibly via concerted quasi-particle tunnelling in localised cyclic structures or in the spirit of a coherent quantum liquid encompassing the entire system, no truly conclusive evidence prevails to date. This urgently clearly calls for intensified research in the future using experimental, theoretical and simulational approaches with the sole aim of either strengthening, modifying, or refuting this emerging concept.
Appendix: computational methods and technical details
Defect-free hexagonal ice Ih exhibits a regular oxygen sublattice, whereas the hydrogen sublattice is disordered but satisfies the ice rules.21–23 Our model of such ordinary ice (shown in Fig. 1) consisted of 48 water molecules placed in an orthorhombic simulation cell of hexagonal symmetry22 subject to periodic boundary conditions. The volume of the simulation cell was 13.54 × 15.64 × 7.37 Å3. A purpose-built software (used in ref. 43 but unpublished) produced overall proton-disordered crystal structures with zero dipole moment and minimal quadrupole moment subject to both the usual ice rules56 and the presence of a central proton-ordered six-membered ring (see Fig. 1). To represent the proton disorder of hexagonal ice, we selected from a set of stochastically generated structures one among those with maximum randomness of the protons.56 Based on this set-up, we studied collective proton transfer, i.e. the transition from the initial to the final state, as illustrated in Fig. 1a.Proton transfer reactions require a quantum-mechanical description of the electronic structure that allows for the breaking and the formation of covalent chemical bonds. We used Kohn–Sham density functional theory with the BLYP exchange–correlation functional57,58 in conjunction with a plane wave basis set expansion and norm-conserving pseudopotentials.59 The cutoff for the plane wave expansion of the valence Kohn–Sham orbitals at the Γ-point of the Brillouin zone was 70 Ry, see e.g.ref. 48 for general background on such plane wave pseudopotential electronic structure calculations. It is stressed that the same electronic structure methodology is used for what we call “classical” and “quantum” (ab initio) simulations in order to represent classical and quantum nuclei, respectively, as specified in more detail below. The accuracy of these plane wave pseudopotential BLYP density functional calculations has been most carefully assessed in comparison to all-electron and frozen-core MP2 and CCSD(T) reference calculations using Gaussian basis sets for representative proton transfer processes sampled in hexagonal ice, as shown in the ESI (see in particular Fig. S8 and S9) of ref. 43.
The present work has focussed on the temperature and mass dependence of collective proton transfer in hexagonal ice. We captured thermal fluctuations of the atoms through ab initio molecular dynamics simulations48 according to the Car–Parrinello algorithm60 with a timestep and a fictitious electron mass of 4 a.u. ≈ 0.1 fs and 400 a.u., respectively. In both classical and quantum simulations, the temperature was controlled by coupling each nuclear positional degree of freedom to a separate Nosé–Hoover-chain thermostat,61 thus implementing so-called “massive thermostatting”, to ensure efficient sampling in particular for ab initio path integral simulations47,48,62 in order to capture nuclear quantum effects. In addition, the electronic degrees of freedom have been thermostatted using a separate Nosé–Hoover chain. For brevity, we call standard ab initio molecular dynamics using classical nuclei and ab initio path integral simulations using quantum nuclei “classical” and “quantum” simulations, respectively, throughout this work. Following a large body of earlier work on nuclear quantum effects in molecular systems, we employed simulations using classical nuclei (either all of them or specific subsets to be defined below) to qualitatively assess the deuteration effects.
The path integral formalism of quantum statistical mechanics maps the many-body quantum system onto an equivalent extended classical system in which each quantum particle is represented by a classical cyclic polymer of P discretised Trotter (or imaginary-time) slices (or beads or replicas), s, where s = P + 1 = 1, in order to time-slice the full imaginary time interval τ ∈ [0,ℏβ] of these so-called Euclidean path integrals in terms of s = 1,2,…,P replicas of the fully interacting system.63 The extended classical system corresponds exactly to the quantum system in the limit of P → ∞. According to quantum statistical mechanics, the average of an operator B in the canonical ensemble is approximated as 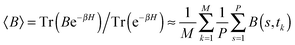 , which becomes exact as P → ∞. Above, Tr is the trace of its argument, β = 1/(kBT) with T being the temperature and kB Boltzmann's constant, H denotes the Hamiltonian, and M denotes the number of sampled closed Feynman paths; as usual, the indistinguishability of identical particles and thus exchange are neglected in our path integral simulations. The “on the fly” combination of path integral sampling of nuclear quantum effects and concurrent electronic structure calculations of the electrons lead to the so-called ab initio path integral simulation technique,46–48,62,64,65 which is used here. Despite using molecular dynamics techniques to evaluate numerically the path integrals, time is fictitious, which implies that these simulations provide exclusively thermal averages of time-independent observables and, therefore, neither quantum dynamics nor physical timescales of processes. Such quantum simulations at 50, 100, 200, and 320 K used P = 32, 16, 8, and 5 imaginary time slices, respectively, to keep ℏβ/P and, hence, the discretisation error along imaginary time roughly constant. In order to assess this level of Trotter discretisation, selected quantum simulations at 50 K using P = 64 Trotter slices were performed to investigate the convergence of observables with respect to P; see ESI of ref. 43. The results for P = 64 and 32 beads were qualitatively identical and quantitatively very close so that 32 replicas were employed to keep the computational effort tractable. Classical reference simulations are obtained in the P = 1 limit and were performed at 50, 100, and 300 K to assess the influence of nuclear quantum effects.
, which becomes exact as P → ∞. Above, Tr is the trace of its argument, β = 1/(kBT) with T being the temperature and kB Boltzmann's constant, H denotes the Hamiltonian, and M denotes the number of sampled closed Feynman paths; as usual, the indistinguishability of identical particles and thus exchange are neglected in our path integral simulations. The “on the fly” combination of path integral sampling of nuclear quantum effects and concurrent electronic structure calculations of the electrons lead to the so-called ab initio path integral simulation technique,46–48,62,64,65 which is used here. Despite using molecular dynamics techniques to evaluate numerically the path integrals, time is fictitious, which implies that these simulations provide exclusively thermal averages of time-independent observables and, therefore, neither quantum dynamics nor physical timescales of processes. Such quantum simulations at 50, 100, 200, and 320 K used P = 32, 16, 8, and 5 imaginary time slices, respectively, to keep ℏβ/P and, hence, the discretisation error along imaginary time roughly constant. In order to assess this level of Trotter discretisation, selected quantum simulations at 50 K using P = 64 Trotter slices were performed to investigate the convergence of observables with respect to P; see ESI of ref. 43. The results for P = 64 and 32 beads were qualitatively identical and quantitatively very close so that 32 replicas were employed to keep the computational effort tractable. Classical reference simulations are obtained in the P = 1 limit and were performed at 50, 100, and 300 K to assess the influence of nuclear quantum effects.
The two partially deuterated systems at 50 K used one proton in the entire system, being located in the proton-ordered six ring, and one proton per six ring, respectively, with one imaginary time slice of these particles in order to mimic the effect of deuteration when compared to the fully protonated system. This approach closely follows earlier work on single-particle proton transfer along an intramolecular hydrogen bond.66 Note that this leads formally to a hybrid QM/MM simulation at the level of the nuclei where the deuteration effect is approximated by invoking the classical limit of a subset of protons whereas all other nuclei are treated fully quantum mechanically throughout.
The collective transfer of six protons between the locally proton-ordered initial (〈Φ〉 ≈ −0.8 Å) and final (〈Φ〉 ≈ +0.8 Å) states is a rare event that is inaccessible on the (fictitious sampling) timescale of ab initio (path integral) molecular dynamics simulations in view of the high energy barrier that separates the final from the initial state. To overcome that free energy barrier and to sample configurations with low probability, we constrained the global (or collective) proton transfer coordinate of the centroid positions, 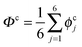 (with ϕcj = dc(O(j)H(j)) − dc(H(j)O(j+1)) and dc(XY) denoting the distance between the centroids of sites X,
(with ϕcj = dc(O(j)H(j)) − dc(H(j)O(j+1)) and dc(XY) denoting the distance between the centroids of sites X, 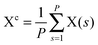 , and Y,
, and Y, 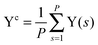 ), at various values of Φc according to (quantum) blue moon sampling.48,67–69 This implements thermodynamic integration70 in the framework of ab initio path integral68 molecular dynamics simulations and generalises what has been done earlier66 in the context of single-particle proton transfer. We computed the constraint force,
), at various values of Φc according to (quantum) blue moon sampling.48,67–69 This implements thermodynamic integration70 in the framework of ab initio path integral68 molecular dynamics simulations and generalises what has been done earlier66 in the context of single-particle proton transfer. We computed the constraint force, 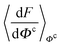 , from at least Φc = −0.8 Å to at least Φc = +0.8 Å in increments of ΔΦc = 0.1
, from at least Φc = −0.8 Å to at least Φc = +0.8 Å in increments of ΔΦc = 0.1![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) Å. The constraint force was then numerically integrated to achieve thermodynamic integration69,70 from the initial to the final state as a function of Φc to yield the free energy profile of Fig. 3. After equilibration, we acquired data for Φc ranging from −0.8 to 0.8 Å for at least 11 and 35 ps in the quantum and classical simulations, respectively. The statistical accuracy of these free energy calculations has been critically assessed in the ESI (see in particular Tables S1 and S2) of ref. 43. In order to prevent proton transfer between the proton-ordered six ring and its environment, we applied one-sided harmonic restraining potentials along the respective bond axes to each of the six hydrogen bonds that connect the six ring to its environment. The protons external to the six ring that are covalently bonded to the six ring were thereby prevented from transferring to the environment, and the restraint became effective for (covalent) O–H bond lengths larger than 1.18 Å. The other protons, being externally hydrogen bonded to the six ring, were prevented from transferring to the six ring, and the restraint became effective for (hydrogen bond) O⋯H distances smaller than 1.58 Å. The force constant of the restraining potential was 0.5 atomic units in both cases.
Å. The constraint force was then numerically integrated to achieve thermodynamic integration69,70 from the initial to the final state as a function of Φc to yield the free energy profile of Fig. 3. After equilibration, we acquired data for Φc ranging from −0.8 to 0.8 Å for at least 11 and 35 ps in the quantum and classical simulations, respectively. The statistical accuracy of these free energy calculations has been critically assessed in the ESI (see in particular Tables S1 and S2) of ref. 43. In order to prevent proton transfer between the proton-ordered six ring and its environment, we applied one-sided harmonic restraining potentials along the respective bond axes to each of the six hydrogen bonds that connect the six ring to its environment. The protons external to the six ring that are covalently bonded to the six ring were thereby prevented from transferring to the environment, and the restraint became effective for (covalent) O–H bond lengths larger than 1.18 Å. The other protons, being externally hydrogen bonded to the six ring, were prevented from transferring to the six ring, and the restraint became effective for (hydrogen bond) O⋯H distances smaller than 1.58 Å. The force constant of the restraining potential was 0.5 atomic units in both cases.
Proton transfer from or to a water molecule that is a member of the proton-ordered six ring to a hydrogen-bonded water molecule outside the ring would formally lead to the formation of an OH− or H3O+ defect, respectively, within the six ring. Thus, the six ring would formally remain proton ordered, but it is expected that the creation of such a net charge defect within the ring would lead to strong structural distortions. It could be speculated that they are at least comparable to (but probably even stronger because more asymmetric than) the intrinsic charge defects that occur at high temperatures due to the proton hopping mechanism. Thus, it is expected that fluctuations in the hydrogen-bonded network that host the proton-ordered six ring leading to net (de)protonation of the six ring would destroy the concerted nature of the process and thus lead to essentially thermally activated high-temperature behaviour.
All classical and quantum simulations were carried out using our in-house version of the CPMD program package71 that has been suitably modified earlier43 for the purpose of this research.
Acknowledgements
Our research into collective proton transfer in hexagonal ice goes back to stimulating discussions with Livia Bove and Stefan Klotz, for which we are grateful. This work was supported by Deutsche Forschungsgemeinschaft through grant MA 1547/16 and is part of the Cluster of Excellence RESOLV EXC 1069. Computer time support from Leibniz Rechenzentrum (SuperMUC) and Bochum Virtual Laboratory (BOVILAB@RUB) is also gratefully acknowledged.References
- D. Marx, ChemPhysChem, 2006, 7, 1848–1870 CrossRef CAS PubMed.
- D. Marx, M. E. Tuckerman, J. Hutter and M. Parrinello, Nature, 1999, 397, 601–604 CrossRef CAS.
- U. W. Schmitt and G. A. Voth, J. Chem. Phys., 1999, 111, 9361–9381 CrossRef CAS.
- M. E. Tuckerman, D. Marx and M. Parrinello, Nature, 2002, 417, 925–929 CrossRef CAS PubMed.
- T. C. Berkelbach, H.-S. Lee and M. E. Tuckerman, Phys. Rev. Lett., 2009, 103, 238302 CrossRef PubMed.
- B. Chen, I. Ivanov, M. L. Klein and M. Parrinello, Phys. Rev. Lett., 2003, 91, 215503 CrossRef PubMed.
- J. A. Morrone and R. Car, Phys. Rev. Lett., 2008, 101, 017801 CrossRef PubMed.
- M. Ceriotti, J. Cuny, M. Parrinello and D. E. Manolopoulos, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 15591–15596 CrossRef CAS PubMed.
- M. Ceriotti, W. Fang, P. G. Kusalik, R. H. McKenzie, A. Michaelides, M. A. Morales and T. E. Markland, Chem. Rev., 2016, 116, 7529–7550 CrossRef CAS PubMed.
- X.-Z. Li, B. Walker and A. Michaelides, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 6369–6373 CrossRef CAS.
- E. A. Cobar, P. R. Horn, R. G. Bergman and M. Head-Gordon, Phys. Chem. Chem. Phys., 2012, 14, 15328–15339 RSC.
- B. Wang, W. Jiang, X. Dai, Y. Gao, Z. Wang and R.-Q. Zhang, Sci. Rep., 2016, 6, 22099 ( Corrigendum , 2016 , 6 , 29148 ) CrossRef CAS PubMed.
- S. Maier and M. Salmeron, Acc. Chem. Res., 2015, 48, 2783–2790 CrossRef CAS PubMed.
- X.-Z. Li, M. I. J. Probert, A. Alavi and A. Michaelides, Phys. Rev. Lett., 2010, 104, 066102 CrossRef PubMed.
- L. R. Merte, G. Peng, R. Bechstein, F. Rieboldt, C. A. Farberow, L. C. Grabow, W. Kudernatsch, S. Wendt, E. Lægsgaard, M. Mavrikakis and F. Besenbacher, Science, 2012, 336, 889–893 CrossRef CAS PubMed.
- F. Madeja and M. Havenith, J. Chem. Phys., 2002, 117, 7162–7168 CrossRef CAS.
- S. D. Ivanov, I. A. Grant and D. Marx, J. Chem. Phys., 2015, 143, 124304 CrossRef PubMed.
- M. Schlabach, H. Rumpel and H.-H. Limbach, Angew. Chem., Int. Ed. Engl., 1989, 28, 76–79 CrossRef.
- G. Mathias and D. Marx, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 6980–6985 CrossRef CAS PubMed.
- Z. P. Nhlabatsi, P. Bhasi and S. Sitha, Phys. Chem. Chem. Phys., 2016, 18, 375–381 RSC.
- J. D. Bernal and R. H. Fowler, J. Chem. Phys., 1933, 1, 515–548 CrossRef CAS.
- V. F. Petrenko and R. W. Whitworth, Physics of ice, Oxford University Press, Oxford, 1999 Search PubMed.
- L. Pauling, J. Am. Chem. Soc., 1935, 57, 2680–2684 CrossRef CAS.
- J. F. Nagle, J. Math. Phys., 1966, 7, 1484–1491 CrossRef CAS.
- P. A. F. P. Moreira and M. de Koning, Phys. Chem. Chem. Phys., 2015, 17, 24716–24721 RSC.
- B. Pamuk, J. M. Soler, R. Ramírez, C. P. Herrero, P. W. Stephens, P. B. Allen and M.-V. Fernández--Serra, Phys. Rev. Lett., 2012, 108, 193003 CrossRef CAS PubMed.
- C. Gainaru, A. L. Agapov, V. Fuentes-Landete, K. Amann-Winkel, H. Nelson, K. W. Köster, A. I. Kolesnikov, V. N. Novikov, R. Richert, R. Böhmer, T. Loerting and A. P. Sokolov, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 17402–17407 CrossRef CAS PubMed.
- L. Masgrau, A. Roujeinikova, J. O. Johannissen, P. Hothi, J. Basran, K. E. Ranaghan, A. J. Mulholland, M. J. Sutcliffe, N. S. Scrutton and D. Leys, Science, 2006, 312, 237–241 CrossRef CAS PubMed.
- S. Koval, J. Kohanoff, R. L. Migoni and E. Tosatti, Phys. Rev. Lett., 2002, 89, 187602 CrossRef CAS PubMed.
- G. F. Reiter, J. Mayers and P. Platzman, Phys. Rev. Lett., 2002, 89, 135505 CrossRef CAS PubMed.
- Y. Feng, C. Ancona-Torres, T. F. Rosenbaum, G. F. Reiter, D. L. Price and E. Courtens, Phys. Rev. Lett., 2006, 97, 145501 CrossRef PubMed.
- M. Benoit, D. Marx and M. Parrinello, Nature, 1998, 392, 258–261 CrossRef CAS.
- M. Benoit, A. H. Romero and D. Marx, Phys. Rev. Lett., 2002, 89, 145501 CrossRef PubMed.
- A. Oppenländer, C. Rambaud, H. P. Trommsdorff and J.-C. Vial, Phys. Rev. Lett., 1989, 63, 1432–1435 CrossRef PubMed.
- Q. Xue, A. J. Horsewill, M. R. Johnson and H. P. Trommsdorff, J. Chem. Phys., 2004, 120, 11107–11119 CrossRef CAS PubMed.
- F. Aguilar-Parrilla, O. Klein, J. Elguero and H.-H. Limbach, Ber. Bunsen-Ges., 1997, 101, 889–901 CrossRef CAS.
- J. M. Lopez, F. Männle, I. Wawer, G. Buntkowsky and H.-H. Limbach, Phys. Chem. Chem. Phys., 2007, 9, 4498–4513 RSC.
- A. J. Horsewill, Prog. Nucl. Magn. Reson. Spectrosc., 2008, 52, 170–196 CrossRef CAS.
- D. F. Brougham, R. Caciuffo and A. J. Horsewill, Nature, 1999, 397, 241–243 CrossRef CAS.
- X. Meng, J. Guo, J. Peng, J. Chen, Z. Wang, J.-R. Shi, X.-Z. Li, E.-G. Wang and Y. Jiang, Nat. Phys., 2015, 11, 235–239 CrossRef CAS.
- C. Drechsel-Grau and D. Marx, Nat. Phys., 2015, 11, 216–218 CrossRef CAS.
- L. E. Bove, S. Klotz, A. Paciaroni and F. Sacchetti, Phys. Rev. Lett., 2009, 103, 165901 CrossRef CAS PubMed.
- C. Drechsel-Grau and D. Marx, Phys. Rev. Lett., 2014, 112, 148302 CrossRef PubMed.
- C. Drechsel-Grau and D. Marx, Angew. Chem., Int. Ed., 2014, 53, 10937–10940 CrossRef CAS PubMed.
- O. Benton, O. Sikora and N. Shannon, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 93, 125143 CrossRef.
- D. Marx and M. Parrinello, Z. Phys. B: Condens. Matter, 1994, 95, 143–144 CrossRef CAS.
- D. Marx, Lect. Notes Phys., 2006, 704, 507–539 Search PubMed.
- D. Marx and J. Hutter, Ab Initio Molecular Dynamics: Basic Theory and Advanced Methods, Cambridge University Press, Cambridge, 2009 Search PubMed.
- P. Hänggi, P. Talkner and M. Borkovec, Rev. Mod. Phys., 1990, 62, 251 CrossRef.
- G. A. Voth, D. Chandler and W. H. Miller, J. Chem. Phys., 1989, 91, 7749 CrossRef CAS.
- M. Messina, G. K. Schenter and B. C. Garrett, J. Chem. Phys., 1995, 103, 3430–3435 CrossRef CAS.
- G. Mills, G. K. Schenter, D. E. Makarov and H. Jónsson, Chem. Phys. Lett., 1997, 278, 91–96 CrossRef CAS.
- W. F. Giauque and J. W. Stout, J. Am. Chem. Soc., 1936, 58, 1144–1150 CrossRef CAS.
- P. Flubacher, A. J. Leadbetter and J. A. Morrison, J. Chem. Phys., 1960, 33, 1751–1755 CrossRef CAS.
- S. J. Smith, B. E. Lang, S. Liu, J. Boerio-Goates and B. F. Woodfield, J. Chem. Thermodyn., 2007, 39, 712–716 CrossRef CAS.
- J. A. Hayward and J. R. Reimers, J. Chem. Phys., 1997, 106, 1518–1529 CrossRef CAS.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- N. Troullier and J. L. Martins, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1993–2006 CrossRef CAS.
- R. Car and M. Parrinello, Phys. Rev. Lett., 1985, 55, 2471–2474 CrossRef CAS PubMed.
- G. J. Martyna, M. L. Klein and M. E. Tuckerman, J. Chem. Phys., 1992, 97, 2635–2643 CrossRef.
- M. E. Tuckerman, D. Marx, M. L. Klein and M. Parrinello, J. Chem. Phys., 1996, 104, 5579–5588 CrossRef CAS.
- D. Chandler and P. G. Wolynes, J. Chem. Phys., 1981, 74, 4078–4095 CrossRef CAS.
- D. Marx and M. Parrinello, J. Chem. Phys., 1996, 104, 4077–4082 CrossRef CAS.
- D. Marx, M. E. Tuckerman and G. J. Martyna, Comput. Phys. Commun., 1999, 118, 166–184 CrossRef CAS.
- M. E. Tuckerman and D. Marx, Phys. Rev. Lett., 2001, 86, 4946–4949 CrossRef CAS PubMed.
- E. A. Carter, G. Ciccotti, J. T. Hynes and R. Kapral, Chem. Phys. Lett., 1989, 156, 472–477 CrossRef CAS.
- D. Laria, G. Ciccotti, M. Ferrario and R. Kapral, Chem. Phys., 1994, 180, 181–189 CrossRef CAS.
- M. Sprik and G. Ciccotti, J. Chem. Phys., 1998, 109, 7737–7744 CrossRef CAS.
- J. G. Kirkwood, J. Chem. Phys., 1935, 3, 300–313 CrossRef CAS.
- J. Hutter, CPMD Copyright IBM Corp., Zurich, and Max Planck Institute, Stuttgart, http://www.cpmd.org.
| This journal is © the Owner Societies 2017 |