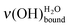Open Access Article
Open Access ArticleInterfacial water on organic substrates at cryogenic temperatures: hydrogen bonding and quantification in the submonolayer regime
D.
Houdoux
,
J.
Houplin
,
L.
Amiaud
,
A.
Lafosse
* and
C.
Dablemont

Institut des Sciences Moléculaires d'Orsay (ISMO), CNRS, Univ. Paris Sud, Université Paris Saclay, F-91405 Orsay, France. E-mail: anne.lafosse@u-psud.fr
First published on 5th January 2017
Abstract
Water molecules were used to probe the physical and chemical properties of a model hydrophilic organic organized layer. To this end, H2O adsorption on mercaptoundecanoic acid self-assembled monolayers (SAMs) was investigated at the molecular level under ultra-high vacuum by high resolution electron energy loss spectroscopy (HREELS), through the sensitivity of the water OH stretching modes to the molecular environment. The water interfacial layer formation and structure were studied upon deposition at 28 K. A direct sensitive quantification in the submonolayer regime (10–80% of completion) was achieved by the sole measurement of the OH stretching mode frequencies, and the dominant basic (–COO−)/acidic (–COOH) forms of the terminal functions could be probed. The surface densities of the water interfacial layer and the SAM terminal functions were measured independently, and demonstrated to be comparable. This means that the SAM terminal functions provided anchors for water adsorption through two hydrogen bonds and that the SAM acted as a template even at 28 K. Upon annealing at 110 K, the water molecules were observed to form clusters of higher molecular density, dewetting the supporting substrate. Finally, the vanishing of the supporting substrate vibrational signature, due to the masking effect by the deposited water layer, was used to estimate the depth probed by HREELS through water layers to be 11 ± 2 Å.
Introduction
Water vapour interaction with surfaces is of general technological interest for preserving or even for manipulating interfacial physical and chemical properties. Dissociative or non-dissociative water adsorption was intensively investigated at the molecular level for metallic1–5 and metal oxide substrates.1,2,6–8 Another important type of interfaces, although less considered, are organic layers.1,9–12 The study of the interaction between vapour-phase probe molecules and supported molecular platforms participates in the fundamental understanding of molecular recognition-based chemical sensors, double-layer structures and biological membrane interfaces.13–15 The main types of molecular interactions driving adsorption on organic interfaces are: electrostatic (ion–ion) binding interactions, covalent bonding, hydrogen bonding and acid–base interactions.13,16–18Self-assembled monolayers (SAMs) are model organic layers, since they are organized surface-confined monolayers of functionalized compounds. They provide structured molecular platforms of controlled chemical composition for developing chemical and biological sensors.15,19 In particular, layers having acidic terminal functions provide chemical anchors suitable for peptide and protein immobilization.16,17,20,21 Therefore, it is of prime interest to study the interaction of such platforms with their surrounding media, and in particular with the ubiquitous compound water.9 As an example, SAMs of 11-mercaptoundecanoic acid (MUA, HS-(CH2)10-COOH) are used as model hydrophilic acid terminated alkanethiolate systems providing 2D-ordered layers of terminal functions. The latter are able to act as water anchors through hydrogen bond(s). The specific behaviour of interfacial water22 will be taken advantage of to probe some physical and chemical properties of the prepared molecular platforms.
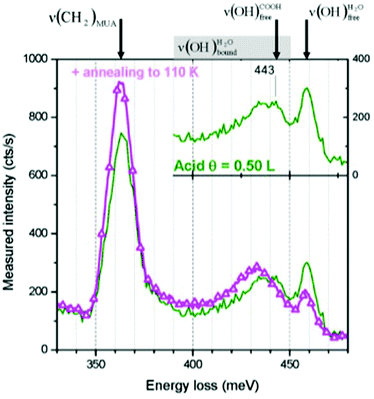
In this paper, in order to study the water–SAM interfacial layer at the molecular level, the H2O adsorption has been studied at its very first stages under ultra-high vacuum (UHV) by high resolution electron energy loss spectroscopy (HREELS), a vibrational spectroscopy technique known for its high surface sensitivity. Isothermal adsorption measurements have been performed at 28 K on base (–COO−) and acid (–COOH) terminated MUA substrates, by exposing them to controlled H2O doses under background deposition conditions. At this temperature, the water sticking and condensation coefficients are equal to unity.23 In this system, the water–SAM interfacial layer structure results from a delicate interplay between different hydrogen bonding interactions: the –COOH terminal functions are embedded into an intralayer hydrogen bond network, water molecules are hydrogen bonded to the acidic/basic terminal functions, and the water molecules also form a hydrogen bond network when close enough.11,12,22,24 The OH stretching modes of water are known to be sensitive to its molecular environment and the ν(OH)H2O vibrations are red-shifting upon the formation of hydrogen bonds.1,3,4,6–8 Therefore, special attention was given to the loss feature extending from 380 to 470 meV.
In the submonolayer regime (0–1 L), a direct quantification of the interfacial water layer completion was achieved, based on the sole peak position of the hydrogen bonded OH stretching band. At the same time, molecular surface packing densities were measured quantitatively for the water-layer under formation as well as for the supporting MUA molecular platforms. The molecular density of the water–MUA interfacial layer has been shown to be low enough to match the MUA terminal function density. In the multilayer regime (2–16 L), the formation of porous amorphous solid water (ASW) layers was observed, as expected from the chosen experimental conditions.23,25,26 The vanishing of the MUA substrate vibrational signature, due to the masking effect,27 has been used to estimate the depth probed by HREELS through the deposited water layers to be 11 ± 2 Å.
The water–MUA interfacial layer structuration is driven by competing hydrogen bonding interactions: anchoring to the substrate terminal functions, and water–water bonding. Therefore, water molecules were used to probe the dominant basic/acidic forms (–COO−/–COOH) of the carboxylic acid terminal functions. The H2O–terminal function interactions were observed to be strong enough for the underlying MUA organized layer to serve as a template for water molecules anchoring at 28 K. Furthermore, when the temperature was raised to 110 K, the mobility of the water molecules was then high enough for long-range diffusion to take place, which leads to the formation of high density water domains and “dewetting” of the SAM.
Experimental
SAMs preparation
The 11-mercaptoundecanoic acid (MUA) SAM preparation at room temperature was described in detail in a previous paper.28 Briefly, MUA was purchased from Sigma-Aldrich (98%, Saint-Quentin Fallavier, France). All solvents were of reagent grade. Reagents were used without any further purification. Glass substrates (11 mm × 11 mm) coated successively with a 2.5 nm thick layer of chromium and a 250 nm thick layer of gold were purchased from Arrandee (Werther, Germany). The gold substrates were annealed by a brief passage in a flame, and then cleaned by 30 minutes of UV-ozone treatment. Then, they were immersed in a freshly prepared 10 mM solution of thiol in absolute ethanol for 2 hours. After thorough rinsing in ethanol (15 minutes), the surfaces were rinsed in aqueous solution for 15 minutes. During the last rinsing step, it was possible to control, to a certain extent, the surface composition by using an acidic (pH 2) or a basic (pH 9) solution.29 Since the pKa of the acidic function of MUA is around 4.5–5 in solution,30 the terminal carboxylic functions of the MUA SAMs were mainly in their acidic (–COOH) or basic (–COO−) form. However, a complete acidic or basic surface can never be obtained because of the existence of an acid–base equilibrium.16,21 After the acidic or basic rinsing step, the surfaces were dried under a flow of dry nitrogen.Water deposition
The SAMs were loaded into the UHV system (base pressure below 2 × 10−10 Torr) through a load-lock chamber, allowing the samples to be transferred into UHV, without baking the vacuum chambers. The SAM samples were then fixed at the end of a He closed-cycle cryostat and cooled down to ∼28 K. Microleak valves allowed depositing fractions of water on the samples. The water amount was controlled by regulating the introduced partial pressure (typically 10−9 Torr or even 10−8 Torr for the higher deposits) and the exposure time. During the experiments, the pressure value was recorded every 10 seconds starting from and ending at 3.8 × 10−10 Torr, threshold pressure for notable variations, and below which the partial pressure of the residual gas is no more negligible. For each exposure, the read pressure was integrated over time to determine precisely the adsorbed amount of water θ in Langmuir (L). The sticking and condensation coefficients for water adsorption are equal to 1 at ∼28 K.23,25,31Absolute measurements of low pressures (<10−9 Torr) in a vacuum chamber are very delicate and depend on many parameters:32–34 temperature, residual gas conductance, non-uniformity of pumping inside the vacuum chamber and gauge history. The read pressure values were corrected by a gauge calibration factor. The uncertainty on the water exposure was estimated to be around 15% because of (i) the uncertainty in the reading of the gauge and its calibration factor and (ii) the additional contribution of the background pressure (UHV system residual vacuum, residual water in the chamber and in the gas inlet).
HREEL characterization of SAMs
The pristine and water exposed MUA SAMs were characterized by HREEL spectroscopy at ∼28 K. The spectrometer consists of a double monochromator and a single analyzer (model IB 500 by Omicron). The energy loss spectra (−15 ≤ Eloss ≤ 500 meV) were recorded for the incident energy Ei = 6 eV, with an overall resolution ΔEFWHM ∼ 6–7 meV, measured at the full width at half maximum (FWHM) of the elastic peak. All the spectra were measured in the specular geometry (θi = θf = 55° with respect to the surface normal) and are presented without any normalization. The electron induced damaging of the films during the long accumulation times was regularly checked for.Results and discussion
1. HREELS characterization of acidic/basic MUA SAMs and ASW multilayers
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) stretching mode observed at 213 meV for the acidic SAM shifts down to 198 meV for the basic SAM, (ii) the out-of-plane bending of two hydrogen bonded terminal functions at 115 meV decreases in intensity (as a consequence of the equilibrium existing between the acidic and the basic forms). The most obvious difference that should be expected between the acidic and basic forms should be related to the vibrational signature of the OH bond, although characterized by weak oscillating forces.38 On one hand, the ν(OH)COOHfree vibration mode is expected at ∼444 meV35,39–43 in a region where strong multiple losses are contributing. On the other hand, the proximity of molecules as well as their flexibility allow the formation of hydrogen bonds between neighbouring COOH groups,24,29,44 broadening and shifting the OH stretching ν(OH)COOHbound down to 325–390 meV.28 Therefore, ν(OH)COOHfree and ν(OH)COOHbound cannot be isolated in the spectrum.
O) stretching mode observed at 213 meV for the acidic SAM shifts down to 198 meV for the basic SAM, (ii) the out-of-plane bending of two hydrogen bonded terminal functions at 115 meV decreases in intensity (as a consequence of the equilibrium existing between the acidic and the basic forms). The most obvious difference that should be expected between the acidic and basic forms should be related to the vibrational signature of the OH bond, although characterized by weak oscillating forces.38 On one hand, the ν(OH)COOHfree vibration mode is expected at ∼444 meV35,39–43 in a region where strong multiple losses are contributing. On the other hand, the proximity of molecules as well as their flexibility allow the formation of hydrogen bonds between neighbouring COOH groups,24,29,44 broadening and shifting the OH stretching ν(OH)COOHbound down to 325–390 meV.28 Therefore, ν(OH)COOHfree and ν(OH)COOHbound cannot be isolated in the spectrum.
 and the sharp peak at 459 meV to the unbound (i.e. without interactions)
and the sharp peak at 459 meV to the unbound (i.e. without interactions) 
2. From a water–SAM interfacial layer to ASW multilayers
 red-shifting at increasing water exposure.
As the deposited water amount increases (Fig. 1c), the sharp peak
red-shifting at increasing water exposure.
As the deposited water amount increases (Fig. 1c), the sharp peak  remains at 459 meV, whereas there is a displacement of the broad peak
remains at 459 meV, whereas there is a displacement of the broad peak  to lower energy losses, as expected.4,7 This displacement will be used to quantify the amount of deposited water thanks to a precise positioning of that peak.
to lower energy losses, as expected.4,7 This displacement will be used to quantify the amount of deposited water thanks to a precise positioning of that peak.
To take into account only the water layer signature, the recorded spectra were corrected from the MUA SAM contribution, as long as the characteristic ν(CH2)MUA signature remained visible (for θ ≲ 2.8 L). Doing so, the small contribution of the multiple loss 88 + 362 meV was removed from the  feature, but not the residual contribution ν(OH)COOHfree of any free –COOH terminal functions expected at 444 meV with weak oscillating force.38 The MUA SAM background contribution was subtracted, after scaling the pristine spectrum (bottom black spectrum on Fig. 1b) to the ν(CH2)MUA peak intensity. The spectrum resulting from the subtraction contains only the water layer contribution and will be called the corrected spectrum in the following section. The position of the water broad peak is determined for each deposited layer thanks to a fitting procedure, using two Gaussians (the position of one being fixed at 459 meV and the second one left free).
feature, but not the residual contribution ν(OH)COOHfree of any free –COOH terminal functions expected at 444 meV with weak oscillating force.38 The MUA SAM background contribution was subtracted, after scaling the pristine spectrum (bottom black spectrum on Fig. 1b) to the ν(CH2)MUA peak intensity. The spectrum resulting from the subtraction contains only the water layer contribution and will be called the corrected spectrum in the following section. The position of the water broad peak is determined for each deposited layer thanks to a fitting procedure, using two Gaussians (the position of one being fixed at 459 meV and the second one left free).
The results of water deposition on a series of acidic and basic SAMs are presented in the calibration curve displayed in Fig. 2. With increasing water exposure, the  peak shifts towards lower energy losses. The water OH bond environment is modified and the hydrogen bond network evolves towards ASW. The asymptotic value is ν0,ASW = 423.6 ± 0.2 meV, which is a signature of amorphous ice and not the crystallized one.3,11,46 A poorly organized water phase involving, for example, only 2.5 hydrogen bonds per water molecule leads to a ν(OH)H2O vibration at 422 meV.6 By contrast, a fully crystallized ice, presenting 4 hydrogen bonds per water molecule, is characterized by a vibration at the 400 meV peak.6
peak shifts towards lower energy losses. The water OH bond environment is modified and the hydrogen bond network evolves towards ASW. The asymptotic value is ν0,ASW = 423.6 ± 0.2 meV, which is a signature of amorphous ice and not the crystallized one.3,11,46 A poorly organized water phase involving, for example, only 2.5 hydrogen bonds per water molecule leads to a ν(OH)H2O vibration at 422 meV.6 By contrast, a fully crystallized ice, presenting 4 hydrogen bonds per water molecule, is characterized by a vibration at the 400 meV peak.6
These experiments have been performed for both acidic and basic samples. The tendency that is observed is independent of the sample type. The curve in Fig. 2 allows the direct determination of the water amount present on the surface, in the submonolayer regime, thanks to the sole value of the 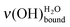 vibrational peak in HREELS. This procedure can be applied to any MUA samples (acidic, basic or mixed) and for any tuning of the spectrometer.
vibrational peak in HREELS. This procedure can be applied to any MUA samples (acidic, basic or mixed) and for any tuning of the spectrometer.
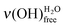 ,
,  and eventually ν(OH)COOHfree. The present study is mainly focused on the water–SAM interfacial layer (i.e. in the very low exposure regime), so that any intrinsic ν(OH)H2O band intensity variation can be neglected since the probed water molecules all primarily interact with the SAM terminal functions.
and eventually ν(OH)COOHfree. The present study is mainly focused on the water–SAM interfacial layer (i.e. in the very low exposure regime), so that any intrinsic ν(OH)H2O band intensity variation can be neglected since the probed water molecules all primarily interact with the SAM terminal functions.
Fig. 3 displays the evolution of the normalized areas Γν(OH) and Γν(CH2) with respect to the water exposure θ. As expected, when water exposure increases the Γν(OH) increases before reaching saturation, while the Γν(CH2) decreases. More specifically, we note that:
 | ||
| Fig. 3 Normalized area Γ under the features attributed to ν(OH)H2O (circles) and ν(CH2)MUA (squares) with respect to the water exposure θ (L) for acidic (red full symbols) and basic (blue open symbols) MUA SAMs. The detection limit is represented by the dashed line at Γ ∼ 0.05. The black curves are the exponential variation laws predicted by a Langmuir model for layer growth (eqn (1) and (2)). They were obtained by adjusting one single parameter θlim over the range 0–2 L, i.e. during the formation of the water–SAM interfacial layer. The green curve represents the exponential law associated with the completion of the ASW multilayer, taking place over the range 2–5.5 L. | ||
(i) The Γν(CH2) signal goes below the detection limit for θ ≳ 2.8 L: the MUA surface is completely covered for θ ≈ 2.8 L.
(ii) The Γν(OH) normalized area saturates to 1 for θ ≳ 5.5 L: the probed depth contains only ASW ice.
(iii) For 2.8 ≲ θ ≲ 5.5 L, the probed depth only contains water and the signal continues to increase, as a sign of increasing quantities of water molecules inside the probed depth.
2.3.1. Low exposure regime θ ≲ 2.0 L. In the low coverage regime θ ≲ 2.0 L, the normalized area Γ experimentally determined under the ν(OH)H2O (respectively ν(CH2)MUA) peak represented in Fig. 3 can be adjusted by exponential variation laws (1) and (2) characterized by a single parameter θlim.
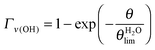 | (1) |
 | (2) |
 and θMUAlim = 0.94 ± 0.14 L. Using a simple Langmuir model of monolayer deposition,47,48θlim is proportional to the adsorption site density N0.
and θMUAlim = 0.94 ± 0.14 L. Using a simple Langmuir model of monolayer deposition,47,48θlim is proportional to the adsorption site density N0.| N0 = θlim × K | (3) |

N
A is Avogadro's constant, R is the perfect gases constant, T is the gas temperature in K (here approximated 300 K), M = 18 × 10−3 kg mol−1 is the molar mass of the gaseous species. The adjusted θlim values leads to  and NMUA0 = 3.8–5.2 × 1014 molecules cm−2. According to Schreiber et al.,49 a thiolated aliphatic molecule occupies a 21.6 Å2 surface inside a SAM, which corresponds to a molecule surface density of 4.6 × 1014 molecules cm−2. This is in a perfect agreement with the density NMUA0 determined above.
and NMUA0 = 3.8–5.2 × 1014 molecules cm−2. According to Schreiber et al.,49 a thiolated aliphatic molecule occupies a 21.6 Å2 surface inside a SAM, which corresponds to a molecule surface density of 4.6 × 1014 molecules cm−2. This is in a perfect agreement with the density NMUA0 determined above.
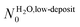 and NMUA0 values are quite comparable. It means that, in the low exposure regime, the impinging entities build a layer having a density comparable to the packing density of the MUA SAM. The SAM terminal functions serve as anchors for the incoming molecules and act as a template for building the water layer even at 28 K. Since the obtained density is far below that expected for water molecule assemblies alone,23,26 the adsorbed water molecules strongly interact with the SAM. According to the diffusion model developed by Kasza et al.,31† at 28 K water molecules linked by one hydrogen bond are still mobile, while two hydrogen bonds immobilize them. So we conclude that the water molecules are anchored to the SAM via two hydrogen bonds, resulting in an adsorption energy estimated to be ∼10 kcal mol−1. This is in accordance with the estimation, obtained by TPD, for water adsorption at a low coverage on a 16-mercaptohexadecanoic acid HS-(CH2)15-COOH SAM.11 Some studies have considered water interfacial layers with silicon oxide6 and muscovite mica8 at room temperature. In both cases, they proposed that the structure of the first water layer is driven by the substrate, in accordance with our observation.
and NMUA0 values are quite comparable. It means that, in the low exposure regime, the impinging entities build a layer having a density comparable to the packing density of the MUA SAM. The SAM terminal functions serve as anchors for the incoming molecules and act as a template for building the water layer even at 28 K. Since the obtained density is far below that expected for water molecule assemblies alone,23,26 the adsorbed water molecules strongly interact with the SAM. According to the diffusion model developed by Kasza et al.,31† at 28 K water molecules linked by one hydrogen bond are still mobile, while two hydrogen bonds immobilize them. So we conclude that the water molecules are anchored to the SAM via two hydrogen bonds, resulting in an adsorption energy estimated to be ∼10 kcal mol−1. This is in accordance with the estimation, obtained by TPD, for water adsorption at a low coverage on a 16-mercaptohexadecanoic acid HS-(CH2)15-COOH SAM.11 Some studies have considered water interfacial layers with silicon oxide6 and muscovite mica8 at room temperature. In both cases, they proposed that the structure of the first water layer is driven by the substrate, in accordance with our observation.
2.3.2. Multilayer deposition regime θ ≳ 2 L. In the higher coverage regime, the adjustment parameter, coming from eqn (1), is θASWlim = 1.52 ± 0.26 L. This means that, in the multilayer formation regime under our experimental conditions, the limit is amorphous porous ice as NASW0 = θASWlim × K = 7.3 ± 1.3 × 1014 molecules cm−2. From this value, an estimate of the water multilayer volumic mass can be obtained through the simple relationship
This is in excellent agreement with the value obtained experimentally by optical density measurements for ice deposited at 20 K.23,50
2.3.3. Direct determination of water coverage in the submonolayer regime. By combining all the experimental data (Fig. 2 and 3), the obtained peak position of the
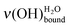 can be directly related to the coverage rates Γ of the SAM platform (Fig. 4). For example, on a sample on which the deposited water amount is unknown, if the position of the water peak is measured at 436 meV, it can be deduced that 70–78% of the MUA molecule sites (and, so, of COOH) are free and that the coverage level is 20–26%. To put it in a nutshell, HREELS is sensitive to the formation of the water interfacial layer, which is on the way to its completion. In the 90–10% domain for the normalized area Γν(CH2), the peak position for the
can be directly related to the coverage rates Γ of the SAM platform (Fig. 4). For example, on a sample on which the deposited water amount is unknown, if the position of the water peak is measured at 436 meV, it can be deduced that 70–78% of the MUA molecule sites (and, so, of COOH) are free and that the coverage level is 20–26%. To put it in a nutshell, HREELS is sensitive to the formation of the water interfacial layer, which is on the way to its completion. In the 90–10% domain for the normalized area Γν(CH2), the peak position for the 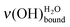 shifts from 440 to 428 meV. This low energy loss limit corresponds to ∼2.4 L exposure and Γν(OH) is ∼80%, confirming that this is the beginning of the multilayer regime. In the domain of the interfacial layer completion, Fig. 4 constitutes an abacus, which is independent of the HREELS settings. It gives a direct determination of the coverage at exposures as low as submonolayer ones. In addition, the morphology of the first water layer is driven by the SAM as shown by the similarity of the surface density of water for the low deposits and the surface density of the MUA SAM. As demonstrated above, a water molecule explores the surface before immobilization on one terminal function through two hydrogen bonds. Consequently, the arrangement of the COOH/COO− terminal functions of the SAM may influence the structure of the first water layer as discussed below.
shifts from 440 to 428 meV. This low energy loss limit corresponds to ∼2.4 L exposure and Γν(OH) is ∼80%, confirming that this is the beginning of the multilayer regime. In the domain of the interfacial layer completion, Fig. 4 constitutes an abacus, which is independent of the HREELS settings. It gives a direct determination of the coverage at exposures as low as submonolayer ones. In addition, the morphology of the first water layer is driven by the SAM as shown by the similarity of the surface density of water for the low deposits and the surface density of the MUA SAM. As demonstrated above, a water molecule explores the surface before immobilization on one terminal function through two hydrogen bonds. Consequently, the arrangement of the COOH/COO− terminal functions of the SAM may influence the structure of the first water layer as discussed below.
3. Water as a probe for determining the acidic/basic character of the MUA SAM
As there is an acid–base equilibrium between COOH and COO− terminal functions, the acidic or basic character of the SAM interface deserves to be probed. The energy loss spectra of the bare acidic and basic MUA SAMs resemble each other with the exceptions of the position of the weak intensity ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) stretching mode and the intensity of the out-of-plane bending of two hydrogen bonded terminal functions. When these two types of SAMs are exposed to water, the positions of the losses are also similar (Fig. 1 – Section 1.1). However, it has been shown that each water molecule diffuses until it forms two hydrogen bonds with one terminal function.
O) stretching mode and the intensity of the out-of-plane bending of two hydrogen bonded terminal functions. When these two types of SAMs are exposed to water, the positions of the losses are also similar (Fig. 1 – Section 1.1). However, it has been shown that each water molecule diffuses until it forms two hydrogen bonds with one terminal function.
In Fig. 5, the features attributed to ν(OH)H2O are compared for acid- and base-terminated MUA SAMs at low water exposures. For the higher doses (∼0.7 and 1.4 L), they are comparable. Only, for the lowest exposures (∼0.3 and 0.4 L), the height of the 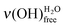 peak is always smaller than the one of the
peak is always smaller than the one of the 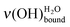 on a basic SAM, whereas it is always higher on an acidic SAM. This can serve as a qualitative probe for determining the acidic/basic state of the MUA SAM interface layer. The
on a basic SAM, whereas it is always higher on an acidic SAM. This can serve as a qualitative probe for determining the acidic/basic state of the MUA SAM interface layer. The  intensity reflects the proportion of terminal functions in their acidic-form –COOH, at disposal for hydrogen bonding with incoming water. As mentioned above (Section 2.3.1), water molecules bind to the SAM terminal functions through two hydrogen bonds. When interacting with an acidic-form –COOH terminal function, a water molecule might involve only one of its covalent OH bonds. As the acidic SAM is both a hydrogen bond donor and acceptor, the second hydrogen bond might come from the covalent OH bond of the carboxylic acid function. On the contrary, basic SAMs are only hydrogen bond acceptors as they have no covalent OH bond to involve into intermolecular interactions with water. So, water molecules create bonds using their two OH covalent bonds to interact with basic SAMs, leading to a reduced
intensity reflects the proportion of terminal functions in their acidic-form –COOH, at disposal for hydrogen bonding with incoming water. As mentioned above (Section 2.3.1), water molecules bind to the SAM terminal functions through two hydrogen bonds. When interacting with an acidic-form –COOH terminal function, a water molecule might involve only one of its covalent OH bonds. As the acidic SAM is both a hydrogen bond donor and acceptor, the second hydrogen bond might come from the covalent OH bond of the carboxylic acid function. On the contrary, basic SAMs are only hydrogen bond acceptors as they have no covalent OH bond to involve into intermolecular interactions with water. So, water molecules create bonds using their two OH covalent bonds to interact with basic SAMs, leading to a reduced 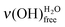 intensity.
intensity.
4. Favouring water/water and COOH/COOH interactions through annealing
The influence of water deposition on an acidic MUA SAM itself is now examined thanks to the as-recorded spectrum of a water layer of 0.50 L deposited at 28 K (green curve of Fig. 6). The vibrational signatures, that are characteristic of a water interfacial layer, are observed with a broad peak between 380 and 450 meV attributed to and a peak at 459 meV
and a peak at 459 meV  . However, there is an additional signature at 443 meV, which can be attributed to ν(OH)COOHfree, meaning that the intra-SAM hydrogen bond network was broken.35,39–43 The associated loss of energy is counterbalanced by the formation of hydrogen bonds between adsorbing water molecules and the SAM. Statistically, a 0.50 L deposit is favourable for the observation of this phenomenon. The probability to have two free COOH functions close enough to each other to regenerate the hydrogen bond network observed in the pristine MUA SAM is quite low.
. However, there is an additional signature at 443 meV, which can be attributed to ν(OH)COOHfree, meaning that the intra-SAM hydrogen bond network was broken.35,39–43 The associated loss of energy is counterbalanced by the formation of hydrogen bonds between adsorbing water molecules and the SAM. Statistically, a 0.50 L deposit is favourable for the observation of this phenomenon. The probability to have two free COOH functions close enough to each other to regenerate the hydrogen bond network observed in the pristine MUA SAM is quite low.
After the deposition of 0.50 L at 28 K, the sample is heated at 110 K (pink curve with triangles in Fig. 6), which is below the temperature desorption of water (≥130 K).12,51,52 The area under the ν(OH) broad peak only slightly decreases (12% ± 5%), while the  peak looses half of its intensity. Consequently, a
peak looses half of its intensity. Consequently, a 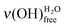 conversion into
conversion into  is observed. The
is observed. The  peak is shifted towards the lower energy losses. Referring to the calibration curve in Fig. 2, it means that the initial 0.50 L amount of water displays, after heating, a hydrogen bond network comparable to the one of a higher deposit. Also it can be noted that the peak attributed to the ν(OH)COOHfree vibration disappears. This is in agreement with the rearrangement of the whole system, the water submonolayer as well as the terminal functions of the supporting SAM. At 110 K, two hydrogen bonds are not enough to prevent water diffusion (see Section 2.3.1).31 The carboxylic acid functions no longer serve as a template for the water submonolayer. The molecules can migrate to build an optimized water network above the SAM. A possible interpretation is that the water submonolayer has now contracted into 2D dense islands, so that their signature mimics the one of a higher deposit. However, this
peak is shifted towards the lower energy losses. Referring to the calibration curve in Fig. 2, it means that the initial 0.50 L amount of water displays, after heating, a hydrogen bond network comparable to the one of a higher deposit. Also it can be noted that the peak attributed to the ν(OH)COOHfree vibration disappears. This is in agreement with the rearrangement of the whole system, the water submonolayer as well as the terminal functions of the supporting SAM. At 110 K, two hydrogen bonds are not enough to prevent water diffusion (see Section 2.3.1).31 The carboxylic acid functions no longer serve as a template for the water submonolayer. The molecules can migrate to build an optimized water network above the SAM. A possible interpretation is that the water submonolayer has now contracted into 2D dense islands, so that their signature mimics the one of a higher deposit. However, this  displacement has to be carefully considered, since the annealing of an ice multilayer would result in comparable experimental evidence.
displacement has to be carefully considered, since the annealing of an ice multilayer would result in comparable experimental evidence.
A stronger evidence of water contraction into 2D islands upon 110 K heating is given by the variation of the ν(CH2) intensity. The normalized area Γν(CH2) increases by ∼0.14–0.16, meaning that the proportion of the MUA surface free from water increases. Thereby, the water molecule surface density N2D,110K0 is multiplied by a factor ∼1.6–1.9. By extrapolation, a hypothetical volumic mass can be estimated in the range 0.7–1.1 g cm−3 from the 2D surface density. Such a water contraction leading to the restoring of domains with available SAM terminal functions was also observed by Engquist in the case of 2 Å water layer deposited on a methyl 16-mercaptohexadecanoate HS-(CH2)15-COO-CH3 SAM on gold.10 The annealing from 100 to 140 K decreases the fraction of water capped C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups from 95% to 36%. Considering that the contraction is the variation of the covered surface over the initial water coverage, a contraction of (95 − 36)/95 = 0.62 was obtained. In our case, on an acidic SAM, the obtained contraction ∼0.46–0.54 is in a reasonable agreement, taking into account that we are working at a much lower coverage well before the start of the multilayer. Such a metastable behaviour of water layers was observed, upon annealing up to 140 K, for films deposited at 80 K on a 16-mercaptohexadecanoic acid HS-(CH2)15-COOH SAM.11
O groups from 95% to 36%. Considering that the contraction is the variation of the covered surface over the initial water coverage, a contraction of (95 − 36)/95 = 0.62 was obtained. In our case, on an acidic SAM, the obtained contraction ∼0.46–0.54 is in a reasonable agreement, taking into account that we are working at a much lower coverage well before the start of the multilayer. Such a metastable behaviour of water layers was observed, upon annealing up to 140 K, for films deposited at 80 K on a 16-mercaptohexadecanoic acid HS-(CH2)15-COOH SAM.11
Conclusions
In this paper, mercaptoundecanoic acid (MUA, HS-(CH2)10-COOH) SAMs were chosen as model hydrophilic organized surface-confined organic layers to study water interaction and adsorption at the molecular level. H2O molecule adsorption was investigated under ultra-high vacuum on both acid (–COOH) and base (–COO−) terminated SAMs. The sensitivity of the water OH stretching modes to the molecular environment was probed by high resolution electron energy loss spectroscopy (HREELS). Two water characteristic losses are particularly observed: one related to free OH bonds at 459 meV and one attributed to OH bonds involved in hydrogen bonding interaction(s)
at 459 meV and one attributed to OH bonds involved in hydrogen bonding interaction(s)  . At the very first stages of water adsorption, the latter was observed to shift from 440 meV down to 428 meV.
. At the very first stages of water adsorption, the latter was observed to shift from 440 meV down to 428 meV.
Working at a low water exposure, the formation of the water interfacial layer was followed by considering both the increase in intensity of the OH stretching feature and the decrease in intensity of the MUA substrate vibrational signature ν(CH2). With the help of a simple Langmuir model, the surface densities of the water interfacial layer and the SAM terminal functions were measured independently, and demonstrated to be comparable. The water layer consists of (5.6 ± 0.9) × 1014 molecules cm−2, which corresponds to a remarkably low extrapolated density of 0.4 ± 0.1 g cm−3. Hence, the SAM terminal functions provide anchors for water adsorption through two hydrogen bonds and the SAM acts as a template for the interfacial water layer formation even at 28 K. A direct quantification of the amount of deposited water was achieved in the submonolayer regime (10–80% of completion) by the sole measurement of the OH stretching mode frequencies, as a consequence of the HREELS surface sensitivity. The dominant basic (–COO−)/acidic (–COOH) forms of the terminal functions could be probed by considering the relative intensities of the  and
and  loss features. Upon annealing at 110 K, the deposited water molecules were observed to migrate and form clusters of higher molecular density, reaching values characteristic for phases where water–water interactions dominate. This contraction was accompanied by the dewetting of the supporting substrate.
loss features. Upon annealing at 110 K, the deposited water molecules were observed to migrate and form clusters of higher molecular density, reaching values characteristic for phases where water–water interactions dominate. This contraction was accompanied by the dewetting of the supporting substrate.
At a higher water exposure at 28 K, the progressive transition to porous ASW ice multilayers was observed as expected and led to characteristic energy losses  and
and 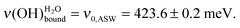 The density of such thicker water layers was here determined to be 0.59 ± 0.16 g cm−3. The vanishing of the MUA substrate vibrational signature ν(CH2), caused by the masking effect of the deposited water layer, was used to estimate the depth probed by HREELS at 6 eV to be 11 ± 2 Å.
The density of such thicker water layers was here determined to be 0.59 ± 0.16 g cm−3. The vanishing of the MUA substrate vibrational signature ν(CH2), caused by the masking effect of the deposited water layer, was used to estimate the depth probed by HREELS at 6 eV to be 11 ± 2 Å.
In this study, water molecules were used to probe the physical and chemical properties of a model hydrophilic organic organized layer. This method, relying on the HREELS analysis of samples exposed to water will be transposed in the near future to surfaces of various hydrophobicities. The water interaction with these substrates will then be characterized at the molecular level, and the structure of the water-interfacial layer will be studied.
Acknowledgements
We thank Dr Christophe Poulard for his help with the UV-Ozone treatment and Prof. Petra Swiderek for fruitful discussions. We acknowledge the financial support by C'Nano, Ile-de-France, Programme Francilien de Recherche en Nanosciences, through the 2009 SAMTOX-NC granted project. This work was conducted within the framework of the COST action CM1301 (CELINA for ‘Chemistry for ELectron-Induced NAnofabrication’). The HREELS electronics was funded by the LabEx PALM Investissement d'Avenir (ANR-10-LABX-0039-PALM, ProDac project).Notes and references
- M. A. Henderson, Surf. Sci. Rep., 2002, 46, 1–308 CrossRef CAS.
- P. A. Thiel and T. E. Madey, Surf. Sci. Rep., 1987, 7, 211–385 CrossRef CAS.
- F. Bensebaa and T. H. Ellis, Prog. Surf. Sci., 1995, 50, 173–185 CrossRef CAS.
- K. Jacobi, K. Bedürfig, Y. Wang and G. Ertl, Surf. Sci., 2001, 472, 9–20 CrossRef CAS.
- H. Ibach and S. Lehwald, Surf. Sci., 1980, 91, 187–197 CrossRef CAS.
- D. B. Asay and S. H. Kim, J. Phys. Chem. B, 2005, 109, 16760–16763 CrossRef CAS PubMed.
- C.-W. Yi and J. Szanyi, J. Phys. Chem. C, 2007, 111, 17597–17601 CAS.
- W. Cantrell and G. E. Ewing, J. Phys. Chem. B, 2001, 105, 5434–5439 CrossRef CAS.
- I. Engquist, I. Lundström, B. Liedberg, A. N. Parikh and D. L. Allara, J. Chem. Phys., 1997, 106, 3038–3048 CrossRef CAS.
- I. Engquist, M. Lestelius and B. Liedberg, J. Phys. Chem., 1995, 99, 14198–14200 CrossRef CAS.
- R. G. Nuzzo, B. R. Zegarski, E. M. Koreniqt and L. H. Dubois, J. Phys. Chem., 1992, 96, 1355–1361 CrossRef CAS.
- L. H. Dubois, B. R. Zegarski and R. G. Nuzzo, J. Am. Chem. Soc., 1990, 112, 570–579 CrossRef CAS.
- L. Sun, R. M. Crooks and A. J. Ricco, Langmuir, 1993, 9, 1775–1780 CrossRef CAS.
- L. Sun, L. J. Kepley and R. M. Crooks, Langmuir, 1992, 8, 2101–2103 CrossRef CAS.
- F. Schreiber, J. Phys.: Condens. Matter, 2004, 16, R881 CrossRef CAS.
- A. Kudelski, Vib. Spectrosc., 2005, 39, 200–213 CrossRef CAS.
- N. Patel, M. C. Davies, M. Hartshorne, R. J. Heaton, C. J. Roberts, S. J. B. Tendler and P. M. Williams, Langmuir, 1997, 13, 6485–6490 CrossRef CAS.
- M. Wells, D. L. Dermody, H. C. Yang, T. Kim, R. M. Crooks and A. J. Ricco, Langmuir, 1996, 12, 1989–1996 CrossRef CAS.
- J. C. Love, L. A. Estroff, J. K. Kriebel, R. G. Nuzzo and G. M. Whitesides, Chem. Rev., 2005, 105, 1103–1170 CrossRef CAS PubMed.
- V. Humblot, P. Thebault, K. Boukerma, J.-F. Yala, A. Héquet, J.-M. Berjeaud and C.-M. Pradier, Biomaterials, 2009, 30, 3503–3512 CrossRef CAS PubMed.
- A. Vallée, V. Humblot, R. Al Housseiny, S. Boujday and C.-M. Pradier, Colloids Surf., B, 2013, 109, 136–142 CrossRef PubMed.
- V. Molinero and B. D. Kay, J. Chem. Phys., 2014, 141, 18C101 CrossRef PubMed.
- D. E. Brown, S. M. George, C. Huang, E. K. L. Wong, K. B. Rider, R. Scott Smith and B. D. Kay, J. Phys. Chem., 1996, 100, 4988–4995 CrossRef CAS.
- F. Tielens, D. Costa, V. Humblot and C.-M. Pradier, J. Phys. Chem. C, 2008, 112, 182–190 CAS.
- G. A. Kimmel, K. P. Stevenson, Z. Dohnalek, R. Scott Smith and B. D. Kay, J. Chem. Phys., 2001, 114, 5284–5294 CrossRef CAS.
- B. Guillot and Y. Guissani, J. Chem. Phys., 2004, 120, 4366–4382 CrossRef CAS PubMed.
- J. J. Pireaux, C. Gregoire and R. Caudano, Langmuir, 1991, 7, 2433–2437 CrossRef CAS.
- J. Houplin, L. Amiaud, V. Humblot, I. Martin, E. Matar, R. Azria, C.-M. Pradier and A. Lafosse, Phys. Chem. Chem. Phys., 2013, 15, 7220–7227 RSC.
- R. Arnold, W. Azzam, A. Terfort and C. Wöll, Langmuir, 2002, 18, 3980–3992 CrossRef CAS.
- I. Pascal and D. S. Tarbell, J. Am. Chem. Soc., 1957, 79, 6015–6020 CrossRef CAS.
- R. V. Kasza, K. Griffiths, V. P. Zhdanov and P. R. Norton, Appl. Surf. Sci., 1995, 84, 97–105 CrossRef CAS.
- K. Jousten, Ultrahigh vacuum gauges CERN, 2007–24 p., CAS – CERN accelerator school and ALBA synchrotron light facility: course on vacuum in accelerators, Platja d'Aro, Spain, 16–24 May 2006.
- K. Jousten, Pressure measurement with ionization gauges, OPEN-2000-271. – CERN, 1999 In: CAS – CERN accelerator school: vacuum technology, Snekersten, Denmark, 28 May–3 Jun 1999.
- Varian Vacuum Technologies, Multi-gauge controller part no L8350301, 2000.
- J. Houplin, PhD thesis, Université Paris Sud, 2015.
- J. Houplin, L. Amiaud, T. Sedzik, C. Dablemont, D. Teillet-Billy, N. Rougeau and A. Lafosse, Eur. Phys. J. D, 2015, 69, 217 CrossRef.
- A. Lafosse and R. Azria, in Low-energy electron scattering from molecules, biomolecules and surfaces, ed. P. Čársky and R. Čurík, CRC Press Taylor & Francis Group, 2012, ch. 7 Search PubMed.
- M. Allan, Phys. Rev. Lett., 2007, 98, 123201 CrossRef PubMed.
- I. Martin, M. Bertin, A. Domanracka, R. Azria, E. Illenberger and A. Lafosse, Int. J. Mass Spectrom., 2008, 277, 262–268 CrossRef CAS.
- R. C. Millikan and K. S. Pitzer, J. Am. Chem. Soc., 1958, 80, 3515–3521 CrossRef CAS.
- National Institute of Standards and Technology (NIST), http://www.nist.gov.
- S. E. Creager and C. M. Steiger, Langmuir, 1995, 11, 1852–1854 CrossRef CAS.
- H. C. Yang, D. L. Dermody, C. Xu, A. J. Ricco and R. M. Crooks, Langmuir, 1996, 12, 726–735 CrossRef CAS.
- R. G. Nuzzo, L. H. Dubois and D. L. Allara, J. Am. Chem. Soc., 1990, 112, 558–569 CrossRef CAS.
- J. J. Pireaux, C. Gregoire, M. Vermeersch, P. A. Thiry and R. Caudano, Surf. Sci., 1987, 189–190, 903–912 CrossRef CAS.
- P. Jenniskens, S. F. Banham, D. F. Blake and M. R. S. McCoustra, J. Chem. Phys., 1997, 107, 1232–1241 CrossRef CAS PubMed.
- G. G. A. Somorjai and M.-P. Delplancke, Chimie des surfaces et catalyse, Ediscience International, 1995 Search PubMed.
- K. Oura, V. G. Lifshits, A. A. Saranin, A. V. Zotov and M. Katayama, Surface science: an introduction, Springer, Berlin, 2003 Search PubMed.
- F. Schreiber, Prog. Surf. Sci., 2000, 65, 151–256 CrossRef CAS.
- Z. Dohnalek, G. A. Kimmel, P. Ayotte, R. Scott Smith and B. D. Kay, J. Chem. Phys., 2003, 118, 364–372 CrossRef CAS.
- Z. Dohnalek, R. L. Ciolli, G. A. Kimmel, K. P. Stevenson, R. Scott Smith and B. D. Kay, J. Chem. Phys., 1999, 110, 5489–5492 CrossRef CAS.
- B. D. Kay, K. R. Lykke, J. Randall Creighton and S. J. Ward, J. Chem. Phys., 1989, 91, 5120–5121 CrossRef CAS.
Footnote |
| † The limit temperatures for diffusion were estimated to be 17 K and 35 K, for water molecules linked by one and two hydrogen bond(s), respectively (taking an average diffusion activation energy of 1.25 kcal mol−1 for a hydrogen bond of 5 kcal mol−1). |
| This journal is © the Owner Societies 2017 |