Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Atomic structure of Mg-based metallic glasses from molecular dynamics and neutron diffraction
Anastasia
Gulenko
a,
Louis
Forto Chungong
b,
Junheng
Gao
c,
Iain
Todd
c,
Alex C.
Hannon
d,
Richard A.
Martin
*b and
Jamieson K.
Christie
 *ae
*ae
aDepartment of Chemistry, University College London, 20 Gordon Street, London, WC1H 0AJ, UK
bAston Institute of Materials Research, School of Engineering and Applied Sciences & Aston Research Centre for Healthy Ageing University of Aston Birmingham, B4 7ET, UK. E-mail: r.a.martin@aston.ac.uk
cFaculty of Engineering, University of Sheffield, Sir Frederick Mappin Building, Mappin Street, Sheffield, S1 3JD, UK
dISIS Facility, Rutherford Appleton Laboratory, Chilton, Didcot, OX11 0QX, UK
eDepartment of Materials, Loughborough University, Loughborough, LE11 3TU, UK. E-mail: j.k.christie@lboro.ac.uk
First published on 3rd March 2017
Abstract
We use a combination of classical molecular dynamics simulation and neutron diffraction to identify the atomic structure of five different Mg–Zn–Ca bulk metallic glasses, covering a range of compositions with substantially different behaviour when implanted in vitro. There is very good agreement between the structures obtained from computer simulation and those found experimentally. Bond lengths and the total correlation function do not change significantly with composition. The zinc and calcium bonding shows differences between composition: the distribution of Zn–Ca bond lengths becomes narrower with increasing Zn content, and the preference for Zn and Ca to avoid bonding to themselves or each other becomes less strong, and, for Zn–Ca, transforms into a positive preference to bond to each other. This transition occurs at about the same Zn content at which the behaviour on implantation changes, hinting at a possible structural connection. A very broad distribution of Voronoi polyhedra are also found, and this distribution broadens with increasing Zn content. The efficient cluster packing model, which is often used to describe the structure of bulk metallic glasses, was found not to describe these systems well.
1 Introduction
Since their discovery over 50 years ago,1 bulk metallic glasses (BMG) have been extensively studied.2 They are of significant fundamental and technological interest due to their exceptional physical, chemical and mechanical properties. Their amorphous structure means that they are not limited to specific stoichiometries, resulting in a wide range of possible glass compositions. This also implies that their macroscopic properties could be continuously variable, hence tunable, within a certain range by changes in the glass composition. One field in which this is potentially very useful is biomedicine.3–5In this work, we investigate Mg–Zn–Ca glasses which are promising candidates for use as medical implants. They consist of elements found within the human body and the glasses themselves are known to be biocompatible.6,7 Their density and elastic modulus are comparable to that of human bone,8 which minimises stress mismatch for orthopaedic applications. In addition, Mg–Zn–Ca glasses have a very good glass-forming ability (GFA); the addition of calcium substantially enhances the GFA over that of Mg–Zn binary glass compositions.9
When crystalline magnesium and its alloys are implanted in the body, unwanted and harmful hydrogen gas pockets are generated by the corrosion reaction, which limits the use of these alloys for biomedical implantation. It was recently shown3 that Mg–Zn–Ca glasses rich in zinc (>28 at% Zn) form a passivating surface layer which prevents the release of hydrogen, implying that these glasses “hold much promise for improving next-generation biodegradable implants”.10
In order to optimise these glasses for use as biomedical implants, or indeed for any other application, we need to understand how the macroscopic properties of interest depend on the atomic structure of the glass and its composition. Due to the potential large impact of these glasses, this has attracted substantial attention, but the structural studies of Mg–Zn–Ca metallic glasses are far from complete. Several recent works showed that the short-range order (SRO) in these glasses is formed to some extent with icosahedral and icosahedral-like structural units,8,11–14 but it is clear that distinguishing the subtle changes in SRO with glass composition is difficult. Based on ab initio molecular dynamics (MD) it was also proposed that a percolated network formed with Zn-centered structural units in Zn-rich Mg–Zn–Ca glasses (i.e. the medium-range order (MRO)) can promote a homogeneous corrosion behavior on the alloy surface.13
Much of this previous work relies on ab initio MD.8,11,13,14Ab initio MD has the great advantage that is free from a priori established assumptions about interatomic interactions, but the associated very high computational expense means that it is restricted to small models, typically a few hundred atoms. This prohibits the possibility of analysing the structure at larger length scales. There has also been very little attempt to complement these computational investigations with experimental study of the glass structure, despite the potential for substantial new insight into the glass properties through a combined modelling and experiment approach.
In this work, we present for the first time, an investigation of the structure of Mg60+xZn35−xCa5, (x = 0, 7, 12, 14, 20 at%) bulk metallic glasses by both classical molecular dynamics and neutron diffraction. This allows us to characterise in detail the local structure, including total and partial coordination numbers, coordination polyhedra distribution and the extent of any preferential bonding. We are able to reveal some subtle structural changes which could explain the compositional dependence of the biodegradable properties of these compositions of bulk metallic glass. The use of the large models accessible through classical MD also allows us to investigate the medium-range order (MRO) in these glasses.
2 Methods
2.1 Experimental
Neutron diffraction expriments were performed for two compositions: Mg60Zn35Ca5 and Mg72Zn23Ca5. Bulk metallic Mg–Zn–Ca glasses were prepared using high-purity elements: magnesium (99.8%), zinc (99.99%) and calcium (99.5%), all purchased at Sigma Aldrich, UK. The metals were weighed to give the desired stoichiometry and mixed thoroughly in a glove box to avoid air before being placed in a boron nitride crucible. Ingots of Mg–Zn–Ca alloys were fabricated using an inductively heated furnace which was initially evacuated to 8 × 10−5 Torr and backfilled with flowing argon. The metals were melted and then held at temperature to homogenise before cooling. Rapidly quenched ribbons were produced by remelting the ingots in quartz crucibles, and ejecting with an overpressure of 40 kPa through a nozzle of the quartz crucibles onto a copper wheel rotating with a surface velocity of 25 m s−1.Neutron diffraction spectra of the resultant glasses were collected using the GEM diffractometer15 at the ISIS spallation neutron source at the Rutherford Appleton Laboratory, UK. The glasses were broken into small pieces and placed inside an 8.3 mm diameter vanadium foil container. Spectra were collected for each of the samples inside the container, the empty container, a vanadium rod of 8.34 mm diameter, and the empty GEM instrument in order to perform the appropriate corrections. Data reduction and corrections were performed using the GUDRUN program.15 The corrections involve the removal of background and container scattering, normalization, correction for absorption, inelastic and multiple scattering effects, and subtraction of the self-scattering term.15
Following these corrections, the resultant coherent scattering intensity, i(Q) is defined by
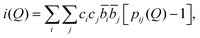 | (1) |
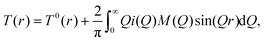 | (2) |
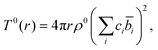 | (3) |
The total correlation function T(r) is related to the total pair distribution function G(r) by
| T(r) = 4πrρ(G(r) − 1), | (4) |
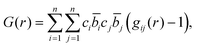 | (5) |
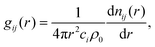 | (6) |
2.2 Simulation
For the classical MD simulations, we used a recently developed many-body, tight-binding (TB) potential12,17 of the form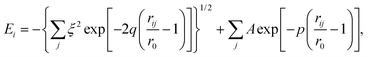 | (7) |
Classical MD simulations were performed using the DLPOLY Classic code.19 All glass models were prepared using the melt-and-quench method: firstly, the starting configuration was equilibrated at high temperature, well above the melting temperature of the glass, and then continuously cooled down to room temperature. The starting configurations for each model were obtained by randomly placing 2000 atoms of the appropriate composition into a cubic periodic simulation box. The size of the box was defined so as to obtain a correct glass density and was about 34.5 Å depending on glass composition. The densities of Mg60Zn35Ca5 and Mg72Zn23Ca5 were obtained experimentally in this work (3.24 and 2.63 g cm−3 respectively, see Section 3.1), those of Mg67Zn28Ca5 and Mg74Zn21Ca5 were taken from the literature,8,13 and the density of Mg80Zn15Ca5, which was not available experimentally, was estimated at 2.32 g cm−3. However, in order to simulate the glass models under realistic conditions, we used the NPT (constant number of particles, pressure and temperature) ensemble allowing the box size to change throughout the simulation. This approach could be more computationally expensive than NVT (constant number of particles, volume and temperature) MD but it helps to avoid high pressures during high-temperature annealing and it was successfully used to obtain glass models consistent with experimental data for other glass compositions.20 Hence, the final glass densities are slightly different from the initial densities, which will be discussed in more detail in Section 3. To ensure that these models were large enough, we also constructed 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000-atom models of two compositions; there were no statistically significant differences in the structure between the two sizes.
000-atom models of two compositions; there were no statistically significant differences in the structure between the two sizes.
Each model was firstly equilibrated at 1500 K for 300 ps and then continuously cooled down to room temperature in 100 K steps being equilibrated for 100 ps at each temperature. Finally, each model was run for 300 ps at 300 K. The MD timestep was 1.0 fs, and the pressure set to zero. The cooling rate of these glasses is 0.7 K ps−1, which is considerably slower than that used in ab initio MD simulations of similar BMG.8,13,14 Although this is still orders of magnitude larger than cooling rates achieved experimentally, simulations using cooling rates of this order have been successful in generating glass structures in agreement with experiment.20–24 Whilst the structures generated using this methodology are in agreement with experimental values, some properties of the glass, such as glass transition temperature, are more difficult to reproduce using simulation methods. We have not attempted to compute the glass transition temperature of our models, but instead we computed structures and diffusion constants to check that the simulations were liquid at high temperature and solid at low temperature, and hence that the final run had equilibrated into an appropriate disordered solid state. The configuration at the final timestep was used for further analysis and only the pair-distribution function data were averaged over the final room-temperature run. Data supporting this paper are available via the Loughborough University Data Repository with DOI: http://10.17028/rd.lboro.4733263.
3 Results
3.1 Density
Table 1 gives the densities for the final configurations of all glass structures. The densities are given in g cm−3 and atoms Å−3 and compared with available experimental data. There is a good agreement in calculated and experimental values that demonstrates the reliability of the interatomic potential, NPT ensemble, and melt-and-quench procedure used to obtain our glass models. The largest discrepancies are observed for the Mg67Zn28Ca5 and Mg74Zn21Ca5 compositions, however, it is worth noting that the experimental densities13 for these compositions were extrapolated from data reported elsewhere.83.2 Pair-distribution functions
Fig. 1 shows the experimental and calculated total correlation functions T(r) for both compositions which we measured with diffraction: Mg72Zn23Ca5 and Mg60Zn35Ca5. In general, there is very good agreement between the simulated and experimental T(r) implying that our simulated structures are consistent with those observed experimentally. The peaks of the calculated T(r) for Mg72Zn23Ca5 occur at very slightly smaller values of r than those seen experimentally, due to the slight (∼3%) overestimation of the calculated atomic density with respect to experiment (Table 1).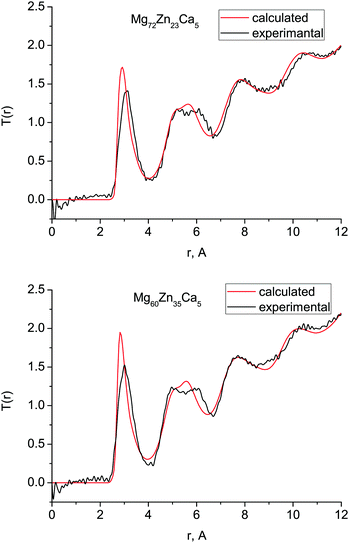 | ||
| Fig. 1 Total correlation functions T(r) obtained with MD simulations (red) and compared with the neutron diffraction data (black) for (a) Mg72Zn23Ca5 and (b) Mg60Zn35Ca5. | ||
For both compositions, the intensity of the simulated first peak in T(r) is larger than for experiment, and the broad peak at 4–7 Å is narrower. This higher first peak is often a feature of simulated correlated functions compared to the broadened data extracted from experimental data. The double nature of the second peak is well-reproduced, which is important as it is a well-known feature of the pair-correlation function of several metallic glasses.2,27,28 The oscillations seen in the experimental T(r) at larger length scales, 7–12 Å, are also present in the simulated T(r).
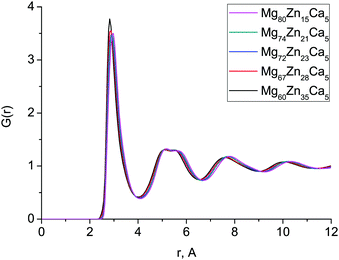
The first peak in T(r) corresponds to interatomic distances in the first coordination shell. It is relatively broad (2.5–4.0 Å) for both compositions and has contributions from overlapping correlations from all the six atom–atom pairs (see Table 2); due to this complexity we have made no attempt to extract partial coordination numbers from the experimental spectrum. Neither the experimental or simulated T(r) differ significantly when the Zn concentration is increased from 23 to 35 at% Zn. In Fig. 2 we show the total distribution functions G(r) for all of our simulated compositions, and see that there is no significant difference across this range of compositions, nor is there substantial variation in the bond lengths, which are given in Table 2, and discussed further below. As discussed in the introduction, these compositions exhibit very different behaviour in terms of their biocompatibility, so to understand this, we must study their structures in more detail.
| r ij (Å) | ||||||
|---|---|---|---|---|---|---|
| Mg–Mg | Mg–Zn | Mg–Ca | Zn–Zn | Zn–Ca | Ca–Ca | |
| Mg80Zn15Ca5 | 3.025 | 2.825 | 3.425 | 2.725 | 3.175 | 3.725 |
| Mg74Zn21Ca5 | 3.025 | 2.825 | 3.425 | 2.675 | 3.175 | 3.775 |
| Mg72Zn23Ca5 | 3.025 | 2.825 | 3.425 | 2.675 | 3.175 | 3.775 |
| Mg67Zn28Ca5 | 3.025 | 2.825 | 3.425 | 2.675 | 3.175 | 3.775 |
| Mg60Zn35Ca5 | 3.025 | 2.825 | 3.425 | 2.675 | 3.175 | 3.725 |
| (rij)aver | 3.025 | 2.825 | 3.425 | 2.685 | 3.175 | 3.755 |
| r m | 3.20 | 2.94 | 3.57 | 2.68 | 3.31 | 3.94 |
| 100%(raver/rm − 1) | −5.47 | −3.91 | −4.06 | 0.19 | −4.08 | −4.70 |
| r c | 2.82 | 2.63 | 3.17 | 2.44 | 2.98 | 3.52 |
| 100%(raver/rc − 1) | 7.27 | 7.41 | 8.04 | 10.04 | 6.54 | 6.68 |
| Crystalline | 3.05–3.18 | 3.04 | 3.62 | 2.53–4.15 | 3.14–4.17 | 3.61–4.32 |
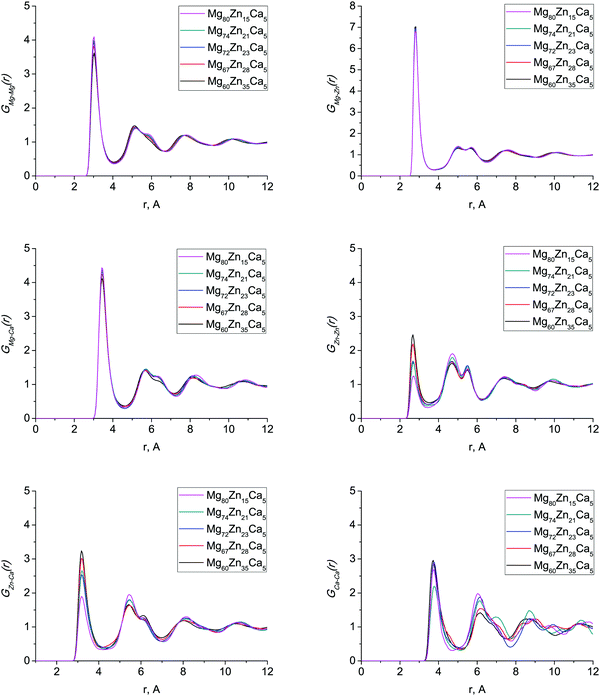
Fig. 3 shows the calculated partial PDFs for all compositions. GMg–Mg(r), GMg–Zn(r) and GMg–Ca(r) partial PDFs do not change significantly with changing composition, indicating that the Mg environment does not depend on composition. As Zn content increases, the first peak of GZn–Zn(r) and GZn–Ca(r) sharpens and becomes more intense; similar features were found in ab initio MD simulations of these and related Mg–Zn–Ca glass compositions.13,14 The GCa–Ca(r) partial PDF has considerable variations in peak shape at larger distances (6–12 Å). This effect has never been considered before as the amount of Ca atoms in models generated with ab initio MD is very low, so that the Ca–Ca partial PDF is liable to strong statistical noise. To check that these variations were not due to remnants of the initial configuration, we computed the Ca diffusion constant at 1500 K, and found it to be about 2 × 10−8 m2 s−1, implying an average Ca atomic displacement of ∼60 Å during the 300 ps run at 1500 K. This is the same order of magnitude as the size of the model, meaning that any memory of the starting configuration will have been destroyed even by the end of the 1500 K part of the trajectory. Statistical noise due to the low Ca content of these models seems the most likely explanation.
Table 2 gives the interatomic bond distances estimated from the first maxima of the simulated partial PDFs. The interatomic bond distances for all pairs of atoms stay virtually constant across this range of composition. This is contrary to other studies8,13,14,29 where, for example, the Zn–Zn interatomic bond distance changes significantly, by up to 0.1 Å. The average interatomic distances, (rij)aver, are generally slightly shorter for the Mg-rich compositions we consider in this system than for the Ca-rich compositions considered in other work,29 which implies a more dense and efficient packing, as we discuss below in Section 3.3.
The values of our calculated interatomic bond distances lie in between covalent, rc, and metallic, rm, bond distances (Table 2). Only the Zn–Zn nearest-neighbour distance is outside this range as it is slightly larger than the corresponding rm. Characteristic bond lengths for several crystalline binary compounds29,30 are also given in Table 2. The bond distances for Mg–Mg, Mg–Zn and Mg–Ca are considerably shorter than those in crystals and those for Zn–Zn, Zn–Ca and Ca–Ca are close to the minimum distance values for crystals indicating that the absence of the long-range order constraints allows shortening of interatomic distances between the nearest-neighbour atoms in the amorphous structure.29
3.3 Coordination numbers
The distributions of the total simulated coordination numbers (CN) for all compositions are given in Fig. 4, and the partial CNs for all pairs are given in Table 3. The coordination number of the atom is defined with Voronoi polyhedra analysis, which will be described further in Section 3.5. The average CN for all species very slightly increases with increasing Zn content: from 14.11 to 14.45 (an increase of 2.4%) for Mg, from 12.38 to 12.84 (an increase of 3.7%) for Zn, and from 17.2 to 17.84 (an increase of 3.5%) for Ca. The largest proportional effect is for Zn atoms. We see from Table 3 that as Mg content decreases and Zn content increases, the number of Mg atoms in the first coordination shell of all species decreases, to be replaced by an increase in the number of Zn atoms, e.g., CNMg–Zn increases from 2.08 to 5.19, CNZn–Zn from 0.81 to 3.21, and CNCa–Zn from 1.4 to 5.08. Although the content of Ca atoms does not change for this range of compositions, CNZn–Ca and CNCa–Ca partial CNs both increase significantly, while CNMg–Ca remains unchanged. This result can indicate some preferences in Zn–Ca and Ca–Ca bonding and will be discussed in Section 3.4 in more detail.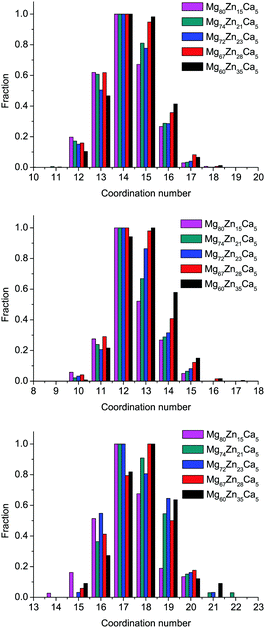 | ||
| Fig. 4 Distributions of Mg-centered, Zn-centered, and Ca-centered clusters by their total coordination number for all simulated compositions. | ||
| Composition | Mg–Mg | Mg–Zn | Mg–Ca | Mg total |
|---|---|---|---|---|
| Mg80Zn15Ca5 | 11.09 | 2.08 | 0.94 | 14.11 |
| Mg74Zn21Ca5 | 10.20 | 3.00 | 0.98 | 14.18 |
| Mg72Zn23Ca5 | 9.97 | 3.30 | 0.97 | 14.24 |
| Mg67Zn28Ca5 | 9.29 | 4.05 | 0.97 | 14.31 |
| Mg60Zn35Ca5 | 8.28 | 5.19 | 0.98 | 14.45 |
| Composition | Zn–Mg | Zn–Zn | Zn–Ca | Zn total |
|---|---|---|---|---|
| Mg80Zn15Ca5 | 11.10 | 0.81 | 0.47 | 12.38 |
| Mg74Zn21Ca5 | 10.57 | 1.34 | 0.60 | 12.51 |
| Mg72Zn23Ca5 | 10.32 | 1.66 | 0.61 | 12.59 |
| Mg67Zn28Ca5 | 9.69 | 2.29 | 0.67 | 12.65 |
| Mg60Zn35Ca5 | 8.90 | 3.21 | 0.73 | 12.84 |
| Composition | Ca–Mg | Ca–Zn | Ca–Ca | Ca total |
|---|---|---|---|---|
| Mg80Zn15Ca5 | 15.1 | 1.4 | 0.7 | 17.2 |
| Mg74Zn21Ca5 | 14.5 | 2.5 | 0.78 | 17.78 |
| Mg72Zn23Ca5 | 13.95 | 2.8 | 0.9 | 17.65 |
| Mg67Zn28Ca5 | 12.99 | 3.73 | 0.96 | 17.68 |
| Mg60Zn35Ca5 | 11.74 | 5.08 | 1.02 | 17.84 |
The exact partial CNs available from the simulated data allow us to calculate the local atomic packing efficiency using the approach of Miracle.31,32 For all of the simulated structures, the packing efficiency for Mg atoms is about 100%, for Zn atoms about 113%, and for Ca atoms about 105% (we note that a ±10% accuracy is anticipated in the calculation of the local packing efficiency32), implying that the atoms in the glass are packed extremely efficiently. This implies that all available space in the first coordination shell of all species is fully occupied contrary to Ca60MgxZn40−x glasses29 where the packing efficiency does not reach its maximum value for the largest Ca atoms. The packing efficiency correlates with glass forming ability (GFA).33,34 The maximum packing efficiency found for our simulated glasses agrees with the experimentally known good GFA of these glasses.9
3.4 Local chemical order
To characterise the local chemical order, one can define a chemical short-range order (CSRO) parameter αi(jk), which for a ternary glass takes the form35| αi(jk) = 1 − (CNij + CNik)/((cj + ck)CNi) for i ≠ j ≠ k, | (8) |
| αij = 1 − CNij/(cjCNi). | (9) |
| αii = (1 − 1/ci)αi(jk), | (10) |
The CSRO parameters αij and αi(jk) are given in Tables 4 and 5. αMgMg and αMgZn are close to zero indicating the absence of CSRO in the distribution of Mg and Zn atoms around Mg atoms, whereas the strongly negative values of αMgCa indicate an increased local concentration of Ca atoms in the first coordination shell of Mg.
| α ij | Mg–Mg | Mg–Zn | Mg–Ca | Zn–Mg | Zn–Zn | Zn–Ca | Ca–Mg | Ca–Zn | Ca–Ca |
|---|---|---|---|---|---|---|---|---|---|
| Mg80Zn15Ca5 | 0.02 | 0.02 | −0.34 | −0.12 | 0.56 | 0.25 | −0.10 | 0.46 | 0.19 |
| Mg74Zn21Ca5 | 0.03 | −0.01 | −0.38 | −0.14 | 0.49 | 0.05 | −0.10 | 0.33 | 0.12 |
| Mg72Zn23Ca5 | 0.03 | −0.01 | −0.36 | −0.14 | 0.43 | 0.03 | −0.10 | 0.31 | −0.02 |
| Mg67Zn28Ca5 | 0.03 | −0.01 | −0.35 | −0.14 | 0.35 | −0.05 | −0.10 | 0.25 | −0.09 |
| Mg60Zn35Ca5 | 0.05 | −0.03 | −0.35 | −0.16 | 0.29 | −0.13 | −0.10 | 0.19 | −0.14 |
| α i(jk), i = | Mg | Zn | Ca |
|---|---|---|---|
| Mg80Zn15Ca5 | −0.07 | −0.10 | −0.01 |
| Mg74Zn21Ca5 | −0.08 | −0.13 | −0.01 |
| Mg72Zn23Ca5 | −0.07 | −0.13 | 0.00 |
| Mg67Zn28Ca5 | −0.06 | −0.14 | 0.00 |
| Mg60Zn35Ca5 | −0.07 | −0.15 | 0.01 |
For Zn and Ca atoms the local environment is far from neutral: negative αZnMg values and positive αZnZn values indicate an enrichment in Mg atoms and a deficit of Zn atoms in Zn-centered clusters. This deficit decreases with increasing Zn content but even for the Mg60Zn35Ca5 composition, it remains significant (αZnZn = 0.29). A similar situation is observed for the local environment of Ca: a slight enrichment in Mg atoms and a deficit of Zn atoms, which reduces with increasing Zn content.
Remarkable changes are observed for αZnCa and αCaCa. With increasing Zn content, these parameters change from 0.25 and 0.19 for Mg80Zn15Ca5 to −0.13 and −0.14 for Mg60Zn35Ca5, i.e., a strong deficit in Ca around Zn and Ca transforms to a slight enrichment as Zn content increases. Remarkably, αZnCa and αCaCa values cross from positive to negative at Zn content of 23–28 at%, i.e., near the threshold value where Mg–Zn–Ca glasses forms the amorphous Zn- and oxygen-rich layer which prevents the harmful release of hydrogen on immersion into the body.3 Across the same range of compositions, αMgZn and αMgCa remain unchanged. This allows us to speculate that Zn–Ca and Ca–Ca bonding play an important role in structural changes which occur with changing Zn content and affect the biocompatibility of Mg–Zn–Ca glass.
The αi(jk) values in Table 5 demonstrate the absence of significant clustering in Mg–Zn–Ca amorphous alloys. All values are zero or slightly negative, indicating no CSRO around Ca and slightly increased order around Mg and Zn respectively.
3.5 Voronoi polyhedra distribution
Voronoi analysis can be used to further characterise the order of BMG providing important information on atoms first coordination shell.37 The Voronoi polyhedron for a given atom is defined as the region of space which is closer to that atom than to any other. Each polyhedron can be described by its signature, (v3, v4, v5, v6,…), where vm is the number of faces on the polyhedron containing m edges. For example, the icosahedral motif, which is important in BMGs, has twelve pentagonal (m = 5) faces and therefore has a Voronoi signature of (0, 0, 12, 0).One can define the coordination number of an atom directly from its Voronoi polyhedron as 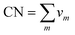 , by defining nearest-neighbour atoms as two atoms which have common faces in their Voronoi polyhedra.38 This gives a different definition of the CN to that often used, where two atoms are nearest neighbours if they are closer than a given cutoff. The coordination number defined in this way is very sensitive to the choice of the cutoff value if the bond length distribution is broad20 as it often is for metallic glasses. Moreover, comparison with other results becomes more difficult if a different cutoff value was used.
, by defining nearest-neighbour atoms as two atoms which have common faces in their Voronoi polyhedra.38 This gives a different definition of the CN to that often used, where two atoms are nearest neighbours if they are closer than a given cutoff. The coordination number defined in this way is very sensitive to the choice of the cutoff value if the bond length distribution is broad20 as it often is for metallic glasses. Moreover, comparison with other results becomes more difficult if a different cutoff value was used.
In this work, the Voro++39 code was used to perform the Voronoi analysis. An example of a simulation box with calculated Voronoi polyhedra is given in Fig. 5.
The distributions of different types of Mg-, Zn-, and Ca-centered coordination Voronoi polyhedra are given in Fig. 6. Note that for Mg- and Zn-centered clusters only polyhedra with ≥2% population in all compositions are given, whereas for Ca-centered clusters polyhedra with >2% population in at least one composition are given.
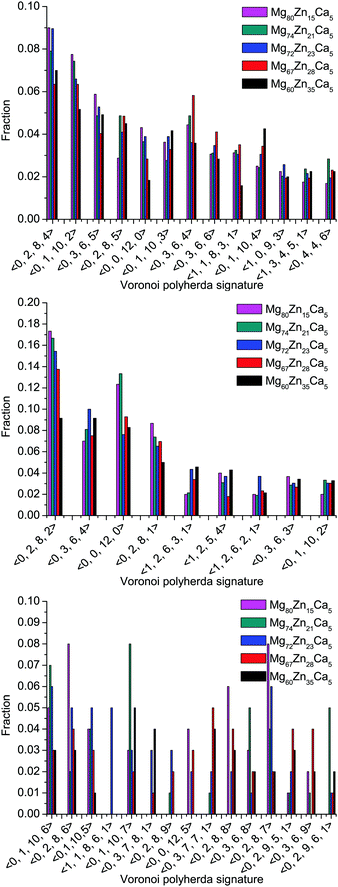 | ||
| Fig. 6 Distribution of different types of Mg- (top), Zn- (middle) and Ca- (bottom) centered coordination polyhedra in all simulated compositions. | ||
It is clear that the distributions for all elements are very broad and it is difficult to distinguish a dominant type of coordination polyhedra. However, for Mg-centered clusters, (0, 2, 8, 4) and (0, 1, 10, 2) polyhedra make up 6–9% and 5–8% respectively of the total population. For Zn-centered clusters, the (0, 2, 8, 2) and (0, 0, 12, 0) polyhedra dominate with 9–17% and 8–14% respectively of the total population. For Ca-centered clusters, it is not possible to define a dominant type of coordination polyhedra for all compositions.
Although the distribution of coordination polyhedra is very broad, it is possible to highlight some trends which occur with changes in composition. In Zn-poor compositions (Mg80Zn15Ca5 and Mg74Zn21Ca5) the distribution of polyhedra is narrower: the fraction of Zn-centered (0, 2, 8, 2) and (0, 0, 12, 0) polyhedra is highest (17% and 14%) and for Ca-centered clusters the fraction of two types of polyhedra ((0, 2, 8, 6) and (0, 8, 8, 7)) reaches 8%. By contrast, for the Zn-rich composition Mg60Zn35Ca5, the maximum value of fraction for any polyhedron type does not exceed 9% and 4% for Zn- and Ca-centered clusters respectively. For Mg-centred polyhedra, no clear tendencies could be found.
3.6 Bond-angle distribution
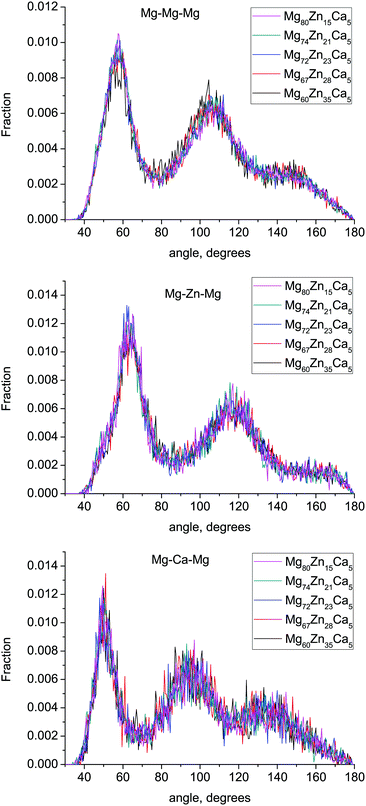
The bond-angle distributions (BAD) for Mg–X–Mg (X = Mg, Zn, Ca) are given in Fig. 7. There are no significant changes in these BADs with composition. The Mg–Mg–Mg and Mg–Zn–Mg BADs have two broad peaks at ≈57° and 106° and ≈63° and 117° respectively. The ideal icosahedral bond angles are ≈63.5° and 116.5°, indicating that Zn-centered clusters are more likely to form icosahedral and related motifs than Mg-centered clusters. This confirms the results of Voronoi tesselation analysis discussed above. The Mg–Ca–Mg BAD has peaks at ≈50° and 95°, which corresponds to the higher Ca atom CN (17.2–17.84) and a larger fraction of polyhedron faces with six edges.3.7 Medium-range order
Structural studies of BMGs over the past decades have shown that many glasses exhibit not just short-range order (SRO) but also order at larger length scales, so-called medium-range order (MRO).29,35,40–44 Generally, MRO in glasses is shown by a pre-peak in the neutron or X-ray scattering structure factor.2 There is no unique explanation of the origin of this feature. Some suggest that icosahedral clusters are the source of MRO,45,46 however, such a pre-peak was also observed from neutron scattering data on a Zr–Ni liquid47 which is reported not to have dominant icosahedral short-range order. It has been suggested44 that “a pre-peak is a manifestation of chemical and topological ordering originating from the most common polyhedral cluster in each system, icosahedral or otherwise”.The extent of MRO in Mg–Zn–Ca glasses is likely to be rather small. Fig. 8 shows the experimental total neutron scattering structure factors for Mg60Zn35Ca5 and Mg72Zn23Ca5 metallic glasses. For our samples, a pre-peak at about 1.2 Å−1 is barely resolved.
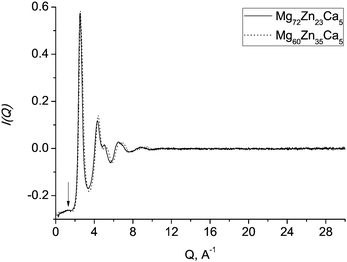 | ||
| Fig. 8 Experimental total neutron scattering structure factors for Mg60Zn35Ca5 (dotted line) and Mg72Zn23Ca5 (solid line) metallic glasses. The arrow indicates a barely resolved pre-peak at ≈1.2 Å−1. | ||
The efficient cluster packing (ECP) model has been recently developed for the structural description of metallic glasses40 and applied to the structure of Ca–Mg–Cu glasses,35 where it was shown that the MRO can be explained as a face-centered-cubic (FCC)-like local ordering of Cu-centered clusters. In our glasses, the Zn-centered clusters could play this role of the MRO formers. Icosahedral (0, 0, 12, 0) and icosahedral-like ((0, 2, 8, 2), (0, 1, 10, 2) and (0, 2, 8, 1)) clusters make up about 33% of the Voronoi polyhedra for Mg72Zn23Ca5, for example, and can be considered as SRO forming structural units, consistent with previous results.11,13 Hence, we assume that Zn-centered clusters form the FCC motif and try to explain the Zn–Zn partial PDF profile, gZnZn(r) (Fig. 3), with the ECP model.35,40 In particular, we are interested in the broad double peak in G(r) at ≈4–6 Å. For conciseness, the analysis is only shown for the Mg72Zn23Ca5 composition.
Within the ECP model,35,40 the FCC lattice has four α sites occupied with Zn-centered clusters and four octahedral (β) and eight tetrahedral (γ) interstitial sites which could be also occupied by alloying elements. The average number of atoms in each Zn-centered cluster is 13.6 (CNZn + 1) and so we can estimate the number of atoms forming the FCC “super-cell” as between 54.3 (no interstitial sites occupied) and 66.3 (all interstitial sites occupied). By using the calculated density, this implies a supercell volume of 1150.5 to 1404.5 Å3, and hence a lattice parameter between 10.5 Å and 11.2 Å. The distance between neighbouring Zn-centred clusters, rc, is the lattice parameter divided by 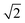 , hence between 7.4 Å and 7.9 Å. The third peak of the simulated Zn–Zn partial PDF, gZnZn(r) (Fig. 3), is at 7.525 Å and, hence, is consistent with this rc value.
, hence between 7.4 Å and 7.9 Å. The third peak of the simulated Zn–Zn partial PDF, gZnZn(r) (Fig. 3), is at 7.525 Å and, hence, is consistent with this rc value.
By using this calculated value, the super-cell parameter is refined to 10.6 Å, which corresponds to 22% of interstitial sites in a super-cell being occupied. For this value of ac, we expect to find the peak corresponding to the octahedral site at 5.3 Å (=ac/2) and the peaks corresponding to the tetrahedral sites at 4.6 Å (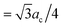 ) and 8.7 Å (
) and 8.7 Å (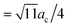 ). The positions for the second and the third peaks in gZnZn(r) are at about 4.73 Å and 5.48 Å respectively. Hence, the second peak could possibly be assigned to the distance between the Zn atom in the center of the cluster and a Zn atom in the nearest tetrahedral position. However, the third peak is further from the predicted distance between α and β (octahedral) sites. The magnesium atom could occupy the octahedral interstitial sites, however, the Mg–Zn partial PDF, gMgZn(r) (Fig. 3), demonstrates that there are no peaks corresponding to the predicted distances. This implies that Mg–Zn–Ca metallic glasses do not possess a MRO which could be described well with the ECP model.
). The positions for the second and the third peaks in gZnZn(r) are at about 4.73 Å and 5.48 Å respectively. Hence, the second peak could possibly be assigned to the distance between the Zn atom in the center of the cluster and a Zn atom in the nearest tetrahedral position. However, the third peak is further from the predicted distance between α and β (octahedral) sites. The magnesium atom could occupy the octahedral interstitial sites, however, the Mg–Zn partial PDF, gMgZn(r) (Fig. 3), demonstrates that there are no peaks corresponding to the predicted distances. This implies that Mg–Zn–Ca metallic glasses do not possess a MRO which could be described well with the ECP model.
It is usual to assume that the largest solute in a multicomponent glass would be the primary structure-forming solute.48 In our system, the largest solute atom is Ca and its concentration is too small. However, for Ca–Mg–Cu glasses, it was suggested that elements with the strongest chemical interaction with solvent atoms form the structure-forming clusters.35 The order of interaction energy in Mg–Zn–Ca system can be estimated with heats of mixing,49 which suggest that the Ca–Zn interaction (−22 kJ mol−1) is much stronger than the Ca–Mg and Mg–Zn interactions (−6 kJ mol−1 and −4 kJ mol−1, respectively). In such a way, in our systems, the dominant solute Zn atoms have the weakest interaction with the solvent Mg atoms. This could possibly be a reason why our systems do not exhibit the explicit medium-range ordering seen in Ca–Mg–Zn29 and Ca–Mg–Cu35 glasses, where the solute atoms interact more strongly with solvent atoms than with other solute atoms.
The formation of chain-like fragments in the modeled glass structure can be considered as a certain degree of a MRO. Indeed, our calculations demonstrate that the Zn–Zn connectivity strongly increases with increasing Zn content. In agreement with ab initio MD simulations,13 the number of Zn atoms connected to two other Zn atoms dramatically increases for zinc-rich compositions (Mg67Zn28Ca5 and Mg60Zn35Ca5), and the number is of course largest for the compositions richest in zinc. In such a way, our calculations confirm the proposed idea13 that “Zn-centered cluster(s) could eventually form a percolated network” and that this can determine the physical and chemical properties of the bulk materials.
4 Conclusions
In this work, we have presented a combined simulation-experiment study of the atomic structure of Mg-based bulk metallic glasses intended for biomedical applications. A good agreement in calculated and experimental densities and in pair-correlation functions for two compositions (Mg60Zn35Ca5 and Mg72Zn23Ca5) let us conclude that our models of glass structure are realistic, and so we studied five different compositions of potential biomedical relevance. There is no significant change in the total pair-correlation functions or in the bond lengths for the range of compositions studied. There were only small increases in the total coordination numbers with increasing zinc content. The bond lengths for all pairs of atoms are smaller or close to minimum bond distances found in crystalline compounds, indicating a dense and efficient packing of atoms within an amorphous system and the bond distance shortening caused by the absence of the long-range order. This is confirmed by calculated packing efficiencies of about 100%, which also corresponds to these compositions' known good glass-forming ability.The greatest variation in the bonding with composition was in the zinc and calcium bonding, which we have characterised by calculating the local chemical short-range order parameter using the partial coordination numbers extracted from our structural models. At low zinc content, zinc and calcium prefer to avoid each other and themselves in their first coordination shell. As zinc content increases, this avoidance becomes less prevalent and in the highest-zinc-content glasses, zinc and calcium prefer to bond to calcium. This is also visible in the sharpening of the first peaks in the Zn–Ca and Ca–Ca partial pair-correlation functions, and the increase in the Zn–Ca and Ca–Ca coordination numbers. The crossover between avoidance and preference occurs at zinc contents of 23–28%, close to the threshold value of 28% where Mg–Zn–Ca glasses change their bio-compatible properties. This implies that the suggestion that the corrosive elements (Mg, Ca) are removed in the body to leave the passive zinc is too simplistic, and that there is substantial preferential bonding in these systems, which will strongly affect the passivation.
The distribution of Voronoi polyhedra is very broad for all simulated glasses and there is no single unambiguously dominant structural unit. Icosahedral and icosahedral-like coordination polyhedra are always present. In Zn-poor glasses, these (0, 2, 8, 2) and (0, 0, 12, 0) coordination polyhedra make up 14–17% of the population of polyhedra and their content decreases with increasing Zn content. This indicates a sort of degradation of the short-range ordering in Zn-rich Mg–Zn–Ca glasses.
In the last section of this paper, we have applied the efficient cluster packing model in order to investigate the medium-range order in these glasses. We conclude that this model cannot describe the MRO in our amorphous systems. This is also confirmed by our experimental total neutron scattering structure factor which does not have the explicit pre-peak which usually indicates the presence of MRO. The only evidence of the MRO for Mg–Zn–Ca glasses is the increasing amount of chains formed with Zn-centered clusters in Zn-rich Mg–Zn–Ca metallic glasses. Our result confirms an earlier suggestion13 that Zn-centered clusters could form a percolated network and that this can determine the physical and chemical properties of the bulk materials.
Acknowledgements
The authors would like to thank the ISIS Pulsed Neutron and Muon Source for the allocation of beam-time (RB1510188). The work of A. G. and J. K. C. was funded by the UK's EPSRC (EP/L024195). Via our membership of the UK's HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202), this work used the ARCHER UK National Supercomputing Service (http://www.archer.ac.uk). The authors also acknowledge the use of the UCL Legion High Performance Computing Facility (Legion@UCL), and associated support services, in the completion of this work.References
- W. Klement, R. H. Willens and P. Duwez, Nature, 1960, 187, 869–870 CrossRef CAS.
- Y. Q. Cheng and E. Ma, Prog. Mater. Sci., 2011, 56, 379–473 CrossRef CAS.
- B. Zberg, P. J. Uggowitzer and J. F. Löffler, Nat. Mater., 2009, 8, 887–891 CrossRef CAS PubMed.
- H. Li and Y. Zheng, Acta Biomater., 2016, 28, 1–20 Search PubMed.
- P. Meagher, E. O'Cearbhaill, J. Byrne and D. Browne, Adv. Mater., 2016, 28, 5755–5762 CrossRef CAS PubMed.
- X. Gu, Y. Zheng, S. Zhong, T. Xi, J. Wang and W. Wang, Biomaterials, 2010, 31, 1093–1103 CrossRef CAS PubMed.
- Y. B. Wang, X. H. Xie, H. F. Li, X. L. Wang, M. Z. Zhao, E. W. Zhang, Y. J. Bai, Y. F. Zheng and L. Qin, Acta Biomater., 2011, 7, 3196–3208 CrossRef CAS PubMed.
- R. Mahjoub, K. J. Laws, J. P. Scicluna, J. E. Daniels and M. Ferry, Comput. Mater. Sci., 2015, 96, 246–255 CrossRef CAS.
- X. Gu, G. J. Shiflet, F. Q. Guo and S. J. Poon, J. Mater. Res., 2005, 20, 1935–1938 CrossRef CAS.
- Q. He, Y.-Q. Cheng, E. Ma and J. Xu, Acta Mater., 2011, 59, 202–215 CrossRef CAS.
- Y. F. Zhao, D. Y. Lin, X. H. Chen, Z. K. Liu and X. D. Hui, Acta Mater., 2014, 67, 266–277 CrossRef CAS.
- S.-P. Ju, H.-H. Huang and J. C.-C. Huang, J. Non-Cryst. Solids, 2014, 388, 23–31 CrossRef CAS.
- S. N. Li, J. B. Liu, J. H. Li, J. Wang and B. X. Liu, J. Phys. Chem. B, 2015, 119, 3608–3618 CrossRef CAS PubMed.
- J. K. Christie, Phys. Chem. Chem. Phys., 2015, 17, 12894–12898 RSC.
- A. C. Hannon, Nucl. Instrum. Methods Phys. Res., Sect. A, 2005, 551, 88–107 CrossRef CAS.
- E. Lorch, J. Phys. C: Solid State Phys., 1969, 2, 229 Search PubMed.
- F. Cleri and V. Rosato, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 22 CrossRef CAS.
- T. Egami, JOM, 2010, 62, 70–75 CrossRef.
- I. T. Todorov, W. Smith, K. Trachenko and M. T. Dove, J. Mater. Chem., 2006, 16, 1911–1918 RSC.
- A. Gulenko, O. Masson, A. Berghout, D. Hamani and P. Thomas, Phys. Chem. Chem. Phys., 2014, 16, 14150–14160 RSC.
- K. Vollmayr, W. Kob and K. Binder, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 15808 CrossRef CAS.
- J. K. Christie and A. Tilocca, J. Phys. Chem. B, 2012, 116, 12614–12620 CrossRef CAS PubMed.
- A. Tilocca and A. N. Cormack, Langmuir, 2009, 26, 545–551 CrossRef PubMed.
- J. K. Christie and A. Tilocca, Chem. Mater., 2010, 22, 3725–3734 CrossRef CAS.
- N. N. Greenwood and A. Earnshaw, Chemistry of the elements, Butterworth Heinemann, 1997 Search PubMed.
- B. Cordero, V. Gómez, A. E. Platero-Prats, M. Revés, J. Echeverría, E. Cremades, F. Barragán and S. Alvarez, Dalton Trans., 2008, 2832–2838 RSC.
- H. Y. Hsieh, T. Egami, Y. He, S. J. Poon and G. J. Shiflet, J. Non-Cryst. Solids, 1991, 135, 248–254 CrossRef CAS.
- Y. H. Liu, T. Fujita, D. P. B. Aji, M. Matsuura and M. W. Chen, Nat. Commun., 2014, 5, 3238 CAS.
- O. N. Senkov, D. B. Miracle, E. R. Barney, A. C. Hannon, Y. Q. Cheng and E. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 104206 CrossRef.
- J. L. C. Daams, J. H. N. van Vucht and P. Villars, Atlas of Crystal Structure Types Of Intermetallic Phases, American Society for Metals, 1992 Search PubMed.
- D. B. Miracle, W. S. Sanders and O. N. Senkov, Philos. Mag., 2003, 83, 2409–2428 CrossRef CAS.
- D. B. Miracle, J. Non-Cryst. Solids, 2004, 342, 89–96 CrossRef CAS.
- A. L. Greer, Nature, 1993, 366, 303–304 CrossRef.
- M. Chen, NPG Asia Mater., 2011, 3, 82–90 CrossRef.
- O. N. Senkov, Y. Q. Cheng, D. B. Miracle, E. R. Barney, A. C. Hannon and C. F. Woodward, J. Appl. Phys., 2012, 111, 123515 CrossRef.
- B. Warren, X-ray Diffraction, Dover, Dover Publications, 1990 Search PubMed.
- G. Voronoi, J. Reine Angew. Math., 1909, 136, 67–182 Search PubMed.
- R. Zallen, The Physics of Amorphous Solids, Wiley Online Library, 1983 Search PubMed.
- C. Rycroft, Voro++: a three-dimensional Voronoi cell library in C++, Lawrence Berkeley National Laboratory, LBNL-1430E, 2009 Search PubMed.
- D. B. Miracle, Acta Mater., 2006, 54, 4317–4336 CrossRef CAS.
- P. Lamparter and S. Steeb, J. Non-Cryst. Solids, 1988, 106, 137–146 CrossRef CAS.
- H. Y. Hsieh, B. H. Toby, T. Egami, Y. He, S. J. Poon and G. J. Shiflet, J. Mater. Res., 1990, 5, 2807–2812 CrossRef CAS.
- T. C. Hufnagel and S. Brennan, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 014203 CrossRef.
- N. A. Mauro, V. Wessels, J. C. Bendert, S. Klein, A. K. Gangopadhyay, M. J. Kramer, S. G. Hao, G. E. Rustan, A. Kreyssig and A. I. Goldman, et al. , Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 184109 CrossRef.
- J. Saida, M. Matsushita and A. Inoue, Appl. Phys. Lett., 2001, 79, 412–414 CrossRef CAS.
- M. H. Lee, R. T. Ott, M. F. Besser, M. J. Kramer and D. J. Sordelet, Scr. Mater., 2006, 55, 505–508 CrossRef CAS.
- D. Holland-Moritz, S. Stüber, H. Hartmann, T. Unruh, T. Hansen and A. Meyer, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 064204 CrossRef.
- D. B. Miracle, D. V. Louzguine-Luzgin, L. V. Louzguina-Luzgina and A. Inoue, Int. Mater. Rev., 2010, 55, 218–256 CrossRef CAS.
- A. Takeuchi and A. Inoue, Mater. Trans., 2005, 46, 2817–2829 CrossRef CAS.
| This journal is © the Owner Societies 2017 |