Open Access Article
Open Access ArticleStructural aspects of partial solid solution formation: two crystalline modifications of a chiral derivative of 1,5-dihydro-2H-pyrrol-2-one under consideration†
Olga A.
Lodochnikova
 *ab,
Liliya S.
Kosolapova
b,
Alina F.
Saifina
a,
Aidar T.
Gubaidullin
*ab,
Liliya S.
Kosolapova
b,
Alina F.
Saifina
a,
Aidar T.
Gubaidullin
 a,
Robert R.
Fayzullin
a,
Robert R.
Fayzullin
 *a,
Ayrat R.
Khamatgalimov
*a,
Ayrat R.
Khamatgalimov
 a,
Igor A.
Litvinov
a and
Almira R.
Kurbangalieva
a,
Igor A.
Litvinov
a and
Almira R.
Kurbangalieva
 b
b
aA.E. Arbuzov Institute of Organic and Physical Chemistry, Kazan Scientific Center, Russian Academy of Sciences, Arbuzov Street, 8, Kazan 420088, Russian Federation. E-mail: lod_olga@mail.ru; robert.fayzullin@gmail.com
bA.M. Butlerov Institute of Chemistry, Kazan Federal University, Kremlyovskaya Street, 18, Kazan 420008, Russian Federation
First published on 16th November 2017
Abstract
The purposeful change of crystallization conditions for rac-3-chloro-5-hydroxy-1-(4-methylbenzyl)-4-[(4-methylphenyl)sulfanyl]-1,5-dihydro-2H-pyrrol-2-one 1 leads to two different crystal modifications, namely, a racemic compound in the triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) with Z′ = 1 (α-1) and a partial solid solution based on a racemic compound in the monoclinic space group P21 with Z′ = 4 (β-1). The first modification, α-1, is characterized by a higher density of the molecular packing in the crystal, while the second one, β-1, by a stronger system of hydrogen bonds and the presence of positional and substitutional disorder simultaneously. The analysis of the crystal structure of modifications α and β allowed us to define some structural aspects of the partial solid solution formation. Namely, the tendency to build a stronger hydrogen bond system enables the solution of enantiomers of 1 to be formed in the crystalline phase, whereas the propensity of the molecules to adopt a more favorable transoid conformation limits the solubility of the minor enantiomer.
with Z′ = 1 (α-1) and a partial solid solution based on a racemic compound in the monoclinic space group P21 with Z′ = 4 (β-1). The first modification, α-1, is characterized by a higher density of the molecular packing in the crystal, while the second one, β-1, by a stronger system of hydrogen bonds and the presence of positional and substitutional disorder simultaneously. The analysis of the crystal structure of modifications α and β allowed us to define some structural aspects of the partial solid solution formation. Namely, the tendency to build a stronger hydrogen bond system enables the solution of enantiomers of 1 to be formed in the crystalline phase, whereas the propensity of the molecules to adopt a more favorable transoid conformation limits the solubility of the minor enantiomer.
Introduction
Chirality is one of the most important concepts in chemistry. Crystallization of a chiral substance with an equal ratio of enantiomers leads to one of the following racemate types: (i) a racemic compound, (ii) a molecular compound having a non-equimolar composition, (iii) a conglomerate of crystals of individual enantiomers, or (iv) a solid solution (in other words, a mixed crystal) with a racemic composition.1 Furthermore, the first three cases can be complicated by a partial solid solution.2 Since pioneering Pasteur's experiments and till the present time, comprehensive research on chiral compounds has greatly succeeded in understanding their phase behaviour and crystal structure3–5 and applying crystallization processes for resolution of racemates.6 Nevertheless, a complete theory of solid solution formation has not been elaborated yet.7 One of the obvious reasons for this is the difficulty in identifying and studying the scarce partial8–14 and continuous15–23 solid solutions of enantiomers.The analysis of literature studies accumulated to date has made it possible to identify some structural features accompanying the formation of an enantiomer solution in the crystalline phase, such as pseudosymmetry, isostructurality, and Z′ > 1 packing of a crystal (pure enantiomer, normal racemic compound), which acts as a constructive pattern for a solid solution phase.7,23
At the same time, the problem of observing multiple molecules in an asymmetric unit is currently at the forefront of modern chemical crystallography.24,25 According to recent reviews on Z′ problems,26,27 the amount of structures with Z′ > 1 is estimated at ca. 10% of the total number of crystals investigated, and structures with Z′ ≥ 4 are even more infrequent. Although the number of symmetry-independent molecules does not relate to the enthalpy or entropy of a solid phase directly, in all probability, Z′ > 1 provides more flexibility to accommodate the packing, which could contribute to or contradict the best crystal formative motif.23,28–30 Moreover, the presence of a second and more “extra” symmetrically independent molecule in crystals is often accompanied by the pseudosymmetry phenomenon,31 which we exemplified earlier in glycerol derivatives20,21 and a pair of mucochloric acid polymorphs.32
1,5-Dihydro-2H-pyrrol-2-ones represent an important class of five-membered nitrogen-containing heterocycles. Their structural moiety is found in different natural molecules and synthesized compounds having a wide range of biological activities. Among the compounds of this class, substances with antimicrobial, anti-inflammatory, antitumor, analgesic, antiviral, nootropic, antiaggregant and other types of biological activities have been found.33–38
In the present work, the polymorphism of an unsaturated γ-lactam, racemic 3-chloro-5-hydroxy-1-(4-methylbenzyl)-4-[(4-methylphenyl)sulfanyl]-1,5-dihydro-2H-pyrrol-2-one 1, was investigated. It is important to note that 1 includes the hydroxyl group O(5)–H(5) (marked with blue color in Chart 1) in its structure. This group is directly bonded to the asymmetric C(5) carbon atom and can be a potential donor in hydrogen bonding. The carbonyl group (marked with red), often acting as an acceptor during the H-bond formation, is also present within the polyfunctional compound 1. The crystallization of lactam 1 from the solution at room temperature leads to the formation of a racemic compound in the triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) with Z′ = 1 (α-1), whereas a partial solid solution in the monoclinic space group P21 with Z′ = 4 (β-1) is formed from the hot solution during the crystallization process. The analysis of the crystal structures of crystalline modifications α and β revealed some structural aspects of racemic compound and partial solid solution formation.
with Z′ = 1 (α-1), whereas a partial solid solution in the monoclinic space group P21 with Z′ = 4 (β-1) is formed from the hot solution during the crystallization process. The analysis of the crystal structures of crystalline modifications α and β revealed some structural aspects of racemic compound and partial solid solution formation.
Experimental
Racemic 3-chloro-5-hydroxy-1-(4-methylbenzyl)-4-[(4-methylphenyl)sulfanyl]-1,5-dihydro-2H-pyrrol-2-one rac-1 was synthesized as described earlier.39FTIR spectroscopy
Infrared spectra of the polycrystalline samples in potassium bromide pellets were recorded on a Bruker Tensor 27 FTIR spectrometer.DSC studies
DSC curves were measured on a Netzsch STA 449 F3 Jupiter differential scanning calorimeter in a temperature range of 20–200 °C with a heating rate of 10 °C min−1. The temperature scale and heat flux were calibrated against the melting data for naphthalene, benzil, acetanilide, benzoic acid, indium, tin, and lead. The mass of the samples usually amounted to approximately 5 mg.DFT calculations
Quantum-chemical calculations were performed at a DFT level using Gaussian 03 software.40 A hybrid functional PBE0 (ref. 41) and a standard basis set 6-31G(d,p) were used. The optimization of geometries was carried out without limitations on the symmetry. Only the positive values of frequency were obtained.Solid phase characterization via PXRD
Powder X-ray diffraction (PXRD) measurements were performed using a Bruker D8 Advance diffractometer equipped with a Vario attachment and a Vantec linear PSD, using CuKα1 radiation (1.5406 Å) monochromated with a curved Johansson monochromator. The performance mode of the X-ray tube was 40 kV and 40 mA. Room-temperature data were collected in the reflection mode with a flat-plate sample. Samples were applied on the surface of a standard zero diffraction silicon plate. The samples were kept spinning (15 rpm) throughout the data collection. Patterns were recorded in the 2θ range between 2° and 50°, in 0.008° steps, with a step time of 0.1–2.0 s.Single crystal X-ray analysis
X-ray diffraction (XRD) data for the single crystals of α-1 and β-1 were collected on a Bruker Smart Apex II CCD diffractometer (ω-scan mode) using graphite-monochromated MoKα (0.71073 Å) radiation at 150 and 293 K. The performance mode of the sealed X-ray tube was 50 kV and 30 mA. The diffractometer was equipped with an Oxford Cryostream LT device.Suitable crystals of appropriate dimensions were mounted on glass fibres in random orientations. Two different crystals of α-1 and the same crystal of β-1 were analyzed at the two above-mentioned temperatures. Preliminary unit cell parameters were determined with three sets of 12 narrow frame scans. Data collection: images were indexed and integrated using the APEX2 data reduction package (v2014.11-0, Bruker AXS). Final cell constants were determined by global refinement of reflections from the complete data set. Analysis of the integrated data did not show any decay. Data were corrected for systematic errors and absorption using TWINABS-2012/1 (for the crystal of α-1 [293 K]) or SADABS-2014/5 (for the other cases) based on the Laue symmetry using equivalent reflections. The crystal of α-1 [293 K] demonstrated non-merohedral twinning: orientation matrices of two components were found by using the CELL_NOW-2008/4 routine and the final model was refined against a combined set of diffraction indices. The minor domain with a fractional contribution of 0.304(2) was rotated from the main one by 179.7° about the reciprocal axis [−0.001 1.000 −0.997] and real axis [−0.170 1.000 −0.871], and the twin law was −0.998 0.002 0.005, −0.185 0.070 −0.933, and 0.177 −1.069 −0.072.
XPREP-2014/2 and the Assign Spacegroup routine of WinGX-2014.1 were used for analysis of systematic absences and space group determination. The structures were solved by direct methods using SHELXT-2014/5 (ref. 42) and refined by full-matrix least-squares on F2 using SHELXL-2017/1.43 Calculations were mainly performed using the WinGX-2014.1 suite of programs.44 The crystal of β-1 turned out to be an inversion twin with a fractional volume contribution of 0.48(7). Non-hydrogen atoms were refined anisotropically. The position of the hydrogen atom H(5) of α-1 [150 and 293 K] was determined based on the difference electron density map and this atom was refined isotropically. The position of the hydrogen atom H(5) of β-1 [150 and 293 K] was inserted using a rotating group refinement with an idealized C(5)–O(5)–H(5) angle. The other hydrogen atoms were inserted at the calculated positions and refined as riding atoms. The N-pivot para-methylbenzyl substituent of symmetrically independent molecules B and D was almost equally disordered into two conformations (relative occupancy of 0.541(33) and 0.556(37) for the major components, respectively). Furthermore, the hydroxyl at the chiral atom C(5D) was disordered into two almost mirror-related positions with an occupancy of 0.753(8) for the main component. The disorder was resolved using free variables and reasonable restraints on geometry and anisotropic displacement parameters. All the compounds studied have no unusual bond lengths and angles. The numbering scheme adopted in this study is shown in Chart 1. The crystal data, data collection and structure refinement details for low-temperature experiments are summarized in Table 1.
| Compound | α-1 | β-1 |
|---|---|---|
| Empirical formula | C19H18ClNO2S | C19H18ClNO2S |
| Formula weight | 359.85 | 359.85 |
| Temperature | 150(2) K | 150(2) K |
| Radiation, wavelength | MoKα, 0.71073 Å | MoKα, 0.71073 Å |
| Crystal system | Triclinic | Monoclinic |
| Space group |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) (no. 2) (no. 2) |
P21 (no. 4) |
| Unit cell dimensions | a = 8.0999(10) Å | a = 8.3442(8) Å |
| b = 10.9970(13) Å | b = 35.108(3) Å | |
| c = 11.7661(14) Å | c = 12.7373(12) Å | |
| α = 113.084(2)° | α = 90° | |
| β = 106.754(2)° | β = 107.1550(10)° | |
| γ = 97.855(2)° | γ = 90° | |
| Volume | 885.35(19) Å3 | 3565.4(6) Å3 |
| Z and Z′ | 2 and 1 | 8 and 4 |
| Calculated density | 1.350 g cm−3 | 1.341 g cm−3 |
| Absorption coefficient | 0.344 mm−1 | 0.342 mm−1 |
| F(000) | 376 | 1504 |
| Crystal size | 0.391 × 0.347 × 0.221 mm3 | 0.381 × 0.329 × 0.280 mm3 |
| θ range for data collection | 2.099° to 28.849° | 1.771° to 28.800° |
| Index ranges | −10 ≤ h ≤ 10 | −11 ≤ h ≤ 11 |
| −14 ≤ k ≤ 14 | −47 ≤ k ≤ 47 | |
| −15 ≤ l ≤ 15 | −17 ≤ l ≤ 16 | |
| Reflections collected | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 081 081 |
33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 856 856 |
| Independent reflections | 4512 [R(int) = 0.0186] | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 821 [R(int) = 0.0438] 821 [R(int) = 0.0438] |
| Observed data [I > 2σ(I)] | 3907 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 547 547 |
| Completeness to θ = 25.242° | 99.3% | 100% |
| Absorption correction | Semi-empirical from equivalents | Semi-empirical from equivalents |
| Max. and min. transmission | 0.7463 and 0.6899 | 0.7459 and 0.6961 |
| Data/restraints/parameters | 4512/0/223 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 821/514/1019 821/514/1019 |
| Goodness-of-fit on F2 | 1.037 | 1.018 |
| Final R indices [I > 2σ(I)] | R 1 = 0.0350, wR2 = 0.0909 | R 1 = 0.0543, wR2 = 0.0936 |
| R indices (all data) | R 1 = 0.0412, wR2 = 0.0952 | R 1 = 0.0991, wR2 = 0.1114 |
| Flack parameter | n/a | 0.48(7) |
| Extinction coefficient | n/a | n/a |
| Largest diff. peak and hole | 0.371 and −0.209 e Å−3 | 0.552 and −0.379 e Å−3 |
Results and discussion
Polymorphism inspection
The crystallization of lactam 1 from benzene solution at room temperature leads to the formation of colorless prismatic crystals of α-1. The experimental and theoretical PXRD patterns of the polycrystalline sample α-1 are shown in Fig. 1 (red and black curves).According to the DSC thermogram presented in Fig. 2a (red curve), solid phase α-1 shows complex behavior at heating. A subsequence of pronounced endothermic, exothermic, and again endothermic events can be identified on the curve. The first endothermic peak can be attributed to melting of α-1 at ca. 136 °C that immediately induces the crystallization of stable β-1 from the just obtained supercooled melt (exothermic process). Obviously, these two events overlap considerably. The contour of the third peak corresponds to the melting of new crystalline phase β-1 at ca. 151 °C. The aforementioned explanation agrees with thermomicroscopic results, as it was observed that crystals of α-1 melted at ca. 136 °C and the melt recrystallized instantly to form β-1 (according to PXRD data).
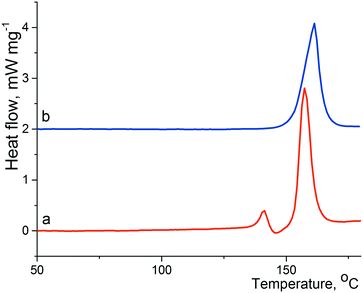 | ||
| Fig. 2 Fragments of DSC curves of α-1 (a; red) and β-1 (b; blue); the heating rate is 10 K min−1. The baseline of curve b was shifted up. | ||
Hence, the β-1 phase is thermodynamically preferred at least at high temperatures. In view of this, we suppose that the crystallization of lactam 1 at high temperatures could promote the nucleation of polymorphic modification β-1. Indeed, the crystallization of lactam 1 from hot benzene solution at 75–80 °C led to the formation of colorless prismatic crystals of β-1. The experimental and theoretical PXRD patterns of the polycrystalline sample β-1 are shown in Fig. 1 (blue and green curves). The DSC curve of pure form β-1 (Fig. 2b, red curve) was characterized by a melting peak at ca. 150 °C and no thermal event up to the melting point was observed. It should be mentioned that the shape of the crystals of α-1 was very similar to that of β-1, so the two phases can be distinguished by spectral or diffraction data.
As illustrated in Fig. 3, there is an evident difference between the IR spectra of crystalline forms α-1 and β-1, which relates to the functional groups potentially involved in H-bonding. For instance, the absorption bands corresponding to the stretching vibrations of both hydroxyl and carbonyl groups for phase β-1 (3238 and 1674 cm−1, respectively) proved to be red-shifted as compared with those for α-1 (3308 and 1694 cm−1, respectively). Therefore, the β-1 form is characterized by the average hydrogen bond system stronger than that of α-1, which fully agrees with the geometry of H-bonds obtained from the X-ray diffraction data. Interestingly, the spectra are characterized by the additional difference in the low frequency region, namely, there is an intense absorption band at 645 cm−1 in the spectrum of α-1, which is practically absent in the spectrum of the β-phase. Obviously, the mentioned band relates to the stretching vibration of the hydroxyl group.
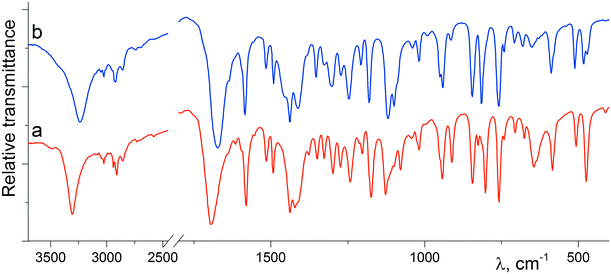 | ||
| Fig. 3 IR spectra of the polycrystalline samples of α-1 (a; red) and β-1 (b; blue) recorded at 20 °C in potassium bromide pellets. | ||
Crystal structure of racemic compound α-1
As follows from Table 1, the α-1 phase obtained from a benzene solution at room temperature crystallizes in the centrosymmetric triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) with one molecule in the asymmetric cell. The analysis of anisotropic displacement ellipsoids (Fig. 4) and the difference electron density map confirm that the molecule is not disordered. Thus, the crystals of the α-1 modification belong to a typical case of a racemic compound.
with one molecule in the asymmetric cell. The analysis of anisotropic displacement ellipsoids (Fig. 4) and the difference electron density map confirm that the molecule is not disordered. Thus, the crystals of the α-1 modification belong to a typical case of a racemic compound.
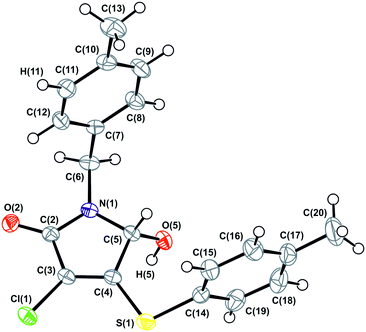 | ||
| Fig. 4 ORTEP projection showing 50% probability anisotropic displacement ellipsoids of non-hydrogen atoms for α-1 according to single crystal XRD data at 150 K. | ||
X-ray experiments were performed at two different temperatures: 293 K and 150 K. While cooling the crystal from room to low temperature, an expected proportional decrease of the thermal ellipsoids was observed, but no significant changes in the structure or phase transition were registered.
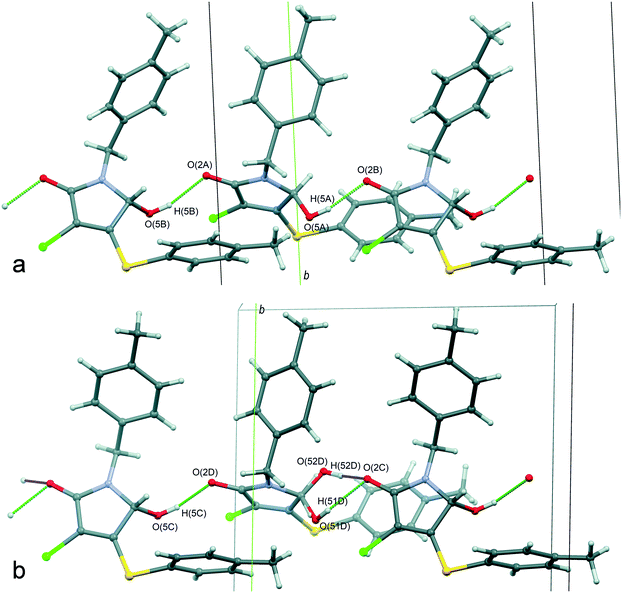
The molecule conformation in the crystals of α-1 can be described as a transoid form: the hydroxyl group is located in an opposite position relative to both of the aromatic rings with respect to the plane of the heterocyclic moiety. As illustrated in Fig. 5a, the main supramolecular motif in the crystals is centrosymmetric heterochiral {R⋯S} dimers formed by means of classical intermolecular hydrogen bonds between the hydroxyl and carbonyl groups. In turn, the dimers are combined with each other by non-classical H-interactions C(11)–H(11)⋯O(2) between the hydrogen atom of aromatic cycles of the N-pivot para-methylbenzyl moiety and the carbonyl group oxygen atom, forming the chains of molecules with an alternating sequence of enantiomers {R⋯S}⋯{R⋯S} along the 0b axis (Fig. 5b). Finally, the three-dimensional crystal packing is arranged by the association of the one-dimensional chains by weak dispersion interactions of the peripheral fragments. The packing index of the racemic compound α-1 is equal to 67.7%.
It should be noted that the transoid conformation of the molecules is a necessary condition for the centrosymmetric dimer formation in the considered case. Namely, the bulky aromatic substituents sterically do not prevent the formation of hydrogen bonds only when they are situated in the periphery of the dimers. However, the strength of hydrogen bonds in such centrosymmetric dimers is limited by van der Waals repulsion of two stacked heterocyclic fragments. By our assumption, this circumstance does not allow hydrogen bonding to be fully realized in the heterochiral centrosymmetric cyclic dimer of compound 1. At the same time, the formation of a homochiral cyclic dimer for such a system seems to be unfeasible, as this would require adopting an unfavorable conformation of molecules.
Crystal structure of partial solid solution β-1
The crystallization of compound 1 from a hot benzene solution at 75–80 °C leads to the formation of colorless prisms visually similar to α-1 crystals. However, according to the powder (Fig. 1b) and single crystal (Table 1) X-ray diffraction data, we obtained crystals of a new phase, belonging to the monoclinic crystal system.It is worth noting that the choice of the space group P21 rather than P21/n was clear for the experiment at 150 K but was more ambiguous for the room temperature data. The E-statistics suggest a centrosymmetric space group but this behavior can be explained, especially at 293 K, by the pseudosymmetry of the crystal structure,21,23,45 which increases with heating. The data measured at 150 K include 137 unique h0l (<I/σ(I)> = 3.9), h + l odd reflections, 41 of which have I > 3σ(I) and 15 have I > 10σ(I). The data at 293 K include 137 unique h0l reflections (<I/σ(I)> = 0.5), 2 of which have I > 3σ(I) and 1 has I > 10σ(I). The refinement of the experiment at 293 K was not stable without geometry restraints. No obvious evidence of phase transitions during heating to room temperature was found.
An attempt to refine the structure (room temperature experiment) in the wrong space group P21/n led to the model with two molecules in the asymmetric cell. In this case, the symmetrically independent site A was ordered, while for site B a weak peak of the residual electron density corresponding to the second minor position of the oxygen atom of the hydroxyl group was observed. The last statement could mean a partial replacement of site B by a molecule of the other enantiomer. We have deposited this preliminary version of the structure solution as a private communication in the Cambridge Crystallographic Data Centre (CCDC 898237). The fact that β-1 structure refinement in a space group with higher symmetry is potentially possible indicates the presence of significant pseudosymmetry.
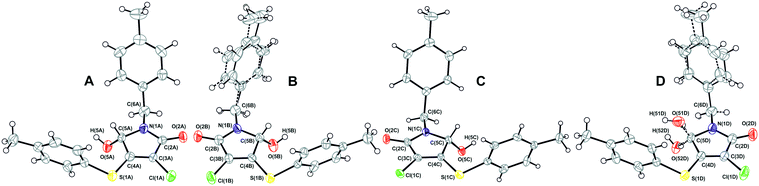
A crystallographically correct model of β-1 was obtained by solving and refining the structure in the Sohncke space group P21 with four independent molecules A–D (Fig. 6) in the asymmetric cell. It should be noted that despite a purposeful search for compounds crystallizing with several symmetrically independent molecules, examples of molecular crystals with four or more molecules are very rare.26 Particular attention was drawn towards the shape and size changes of the anisotropic displacement ellipsoids for the experiments performed at different temperatures. Thus, the decrease of thermal ellipsoids in the case of molecules A and C was expected, whereas the ellipsoids of the benzyl fragments in molecules B and D retained an elongated cigar-like shape, which is obvious evidence of disorder of the considered fragments into two positions. Hence, molecules A and C are completely ordered, while the positional disorder of the N-pivot para-methylbenzyl substituents of molecules B and D is observed. Moreover, according to analysis of residual electron density, molecule D is characterized by extra disorder of the substituents at the C(5D) chiral center, namely, the hydroxyl group is disordered into two almost mirror-related positions O(51D), H(51D) and O(52D), H(52D) with a relative occupancy of ca. 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, respectively. Thus, molecule D undergoes substitutional disorder and the corresponding site contains either (S)-1 or (R)-1, preferably the isomer with a configuration opposite to that of molecule C. In other words, the β-1 phase is a racemic compound complicated by a partial solid solution of enantiomers. From the crystallographic point of view, the limited solubility corresponds to the population of the minor component-enantiomer and is manifested in the fact that only one of four symmetrically independent sites is structurally pre-organized to include both enantiomers. The fact that only one site is prone to chiral disorder (and at the same time, the corresponding molecule connected by the pseudoinversion is not) could be considered as an important argument in favor of choosing the space group P21. Thus, the choice of the higher symmetry group P21/n does not allow description of the crystal structure completely.
1, respectively. Thus, molecule D undergoes substitutional disorder and the corresponding site contains either (S)-1 or (R)-1, preferably the isomer with a configuration opposite to that of molecule C. In other words, the β-1 phase is a racemic compound complicated by a partial solid solution of enantiomers. From the crystallographic point of view, the limited solubility corresponds to the population of the minor component-enantiomer and is manifested in the fact that only one of four symmetrically independent sites is structurally pre-organized to include both enantiomers. The fact that only one site is prone to chiral disorder (and at the same time, the corresponding molecule connected by the pseudoinversion is not) could be considered as an important argument in favor of choosing the space group P21. Thus, the choice of the higher symmetry group P21/n does not allow description of the crystal structure completely.
Interestingly, the configurations of molecules B and C are the same and opposite to those of the pair A and D (hereinafter, the main component of site D is considered, if it is not noted otherwise). Accordingly, the racemic sample of β-1 would be a mechanical mixture of single crystals enriched with either (S)-1 or (R)-1.13 But it turned out that β-1 crystals were affected by inversion twinning, which could be caused by kinetic3 and structural factors.46 This led to an equimolar ratio of the enantiomers in the investigated crystals.
A comparative analysis of the geometry of four independent molecules shows that the conformations of molecules in pairs of AC and BD are similar. These two pairs of molecules differ mainly in the rotation angle of the N-pivot para-methylbenzyl substituent relative to the plane heterocyclic fragment. For all four molecules (when choosing the prevailing component in site D), the hydroxyl group is located on the back side of both aromatic fragments with respect to the pyrrolinone cycle. Actually, the main and minor enantiomers are forcedly located on site D in different conformations: the transoid form for the main enantiomer and the cisoid form for the minor one.
We assumed that these conformations might be noticeably different in energy. Consequently, we performed a preliminary calculation of the energy of cisoid and transoid conformations for free molecules by means of the DFT method. For this, we optimized the geometry of the conformations using the molecular structure of the main and minor enantiomers of site D as starting coordinates. Indeed, according to quantum-chemical calculations, the optimized geometries of the conformations differ by the angles of rotation of aromatic fragments relative to the heterocyclic skeleton (Fig. 7). The energy advantage of the transoid form, which is realized in crystals of the true racemate α-1, as well as in sites A–D (in the latter case for the predominant component) of β-1, was ca. 0.8 kcal mol−1 compared with the cisoid conformation. Thus, the preference for the transoid conformation can be considered as one of the main factors determining and restricting the enantiomer solubility limit, or in other words, the observed population ratio of site D with (S)- and (R)-1 molecules.
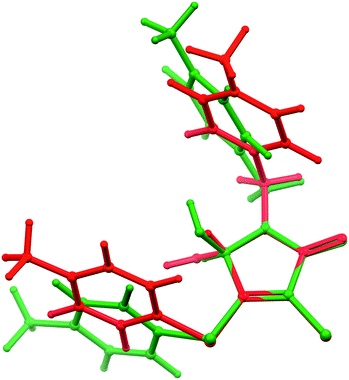 | ||
| Fig. 7 Overlapping the cisoid (green) and transoid (red) conformations of opposite enantiomer molecules, obtained from DFT calculations (modeling of site D). Details are discussed in the text. | ||
As discussed earlier, we detected two fundamentally different types of disorder in the β-1 crystals: (i) the “achiral” positional disorder of the N-pivot para-methylbenzyl substituents of the B and D molecules and (ii) the “chiral” substitutional disorder in site D. The numerically different ratios of occupancy values for the “chiral” and “achiral” disorder do not allow us to assert that there is an unambiguous correlation between them. Nevertheless, the analysis of the crystal structure of β-1 permits us to conclude that some “loose packing” takes place in the regions, where the disordered methylbenzyl fragments of molecules B and D are situated. It is reasonable to assume that this “looseness” creates the appropriate conditions for the partial replacement of the main enantiomer with the opposite one. Why is the “chiral” disorder not observed for site B (and for sites A and C as well)? We tried to find the answer by detailed analysis of molecular packing in the β-1 crystals.
The main supramolecular motif in the β-1 crystals is one-dimensional heterochiral chains with sequences of A⋯B⋯A⋯B and C⋯D⋯C⋯D, oriented along the 0c axis and formed by the O(5)–H(5)⋯O(2) hydrogen bonds between the hydroxyl and carbonyl groups (Fig. 8). Although these chains are not related to each other by a strict crystallographic symmetry, their interrelation through the pseudo-glide plane and pseudo-inversion centers is evident and discussed above. The hydrogen bond parameters in the β-1 crystals prove their greater strength in comparison with the α-1 crystals, which is in full agreement with the infrared spectroscopy data given above. Due to the dispersive interactions of peripheral fragments, the one-dimensional chains are connected in the three-dimensional crystal structure. The packing index of the mixed crystal phase β-1 is equal to 67.0%, which is evidence of more friable packing of molecules of 1 compared with the racemic compound α-1 (67.7%). It should be noted that the above-mentioned difference in the rotation angles of N-pivot para-methylbenzyl substituents in the pairs AB and CD is probably caused by the steric requirements for the H-bonded chain formation.
It thus appears that the analysis of the hydrogen bond parameters makes it possible to explain why both of the lactam 1 enantiomers can be included in site D and find the structural reasons for this. Indeed, the packing of molecules in the C⋯D⋯C⋯D chain provides the geometrical conditions for the formation of a significantly stronger hydrogen bond when a minor enantiomer in site D participates in bonding. Moreover, as follows from Table 2, the hydrogen bond O(52D)–H(52D)⋯O(2C) is characterized by the shortest donor–acceptor and H-atom–acceptor distance, whereas the contact O(51D)–H(51D)⋯O(2C) can be considered as one of the weakest. At the same time, this minor enantiomer occupies site D in an unfavorable cisoid conformation. Obviously, the presence of “chiral” disorder and the enantiomer ratio in site D can be explained by the balance of two opposite tendencies, namely, the realization of the favorable transoid conformation and the formation of the strong hydrogen bond. It is important to note that the independent molecules A–C form noticeably stronger hydrogen bonds than the main enantiomer of site D. It is possibly one of the reasons for the absence of “chiral” disorder in sites A–C.
| D–H⋯A | d(D–H) | d(H⋯A) | d(D⋯A) | ∠(DHA) |
|---|---|---|---|---|
| Crystal α-1 | ||||
| Symmetry transformations used to generate equivalent atoms: #1 −x + 1, −y + 1, −z + 1; #2x, y, z + 1. | ||||
| O(5)–H(5)⋯O(2)#1 | 0.84(2) | 1.94(2) | 2.7823(14) | 175(2) |
| Crystal β-1 | ||||
|---|---|---|---|---|
| O(5A)–H(5A)⋯O(2B) | 0.84 | 1.89 | 2.700(5) | 162.7 |
| O(5B)–H(5B)⋯O(2A)#2 | 0.84 | 1.91 | 2.725(5) | 163.1 |
| O(5C)–H(5C)⋯O(2D)#2 | 0.84 | 1.90 | 2.710(5) | 161.2 |
| O(51D)–H(51D)⋯O(2C) | 0.84 | 2.04 | 2.789(6) | 147.7 |
| O(52D)–H(52D)⋯O(2C) | 0.84 | 1.79 | 2.600(14) | 160.8 |
Conclusions
The purposeful modification of crystallization conditions for racemic 3-chloro-5-hydroxy-1-(4-methylbenzyl)-4-[(4-methylphenyl)sulfanyl]-1,5-dihydro-2H-pyrrol-2-one 1 allows two crystal modifications, α and β, to be obtained. The α-1 crystals are a usual racemic compound in the triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) . The second phase, β-1, crystallizes in the monoclinic space group P21 with four independent molecules in the asymmetric cell and belongs to a rare racemate type – partially mixed crystals of enantiomers based on a racemic compound.
. The second phase, β-1, crystallizes in the monoclinic space group P21 with four independent molecules in the asymmetric cell and belongs to a rare racemate type – partially mixed crystals of enantiomers based on a racemic compound.
The crystal structure of β-1 is characterized by the presence of two disorder types: the “achiral” positional (conformational) disorder of the N-pivot para-methylbenzyl fragments of molecules B and D and the “chiral” substitutional disorder in site D. In fact, the main and minor enantiomers of 1 in site D are in different conformations: the more favorable transoid form is observed for the main enantiomer and the less favorable cisoid conformation for the minor one. On the other hand, the stronger hydrogen bond in site D is formed involving the minor enantiomer. Hence, the system of directional hydrogen bonds, which usually plays a fundamental role in chiral discrimination and in the realization of a regular molecular crystal packing, causes the formation of mixed crystals in the case of γ-lactam 1. Thus, we have found two counteractive structural aspects that mainly allow defining and controlling the formation of a solid solution of enantiomers for compound 1, i.e. the tendency of molecules to adopt the favorable transoid conformation vs. that to form the stronger hydrogen bond.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The crystallographic and physicochemical studies were financially supported by the Russian Science Foundation (grant no. 17-13-01209). The synthetic part of this work was funded by the subsidy allocated to Kazan Federal University for the state assignment in the sphere of scientific activities (4.1493.2017/4.6 and 4.5151.2017/6.7).Notes and references
- J. Jacques, A. Collet and S. H. Wilen, Enantiomers, Racemates, and Resolutions, Krieger Publishing Company, Malabar, FL, 1994 Search PubMed.
- G. Coquerel, Enantiomer, 2000, 5, 481–498 CAS.
- C. P. Brock, W. B. Schweizer and J. D. Dunitz, J. Am. Chem. Soc., 1991, 113, 9811–9820 CrossRef CAS.
- A. A. Bredikhin, Z. A. Bredikhina and D. V. Zakharychev, Mendeleev Commun., 2012, 22, 171–180 CrossRef CAS.
- G. Coquerel, in Advances in Organic Crystal Chemistry, ed. R. Tamura and M. Miyata, Springer Japan, Tokyo, 2015, ch. 20, pp. 393–420 Search PubMed.
- H. Lorenz and A. Seidel-Morgenstern, Angew. Chem., Int. Ed., 2014, 53, 1218–1250 CrossRef CAS PubMed.
- C. Brandel, S. Petit, Y. Cartigny and G. Coquerel, Curr. Pharm. Des., 2016, 22, 4929–4941 CrossRef CAS PubMed.
- J. Lajzerowicz-Bonneteau, J. Lajzerowicz and D. Bordeaux, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 6453–6463 CrossRef CAS.
- H. E. Gallis, P. J. van Ekeren, J. C. van Miltenburg and H. A. J. Oonk, Thermochim. Acta, 1999, 326, 83–90 CrossRef CAS.
- N. Wermester, E. Aubin, M. Pauchet, S. Coste and G. Coquerel Tetrahedron, Asymmetry, 2007, 18, 821–831 CrossRef CAS.
- L. Renou, T. Morelli, S. Coste, M.-N. Petit, B. Berton, J.-J. Malandain and G. Coquerel, Cryst. Growth Des., 2007, 7, 1599–1607 CAS.
- N. V. Taratin, H. Lorenz, E. N. Kotelnikova, A. E. Glikin, A. Galland, V. Dupray, G. Coquerel and A. Seidel-Morgenstern, Cryst. Growth Des., 2012, 12, 5882–5888 CAS.
- A. A. Bredikhin, D. V. Zakharychev, A. T. Gubaidullin, R. R. Fayzullin, A. V. Pashagin and Z. A. Bredikhina, Cryst. Growth Des., 2014, 14, 1676–1683 CAS.
- T. Rekis, A. Bērziņš, L. N. Orola, T. Holczbauer, A. Actiņš, A. Seidel-Morgenstern and H. Lorenz, Cryst. Growth Des., 2017, 17, 1411–1418 CAS.
- F. Baert, R. Fouret, H. A. J. Oonk and J. Kroon, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1978, 34, 222–226 CrossRef.
- B. Chion, J. Lajzerowicz, D. Bordeaux, A. Collet and J. Jacques, J. Phys. Chem., 1978, 82, 2682–2688 CrossRef CAS.
- J. M. Rollinger and A. Burger, J. Pharm. Sci., 2001, 90, 949–959 CrossRef CAS PubMed.
- F. G. Vogt, R. C. B. Copley, R. L. Mueller, G. P. Spoors, T. N. Cacchio, R. A. Carlton, L. M. Katrincic, J. M. Kennady, S. Parsons and O. V. Chetina, Cryst. Growth Des., 2010, 10, 2713–2733 CAS.
- D. H. Lopez, A. D. Bond and R. J. Dancer, Chirality, 2011, 23, 408–416 CrossRef PubMed.
- A. A. Bredikhin, Z. A. Bredikhina, D. V. Zakharychev, A. T. Gubaidullin and R. R. Fayzullin, CrystEngComm, 2012, 14, 648–655 RSC.
- A. A. Bredikhin, A. T. Gubaidullin, Z. A. Bredikhina and R. R. Fayzullin, J. Mol. Struct., 2013, 1032, 176–184 CrossRef CAS.
- R. R. Fayzullin, O. A. Antonovich, D. V. Zakharychev, Z. A. Bredikhina, A. V. Kurenkov and A. A. Bredikhin, Russ. J. Org. Chem., 2015, 51, 202–209 CrossRef CAS.
- R. R. Fayzullin, D. V. Zakharychev, A. T. Gubaidullin, O. A. Antonovich, D. B. Krivolapov, Z. A. Bredikhina and A. A. Bredikhin, Cryst. Growth Des., 2017, 17, 271–283 CAS.
- C. P. Brock and J. D. Dunitz, Chem. Mater., 1994, 6, 1118–1127 CrossRef CAS.
- D. J. Watkin, Crystallogr. Rev., 2010, 16, 197–230 CrossRef CAS.
- K. M. Steed and J. W. Steed, Chem. Rev., 2015, 115, 2895–2933 CrossRef CAS PubMed.
- C. P. Brock, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 2016, 72, 807–821 CAS.
- K. M. Anderson, A. E. Goeta and J. W. Steed, Cryst. Growth Des., 2008, 8, 2517–2524 CAS.
- O. A. Lodochnikova, A. B. Dobrynin, O. V. Andreeva, I. Yu. Strobykina, V. E. Kataev and I. A. Litvinov, CrystEngComm, 2014, 16, 6234–6243 RSC.
- O. A. Lodochnikova, V. A. Startseva, L. E. Nikitina, A. V. Bodrov, A. E. Klimovitskii, E. N. Klimovitskii and I. A. Litvinov, CrystEngComm, 2014, 16, 4314–4321 RSC.
- L. N. Kuleshova, M. Y. Antipin and I. V. Komkov, J. Mol. Struct., 2003, 647, 41–51 CrossRef CAS.
- O. A. Lodochnikova, R. M. Khakimov, I. A. Litvinov, L. Z. Latypova and A. R. Kurbangalieva, Russ. Chem. Bull., 2015, 64, 2444–2453 CrossRef CAS.
- F. Ghelfi, C. V. Stevens, I. Laureyn, E. V. Meenen, T. M. Rogge, L. De Buyck, K. V. Nikitin, R. Grandi, E. Libertini, U. M. Pagnoni and L. Schenetti, Tetrahedron, 2003, 59, 1147–1157 CrossRef CAS.
- F. Bellina and R. Rossi, Tetrahedron, 2006, 62, 7213–7256 CrossRef CAS.
- K. D. Sarma, J. Zhang, Y. Huang and J. G. Davidson, Eur. J. Org. Chem., 2006, 16, 3730–3737 CrossRef.
- S. Ma and H. Xie, Org. Lett., 2000, 2, 3801–3803 CrossRef CAS PubMed.
- C. H. Lim, S. H. Kim and J. N. Kim, Bull. Korean Chem. Soc., 2012, 33, 1622–1626 CrossRef CAS.
- N. Saygili, A. Altunbaş and A. Yeşilada, Turk. J. Chem., 2006, 30, 125–130 CAS.
- L. S. Kosolapova, M. F. Valiev, A. R. Kurbangalieva, O. A. Lodochnikova, E. A. Berdnikov and G. A. Chmutova, presented in part at International Congress on Organic Chemistry dedicated to the 150-th anniversary of the Butlerov's Theory of Chemical Structure of Organic Compounds, Kazan, September, 2011 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. G. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, GAUSSIAN 03, Gaussian, Inc., Wallingford, CT, 2003 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8 CrossRef PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 CrossRef PubMed.
- L. J. Farrugia, J. Appl. Crystallogr., 2012, 45, 849–854 CrossRef CAS.
- M. Walker, E. Pohl, R. Herbst-Irmer, M. Gerlitz, J. Rohr and G. M. Sheldrick, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1999, 55, 607–616 Search PubMed.
- V. Y. Torbeev, K. A. Lyssenko, O. N. Kharybin, M. Y. Antipin and R. G. Kostyanovsky, J. Phys. Chem. B, 2003, 107, 13523–13531 CrossRef CAS.
Footnote |
| † The crystallographic data have been deposited in the Cambridge Crystallographic Data Centre as supplementary publication numbers CCDC 1575691, 1575692, 1575693, and 1575694 for α-1 [293 K], α-1 [150 K], β-1 [293 K], and β-1 [150 K], respectively. For crystallographic data in CIF or other electronic format see DOI: 10.1039/c7ce01717k |
| This journal is © The Royal Society of Chemistry 2017 |