Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Novel drug–drug cocrystals of carbamazepine with para-aminosalicylic acid: screening, crystal structures and comparative study of carbamazepine cocrystal formation thermodynamics†‡
Ksenia V.
Drozd
a,
Alex N.
Manin
 a,
Andrei V.
Churakov
b and
German L.
Perlovich
a,
Andrei V.
Churakov
b and
German L.
Perlovich
 *a
*a
aG.A. Krestov Institute of Solution Chemistry of the Russian Academy of Sciences, 1, Akademicheskaya St., 153045, Ivanovo, Russia. E-mail: glp@isc-ras.ru; Fax: +7 4932 336237; Tel: +7 4932 533784
bInstitute of General and Inorganic Chemistry RAS, Leninsky Prosp. 31, 119991 Moscow, Russia
First published on 23rd June 2017
Abstract
The cocrystal formation of the anticonvulsant drug carbamazepine (CBZ) with para-aminosalicylic acid (PASA, antituberculous drug) has been studied by varying the molar ratios of CBZ to PASA (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 2
1 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) and using liquid-assisted grinding (LAG), slurrying and solution crystallization methods. Three novel cocrystal forms of CBZ and PASA have been synthesized: [CBZ + PASA] (1
1) and using liquid-assisted grinding (LAG), slurrying and solution crystallization methods. Three novel cocrystal forms of CBZ and PASA have been synthesized: [CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), [CBZ + PASA + H2O] (2
1), [CBZ + PASA + H2O] (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) and [CBZ + PASA + MeOH] (2
1) and [CBZ + PASA + MeOH] (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), and their crystal structures have been described. Conformational analysis of the CBZ molecule in its polymorphic forms, its cocrystals and solvates has been conducted. Calculations of intermolecular interaction energies using the PIXEL approach have been carried out for CBZ cocrystals with 1
1), and their crystal structures have been described. Conformational analysis of the CBZ molecule in its polymorphic forms, its cocrystals and solvates has been conducted. Calculations of intermolecular interaction energies using the PIXEL approach have been carried out for CBZ cocrystals with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry. The melting and desolvation processes of the [CBZ + PASA] (1
1 stoichiometry. The melting and desolvation processes of the [CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), [CBZ + PASA + H2O] (2
1), [CBZ + PASA + H2O] (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) and [CBZ + PASA + MeOH] (2
1) and [CBZ + PASA + MeOH] (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) cocrystals have been studied. The temperature dependence of the CBZ (form III) saturation vapor pressure has been studied, and the sublimation thermodynamic functions have been calculated. Based on the sublimation thermodynamics database of molecular crystals, the standard sublimation thermodynamic functions of PASA have been evaluated. The thermodynamic functions of cocrystal formation based on CBZ have been calculated and analyzed. The dissolution process of the [CBZ + PASA] cocrystal (1
1) cocrystals have been studied. The temperature dependence of the CBZ (form III) saturation vapor pressure has been studied, and the sublimation thermodynamic functions have been calculated. Based on the sublimation thermodynamics database of molecular crystals, the standard sublimation thermodynamic functions of PASA have been evaluated. The thermodynamic functions of cocrystal formation based on CBZ have been calculated and analyzed. The dissolution process of the [CBZ + PASA] cocrystal (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
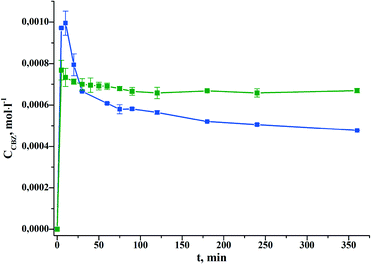
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) in water (pH 7.4) has been studied. CBZ cocrystallization with PASA has been shown to lead to a dramatic decrease of the CBZ rate of conversion from the anhydrous to the hydrate form, and as a consequence, to solubility improvement by approximately 1.5 times.
1) in water (pH 7.4) has been studied. CBZ cocrystallization with PASA has been shown to lead to a dramatic decrease of the CBZ rate of conversion from the anhydrous to the hydrate form, and as a consequence, to solubility improvement by approximately 1.5 times.
Introduction
Today, the approach of combining several drugs to treat many serious diseases (such as virulent diseases, HIV/AIDS, cancer, diabetes, cardiovascular diseases) definitely forces out monotherapy (aimed at a definite receptor).1 The use of cost-effective and multi-target fixed-dose drug combinations (FDC) can help reduce the pill load without the additional risk of adverse events or drug resistance, thereby improving patient compliance by simplified disease management.2 An alternative approach to using drug combinations is the use of multi-component crystals such as salts, complexes, and cocrystals containing more than one active pharmaceutical ingredient.3 Among all the mentioned multi-component systems, cocrystals attract the biggest attention of the pharmaceutical industry4 due to the introduction of regulatory guidelines by the US Food and Drug Administration (FDA)5 as a result of expanded patent portfolios.2 Unfortunately, cocrystal studies mainly focus on crystal engineering and supramolecular synthesis of API-based cocrystals. For example, the pharmaceutical properties have not been evaluated for the [sulfadimidine + aspirin] cocrystal6 which can be regarded as an antibacterial and an NSAID therapeutic drug. Another example is the two-component crystal of piracetam (a nootropic agent) with gentisic acid (NSAID),7 for which no studies have been conducted except those of the synthons' nature in the cocrystal formation. The study of drug–drug cocrystals in terms of their further use in the pharmaceutical industry is much less intensive,8,9 though designing drug–drug cocrystals of marketed drugs may shorten the development period (including clinical trials) compared to those of New Chemical Entities, as cocrystals do not involve structural modification of the APIs.10Carbamazepine (CBZ) is an anticonvulsant and a mood-stabilizing drug used primarily to treat epilepsy, bipolar disorder and trigeminal neuralgia (Fig. 1). According to the biopharmaceutical classification system, carbamazepine is classified as a class II drug11 having low water solubility which limits its absorption. CBZ cocrystallization with more soluble coformers is one of the solutions to this problem.12 The Cambridge Structural Database (CSD) so far contains over 50 crystalline forms of CBZ, most of which are cocrystals, including drug–drug cocrystals, as well as their solvates/hydrates and polymorphs.13
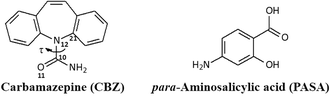 | ||
| Fig. 1 Molecular structures of carbamazepine and para-aminosalicylic acid. The flexible torsion angle in carbamazepine is numbered and is indicated by τ. | ||
The purpose of our research was to obtain and study drug–drug carbamazepine cocrystals with antituberculosis drugs. Recent studies have shown that pharmacological stimulation of autophagy by carbamazepine avoids the immunosuppressive effects of mTOR inhibition seen with rapamycin, promoting both innate and adaptive immune responses to mycobacterial infection and proves the concept for a novel therapeutic strategy unaffected by bacterial resistance to conventional antibiotics.14 Earlier, Swart A. and Harris V.15 reported on the CBZ interaction with first-line antituberculosis drugs: isoniazid and rifampicin. According to this report, their simultaneous administration leads to serious side effects. Therefore, para-aminosalicylic acid (PASA), a second-line antituberculosis drug, was chosen for cocrystallization with CBZ (Fig. 1).
In this context, we conducted cocrystal screening of carbamazepine with para-aminosalicylic acid. The cocrystals and their solvates were characterized by single crystal X-ray diffraction and differential scanning calorimetry. The cocrystal aqueous dissolution and solution stability were also investigated. In addition, analysis of the intermolecular interaction and crystal lattice energies of the carbamazepine cocrystals was performed using the PIXEL approach.
One of the most important fundamental problems of cocrystallization studies is the prediction of the stability of the new cocrystal . An approach is proposed for estimating the thermodynamic parameters of the cocrystal formation based on the thermodynamic functions of the components of known CBZ cocrystals.
Materials and methods
Compounds and solvents
Carbamazepine was purchased from Acros Organics while para-aminosalicylic acid was supplied by Sigma-Aldrich. All the compounds were used without further purification. Analytical grade solvents were used for the crystallization experiments.Cocrystal preparation
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 2
1 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometries of CBZ and PASA (the total physical mixture weight was ca. 50 mg). Solvent-drop grinding experiments were conducted prior to the grinding by adding ca. 0.05 ml of the solvent to the reactants using a micropipette. The resulting powder samples were analyzed by PXRD for the cocrystal formation.
1 stoichiometries of CBZ and PASA (the total physical mixture weight was ca. 50 mg). Solvent-drop grinding experiments were conducted prior to the grinding by adding ca. 0.05 ml of the solvent to the reactants using a micropipette. The resulting powder samples were analyzed by PXRD for the cocrystal formation.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 2
1 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometries were mixed in a 2 mL test tube with the solvent amount sufficient to produce a wet paste. The mixture was sonicated at room temperature for 15–20 min at maximum power.16 The resulting solids were air-dried prior to subsequent analysis.
1 stoichiometries were mixed in a 2 mL test tube with the solvent amount sufficient to produce a wet paste. The mixture was sonicated at room temperature for 15–20 min at maximum power.16 The resulting solids were air-dried prior to subsequent analysis.
Solution crystallization
A slow evaporation method was used to grow single crystals. Cocrystallization experiments were carried out by dissolving 80 mg of either a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 or a 2
1 or a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of CBZ and PASA in a minimum amount of the solvent selected from acetonitrile (ACN), acetone (AO), ethanol (EtOH), methanol (MeOH), tetrahydrofuran (THF) and ethyl acetate (EtOCH3). The vials containing the dissolved mixtures were covered with a parafilm, punctured with 3–5 holes and allowed to slowly evaporate under ambient conditions. The crystallization experiment results are given below (Table 1).
1 mixture of CBZ and PASA in a minimum amount of the solvent selected from acetonitrile (ACN), acetone (AO), ethanol (EtOH), methanol (MeOH), tetrahydrofuran (THF) and ethyl acetate (EtOCH3). The vials containing the dissolved mixtures were covered with a parafilm, punctured with 3–5 holes and allowed to slowly evaporate under ambient conditions. The crystallization experiment results are given below (Table 1).
| Solvent | Molar ratio | [CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
[CBZ + PASA + H2O] (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
[CBZ + PASA + MeOH] (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
|---|---|---|---|---|
| ACN | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
Yes | — | — |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
— | Yes | — | |
| MeOH | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
— | — | Yes |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
— | — | — | |
| EtOH | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
— | — | — |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
— | — | — | |
| THF | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
Yes | — | — |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
Yes | — | — | |
| AO | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
— | — | — |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
— | — | — | |
| EtOCH3 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
— | Yes | — |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
— | — | — |
Single crystal X-ray diffraction
Single-crystal X-ray diffraction data were collected using a Bruker SMART APEX II diffractometer with graphite-monochromated Mo-Kα radiation (λ = 0.71073 Å) in the ω-scan mode. Absorption corrections based on measurements of equivalent reflections were applied.17 The structures were solved by direct methods and refined by full matrix least-squares on F2 with anisotropic thermal parameters for all the non-hydrogen atoms.18 All hydrogen atoms were found from a difference Fourier map and refined with isotropic thermal parameters.Powder X-ray diffraction (PXRD)
X-ray powder diffraction data were recorded under ambient conditions in Bragg–Brentano geometry on a Bruker D8 Advance diffractometer with Cu Kα radiation (λ = 1.5406 Å) at 40 kV and 40 mA power. The X-ray diffraction patterns were collected over the 2θ range 5–30°, with a 0.03° step size.Crystal lattice energy calculations
Intermolecular interaction energies were calculated using the PIXEL approach developed by Gavezzotti.19,20 This method provides quantitative determination of crystal lattice energies and pairwise intermolecular interactions, with a breakdown of these energies into Coulombic, polarization, dispersion and repulsion terms. The molecular electron densities for the cocrystals were calculated at the MP2/6-31G** level of theory in the GAUSSIAN09 program. All the hydrogen atoms in the structures were set to the standard neutron values according to the default procedure in the PIXEL program.Differential scanning calorimetry (DSC)
DSC was performed using a Perkin Elmer DSC 4000 differential scanning calorimeter with a refrigerated cooling system (USA). The sample was heated in sealed aluminum sample holders from 30 to 210 °C at a heating rate of 10 °C min−1 in a nitrogen atmosphere. The unit was calibrated with indium and zinc standards. The accuracy of the weighing procedure was ±0.01 mg.Thermogravimetric analysis (TGA)
TGA was performed using a TG 209 F1 Iris thermomicrobalance (Netzsch, Germany). Approximately 10 mg of the sample was put in a platinum crucible. The samples were heated over the temperature range of 30 to 210 °C at a heating rate of 10 °C min−1. The samples were purged with a stream of flowing dry Ar at 30 ml min−1 throughout the experiment.Sublimation measurements
The sublimation experiments were carried out by the transpiration method as described elsewhere.21,22 In brief, a stream of an inert gas passes above the sample at a constant temperature and at a known slow constant flow rate in order to achieve saturation of the carrier gas with the vapor of the substance under investigation. The vapor is condensed at some point downstream, and the mass of the sublimate and its purity are determined by UV-Vis spectrophotometry and DSC. The vapor pressure over the sample at this temperature can be calculated by means of the amount of the sublimated sample and the volume of the inert gas used.Aqueous dissolution experiment
The dissolution measurements were made by the shake-flask method in phosphate buffer with pH 7.4 at 25.0 ± 0.1 °C for 6 h. An excess amount of the sample was suspended in the respective buffer solution in Pyrex glass tubes. The dissolved drug amount was measured by taking aliquots of the media. The suspension was filtered through a 0.2 μm PTEF syringe filter (Rotilabo), and the concentration was determined by high-performance liquid chromatography (HPLC). HPLC was conducted on a Shimadzu Prominence model LC-20 AD equipped with a PDA detector and a C-18 column (150 mm × 4.6 mm i.d., 5 μm particle size and 100 Å pore size). The elution was achieved by a mobile phase consisting of 50% phosphate buffer pH 3.5 (A) and 50% methanol, and the flow rate was 0.5 mL min−1. The concentration of the components was measured at the wavelength of 284 (CBZ) and 266 and 298 nm (PASA).Results and discussion
Cocrystal production and preliminary identification
The initial stage of our research was to identify the formation of new crystalline species (cocrystal) between carbamazepine and para-aminosalicylic acid. The cocrystal formation feasibility was verified by the DSC and XRPD methods. At first the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio of the studied compounds was tested. The DSC curves for the individual components and the mixture after cogrinding are shown in Fig. 2a. The CBZ DSC thermogram represents the characteristic thermal events of CBZ form III (p-monoclinic): two endotherms and one exotherm (Fig. 2a), as reported by Grzesiak.23 The DSC thermogram of the 1
1 molar ratio of the studied compounds was tested. The DSC curves for the individual components and the mixture after cogrinding are shown in Fig. 2a. The CBZ DSC thermogram represents the characteristic thermal events of CBZ form III (p-monoclinic): two endotherms and one exotherm (Fig. 2a), as reported by Grzesiak.23 The DSC thermogram of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture shows only one major endothermic event at 154.0 °C (onset), which differs from the melting points of both CBZ (191 °C) and PASA (139.1 °C). This indicates that during the cogrinding experiment, a new phase (cocrystal) was formed between CBZ and PASA. The XRPD patterns for CBZ, PASA and their 1
1 mixture shows only one major endothermic event at 154.0 °C (onset), which differs from the melting points of both CBZ (191 °C) and PASA (139.1 °C). This indicates that during the cogrinding experiment, a new phase (cocrystal) was formed between CBZ and PASA. The XRPD patterns for CBZ, PASA and their 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
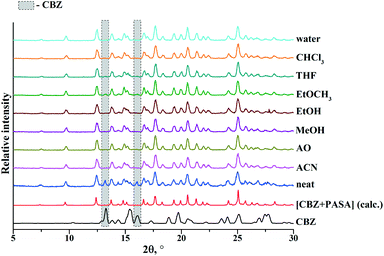
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture are illustrated in Fig. 2b. The diffraction pattern of the ground mixture was found to be distinctly different (new peaks at 2θ angles of 9.7°, 12.5°, 14.9°, 16.7°, 17.7°, 18.3°, 19.3°, 21.3° and 28.3°) as compared to the starting compounds, indicating the formation of a new solid, i.e. a cocrystal.
1 mixture are illustrated in Fig. 2b. The diffraction pattern of the ground mixture was found to be distinctly different (new peaks at 2θ angles of 9.7°, 12.5°, 14.9°, 16.7°, 17.7°, 18.3°, 19.3°, 21.3° and 28.3°) as compared to the starting compounds, indicating the formation of a new solid, i.e. a cocrystal.
 | ||
Fig. 2 (a) DSC heating curves and (b) experimental XRPD patterns of pure carbamazepine (black), para-aminosalicylic acid (red), and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (blue) and 2 1 (blue) and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (purple) mixtures of compounds after cogrinding. 1 (purple) mixtures of compounds after cogrinding. | ||
There are known cases when some compounds (which include APIs) can form cocrystals in multiple stoichiometries with the same coformer: [CBZ + para-aminobenzoic acid (PABA)] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 2
1, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 4
1 and 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1),24,25 [caffeine + maleic acid] (1
1),24,25 [caffeine + maleic acid] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 2
1 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1),26,27 [nicotinamide + (R)-mandelic acid] (1
1),26,27 [nicotinamide + (R)-mandelic acid] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 4
1, 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2)28 and others. Consequently, the 2
2)28 and others. Consequently, the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio with an excess of CBZ was additionally tested. The DSC curves and XRPD patterns of the 2
1 molar ratio with an excess of CBZ was additionally tested. The DSC curves and XRPD patterns of the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture prepared by grinding are shown in Fig. 2versus the starting components and cocrystal in a 1
1 mixture prepared by grinding are shown in Fig. 2versus the starting components and cocrystal in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio. The DSC thermogram of the 2
1 molar ratio. The DSC thermogram of the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture shows a broad and low melting peak at 153.4 °C (onset) versus the sharp peak of the 1
1 mixture shows a broad and low melting peak at 153.4 °C (onset) versus the sharp peak of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 cocrystal. The XRPD pattern of the 2
1 cocrystal. The XRPD pattern of the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture presents the peaks of the 1
1 mixture presents the peaks of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 cocrystal, CBZ and the new double peak at 9° 2θ. Thus, the carbamazepine cocrystal with para-aminosalicylic acid can be produced by grinding the compounds in 1
1 cocrystal, CBZ and the new double peak at 9° 2θ. Thus, the carbamazepine cocrystal with para-aminosalicylic acid can be produced by grinding the compounds in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 or 2
1 or 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometries. Moreover, the cocrystal formation leads to a ca. 30 °C decrease in the melting point compared to the pure CBZ.
1 stoichiometries. Moreover, the cocrystal formation leads to a ca. 30 °C decrease in the melting point compared to the pure CBZ.
Screening by slow crystallization from the solution was the next stage of the investigation. The experiment was carried out by using six different solvents. All the single crystals of carbamazepine cocrystals with para-aminosalicylic acid were obtained by slow evaporation (Table 1). Colorless crystalline materials were obtained within 5 days. As a result, we produced single crystals of [CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), [CBZ + PASA + H2O] (2
1), [CBZ + PASA + H2O] (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) and [CBZ + PASA + MeOH] (2
1) and [CBZ + PASA + MeOH] (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). Unfortunately, the pure crystal form of the [CBZ + PASA] cocrystal (2
1). Unfortunately, the pure crystal form of the [CBZ + PASA] cocrystal (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) was not obtained.
1) was not obtained.
Liquid-assisted grinding (LAG) and slurry experiments for [CBZ + PASA] cocrystallization discovery
The screening of [CBZ + PASA] crystals by slow crystallization from the solution has shown that there are at least 3 new forms: cocrystal (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), cocrystal methanol solvate (2
1), cocrystal methanol solvate (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) and cocrystal hydrate (2
1) and cocrystal hydrate (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). Two methods were tested to obtain the required quantity of new cocrystal forms: cogrinding and slurrying.
1). Two methods were tested to obtain the required quantity of new cocrystal forms: cogrinding and slurrying.
The influence of liquid-assisted grinding and sonication conditions on the outcome of CBZ cocrystal forms was investigated by adding the solvent to the physical mixtures in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 2
1 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometries. The results of the experiment are summarized in Table 2.
1 stoichiometries. The results of the experiment are summarized in Table 2.
| Solvent | LAG | Slurry technique | ||
|---|---|---|---|---|
(1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
(2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
(1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
(2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
|
| CBZ dihyd – dihydrate form of carbamazepine (CSD refcode FEFNOT04).29 | ||||
| Neat grinding | [CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1); CBZ 1); CBZ |
[CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1); CBZ 1); CBZ |
— | — |
| Acetonitrile | [CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
[CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1); CBZ 1); CBZ |
[CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
[CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1); CBZ dihyd; CBZ 1); CBZ dihyd; CBZ |
| Acetone | [CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
[CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1); CBZ 1); CBZ |
[CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1); CBZ dihyd 1); CBZ dihyd |
[CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1); CBZ dihyd; CBZ 1); CBZ dihyd; CBZ |
| Methanol | [CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
[CBZ + PASA + MeOH] (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
[CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
[CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1); CBZ dihyd 1); CBZ dihyd |
| Ethanol | [CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
[CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1); CBZ 1); CBZ |
[CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
[CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1); CBZ; PASA 1); CBZ; PASA |
| Ethyl acetate | [CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1); CBZ 1); CBZ |
[CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1); CBZ 1); CBZ |
[CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
[CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1); CBZ 1); CBZ |
| Tetrahydrofuran | [CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
[CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1); CBZ 1); CBZ |
[CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
[CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1); CBZ dihyd; CBZ 1); CBZ dihyd; CBZ |
| Chloroform | [CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
[CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1); CBZ 1); CBZ |
[CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1); CBZ dihyd; CBZ 1); CBZ dihyd; CBZ |
[CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1); CBZ 1); CBZ |
| Water | [CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
[CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1); CBZ; CBZ dihyd 1); CBZ; CBZ dihyd |
[CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1); CBZ dihyd; CBZ 1); CBZ dihyd; CBZ |
[CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1); CBZ 1); CBZ |
The findings have revealed that the grinding of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 physical mixture with acetonitrile (ACN), acetone (AO), methanol (MeOH), ethanol (EtOH), tetrahydrofuran (THF), chloroform (CHCl3) and water (H2O) leads to [CBZ + PASA] (1
1 physical mixture with acetonitrile (ACN), acetone (AO), methanol (MeOH), ethanol (EtOH), tetrahydrofuran (THF), chloroform (CHCl3) and water (H2O) leads to [CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) cocrystal formation. The neat grinding and grinding with ethyl acetate have produced a [CBZ + PASA] (1
1) cocrystal formation. The neat grinding and grinding with ethyl acetate have produced a [CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) cocrystal with a small amount of unconverted CBZ (Fig. 3).
1) cocrystal with a small amount of unconverted CBZ (Fig. 3).
A pure [CBZ + PASA + MeOH] (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) form was obtained only by grinding the compounds with an excess amount of CBZ with methanol. In the case of cogrinding of the 2
1) form was obtained only by grinding the compounds with an excess amount of CBZ with methanol. In the case of cogrinding of the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture with water, the unreacted CBZ was partially converted to the dihydrate form (Fig. 4).
1 mixture with water, the unreacted CBZ was partially converted to the dihydrate form (Fig. 4).
It should be noted that no evidence of [CBZ + PASA + H2O] (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) formation in any of the mechanochemical and slurry experiments (Fig. S1 and S2, see the ESI‡) has been found. Moreover, in comparison with the grinding experiments, CBZ and PASA slurrying in 1
1) formation in any of the mechanochemical and slurry experiments (Fig. S1 and S2, see the ESI‡) has been found. Moreover, in comparison with the grinding experiments, CBZ and PASA slurrying in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 2
1 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometries more often leads to CBZ hydration (Table 2).
1 stoichiometries more often leads to CBZ hydration (Table 2).
Crystal structure analysis
Diffraction quality single crystals of [CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) were grown by slow evaporation of an acetonitrile or tetrahydrofuran solution at room temperature.
1) were grown by slow evaporation of an acetonitrile or tetrahydrofuran solution at room temperature.
The solution was prepared by dissolving a mixture of CBZ and PASA in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and/or 2
1 and/or 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratios in the case of tetrahydrofuran. Single crystals of [CBZ + PASA] cocrystal monohydrate (2
1 molar ratios in the case of tetrahydrofuran. Single crystals of [CBZ + PASA] cocrystal monohydrate (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) were grown from acetonitrile by dissolving CBZ and PASA in a 2
1) were grown from acetonitrile by dissolving CBZ and PASA in a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio and from ethyl acetate in a 1
1 molar ratio and from ethyl acetate in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio. We were also able to obtain single crystals of the [CBZ + PASA] (2
1 molar ratio. We were also able to obtain single crystals of the [CBZ + PASA] (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) methanol solvate which were crystallized from the methanol solution of CBZ and PASA mixture with 1
1) methanol solvate which were crystallized from the methanol solution of CBZ and PASA mixture with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry.
1 stoichiometry.
The crystallographic data for the cocrystals are summarized in Table 3, whereas the hydrogen bonding geometries are listed in Table S1 (see the ESI‡).
| 1 | 2 | 3 | |
|---|---|---|---|
[CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
[CBZ + PASA + H2O] (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
[CBZ + PASA + MeOH] (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
|
| CCDC no. | 1544195 | 1544196 | 1544197 |
| Chemical formula | C15H12N2O·C7H7NO3 | 2(C15H12N2O)·C7H7NO3·H2O | 2(C15H12N2O)·C7H7NO3·CH4O |
| Formula weight | 389.40 | 643.68 | 657.71 |
| Crystal structure | Monoclinic | Monoclinic | Monoclinic |
| Space group | C2/c | P21/n | P21/c |
| Crystal size, mm | 0.30 × 0.20 × 0.20 | 0.30 × 0.30 × 0.20 | 0.40 × 0.25 × 0.20 |
| a, Å | 27.427(5) | 13.6727(12) | 12.6443(18) |
| b, Å | 7.6402(15) | 17.6172(15) | 7.5232(11) |
| c, Å | 21.038(4) | 14.836(13) | 34.674(5) |
| β, ° | 119.263(2) | 116.334(1) | 96.811(3) |
| Unit cell volume, Å3 | 3845.8(13) | 3202.8(5) | 3275.1(8) |
| No. of formula units per unit cell, Z | 8 | 4 | 4 |
| D calc, g cm−3 | 1.345 | 1.335 | 1.334 |
| T, K | 150(2) | 150(2) | 183(2) |
| Absorption coefficient, μ, mm−1 | 0.094 | 0.092 | 0.092 |
| Data collection | |||
| No. of reflections measured | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 588 588 |
32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 373 373 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 975 975 |
| No. of independent reflections | 5123 | 7715 | 6390 |
| Reflections with I > 2σ(I) | 4512 | 6313 | 5050 |
| R int | 0.0199 | 0.0271 | 0.0379 |
| Θ max, ° | 29.00 | 28.00 | 26.00 |
| Refinement | |||
| No. of parameters | 338 | 565 | 583 |
| R 1 values (I > 2σ(I)) | 0.0385 | 0.0382 | 0.0377 |
| wR2 values (all data) | 0.1058 | 0.1026 | 0.0915 |
| Goodness of fit on F2 | 1.054 | 1.026 | 1.012 |
| Largest diff peak and hole, e Å−3 | 0.342/−0.214 | 0.255/−0.255 | 0.191/−0.187 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 1 cocrystal (1).
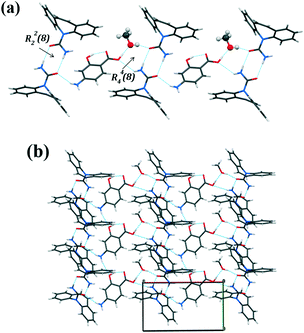
The colorless prism-shaped crystals grown from acetonitrile and tetrahydrofuran (Table 1) were found to belong to the monoclinic, C2/c space group (Table 3). The asymmetric unit consists of one CBZ and one PASA molecule (Fig. 5a). The primary interaction that holds CBZ and PASA molecules is the heterosynthon interaction (R22(8) ring motif) between the carboxamide group of CBZ and the acid group of PASA via N–H⋯O (2.01(2) Å, 165(2)°) and O–H⋯O (1.60(2) Å, 167(2)°) hydrogen bonds. The resulting two-component supramolecular units then interact with each other via the N–H⋯O (2.22(2) Å, 163(2)°) hydrogen bond among PASA molecules to form a zigzag chain along the b-axis with a C(6) graph set notation (Fig. 5b).30,31 The anti-oriented NH amide H11 atom of CBZ is not involved in any strong hydrogen bonding.
1 cocrystal (1).
The colorless prism-shaped crystals grown from acetonitrile and tetrahydrofuran (Table 1) were found to belong to the monoclinic, C2/c space group (Table 3). The asymmetric unit consists of one CBZ and one PASA molecule (Fig. 5a). The primary interaction that holds CBZ and PASA molecules is the heterosynthon interaction (R22(8) ring motif) between the carboxamide group of CBZ and the acid group of PASA via N–H⋯O (2.01(2) Å, 165(2)°) and O–H⋯O (1.60(2) Å, 167(2)°) hydrogen bonds. The resulting two-component supramolecular units then interact with each other via the N–H⋯O (2.22(2) Å, 163(2)°) hydrogen bond among PASA molecules to form a zigzag chain along the b-axis with a C(6) graph set notation (Fig. 5b).30,31 The anti-oriented NH amide H11 atom of CBZ is not involved in any strong hydrogen bonding.
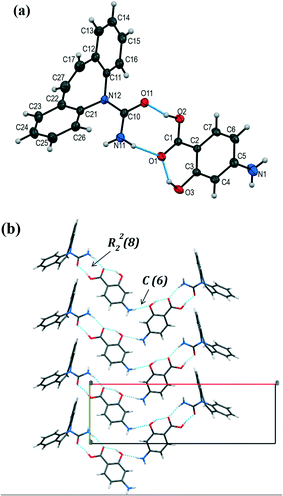 | ||
Fig. 5 (a) Asymmetric unit in [CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). The displacement ellipsoids are shown at the 50% probability level. (b) Molecular packing projection for [CBZ + PASA] (1 1). The displacement ellipsoids are shown at the 50% probability level. (b) Molecular packing projection for [CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). 1). | ||
Interestingly, the crystal packing of [CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) is significantly different from the crystal packing of a known CBZ cocrystal with PABA in a 1
1) is significantly different from the crystal packing of a known CBZ cocrystal with PABA in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio (CSD refcode XOXHEY).24 This is due to the fact that the PASA molecule has an additional –OH group functioning as an H-bond donor (intramolecular hydrogen bond, O3–H3⋯O1 (1.70(2) Å, 152(2)°) and an acceptor (intermolecular hydrogen bond, N1–H1⋯O3 (2.22(2) Å, 163(2)°) simultaneously in contrast with the PABA molecule.
1 molar ratio (CSD refcode XOXHEY).24 This is due to the fact that the PASA molecule has an additional –OH group functioning as an H-bond donor (intramolecular hydrogen bond, O3–H3⋯O1 (1.70(2) Å, 152(2)°) and an acceptor (intermolecular hydrogen bond, N1–H1⋯O3 (2.22(2) Å, 163(2)°) simultaneously in contrast with the PABA molecule.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 1 cocrystal hydrate (2).
The colorless block-shaped crystals grown from ethyl acetate and acetonitrile (Table 1) belong to the monoclinic, P21/n space group (Table 3). The asymmetric unit contains two CBZ molecules and one molecule each of PASA and water (Fig. 6a). In this case, the crystal structure of [CBZ + PASA + H2O] shows the same packing arrangement as that of the carbamazepine cocrystal monohydrate with PABA in a 2
1 cocrystal hydrate (2).
The colorless block-shaped crystals grown from ethyl acetate and acetonitrile (Table 1) belong to the monoclinic, P21/n space group (Table 3). The asymmetric unit contains two CBZ molecules and one molecule each of PASA and water (Fig. 6a). In this case, the crystal structure of [CBZ + PASA + H2O] shows the same packing arrangement as that of the carbamazepine cocrystal monohydrate with PABA in a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio (CSD refcode XAQREN).32 The crystal structure of [CBZ + PASA + H2O] forms an 8-membered supramolecular discrete unit consisting of four carbamazepine molecules, two para-aminosalicylic acid molecules and two water molecules (Fig. 6b). Carbamazepine does not form a carboxyl-amide heterosynthon with PASA due to the incorporation of water molecules in the crystal structure. Instead, the molecules of 2 form two types of trimeric ring motifs with R33(10) and R33(8) graph set notations. The fist trimer (R33(10)) is composed of one molecule each of carbamazepine, para-aminosalicylic acid and water, in which the strongest O2–H2⋯O5 (1.66(2) Å, 174(2)°), between PASA and H2O molecules) hydrogen bond in the structure (2) is realized. The second trimer (R33(8)) is composed of two carbamazepine molecules and one methanol molecule. As in [CBZ + PASA], the anti-oriented NH amide H11 and H21 atoms are not involved in any hydrogen bonding.
1 molar ratio (CSD refcode XAQREN).32 The crystal structure of [CBZ + PASA + H2O] forms an 8-membered supramolecular discrete unit consisting of four carbamazepine molecules, two para-aminosalicylic acid molecules and two water molecules (Fig. 6b). Carbamazepine does not form a carboxyl-amide heterosynthon with PASA due to the incorporation of water molecules in the crystal structure. Instead, the molecules of 2 form two types of trimeric ring motifs with R33(10) and R33(8) graph set notations. The fist trimer (R33(10)) is composed of one molecule each of carbamazepine, para-aminosalicylic acid and water, in which the strongest O2–H2⋯O5 (1.66(2) Å, 174(2)°), between PASA and H2O molecules) hydrogen bond in the structure (2) is realized. The second trimer (R33(8)) is composed of two carbamazepine molecules and one methanol molecule. As in [CBZ + PASA], the anti-oriented NH amide H11 and H21 atoms are not involved in any hydrogen bonding.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 1 cocrystal MeOH solvate (3).
The colorless block-shaped crystals grown from methanol in a 1
1 cocrystal MeOH solvate (3).
The colorless block-shaped crystals grown from methanol in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio (Table 1) belong to the monoclinic, P21/c space group (Table 3). The asymmetric unit contains two CBZ molecules, one PASA molecule and one methanol molecule (Fig. 7).
1 molar ratio (Table 1) belong to the monoclinic, P21/c space group (Table 3). The asymmetric unit contains two CBZ molecules, one PASA molecule and one methanol molecule (Fig. 7).
 | ||
Fig. 7 Asymmetric unit in [CBZ + PASA + MeOH] (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). The displacement ellipsoids are shown at the 50% probability level. 1). The displacement ellipsoids are shown at the 50% probability level. | ||
Analysis of the packing diagram of the [CBZ + PASA + MeOH] cocrystal reveals that the structure is made up of hydrogen bonded tetramers (Fig. 8a). The hydrogen bonding motif is described by a carboxamide dimer between crystallographically different molecules of carbamazepine with an additional bent N11–H11 (anti-oriented)⋯O2 (2.59(2) Å, 126.4(1)°) hydrogen bond from CBZ to PASA and an O4–H41⋯O21 (1.78(2) Å, 161(2)°) hydrogen bond from methanol to CBZ. para-Aminosalicylic acid and methanol molecules are connected to each other via the strongest O2–H2⋯O4 (1.66(2) Å, 177(2)°) interaction in the structure (3). The hydrogen bonded tetramers form a layer along the a-axis via the N1–H1⋯O11 (2.17(2) Å, 156(2)°) hydrogen bond between the PASA and CBZ molecules. The neighboring layers are linked by the weak N1–H10⋯O3 (2.43(2) Å, 166(2)°) interaction between the PASA molecules forming a 2D structure along the b-axis (Fig. 8b).
Conformational analysis of polymorphs of CBZ and its cocrystals
CBZ is an excellent example of crystal polymorphism, wherein the conformation and the network of strong hydrogen bonds remain unchanged in all its forms. The differences between the crystal forms lie solely in the packing of the carboxamide dimer units.23 An exception is the fifth CBZ polymorph for which the hydrogen bond network changes from the dimer motif to the catemeric hydrogen bond.33 Moreover, the molecules in CBZ form III were found to exist in two forms that differ only in the relative orientation of the carboxamide moiety (Fig. S3, see the ESI‡).34The molecule conformation of CBZ can be defined in terms of the torsion angle τ (∠C21–N12–C10–O11, Fig. 1) and one dihedral angle β between the two rings (Fig. 9) which is responsible for the mutual orientation of the different phenyl rings R1 and R2. The overlay of the CBZ molecular conformations in the polymorphic forms is shown in Fig. S4 (see the ESI‡), which confirms that CBZ is a conformationally rigid molecule. And, in the case of polymorphic forms, the dihedral and torsion angles remain practically the same.
In order to investigate the conformational preferences of the CBZ molecule cocrystals, a search of the CSD (v 5.36, May 2015 update)35 for crystal structures of CBZ cocrystals was performed. The search constraints were as follows: 3D coordinates were determined; only organics; no powder structures; not disordered; R ≤ 0.1. As a result, 40 hits, including cocrystals and their hydrates and solvates were retrieved and analyzed. The distribution of the torsion angle and the dihedral angle between the two rings from the retrieved CSD set is presented in Fig. 10a and b. The values of the selected torsion and dihedral angles for the CBZ molecule in all polymorphic forms and in all cocrystals are collected in Table S2 (see the ESI†).
 | ||
| Fig. 10 (a) Distribution of torsion, τ, and (b) dihedral angle between benzene rings, β, in CBZ polymorphs, cocrystals and cocrystal solvates/hydrates retrieved from the CSD set (40 hits). | ||
As previously noted, CBZ is a rather rigid molecule. This CBZ feature is also traced in its cocrystals. The torsion angle value of the carboxamide moiety of the CBZ molecule most often ranges from 175 to 179°, which is the closest to the torsion angle value of CBZ form III. This immobility of the functional group can be explained by the fact that it is stabilized via the carboxamide homosynthon or the acid-amide heterosynthon in cocrystals. The torsion angle values decrease to 160–165° in cases where rather strong N–H⋯O or O–H⋯O anti-oriented hydrogen bonds are formed (CBZ cocrystals with saccharin,36 nicotinamide,36para-aminobenzoic acid24 or adamantine-1,3,5,7-tetracarboxylic acid36).
Most of the structures are located between 124° and 126° dihedral angle values. The smallest dihedral angle for the CBZ molecule (119.6°) is observed in the CBZ cocrystal with isonicotinamide form I (refcode LOFKIB37). Such a significant alteration is explained by the formation of strong π–π interactions between the CBZ benzene ring and the isonicotinamide molecule, which are located approximately 3.8 Å apart. Moreover, the PABA and PASA cocrystal hydrates are characterized by the minimum β values. The deviation from the optimal geometry of the CBZ molecule is explained by the influence of the supramolecular environment. These cocrystal hydrates are characterized by the same packing arrangement type: the 8-membered supramolecular discrete unit consists of four carbamazepine molecules, two para-aminosalicylic acid molecules and two water molecules. The different discrete units “rest” on dibenzazepine fragments of CBZ, which leads to an additional stress and the “unfolding” of two benzene rings.
Crystal lattice energy calculation
The intermolecular interaction energies in the studied CBZ cocrystals with stoichiometry (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) were analyzed according to the PIXEL approach developed by Gavezzotti.19 The calculation results are summarized in Table 4.
1) were analyzed according to the PIXEL approach developed by Gavezzotti.19 The calculation results are summarized in Table 4.
| Ref. | E coul | E pol | E disp | E rep | E latt | |
|---|---|---|---|---|---|---|
| HQ – Hydroquinone; BA – benzoic acid; SA – salicylic acid; 4-OHBA – 4hydroxybenzoic acid; NAM – nicotinamide; iNAM – isonicotinamide; Schr – saccharin; GltAc – glutaric acid. | ||||||
| [CBZ + PASA] | [tw] | −184.4 | −83 | −227 | 217.4 | −277 |
| [CBZ + HQ] | 38 | −175.6 | −83.8 | −226 | 216.4 | −269 |
| [CBZ + BA] | 39 | −123.6 | −54.8 | −217.6 | 151.6 | −244.6 |
| [CBZ + SA] | 39 | −137.4 | −55.8 | −210.8 | 166.6 | −237.4 |
| [CBZ + 4-OHBA] form A | 39 | −193 | −89.2 | −228.6 | 236.2 | −274.8 |
| [CBZ + 4-OHBA] form C | 39 | −191.6 | −81 | −226.4 | 217.6 | −281.2 |
| [CBZ + PABA] | 24 | −196.6 | −89.8 | −243.2 | 240.4 | −289.2 |
| [CBZ + NAM] | 36 | −131.2 | −48.2 | −222.8 | 135.4 | −266.8 |
| [CBZ + iNAM] form A | 37 | −148.8 | −54.6 | −233.4 | 168.6 | −268.2 |
| [CBZ + iNAM] form B | 40 | −132.6 | −51 | −214.6 | 135.8 | −262.4 |
| [CBZ + Schr] form A | 36 | −136.2 | −53.2 | −248.8 | 151 | −287.2 |
| [CBZ + Schr] form B | 41 | −148.8 | −61.2 | −237 | 167.8 | −279.4 |
| [CBZ + GltAc] | 39 | −216.6 | −97.8 | −222.4 | 255.8 | −281 |
The calculations show that the total lattice energy for [CBZ + PASA] is ca. 11 kJ mol−1 less stabilizing than that for the [CBZ + PABA] cocrystal. The stability decrease is most likely a consequence of the presence of an intramolecular hydrogen bond in the PASA molecule, which affects the structure-forming intermolecular hydrogen bond energy in the acid-amide heterosynthon between PASA and CBZ. The same is observed for other benzoic acid derivatives. Comparing the total lattice energy in the series benzoic acid, salicylic acid, 4-hydroxybenzoic acid, PABA and PASA coformers, we can see that an increase in the number of hydrogen bond donors and acceptors leads to an increase in the total crystal lattice energy. Cocrystals with PASA and salicylic acid are exceptions due to the presence of an intramolecular hydrogen bond in the coformer molecules. The total lattice energy for [CBZ + salicylic acid] is lower than those of both the CBZ cocrystal with the structural isomer [salicylic acid + 4-hydroxybenzoic acid] (more than 20 kJ mol−1) and the cocrystal [CBZ + benzoic acid] (at 7.2 kJ mol−1).
However, PIXEL gives an opportunity not only to estimate the total lattice energy of the studied systems but also to partition the total energy into electrostatic, polarization, dispersion and repulsion terms. Table 4 shows that the dispersion interactions dominate the structures of the cocrystals, while the Coulombic term also contributes significantly to the lattice energies, particularly in [CBZ + PASA].
The maximum difference between the dispersion and Coulombic terms is observed in the [CBZ + benzoic acid], [CBZ + salicylic acid] and [CBZ + nicotinamide] cocrystals, which are characterized by the formation of separate clusters of dimers (discrete units) not bound by hydrogen bonds to the adjacent rows of cocrystal molecules. The minimum difference between the dispersion and Coulombic terms and, as a consequence, the maximum contribution of electrostatic interactions are observed in the [CBZ + glutaric acid] cocrystal with the biggest number of strong hydrogen bonds (5) attributable to the molecules of coformers. In [CBZ + 4-hydroxybenzoic acid] cocrystal form A, there are also 5 unique hydrogen bonds on two coformer molecules, but there is no acid-amide heterosynthon.
Table 5 shows the sums of the intermolecular interaction energies between the different types of molecules. In most cases, the CBZ–CF interactions make the largest contribution to the lattice energy (more than 50%). The maximum contribution of such interactions to the crystal lattice energy is found for the CBZ cocrystals with benzoic acid derivatives. The CBZ–CBZ interactions comprise approximately a third of the total energy, while less than 20% is left for the interaction between the CF molecules.
| CBZ–CBZ | CBZ–CF | CF–CF | Total | |
|---|---|---|---|---|
| [CBZ + PASA] | −79.9 (28.9%) | −147.3 (53.2%) | −49.8 (18%) | −277 |
| [CBZ + HQ] | −103.8 (38.6%) | −141.3 (52.5%) | −23.9 (8.9%) | −269 |
| [CBZ + BA] | −84.1 (34.4%) | −139.7 (57.1%) | −20.8 (8.5%) | −244.6 |
| [CBZ + SA] | −83.5 (35.2%) | −136.6 (57.5%) | −17.3 (7.3%) | −237.4 |
| [CBZ + 4-OHBA] form A | −103.9 (37.8%) | −155.7 (56.7%) | −15.1 (5.5%) | −274.8 |
| [CBZ + 4-OHBA] form C | −112.7 (40.1%) | −142.4 (50.6%) | −26.0 (9.2%) | −281.2 |
| [CBZ + PABA] | −119.0 (41.2%) | −153.0 (52.9%) | −17.1 (5.9%) | −289.2 |
| [CBZ + NAM] | −98.9 (37.1%) | −116.5 (43.7%) | −51.4 (19.3%) | −266.8 |
| [CBZ + iNAM] form A | −87.5 (32.6%) | −146.7 (54.7%) | −34.0 (12.7%) | −268.2 |
| [CBZ + iNAM] form B | −103.1 (39.3%) | −113.0 (43.0%) | −46.3 (17.6%) | −262.4 |
| [CBZ + Schr] form A | −82.8 (28.9%) | −174.3 (60.7%) | −30.1 (10.5%) | −287.2 |
| [CBZ +Schr] form B | −97.9 (35.0%) | −118.7 (42.5%) | −62.8 (22.5%) | −279.4 |
| [CBZ + GltAc] | −119.4 (42.5%) | −111.4 (39.7%) | −50.3 (17.9%) | −281.0 |
A similar relation between the CBZ–CBZ and CBZ–CF relative contributions to the total energy (ca. 35/55%) is observed in the CBZ cocrystals with benzoic acid derivatives. It seems that this fact can be attributed to the similarity of the packing arrangements of the considered cocrystals.
The contributions of CBZ–CBZ and CF–CF interactions are enhanced, while the contribution from CBZ–CF interactions is reduced to 40–45% for the systems where the acid-amide heterosynthon between the coformers is not realized, as well as for the systems with nicotinamide and isonicotinamide.
Thermal analysis
The DSC curves of [CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), [CBZ + PASA + H2O] (2
1), [CBZ + PASA + H2O] (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) and [CBZ + PASA + MeOH] (2
1) and [CBZ + PASA + MeOH] (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) are presented in Fig. 11. The melting points of the studied cocrystals and their individual components are summarized in Table 6.
1) are presented in Fig. 11. The melting points of the studied cocrystals and their individual components are summarized in Table 6.
 | ||
Fig. 11 DSC curves of CBZ, PASA, [CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), [CBZ + PASA + H2O] (2 1), [CBZ + PASA + H2O] (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) and [CBZ + PASA + MeOH] (2 1) and [CBZ + PASA + MeOH] (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) recorded at 10 °C min−1 heating rate. 1) recorded at 10 °C min−1 heating rate. | ||
| T desolv, °C (onset) | ΔHTdesolv, J g−1 | ΔmS, % | T fus, °C (onset) | ΔHTfus, kJ mol−1 | ΔHS, kJ mol−1 | |
|---|---|---|---|---|---|---|
[CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
— | — | — | 154.0 ± 2.1 | 77.8 | — |
[CBZ + PASA + H2O] (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
81.9 | 72.4 | 2.20 | 154.5 ± 0.8 | 136.7 | 59.3 |
[CBZ + PASA + MeOH] (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
74.7 | 76.5 | 4.56 | 150.8 ± 3.0 | 103.5 | 53.7 |
The DSC curves of CBZ, PASA and [CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) show one endotherm which corresponds to the melting process, whereas no other phase transitions are observed. The melting temperature of the [CBZ + PASA] cocrystal is found to be ca. 15 °C higher than the PASA one. The melting temperature values of [CBZ + PASA] [1
1) show one endotherm which corresponds to the melting process, whereas no other phase transitions are observed. The melting temperature of the [CBZ + PASA] cocrystal is found to be ca. 15 °C higher than the PASA one. The melting temperature values of [CBZ + PASA] [1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1] and [CBZ + PASA] (2
1] and [CBZ + PASA] (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) after desolvation are equal within the experimental error.
1) after desolvation are equal within the experimental error.
For [CBZ + PASA + H2O] (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), the desolvation process is registered by TG at the desolvation onset temperature equaling 81.9 °C (Fig. S5, see the ESI‡).
1), the desolvation process is registered by TG at the desolvation onset temperature equaling 81.9 °C (Fig. S5, see the ESI‡).
The binding strength of the solvent in the cocrystal solvate and hydrate can be estimated by calculating the vaporization enthalpy (ΔHS) of the cocrystal-bound solvent using the following relationship:42,43
| ΔHS = (ΔHTdesolv·100/ΔmS)·MS | (1) |
The ΔHS value for [CBZ + PASA + H2O] indicates 45% (59.3 kJ mol−1) stronger interactions of water with the host structure than pure water (40.66 kJ mol−1). The enthalpy of pure methanol vaporization (35.21 kJ mol−1) is found to be ca. 18.5 kJ mol−1 lower than the ΔHS value in the solvate cocrystal. The binding strength of the solvent molecules depends on different factors, such as the packing arrangement of the host structure, the solvent accommodation, etc. In the case of the hydrate under investigation, the differences in ΔHS values correlate well with the hydrate crystal structure features. The water molecules in the cocrystal hydrate interact with three neighboring coformer molecules forming the three strongest hydrogen bonds of the system: O2–H2⋯O5 (1.66 Å), O5–H52⋯O21 (1.78 Å) and O5–H51⋯O11 (1.91 Å). Similarly, the methanol molecules in [CBZ + PASA + MeOH] are bound to the coformers by strong hydrogen bonds, but there are only two such bonds: O2–H2⋯O4 (1.66 Å) and O4–H41⋯O21 (1.78 Å) (Table S1, see the ESI‡).
Cocrystal formation thermodynamics
The approach to prediction of the thermodynamic functions of cocrystal formation (ΔG0,298f(CC), ΔH0,298f(CC)) based on the knowledge of the melting temperatures of active pharmaceutical ingredients (API) (Tm(API)), coformers (CF) (Tm(CF)), cocrystals (Tm(CC)) and also on the sublimation Gibbs energies and enthalpies of the individual components included in the cocrystal (ΔG0,298sub(API), ΔG0,298sub(CF), ΔH0,298sub(API), ΔH0,298sub(CF)) has been developed by us earlier.44 Literature data analysis of the sublimation thermodynamics of the individual compounds has shown that there are no sublimation data for either CBZ or PASA. If we keep in mind that CBZ is quite a common compound with a great number of cocrystals with different coformers, the study of its sublimation seems timely and relevant.| T, °C | P, Pa | T, °C | P, Pa |
|---|---|---|---|
a ln(P[Pa]) = (32.7 ± 0.3) − (13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 343 ± 97)/T; σ = 3.97 × 10−2; r = 0.9991; F = 19 343 ± 97)/T; σ = 3.97 × 10−2; r = 0.9991; F = 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 078; n = 18.
b
C
298
p,cr has been calculated using Chickos's additive scheme;45 the calculation procedure error corresponds to a significant digit.
c ςH = (ΔH298sub/(ΔH298sub + T·ΔS298sub))·100%; ςTS = (T·ΔS298sub/(ΔH298sub + T·ΔS298sub))·100%. 078; n = 18.
b
C
298
p,cr has been calculated using Chickos's additive scheme;45 the calculation procedure error corresponds to a significant digit.
c ςH = (ΔH298sub/(ΔH298sub + T·ΔS298sub))·100%; ςTS = (T·ΔS298sub/(ΔH298sub + T·ΔS298sub))·100%.
|
|||
| 80.0 | 6.10 × 10−3 | 108.0 | 8.89 × 10−2 |
| 81.0 | 6.87 × 10−3 | 110.0 | 1.09 × 10−1 |
| 82.0 | 7.45 × 10−3 | 115.0 | 1.76 × 10−1 |
| 83.0 | 8.31 × 10−3 | 118.0 | 2.35 × 10−1 |
| 85.0 | 1.02 × 10−2 | 120.0 | 2.87 × 10−1 |
| 90.0 | 1.83 × 10−2 | 123.0 | 3.79 × 10−1 |
| 95.0 | 2.93 × 10−2 | 125.0 | 4.40 × 10−1 |
| 100.0 | 4.24 × 10−2 | 127.0 | 5.33 × 10−1 |
| 105.0 | 6.72 × 10−2 | 130.0 | 6.84 × 10−1 |
| ΔG298sub, kJ mol−1 | 58.5 | ΔS298sub, J mol−1 K−1 | 187 ± 3 |
| ΔHTsub, kJ mol−1 | 110.9 ± 0.8 | ς H, %c | 67.2 |
| ΔH298sub, kJ mol−1 | 114.2 ± 0.8 | ς TS, %c | 32.8 |
| C 298 p,cr, J mol−1 K−1b | 277.3 | T m, K | 190.1 |
| T·ΔS298sub, kJ mol−1 | 55.7 | ΔHTfus, kJ mol−1 | 28.8 |
| ΔG0,298sub = A + B·Tm | (2) |
| Tc = N(A & B)/[N(A) + N(B) − N(A & B)] | (3) |
In this program, molecular fragments are defined as atom-centered concentric environments. The fragments consist of a central atom and neighboring atoms connected to it within a predefined sphere size (the number of the bonds between the central and edge atoms). For each atom in a fragment, information on the atom and bond type, charge, valency, cycle type and size is coded into fixed-length variables which are subsequently used to define a pseudo-random hash value for this fragment. The program permits an estimation of the similarity of each molecule in the database to all the other molecules by sorting them according to the value of similarity to the initial molecule.
We have formed a cluster for PASA including the structurally related compounds selected by the criterion 0.4 < Tc. Fig. S6 (see the ESI‡) illustrates the experimental values ΔG298sub for cluster elements versus Tm described by the correlation equation:
| ΔG0,298sub = −(23.4 ± 5.5) + (0.175 ± 0.012)·TmR = 0.9119; σ = 4.08; n = 44 | (4) |
On the other hand, we can estimate ΔH0,298sub(PASA) using the equation relating the sublimation enthalpies and Gibbs energies of molecular crystals in a cluster (the so-called “compensation” effect). Fig. S7 (see the ESI‡) illustrates this dependence for the PASA cluster, which can be described by the equation:
| ΔH0,298sub = (52.2 ± 3.7) + (1.26 ± 0.07)·ΔG0,298subR = 0.9469; σ = 4.25; n = 44 | (5) |
It is easy to estimate the thermodynamic functions of the PASA sublimation: ΔG0,298sub(PASA) = 48.7 kJ mol−1 and ΔH0,298sub(PASA) = 113.6 kJ mol−1, using eqn (4) and (5) and knowing the melting point (Tm(PASA) = 412.2 K).
| N | API | Coformer (CF) | Ref | Stoich | T m (API), °C | T m (CF), °C | T m (CC), °C | ΔG0,298sub(API), kJ mol−1 | ΔH0,298sub(API), kJ mol−1 | ΔG0,298sub(CF), kJ mol−1 | ΔH0,298sub(CF), kJ mol−1 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| a T m (API), Tm (CF), Tm (CC) are the melting temperatures of the active pharmaceutical ingredient, coformer and cocrystal, respectively; ΔG0,298sub(API), ΔH0,298sub(API), ΔG0,298sub(CF), ΔH0,298sub(CF) are the sublimation Gibbs energies and enthalpies of the active pharmaceutical ingredient and coformer; the bold values correspond to the sublimation Gibbs energy and enthalpy predicted by the clusterization approach (see text). | |||||||||||
| 1 | CBZ | 4,4′-Bipyridine | 32 | 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
190.1 | 111.8 | 159.0 | 58.5 | 114.20 | 33.6 | 106.3 |
| 2 | CBZ | Hydroquinone | 38 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
190.1 | 173.5 | 168.1 | 58.5 | 114.20 | 43.8 | 103.9 |
| 3 | CBZ | Benzoic acid | 13 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
190.1 | 122.0 | 112.5 | 58.5 | 114.20 | 34.4 | 90.5 |
| 4 | CBZ | Malonic acid | 13 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
190.1 | 136.0 | 143.4 | 58.5 | 114.20 | 46.7 | 111.4 |
| 5 | CBZ | Malonic acid | 48 | 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
190.1 | 134.0 | 142.0 | 58.5 | 114.20 | 46.7 | 111.4 |
| 6 | CBZ | Adipic acid | 13 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
190.1 | 152.0 | 136.8 | 58.5 | 114.20 | 57.5 | 129.3 |
| 7 | CBZ | 4-OHBA (form A) | 13 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
190.1 | 213.0 | 171.5 | 58.5 | 114.20 | 55.0 | 113.3 |
| 8 | CBZ | 4-OHBA (form C) | 13 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
190.1 | 213.0 | 170.0 | 58.5 | 114.20 | 55.0 | 113.3 |
| 9 | CBZ | Fumaric acid | 13 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
190.1 | 287.0 | 188.7 | 58.5 | 114.20 | 26.1 | 123.9 |
| 10 | CBZ | Trimesic acid | 36 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
190.1 | 375.0 | 278.0 | 58.5 | 114.20 | 100.2 | 159.4 |
| 11 | CBZ | Glutaric acid | 48 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
190.1 | 97.7 | 125.9 | 58.5 | 114.20 | 49.1 | 119.8 |
| 12 | CBZ | Glutaric acid | 49 | 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
190.1 | 98.0 | 125.0 | 58.5 | 114.20 | 49.1 | 119.8 |
| 13 | CBZ | Succinic acid | 48 | 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
190.1 | 188.1 | 188.9 | 58.5 | 114.20 | 58.0 | 123.2 |
| 14 | CBZ | Salicylic acid | 48 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
190.1 | 160.9 | 160.1 | 58.5 | 114.20 | 38.5 | 96.6 |
| 15 | CBZ | Nicotinamide | 49 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
190.1 | 130.6 | 160.0 | 58.5 | 114.20 | 49.0 | 111.8 |
| 16 | CBZ | Urea | 49 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
190.1 | 133.0 | 169.0 | 58.5 | 114.20 | 44.5 | 89.0 |
| 17 | CBZ | Cinnamic acid | 50 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
190.1 | 133.5 | 144.0 | 58.5 | 114.20 | 43.8 | 107.1 |
| 18 | CBZ | PASA | tw | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
190.1 | 139.1 | 154.0 | 58.5 | 114.20 | 48.7 | 113.6 |
| 19 | CBZ | PASA | tw | 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
190.1 | 139.1 | 154.5 | 58.5 | 114.20 | 48.7 | 113.6 |
Based on the approach developed by us,44 we calculated the thermodynamic functions of the cocrystal formation. The results of the calculations are presented in Fig. 11 as a diagram, where the abscissa corresponds to the formation enthalpy (ΔH0,298f), and the ordinate corresponds to the entropic term (TΔS0,298f). The dotted lines correspond to the isoenergetic cocrystal formation Gibbs energy values ΔG0,298f. The diagram is divided into eight sectors, each corresponding to a different ratio of the enthalpy and entropy contributions to the Gibbs energy. Each sector is formed by two lines: on one side – the line corresponding to the zero ΔH0,298f or TΔS0,298f-value; on the other side – the bisector of the angles formed at the intersection of the coordinates (ΔH0,298f; TΔS0,298f). The isoenergetic curves of Gibbs energy are marked by dotted lines. Thus, the diagram can be divided into the following areas: (TΔS0,298f > ΔH0,298f > 0) ≡ sector A, (ΔH0,298f < 0; TΔS0,298f > 0; |TΔS0,298f| > |ΔH0,298f|) ≡ sector B, (TΔS0,298f < ΔH0,298f < 0) ≡ sector E, and (ΔH0,298f > 0; TΔS0,298f < 0; |TΔS0,298f| > |ΔH0,298f|) ≡ sector F belonging to the entropy determined processes. The segments of the diagram where (ΔH0,298f < 0; TΔS0,298f > 0; |ΔH0,298f| > |TΔS0,298f|) ≡ sector C, (ΔH0,298f < 0; TΔS0,298f < 0; |ΔH0,298f| > |TΔS0,298f|) ≡ sector D, (ΔH0,298f > TΔS0,298f > 0) ≡ sector H and ((ΔH0,298f > 0; TΔS0,298f < 0; |ΔH0,298f| > |TΔS0,298f|) ≡ sector G correspond to the enthalpy determined processes (Fig. 12).
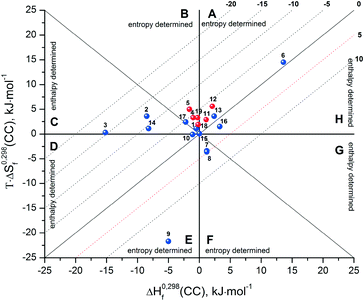 | ||
| Fig. 12 Thermodynamic functions of cocrystal formation processes in coordinates of entropy term vs. enthalpy. The isoenergetic curves of the ΔG0f function are marked by dotted lines. The numbering of the cocrystals corresponds to that in Table 8. The red points correspond to the cocrystals with the same composition but different stoichiometry (see text). | ||
In our previous work,44 we justified the selection criterion for thermodynamically stable cocrystals. This criterion claims that ΔG0,298f < 5 kJ mol−1, which can be explained by the possible existence of polymorphic modifications both for individual compounds and for cocrystals. Based on this criterion, eighteen out of the nineteen cocrystals selected in the literature were predicted correctly (95% correct coincidences). It should be noted that the formation of most cocrystals is an entropically controlled process: 14 cocrystals out of 19 examined. For these, the Gibbs energies of formation, as a rule, do not exceed (in modulus) the value −8 kJ mol−1. In contrast, the Gibbs energies of formation are higher (in modulus) than the value −8 kJ mol−1 for cocrystals with entropically controlled formation (2, 3, 14).
It is interesting to compare cocrystals with identical compositions but with different stoichiometry: [CBZ + Malonic acid] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) – (4) and (2
1) – (4) and (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) – (5); [CBZ + Glutaric acid] (1
1) – (5); [CBZ + Glutaric acid] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) – (11) and (2
1) – (11) and (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) – (12); [CBZ + PASA] (1
1) – (12); [CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) – (18) and (2
1) – (18) and (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) – (19). It is evident that the cocrystals with 2
1) – (19). It is evident that the cocrystals with 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry are slightly thermodynamically more stable than similar cocrystals with 1
1 stoichiometry are slightly thermodynamically more stable than similar cocrystals with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry.
1 stoichiometry.
Dissolution experiments and stability studies
Carbamazepine is a poorly soluble drug that transforms into its dihydrate form in aqueous media, whose solubility is even worse.51 Moreover, CBZ solubility does not depend on the change in the medium pH, since this compound is not capable of ionization. It was proved earlier that CBZ solubility can be enhanced by CBZ cocrystallization with ionizable coformers: PABA, saccharin, salicylic acid.52,53 We used PASA as the coformer – a drug whose solubility increases with rising pH.54 The measurements were carried out in a pH 7.4 phosphate buffer as PASA dissolves almost 9 times better than CBZ. Table 9 shows the results of the solubility experiment for both pure CBZ and its cocrystal in pH 7.4 buffer medium at 25 °C. According to the obtained data, the CBZ cocrystallization with PASA reduces the maximum CBZ concentration in the first 20 minutes but increases its equilibrium concentration, which is reached 2 hours after the start of the experiment.| C max,a mol l−1 | Equilibrium solubility,b mol l−1 | Solid phase recovered after solubility experimentc | |
|---|---|---|---|
| a Is the maximum concentration of CBZ in solution. b Is the equilibrium solubility after 6 hours of the experiment. c The residual materials were identified by XRPD analysis (Fig. S8, see the ESI). | |||
| CBZ | 9.94 × 10−4 ± 5.79 × 10−5 | 4.77 × 10−4 ± 2.23 × 10−7 | CBZ dihyd |
[CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
7.68 × 10−4 ± 4.75 × 10−5 | 6.69 × 10−4 ± 1.08 × 10−5 | CBZ + CBZ dihyd + cocrystal |
Besides measuring the CBZ solubility, it was also important to check how cocrystallization affected the CBZ stability (process of hydration) in an aqueous medium. Fig. 13 illustrates that CBZ in pH 7.4 phosphate buffer begins to quickly convert into its dihydrate form after remaining in the aqueous medium for 20 minutes. This results in a sharp drop in CBZ solubility. This CBZ transformation is also confirmed by the analysis of the solid phase after the experiment (Fig. S8, see the ESI‡); its XRPD pattern coincides with the XRPD pattern of the dihydrate CBZ. In turn, cocrystallization leads to a significant deceleration of CBZ hydration, which is reflected by the absence of a characteristic peak during pure CBZ dissolution. The cocrystal solid phase analysis after the experiment also confirms that after 6 hours in water, CBZ is only partly transformed into its dihydrate form. In the XRPD pattern, there are peaks related to both the dihydrate CBZ form and the unhydrated CBZ. Thus, CBZ cocrystallization with PASA leads to a significant decrease (up to several hours) of the CBZ rate of conversion from the anhydrous to the hydrate form, and as a consequence, a solubility increase of approximately 1.5 times.
Conclusions
Three new CBZ cocrystals with para-aminosalicylic acid, a second-line antituberculosis drug, have been prepared by both solvent-drop grinding and solution techniques. The pure [CBZ + PASA + MeOH] (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) form was obtained only by grinding of CBZ and PASA in (2
1) form was obtained only by grinding of CBZ and PASA in (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) stoichiometry with the addition of methanol. [CBZ + PASA + H2O] (2
1) stoichiometry with the addition of methanol. [CBZ + PASA + H2O] (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) was produced only by solution crystallization from acetonitrile and ethyl acetate.
1) was produced only by solution crystallization from acetonitrile and ethyl acetate.
The crystal structures of [CBZ + PASA] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), [PASA + CBZ + H2O] (2
1), [PASA + CBZ + H2O] (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) and [PASA + CBZ + MeOH] (2
1) and [PASA + CBZ + MeOH] (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) have been analyzed. Comparative analysis of the molecular packing in the obtained cocrystal and in a structurally related [CBZ + PABA] cocrystal has been conducted . It has been found that the presence of an additional donor and an additional acceptor of the hydrogen bond in the PASA molecule leads to the formation of an acid-amide heterosynthon with CBZ versus PABA. This difference significantly affects the molecular packing in the cocrystals.
1) have been analyzed. Comparative analysis of the molecular packing in the obtained cocrystal and in a structurally related [CBZ + PABA] cocrystal has been conducted . It has been found that the presence of an additional donor and an additional acceptor of the hydrogen bond in the PASA molecule leads to the formation of an acid-amide heterosynthon with CBZ versus PABA. This difference significantly affects the molecular packing in the cocrystals.
We have conducted a conformational analysis of the CBZ molecule in the crystals obtained by us in this work in comparison with polymorphs of CBZ, its cocrystals and solvates described in the CSD. It has been shown that the torsion angle value of the carboxamide moiety varies between 175° and 179°, which is the closest to the torsion angle value of CBZ form III. The position of the functional group is stabilized by the carboxamide homosynthon or acid-amide heterosynthon in the cocrystals. The torsion angle value decreases to 160–165° in cases where there are strong N–H⋯O or O–H⋯O anti-oriented hydrogen bonds. Most of the structures are located between 124° and 126° dihedral angle values between the two rings.
The intermolecular interaction energies in the studied CBZ cocrystals with (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) stoichiometry were analyzed according to the PIXEL approach. The analysis of the total lattice energy values in the series of CBZ cocrystals with benzoic acid derivatives has shown that a bigger number of hydrogen bond donors and acceptors leads to an increase in the total crystal lattice energy except in compounds with an intramolecular hydrogen bond. The results of PIXEL calculations show that the dispersion interactions dominate the structures of the cocrystals, while the Coulombic term also contributes significantly to the lattice energies. The largest difference between the dispersion and Coulombic terms was observed in cocrystals characterized by the formation of separate dimer clusters not connected by hydrogen bonds with the neighboring rows of cocrystal molecules. The CBZ–CF interactions provide the largest contribution to the lattice energy (more than 50%). The contributions of CBZ–CBZ and CF–CF interactions increase, while the contribution of the CBZ–CF interactions decreases to 40–45% for systems in which the acid-amide heterosynthon is not realized.
1) stoichiometry were analyzed according to the PIXEL approach. The analysis of the total lattice energy values in the series of CBZ cocrystals with benzoic acid derivatives has shown that a bigger number of hydrogen bond donors and acceptors leads to an increase in the total crystal lattice energy except in compounds with an intramolecular hydrogen bond. The results of PIXEL calculations show that the dispersion interactions dominate the structures of the cocrystals, while the Coulombic term also contributes significantly to the lattice energies. The largest difference between the dispersion and Coulombic terms was observed in cocrystals characterized by the formation of separate dimer clusters not connected by hydrogen bonds with the neighboring rows of cocrystal molecules. The CBZ–CF interactions provide the largest contribution to the lattice energy (more than 50%). The contributions of CBZ–CBZ and CF–CF interactions increase, while the contribution of the CBZ–CF interactions decreases to 40–45% for systems in which the acid-amide heterosynthon is not realized.
The thermodynamic parameters of the sublimation process of carbamazepine form III were obtained for the prediction of the thermodynamic functions of cocrystal formation based on the knowledge of the melting temperatures of active pharmaceutical ingredients, coformers, and cocrystals and also on the sublimation Gibbs energies and enthalpies of individual components included in the cocrystals. The thermodynamic functions of the CBZ cocrystal formation with a number of known cocrystals were calculated. Based on the conducted calculations, eighteen out of the nineteen cocrystals selected in the analyzed literature were predicted correctly (95% correct coincidences). It has been shown that the formation of most cocrystals is an entropically controlled process (14 cocrystals out of 19 examined).
The dissolution process of the [CBZ + PASA] cocrystal (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) in pH 7.4 phosphate buffer has been studied. The cocrystallization of CBZ with PASA leads to a significant decrease (up to several hours) of the CBZ rate of conversion from the anhydrous to the hydrate form, and as a result, a CBZ solubility increase by approximately 1.5 times.
1) in pH 7.4 phosphate buffer has been studied. The cocrystallization of CBZ with PASA leads to a significant decrease (up to several hours) of the CBZ rate of conversion from the anhydrous to the hydrate form, and as a result, a CBZ solubility increase by approximately 1.5 times.
Acknowledgements
This work was supported by the Russian Foundation of Basic Research (grant No. 16-53-150007). The single crystal X-ray diffraction studies were performed at the Centre of Shared Equipment of IGIC RAS. We thank “the Upper Volga Region Centre of Physicochemical Research” for technical assistance with TGA and XRPD experiments.Notes and references
- X. Wan, P. Ma and X. Zhang, Asian J. Pharm. Sci., 2014, 9, 1 CrossRef.
- R. Thipparaboina, D. Kumar, R. B. Chavan and N. R. Shastri, Drug Discovery Today, 2016, 21, 481 CrossRef CAS PubMed.
- N. Schultheiss and A. Newman, Cryst. Growth Des., 2009, 9, 2950 CAS.
- R. Thakuria, A. Delori, W. Jones, M. P. Lipert, L. Roy and N. Rodriguez-Hornedo, Int. J. Pharm., 2013, 453, 101 CrossRef CAS PubMed.
- FDA, Guidance for industry, 2011, https://www.fda.gov/downloads/Drugs/GuidanceComplianceRegulatoryInformation/Guidance1054s/UCM281764.pdf Search PubMed.
- G. R. Desiraju, Angew. Chem., Int. Ed. Engl., 1995, 34, 2311 CrossRef CAS.
- R. Chadha, A. Saini, P. Arora, D. S. Jain, A. Dasgupta and T. N. G. Row, CrystEngComm, 2011, 13, 6271 RSC.
- S. Aitipamula, P. S. Chow and R. B. H. Tan, CrystEngComm, 2009, 11, 1823 RSC.
- M. L. Cheney, D. R. Weyna, N. Shan, M. Hanna, L. Wojtas and M. J. Zaworotko, J. Pharm. Sci., 2011, 100, 2172 CrossRef CAS PubMed.
- B. S. Sekhon, Daru, J. Pharm. Sci., 2012, 20, 45 CrossRef CAS PubMed.
- WHO, Expert committee on specifications for pharmaceutical preparations, Fortieth report, 2006, p. 402 Search PubMed.
- Z. Rahman, C. Agarabi, A. S. Zidan, S. R. Khan and M. A. Khan, AAPS PharmSciTech, 2011, 12, 693 CrossRef CAS PubMed.
- S. L. Childs, N. Rodriguez-Hornedo, L. S. Reddy, A. Jayasankar, C. Maheshwari, L. McCausland, R. Shipplett and B. C. Stahly, CrystEngComm, 2008, 10, 856 RSC.
- M. Schiebler, K. Brown, K. Hegyi, S. M. Newton, M. Renna, L. Hepburn, C. Klapholz, S. Coulter, A. Obregon-Henao, M. Henao Tamayo, R. Basaraba, B. Kampmann, K. M. Henry, J. Burgon, S. A. Renshaw, A. Fleming, R. R. Kay, K. E. Anderson, P. T. Hawkins, D. J. Ordway, D. C. Rubinsztein and R. A. Floto, EMBO Mol. Med., 2015, 7, 127 CrossRef CAS PubMed.
- A. Swart and V. Harris, Continuing Medical Education, 2005, 23, 56 Search PubMed.
- A. V. Yadav, A. S. Shete, A. P. Dabke, P. V. Kulkarni and S. S. Sakhare, Indian J. Pharm. Sci., 2009, 71, 359 CrossRef CAS PubMed.
- G. M. Sheldrick, SADABS, Program for scaling and correction of area detector data, University of Göttingen, Germany, 1997 Search PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112 CrossRef CAS PubMed.
- A. Gavezzotti, Mol. Phys., 2008, 106, 1473 CrossRef CAS.
- L. Maschio, B. Civalleri, P. Ugliengo and A. Gavezzotti, J. Phys. Chem. A, 2011, 115, 11179 CrossRef CAS PubMed.
- A. N. Manin, A. P. Voronin and G. L. Perlovich, Thermochim. Acta, 2014, 583, 72 CrossRef CAS.
- W. Zielenkiewicz, G. L. Perlovich and M. Wszelaka-Rylik, J. Therm. Anal. Calorim., 1999, 57, 225 CrossRef CAS.
- A. L. Grzesiak, M. Lang, K. Kim and A. J. Matzger, J. Pharm. Sci., 2003, 92, 2260 CrossRef CAS PubMed.
- A. Jayasankar, L. S. Reddy, S. J. Bethune and N. Rodrigues-Hornedo, Cryst. Growth Des., 2009, 9, 889 CAS.
- Z. Li and A. J. Matzger, Mol. Pharmaceutics, 2016, 13, 990 CrossRef CAS PubMed.
- A. V. Trask, W. D. S. Mothrwell and W. Jones, Cryst. Growth Des., 2005, 5, 1013 CAS.
- K. Guo, G. Sadiq, C. Seaton, R. Davey and Q. Yin, Cryst. Growth Des., 2010, 10, 268 CAS.
- S.-W. Zhang, M. T. Harasimowicz, M. M. de Villiers and L. Yu, J. Am. Chem. Soc., 2013, 135, 18981 CrossRef CAS PubMed.
- A. Kogan, I. Popov, V. Uvarov, S. Cohen, A. Aserin and N. Garti, J. Dispersion Sci. Technol., 2007, 28, 1008 CrossRef CAS.
- M. C. Etter, Acc. Chem. Res., 1990, 23, 120 CrossRef CAS.
- J. Bernstein, R. E. Davis, L. Shimoni and N.-L. Chang, Angew. Chem., Int. Ed. Engl., 1995, 34, 1555 CrossRef CAS.
- J. A. McMahon, J. A. Bis, P. Vishweshwar, T. R. Shattock, O. L. McLaughlin and M. J. Zaworotko, Z. Kristallogr., 2005, 220, 340 CAS.
- J.-B. Arlin, L. S. Price and S. L. Price, Chem. Commun., 2011, 47, 7074 RSC.
- T. Gelbrich and M. B. Hursthouse, CrystEngComm, 2006, 8, 448 RSC.
- F. H. Allen, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 380 CrossRef.
- S. G. Fleischman, S. S. Kuduva, J. A. McMahon, B. Moulton, R. D. B. Walsh, N. Rodriguez-Hornedo and M. J. Zaworotko, Cryst. Growth Des., 2003, 3, 909 CAS.
- J. H. ter Horst and P. W. Cains, Cryst. Growth Des., 2008, 8, 2537 CAS.
- S. Aitipamula, P. S. Chow and R. B. H. Tan, J. Chem. Crystallogr., 2011, 41, 1604 CrossRef CAS.
- S. L. Childs, P. A. Wood, N. Rodriguez-Hornedo, L. S. Reddy and K. I. Hardcastle, Cryst. Growth Des., 2009, 9, 1869 CAS.
- M. Habgood, M. A. Deij, J. Mazurek, S. L. Price and J. H. ter Horst, Cryst. Growth Des., 2010, 10, 903 CAS.
- W. W. Porter III, S. C. Elie and A. J. Matzger, Cryst. Growth Des., 2008, 8, 14 Search PubMed.
- M. R. Caira, G. Bettinetti and M. Sorrenti, J. Pharm. Sci., 2002, 91, 467 CrossRef CAS PubMed.
- A. O. Surov, A. N. Manin, A. P. Voronin, K. V. Drozd, A. A. Simagina, A. V. Churakov and G. L. Perlovich, Eur. J. Pharm. Sci., 2015, 77, 112 CrossRef CAS PubMed.
- G. L. Perlovich, CrystEngComm, 2015, 17, 7019 RSC.
- J. S. Chickos and W. E. Acree Jr., J. Phys. Chem. Ref. Data, 2002, 31, 537 CrossRef CAS.
- G. L. Perlovich and O. A. Raevsky, Cryst. Growth Des., 2010, 10, 2707 CAS.
- O. A. Raevsky, V. A. Gerasimenko and S. V. Trepalin, MOLDIVS (MOLecular DIVersity& Similarity) program package, Registration by Russian State Patent Agency No. 990093 of 26.02.99 Search PubMed.
- D. J. Good and N. Rodriguez-Hornedo, Cryst. Growth Des., 2009, 9, 2252 CAS.
- E. Lu, N. Rodriguez-Hornedo and R. Suryanarayanan, CrystEngComm, 2008, 10, 665 RSC.
- A. Shayanfar, K. Asadpour-Zeynali and A. Jouyban, J. Mol. Liq., 2013, 187, 171 CrossRef CAS.
- F. Keramathnia, A. Shayanfar and A. Jouyban, J. Pharm. Sci., 2015, 104, 2559 CrossRef PubMed.
- S. J. Bethune, N. Huang, A. Jayasankar and N. Rodriguez-Hornedo, Cryst. Growth Des., 2009, 9, 3976 CAS.
- A. Alhalaweh, L. Roy, N. Rodriguez-Hornedo and S. P. Velaga, Mol. Pharmaceutics, 2012, 9, 2605 CrossRef CAS PubMed.
- K. V. Drozd, A. N. Manin, A. V. Churakov and G. L. Perlovich, Eur. J. Pharm. Sci., 2017, 99, 228 CrossRef CAS PubMed.
Footnotes |
| † The authors declare no competing financial interest. |
| ‡ Electronic supplementary information (ESI) available: XRPD patterns of samples obtained by slurrying and from dissolution experiments, DSC/TG thermograms, estimation of sublimation thermodynamic functions, conformational analysis of polymorphs of CBZ and its cocrystals, hydrogen bond details and CIFs. CCDC 1544195–1544197. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c7ce00831g |
| This journal is © The Royal Society of Chemistry 2017 |