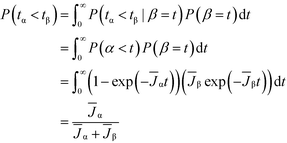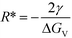Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Induction time of a polymorphic transformation
Wenhao
Sun
 *ab and
Gerbrand
Ceder
*ab and
Gerbrand
Ceder
 abc
abc
aDepartment of Materials Science and Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: wenhaosun@lbl.gov
bMaterials Sciences Division, Lawrence Berkeley National Laboratory, Berkeley, California 94720, USA
cDepartment of Materials Science and Engineering, UC Berkeley, Berkeley, California 94720, USA
First published on 21st July 2017
Abstract
When a solution is supersaturated with respect to multiple polymorphs, the polymorph with the lowest nucleation barrier will form first. If this is a metastable polymorph, it will persist until the induction of nuclei of a lower free-energy phase, marking the onset of a polymorphic transformation. Induction of a more stable polymorph can occur under two conditions: a.) during steady-state nucleation, or b.) after complete crystal growth of the metastable phase. Using the theory of competing stochastic processes, we derive the rare probability of forming a higher-barrier, more-stable polymorph during steady-state nucleation, and use this to explain variations in crystallization products between repeat experiments, which may underlie the phenomenon of “Disappearing Polymorphs”. We also derive the induction time of a stable phase from a solution equilibrated with a metastable phase, and show that once the stable phase nucleates, bulk metastable crystals will spontaneously ripen onto nanoscale nuclei or seeds of a more stable phase, thermodynamically driving dissolution–reprecipitation processes. Existing strategies to prolong or shorten the lifetimes of transient metastable phases are reviewed and interpreted within the context of polymorphic induction. The analyses in this work are conducted from classical nucleation and crystal growth theories, suggesting that paradigms shifts to ‘non-classical’ nucleation theories may not be necessary to rationalize multistage crystallization.
Crystallization from a supersaturated solution frequently proceeds through a series of transient, metastable phases prior to the formation of the lowest-energy, stable polymorph. This phenomenon, popularly referred to as “Ostwald's Rule of Stages”,1 has been observed across nearly all classes of solid-state materials:2 from inorganic minerals3–5 and functional technological materials6,7 to organic crystals8,9 and biological protein crystals.10,11 Despite there being a lower thermodynamic driving force for the formation of a metastable polymorph, a metastable phase can still dominate the kinetics of crystallization if it has a lower nucleation barrier than the equilibrium phase.12,13 Following the complete crystallization of a metastable phase, the next more-stable polymorph nucleates and grows – consuming the previous metastable phase in a recursive, energetically-cascading series of polymorphic stages down to the lowest-energy, equilibrium phase.
Although a phenomenological understanding of Ostwald's Rule of Stages exists, there is no quantitative theory for the lifetime of the intermediate metastable phases, which can vary anywhere from minutes to millions of years. Numerous technologies and applications would benefit from such a theory. In cases where a transient metastable polymorph is a functional material, polymorphic transformation to a more stable phase can compromise materials performance and be technologically disruptive. Understanding how long it takes to proceed through Ostwald's Rule of Stages could also enable better control over synthesis of metastable materials by soft-chemistry routes, such as chemie douce or hydrothermal synthesis. Most importantly, understanding the parameters that determine the lifetime of a transient metastable phase could lead to strategies to prolong the existence of a functional metastable phase, or to accelerate crystallization through non-functional metastable phases to a desired equilibrium phase.
The Johnson–Mehl–Avrami–Kolmogorov (JMAK) model is the prevailing theory for the kinetics of polymorphic transformations, but the theory presupposes the existence of nuclei of the stable phase.14 However, formation of nuclei of the stable phase is often the limiting step in a polymorphic transformation. In some classic “Disappearing Polymorphs” – metastable pharmaceutical crystals can be crystallized in several hours, and undergo industrial production for months or years before the sudden appearance of a stable phase, which then dominates all ensuing crystallization events.15,16 This suggests that the lifetime of a metastable phase is governed by the time to the formation of the first nucleus of the stable phase. Assuming that the initial formation of a metastable phase is due to a lower nucleation barrier, the lifetime of a metastable polymorph can be framed as quantifying the induction time until the formation of a more-stable polymorph with a higher nucleation barrier.
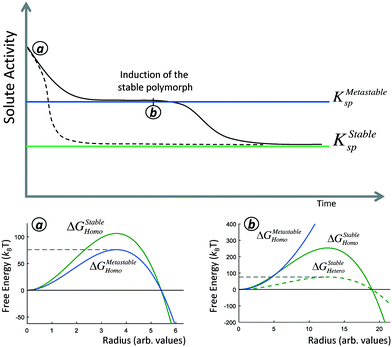
There are two opportunities during the crystallization of a polymorphic system to form a phase with a higher nucleation barrier. The first is during steady-state nucleation from a supersaturated solution, when primary nuclei are forming (Fig. 1, dashed line). Because of the stochastic nature of nucleation, while the solution will predominantly nucleate the phase with the lowest nucleation barrier, there is a non-zero probability that a nucleus of the higher-nucleation barrier stable phase will form (Fig. 1a). We can thus characterize the probability that a nucleus of the stable phase will form by considering the relative stochastic induction probability between competing polymorphs. This scenario is most relevant in open or replenished solutions, where the supersaturation remains relatively constant even as crystallization occurs, such as mineralization in flowing geological systems like oceans or streams, or for industrial crystallization processes in large reaction vessels where thousands or millions of primary nucleation events occur.
We will find that in general, it is rare for nuclei of a higher-barrier phase to form during steady-state nucleation, and in a closed system with a fixed amount of solute, crystallization typically proceeds by nucleation and growth of the bulk metastable phase (Fig. 1, solid line). However, even if the metastable phase proceeds to complete crystal growth, i.e. consuming solute until the solution is no longer supersaturated with respect to KMetastablesp, the solution will still remain supersaturated with respect to KStablesp. The time to the formation of the stable phase will thus be the induction time of the stable phase at this supersaturation. However, the induction time of the stable polymorph can be drastically reduced in the presence of a metastable phase. This is because the pre-existing bulk metastable phase can serve a substrate for heterogeneous nucleation, thereby reducing the nucleation barrier of the stable phase compared to pseudo-homogeneous nucleation (Fig. 1b). In this sense, the presence of the metastable polymorph ‘catalyzes’ the formation of the stable phase.
A polymorphic transformation to the stable phase proceeds only if the system can reduce its free-energy by doing so. By the Gibbs–Thomson equation, large crystallites have a lower chemical potential than small crystallites. This might suggest that new nanoscale nuclei of the stable phase may ripen away immediately onto bulk crystallites of a metastable phase before they have the chance to initiate crystal growth. However, we will demonstrate that this intuition does not apply in competing polymorphic systems. We will derive that the size-dependent solubility of a critical nucleus of the stable phase is equal to the bulk solubility of the metastable phase. This means that so long as the stable phase nucleates, the bulk metastable phase will spontaneously ripen onto nascent nuclei of the stable phase, and a JMAK-style polymorphic transformation will proceed.
In this work, we limit our analysis to polymorphic transformations that proceed through a melt or solvent phase by dissolution–reprecipitation, rather than directly in the solid-state by diffusionless ‘martensitic’ atomic reshuffling. There is increasing evidence that dissolution–reprecipitation is the relevant transformation mechanism between polymorphs that are not topotactically-related.17,18 Our analysis is conducted within the framework of classical nucleation and crystal growth theories, which suggests that recently proposed ‘non-classical’ models of crystal nucleation and growth19–21 may not be necessary to rationalize Ostwald Rules of Stages. We will also discuss how prenucleation clusters, dense liquid phases, and amorphous precursors can be reconciled within a classical nucleation and crystal growth framework.
In this work we reference two-polymorph systems, where one polymorph is metastable and the other is stable, but our analysis applies generally to systems with multiple polymorphic phases. In these cases, the ‘stable phase’ in our analysis simply refers to the next more-stable phase.
Competitive nucleation in polymorphic systems
We begin our analysis with a discussion of steady-state nucleation rates in competitive polymorphic systems. If a solution is supersaturated with respect to multiple polymorphs, then there is a thermodynamic driving force for all of these polymorphs to form. The classical nucleation barrier to their formation, ΔG*, is given by: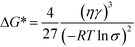 | (1) |
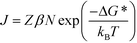 | (2) |
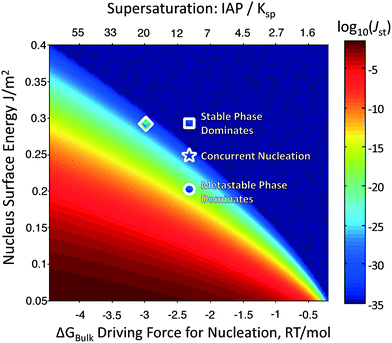
Fig. 2 plots the steady-state nucleation rate (colored) of a polymorph as a function of its surface energy and the driving force for nucleation, for phases of density 10 cm3 mol−1 – typical of most inorganic sparingly-soluble salts. Because the nucleation barrier depends on the cube of the surface energy, but is only reduced by (ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σ)2, a metastable phase can still nucleate faster than the stable phase, so long as its surface energy is sufficiently lower than the stable phase. Calorimetry experiments have revealed that the surface energies of metastable oxides are often lower than their stable counterparts, driving nanoscale crossovers in phase stability.25 This might be rationalized by metastable phases possessing a lower cohesive energy, and thus cleavage energy, than the stable phases. It might also be because there is only one stable phase, while there are hypothetically many potential metastable phases,26,27 and it is probable that at least one of these metastable phases has a lower surface energy than the stable phase. Regardless of the physical mechanism, the lower surface energy of metastable phases explains the initial precipitation of metastable polymorphs during crystallization. Manipulating solution chemistry can also promote the formation of a metastable phase, as solvent or solution additives may selectively influence the surface energies of competing polymorphs,28–32 which could manifest in orders of magnitude changes in their relative nucleation rates.
σ)2, a metastable phase can still nucleate faster than the stable phase, so long as its surface energy is sufficiently lower than the stable phase. Calorimetry experiments have revealed that the surface energies of metastable oxides are often lower than their stable counterparts, driving nanoscale crossovers in phase stability.25 This might be rationalized by metastable phases possessing a lower cohesive energy, and thus cleavage energy, than the stable phases. It might also be because there is only one stable phase, while there are hypothetically many potential metastable phases,26,27 and it is probable that at least one of these metastable phases has a lower surface energy than the stable phase. Regardless of the physical mechanism, the lower surface energy of metastable phases explains the initial precipitation of metastable polymorphs during crystallization. Manipulating solution chemistry can also promote the formation of a metastable phase, as solvent or solution additives may selectively influence the surface energies of competing polymorphs,28–32 which could manifest in orders of magnitude changes in their relative nucleation rates.
Competitive induction in polymorphic systems
During steady-state nucleation, when nuclei are constantly forming, there is a non-zero probability that a nucleus of the higher nucleation barrier phase forms instead of the lower nucleation barrier phase. This scenario is particularly relevant in systems with constant or replenished supersaturation, such as mineralization in rivers and oceans, or in continuous crystallization processes, such as during industrial crystallization.The macroscopic steady-state nucleation rate provides the average number of nuclei formed per time per volume. However, the local, microscopic formation of each nucleus can be treated as a stochastic event, and the time to formation, known as the induction time (also referred to as the incubation time), can be modeled by a Poisson process,33,34 where the probability of forming m nuclei (in a single-polymorph system) by a given time is dependent on its steady-state nucleation rate, J, and solution volume, V, by
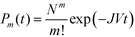 | (3) |
The induction probability for the formation of the first, local nucleus as a function of time is given by
| P0(t) = 1 − exp(−JVt) | (4) |
Eqn (4) is often used to model the time until the formation of the first nucleus from a metastable supersaturated solution.35,36 However, the exponential form of eqn (4) means that this induction probability is memoryless – allowing any arbitrary time to be set as t = 0. In other words, in addition to describing the time until the first nucleation event from a supersaturated solution, eqn (4) can also be applied to a system undergoing steady-state nucleation, in which it describes the time until the next local nucleation event. Although each individual nucleation event occurs stochastically, the rate constant for this Poisson process is the steady-state nucleation rate, JV, meaning that the induction equation is a microscopic probabilistic model of the macroscopic steady-state nucleation rate. We can thus model competitive polymorphism during steady-state nucleation from the perspective of competing induction processes.
We now analyze competitive induction between polymorphs with different nucleation barriers, and therefore different J. Because both polymorphs are forming in the same vessel, we consider our analysis for the volume-normalized nucleation rate of a polymorph, ![[J with combining macron]](https://www.rsc.org/images/entities/i_char_004a_0304.gif) = JV. We review in Fig. 3a the induction probability for two non-competing polymorphs; i.e. the hypothetical situation where the two polymorphs are independent and are not competing for the same solute. The higher nucleation barrier stable phase has a much longer characteristic induction time than the metastable phase. However, at short times (consider t = 2 on Fig. 3a), there is a probability that the metastable phase has not formed, but there is also a probability that the stable phase has formed. If the two polymorphs are competing in the same local region of space, the polymorph that nucleates first will be the polymorph that crystallizes. In stochastic systems with competing exponential Poisson processes, this scenario is known as an ‘exponential race’.37 In a two polymorph system, α and β, the overall probability that polymorph α has a shorter induction time than polymorph β can be calculated as
= JV. We review in Fig. 3a the induction probability for two non-competing polymorphs; i.e. the hypothetical situation where the two polymorphs are independent and are not competing for the same solute. The higher nucleation barrier stable phase has a much longer characteristic induction time than the metastable phase. However, at short times (consider t = 2 on Fig. 3a), there is a probability that the metastable phase has not formed, but there is also a probability that the stable phase has formed. If the two polymorphs are competing in the same local region of space, the polymorph that nucleates first will be the polymorph that crystallizes. In stochastic systems with competing exponential Poisson processes, this scenario is known as an ‘exponential race’.37 In a two polymorph system, α and β, the overall probability that polymorph α has a shorter induction time than polymorph β can be calculated as
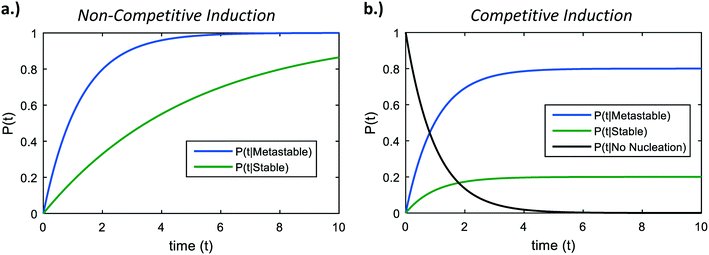 | ||
| Fig. 3 a) Induction times of two non-competing polymorphs – a metastable phase with nucleation barrier 76 kBT, and a stable phase with nucleation barrier 77.5 kBT. b) Induction probabilities in a system with competitive induction. The asymptotic probabilities as time proceeds to infinity are given in eqn (5). | ||
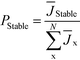
This result can easily be extended to the general case with N competing polymorphs, where both the instantaneous and the ultimate probability of forming polymorph i is the probability that polymorph i has a shorter induction time than all other N competing polymorphs, which is given by
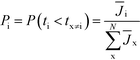 | (5) |
Note that these expressions would yield the same results with ![[J with combining macron]](https://www.rsc.org/images/entities/i_char_004a_0304.gif) = JV, meaning the relative induction probabilities between polymorphs are independent of the volume of the crystallization vessel. Also note that this expression makes no assumptions as to whether the different nucleation rates of competing polymorphs originate from their thermodynamic barriers, ΔG* (eqn (1)), or their kinetic barriers, βN (from eqn (2)).
= JV, meaning the relative induction probabilities between polymorphs are independent of the volume of the crystallization vessel. Also note that this expression makes no assumptions as to whether the different nucleation rates of competing polymorphs originate from their thermodynamic barriers, ΔG* (eqn (1)), or their kinetic barriers, βN (from eqn (2)).
As a function of time, the relative probability that polymorph i forms, is given by
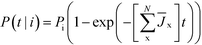 | (6) |
On the other hand, the probability that no polymorph has nucleated by time t is
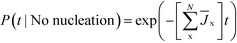 | (7) |
Fig. 3b shows representative curves for eqn (6) and (7) in a hypothetical two-polymorph system, where we assign the stable phase a nucleation barrier only 2% higher than the metastable phase. For competing induction processes, there is only a short window of time for the possible nucleation of the stable phase, which is before the induction probability for forming the metastable phase approaches 1 in the non-competing case (Fig. 3a). Even though the induction period of the stable phase would have been very long if it were not in competition with the metastable phase (Fig. 3a, green line), in a competitive polymorphic system, the characteristic induction time for all polymorphs is the same, and is approximately the characteristic induction time of the lowest-barrier phase. If there is a crossover in induction times, where the stable phase nucleates before the metastable phase, this would bring about a change from an ‘indirect’, two-stage crystallization through a metastable phase (Fig. 1, solid line) to a ‘direct’ crystallization pathway to the stable phase (Fig. 1, dashed line), as was often observed during in situ liquid-cell TEM observations of multistage crystallization.38
One surprising result from this analysis is that even between reaction vessels with identical preparation – reactants, supersaturation, thermodynamic conditions, etc. – there is a non-zero probability that different polymorphs can form. This can address the deep frustration involved with the fickleness of crystallization – occasionally experiments that have been reliably prepared and completed numerous times can still yield different polymorphs! This is especially frustrating as a central tenet of the scientific method is reproducibility – if two crystallization experiments are prepared in the exact same manner, we should expect the same resulting polymorph. Our analysis demonstrates that because of the stochastic nature of exponential races, not only is it expected that identical crystallization experiments occasionally attain different polymorphs, but one can even quantify the probability that such an occurrence should happen.
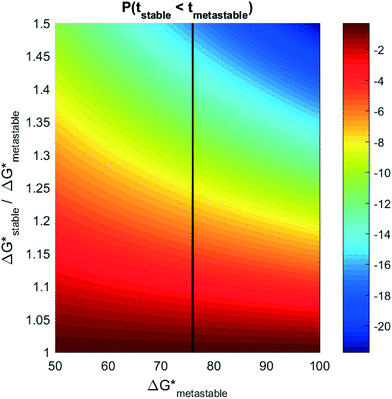
Experiments measuring induction time often involve high-throughput microcrystallization arrays, where the induction probability, P0 (eqn (2)) is obtained explicitly by measuring how many plates crystallize as a function of time.34,35,39 In principle, if multiple polymorphs form in such experiments, eqn (5) could be used to extract the relative nucleation rates (and thereby, relative nucleation barriers) between competing polymorphs. Unfortunately, a very small difference in nucleation barrier between polymorphs can yield exceedingly small probabilities of forming the higher barrier phase. Fig. 4 plots the log10 probability for competitive induction of the stable phase, as a function of the metastable phase nucleation barrier, and the relative ratio of the nucleation barriers between the stable phase and the metastable phase. If the onset of nucleation occurs for a metastable phase with a nucleation barrier of 76 kBT, then even a 20% higher nucleation barrier can result in the probability for a stable nucleus forming to be 1 out of 107 nuclei. To measure relative nucleation rates in practice, the crystallization arrays would have to be correspondingly large (spanning millions or billions of plates) to achieve statistically confident measurements of relative nucleation rates and barriers.
While billion-plate crystallization arrays are probably infeasible, such an induction probability between competing polymorphs would be present each time a nucleation event occurs. For a nucleation rate of 1 nucleus per cm3 per second, and assuming that all nucleation events are independent, large reaction vessels >1 liter in size may have the opportunity for thousands or millions of primary nucleation events. In industrial crystallization processes involving continuous precipitation reactions inside of large vessels, even a 1-in-a-billion chance for the formation of a stable phase may eventually transpire. This may result in a “Disappearing Polymorph” – where the sudden appearance of a stable phase forever prevents the synthesis of a previously-attainable metastable phase.15 An infamous example of a disappearing polymorph was the transformation of the AIDS drug ritonavir from a metastable crystalline form to a stable, bio-inert form two years after production.16 This resulted in the withdrawal of the drug from the market, and resulted in tens of thousands of AIDS patients without crucial medication. Most aggravatingly, seeding by residual nanoparticles of the stable phase made it impossible to recover the functional metastable phase from the same reaction vessel (or even facility). Our analysis here provides an explanation for why the stable phases of “Disappearing Polymorphs” may not appear until many months or years following the production of a metastable crystalline phase.
If the relative induction probability of a higher-barrier phase is too small to be accessed experimentally, we have previously shown that relative nucleation rates between polymorphs can also be evaluated computationally, using density functional theory calculations of nanoparticle surface and bulk energies in equilibrium with a solvent.28,40,41 This enables the calculation of relative Ji between polymorphs (eqn (2)), and thereby Pi in eqn (5). With these relative nucleation rates, the induction probability of the stable phase can be formulated as:
| P(Stable|n) = 1 − exp(−PStablen) |
and n is the total number of nucleation events that occur. This equation can be directly related to an induction time by n(t) – the number of primary nucleation events as a function of time. In the case that only a single polymorph has been observed, the existence of polymorphs with lower free energy can be probed using computational crystal structure prediction methods,42,43 enabling risk-analyses for predicting ‘Disappearing Polymorphs’. As first-principles methods to rank relative polymorph lattice free-energies continue to improve in accuracy,44–46 so will confidence in these predictions.
Formation of stable phase nucleus after bulk crystal growth of a metastable phase
Because it is rare that a stable phase will form during steady-state nucleation, we next discuss the formation of a stable phase after the nucleation and growth of a metastable polymorph. This scenario is primarily relevant in closed chemical systems, where there is a fixed amount of solute in either the solution-state or in the solid-state.In the limit that a metastable polymorph has grown to bulk sizes, and is in equilibrium with a solution, then the activity of the solute in solution (represented by IAP – the ionic activity product) will be the same as the solubility product of the metastable polymorph:
| IAP = KMetastablesp | (8) |
In this case, the solution is still supersaturated with respect to the equilibrium phase, and the driving force for the crystallization of the stable phase can be written as
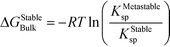 | (9) |
In this case, the induction time to the formation of the stable phase is simply
| PStable(t) = 1 − exp(−JHetAt) | (10) |
However, the intermediate metastable phase can serve as a substrate for heterogeneous nucleation. The heterogeneous nucleation barrier can be an order of magnitude lower than a homogeneous nucleation barrier, and indeed it has been observed that the equilibrium phase often nucleates directly on an existing metastable phase, rather than pseudo-homogeneously in the solvent.37 It may even be considered that the metastable phase “catalyzes” the formation of the stable phase. If growth of the metastable phase is slow compared to the heterogeneous induction time of the stable phase, heterogeneous nucleation of the stable phase can initiate even when the metastable phase has not grown to completion. This would yield coexisting polymorphs, although eventually the stable phase should consume the metastable compound.
It is valuable to assign an order of magnitude ‘characteristic time’ for the induction of the stable phase. For equations of the exponential form in eqn (10), the characteristic time is often chosen as the ‘expectation’ time (the mean-average time), τ, where τ is
| P0(t) = 1 − exp(−t/τ) | (11) |
In this case, we see that
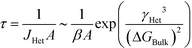 | (12) |
Eqn (12) suggests that viable handles to engineer the induction time of a stable phase are A, the area of the substrate for heterogeneous nucleation; β, the rate of monomer attachment to growing nuclei; γHet, the effective surface energy for heterogeneous nucleation; and ΔGBulk, the thermodynamic driving force for crystallization.
Many of these handles have already been identified to influence polymorphic transformation times; here we explicitly discuss them within the context of manipulating the induction time of a stable phase. Because the heterogeneous nucleation rate scales with substrate area, induction times will be shorter on substrates with large specific areas, such as on textured surfaces or fractal mesostructures of a metastable phase. On smooth substrates, substrate area scales approximately with V2/3, and metastable phases have indeed been shown to resist transformation to the stable phase when under nanoconfinement to small volumes.47–49 High viscosity solutions can slow solute transport and monomer attachment, particularly in protein solutions, which can increase induction times.50 The solid–solid interfacial energy term of the heterogeneous nucleation barrier can be increased by reducing the surface energy of the substrate phase by nanostructuring or with surfactants,51 whereas epitaxial matching or chemical compatibility of the solid–solid interface can lower the interfacial energy, accelerating heterogeneous nucleation.52,53 Although ΔGBulk is fixed by the intrinsic solubilities of the competing polymorphs, increasing the ionic strength of a solution may slow the dissolution rate of a metastable phase,54 possibly by reducing its solubility via the common-ion effect.
Many of these heuristics are still qualitative in nature; to apply these principles in a quantitative and predictive manner requires better characterization of the structural, compositional, and thermochemical properties of the bulk and the interfaces of these transient metastable phases. Nevertheless, while much of the necessary data are not available today, eqn (12) can still offer principles on the design of crystallization conditions to accelerate the induction of stable phases with desirable properties during materials synthesis, or inhibit the induction of more stable phases in order to retain a functional metastable compound.
Ripening of a bulk metastable phase onto a nucleus of the stable phase
So far, our discussion has focused on the induction of the stable phase. To conclude, we demonstrate that so long as this induction occurs, dissolution–reprecipitation of a bulk metastable phase onto nuclei of the stable phase proceeds spontaneously and monotonically downhill in free-energy.As crystal growth proceeds, the total number of crystallites in a system decreases by Ostwald Ripening, where “les grands mangent les petits” – the large particles consume the small particles.55 The thermodynamic driving force for this process originates from the system reducing its free energy by eliminating surface area, which has positive energy. By the Gibbs–Thomson equation, small particles possess higher surface curvature, and therefore greater chemical potential, than the large particles, and the system evolves to lower chemical potential when small particles dissolve and the dissolved solute reprecipitates onto the larger particles.
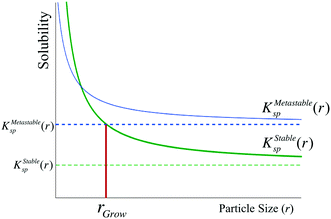
In a single-polymorph system, after crystal growth has proceeded into the bulk regime, the chemical potential of new nuclei is too high to persist, such that they dissolve and ripen onto the larger particles faster than they can grow. However, this intuition may not necessarily apply to a multi-polymorph system, as the size-dependent chemical potential of the stable phase may be lower than the bulk chemical potential of the metastable phase. Thus, the condition for the transformation of a bulk metastable phase to the stable polymorph is that the size-dependent solubility of the stable phase must be lower than the bulk solubility of the metastable phase (Fig. 5). We term this critical size of the stable phase as rgrow, and we formulate this condition as
| KStablesp(rgrow) ≤ KMetastablesp(r = ∞) | (13) |
We now demonstrate that the critical nucleation radius of the stable phase is exactly equal to rgrow, meaning that so long as the stable phase nucleates, the system will spontaneously undergo the polymorphic transformation. We first determine rgrow, the radius of a particle of the stable phase such that its solubility is lower than that of the bulk metastable phase. For the spherical case, the size-dependent solubility is given by the Ostwald–Freundlich equation
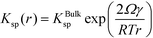 | (14) |
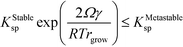 | (15) |
Rearranging and substituting ΔGStableBulk from eqn (9),
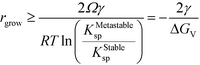 | (16) |
This simple derivation shows that rgrow is equal to R*Stable, meaning that the induction or presence of any nuclei of the stable phase will be at least at a size where the system can spontaneously ripen from the bulk metastable phase onto the nanoscale nuclei or seeds of the stable phase. This transformation will then proceed to completion as predicted in a JMAK-model of phase transformation.56 Our analysis suggests that engineering the induction time of the stable phase is the crucial step for inhibiting or accelerating polymorphic transformations from a metastable phase.
Reconciling multistage crystallization with classical nucleation theory
We have thus provided a theoretical framework to explain and evaluate the lifetime of transient metastable phases in Ostwald's Rule of Stages. Our analysis is performed using traditional concepts from classical nucleation theory, suggesting that observations of two-step and multi-step crystallization processes can be reconciled with conventional nucleation theory. In a solution supersaturated with respect to numerous polymorphs, all competing polymorphs will form via steady-state nucleation, but at a rate proportional to the negative exponential of their nucleation barrier. However, tiny differences between nucleation barriers of competing polymorphs can manifest in many orders of magnitude differences in nucleation rates, so crystallization will be dominated by the phase with the lowest-nucleation barrier. If this is a metastable phase, then as it grows and consumes solute, the solution will equilibrate with this metastable phase and its driving force for crystallization will become zero, but the solution will still be supersaturated with respect to the next more-stable phases. Crystallization then proceeds to the next polymorphic stages in iterative dissolution–reprecipitation processes – although the latter phases have the kinetic advantage of heterogeneous nucleation on pre-existing metastable phases. The crystal growth and transformation times of these intermediate metastable phases can be characterized by traditional JMAK models of crystal growth, but with the addition of an induction time for the next more stable phase. Because induction is inherently probabilistic, crossovers in induction times between competing polymorphs can occasionally result in direct or indirect crystallization pathways to the stable phase,37 even between repeat experiments under the same preparations and thermodynamic conditions. Most importantly, the surface energy in the nucleation barrier is a function of solution chemistry, so minor alterations to the solution chemistry can drive drastic changes in the nucleation rate of a polymorph. This can explain why polymorphism can be so sensitive to solvent selection, minor additives in solution, pH, ionic strength, and other solution parameters that are seemingly irrelevant in a thermodynamic picture.Finally, we suggest that recent observations of dense liquid phases,57,58 prenucleation clusters,59 and amorphous precursors,60 which have been described as ‘non-classical nucleation’,19,20,61 can still be reconciled within the framework of classical nucleation theory. The solute in a non-crystalline phase still possesses a bulk chemical potential, proportional to its cohesive energy, corresponding to an ‘infinite’ macroscopic quantity of this phase, even if the non-crystalline phase never grows to such sizes. The cohesive energy of a prenucleation precursor will be significantly weaker than for a crystalline polymorph, and thus will have a correspondingly weaker cleavage energy, i.e. a much lower surface energy. From our description of competitive nucleation, these phases would form rapidly and immediately, with potentially negligible barriers (resulting in spinodal decomposition).62 Therefore, these prenucleation phases can be treated as simply the initial polymorphic stages of Ostwald's Rule of Stages, which as we have shown, can be approached classically. Solvated prenucleation clusters, or solvent inclusions in amorphous solids, should simply be treated as intermediate compositions in a classical phase-separating system between a pure chemical solid and its solvent.
Our approach may also resolve the observation that classical nucleation theory ‘overpredicts’ the steady-state nucleation rate.63–65 The free-energy of prenucleation phases will be lower than that of a supersaturated solution, but still higher than the crystalline phases. In the presence of a prenucleation phase, the bulk driving force for crystallization (ΔGBulk) should not be calculated with respect to the IAP of the solution, but rather with respect to an appropriate Ksp of the prenucleation phases, as in eqn (9). This lower driving force for formation would yield a correspondingly higher nucleation barrier, and thereby a (significantly) lower nucleation rate.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by the Center for Next-Generation of Materials by Design, an Energy Frontier Research Center funded by U.S. Department of Energy, Office of Basic Energy Sciences under Contract No. DE-AC36-08GO28308. WS thanks Paul Park (Northwestern University) for valuable discussions. WS thanks Shirley Chan for thought-provoking insights. Much of the insight in this manuscript was attained from the excellent Faraday Discussion: “Nucleation, A Transition State to the Directed Assembly of Materials” in Leeds, UK, 2015.Notes and references
- W. Ostwald, Z. Phys. Chem., 1897, 22, 289–300 CAS.
- J. J. De Yoreo, P. U. Gilbert, N. A. Sommerdijk, R. L. Penn, S. Whitelam, D. Joester, H. Zhang, J. D. Rimer, A. Navrotsky, J. F. Banfield and A. F. Wallace, Science, 2015, 349(6247), aaa6760 CrossRef PubMed.
- P. Bots, L. G. Benning, J. D. Rodriguez-Blanco, T. Roncal-Herrero and S. Shaw, Cryst. Growth Des., 2012, 12(7), 3806–3814 CAS.
- A. E. S. Van Driessche, L. G. Benning, J. D. Rodriguez-Blanco, M. Ossorio, P. Bots and J. M. García-Ruiz, Science, 2012, 336(6077), 69–72 CrossRef CAS PubMed.
- A. Putnis, Rev. Mineral. Geochem., 2009, 70(1), 87–124 CrossRef CAS.
- A. L. Washington, M. E. Foley, S. Cheong, L. Quffa, C. J. Breshike, J. Watt, R. D. Tilley and G. F. Strouse, J. Am. Chem. Soc., 2012, 134(41), 17046–17052 CrossRef CAS PubMed.
- S. Y. Chung, Y. M. Kim, J. G. Kim and Y. J. Kim, Nat. Phys., 2009, 5(1), 68–73 CrossRef CAS.
- E. B. Sirota and A. B. Herhold, Science, 1999, 283(5401), 529–532 CrossRef CAS PubMed.
- D. Erdemir, A. Y. Lee and A. S. Myerson, Acc. Chem. Res., 2009, 42(5), 621–629 CrossRef CAS PubMed.
- P. G. Vekilov, Nanoscale, 2010, 2(11), 2346–2357 RSC.
- D. Kurouski, W. Lauro and I. K. Lednev, Chem. Commun., 2010, 46(24), 4249–4251 RSC.
- A. Navrotsky, Proc. Natl. Acad. Sci. U. S. A., 2004, 101(33), 12096–12101 CrossRef CAS PubMed.
- I. N. Stranski and D. Totomanow, Z. Phys. Chem, 1933, 163, 399–408 Search PubMed.
- M. Avrami, J. Chem. Phys, 1939, 7(12), 1103–1112 CrossRef CAS.
- D. K. Bučar, R. W. Lancaster and J. Bernstein, Angew. Chem., Int. Ed., 2015, 54(24), 6972–6993 CrossRef PubMed.
- J. Bauer, S. Spanton, R. Henry, J. Quick, W. Dziki, W. Porter and J. Morris, Pharm. Res., 2001, 18(6), 859–866 CrossRef CAS.
- A. J. Giuffre, A. C. Gagnon, J. J. De Yoreo and P. M. Dove, Geochim. Cosmochim. Acta, 2015, 165, 407–417 CrossRef CAS.
- Y. Peng, F. Wang, Z. Wang, A. M. Alsayed, Z. Zhang, A. G. Yodh and Y. Han, Nat. Mater., 2015, 14(1), 101–108 CrossRef CAS PubMed.
- R. P. Sear, Int. Mater. Rev., 2012, 57(6), 328–356 CrossRef CAS.
- D. Gebauer and H. Cölfen, Nano Today, 2011, 6(6), 564–584 CrossRef CAS.
- D. Zahn, ChemPhysChem, 2015, 16(10), 2069–2075 CrossRef CAS PubMed.
- R. W. Balluffi, S. Allen and W. C. Carter, Kinetics of materials, John Wiley & Sons, 2005 Search PubMed.
- A. J. Cruz-Cabeza and J. Bernstein, Chem. Rev., 2013, 114(4), 2170–2191 CrossRef PubMed.
- D. Chakraborty, N. Sengupta and D. J. Wales, J. Phys. Chem. B, 2016, 120(19), 4331–4340 CrossRef CAS PubMed.
- A. Navrotsky, ChemPhysChem, 2011, 12(12), 2207–2215 CrossRef CAS PubMed.
- W. Sun, S. Dacek, S. P. Ong, G. Hautier, A. Jain, W. D. Richards, A. C. Gamst, K. A. Persson and G. Ceder, Sci. Adv., 2016, 2, 11 Search PubMed.
- S. L. Price, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2013, 69(4), 313–328 CrossRef CAS PubMed.
- W. Sun, S. Jayaraman, W. Chen, K. A. Persson and G. Ceder, Proc. Natl. Acad. Sci. U. S. A., 2015, 112(11), 3199–3204 CrossRef CAS PubMed.
- G. G. Poon, S. Seritan and B. Peters, Faraday Discuss., 2015, 179, 329–341 RSC.
- C. C. Sun, W. Sun, S. Price, C. Hughes, J. Ter Horst, S. Veesler, K. Lewtas, A. Myerson, H. Pan, G. Coquerel and J. van den Ende, Faraday Discuss., 2015, 179, 383–420 RSC.
- K. R. Devi and K. Srinivasan, CrystEngComm, 2014, 16(4), 707–722 RSC.
- M. Salvalaglio, M. Mazzotti and M. Parrinello, Faraday Discuss., 2015, 179, 291–307 RSC.
- S. Toschev, A. Milchev and S. Stoyanov, J. Cryst. Growth, 1972, 13, 123–127 CrossRef.
- D. Kashchiev, D. Verdoes and G. M. Van Rosmalen, J. Cryst. Growth, 1991, 110(3), 373–380 CrossRef.
- C. Brandel and J. H. ter Horst, Faraday Discuss., 2015, 179, 199–214 RSC.
- Z. Hammadi, R. Grossier, S. Zhang, A. Ikni, N. Candoni, R. Morin and S. Veesler, Faraday Discuss., 2015, 179, 489–501 RSC.
- D. P. Bertsekas and J. N. Tsitsiklis, Introduction to Probability, Athena Scientific, Belmont, MA, 2002, vol. 1 Search PubMed.
- M. H. Nielsen, S. Aloni and J. J. De Yoreo, Science, 2014, 1158–1162 CrossRef CAS PubMed.
- A. J. Alvarez, A. Singh and A. S. Myerson, Cryst. Growth Des., 2009, 9(9), 4181–4188 CAS.
- W. Sun and G. Ceder, Surf. Sci., 2013, 617, 53–59 CrossRef CAS.
- K. A. Persson, B. Waldwick, P. Lazic and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85(23), 235438 CrossRef.
- S. L. Price, Chem. Soc. Rev., 2014, 43(7), 2098–2111 RSC.
- R. K. Hylton, G. J. Tizzard, T. L. Threlfall, A. L. Ellis, S. J. Coles, C. C. Seaton, E. Schulze, H. Lorenz, A. Seidel-Morgenstern, M. Stein and S. L. Price, J. Am. Chem. Soc., 2015, 137(34), 11095–11104 CrossRef CAS PubMed.
- D. A. Kitchaev, H. Peng, Y. Liu, J. Sun, J. P. Perdew and G. Ceder, Phys. Rev. B., 2016, 93(4), 045132 CrossRef.
- J. Yang, W. Hu, D. Usvyat, D. Matthews, M. Schütz and G. K. L. Chan, Science, 2014, 345(6197), 640–643 CrossRef CAS PubMed.
- G. J. Beran, Chem. Rev., 2016, 116(9), 5567–5613 CrossRef CAS PubMed.
- A. S. Schenk, E. J. Albarracin, Y. Y. Kim, J. Ihli and F. C. Meldrum, Chem. Commun., 2014, 50(36), 4729–4732 RSC.
- Y. W. Wang, H. K. Christenson and F. C. Meldrum, Chem. Mater., 2014, 26(20), 5830–5838 CrossRef CAS.
- M. Beiner, G. T. Rengarajan, S. Pankaj, D. Enke and M. Steinhart, Nano Lett., 2007, 7(5), 1381–1385 CrossRef CAS PubMed.
- O. Galkin, R. L. Nagel and P. G. Vekilov, J. Mol. Biol., 2007, 365(2), 425–439 CrossRef CAS PubMed.
- S. Bengaluru Subramanyam, V. Kondrashov, J. Rühe and K. K. Varanasi, ACS Appl. Mater. Interfaces, 2016, 8(20), 12583–12587 CAS.
- A. J. Giuffre, L. M. Hamm, N. Han, J. J. De Yoreo and P. M. Dove, Proc. Natl. Acad. Sci. U. S. A., 2013, 110(23), 9261–9266 CrossRef CAS PubMed.
- H. Ding, S. S. Dwaraknath, L. Garten, P. F. Ndione, D. S. Ginley and K. A. Persson, ACS Appl. Mater. Interfaces, 2016, 8(20), 13086–13093 CAS.
- M. Kowacz and A. Putnis, Geochim. Cosmochim. Acta, 2008, 72(18), 4476–4487 CrossRef CAS.
- P. W. Voorhees, J. Stat. Phys., 1985, 38(1–2), 231–252 CrossRef.
- D. Kashchiev and K. Sato, J. Chem. Phys., 1998, 109(19), 8530–8540 CrossRef CAS.
- J. F. Lutsko and G. Nicolis, Phys. Rev. Lett., 2006, 96(4), 046102 CrossRef PubMed.
- P. G. Vekilov, Cryst. Growth Des., 2004, 4(4), 671–685 CAS.
- D. Gebauer, A. Völkel and H. Cölfen, Science, 2008, 322(5909), 1819–1822 CrossRef CAS PubMed.
- W. J. Habraken, J. Tao, L. J. Brylka, H. Friedrich, L. Bertinetti, A. S. Schenk, A. Verch, V. Dmitrovic, P. H. Bomans, P. M. Frederik and J. Laven, Nat. Commun., 2013, 4, 1507 CrossRef PubMed.
- J. Lee, J. Yang, S. G. Kwon and T. Hyeon, Nat. Rev. Mater., 2016, 16034 CrossRef CAS.
- A. F. Wallace, L. O. Hedges, A. Fernandez-Martinez, P. Raiteri, J. D. Gale, G. A. Waychunas, S. Whitelam, J. F. Banfield and J. J. De Yoreo, Science, 2013, 341(6148), 885–889 CrossRef CAS PubMed.
- S. Auer and D. Frenkel, Nature, 2001, 409(6823), 1020–1023 CrossRef CAS PubMed.
- O. Galkin and P. G. Vekilov, J. Am. Chem. Soc., 2000, 122(1), 156–163 CrossRef CAS.
- N. E. Zimmermann, B. Vorselaars, D. Quigley and B. Peters, J. Am. Chem. Soc., 2015, 137(41), 13352–13361 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2017 |