Molecular and crystalline architectures based on HgI₂: from metallamacrocycles to coordination polymers

Abstract

Three metallamacrocycles and one coordination polymer were obtained by using coordination driven self-assembly of the HgI₂ salt with four different ligands: 2,2′-butan-1,4-diylbis(oxy)dianiline (L1), 1,4-bis(2′-formylphenyl)-1,4-dioxabutane bis(isonicotinoylhydrazone) (L2), (E)-N′-(pyridin-3-ylmethylene)isonicotinohydrazide (L3) and (E)-1-(pyridin-3-yl)-N-(pyridin-3-ylmethyl)methanimine (L4). The coordination compounds were studied by elemental analysis, FT-IR spectroscopy and single-crystal X-ray diffraction analyses. Reaction of the HgI₂ salt with L1, L2 and L3 yields metallamacrocycles of formula [(HgI₂)₂(μ-L1)₂] (1), [(HgI₂)₂(μ-L2)₂] (2), [HgI₂(μ-L3)]₄ (3). In contrast, the reaction with L4 under the same conditions yields a coordination polymer of formula [{HgI₂(L4)}]_n (4). In addition, the X-ray structure of L2 is also reported. The influence of the flexibility of the ligand on the final shape and nuclearity of the macrocycle is also analysed. Hirshfeld surface analysis and fingerprint plots facilitate a comparison of intermolecular interactions in all compounds, which are crucial in the construction of the supramolecular architectures. Finally, some noncovalent interactions have been evaluated energetically using DFT calculations and characterized using Bader's theory of atoms-in-molecules.

---

1. Introduction

Interest in molecular crystal engineering has been driven not only due to attractiveness of crystal topologies, but also for possible applications of the compounds synthesised. Several factors, such as the organic ligand (shape, rigidity, number and disposition of the coordinating sites) as well as the stereochemical requirements of the metal centre (oxidation state, geometry, number and disposition of free coordination sites).¹ To this respect, research in supramolecular chemistry has emerged as a promising new area of coordination chemistry.² It is devoted to the construction of well-defined, discrete two- (2D) and three-dimensional (3D) molecular architectures prepared by the coordination-driven self-assembly of metal centers with ligands containing multiple binding sites.³ At the same time, some useful methodologies for the rational design and synthesis of these systems have also been developed and a number of reviews provide a global perspective of discrete self-assemblies with various topologies including their application in different fields.^4,5 The most ubiquitous ionization state of mercury, Hg²⁺, is a d¹⁰ metal ion, which lacks strong coordination number and geometry preferences. This causes a flexible coordination environment around the mercury ion that can vary from linear to octahedral. In connection with this, structural characterization of its complexes by X-ray crystallography is crucial. The structure and functionality of Hg(II) halide complexes strongly rely on the selection of bridging organic spacers besides reaction conditions, including temperature, time, pH, etc., which severely hinder the rational design and prediction of the coordination driven assemblies.⁶ One possibility is the use of conformationally rigid organic ligands and metal centers with well-defined coordination spheres. Another approach requires the use of flexible ligands that can lead to distinct entities during the self-assembly process due to the different conformations adopted by the ligand. The incorporation of flexible components may endow molecular architectures having adaptive recognition properties to host solvent molecules or counterions.⁷

Herein, as part of our continuous interest in the investigation and design of Hg(II) complexes,⁸ we describe the formation of three neutral metallamacrocycles and one coordination polymer based on the use of dianiline or bis(pyridyl) ligands (see Scheme 1) with HgI₂. We have used ligands of different degrees of flexibility (see Scheme 1) in order to investigate their influence on the nuclearity and how the conformation of these ligands can define the primary structure of the self-assembled macromolecule. Remarkably, L1 presents an sp³-hybridized N donor atom with a high degree of flexibility and two of these ligands (L2 and L3) are unsymmetrical, which is a quite uncommon feature for the construction of discrete macrocycles.⁹ Compounds 1–4 (see Scheme 2) and ligand L2 have been characterized by spectroscopic methods, elemental and single crystal X-ray diffraction analyses. Additionally, we have analysed the noncovalent interactions of these compounds in solid state by using Hirshfeld surface analysis and density functional theory (DFT) calculations.

Scheme 1 Ligands used in this work.

Scheme 2 Macrocycles 1–3 and polymer 4 synthesized in this work.

2. Experimental

2.1. Materials and measurements

The Schiff base was prepared following the reported method as described elsewhere and used without further purification. All other reagents and solvents used for the synthesis and analysis were commercially available and used as received. FT-IR spectra were recorded on a Bruker Tensor 27 spectrometer. Microanalyses were performed using a Heraeus CHN–O-Rapid analyser.

The synthesis of ligands L1, L3 and L4 has been carried out following the methodology available in the literature.¹⁰

2.2.1. Synthesis of L2. The ligand 2,2′-[ethane-1,2-diylbis(oxy)]dibenzaldehyde was prepared by mixing a solution of salicylaldehyde and 1,2-dibromoethane in ethanol (96%) with isonicotinohydrazide (0.137 g, 1 mmol in 10 ml of ethanol) and heated under reflux for 4 h in the presence of a catalytic amount of acetic acid. Yield: 0.23 g (91%).

2.2.2. Synthesis of [(HgI₂)₂(μ-L1)₂] (1), [(HgI₂)₂(μ-L2)₂] (2), [HgI₂(μ-L3)]₄ (3) and [{HgI₂(L4)}]_n(4). L1 (0.03 g, 0.1 mmol) and mercury(II) iodide (0.1 g, 0.2 mmol) were placed in the main arm of a branched tube. Methanol was carefully added to fill the arms. The tube was sealed and immersed in an oil bath at 60 °C while the branched arm was kept at ambient temperature. After 6 days, crystals of 1 were isolated in the cooler arm and filtered off, washed with acetone and ether, and dried in air.

Crystals of 2–4 were isolated by mixing mercury(II) iodide with L2–L4, respectively, following the same method as for compound 1, for both the synthesis and crystallisation.

[(HgI₂)₂(μ-L1)₂] (1). Isolated yield was 85%. Anal. calcd. (found) for C₃₂H₄₀Hg₂I₄N₄O₄; C, 26.44 (26.50); H, 2.77 (2.61); N, 3.85 (3.74)%. IR (cm⁻¹) selected bands: [small nu, Greek, tilde] = CH b (oop): 743 (m) and 776 (s); CC st: 1457 (m); C–N st: 1500 and 1557 (m); CH st: 2926 (w), NH st: 3273 and 3356 (w) cm⁻¹.
[(HgI₂)₂(μ-L2)₂] (2). Isolated yield was 80%. Anal. calcd. (found) for C₃₀H₃₂HgI₂N₆O₆; C, 35.08 (35.14); H, 3.14 (3.26); N, 8.18 (8.24)%. IR (cm⁻¹) selected bands: [small nu, Greek, tilde] = CH b (oop): 683 (m) and 841 (m); C–O–C (sym): 1063; C–O–C (asym): 1295; CC st: 1481 (m); C=N st: 1548 and 1602 (m); C=O st (ligand) 1668; CH st: 3011 (w), NH st: 3263 (w) cm⁻¹.
[HgI₂(μ-L3)]₄ (3). Isolated yield was 75%. Anal. calcd. (found) for C₂₄H₂₀Hg₂I₄N₈O₂; C, 21.18 (21.30); H, 1.48 (1.36); N, 8.23 (8.34)%. IR (cm⁻¹) selected bands: [small nu, Greek, tilde] = CH b (oop): 616 (m) and 748 (m); CC st: 1476 (m); C=N st: 1550 and 1616 (m); C=O st (ligand) 1639; CH st: 2922 (w), NH st: 3236 (w) cm⁻¹.
[{HgI₂(L4)}]_n (4). Isolated yield was 65%. Anal. calcd. (found) for C₁₂H₁₁HgI₂N₃; C, 22.12 (22.20); H, 1.70 (1.81); N, 6.45 (6.34)%. IR (cm⁻¹) selected bands: [small nu, Greek, tilde] = CH b (oop): 637 (m) and 692 (m); CC st: 1470 (m); C=N st: 1618 and 1639 (m); CH st: 2865 (w) cm⁻¹.

2.2. X-ray crystallography

Single crystals of complexes 1–4 suitable for X-ray analyses were selected and crystallographic data were collected on an Oxford Diffraction Xcalibur Ruby Gemini, Bruker APEX-II CCD, CAD4 Enraf Nonius FR590, and Oxford Diffraction Xcalibur Sapphire3 diffractometer, respectively. On the other hand intensity data for the crystal of ligand L2 were collected on a Bruker SMART1000 CCD diffractometer. Data of 1 were collected with copper radiation, while for the other complexes, Mo-Kα radiation was employed at a temperature indicated in each case in Table 1. Data reductions were performed with CrysAlisPro, Bruker SAINT and XCAD4 programs.¹¹ Empirical absorption corrections were applied by means of programs ABSPACK,^11a SADABS and Refdef.¹² All the structures were solved by direct methods and refined by full matrix least-squares procedures using SHELXTL.¹³ All non-hydrogen atoms were refined with anisotropic displacement parameters and the contribution of hydrogen atoms placed in calculated positions is included in the final cycles of refinement. In the Fourier map of ligand L2 and of complex 2, two lattice methanol molecules were detected. Materials for publication were prepared using Cameron¹⁴ and Diamond 3.2k¹⁵ programs. Details of crystallographic data are given in Table 1.

Table 1 Crystallographic data and details of refinements for ligand L2 and complexes 1–4

	L2.2(CH3OH)	1	2.2(CH3OH)	3	4
a R 1 = ∑∥Fo| − |Fc∥/∑|Fo|, wR2 = [∑w (Fo^2 − Fc^2)^2/∑w(Fo^2)^2]^½. b Residuals close to the metals.
Empirical formula	C30H32N6O6	C32H40Hg2I4N4O4	C30H32HgI2N6O6	C24H20Hg2I4N8O2	C12H11HgI2N3
Formula weight	572.61	1453.46	2054.01	1361.26	651.63
Temperature (K)	193(2)	296(2)	193(2)	293(2)	173(2)
Wavelength (Å)	0.71073	1.54184	0.71073	0.71073	0.71069
Crystal system	Monoclinic	Monoclinic	Triclinic	Triclinic	Orthorhombic
Space group	P21	P21/c	P1̄	P1̄	Pbca
a (Å)	8.6824(13)	14.1519(3)	11.0638(18)	10.151(10)	16.861(2)
b (Å)	20.009(3)	17.9729(4)	12.0651(18)	11.85(2)	8.7293(8)
c (Å)	8.9455(13)	8.0831(2)	14.522(2)	15.410(18)	21.760(2)
α (°)	90.00	90.00	72.328(3)	81.36(14)	90.00
β (°)	107.123(3)	97.051(2)	69.217(3)	89.39(9)	90.00
γ (°)	90.00	90.00	84.581(3)	87.30(13)	90.00
V/(Å^3)	1485.2(4)	2040.39(8)	1726.6(5)	1831(5)	3202.7(6)
Z	2	2	1	2	8
D calcd (mg m^−3)	1.280	2.366	1.975	2.469	2.703
μ (Mo-Kα) (mm^−1)	0.091	37.366	6.294	11.780	13.454
F(000)	604	1328	976	1216	2320
θ range (°)	2.04–25.06	3.15–70.70	1.57–25.04	1.34–26.98	4.38–29.46
Collected reflections	7915	16 069	9248	8165	23 170
Indep reflections	4671	3812	6019	7856	3888
R int	0.0315	0.0506	0.0443	0.0430	0.1196
Obs reflections [I > 2σ(I)]	3560	2965	3917	3846	2408
Parameters	393	264	410	362	163
R 1 [I > 2σ(I)]^a	0.0430	0.0311	0.0525	0.1020	0.0742
wR2 [I > 2σ(I)]^a	0.0970	0.0596	0.1398	0.2366	0.2121
GOF on F^2	1.060	1.031	1.048	0.946	1.009
Residuals (e Å^−3)^b	0.240, −0.180	0.977, −0.600	1.936, −2.245	2.721, −3.126	4.018, −2.049

---

2.3. Hirshfeld surface analysis

The Hirshfeld surfaces (HS)¹⁶ and the related 2D-fingerprint plots (FP)¹⁷ were calculated using Crystal Explorer.¹⁸ The CIF file of each structure was imported into Crystal Explorer and high resolution Hirshfeld surfaces were mapped with the function d_norm. Before starting the calculations, the bond lengths to hydrogen atoms were set to standardized neutron values (O–H = 0.983 Å, N–H = 1.009 Å and C–H = 1.083 Å). Then, the HS surfaces were resolved into 2D-fingerprint plots, in order to quantitatively determine the nature and type of all intermolecular contacts experienced by the molecules in the crystal.

2.4. Theoretical methods.

The geometries of the complexes included in this study were computed at the M06-2X/def2-TZVP level of theory using the crystallographic coordinates within the TURBOMOLE program.¹⁹ This level of theory that intrinsically includes the latest available dispersion correction (D3) is adequate for studying noncovalent interactions dominated by dispersion effects like π-stacking. The basis set superposition error for the calculation of interaction energies has been corrected using the counterpoise method.²⁰ The “atoms-in-molecules” (AIM)²¹ analysis of the electron density has been performed at the same level of theory using the AIMAll program.²²

3. Results and discussion

3.1. Synthesis and spectroscopic results

The one-pot synthesis of a 2 : 1 molar ratio of mercury(II) salts and L in MeOH afforded the mono-, di- and polynuclear mercury(II) compounds 1–4 in good yields. The IR spectra of all complexes exhibit the characteristic strong absorption for the carbonyl groups and C=N groups. The strong bands centered at 800–600 cm⁻¹ are attributed to the ring of pyridines.

3.2. Crystal structure descriptions

Complexes 1 and 2, built from ligands with high degree of flexibility, are dinuclear Hg species featuring a 26-, and a 50-membered macrocycle, respectively, of formulation [(HgI₂)₂(μ-L1)₂] and [(HgI₂)₂(μ-L2)₂]. Fig. 1 and 2 depict ORTEP pictures of the neutral complexes and a selection of bond distances and angles is reported in Table 2. These complexes have a crystallographic inversion center at the midpoint and thus each macrocycle contains two symmetry related HgI₂ units having a rather distorted tetrahedral stereochemistry. The different natures of coordinating nitrogen (amino group in 1 and pyridine in 2) lead to Hg–N bond distances of 2.439(6) and 2.525(6) Å in the former and of 2.480(13) and 2.428(12) Å in 2. The Hg–I bond lengths are rather comparable in the two complexes and fall in the range from 2.6323(14) to 2.6721(5) Å. The distortions from the ideal tetrahedral geometry are evident from the N–Hg–N and I–Hg–I bond angles of 88.2 and 142.0° (mean values for the two complexes, see Table 2). In complex 1, intramolecular hydrogen bonds are detected between N1–H⋯I1 (3.697(6) Å, angle of 150(7)°) and between N2⋯O2 (2.633(8) Å, 105(7)°), which reinforce the overall structure. It is worth noting that the ligand 2,2′-butan-1,4-diylbis(oxy)dianiline (L1) was observed to form polymeric chains when used with silver(I) ions,²³ while in the present Hg complex the conformation adopted by the ligand allows the formation of the macrocycle where Hg metals are separated by 7.001 Å.

Fig. 1 ORTEP drawing (ellipsoid probability at 35%) of 1 with the atom label scheme of the independent unit.

Fig. 2 ORTEP drawing (top, ellipsoid probability at 50%) of complex 2 and its space-filling structure (bottom).

Table 2 Selected bond distances (Å) and angles (°) of complexes 1, 2 and 4

	1	2	4
Hg–N(1)	2.439(6)	2.480(13)	2.384(13)
Hg–N(2)	2.525(6)	2.428(12)	2.391(13)
Hg–I(1)	2.6721(5)	2.6541(13)	2.6537(14)
Hg–I(2)	2.6333(5)	2.6323(14)	2.6825(14)
N(1)–Hg–N(2)	89.7(2)	86.8(5)	90.3(5)
N(1)–Hg–I(1)	98.66(16)	102.9(3)	103.4(3)
N(1)–Hg–I(2)	110.84(14)	101.8(3)	108.2(4)
N(2)–Hg–I(1)	106.08(16)	98.8(3)	101.8(3)
N(2)–Hg–I(2)	102.78(16)	106.0(3)	101.1(4)
I(2)–Hg–I(1)	138.433(17)	145.67(5)	140.77(5)
C(2)–N(1)–Hg	115.0(4)	—	—
C(8)–N(2)–Hg	115.1(4)	—	—

---

Differently from 1, the molecular structure of 2, with an intermetallic distance between the HgI₂ moieties of 13.831 Å, presents a large cavity as evidenced from the space-filling representation of Fig. 2 (bottom). The crystal packing shows the complexes arranged along the crystallographic axis a and each complex ring is occupied by two phenyl rings of adjacent symmetry related complexes. This arrangement allows the formation of H bonds between the hydrazone N3–H and carbonyl oxygen O4 of a symmetry related complex (N⋯O distance 2.869(19) Å, N–H⋯O angle 162°), as shown in Fig. 3. The lattice methanol molecules are appended through H-bonds to the 1D supramolecular polymeric chains built from the aforementioned N–H⋯OH bonding interactions. Details of the H-bonds are reported in Table 4.

Fig. 3 Crystal packing of complex 2 showing the N3–H⋯O4 hydrogen bonds connecting the complexes.

The structurally characterized ligand 1,4-bis(2′-formylphenyl)-1,4-dioxabutane bis(isonicotinoylhydrazone) (L2) used for the synthesis of complex 2 has been found to crystallize with two lattice methanol molecules in monoclinic space group P2₁, (Fig. 4) thus in a chiral conformation,^7b while both chiral conformations are present in the centrosymmetric complex 2. The bond lengths and angles in the molecule are found in the normal range with an E configuration at the C7–N4 and C22–N6 bonds, as found in the dinuclear Hg complex. The crystal packing (Fig. 5) shows the pyridine N atoms are connected to the N3–H and N5–H hydrazone groups of symmetry related molecules to form a 2D layered structure in the ac plane. In addition, a π⋯π interaction between pyridine N2 and ring C16/C21 (at x, y, 1 + z) is detected among the molecules (centroid-to-centroid distance of 3.881(3) Å). The distance between the pyridine nitrogen donors is 8.228 Å, indicating that lattice methanol molecules affect the conformation of this molecule. In fact in a different crystal form,²⁴ triclinic space group P1̄, molecule L2 has a conformation with a distance between the py nitrogens of 11.496 Å, thus closely comparable to the value of 11.261 Å measured in complex 2.

Fig. 4 ORTEP drawing (ellipsoid probability at 50%) of ligand L2.

Fig. 5 The 2D layered structure of ligand L2 connected by H-bonds.

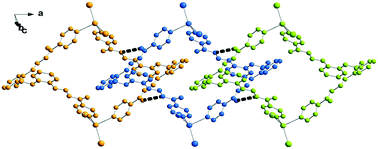
Complex 3 is a tetranuclear centrosymmetric complex [HgI₂(μ-L3)]₄ built from two crystallographic independent ligands connecting through pyridine donors to the HgI₂ moieties at the corners with a rhomboid shape structure. An Ortep drawing is shown in Fig. 6 and a selection of bond lengths and angles is reported in Table 3. The metal centers along the edges are spaced by 14.121 and 14.851 Å, while angles at the mercury corners are of 108.43 and 71.57°. Besides these geometrical features, distortions are also evidenced by the C_p–N1–Hg1 angle of 149° (C_p indicates the carbon atom in the para position of the pyridine). This affects the Hg(1)–N(1) bond distance that is the longest 2.54(3) Å in comparison to other Hg–N values in between 2.41(2)–2.45(2) Å, taking into account here the lower accuracy of bond distances. In contrast, the other pyridine rings are linearly coordinated with Cp–N–Hg angles that average to 175.0°. The crystal packing shows the complexes interdigitated and piled along the axis a (see Fig. 7). As far as we know, this is the first tetranuclear complex built from HgI₂ moieties.

Fig. 6 ORTEP drawing (ellipsoid probability at 50%) of 3.

Table 3 Selected bond distances (Å) and angles (°) of complex 3

N(2)′ atom at 2−x, 2 − y, −1 − z.
Hg(1)–N(1)	2.54(3)	Hg(2)–N(2)′	2.42(2)
Hg(1)–N(6)	2.406(19)	Hg(2)–N(5)	2.45(2)
Hg(1)–I(1)	2.650(5)	Hg(2)–I(3)	2.647(6)
Hg(1)–I(2)	2.614(4)	Hg(2)–I(4)	2.637(5)
N(1)–Hg(1)–N(6)	90.5(8)	N(2)′–Hg(2)–N(5)	89.3(8)
N(1)–Hg(1)–I(1)	92.1(6)	N(2)′–Hg(2)–I(3)	102.4(5)
N(1)–Hg(1)–I(2)	105.9(5)	N(2)′–Hg(2)–I(4)	103.2(5)
N(6)–Hg(1)–I(1)	103.6(4)	N(5)–Hg(2)–I(3)	102.0(7)
N(6)–Hg(1)–I(2)	103.2(5)	N(5)–Hg(2)–I(4)	99.2(6)
I(1)–Hg(1)–I(2)	147.40(9)	I(3)–Hg(2)–I(4)	146.70(11)

---

Fig. 7 Crystal packing of complex 3 (top) and a detail showing the N–H⋯O interactions between adjacent complexes (bottom).

In the solid state, complex 4 exists as a helical polymer [{HgI₂(L4)}]_n wrapped about a two-fold improper rotation axis. The ORTEP drawing of the polymer is shown in Fig. 8. The mercury atoms are connected by the pyridine N donors separated at a distance of 7.925 Å with an intermetallic Hg⋯Hg⋯Hg angle of 66.83°. This arrangement is allowed by the conformation of the ligand that leads the two py planes to form a dihedral angle of 67.7°. Here the Hg–N bond distances are the shortest (of 2.384(13) and 2.391(13) Å) among those measured in the other complexes, while Hg–I distances (2.6537(14) and 2.6825(14) Å) and bond angles confirm the trend discussed above (Table 2). The polymers extended in the direction of the b axis (Fig. 9) are strongly connected by π⋯π interactions between a pair of py(N2) having a centroid-to-centroid distance of 3.573(11) Å.

Fig. 8 ORTEP drawing (ellipsoid probability at 35%) of the polymeric structure of 4 with the atom label scheme of an independent unit.

Fig. 9 A perspective view showing the crystal packing of polymers of 4 connected by π⋯π interactions.

3.3. Hirshfeld surface analysis

The share and nature of different kinds of non-covalent intermolecular interactions in crystals of 1–4 and L2 were identified and analysed through Hirshfeld surface analysis. We based our analysis on three different datasets: the Hirshfeld surface map, the two-dimensional (2D) fingerprint plots, and the percentage contribution for different kinds of non-covalent interactions. The dominant intermolecular interactions are viewed by the bright red area of the d_norm surface. Fig. 10 illustrates the Hirshfeld surfaces for structures of 1–4 and L2. This analysis reveals that the crystal packing in all structures is largely dominated by the common planar aromatic rings of the ligands, leading to close H⋯H intercontacts, as well as to π-stacking contacts, namely C–H⋯π and π⋯π interactions. Moreover, there is a strong participation of I⋯H interactions in the stabilization of the structures. In addition, for structures 2 and L2 we observe a higher level of O⋯H interactions due to the hydrogen bonds between the methanol solvate and the macrocycle/ligand.

Fig. 10 Views of the Hirshfeld surfaces for 1–4 and L2 mapped with d_norm.

Unexpectedly, there is a certain level of Hg⋯H interactions observed in structures 1 and 4. The FPs (Fig. S1† and Table 4) of the compounds show that the dominant interactions are H⋯H (16.7–44.9%) and C⋯H (7.7–24.6.%). The analysis for 3 shows the lowest proportion of H⋯H interactions of the whole set, making up only 16.7% of the surface. Also, the I⋯H interactions are quite relevant, corresponding to 15–38.7% of the surface. The C⋯H contacts represent the C–H⋯π interactions in the crystals, and the highest values were measured for L2. For π⋯π interactions, which correspond to C⋯C (4.5–5.7%) contacts, the highest values were measured in 2, L2 and 4, respectively. The O⋯H hydrogen bonding interactions between solvent and complex molecules play also important roles in stabilizing the structures. The O⋯H interactions vary from 9.8, to 13.3, and 15.8% in 3, 2, L2, respectively (Table 5).

Table 4 H-bond parameters in L2 and complexes 1–3Å/°

D–H	d(D–H)	d(H⋯A)	<DHA	d(D⋯A)
Symmetry codes: i: x, y, −1 + z; ii: −1 + x, y, z; iii: −x, ½ + y, 1 − z; iv: 1 −x, −y, 1 − z; v: 1 + x, y, z; vi: x, 1 + y, z; vii; 1 − x, 1 −y, −z; viii: 1 −x, 1 −y, 1 −z; ix: −1 + x, 1 + y, z; x: x, −1 + y, z.
L2
N3–H3⋯N2^i	0.91(4)	2.12(4)	173(4)	3.025(5)
N5–H5⋯N1^ii	1.03(4)	1.96(4)	170(4)	2.987(6)
O31–H31⋯O4	0.92(5)	2.00(6)	150(6)	2.836(6)
O32–H32⋯O1^iii	0.90(6)	1.94(7)	156(6)	2.782(7)
1
N1–H21⋯I1^iv	0.79(9)	3.00(9)	150(7)	3.697(6)
N2–H22⋯O2	0.80(8)	2.31(8)	105(7)	2.633(8)
2
N3–H3⋯O4^v	0.88	2.02	162	2.869(19)
N5–H5⋯O31^vi	0.88	2.07	146	2.84(2)
O31–H31⋯I1^vii	0.84	2.67	163	3.479(15)
O41–H41⋯O1^viii	0.84	2.35	111	2.765(19)
3
N3–H3⋯O2^ix	0.86	2.19	147	2.95(2)
N7–H7⋯O1^x	0.86	2.16	155	2.96(2)

---

Table 5 Summary of the various contact contributions greater than 2% in the Hirshfeld surfaces area for all analyzed structures

Contact type/structure	1	2	3	4	L2
H⋯H	44.9	30.2	16.7	24.4	39.4
O⋯H/H⋯O	—	13.3	9.8	—	15.8
C⋯H/H⋯C	20.2	17.9	11.0	7.7	24.6
C⋯C	—	4.5	—	5.7	5.1
N⋯H/H⋯N	—	9.7	4.5	5.9	13.7
I⋯H/H⋯I	29.8	15.0	27.9	38.7	—
I⋯C/C⋯I	—	3.3	8.7	4.3	—
Hg⋯H/H⋯Hg	2.1	—	—	5.5	—

---

3.4. Theoretical study

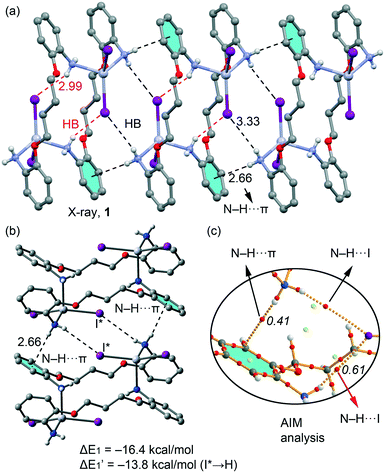
We have focused the theoretical study on the comparison of the energetic features of the different types of π-stacking and H-bonding interactions observed in the crystal packing of macrocyclic compounds 1–3 described above.

In Fig. 11a we represent a fragment of the X-ray solid state structure of compound 1 where an infinite 1D supramolecular chain is formed governed by a combination of very long (3.33 Å) N–H⋯I hydrogen bonds and N–H⋯π interactions (see black dashed lines). Each I atom that participates in the intermolecular H-bond also forms shorter (2.99 Å) intramolecular H bonds with the amino group coordinated to the opposite HgI₂ moiety (see red dashed lines in Fig. 11a). We have used a dimer retrieved from this supramolecular chain (see Fig. 12b) and computed the interaction energy, which is large and negative (ΔE₁ = −16.4 kcal mol⁻¹) due to the formation of two symmetrically equivalent H-bonds and two N–H⋯π interactions that are very short compared to similar interactions likely due to the enhanced acidity of the H atoms due to the coordination of the amino group to Hg(II). In order to evaluate the contribution of each interaction in the formation of the dimer, we have used a theoretical model where the I atoms that form the H-bonds have been replaced by hydrido ligands. In this model the H-bonds are not formed and the resulting interaction energy is reduced to ΔE^′₁ = −13.8 kcal mol⁻¹, which is the contribution of the N–H⋯π interactions and confirm their important contribution in the formation of the supramolecular chain in the solid state of 1. The contribution of the H-bonds can be estimated by difference, that is only −2.6 kcal mol⁻¹ in line with the long H-bonding distance. We have used Bader's theory of atoms in molecules²⁰ to characterize the N–H⋯π interactions. The existence of a bond critical point (CP) and bond path connecting two atoms is a clear evidence of interaction, since it indicates that electron density is accumulated between the nuclei that are linked by the associated atomic interaction line.²¹ In Fig. 11c we represent a partial distribution of CPs and bond paths of the dimer focusing on the H-bonds and N–H⋯π interactions. The distribution of CPs shows that both intra and intermolecular H-bonds are characterized by a bond CP (red sphere) and bond path connecting the H atoms to the I atom (ρ_BCP = 0.0061 a.u.), thus confirming the existence of the long HB. Moreover, the N–H⋯π interaction is characterized by a bond CP and bond path connecting the N–H to one carbon atom of the aromatic ring (ρ_BCP = 0.0061 a.u.).

Fig. 11 (a) Partial view of the crystal packing of 1. (b) Theoretical model used to evaluate the binding energy. (c) AIM distribution of bond and ring critical points (red and yellow spheres, respectively) and bond paths corresponding to the N–H⋯π and N–H⋯I interactions. The values of ρ(r) (× 10² in a.u.) at the bond CPs are given in italics.

Fig. 12 (a) Dimer formed in the crystal packing of 2. (b) AIM distribution of bond and ring critical points (red and yellow spheres, respectively) and bond paths corresponding to the N⋯C interactions. (c) Dimer formed in the X-ray packing of 3. (d) AIM distribution of bond, ring and cage critical points (red, yellow and green spheres, respectively) and bond paths corresponding to the HgI₂⋯π interaction. The values of ρ(r) (× 10² in a.u.) at the bond CPs are given in italics.

For compounds 2 and 3 we have studied the supramolecular assemblies presented in Fig. 3 and 7. Both compounds form 1D supramolecular polymeric chains in the solid state and we have evaluated the interaction energies of dimeric models extracted from them. They are shown in Fig. 12a and c and in addition to the strong N–H⋯O=C H-bonds (2.02 Å and 2.16 Å for 2 and 3, respectively), they are also stabilized by unconventional interactions. In complex 2, it is worth mentioning the antiparallel arrangement of the hydrazone groups allowing the formation of two symmetrically equivalent N⋯C interactions (highlighted in Fig. 12a). The formation energy of the dimer is very large (ΔE₂ = −45.8 kcal mol⁻¹) due to the presence of an intricate combination of interactions including both H-bonds, the antiparallel stacking of the hydrazone groups and additional long range van der Waals and aromatic π-stacking interactions. We have used the AIM analysis to confirm the existence of the N⋯C, which are characterized by a bond CP (ρ = 0.0052 a.u.) and bond path inter-connecting both atoms (see Fig. 12b). In complex 3, it is worth emphasizing the location of the HgI₂ group over one pyridine ring of the ligand, interacting with the π-cloud. The interaction energy of the dimer of 3 (ΔE₃ = −45.8 kcal mol⁻¹) is similar to that computed for the dimer of 2. Interestingly the AIM analysis (see Fig. 12d) confirms the HgI₂⋯π interaction, where the Hg and I atoms are connected to two carbon atoms of the aromatic ring, each one characterized by a bond CP and bond path (ρ_BCP = 0.0045 a.u. and ρ_BCP = 0.0055 a.u., respectively). Interestingly, the other I atom is also connected by a bond CP and bond path to one carbon atom of other pyridine ring (ρ_BCP = 0.0052 a.u.), thus confirming the existence of this mixed cation/anion–π interaction.

4. Concluding remarks

In this study the coordination chemistry of ditopic ligands of different flexibilities, symmetries and types of N donors towards HgI₂ salt has been investigated. One unpredicted tetranuclear and two dinuclear metallamacrocycles were generated through the coordination driven self-assembly approach. However, under the same reaction conditions, by using bis(pyridyl)methanimine ligand (L4) a coordination polymer was obtained. In all cases the HgI₂ fragments were preserved with the metal in a tetrahedral coordination sphere, and flexible ligands play different roles giving rise to particular motifs in the self-assembly process. A polymer–macrocycle equilibrium in solution may explain the formation of the 1D array in 4, as already observed in complexes built from dipyridine ligands and mercury halides.²⁵ The packing effect due to the different kinds of non-covalent intermolecular interactions could have favoured this result. In fact a number of H-bonding and π–π stacking interactions in the solid state of these compounds have been pointed out using DFT calculations and Hirshfeld analysis. The HgI₂⋯π interaction observed in compound 3 is remarkable, with a mixed cation/anion⋯π character. These interactions and associated energies appear to be crucial for the formation of supramolecular architectures detected in the crystal.

Acknowledgements

This work was supported by the Ministry of Education and Science of the Russian Federation (the Agreement number 02.a03.21.0008). We are grateful to the University of Maragheh for the financial support of this research. AB and AF thank DGICYT of Spain (projects CTQ2014-57393-C2-1-P, FEDER funds) for funding and the CTI (UIB) for free allocation of computer time.

References

1. P. J. Stang and B. Olenyuk, Acc. Chem. Res., 1997, 30, 502–518.
2. R. W. Saalfrank, H. Maid and A. Scheurer, Angew. Chem., Int. Ed., 2008, 47, 8794–8824.
3. Y.-Y. Zhanga, W.-X. Gaoa, L. Lina and G.-X. Jina, Coord. Chem. Rev., 2017 DOI:10.1016/j.ccr.2016.09.010.
4. (a) R. Chakrabarty, P. S. Mukherjee and P. J. Stang, Chem. Rev., 2011, 111, 6810–6918; (b) T. R. Cook and P. J. Stang, Chem. Rev., 2015, 115, 7001–7045; (c) Y.-F. Han and G.-X. Jin, Acc. Chem. Res., 2014, 47, 3571–3579; (d) P. Jin, S. J. Dalgarno and J. L. Atwood, Coord. Chem. Rev., 2010, 254, 1760–1768; (e) W.-H. Zhang, Q. Liu and J.-P. Lang, Coord. Chem. Rev., 2015, 293–294, 187–210.
5. (a) T. R. Cook, Y.-R. Zheng and P. J. Stang, Chem. Rev., 2013, 113, 734; (b) M. Yoshizawa and J. K. Klosterman, Chem. Soc. Rev., 2014, 43, 1885; (c) C. G. Oliveri, P. A. Ulmann, M. J. Wiester and C. A. Mirkin, Acc. Chem. Res., 2008, 41, 1618.
6. (a) Z.-Z. Yuan, F. Luo, Y.-M. Song, G.-M. Sun, X.-Z. Tian, H.-X. Huang, Y. Zhu, X.-F. Feng, M.-B. Luo, S.-J. Liu and W.-Y. Xu, Dalton Trans., 2012, 41, 12670–12673; (b) C.-Y. Su, A. M. Goforth, M. D. Smith and H.-C. zur Loye, Inorg. Chem., 2003, 42, 5685–5692; (c) N. Masciocchi, A. Figini Albisetti, A. Sironi, C. Pettinari, C. Di Nicola and R. Pettinari, Inorg. Chem., 2009, 48, 5328–5337; (d) L. Li, Y. Song, H. Hou, Z. Liu, Y. Fan and Y. Zhu, Inorg. Chim. Acta, 2005, 358, 3259–3266.
7. (a) C.-L. Chen, J.-Y. Zhang and C.-Y. Su, Eur. J. Inorg. Chem., 2007, 2997; (b) T. J. Burchell, D. J. Eisler and R. J. Puddephatt, Inorg. Chem., 2004, 43, 5550–5557.
8. (a) G. Mahmoudi, A. Bauzá, A. V. Gurbanov, F. I. Zubkov, W. Maniukiewicz, A. Rodríguez-Diéguez, E. López-Torres and A. Frontera, CrystEngComm, 2016, 18, 9056–9066; (b) G. Mahmoudi, V. Stilinović, M. Servati Gargari, A. Bauzá, G. Zaragoza, W. Kaminsky, V. Lynch, D. Choquesillo-Lazarte, K. Sivakumar, A. A. Khandar and A. Frontera, CrystEngComm, 2015, 17, 3493–3502; (c) S. Dehghanpour, A. Mahmoudi, L. Najafi, M. Khalafbeigi and K. Jahani, Polyhedron, 2013, 53, 91.
9. (a) G. Saha, K. K. Sarkar, T. K. Mondal and C. Sinha, Inorg. Chim. Acta, 2012, 387, 240; (b) Z. Y. Zhang, Z. P. Deng, X. F. Zhang, L. H. Huo, H. Zhao and S. Gao, CrystEngComm, 2014, 16, 359.
10. (a) P. A. Tasker and E. B. Fleischer, J. Am. Chem. Soc., 1970, 92, 7072; (b) W.-X. Ni, M. Li, S.-Z. Zhan, J.-Z. Hou and D. Li, Inorg. Chem., 2009, 48, 1433.
11. Oxford Diffraction, CrysAlis CCD and CrysAlis RED, including ABSPACK Versions 1.171.32.3, Oxford Diffraction Ltd, Abingdon, Oxfordshire, England, 2006; SAINT Plus, Data Reduction and Correction Program, v. 6.01, Bruker AXS, Madison, Wisconsin, USA, 1998; K. Harms and S. Wocadlo, XCAD4, University of Marburg, Germany, 1995.
12. (a) SADABS v.2.01, Bruker/Siemens Area Detector Absorption Correction Program, Bruker AXS, Madison, Wisconsin, USA; (b) N. Walker and D. Stuart, Acta Crystallogr., Sect. A: Found. Crystallogr., 1983, 39, 158–166.
13. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112.
14. D. J. Watkin, C. K. Prout and L. J. Pearce, CAMERON, Chemical Crystallography Laboratory, Oxford, England, 1996.
15. K. Brandenburg, DIAMOND, Crystal Impact GbR, Bonn, Germany, 1999.
16. (a) J. J. McKinnon, D. Jayatilaka and M. A. Spackman, Chem. Commun., 2007, 3814–3816; (b) M. A. Spackman, J. J. McKinnon and D. Jayatilaka, CrystEngComm, 2008, 10, 377–388; (c) M. A. Spackman and D. Jayatilaka, CrystEngComm, 2009, 11, 19–32; (d) F. L. Hirshfeld, Theor. Chim. Acta, 1977, 44, 129–138; (e) H. F. Clausen, M. S. Chevallier, M. A. Spackman and B. B. Iversen, New J. Chem., 2010, 3, 193–199.
17. M. A. Spackmann and J. J. McKinnon, CrystEngComm, 2002, 4, 378–392.
18. S. K. Wolff, D. J. Grimwood, J. J. McKinnon, M. J. Turner, D. Jayatilaka and M. A. Spackman, Crystal Explorer (Version 3.1), University of Western Australia, 2012.
19. R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169.
20. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
21. R. F. W. Bader, Chem. Rev., 1991, 91, 893–928.
22. T. A. Keith, AIMAll (Version 13.05.06), TK Gristmill Software, Overland Park KS, USA, 2013.
23. Q.-L. Zhang, Fenzi Kexue Xuebao, 2011, 27, 112–115.
24. X.-S. Tai, L.-H. Wang, Y.-Z. Li and M.-Y. Tan, Z. Kristallogr. - New Cryst. Struct., 2004, 219, 407–408.
25. T. J. Burchell and R. J. Puddephatt, Inorg. Chem., 2005, 44, 3718–3730.

---

Footnote

† Electronic supplementary information (ESI) available: CCDC 1541661–1541665 contain the supplementary crystallographic data for ligand L2 and complexes 1–4. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c7ce00628d

---