Two-component molecular crystals: evaluation of the formation thermodynamics based on melting points and sublimation data

Abstract

Based on literature analysis, we have built up a database containing the fusion temperatures of two-component molecular co-crystals and individual compounds (1175 co-crystals/salts). In order to estimate the thermodynamics of two-component crystal formation, we have created a database on the basis of values reported in the literature from 1900 till 2016 inclusive. The database includes values of the enthalpies and Gibbs energies of individual molecular crystals obtained by various methods. The distribution functions of two-component crystals have been analysed using their fusion temperatures, both for the full sample and separately for the salts and the co-crystals. A comparative analysis was conducted to determine the differences in the melting temperatures of monotropic polymorphic forms, as well as a similar analysis of two-component crystals with the same composition and different stoichiometries. Correlation equations have been obtained, connecting the melting points of co-crystals/salts and individual components for 74 active pharmaceutical ingredients and coformers, which enabled us to design co-crystals with predictable melting temperatures. An approach to estimating co-crystal sublimation thermodynamic characteristics has been developed. The thermodynamic functions of the formation process of 281 co-crystals have been obtained and analyzed. The diagram method has been used to analyze the parameters under study. Analysis of experimental data distribution in the diagram sectors has shown that the number of two-component crystals with enthalpy determined processes of co-crystal/salt formation corresponds to 70.9%, whereas the number of those with entropy determined processes corresponds to 29.1%. A general algorithm for estimating the thermodynamics of the formation of two-component crystals is proposed.

---

1. Introduction

Co-crystallization has become an important research area in recent years because of the great potential of fine-tuning the physical properties of multi-component crystal components. The term “compound” has long been used to denote co-crystals with a fixed component ratio, while those with variable stoichiometry were named “mixed crystals”.^1,2 Despite numerous studies, the nature of co-crystallization remains inadequately understood. Moreover, understanding and controlling the main driving forces of co-crystal formation is a significant fundamental task. In the past decades, considerable efforts have been made to apply co-crystallization techniques to improving factors such as dissolution rate, thermal stability, and bioavailability in the pharmaceutical industry.^3–6 Encouraged by the great success of pharmaceutical co-crystallization, the development of new functional materials by co-crystallization techniques in other fields is attracting more and more interest. Nowadays, energetic co-crystallization becomes very promising as an alternative method of tuning explosive materials and properties by rearranging existing molecules, instead of synthesizing new compounds.^7,8 Another application of co-crystals is in organic nonlinear optical materials with high second-order nonlinear susceptibilities. These materials are used in electro-optical devices such as optical waveguides or frequency modulators.^9,10 Obtaining co-crystals is a spontaneous, unpredictable process that determines the existence of different screening algorithms. In turn, the need for screening procedures makes the co-crystal technology itself expensive and time-consuming. All this makes it necessary to develop algorithms for predicting thermodynamically stable co-crystals/salts (from the available set of individual substances), in order to minimize the number of screening operations and to know in advance the thermodynamic stability of the new materials.

There is a number of works analyzing the co-crystal formation enthalpy. One of the approaches relies on crystal structure prediction (CSP) using anisotropic potential^11,12 and quick methods of energy estimation based on molecular electrostatic potential surfaces.¹³ Abramov et al.¹⁴ applied COSMO-RS fluid-phase thermodynamics computations describing the miscibility of co-crystal formers in a supercooled liquid (melt) phase to virtual coformer screening. Moreover, Hansen solubility parameters were recently used to describe the miscibility of APIs and coformers to predict co-crystal formation in order to guide co-crystal screening.¹⁵ An essential fault of all these approaches is that they analyze the enthalpic characteristics of co-crystal formation, while the entropic terms are not taken into account. The existence of such approaches can be attributed to the fact that there are almost no experimental data about the Gibbs energies of co-crystal formation.

Development of approaches for estimating the thermodynamic characteristics of multi-component crystal formation requires experimental data. Unfortunately, there is a limited number of experimental works in this field so far, and they can be conditionally divided into several groups. The most informative works are those containing data on all the thermodynamic functions of the co-crystal/salt formation (Gibbs energy, enthalpy and entropy). As a rule, such information is obtained by co-crystal equilibrium solubility experiments conducted at different temperatures.^16–31 However, there are works where two independent techniques – solubility calorimetry (to analyze the enthalpic term) and solubility measured by the saturation method (to analyze the Gibbs energy) – are used to determine all the thermodynamic parameters. For example, Oliveira et al.³² studied the thermodynamics of [Carbamazepine + Saccharin] co-crystal formation by this method. The second group of experimental approaches focuses on studying the co-crystal component complex formation at one temperature.^33–35 In this case, only the Gibbs energy of the co-crystal/salt formation can be calculated.

Several years ago, we proposed an approach³⁶ to estimating the thermodynamic characteristics of two-component crystal formation based on the melting temperatures of the co-crystal and its individual components, as well as on the analysis of the sublimation thermodynamic characteristics of the individual substances. The main sources of such analysis were the databases of the melting points of the co-crystals/salts and the sublimation thermodynamics of the molecular crystals created by us. Because the number of occurrences in the designated databases has risen significantly since the publication of our article, we have attempted to systematize the obtained material and analyze the processes of formation of two-component crystals from the standpoint of the main contributions (enthalpy or entropic) to the Gibbs energy. We also tried to present and justify a general scheme/algorithm for estimating the thermodynamic stability of any co-crystal of interest.

2. Experimental section

2.1. Databases

2.1.1. Database of melting points of two-component crystals. In order to build up a database of melting temperatures of co-crystals and their individual components, we analyzed the relevant literature, as described earlier.³⁶ It should be noted that in order to simplify the process of finding regularities, we selected only two-component systems/co-crystals for the study. The relevant literature was selected through the SciFinder³⁷ system by using two key word forms: “cocrystal” and “co-crystal”. After that, we chose the papers where the melting points of two-component crystals were analysed by different methods (DSC, Kofler and others). Crystals and individual compounds which melt with decomposition (or partial decomposition) were excluded from the study. The melting points obtained by DSC experiments corresponded to T_onset. The melting points obtained by alternative methods were used as they were.

The database included both co-crystals and salts (proton transfer between the co-crystal components). In contrast to our previous analysis, in this paper we tried to make a clear distinction between salts and co-crystals, using the single crystal X-ray diffraction results. Where this was impossible (there were no single crystal X-ray diffraction data), two-component systems were referred to as co-crystals. In addition, for each two-component crystal, we included the following information in the database: 1) data from single crystal X-ray (refcode/cif file); 2) evidence (yes or no) of the existence of a co-crystal/salt using XRPD (comparative analysis of diffractograms for a two-component crystal and crystals of individual compounds); 3) data about the presence of DSC experiment results (yes or no) and evidence of the existence of a co-crystal/salt (comparative analysis of DSC curves for two-component crystals and crystals of individual compounds); 4) data about the presence of the results of experiments aimed at determining the crystal/salt melting temperature using Kofler's method; 5) data about the presence of solubility experiments, and 6) data about the presence of the results of biological experiments. Special attention was paid to the presence of polymorphic modifications of two-component crystals: each polymorphic phase was described as an independent system (occurrence). The data on the melting points of the co-crystals/salts obtained from crystalline hydrates/crystalline solvates should be mentioned in particular. The literature contains data on DSC and TG experiments which describe the dehydration/desolvation processes of co-crystals/salts with the temperatures substantially different from the melting points of the non-solvated two-component crystals. For such systems, the resulting melting temperatures were analyzed together with a common data set. For the analysis, we selected only those co-crystals/salts in which the melting temperature of the individual components was over 25 °C. Based on the literature analysis, we have obtained 1175 co-crystals/salts. For 941 (80.2%) crystals, single crystal X-ray diffraction experiments with the solved crystal structures were carried out. Whereas 233 (19.8%) two-component crystals were characterized using only XRPD. The data of single X-ray diffraction experiments allow us to unambiguously interpret the state of the molecules in the crystal: they either take the form of salts (proton transfer between two organic molecules) or a cocrystal (no proton transfer). It should be noted that 233 two-component crystals (described by XRPD experiments) were referred to as co-crystals as this technique does not allow us to make an unambiguous interpretation of the molecule state in the crystal. With such assumptions, the database under consideration contained 184 salts (15.7%) and 991 co-crystals (84.3%). There were 86 occurrences of polymorphic forms (7.3%) (different polymorphic modifications of the same two-component crystal were considered different occurrences). Of these, 70 were monotropic and 16 – enantiotropic phases (81%/19%).

All the data can be divided into several groups based on their reliability levels: a) those describing the crystal structure of single crystals by using X-ray analysis and the DSC melting curve (745 crystals (63.4%)) (the highest reliability); b) those describing the crystal structure of single crystals by using X-ray analysis and the melting temperature (Kofler's method) (196 occurrences (16.7%)); c) those proving co-crystal formation by comparing the X-ray powder diffraction patterns of the co-crystal/salt and its individual components, and providing the DSC melting curve of the co-crystal/salt (219 occurrences (18.7%)); d) those proving co-crystal/salt formation by comparing the X-ray powder diffraction patterns of the co-crystal/salt and its individual components, and providing the co-crystal/salt melting temperature without a DSC curve (14 occurrences (1.2%)). When different sources described the same two-component crystal, the choice was made in favour of systems belonging to a higher reliability level.

2.1.2. Database of thermodynamic characteristics of sublimation processes of molecular crystals. In order to analyze the experimental data, we used a database created by us on the basis of the values published in the literature from 1900 till 2016 inclusive. The database contains the following information: the method used to measure the thermodynamic characteristics; the experimental temperature interval; the equation describing the temperature dependence of saturated vapor pressure; the sublimation enthalpies both at the experimental temperature, ΔH^T_sub(exp), and at 298.15 K, ΔH²⁹⁸_sub(exp), in kJ mol⁻¹; the standard Gibbs energy values, ΔG²⁹⁸_sub(exp), in kJ mol⁻¹; the fusion enthalpies and melting temperatures of molecular crystals and, finally, the refcodes³⁸ of the compounds described by the X-ray diffraction experiments. The database includes enthalpies and Gibbs energies obtained by various methods and at different experimental temperatures; therefore, we used a special algorithm to reduce the experimental values to comparable conditions. For this purpose, we calculated the standard Gibbs energy values at 298 K using the temperature dependences of vapour pressure. In a similar way, if the sublimation enthalpies were obtained at elevated temperatures, these values were recalculated at 298 K based on the heat capacities of the studied compounds. If the same substance had been earlier described in the literature by several methods, preference was given to methods that allowed us to obtain both the sublimation enthalpy and Gibbs energy (saturated vapor pressure) data at the same time: transpiration, torsion effusion, mass effusion, isoteniscope, mercury manometer methods, etc. Moreover, with other conditions being identical, preference was given to the data received at temperatures closest to the standard condition (298.15 K). The saturated vapor pressure at 298.15 K was calculated from the temperature dependence. If the data were only taken for sublimation enthalpies, preference was given to the values obtained by the calorimetric method. In the final analysis, the database included 2899 sublimation enthalpy values. Among these compounds, only 1780 values of the Gibbs energies were known. So, it was evident that the number of the sublimation enthalpy values was 1.6 times bigger than the Gibbs energy ones. This relationship can be explained by the fact that the earlier works described a lot of calorimetric experiments which did not allow for saturated vapor pressure estimation. The experimental data for the sublimation enthalpies were derived by the following methods: 1136 – mass effusion – Knudsen effusion; 494 – transpiration; 306 – calorimetry; 111 – torsion; 79 – manometer (mercury, piston); 181 – calculation/estimation from vaporization and fusion enthalpies (DSC); 18 – head space analysis; 7 – isoteniscope, and 567 – others. The melting points were known for 2542 molecular crystals. It should be noted that the main reason for the lack of melting temperatures was the decomposition of the compounds under fusion (porphyrins and other substances with a high molecular weight). However, there were a few newly synthesized compounds for which there was no information about the melting points in the original papers. Because the main idea of the work was to find out the relationship between the sublimation Gibbs energies and melting temperatures, we selected 1515 compounds having sublimation Gibbs energies, enthalpies and melting points at the same time.

2.2. Algorithm for co-crystal thermodynamic function estimation

The literature data show that in structurally similar compounds (according to Tanimoto similarity coefficients), there is a linear correlation between ΔG²⁹⁸_sub and T_fus.³⁹ The crystal structure of a two-component co-crystal (with any stoichiometry) can be considered structurally similar to that of the individual compounds. In other words, the experimental values of ΔG²⁹⁸_subvs. T_fus of the individual compounds and the co-crystal belong to one (and the same) cluster. Therefore, the coefficients A and B of eqn (1) can be calculated if ΔG²⁹⁸_sub and T_fus of the individual compounds are known.

ΔG²⁹⁸_sub = A + B·T_fus (1)

Knowing coefficients A, B and T_fus(CC), we can calculate the ΔG²⁹⁸_sub(CC)value:

ΔG²⁹⁸_sub(CC) = A + B·T_fus(CC) (2)

In order to calculate the Gibbs energy of co-crystal formation with the stoichiometric ratio (API)_n(CF)_m ΔG²⁹⁸_f(CC), we should use the following equations:

ΔG²⁹⁸_sub(PM) = X₁·ΔG²⁹⁸_sub(API) + X₂ΔG²⁹⁸_sub(CF) (3)

where (API)_n(CF)_m: X₁ = n/(n + m); X₂ = m/(n + m). ΔG²⁹⁸_sub(PM), ΔG²⁹⁸_sub(API), ΔG²⁹⁸_sub(CF) are the sublimation Gibbs energies of the physical mixture, API and CF, respectively.

ΔG²⁹⁸_f(CC) = ΔG²⁹⁸_sub(CC) − ΔG²⁹⁸_sub(PM) (4)

The co-crystal formation enthalpy value, ΔH²⁹⁸_f(CC), was obtained using the following algorithm. It is well known that there is a linear dependence between ΔG²⁹⁸_sub and ΔH²⁹⁸_sub (the so-called compensation effect).⁴⁰ Thus, knowing the experimental values ΔG²⁹⁸_sub and ΔH²⁹⁸_sub, it is possible to calculate the coefficients of eqn (5):

ΔG²⁹⁸_sub = C + D·ΔH²⁹⁸_sub (5)

and then calculate the necessary value:

ΔH²⁹⁸_f(CC) = ΔH²⁹⁸_sub(CC) − ΔH²⁹⁸_sub(PM) (6)

ΔH²⁹⁸_sub(CC) = (ΔG²⁹⁸_sub(CC) − C)/D (7)

ΔH²⁹⁸_sub(PM) = X₁·ΔH²⁹⁸_sub(API) + X₂·ΔH²⁹⁸_sub(CF) (8)

3. Results and discussion

3.1. Comparative analysis of the melting points of co-crystals and individual compounds

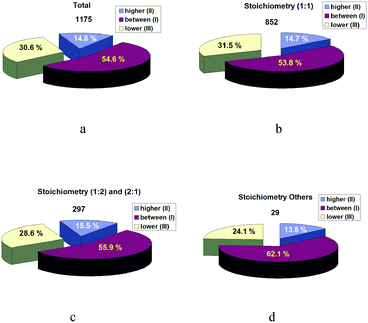
It was interesting to analyze the relationship between the melting temperatures of the co-crystal and its individual components. It is worth mentioning that the division of the co-crystal components into API and CF is done only for convenience in order to separate the components from each other. And in some cases, API molecules are not the molecules for pharmaceutical application. Nevertheless, we used this symbol because most of the analyzed literature reports are devoted to pharmaceutical co-crystals. The melting points in the figures considered below are presented in Celsius for clarity of the analysis. Fig. 1 shows the results of this analysis.

Fig. 1 Distribution of two-component crystal melting points (T_fus(CC)) from the analyzed database relative to individual compounds (T_fus(CF) and T_fus(API)) according to: the total number of crystals (a); stoichiometry (1 : 1) (b); stoichiometry (1 : 2) and (2 : 1) (c); other stoichiometry (d). “Higher (II)” corresponds to T_fus(API) < T_fus(CC), “Between (I)” corresponds to T_fus(CF) < T_fus(CC) < T_fus(API) and “Lower (III)” corresponds to T_fus(CC) < T_fus(CF).

Fig. 1a summarizes the results for all the co-crystals with all possible stoichiometric compositions. These results show that most of the co-crystals/salts have the melting point between the melting points of the individual components (54.6%). In turn, 30.6% (one-third) of the co-crystals/salts have the melting point below the melting points of the individual components (and these are the potential candidates for pharmaceutical co-crystals/salts as their Gibbs energies of crystal lattices are lower than those of the crystals of the individual compounds). However, in this case it should be kept in mind that a melting temperature decrease will reduce the crystal thermodynamic stability. Therefore, pharmaceutical applications require a compromise between the crystal thermodynamic stability and solubility. Finally, 14.8% of co-crystals/salts have the melting temperatures above those of the individual compounds which are the co-crystal/salt components. It is this fact/circumstance that classifies this category of the systems as unfavorable in terms of improving the solubility of poorly soluble components. Fig. 1(b–d) present similar histograms detailed based on different stoichiometric compositions. Each group has its variations, but the general trend remains.

As noted above, the database includes 184 salts and 774 co-crystals (taken from single crystal X-ray diffraction data). It was interesting to compare the distribution of the melting temperatures of two-component crystals among the dedicated groups (I–III) for the co-crystals and salts. The analysis of the results is shown in Fig. 2.

Fig. 2 Distribution of two-component crystals included in the database among the selected groups (I–III) for cocrystals and salts.

It is evident that for the salts, the proportion of two-component crystals with melting temperatures higher than that of the most high-melting component (Higher-II) increases from 13.3% (co-crystals) to 23.4% (1.8 times). In turn, for the salts, the share of two-component crystals of the group (Low-III) remains practically the same in comparison with the co-crystals: 27.2 and 27.7%, respectively. Finally, for the salts, the share of two-component crystals of the group (Between-I) decreases by 9.6% as compared to the co-crystals (from 59.0 to 49.4%).

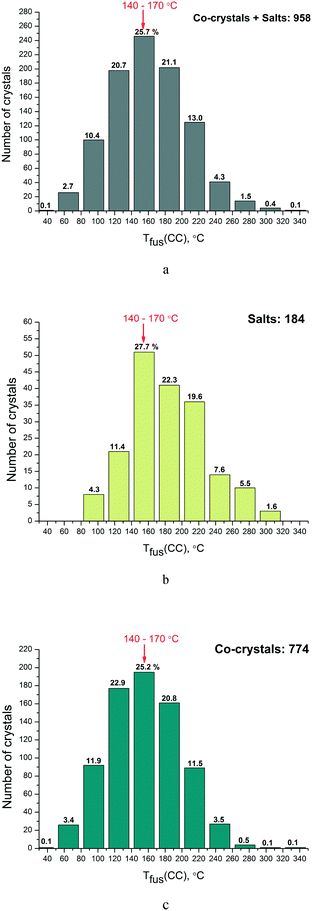
Then we analyzed the distribution functions of two-component crystals according to their melting points both for the full set obtained by single crystal diffraction experiments (958) and separately for the salts (189) and co-crystals (774). The results are given in Fig. 3(a–c). It is clearly seen that the most frequently encountered melting point for the two-component crystals from the analyzed database for both salts and co-crystals lies in the range of 140–170 °C (about 25–28% of the systems based on the total number of samples).

Fig. 3 Distribution of two-component crystals according to their melting points for: the total number of occurrences (a), salts (b) and cocrystals (c). The figures correspond to percentages of the total number of crystals.

Thus, there is no shift in the maximum of the melting temperature distribution function for the salts in the higher-melting region as compared to co-crystals (as is often asserted in the literature).

30 two-component molecular crystals in the analyzed database had two monotropic polymorphic modifications (i.e. polymorphs did not transform into one another when heated and melted at different temperatures). As mentioned above in section 2.1.1, there are 70 occurrences in the database which are associated with monotropic phases. It should be noted that 10 occurrences are associated with three or more polymorphic modifications, so to simplify the analysis we excluded them from consideration. Therefore, it was useful to compare how strongly the melting temperatures of monotropic forms differed from each other. Fig. 4 shows a histogram illustrating the relation between the distribution of the number of polymorphic modifications (two polymorphic forms for one two-component crystal) and the difference in the melting temperatures of these forms (absolute value). The results show that the maximum of the distribution function is in the temperature range from 0 to 5 °C (50% of the polymorph pairs under consideration). However, there are polymorphic modifications (20% of the sample used), in which the difference in the melting temperatures lies between 10 and 20 °C. This circumstance essentially distinguishes the polymorphic forms of two-component crystals from those of single-component crystals, where the differences in melting temperatures of monotropic modifications of the latter rarely exceed 10 °C.⁴¹ Another characteristic feature of the two-component systems (in contrast to the one-component crystals) is that there are monotropic forms in which the melting points differ by more than 40 and 50 °C. Thus, for the two-component crystals, polymorphism gives more possibilities to change the Gibbs energy (the energy of the crystal lattice) in comparison with the individual compounds. This, in turn, is one of the ways to obtain pharmaceutical crystals with improved API solubility.

Fig. 4 Distribution of monotropic polymorphic forms of the two-component crystals according to differences in their melting points (absolute value). The figures correspond to percentages of the total number of crystals.

A similar analysis was carried out for two-component crystals with the same composition and different stoichiometries. 42 co-crystals/salts with stoichiometries of (1 : 1) and (1 : 2)/(2 : 1) were chosen. Fig. 5 shows the distribution function of two-component crystals based on the difference in melting temperatures between co-crystals/salts with the selected stoichiometric compositions. As in the case of monotropic polymorphic forms, the maximum of the distribution function falls within the temperature range of 0–5 °C.

Fig. 5 Distribution of two-component crystals with the same composition and various stoichiometries according to differences in their melting points (absolute value). The figures correspond to percentages of the total number of crystals.

However, unlike the previous case, the maximum value is much lower: 31% compared to 50% for the polymorphic forms. The distribution of the co-crystals in the interval from 5 to 10 °C is comparable to polymorphs and co-crystals with different stoichiometries (about 23%). However, for the latter (co-crystals), the number of two-component crystals in the interval from 10 to 30 °C considerably exceeds that for the former (polymorphs). The number of co-crystals/salts with melting points differing by more than 40 °C for polymorphous modifications is comparable with the case under consideration. Thus, a change in the stoichiometric composition of two-component co-crystals makes it possible to lower the melting temperatures much more efficiently than the production of various monotropic polymorphic modifications. This fact becomes one more way of obtaining pharmaceutical co-crystals/salts with improved solubility of the poorly soluble component.

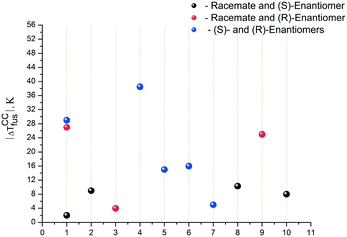
In conclusion, we analyzed the difference in the melting temperatures of co-crystals/salts, where the racemate or its enantiomer is one of the components, while the second component remains unchanged. Fig. 6 presents the analysis results.

Fig. 6 Plot of the melting point differences (absolute value) of cocrystals/salts where one component corresponds to the racemate or its enantiomer, whereas the second component is still the same. The numbering corresponds to: 1 – [(S)-naproxen + proline]; 2 – [(RS)-naproxen + proline]; 3 – [gabapentin + mandelic acid]; 4 – [R-proline amide + mandelic acid]; 5 – [meloxicam + malic acid]; 6 – [4,4′-bipyridine + naproxen]; 7 – [piperazine + naproxen]; 8 – [carbamazepine + tartaric acid]; 9 – [gabapentin + tartaric acid]; 10 – [acyclovir + tartaric acid].

The black dots correspond to the difference in melting temperatures of the co-crystals/salts if one of the components is a racemate or an (S)-enantiomer, the red dots represent a racemate or an (R)-enantiomer, and finally, the blue dots correspond to different enantiomers. Evidently, the analyzed temperature differences can reach significant values – up to 40 °C. Therefore, this variant of co-crystal/salt design can be also considered as a way of obtaining pharmaceutical systems with improved solubility.

3.2. Thermodynamics of two-component crystal formation

Earlier, we developed an approach to estimating the thermodynamic parameters (Gibbs energy, enthalpy, entropy term) for the formation of co-crystals.³⁶ The basic equations for calculations are given above (see section 2.2). Thus, in order to evaluate the thermodynamic characteristics of the formation of a two-component crystal, it is necessary to know the following parameters: the melting points of the individual components (T_fus(API), T_fus(CF)) and the two-component crystal (T_fus(CC)), and also the Gibbs energy and the sublimation enthalpy of the individual compounds (ΔG²⁹⁸_sub(API), ΔG²⁹⁸_sub(CF), ΔH²⁹⁸_sub(API), ΔH²⁹⁸_sub(CF)). To begin with, let us consider the simplest case, when the melting points of the individual substances and two-component crystals are known. There are 1175 such two-component crystals in the database we created. As the next step, we need to select only the co-crystals for which there are data about the Gibbs energies and sublimation enthalpies of the individual compounds – co-crystal/salt components. For this, we will use the molecular crystal sublimation thermodynamics database created by us (described in section 2.1.2). Analysis of the intersections of the two databases (two-component crystals and sublimation thermodynamics) has shown that for 281 co-crystals/salts, all the necessary information for evaluating the thermodynamic characteristics of their formation is available. For 198 two-component crystals, the databases contain only the melting points and no values of the thermodynamic sublimation functions of the individual substances constituting the co-crystal/salt. For 523 two-component crystals, there are melting points, and the Gibbs energy and sublimation enthalpy values for only one component of the co-crystal/salt. Finally, for 173 two-component crystals, the databases contain melting points, and sublimation enthalpy values for one or two components of the co-crystal/salt.

3.2.1. Two-component crystals with known melting points and sublimation thermodynamic characteristics of individual components. Thus, for 281 two-component crystals, all the necessary information for estimating the thermodynamic characteristics of their formation is available. In order to simplify the analysis of the thermodynamic functions of the co-crystal formation we used the diagram method applied by us in a previous work.³⁶ In short, it can be described as follows. Every process can be described by three thermodynamic functions (Gibbs energy, enthalpy and entropy). If we plot the enthalpy term along the OX axis in the coordinate plane, and the entropy term along the OY axis, the obtained point accurately describes the thermodynamic process. In this case the Gibbs energy can be evaluated by means of the point position on the isoenergetic curves (straight lines in this case) that are parallel to the YOX angle bisector. Fig. 7 shows the results of calculating the entropy term versus the enthalpy term in the coordinates.

Fig. 7 Thermodynamic functions of two-component crystal formation in the entropy vs. enthalpy co-ordinates. The isoenergetic curves of the ΔG²⁹⁸_f function are marked by dotted lines. The blue points correspond to the cocrystals/salts with a stoichiometry of (1 : 1), whereas the red points correspond to the cocrystals/salts with a stoichiometry of (2 : 1).

The blue dots denote two-component crystals with a stoichiometry of (1 : 1), whereas the red ones represent the remaining stoichiometry (mainly (1 : 2) and (2 : 1)). The regions of triangular sectors C, D, G and H in Fig. 7 correspond to the enthalpy-determined processes [sector C: ΔH²⁹⁸_f < 0, T·ΔS²⁹⁸_f > 0, |ΔH²⁹⁸_f| > |T·ΔS²⁹⁸_f|; sector D: ΔH²⁹⁸_f < 0, T·ΔS²⁹⁸_f < 0, |ΔH²⁹⁸_f| > |T·ΔS²⁹⁸_f|; sector G: ΔH²⁹⁸_f > 0, T·ΔS²⁹⁸_f < 0, |ΔH²⁹⁸_f| > |T·ΔS²⁹⁸_f|; sector H: ΔH²⁹⁸_f > T·ΔS²⁹⁸_f > 0]. The regions of triangular sectors A, B, E and F correspond to the entropy-determined processes [sector A: T·ΔS²⁹⁸_f > ΔH²⁹⁸_f > 0; sector B: ΔH²⁹⁸_f < 0, T·ΔS²⁹⁸_f > 0, |T·ΔS²⁹⁸_f| > |ΔH²⁹⁸_f|; sector E: ΔH²⁹⁸_f < 0, T·ΔS²⁹⁸_f < 0, |T·ΔS²⁹⁸_f| > |ΔH²⁹⁸_f|; sector F: ΔH²⁹⁸_f < 0, T·ΔS²⁹⁸_f < 0, |T·ΔS²⁹⁸_f| > |ΔH²⁹⁸_f|]. The isoenergetic curves of the ΔG²⁹⁸_f function are marked as dotted lines in Fig. 7. The calculation accuracy of ΔG²⁹⁸_f(CC)values was 6–10%. However, several reservations should be made. Firstly, both the obtained co-crystals and the individual compounds can have different polymorphic modifications. It is difficult to predict which polymorphic modifications of individual compounds should be chosen to make the suggested calculations. Moreover, there are no experimental data about the sublimation thermodynamic parameters of some polymorphic modifications. Therefore, we assume that the criterion of thermodynamically stable co-crystal formation must meet the following requirement:

ΔG²⁹⁸_f(CC) < 5 kJ mol⁻¹ (9)

It is the threshold value of 5 kJ mol⁻¹ that allows assuming that it is possible to obtain different polymorphic modifications. It should also be noted that the proposed algorithm for estimating the thermodynamics of the formation of two-component crystals does not work if the melting points of individual substances of the co-crystal are close to each other. Based on this limitation, 40 out of 281 two-component crystals were excluded (14.2%). Taking into account the proposed criterion of the thermodynamic stability of co-crystals/salts, 196 crystals out of 241 were predicted correctly (81.3%). If we take into account the crystals excluded because it was impossible to estimate the melting points of the co-crystal components at close melting temperatures, then the prediction accuracy is 69.8%.

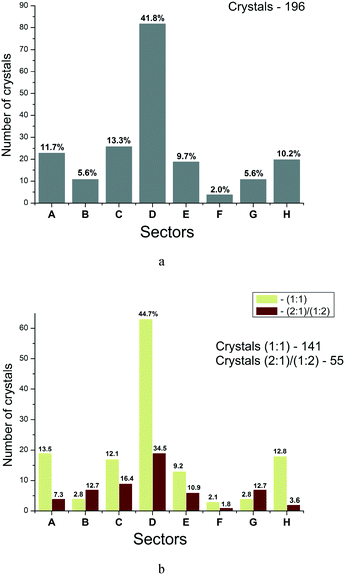
Each sector of the diagram corresponds to a definite relationship between the enthalpy and entropy terms of the two-component crystal formation. Therefore, we tried to construct the distribution functions for crystals (thermodynamically stable) by sectors. Fig. 8 illustrates these functions for all the crystals (a) and the crystals with different stoichiometries (b). It is evident that for all the crystals considered, the maximum distribution is in sector D (41.8%). The next (in descending order) are sectors C, A and H with the number of points about 3.6 times smaller than in sector D. If all the analyzed crystals are grouped into enthalpy and entropy determined ones, then the following regularity is obtained: the number of two-component crystals with enthalpy determined processes of co-crystals/salts formation corresponds to 70.9% (139), whereas the entropy determined processes –29.1% (57). Apparently, the obtained regularity partly justifies the criteria of thermodynamic stability of multicomponent crystals used in the literature, analyzing the enthalpy terms only.^14,42 However, such approaches are “not impeccable”, and as our analysis shows, the formation of every third multicomponent crystal is determined by entropy factors.

Fig. 8 Distribution of two-component crystals according to sectors of the diagram for: the all evaluated crystals (a); the crystals with stoichiometry (1 : 1) and (2 : 1)/(1 : 2) separately (b). The figures correspond to percentages of the total number of crystals.

Fig. 8b represents a similar analysis for different crystal stoichiometries separately. The observed regularities are similar to those of the general sample with small variations for each group. The number of crystals with enthalpy determined processes of co-crystals/salts formation corresponds to 72.4% (102) for (1 : 1) and 67.2% (37) for (2 : 1)/(1 : 2).

It was interesting to analyze whether there is a regularity in the thermodynamic stability of multicomponent crystals relative to different stoichiometric compositions. For this purpose, 12 co-crystals/salts with the same composition and different stoichiometries: (1 : 1) and (2 : 1)/(1 : 2) were selected for 241 two-component crystals. For the convenience of the analysis, the thermodynamic functions of the phase transition ΔY²⁹⁸_tr(CC(1 : 1) → CC((2 : 1)/(1 : 2))) (where Y corresponds to G, H, S) were calculated. Fig. 9 shows the results of the calculations in the coordinates of entropy versus enthalpy terms of the phase transition being analyzed. It is evident that for 75% of the examined co-crystals/salts (9), the two-component crystals with a stoichiometry of (2 : 1)/(1 : 2) are more thermodynamically stable than those with (1 : 1).

Fig. 9 Thermodynamic functions of the phase transition ΔY²⁹⁸_tr(CC(1 : 1) → CC((2 : 1)/(1 : 2))) (where Y corresponds to G, H, S) of the two-component crystals in entropy vs. enthalpy co-ordinates. The isoenergetic curves of the ΔG²⁹⁸_tr function are marked by dotted lines. The numbering corresponds to: 1 – [felodipine + 4-4′-bipyridine]; 2 – [carbamazepine + succinic acid]; 3 – [carbamazepine + malonic acid]; 4 – [carbamazepine + glutaric acid]; 5 – [isonicotinamide + benzoic acid]; 6 – [isonicotinamide + glutaric acid]; 7 – [nicotinamide + fumaric acid]; 8 – [pyrazinamide + 4-nitrobenzoic acid]; 9 – [ciprofloxacin + succinic acid]; 10 – [theophylline + glutaric acid]; 11 – [TNT + anthranilic acid]; 12 – [urea + succinic acid].

3.2.2. Two-component crystals with known melting points and unknown sublimation thermodynamic characteristics of individual components. As shown above, for 198 two-component crystals the databases contain only the melting points, and there are no data about the sublimation thermodynamic functions of the individual substances constituting the co-crystal/salt. For 523 two-component crystals, the databases have records about the melting points and the values of the sublimation Gibbs energy and enthalpy for only one component of the co-crystal/salt. Finally, for 173 two-component crystals, they contain the melting points and values of the sublimation enthalpy for one or two components of the co-crystal/salt. For such co-crystals with unknown values of the thermodynamic sublimation functions of the individual compounds, we are developing an approach based on using the database collected by us for the sublimation processes of molecular crystals (see section 2.1.2). The main idea is to select (using the Tanimoto similarity coefficient) from the database the structurally similar compounds with known sublimation thermodynamic functions to the compound with the unknown sublimation characteristics. Within this cluster, a linear correlation model that relates the sublimation Gibbs energies and the melting temperatures of the compounds is constructed. Knowing the melting point of our compound, we can estimate the sublimation Gibbs energy. At the next stage, using the correlation between the sublimation Gibbs energies and the molecular crystal enthalpy in the selected cluster (“compensation effect”), one can estimate the sublimation enthalpy of the unknown compound. The more representative the sample for each cluster is, the more accurately the values of the thermodynamic functions can be estimated. Some ideas of the presented approach are described in the work by Perlovich and Raevsky.³⁹

3.2.3. Two-component crystals with unknown melting points. The melting temperature of a two-component crystal can only be determined if the crystal itself is obtained. However, it would be very useful to estimate the melting temperature of a co-crystal/salt and its thermodynamic parameters of formation before the screening procedure. In this case, it would be possible to make conclusions about the reasonability of starting the screening procedures. In our previous paper,³⁶ we presented/described an algorithm for estimating the melting temperature of an unknown co-crystal/salt (T_fus(CC)) using the database of the melting points of two-component crystals. In order to do that, we divided all the co-crystals/salts into groups/clusters. Each of the groups contained two-component co-crystals, in which one component was the same (conventionally marked as API) for all the co-crystals, while the second one was different (conventionally marked as CF). Within each of the clusters, we correlated the melting temperatures of co-crystals with those of coformers using the following equation:

T_fus(CC) = A + B·T_fus(CF) (10)

By substantially increasing the database from 729 to 1175 two-component crystals, we were able to analyze 112 independent clusters and to obtain for 74 of them the correlation equations for the individual compounds – components of the co-crystal/salt. The results are presented in Table 1. Unfortunately, for 38 clusters, no correlations were found. Table 1 clearly shows that the pair correlation coefficients for the obtained correlation equations are relatively low but high enough to predict T_fus(CC) values with mean square deviations from 3 to 24° (only for 1,2-phenylenediamine, this value reaches 38.9° due to a small number of points in the cluster). The number of points in the cluster varies from 4 to 48. Thus, we can estimate the melting temperature of the unknown co-crystal/salt, one of the components of which is the compound selected for screening, and the second component is the compound for which there is a correlation equation given in Table 1. After that, we can begin to determine the thermodynamic characteristics of the co-crystal formation according to the algorithms described in sections 3.2.1 and 3.2.2.

Table 1 Coefficients of the correlation equation T_fus(CC) = A + B·T_fus(CF) for the clusters including the considered compound as one of the components of the two-component crystal

Compound	Stoichiometry			A	B	R	σ	n	T fus/°C
a Pair correlation coefficient. b Standard deviation. c The number of points in the cluster. d Correlation is not observed (cno).
1,2-Phenylenediamine	1 : 1			−286 ± 190	1.767 ± 0.445	0.9420	38.9	4	102.1
1-Hydroxy-2-naphthoic acid	1 : 1			−57 ± 113	1.060 ± 0.240	0.9320	16.3	5	192.0
2,3,5,6-F-4-I-Benzoic acid	1 : 1			31 ± 77	1.065 ± 0.211	0.9458	12.0	5	151.0
2,4-Dihydroxybenzoic acid	1 : 1			168 ± 120	0.627 ± 0.255	0.8177	10.4	5	213.0
2,5-Dihydroxybenzoic acid	1 : 1			43 ± 68	0.887 ± 0.144	0.9512	12.5	6	205.0
2-Acetaminopyridine		2 : 1		150 ± 46	0.579 ± 0.104	0.8922	20.5	10	69.0
o-Aminobenzoic acid (anthranilic acid)				cno^d				6	146.0
2-Hydroxybenzamide (salicylamide)	1 : 1			173 ± 48	0.525 ± 0.104	0.9458	10.7	5	140.8
2-Pyridone	1 : 1			105 ± 45	0.648 ± 0.107	0.9494	14.8	6	107.8
3,3′-Azopyridine				cno				10	133.0
3,5-Dihydroxybenzoic acid				cno				5	237.5
3-Hydroxybenzoic acid				cno				21	203.0
4,4′-Azopyridine				cno				11	105.5
4-Br-Benzoic acid				cno				5	234.0
4-Bromobenzamide		2 : 1		142 ± 115	0.704 ± 0.271	0.7576	19.8	7	191.5
4-(Dimethylamino)pyridine				cno				15	111.5
4-Aminobenzoic acid	1 : 1			159 ± 27	0.622 ± 0.060	0.9359	13.9	17	189.0
4-Nitrophenol	1 : 1	2 : 1		175 ± 39	0.612 ± 0.097	0.9031	19.3	11	113.5
4-Hydroxybenzoic acid	1 : 1			128 ± 28	0.703 ± 0.061	0.9283	14.7	23	214.5
4-Hydroxybenzamide	1 : 1		1 : 2	225 ± 51	0.484 ± 0.109	0.9123	10.2	6	161.5
4-Phenylpyridine	1 : 1		1 : 2	238 ± 38	0.289 ± 0.094	0.8387	14.3	6	69.5
p-Toluenesulfonic acid	1 : 1			251 ± 56	0.352 ± 0.109	0.8806	18.9	5	106.5
4-4′-Bipyridine		2 : 1		78 ± 11	0.429 ± 0.067	0.7937	16.7	26	111.8
1,1′-Bis(pyridin-4-ylmethyl)-2,2′-Biimidazole			1 : 2	251 ± 39	0.421 ± 0.099	0.8854	12.2	7	158.5
Acetazolamide	1 : 1		1 : 2	135 ± 52	0.773 ± 0.130	0.9477	16.5	6	258.5
Acridine	1 : 1		1 : 2	−93 ± 95	1.133 ± 0.218	0.8781	21.1	10	108.5
Acyclovir				cno				5	253.6
Adipic acid	1 : 1	2 : 1		203 ± 27	0.529 ± 0.062	0.9112	13.5	17	152.1
Agomelatine	1 : 1			cno				7	113.0
AMG517	1 : 1	2 : 1		224 ± 31	0.547 ± 0.077	0.8721	15.0	18	230.0
Arbidol	1 : 1	2 : 1		329 ± 28	0.190 ± 0.061	0.8728	8.02	5	124.8
Azelaic acid				cno				7	106.5
Benzamide	1 : 1			136 ± 63	0.593 ± 0.143	0.9227	13.3	5	128.5
Benzoic acid	1 : 1			116 ± 35	0.667 ± 0.079	0.9255	16.9	14	122.0
Benzotrifuroxan	1 : 1			231 ± 38	0.545 ± 0.091	0.9488	12.5	6	197.4
1,2-Bis(4-pyridyl)ethylene	1 : 1	2 : 1		212 ± 32	0.527 ± 0.075	0.8839	18.3	16	151.5
1,2-Bis(4-pyridyl)propane	1 : 1			250 ± 40	0.367 ± 0.090	0.8217	19.1	10	54.5
1,2-Bis(4-pyridyl)ethane	1 : 1			229 ± 20	0.310 ± 0.046	0.8686	13.2	17	112.0
Caffeine	1 : 1			153 ± 17	0.635 ± 0.037	0.9806	9.46	14	227.0
Carbamazepine	1 : 1			242 ± 17	0.430 ± 0.037	0.8981	13.2	34	190.1
trans-Cinnamic acid (alfa)	1 : 1			108 ± 68	0.663 ± 0.148	0.8943	19.3	7	134.0
Ciprofloxacin				cno				9	271.7
Citric acid				cno				11	155.2
CL20	1 : 1			74 ± 97	0.916 ± 0.240	0.9376	20.4	4	244.0
Clotrimazole	1 : 1	2 : 1		210 ± 41	0.461 ± 0.091	0.9298	7.36	6	148.0
Dapson	1 : 1	2 : 1	1 : 2	208 ± 36	0.484 ± 0.087	0.9407	10.8	6	177.5
Diflunisal				cno				5	211.8
Edaravone	1 : 1			165 ± 29	0.421 ± 0.099	0.9690	11.5	7	128.0
Febuxostat	1 : 1			350 ± 34	0.213 ± 0.079	0.8420	9.03	5	201.0
Flufenamic acid	1 : 1	2 : 1		204 ± 21	0.502 ± 0.049	0.9815	6.94	6	133.9
Fumaric acid	1 : 1			308 ± 22	0.325 ± 0.049	0.9105	8.30	11	287.0
Furosemide	1 : 1			147 ± 32	0.712 ± 0.075	0.9735	8.76	7	203.0
Gabapentin	1 : 1			205 ± 31	0.470 ± 0.071	0.9198	6.74	10	161.0
Gallic acid	1 : 1	2 : 1		256 ± 60	0.425 ± 0.130	0.8254	19.2	7	250.0
Glutaric acid				cno				29	96.5
Glycolic acid	1 : 1			209 ± 34	0.414 ± 0.069	0.9492	8.62	6	75.0
Hydrochlorothiazide	1 : 1			130 ± 60	0.787 ± 0.137	0.9321	18.4	7	269.0
Octahydro-1,3,5,7-tertranitro-1,3,5,7-tetrazocine (HMX)				cno				13	279.0
Hydroquinone				cno				6	173.5
Imatinib mesylate	1 : 1		1 : 2	375 ± 12	0.175 ± 0.022	0.9397	4.30	10	223.3
Indomethacin	1 : 1			181 ± 37	0.548 ± 0.081	0.9490	10.2	7	160.8
Isoniazid	1 : 1			163 ± 32	0.570 ± 0.070	0.9042	13.5	17	171.5
Isonicotinamide				cno				36	156.0
Ketoconazole				cno				5	148.0
Proline				cno				10	235.2
Lamotrigine	1 : 1			45 ± 12	0.980 ± 0.027	0.9988	2.83	5	217.3
Lornoxicam	1 : 1			364 ± 24	0.246 ± 0.057	0.9274	5.88	5	227.5
Maleic acid	1 : 1	2 : 1		175 ± 34	0.554 ± 0.069	0.9371	12.4	11	139.0
L-Malic acid				cno				7	101.0
Malonic acid	1 : 1			−9 ± 128	0.888 ± 0.252	0.8208	20.0	8	136.0
Mandelic acid				cno				9	132.6
Me-Paraben	1 : 1	3 : 1	3 : 2	−13 ± 18	0.910 ± 0.042	0.9968	3.11	5	126.5
Meloxicam	1 : 1			251 ± 37	0.508 ± 0.087	0.8688	14.5	13	254.0
Minoxidil				cno				8	273.0
3-(6-Methoxypyridin-3-yl)-5-(4-methylsulfonyl phenyl)-pyridin-2-amine (MMP)				cno				6	195.0
Naproxen	1 : 1	2 : 1	1 : 2	185 ± 43	0.512 ± 0.095	0.8627	15.0	12	155.6
Niclosamide				cno				6	229.5
Nicotinamide	1 : 1			204 ± 17	0.454 ± 0.036	0.8802	16.7	48	128.4
Nicotinic acid	1 : 1			11 ± 58	0.957 ± 0.120	0.9701	15.9	6	232.0
Norfloxacin	1 : 1			216 ± 65	0.557 ± 0.148	0.8389	23.7	8	220.6
Nitrofurantoin (NTF)				cno				7	268.4
Oxalic acid				cno				24	189.0
p-Coumaric acid	1 : 1			292 ± 22	0.347 ± 0.047	0.9571	7.94	7	211.5
Paracetamol	1 : 1			284 ± 23	0.291 ± 0.046	0.9529	7.53	6	170.0
p-Aminosalicylic acid				cno				11	150.5
Phenazine	1 : 1	2 : 1	1 : 2	16 ± 83	0.968 ± 0.178	0.9252	25.9	7	177.0
Phloroglucinol				cno				7	216.0
Pimelic acid	1 : 1	2 : 1		112 ± 47	0.667 ± 0.113	0.9352	12.5	7	104.0
Pyrazinamide	1 : 1			99 ± 39	0.704 ± 0.085	0.8962	14.7	19	189.0
Pyrazine				cno				8	52.0
Quercetin				cno				21	321.4
Resorcinol	1 : 1	2 : 1		221 ± 55	0.458 ± 0.119	0.8245	21.9	9	110.5
Saccharin	1 : 1			289 ± 19	0.366 ± 0.042	0.8476	9.79	32	227.9
2-Hydroxybenzoic acid (salicylic acid)	1 : 1			189 ± 35	0.533 ± 0.073	0.8305	20.2	26	159.0
Sebacic acid	1 : 1			233 ± 53	0.465 ± 0.127	0.8532	17.7	7	132.0
Sildenafil				cno				9	188.7
Sorbic acid				cno				6	133.5
Sertraline (STL(+))				cno				12	247.5
Suberic acid				cno				18	142.5
Succinic acid		2 : 1		147 ± 42	0.636 ± 0.091	0.8311	18.2	24	184.0
Sulfacetamide				cno				5	184.0
Sulfadimidine	1 : 1			360 ± 27	0.219 ± 0.060	0.6847	10.0	17	197.0
Tartaric acid				cno				16	172.5
Tegafur	1 : 1			288 ± 58	0.262 ± 0.126	0.7683	15.5	5	171.7
Temozolomide				cno				6	210.0
Tenoxicam	1 : 1			324 ± 72	0.341 ± 0.182	0.7348	7.76	5	209.5
Tetra-me-pyrazine			1 : 2	335 ± 28	0.180 ± 0.065	0.7477	9.55	8	85.0
Theophylline	1 : 1			−173 ± 76	1.400 ± 0.168	0.9347	21.2	12	273.6
2,4,6-Trinitrotoluene (TNT)	1 : 1			242 ± 27	0.331 ± 0.063	0.8451	14.6	13	80.5
Urea	1 : 1	2 : 1	1 : 2	47 ± 59	0.845 ± 0.118	0.9068	22.0	13	134.3
Vanillic acid	1 : 1	2 : 1	1 : 2	285 ± 26	0.308 ± 0.053	0.9104	10.9	9	209.2
Voriconazole				cno				8	129.6

---

3.2.4. General algorithm for estimating the thermodynamics of two-component crystal formation. In general, the application of the developed approach might look like this (Fig. 10). Let us assume that before obtaining the co-crystal/salt experimentally, we need to evaluate the possibility of its formation between the pre-selected API and the coformer. At the initial stage, we must analyze the available correlation equations in order to find out if there is an equation relating the melting temperatures of two-component crystals including the chosen coformer among them. If such an equation exists, then by knowing the melting temperature of the API we can estimate the co-crystal/salt melting temperature. The next step is to find out if the database of the sublimation thermodynamic parameters contains the values of the sublimation thermodynamic functions for both the API and the coformer. If such values are included in the database, we can calculate the thermodynamics of co-crystal formation. If not, then there are two possible ways to solve the problem. Firstly, it is possible to perform the sublimation experiments for the co-crystal components. It should be noted that these experiments are quite routine. As a rule, it takes one to several weeks (depending on the compound being studied) to obtain a complete thermodynamic picture of the sublimation of a single molecular crystal. However, it should be emphasized that the set of coformers used to design co-crystals is usually the same. Therefore, over time, a library of the sublimation thermodynamic parameters for these compounds will be formed and it will not be necessary to waste time on carrying out the indicated experiments. Secondly, if it is not possible to conduct the sublimation experiments, we can estimate the thermodynamic parameters of sublimation using the sublimation database for molecular crystals and the clusterization approach described briefly in section 3.2.2. After that, one can calculate the necessary thermodynamic functions for the co-crystal/salt formation. If the Gibbs energy of the crystal formation is lower than the value chosen as the criterion (5 kJ mol⁻¹), then the probability of obtaining a co-crystal/salt is high, and one can proceed to its production. Otherwise, you need to use a different coformer. It is of interest that if ΔG²⁹⁸_f(CC) < −5 kJ mol⁻¹ (i.e. greater than the energies of polymorphic transitions), then any method can be safely chosen for screening (dry grinding techniques, with an addition of solvent, slurry, recrystallization). If ΔG²⁹⁸_f(CC) does not fit into the indicated criterion, it is necessary to carefully choose the method with which to start. In our opinion, for the reaction to run at low driving force values, the crystals of the initial substances must have an excessive number of defects. Such conditions can be achieved by dry grinding techniques and grinding with an addition of solvent.

Fig. 10 Chart of general algorithm for the estimation of two-component crystal formation thermodynamics.

Conclusions

Based on literature analysis, we have built up a database including the melting temperatures of two-component molecular co-crystals and individual compounds (1175 co-crystals/salts). In order to estimate the thermodynamics of two-component crystal formation, we created a database based on the values published in the literature from 1900 till 2016 inclusive. The database includes enthalpies and Gibbs energies of individual molecular crystals obtained by various methods.

Having analyzed all the co-crystals/salts, we have found out that the melting points of 54.6% of the co-crystals are in the range between (I), of 14.8% higher (II) than, and of 30.6% lower (I) than those of the individual compounds.

A comparative analysis of the distribution of the melting temperatures of two-component crystals has been carried out for the selected groups (I–III) of the co-crystals and salts. It has been found that for the salts, the share of two-component crystals with melting temperatures higher than those of the highest-melting component (Higher-II) increases from 13.3% (co-crystals) to 23.4% (1.8 times). In turn, for the salts, the share of two-component crystals of the group (Low-III) remains practically the same in comparison with the co-crystals: 27.2 and 27.7%, respectively. Finally, for the salts, the share of two-component crystals of the group (Between-I) decreases by 9.6% as compared to the co-crystals (from 59.0 to 49.4%).

The distribution functions of the two-component crystals were analyzed according to their melting points both for the full set obtained by single crystal diffraction experiments (958) and separately for the salts (189) and co-crystals (774). It has been found that the most frequently encountered melting temperature for the two-component crystals from the analyzed database for both the salts and the co-crystals is 140–170 °C (about 25–28% of the systems based on the total number of samples). Thus, there is no shift in the maximum of the salt melting temperature distribution function in the region of higher-melting as compared to the co-crystals (as is often asserted in the literature).

We have compared the differences in the melting temperatures of the monotropic polymorphic forms, as well as of two-component crystals with the same composition and different stoichiometries. It has been found that changing the stoichiometric composition of two-component co-crystals makes it possible to lower the melting temperatures much more efficiently than the production of various monotropic polymorphous modifications. This circumstance is one of the ways to obtain pharmaceutical co-crystals/salts with improved solubility of the poorly soluble component.

Correlation equations have been obtained, connecting the melting points of co-crystals/salts and individual components for 74 active pharmaceutical ingredients and coformers, which enables designing co-crystals with predictable melting temperatures.

An approach to estimation of co-crystal sublimation thermodynamic characteristics has been developed. The thermodynamic functions of the formation process of 281 co-crystals have been obtained and analyzed. The diagram method has been used to analyze the parameters under study. Taking into account the proposed criterion of the thermodynamic stability of the co-crystals/salts, 196 crystals from 281 were predicted correctly (69.8%).

The analysis of experimental data distribution in the diagram sectors has shown that the number of two-component crystals with enthalpy determined processes of co-crystal/salt formation corresponds to 70.9%, whereas the number of those with entropy determined processes –29.1%. The thermodynamic stability of multicomponent crystals relative to different stoichiometric compositions has been analyzed. 75% of the examined co-crystals/salts with (2 : 1)/(1 : 2) stoichiometry were shown to be more thermodynamically stable than those with the (1 : 1) stoichiometry. A general algorithm for estimating the thermodynamics of two-component crystal formation has been proposed.

Acknowledgements

This work was supported by the Russian Foundation of Basic Research (grant no. 16-53-150007).

Notes and references

1. A. Findlay, A. N. Campbell and N. O. Smith, Phase Rule and Its Applications, Dover, Mineola, NY, 1951.
2. A. I. Kitaigorodski, Molecular crystals, Nauka, Moscow, 1971.
3. G. P. Stahly, Cryst. Growth Des., 2009, 9, 4212.
4. S. L. Childs and M. J. Zaworotko, Cryst. Growth Des., 2009, 9, 4208.
5. A. V. Trask, Mol. Pharmaceutics, 2007, 4(3), 301.
6. M. R. Caira, Mol. Pharmaceutics, 2007, 4(3), 310.
7. C. Zhang, Z. Yang, X. Zhou, C. Zhang, Y. Ma, J. Xu, Q. Zhang, F. Nie and H. Li, Cryst. Growth Des., 2014, 14, 3923.
8. H. Zhang, Z. Cuo, X. Wang, J. Xu, X. He, Y. Liu, X. Liu, H. Huang and J. Sun, Cryst. Growth Des., 2013, 13, 679.
9. I. M. Pavlovetc, S. Draguta, M. I. Fokina, T. V. Timofeeva and I. Yu. Denisyuk, Opt. Commun., 2016, 362, 64.
10. H. Figi, M. Jazbinšek, C. Hunziker, M. Koechlin and P. Günter, Opt. Express, 2008, 16(15), 11310.
11. N. Issa, P. Karamertzanis, G. Wellch and S. Price, Cryst. Growth Des., 2009, 9(1), 442.
12. P. Karamertzanis, A. Kazantsev, N. Issa, G. Wellch, C. Adjiman, C. Pantelides and S. Price, J. Chem. Theory Comput., 2009, 5(5), 1432.
13. D. Musumeci, C. Hunter, R. Prohens, S. Scuderi and F. McCabe, Chem. Sci., 2011, 2(5), 883.
14. Y. A. Abramov, C. Loschen and A. Klamt, J. Pharm. Sci., 2012, 101(10), 3687.
15. M. A. Mohammad, A. Alhalaweh and S. P. Velaga, Int. J. Pharm., 2011, 407, 63.
16. Y. Lin, H. Yang, C. Yang and J. Wang, Pharm. Res., 2014, 31, 566.
17. S. Zhang and Å. C. Rasmuson, Cryst. Growth Des., 2013, 13, 1153.
18. S. Zhang and Å. C. Rasmuson, CrystEngComm, 2012, 14, 4644.
19. L. Zhao, V. Raval, N. E. B. Briggs, R. M. Bhardwaj, T. McGlone, I. D. H. Oswald and A. J. Florence, CrystEngComm, 2014, 16, 5769.
20. Z. Q. Yu, P. S. Chow and R. B. H. Tan, Cryst. Growth Des., 2010, 10, 2382.
21. A. O. L. Évora, R. A. E. Castro, T. M. R. Maria, M. R. Silva, J. H. ter Horst, J. Canotilho and M. E. S. Eusébio, Int. J. Pharm., 2014, 466, 68.
22. S. Jung, J. Lee and I. W. Kim, J. Cryst. Growth, 2013, 373, 59.
23. K.-S. Lee, K.-J. Kim and J. Ulrich, Chem. Eng. Technol., 2015, 38(6), 1073.
24. K. Ma, Y. Zhang, H. Kan, L. Cheng, L. Luo, Q. Su, J. Gao, Y. Gao and J. Zhang, Pharm. Res., 2014, 31, 1766.
25. T. Rager and R. Hilfiker, Z. Phys. Chem., 2009, 223, 793.
26. X. Sun, Q. Yin, S. Ding, Z. Shen, Y. Bao, J. Gong, B. Hou, H. Hao, Y. Wang, J. Wang and C. Xie, J. Chem. Eng. Data, 2015, 60(4), 1166.
27. X. Sun, Q. Yin, S. Ding, Z. Shen, Y. Bao, J. Gong, B. Hou, H. Hao, Y. Wang, J. Wang and C. Xie, J. Chem. Thermodyn., 2015, 85, 171.
28. A. O. Surov, A. P. Voronin, A. A. Simagina, A. V. Churakov, S. Y. Skachilova and G. L. Perlovich, New J. Chem., 2015, 39, 8614.
29. A. O. Surov, A. N. Manin, A. V. Churakov and G. L. Perlovich, Mol. Pharmaceutics, 2015, 12(11), 4154.
30. A. Shayanfara, S. P. Velaga and A. Jouyban, Fluid Phase Equilib., 2014, 363, 97.
31. A. O. Surov, K. A. Solanko, A. D. Bond, A. Bauer-Brandl and G. L. Perlovich, CrystEngComm, 2016, 18, 4818.
32. M. A. Oliveira, M. L. Peterson and R. J. Davey, Cryst. Growth Des., 2011, 11, 449.
33. A. Alhalaweh, L. Roy, N. Rodríguez-Hornedo and S. P. Velaga, Mol. Pharmaceutics, 2012, 9, 2605.
34. D. J. Good and N. Rodríguez-Hornedo, Cryst. Growth Des., 2009, 9(5), 2252.
35. C. Grossjohann, D. R. Serrano, K. J. Paluch, P. O'Connell, L. Vella-Zarb, P. Manesiotis, T. McCabe, L. Tajber, O. I. Corrigan and A. M. Healy, J. Pharm. Sci., 2015, 104(4), 1385.
36. G. L. Perlovich, CrystEngComm, 2015, 17, 7019.
37. Copyright© 2015 American Chemical Society, Last Updated, April 2017.
38. F. H. Allen and O. Kennard, J. Mol. Graphics, 1993, 8, 31 , http://www.ccdc.cam.ac.uk/.
39. G. L. Perlovich and O. A. Raevsky, Cryst. Growth Des., 2010, 10(6), 2707.
40. G. L. Perlovich, S. V. Kurkov, A. N. Kinchin and A. Bauer-Brandl, Eur. J. Pharm. Biopharm., 2004, 57(2), 411.
41. M. Pudipeddi and A. T. M. Serajuddin, J. Pharm. Sci., 2005, 94, 929.
42. L. N. Kuleshova, D. W. M. Hofmann and R. Boese, Chem. Phys. Lett., 2013, 564, 26.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ce00554g

---