Open Access Article
Open Access ArticleClosed-shell paramagnetic porphyrinoids†
Rashid R.
Valiev
 *ab,
Heike
Fliegl
*c and
Dage
Sundholm
*ab,
Heike
Fliegl
*c and
Dage
Sundholm
 *b
*b
aTomsk State University, Lenina 36, Tomsk, Russian Federation. E-mail: valievrashid@gmail.com
bDepartment of Chemistry, University of Helsinki, P.O. Box 55 (A. I. Virtanens plats 1), FIN-00014, Finland. E-mail: dage.sundholm@helsinki.fi
cCentre for Theoretical and Computational Chemistry (CTCC), Department of Chemistry, University of Oslo, P.O. Box 1033 Blindern, 0315 Oslo, Norway. E-mail: heike.fliegl@kjemi.uio.no
First published on 21st August 2017
Abstract
Magnetizabilities and magnetically induced ring-current strength susceptibilities have been calculated at the Hartree–Fock, density functional theory and second order Møller–Plesset levels for a number of antiaromatic closed-shell carbaporphyrins, carbathiaporphyrins and isophlorins. The calculations yield a linear relation between magnetizabilities and ring-current strength susceptibilities. The calculations show that the porphyrinoids with the largest ring-current strength susceptibility are closed-shell paramagnetic molecules with positive magnetizabilities. The closed-shell paramagnetism is due to the large paramagnetic contribution to the magnetizability originating from the strong paratropic ring current in the antiaromatic porphyrinoids.
Paramagnetism is usually associated with the non-zero electronic spin of open-shell electronic configurations,1 whereas closed-shell paramagnetic molecules are rare.2 The classic example for a paramagnetic closed-shell molecule is BH and the isoelectronic CH+ and BeH− ions, whose magnetic response is characterized by strong paratropic currents.3–5 Closed-shell paramagnetism has also been predicted for the MnO4− anion,6 antiaromatic molecules,7 carbon nanotube tori,8 and for molecules in strong magnetic fields.9,10 Recently, a large positive magnetic susceptibility was measured for a closed-shell molecular nanoring in its 4+ oxidation state.11
Here, we propose that strongly antiaromatic porphyrinoids according to the magnetic criterion may be closed-shell paramagnetic molecules. We have calculated the isotropic magnetizabilities and ring-current strength susceptibilities at the Hartree–Fock (HF), second-order Møller–Plesset (MP2) perturbation theory and density functional theory (DFT) levels. The magnetizabilities and ring-current strength susceptibilities of three carbaporphyrins, two carbathiaporphyrins and two synthesized isophlorins show that porphyrinoids sustaining strong paratropic ring currents when exposed to an external magnetic field may have positive magnetizabilities indicating paramagnetism.
Isophlorin belongs to a class of porphyrin derivatives with a formal aromatic pathway consisting of 20 π electrons making them antiaromatic.12–15 Aromatic pathways are discussed in the ESI.† Tetraoxa-isophlorin and dioxa-dithia-isophlorin are the first air-stable isophlorins that have been synthesized.16 They are antiaromatic with formally 4n π electrons, since all four pyrrole nitrogen moieties are replaced by either oxygen or sulfur.16–19
Classic aromatic porphyrins like porphin are considered to have 18 π electrons.16,17,20 However, since the ring current of the porphyrins flows along all chemical bonds of the macroring, the number of π electrons participating in the ring-current flow is 26 for the aromatic porphyrins and 28 for the antiaromatic isophlorins.13,14 The porphyrinoids fulfil Hückel's (4n + 2) and (4n) aromaticity rules. Calculations on antiaromatic molecules show that they have a closed-shell singlet ground state.
Carbaporphyrins can be constructed by replacing one or several of the nitrogen moieties with CH2 units.21 Since CH2 is isoelectronic with oxygen, antiaromatic carbaporphyrins are obtained when all four nitrogen moieties in porphin are replaced with CH2.15 The first carbaporphyrins were synthesized 20 years ago.22,23 Recently, we studied the electronic structure and spectroscopic properties of isophlorins.14 Calculations of magnetically induced current densities showed that the isophlorins and carbaporphyrin with four CH2 moieties are strongly antiaromatic.14,15 Time-dependent density functional theory and approximate second-order coupled-cluster calculations showed that they have a closed-shell singlet ground state with an optical gap of about 1 eV. The lowest electronic excited state of the isophlorins is reached by an electronic dipole-forbidden (parity-forbidden) but magnetic dipole-allowed (angular-momentum-allowed) transition. Isophlorins have five low-lying excited singlet states as compared to the four Gouterman states of porphyrins.24
The magnetically induced current density can be expressed using perturbation theory as a gauge-origin dependent sum of diamagnetic and paramagnetic contributions.25–27 Details are discussed in the ESI.†
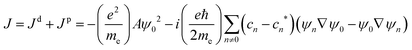 | (1) |
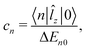 | (2) |
![[l with combining circumflex]](https://www.rsc.org/images/entities/i_char_006c_0302.gif) z is the z-component of the angular momentum operator. The terms containing the matrix elements 〈n|
z is the z-component of the angular momentum operator. The terms containing the matrix elements 〈n|![[l with combining circumflex]](https://www.rsc.org/images/entities/i_char_006c_0302.gif) z|0〉 represent the paramagnetic contribution to the total current density, while the diamagnetic contribution is fully described by the ground-state wave function.
z|0〉 represent the paramagnetic contribution to the total current density, while the diamagnetic contribution is fully described by the ground-state wave function.
When discussing magnetizabilities one usually refers to the experimentally measurable bulk quantity as magnetic susceptibility and to the molecular property as magnetizability.28 The magnetizability χm of a molecule is defined as the second derivative of its ground-state energy E with respect to the external magnetic field B,
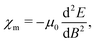 | (3) |
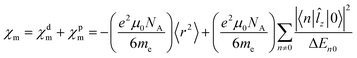 | (4) |
![[l with combining circumflex]](https://www.rsc.org/images/entities/i_char_006c_0302.gif) z|0〉 also appear in the expression for the magnetizability. The largest contributions to χpm are expected from the lowest excited electronic states, because of the small energy denominator. We investigate how the magnetizability is related to the magnetically induced ring-current strength susceptibility of antiaromatic porphyrinoids. The similarities between the expressions in eqn (1) and (2) and in eqn (4) suggest that measurements of magnetic dipole-allowed transitions and magnetizabilities can be used for providing information about magnetically induced current densities, which are only indirectly detectable.29–31
z|0〉 also appear in the expression for the magnetizability. The largest contributions to χpm are expected from the lowest excited electronic states, because of the small energy denominator. We investigate how the magnetizability is related to the magnetically induced ring-current strength susceptibility of antiaromatic porphyrinoids. The similarities between the expressions in eqn (1) and (2) and in eqn (4) suggest that measurements of magnetic dipole-allowed transitions and magnetizabilities can be used for providing information about magnetically induced current densities, which are only indirectly detectable.29–31
The magnetizability can be obtained by integrating the current density susceptibility (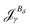 ) multiplied with the vector potential of the external magnetic field (rβ)26
) multiplied with the vector potential of the external magnetic field (rβ)26
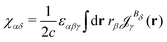 | (5) |
Magnetizabilities were calculated at the DFT, HF, and MP2 levels. The ring-current strength susceptibilities have been obtained by integrating the current-density susceptibilities.27,36 The optimized molecular structures shown in Fig. 1 were taken from ref. 14, 15 and 37. The multi-configuration character of the ground-state of molecule VII having the largest ring-current strength susceptibility was investigated by performing calculations at the complete active space (CASSCF) and extended multi-configuration quasi-degenerate perturbation theory at second order (XMC-QDPT2) levels. The computational details are given in the ESI.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 38–44 The XMC-QDPT2 calculations show that molecule VII has a closed-shell singlet ground state with a weight of 0.94 for the main configuration. The XMC-QDPT2 calculations yield vertical excitation energies of 0.81 eV and 0.52 eV for the lowest singlet (S1) and triplet (T1) states, respectively, which can be compared to the lowest singlet excitation energy of 0.45 eV calculated at the B3LYP level.
38–44 The XMC-QDPT2 calculations show that molecule VII has a closed-shell singlet ground state with a weight of 0.94 for the main configuration. The XMC-QDPT2 calculations yield vertical excitation energies of 0.81 eV and 0.52 eV for the lowest singlet (S1) and triplet (T1) states, respectively, which can be compared to the lowest singlet excitation energy of 0.45 eV calculated at the B3LYP level.
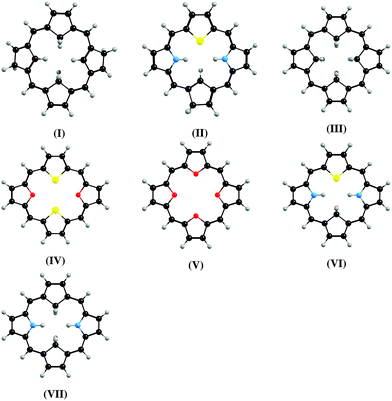 | ||
| Fig. 1 The molecular structures of the investigated carbaporphyrins, carbathiaporphyrins and isophlorins. | ||
The magnetizability calculations at the MP2 level are assumed to be the most reliable ones, because MP2 calculations consider electron correlation effects and do not suffer from self-interaction problems as many DFT functionals do.45 Previous magnetizability calculations at the HF level yielded values that agreed qualitatively with magnetizabilities calculated at coupled-cluster levels,46 whereas the accuracy of the magnetizabilities calculated at the DFT level depend on the employed functional.45 The MP2 calculations suggest that compounds IV–VII are paramagnetic, since the calculated magnetizabilities of the four porphyrinoids are positive. The magnetizabilities calculated at the DFT, HF and MP2 levels are compared in Table 1. The reason for the paramagnetism is the large paramagnetic contribution due to the strong paratropic ring current that contributes to the second term of eqn (4). B3LYP tends to overestimate the paramagnetic character, whereas HF calculations underestimate it. The magnetizabilities calculated at the HF level are negative for all the studied porphyrinoids. For the molecules with weak paratropic ring currents, the magnetizabilities calculated at the HF and MP2 levels qualitatively agree, whereas for the strongly antiaromatic molecules, electron correlation effects seem to be important for the magnetizabilities.
| Molecule | χ m(B3LYP) | χ m(HF) | χ m(MP2) |
|---|---|---|---|
| I | −35.2 | −38.4 | −39.5 |
| II | −21.8 | −36.3 | −32.3 |
| III | 25.4 | −23.9 | −8.7 |
| IV | 44.4 | −19.2 | 7.11 |
| V | 65.9 | −11.6 | 15.8 |
| VI | 90.2 | −14.0 | 21.8 |
| VII | 204.9 | −3.8 | 48.3 |
Correlation effects are missing at the HF level, whereas self-interaction problems of the B3LYP functional are most likely the reason for overestimating the paramagnetic character at the DFT level.45 The performance of other DFT functionals was investigated by calculating the magnetizability of the most antiaromatic molecule (VII) using the CAM-B3LYP47 and B97D48 functionals, which have a more correct form of the long-ranged potential than the B3LYP functional has. At the CAM-B3LYP level, we obtained a magnetizability for molecule VII of 65.5 a.u. and the B97D functional yielded a value of 54.2 a.u. These values are in close agreement with the MP2 value of 48.3 a.u. suggesting that VII is indeed a paramagnetic molecule.
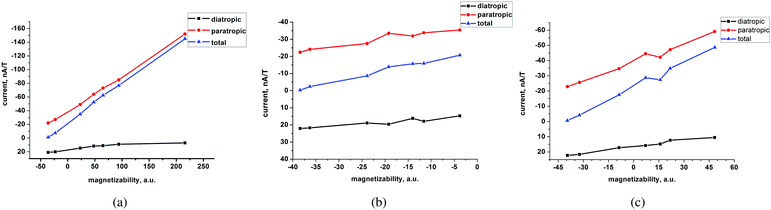
At the MP2 level, molecules I–III are diamagnetic even though molecule III sustains at the MP2 level a paratropic ring current of −17.5 nA T−1. Molecules I and II are practically non-aromatic according to the ring-current criterion. The magnetizabilities and ring-current strength susceptibilities in Tables 1 and 2 show that porphyrinoids with a stronger ring-current strength susceptibility than about −20 nA T−1 are paramagnetic.
| Molecule | I(B3LYP) | I(HF) | I(MP2) |
|---|---|---|---|
| I | −1.1 | −0.3 | −0.6 |
| II | −7.4 | −2.4 | −4.2 |
| III | −35.0 | −8.6 | −17.5 |
| IV | −52.5 | −13.9 | −28.7 |
| V | −62.5 | −15.9 | −27.4 |
| VI | −76.8 | −18.5 | −34.9 |
| VII | −145.0 | −20.7 | −48.6 |
A linear correlation between the paratropic ring-current strength susceptibility and the magnetizability is obtained as shown in Fig. 2. A similar relation has previously been proposed for small molecular rings.49 Since the diatropic ring-current strength susceptibility is almost constant for the studied molecules, the total ring-current strength susceptibility is also a linear function of the magnetizability implying that the ring-current strength susceptibility can be estimated for the investigated class of porphyrinoids by measuring the magnetizability. The linear relation is not completely unexpected, because the magnetizability can be calculated by integrating the current density susceptibility tensor multiplied with the vector potential of the external magnetic field as shown in eqn (5). Since the studied molecules have similar geometries, they have almost the same shape of the current density and the ring current. Thus, the value of the integral obtained in eqn (5) depends mainly on the size of the ring-current strength susceptibility. For the same reason, a linear relation between the magnetizability and the ring-current strength susceptibility is also expected for aromatic porphyrinoids. Thus, the magnetically induced ring-current strength susceptibility for porphyrinoids can be estimated by measuring magnetizabilities. The calculated magnetizabilities and ring-current strength susceptibilities indicate that antiaromatic porphyrins with a stronger negative ring-current strength susceptibility than −20 nA T−1 are paramagnetic molecules with positive magnetizabilities.
This work was supported by The Academy of Finland through projects 275845 and 297304. We acknowledge CSC – IT Center for Science, Finland for computational resources. H. F. thanks for the support by the Norwegian Research Council through the CoE Centre for Theoretical and Computational Chemistry (Grant No. 179568/V30 and 231571/F20). This work has received support from the Norwegian Supercomputing Program (NOTUR) through a grant of computer time (Grant No. NN4654K).
Conflicts of interest
There are no conflicts to declare.References
- J. H. van Vleck, The Theory of Electric and Magnetic Susceptibilities, Oxford University Press, London, 1932, pp. 1–384 Search PubMed.
- R. A. Hegstrom and W. N. Lipscomb, Rev. Mod. Phys., 1968, 40, 354–358 CrossRef CAS.
- P. W. Fowler and E. Steiner, Mol. Phys., 1991, 74, 1147–1158 CrossRef CAS.
- S. P. A. Sauer, T. Enevoldsen and J. Oddershede, J. Chem. Phys., 1993, 98, 9748–9757 CrossRef CAS.
- K. Ruud, T. Helgaker, K. L. Bak, P. Jørgensen and J. Olsen, Chem. Phys., 1995, 195, 157–169 CrossRef CAS.
- P. W. Fowler and E. Steiner, J. Chem. Phys., 1992, 97, 4215–4223 CrossRef CAS.
- E. Steiner and P. W. Fowler, Chem. Commun., 2001, 2220–2221 RSC.
- R. Tamura, R. Ikuta, M. Hirahara and M. Tsukada, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 045418 CrossRef.
- E. I. Tellgren, T. Helgaker and A. Soncini, Phys. Chem. Chem. Phys., 2009, 11, 5489–5498 RSC.
- K. K. Lange, E. I. Tellgren, M. R. Hoffmann and T. Helgaker, Science, 2012, 337, 327–331 CrossRef CAS PubMed.
- M. D. Peeks, T. D. W. Claridge and H. L. Anderson, Nature, 2017, 541, 200–203 CrossRef CAS PubMed.
- R. B. Woodward, Angew. Chem., 1960, 72, 651–662 CrossRef CAS.
- H. Fliegl and D. Sundholm, J. Org. Chem., 2012, 77, 3408–3414 CrossRef CAS PubMed.
- R. R. Valiev, H. Fliegl and D. Sundholm, J. Phys. Chem. A, 2013, 117, 9062–9068 CrossRef CAS PubMed.
- R. R. Valiev, H. Fliegl and D. Sundholm, Phys. Chem. Chem. Phys., 2015, 17, 14215–14222 RSC.
- J. S. Reddy and V. G. Anand, J. Am. Chem. Soc., 2008, 130, 3718–3719 CrossRef CAS PubMed.
- T. Higashino and A. Osuka, Chem. Sci., 2013, 4, 1087–1091 RSC.
- C. Liu, D.-M. Shen and Q.-Y. Chen, J. Am. Chem. Soc., 2007, 129, 5814–5815 CrossRef CAS PubMed.
- Y. Matano, T. Nakabuchia, S. Fujishige, H. Nakano and H. Imahori, J. Am. Chem. Soc., 2008, 130, 16446–16447 CrossRef CAS PubMed.
- A. K. Jissy and A. Datta, J. Comput. Methods Sci. Eng., 2010, 10, 203–218 CAS.
- D. Li and T. D. Lash, J. Org. Chem., 2014, 79, 7112–7121 CrossRef CAS PubMed.
- K. Berlin, Angew. Chem., Int. Ed., 1996, 35, 1820–1822 CrossRef CAS.
- T. D. Lash and M. J. J. Hayes, Angew. Chem., Int. Ed., 1997, 36, 840–842 CrossRef CAS.
- M. Gouterman, J. Mol. Spectrosc., 1961, 6, 138–163 CrossRef CAS.
- P. W. Atkins and R. S. Friedman, Molecular Quantum Mechanics, Oxford University Press, 1997 Search PubMed.
- P. Lazzeretti, Prog. Nucl. Magn. Reson. Spectrosc., 2000, 36, 1–88 CrossRef CAS.
- D. Sundholm, H. Fliegl and R. J. Berger, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 6, 639–678 CrossRef CAS.
- K. Ruud, H. Skaane, T. Helgaker, K. L. Bak and P. Jørgensen, J. Am. Chem. Soc., 1994, 116, 10135–10140 CrossRef CAS.
- J. A. Pople, Mol. Phys., 1958, 1, 175–180 CrossRef CAS.
- R. McWeeny, Mol. Phys., 1958, 1, 311–321 CrossRef CAS.
- J. A. N. F. Gomes and R. B. Mallion, Chem. Rev., 2001, 101, 1349–1384 CrossRef CAS PubMed.
- R. F. W. Bader and T. A. Keith, J. Chem. Phys., 1993, 99, 3683–3693 CrossRef CAS.
- P. Pascal, Ann. Chim. Phys., 1910, 19, 5–70 CAS.
- A. Pacault, Rev. Sci., 1948, 86, 38–61 CAS.
- P. Pascal, F. Gallais and S. F. C. R. Labarre, C. R. Acad. Sci., 1961, 252, 2644–2649 CAS.
- J. Jusélius, D. Sundholm and J. Gauss, J. Chem. Phys., 2004, 121, 3952–3963 CrossRef PubMed.
- R. R. Valiev, H. Fliegl and D. Sundholm, J. Phys. Chem. A, 2015, 119, 1201–1207 CrossRef CAS PubMed.
- S. Loibl and M. Schutz, J. Chem. Phys., 2014, 141, 024108 CrossRef PubMed.
- J. A. Bohmann, F. Weinhold and T. C. Farrar, J. Chem. Phys., 1997, 107, 1173–1184 CrossRef CAS.
- K. Ruud, T. Helgaker, K. L. Bak, P. Jørgensen and H. J. A. Jensen, J. Chem. Phys., 1993, 99, 3847–3859 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- F. Furche, R. Ahlrichs, C. Hättig, W. Klopper, M. Sierka and F. Weigend, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 91–100 CrossRef CAS.
- M. P. Johansson and M. Swart, J. Chem. Theory Comput., 2010, 6, 3302–3311 CrossRef CAS PubMed.
- O. B. Lutnæs, A. M. Teale, T. Helgaker, D. J. Tozer, K. Ruud and J. Gauss, J. Chem. Phys., 2009, 131, 144104 CrossRef PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- S. Grimme and M. Waletzke, J. Chem. Phys., 1999, 111, 5645–5655 CrossRef CAS.
- C. Foroutan-Nejad, J. Phys. Chem. A, 2011, 115, 12555–12560 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cc05232d |
| This journal is © The Royal Society of Chemistry 2017 |