A topologically unique alternating {Co^III₃Gd^III₃} magnetocaloric ring

Abstract

The adiabatic temperature change of the star-shaped {Co^III₃Gd^III₃} magnetocaloric ring is enhanced via topological control over the assembly process, by using a pre-formed {Co^II(H₆L)} building block that undergoes oxidation to Co^III, successfully separating the Gd^III ions.

---

The magnetocaloric effect (MCE) is described as the reversible adiabatic temperature change (ΔT_ad) and magnetic entropy change (ΔS_m) of a material, following the application or removal of a magnetic field. Promising magnetic refrigerants benefit from the large MCE displayed by certain molecular materials.¹ This is where coordination chemistry and molecular magnetism become powerful tools for optimising design towards the ideal magnetic refrigerant. A large MCE at low temperatures is favoured by a negligible magnetic anisotropy.^1b,2 Hence, several molecule-based refrigerants are complexes of isotropic Gd(III) ions.³ Another common trend is to maximise the magnetic : non-magnetic ratio, so as to increase values of the refrigeration power and −ΔS_m, when reported per unit mass or unit volume.^3a,4 The inherent drawback of this approach is that spin–spin correlations increase unavoidably, which ultimately limit the lower bound of ΔT_ad and the lowest temperature that can be attained in an adiabatic demagnetisation process.^3d Therefore, a compromise becomes necessary. Some recent studies explore the combined use of 3d/4f ions in search of the enhancement of magnetocaloric properties, such as Co/Gd.⁵ As expected, Co(II) ions influence negatively the MCE, because of the characteristic large magnetic anisotropy, which makes reorientation of the magnetic moment more difficult.^1b Herein, we explore an attractive solution to this problem, namely tuning the oxidation state, by changing anisotropic Co(II) to diamagnetic Co(III), concomitantly with an effective dilution of the Gd(III) ions, in order to favour ΔT_ad.

We recently reported large heterometallic {Mn₁₈Cu₆} complexes, obtained by following a directed synthesis approach, based on the use of the metallo–organic precursor [Cu(H₆L)Cl]Cl (H₆L = bis–tris propane).⁶ This prompted us to investigate the reactivity of bis–tris propane with 4f ions in the presence of 3d ions.⁷ Similar aminopolyol-type ligands seem to promote the oxidation of different Co(II) starting materials.⁸ Therefore, the exploration of Co(II) precursors containing H₆L in the design of new magnetic refrigerants becomes highly attractive. Our approach is to use {Co^II(H₆L)} precursors that can undergo facile oxidation to diamagnetic Co(III), whilst encapsulating the cobalt centres and directing/separating the Ln(III) ions. Using this strategy, we present the magnetocaloric properties of a new {Co^III₃Gd^III₃} star-shaped ring, showing that the Co(III) ions have a significant impact on the adiabatic temperature change in this system, by separating the Gd(III) ions and weakening the Gd(III)⋯Gd(III) interaction. In terms of ΔT_ad, this complex is among the best gadolinium-based molecular refrigerants reported so far (vide infra).

By combining the metalloligand [Co(H₆L)(CH₃COO)₂] (1) and Gd(acac)₃·H₂O we are able to obtain a new hexametallic complex [Co^III₃Gd^III₃(H₂L)₃(acac)₂(CH₃COO)₄(H₂O)₂] (2) with a unique alternating wheel-like structure (Fig. 1 and Fig. S4, S12, Table S1, ESI†). The pre-formation of the metalloligand (see Fig. S1–S3 and S10, ESI†) seems to be essential for the assembly of 2, as previously seen for the {Mn₁₈Cu₆} complexes. During the reaction, under aerobic conditions in the presence of bis–tris propane, Co(II) is oxidised to Co(III) and hence, the magnetic properties of 2 are defined exclusively by the paramagnetic Gd(III) ions. The structure of 2 contains three octahedral Co(III) ions, each one encapsulated by one tetra-deprotonated H₂L⁴⁻ ligand through four O and two N atoms. The two remaining ligand arms are uncoordinated. Each {Co(H₂L)} unit is linked to two octa-coordinated Gd(III) ions through four μ-O bridging atoms forming a ring-like structure, in which Co(III) and Gd(III) centres alternately occupy the corners of a six-pointed star.

Fig. 1 Synthetic approach and structure of 2. C, grey; Co, fuchsia; Gd, green; N, blue; O, red; hydrogen atoms and solvent molecules are omitted for clarity.

The oxidation state of each cobalt centre has been confirmed by bond valence sum calculations (BVS).⁹ Two different triangular dodecahedral Gd ions can be distinguished based on the co-ligands that complete their coordination sphere: two bidentate acetates for Gd1, or one acac⁻, one monodentate acetate and one water ligand for Gd2 and Gd2′ (see Table S2, ESI†). The average intramolecular Gd⋯M distances (M = Co, Gd) are d_(Gd⋯Co) = 3.389(1) Å, and d_(Gd⋯Gd′) = 5.802(9) Å. Note that the {Co^III₃Gd^III₃} wheel is not perfectly planar (see Fig. S5, ESI†), with a dihedral angle between the {Co₃} and {Gd₃} planes of 9°. To the best of our knowledge, the structure shown by {Co^III₃Gd^III₃} is unprecedented for Co/4f complexes (CSD 5.37, November 2016, where 3d = Sc → Zn, 4f = La → Lu) and remarkably only larger alternating 3d/4f rings (where 3d = Mn or Fe only), such as {Mn₄Ln₄}, {Mn₈Ln₈} or {Fe₁₀Yb₁₀} have been reported to date, where the structures are all more puckered than in 2.¹⁰

The experimental value of the static magnetic susceptibility temperature product χ_MT at 290 K (23.37 cm³ mol⁻¹ K) for 2 is consistent with that expected for three uncoupled Gd(III) centres (23.63 cm³ mol⁻¹ K, ⁸S_7/2, s = 7/2, g = 2). χ_MT displays an almost imperceptible decrease between 290 and 26 K and then drops to 21.33 cm³ mol⁻¹ K at 2 K (Fig. 2), consistent with very weak spin ordering promoted either by antiferromagnetic correlations or zero-field splitting (ZFS) of the ground multiplet. Exchange coupling through the diamagnetic Co(III) ions is a potential pathway for very weak Gd⋯Gd′ intramolecular interactions, similar to previous Cu⋯Cu′ coupling through Zn(II) in heterometallic Cu/Zn bis–tris propane complexes.¹¹ Within the exchange coupling model, the simultaneous fit of the susceptibility and magnetisation data at T = 2 to 10 K, step 1 K (see spin Hamiltonian below, and magnetic model in Fig. S11, ESI†) gives , and g = 1.988 ± 0.002.¹²

Fig. 2 Temperature dependence of χ_MT for 2 in an applied field of 0.1 T (inset shows magnetisation vs. field at 2 to 10 K, step 1 K). The solid lines correspond to the simultaneous fit (see text for details).

In the mean-field approximation, we can interpret as an effective interaction constant resulting from dipole–dipole magnetic interactions, which are well documented for molecular materials.¹³ The g value obtained from the fit is reasonable for Gd(III) ions considering similar complexes.¹⁴ The small deviation from the expected spin-only g value could be a consequence of a small ZFS, induced by crystal-field effects combined with spin–orbit coupling.^2b,15 Considering the relatively large average Gd⋯Gd′ distance (5.802(9) Å), one could argue that exchange coupling is likely to be less effective for spin ordering. All sources, though, are extremely weak and we cannot discriminate between them, on the basis of the experimental data. The DC experiments suggest, therefore, that 2 should display a relatively large MCE, arising from the weakly-interacting Gd(III) ions.^1b,16 The MCE is best evaluated from heat capacity c_p experiments (Fig. 3, top). As is typical for molecular magnetic materials,^1a lattice vibrations contribute predominantly to c_p as a rapid increase above ca. 5–10 K. The non-magnetic lattice contribution can be described by the Debye model (dotted line in Fig. 3), which simplifies to a c_latt/R = aT³ dependence at the lowest temperatures, where a = 6.7 × 10⁻³ K⁻³ for 2. At such low temperatures, c_p is mainly determined by a Schottky-like anomaly, which is strongly dependent on B and can be well modelled by Hamiltonian (1), using the same parameters obtained from fitting the susceptibility and magnetisation data. For B = 0, the system becomes sensitive to any perturbation, hence the need to add an effective internal field B_eff ≈ 0.3 T to our model, in order to simulate the zero-applied-field c_p. For B ≥ 1 T, such a correction is not necessary. We ascribe B_eff to the dipole–dipole magnetic interactions, although to a minor extent, it could also be associated with a small ZFS at the Gd(III) sites. From the experimental heat capacity data, we derive the entropy S of the system, according to . Similarly, we derive the lattice entropy S_latt from c_latt and the magnetic entropy S_m from c_m, that is, the magnetic contribution to c_p, viz., the aforementioned Schottky-like anomaly, calculated on basis of Hamiltonian (1). The bottom panel of Fig. 3 shows the resulting temperature dependence of the experimental entropy S, which thus corresponds to the sum of S_latt (dotted line) and S_m (solid lines), for any applied magnetic field employed. Because of the very weak ZFS and interactions present, temperatures as low as ca. 3–4 K are already sufficient for fully decoupling the Gd(III) spins. Therefore, within the investigated temperature range, the zero-applied-field S reaches the maximum entropy value per mole involved, which corresponds to three non-interacting Gd(III) spins s = 7/2 and is calculated as 3 × R ln(2s + 1) ≈ 6.2R (see Fig. 3).

Fig. 3 Top: Temperature dependence of the heat capacity, normalised to the gas constant, c_p/R for 2 for selected applied fields, as labelled. Bottom: Temperature dependence of the entropy, normalised to the gas constant, S/R for 2 for selected applied fields, as labelled. The dotted line is the lattice while the solid lines correspond to the magnetic modelling (see text for details).

Next, we evaluate ΔS_m and ΔT_ad, following a change of the applied magnetic field ΔB. The temperature dependencies of both ΔS_m and ΔT_ad can be calculated straightforwardly from the experimental entropy (Fig. 3, bottom panel).^1b Likewise, ΔS_m can also be calculated from the magnetisation data (Fig. 2) by making use of the Maxwell relation 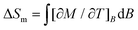. Fig. 4 shows the so-obtained dependence of ΔS_m and ΔT_ad for 2versus temperature for selected ΔB values. Note the nice agreement between the ΔS_m results obtained through both methods, thus validating the approaches employed. For the largest applied field change ΔB = (7–0) T, i.e., after a full demagnetisation from 7 T, the maximum value of −ΔS_m is 5.6R at T = 1.9 K, which corresponds to 90% of the available entropy content and is equivalent to 23.6 J kg⁻¹ K⁻¹ per unit mass. Concomitantly, we obtain ΔT_ad = 10.7 K at T = 1.5 K for the same field change, that is, the temperature decreases down to a final temperature T_f = 1.5 K, on demagnetising adiabatically from B = 7 T and an initial temperature T_i = T_f + ΔT_ad = 12.2 K. Note that ΔT_ad is limited in T_f by sources of magnetic ordering (spin–spin interactions and magnetic anisotropies) and in T_i by the lattice entropy, which soon becomes the dominating contribution on increasing the temperature (see Fig. 3).

Fig. 4 Temperature dependence of the magnetic entropy change ΔS_m (top) and adiabatic temperature change ΔT_ad (bottom) for 2 for selected changes of the applied magnetic field ΔB, as labelled. Values of ΔS_m are reported per unit mole (left) and mass (right), and are obtained from heat capacity (empty dots) and magnetisation (filled dots) data.

The precursor [Co(H₆L)(CH₃COO)₂] (1) has successfully directed the molecular assembly in [Co^III₃Gd^III₃(H₂L)₃(acac)₂(CH₃COO)₄(H₂O)₂] (2), so that the Gd(III) ions are isolated, thus promoting the discussed magnetocaloric properties. Several Co(II)/Gd(III) molecular coolers have been studied so far.^5a,17 The biggest hindrance to a large MCE in those compounds is the large magnetic anisotropy of the Co(II) ions.^1b,2 In 2 we circumvent this impediment by oxidising Co(II) into Co(III) during the synthesis, thus leaving only the Gd(III) ions to contribute magnetically. In terms of the magnetocaloric properties of 2, the diamagnetic Co(III) ions still play a role, though passively. On the one hand, they influence negatively on the entropy change per unit mass. The lower the magnetic : non-magnetic ions ratio, the lower are the magnetic heat capacity and entropy per unit mass. The maximum value observed of −ΔS_m = 23.6 J kg⁻¹ K⁻¹ at T = 1.9 K for 2 is large, though not outstanding. However, the key point is that the Co(III) centres impact positively on the adiabatic temperature change. In 2, the Co(III) and Gd(III) ions alternate with respect to one another. Therefore, the intermediate presence of the Co(III) ions weakens extremely the magnetic interaction between the Gd(III) ions, so the temperature-dependence of ΔT_ad has a maximum at a relatively lower temperature than usually found for pure-Gd molecular complexes. Among the few known systems that have a ΔT_ad maximum below e.g., 2 K for 7 T, complex 2 with ΔT_ad = 10.7 K at T = 1.5 K lags behind only the extraordinary {Gd₂-ac} with ΔT_ad = 12.6 K at T = 1.4 K,^3a while it outdoes {Zn₂Gd₂} with ΔT_ad = 9.6 K at T = 1.4 K,¹⁸ and {Gd₇} with ΔT_ad = 9.4 K at T = 1.8 K.¹⁹

The UK Engineering and Physical Sciences Research Council are thanked for financial support (grant ref. EP/I027203/1). GL and ME thank the Spanish Ministry of Economy, Industry and Competitiveness for funding (MAT2015-68204-R) and a postdoctoral contract (to GL). The data which underpin this work are available at http://dx.doi.org/10.5525/gla.researchdata.223.

Notes and references

1. (a) M. Evangelisti, F. Luis, L. J. de Jongh and M. Affronte, J. Mater. Chem., 2006, 16, 2534–2549; (b) M. Evangelisti and E. K. Brechin, Dalton Trans., 2010, 39, 4672–4676; (c) J. W. Sharples and D. Collison, Polyhedron, 2013, 54, 91–103; (d) Y.-Z. Zheng, G.-J. Zhou, Z. Zheng and R. E. P. Winpenny, Chem. Soc. Rev., 2014, 43, 1462–1475.
2. (a) G. Karotsis, M. Evangelisti, S. J. Dalgarno and E. K. Brechin, Angew. Chem., Int. Ed., 2009, 48, 9928–9931; (b) F. Luis and M. Evangelisti, Struct. Bonding, 2015, 164, 431–460.
3. (a) M. Evangelisti, O. Roubeau, E. Palacios, A. Camón, T. N. Hooper, E. K. Brechin and J. J. Alonso, Angew. Chem., Int. Ed., 2011, 50, 6606–6609; (b) J. W. Sharples, Y.-Z. Zheng, F. Tuna, E. J. L. McInnes and D. Collison, Chem. Commun., 2011, 47, 7650–7652; (c) F.-S. Guo, J.-D. Leng, J.-L. Liu, Z.-S. Meng and M.-L. Tong, Inorg. Chem., 2012, 51, 405–413; (d) M.-J. Martínez-Pérez, O. Montero, M. Evangelisti, F. Luis, J. Sesé, S. Cardona-Serra and E. Coronado, Adv. Mater., 2012, 24, 4301–4305; (e) T. N. Hooper, J. Schnack, S. Piligkos, M. Evangelisti and E. K. Brechin, Angew. Chem., Int. Ed., 2012, 51, 4633–4636; (f) P.-F. Shi, Y.-Z. Zheng, X.-Q. Zhao, G. Xiong, B. Zhao, F.-F. Wan and P. Cheng, Chem. – Eur. J., 2012, 18, 15086–15091; (g) G. Lorusso, M. A. Palacios, G. S. Nichol, E. K. Brechin, O. Roubeau and M. Evangelisti, Chem. Commun., 2012, 48, 7592–7594; (h) R. Sibille, T. Mazet, B. Malaman and M. François, Chem. – Eur. J., 2012, 18, 12970–12973; (i) L.-X. Chang, G. Xiong, L. Wang, P. Cheng and B. Zhao, Chem. Commun., 2013, 49, 1055–1057; (j) J. W. Sharples, D. Collison, E. J. L. McInnes, J. Schnack, E. Palacios and M. Evangelisti, Nat. Commun., 2014, 5, 5321.
4. G. Lorusso, J. W. Sharples, E. Palacios, O. Roubeau, E. K. Brechin, R. Sessoli, A. Rossin, F. Tuna, E. J. L. McInnes, D. Collison and M. Evangelisti, Adv. Mater., 2013, 25, 4653–4656.
5. (a) Y.-Z. Zheng, M. Evangelisti, F. Tuna and R. E. P. Winpenny, J. Am. Chem. Soc., 2012, 134, 1057–1065; (b) J.-B. Peng, Q.-C. Zhang, X.-J. Kong, Y.-Z. Zheng, Y.-P. Ren, L.-S. Long, R.-B. Huang, L.-S. Zheng and Z. Zheng, J. Am. Chem. Soc., 2012, 134, 3314–3317; (c) S. K. Gupta, A. A. Dar, T. Rajeshkumar, S. Kuppuswamy, S. K. Langley, K. S. Murray, G. Rajaraman and R. Murugavel, Dalton Trans., 2015, 44, 5961–5965.
6. V. A. Milway, F. Tuna, A. R. Farrell, L. E. Sharp, S. Parsons and M. Murrie, Angew. Chem., Int. Ed., 2013, 52, 1949–1952.
7. M. Heras Ojea, V. A. Milway, G. Velmurugan, L. H. Thomas, S. J. Coles, C. Wilson, W. Wernsdorfer, G. Rajaraman and M. Murrie, Chem. – Eur. J., 2016, 22, 12839–12848.
8. (a) S. K. Langley, N. F. Chilton, L. Ungur, B. Moubaraki, L. F. Chibotaru and K. S. Murray, Inorg. Chem., 2012, 51, 11873–11881; (b) J. A. Sheikh, S. Goswami and S. Konar, Dalton Trans., 2014, 43, 14577–14585; (c) J. A. Sheikh and A. Clearfield, Inorg. Chem., 2016, 55, 8254–8256.
9. (a) I. D. Brown and D. Altermatt, Acta Crystallogr., Sect. B: Struct. Sci., 1985, 41, 244–247; (b) N. E. Brese and M. O'Keeffe, Acta Crystallogr., Sect. B: Struct. Sci., 1991, 47, 192–197; (c) R. M. Wood and G. J. Palenik, Inorg. Chem., 1998, 37, 4149–4151.
10. (a) M. Li, A. M. Ako, Y. Lan, W. Wernsdorfer, G. Buth, C. E. Anson, A. K. Powell, Z. Wang and S. Gao, Dalton Trans., 2010, 39, 3375–3377; (b) A. Baniodeh, C. E. Anson and A. K. Powell, Chem. Sci., 2013, 4, 4354–4361; (c) K. R. Vignesh, S. K. Langley, B. Moubaraki, K. S. Murray and G. Rajaraman, Chem. – Eur. J., 2015, 21, 16364–16369.
11. M. Heras Ojea, C. Wilson, S. J. Coles, F. Tuna and M. Murrie, Dalton Trans., 2015, 44, 19275–19281.
12. N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, J. Comput. Chem., 2013, 34, 1164–1175.
13. (a) A. Bino, D. C. Johnston, D. P. Goshorn, T. R. Halbert and E. I. Stiefel, Science, 1988, 241, 1479–1481; (b) A. Morello, F. L. Mettes, F. Luis, J. F. Fernández, J. Krzystek, G. Aromí, G. Christou and L. J. de Jongh, Phys. Rev. Lett., 2003, 90, 017206; (c) M. Evangelisti, A. Candini, A. Ghirri, M. Affronte, G. W. Powell, I. A. Gass, P. A. Wood, S. Parsons, E. K. Brechin, D. Collison and S. L. Heath, Phys. Rev. Lett., 2006, 97, 167202; (d) F. Luis, Dipolar magnetic order in crystals of molecular nanomagnets, in Molecular Magnets: Physics and Applications, NanoScience and Technology, ed. J. Bartolomé, F. Luis and J. F. Fernández, Springer-Verlag, Berlin, Heidelberg, 2014, pp. 161–190.
14. (a) C. Lampropoulos, T. C. Stamatatos, K. A. Abboud and G. Christou, Inorg. Chem., 2009, 48, 429; (b) C. Y. Chow, H. Bolvin, V. E. Campbell, R. Guillot, J. W. Kampf, W. Wernsdorfer, F. Gendron, J. Autschbach, V. L. Pecoraro and T. Mallah, Chem. Sci., 2015, 6, 4148–4159; (c) K. Wang, Z.-L. Chen, H.-H. Zou, K. Hu, H.-Y. Li, Z. Zhang, W.-Y. Sun and F.-P. Liang, Chem. Commun., 2016, 52, 8297–8300.
15. S. A. Stoian, C. Paraschiv, N. Kiritsakas, F. Lloret, E. Münck, E. L. Bominaar and M. Andruh, Inorg. Chem., 2010, 49, 3387–3401.
16. (a) R. Sessoli, Angew. Chem., Int. Ed., 2012, 51, 43–45; (b) Y.-Z. Zheng, E. M. Pineda, M. Helliwell and R. E. P. Winpenny, Chem. – Eur. J., 2012, 18, 4161–4165.
17. (a) Y.-Z. Zheng, M. Evangelisti and R. E. P. Winpenny, Chem. Sci., 2011, 2, 99–102; (b) J.-B. Peng, Q.-C. Zhang, X.-J. Kong, Y.-P. Ren, L.-S. Long, R.-B. Huang, L.-S. Zheng and Z. Zheng, Angew. Chem., Int. Ed., 2011, 50, 10649–10652; (c) R. Sibille, T. Mazet, B. Malaman, T. Gaudisson and M. François, Inorg. Chem., 2012, 51, 2885–2892; (d) E. Moreno Pineda, F. Tuna, R. G. Pritchard, A. C. Regan, R. E. P. Winpenny and E. J. L. McInnes, Chem. Commun., 2013, 49, 3522–3524; (e) D. I. Alexandropoulos, L. Cunha-Silva, G. Lorusso, M. Evangelisti, J. Tang and T. C. Stamatatos, Chem. Commun., 2016, 52, 1693–1696; (f) T. N. Hooper, R. Inglis, G. Lorusso, J. Ujma, P. E. Barran, D. Uhrin, J. Schnack, S. Piligkos, M. Evangelisti and E. K. Brechin, Inorg. Chem., 2016, 55, 10535–10546.
18. J. Ruiz, G. Lorusso, M. Evangelisti, E. K. Brechin, S. J. A. Pope and E. Colacio, Inorg. Chem., 2014, 53, 3586–3594.
19. E. M. Pineda, G. Lorusso, K. H. Zangana, E. Palacios, J. Schnack, M. Evangelisti, R. E. P. Winpenny and E. J. L. McInnes, Chem. Sci., 2016, 7, 4891–4895.

---

Footnotes

† Electronic supplementary information (ESI) available: Experimental sections, spectroscopic studies, magnetic studies, crystallographic details. CCDC 1533722. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c7cc02243c

‡ Current address: Institute for Integrated Cell-Material Science (WPI-iCeMS), Kyoto University, Yoshida, Sakyo-ku, Kyoto 606-8501, Japan.

---