Reversible restructuring of supported Au nanoparticles during butadiene hydrogenation revealed by operando GISAXS/GIWAXS

Abstract

Periodically arranged, monodisperse gold nanoparticles supported on flat silicon substrates were studied for the hydrogenation of 1,3-butadiene under operando conditions using Grazing Incidence Small- and Wide-Angle X-ray Scattering (GISAXS/GIWAXS). It was found that the composition and shape of the nanoparticles depends very much on the chemical environment; the particles are shown to be dynamic, undergoing reversible size and shape change particularly during catalytic reaction, highlighting a dynamism often not observed in traditional studies. Specifically, the size of the Au nanoparticles increases during butadiene hydrogenation and this is attributed to the partial removal of a Au₂O₃ at the metal–oxide interface and consequential shape change of the nanoparticle from a more hemispherical particle to a particle with a larger height to width ratio.

---

Heterogeneous catalysts comprising oxide-supported noble metal nanoparticles (NPs) are the backbone of the chemical and fuel industries. Obtaining a better understanding of the properties required of an active catalyst is routinely investigated in the belief that the traits of an active catalyst can be identified and translated to yield improved catalytic materials/catalytic processes. Size and shape dependent effects such as surface atom fraction and quantum confinement have been proposed to affect nanoparticle reactivity, yet there is still a considerable debate within the community as to the importance/influence of nanoparticle size and shape for specific catalytic reactions.¹ Haruta and Hutchings initially demonstrated the catalytic activity of supported gold nanoparticles for oxidation of CO and hydrochlorination of acetylene.^2,3 A size–activity relationship has since been shown to exist for oxidation, epoxidations and hydrogenation reactions amongst others over gold nanoparticle catalysts.⁴ However, there are a number of other pertinent examples of size/support–activity relationships in the literature concerning a range of catalysts, for example cobalt based Fischer–Tropsch catalysts and even palladium catalysts for 1,3-butadiene hydrogenation.^5–7 As a common undesired side product in C₄ streams from naphtha crackers, butadiene can be ‘upgraded’ via hydrogenation over catalysts such as Au/Pd on oxidic supports. Previous research has hinted at both a potentially complex support and particle size dependency due to contrasting reports (of particle size dependency and independency), and theoretical studies suggest a Horiuti–Polanyi type reaction process with C₄H₆ molecules adsorbing more strongly at the (100) surface than at the (111).^6,8,9 However in the many reports detailing size¹⁰ and/or shape¹¹ effects of nanoparticles, there often lies a problem where the preparation method yields broad particle size distributions where the standard deviation ‘σ’ is large (greater than 1 nm). Therefore, the identification of an ideal particle size for catalytic reactions has proven challenging and any proposal for or against particle size/shape sensitivity could at best be considered partial. Furthermore, in many cases, commonly used colloidal methods such as those used by Rogers et al. to prepare catalysts appear to offer good control over particle size (σ ∼ 0.6 nm), however, they can also yield secondary (and often highly active) sub-nanometer atomic species.¹² Thus, in order to properly assess the importance of a particular particle size, more advanced preparation methods are required, such as those based on reverse micelle encapsulation pioneered by Spatz and co-workers.¹³ This method yields nanoparticle populations with extremely small particle size distributions (σ ≪ 1 nm) and at the same time by ensuring full metal ion encapsulation, preventing the occurrence of sub-species. Recently we demonstrated that it is possible to combine this aforementioned synthesis technique with nano-beam X-ray Absorption Spectroscopy (XAS) to study the behaviour of just 20 nanoparticles with an extremely small particle size distribution during CO oxidation, almost eliminating statistical averaging effects associated with standard XAS.¹⁴

Herein, we demonstrate the benefit of marrying a highly controlled nano-catalyst preparation procedure with scattering techniques able to probe nanoparticle behaviour, yielding a deeper understanding of catalyst behavior under operando conditions. Specifically, GISAXS and GIWAXS were used to uncover a previously unseen dynamic structural transformation (including size, shape, and crystallinity) of supported Au NPs under various gas atmospheres and ultimately during the hydrogenation of 1,3-butadiene under realistic working conditions.

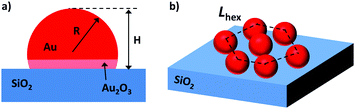
Operando GISAXS/GIWAXS studies were conducted on I07 at Diamond Light Source, using a dedicated gas flow reactor (Fig. S1, ESI†).¹⁵ The 1 × 1 cm² silicon supported Au nanoparticle arrays were exposed to various gases at different temperatures, simulating the industrial catalytic conditions of butadiene hydrogenation. The Au NP arrays were deposited onto a Si(111) wafer (with a native SiO₂ layer) using the reverse micelle method.¹³ The average nanoparticle diameter as determined by FE-SEM was 9.0 ± 0.9 nm, height as determined by AFM was 6.2 ± 0.5 nm, and average interparticle distance in a hexagonal array was 78.8 ± 9.9 nm (Fig. 1 and Fig. S2, ESI†). Details regarding the exact methodology are included within the ESI.†

Fig. 1 Schematic representation of the model used to fit the GISAXS data for the Au/SiO₂–Si catalysts; (a) a spherical Au NP submerged in the SiO₂–Si(111) support, (b) Au NP hexagonal superlattice with the interparticle distance (L_hex) 77.4 nm.

Fig. 2(a and b) show experimental and theoretical 2D operando GISAXS patterns of the Au NP arrays during butadiene hydrogenation at 548 K. The experimental pattern displays a number of peaks with the position ratio of 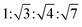corresponding to the (10), (11), (20) and (21) reflections of the 2D hexagonal superlattice. The simulated pattern using the model from Fig. 1 shows there should also be four interference peaks in an idealized hexagonal lattice with the same lattice parameter and particle size distribution.

Fig. 2 Experimental (a) vs. theoretical (b) 2D GISAXS images during butadiene hydrogenation with the diffuse Kiessig fringes typical of NP monolayers with the narrow height distribution. (c and d) 1D GISAXS horizontal (q_z = 0.63 nm⁻¹) and vertical (q_xy = 0.16 nm⁻¹) experimental profiles (points) and corresponding fits (red lines) using IsGISAXS software of the supported Au NPs under various conditions.

Fig. 2(c and d) show the reduced and fitted (using the distorted-wave Born approximation (DWBA)) 1D GISAXS profiles under various conditions. All horizontal profiles (at constant q_z = 0.63 nm⁻¹) have a main interference (10) peak at 0.095 nm⁻¹ (Fig. 2c) that corresponds to the in-plane Au NP hexagonal arrangement as shown in Fig. 1. The fitted data shows this peak corresponds to a real space distance of 77.4 nm (Fig. S2b, ESI†), which is in excellent agreement with the SEM data (78.8 ± 9.9 nm). Furthermore, the peak is ever-present throughout the reaction, and therefore there is no evidence of sintering or Ostwald ripening (inter-particle effects). When the Au catalyst starts to convert butadiene to but-1-enes and but-2-enes (the two are difficult to distinguish by MS, see Fig. S3, ESI†), there is further rise in coherent scattering demonstrated by an increase in intensity of higher order peaks (Fig. 2c). Qualitatively, these observed changes could be attributed to the nanoparticles becoming more identical in some way; akin to an inverse melting effect.¹⁶ Furthermore, the Yoneda peak in Fig. 2d (vertical profile) appears to change shape and becomes much sharper, shifting to a higher critical angle only during butadiene hydrogenation (Fig. 2b). Details regarding GISAXS analysis can be found in the ESI.†

Table S1 (ESI†) summarizes the resulting structural parameters for the Au NP arrays on SiO₂–Si(111) from GISAXS fitting using the software package IsGISAXS,¹⁷ based on schematic model shown in Fig. 1. The calculated NPs radius of 4.2 ± 0.1 nm and height of 4.8 ± 0.4 nm under helium flow are in good agreement with SEM (R = 4.5 nm) and AFM (H = 6.2 nm) data, and the radius/height doesn’t significantly change when exposed to butadiene either. However, during the hydrogenation of butadiene, the average height of the nanoparticles increases tremendously, from 4.8 to 9.3 nm (H/R = 2.0). The radius of the NP array only increases by ca. 0.45 nm, meaning that the average particle within the array is simultaneously growing, and changing shape to have a taller aspect ratio most probably due to the removal of the gold oxide layer at the metal–oxide interface. Interestingly however, the (10) peak position in Fig. 2c which represents the interparticle distance, does not change, and thus we can rule out Ostwald ripening as the cause of mass nanoparticle growth. After the reaction, the atmosphere is switched to helium, and accordingly, the nanoparticles return to a similar size and height as before the reaction (H/R = 1.15).

GISAXS alone cannot give a complete picture, nor reveal entirely why the Au NP arrays change shape so drastically, and therefore it is useful to collect wide-angle scattering data also. Fig. 3a shows the operando GIWAXS data under different gas atmospheres and temperatures, and illustrates the variation in the (200) diffraction peak at q = 3.12 Å⁻¹, which corresponds to metallic Au (Fm3̄m (225), ICSD PDF: 01-071-3755/4-784). From Fig. 3b, one can see that area of the (200) reflection is highest during butadiene hydrogenation, and in fact lowest during hydrogen treatment (Table S2, ESI†). In addition to the signal from metallic gold, a relatively weak diffraction peak at q = 1.81 Å⁻¹ was observed (Fig. 3c) and indexed as the (111) reflection of the orthorhombic unit cell of Au₂O₃.¹⁸ We believe this signal originates from an oxide layer formed at the interface between gold and the native SiO₂ layer of the Si substrate, whose existence was also confirmed on the Au/SiO₂–Si(111) sample after the reaction using ex situ XPS (Fig. S4, Table S3 and discussion on XPS in ESI†). Fig. 3c shows that at the fixed temperature of 473 K the area of the (111) reflection decreases by 30% during butadiene conversion and increases again after the reaction (post He and post He (RT)). The observed changes can be explained by the partial removal of the oxide layer at the Au–SiO₂ interface and correlate well with the increase in intensity of the metallic Au (200) reflection during hydrogenation (Fig. 3b). Our hypothesis is also supported by the GISAXS fit results showing that the contact surface area between the NPs and the support decreases as shown by the H/R ratio in Table S1 (ESI†). After the reaction, the Au₂O₃ layer recovers as indicated by the GIWAXS data in Fig. 3c whereby an observed increase in the Au₂O₃ (111) peak occurs. The subsurface gold oxide buried in the oxide support can also contribute to the (111) reflection.¹⁹ As this phenomenon appears to be reversible, using other, non-operando techniques would not be able to identify these never-before-seen changes.

Fig. 3 (a–c) Changes in metallic gold content in the Au/SiO₂–Si catalyst during butadiene hydrogenation monitored under operando conditions by GIWAXS. (a) 1D GIWAXS profiles showing the (200) reflection of Au fcc lattice. Histograms showing calculated peak areas (b) under various gas atmospheres, using a Voigt function for peak fitting. (c) 1D GIWAXS profiles of the (111) reflection of the Au₂O₃ crystal lattice.

The melting temperatures of solids strongly depends on their size.²⁰ For 9 nm AuNPs the melting temperature was reported to be below 1200 K that is ca 140 K lower than T_m measured for the bulk material.²⁰ However surface atoms become mobile at the Hüttig temperature (T_H = 0.3T_m = 400 K) and bulk atoms can start to move by reaching Tammann temperature (T_T = 0.5T_m = 600 K).²¹ Taking into account that the Au/SiO₂–Si catalyst was heated up to 548 K the solid-state diffusion of gold atoms can play an important role during catalysis. Since the butadiene hydrogenation is an exothermic reaction it can result in the temperature rise at the surface of AuNPs that further accelerates the atoms mobility and can help further explain the observed reversible structural changes in Au/SiO₂–Si catalyst.

It is known that butadiene hydrogenation is facet selective and therefore the expression of a particular facet during catalysis could be expected, similar to other reports, e.g. DFT studies on CO absorption on Au.²² However, butadiene and hydrogen adsorb relatively weakly on Au surfaces (0.01–0.1 eV), as summarised by Bu or Sault,^23,24 yet in our findings a significant structural changes occur according to GISAXS/GIWAXS data. DFT calculations have shown that H₂ cannot dissociate on gold surfaces alone, and in fact this dissociation occurs at the interface between low coordinated Au nanoparticles and support.^25–27 In simple single atom DFT studies, which represent undercoordinated species well, metallic Au is unlikely to be present on oxide surfaces (in the study by Liu, ZrO₂ is used), and in fact Au^III is expected to be the dominant species.²⁸ This is in accordance with our detection of an Au₂O₃ layer. At elevated temperatures, DFT calculations expect Au^III to be reduced to Au^I. Experimentally however, this possible subtle shift in interfacial species does not produce any noticeable change in our scattering data at elevated temperatures alone or in the presence of butadiene/helium (Fig. 2 and 3). However, upon the introduction of hydrogen in addition to that of butadiene, there occurs what we believe is a reversible mass transport phenomenon, fueled by the exothermic catalytic reaction itself providing the energy for the transformation (Fig. 4). Theoretical calculations show that the hydrogenation of butadiene also causes gold–oxygen lattice (Au–O_latt) bonds to be broken, which could fuel interfacial reconstruction.²⁸

Fig. 4 Temperature and gas atmosphere profile during the hydrogenation of butadiene under operando conditions. The Au particles begin with an interface oxide layer under the flow of helium, and then during the hydrogenation of butadiene, the oxide layer at the metal–oxide contact is mostly removed and the H : R ratio of the Au nanoparticles increases. After the reaction the atmosphere is switched back to helium and the contact area between the metal NP and support increases resulting in recovering of NP's dampened hemispherical shape.

As shown experimentally by Nolte et al., reversible facet growth/shrinking caused by intraparticle mass transport is one of the main reasons behind shape and size changes in Rh nanoparticles.²⁹ Therefore in our case it is proposed that a similar phenomenon occurs, however more extreme, energetically possible during an exothermic reaction (ΔH = −126.8 kJ mol⁻¹). Under operating conditions, the Au oxide layer is partially removed, and Au from the metal–oxide interface migrates, increasing the height of the nanoparticle by a factor of 2. Whilst this is indeed a drastic change, we have also shown that it is reversible (Fig. 2 and 3), therefore dependant on the energy released from the reaction itself, and consequently unstable, eventually reverting to their lowest surface energy state/configuration after the reaction has ceased.

To conclude, for the first time we have demonstrated that it is possible to observe real changes in catalytically active NPs using GISAXS/GIWAXS under operando conditions (relevant temperatures and pressures). We show that during butadiene hydrogenation, Au nanoparticles are not inanimate and in fact exist in a resting state prior to catalysis, complete with a Au₂O₃ passivation layer, and the catalytically active state is drastically different than the resting state. We observe a reversible dynamism which is a combination of size, shape and phase change, with NPs height increasing from 4.8 to 9.3 nm.

This approach could be key in identifying the true active state of a NP catalyst, e.g. designing high form, high surface energy nano rods or other polyhedral to increase reactivity. The setup could also be used to monitor other important catalytic systems in the future, e.g. cobalt NPs for Fischer–Tropsch synthesis (FTS), and has the potential to become a valuable technique in the catalysis researchers' toolbox.

The authors would like to thank the EPSRC for funding (grant EP/K007467/1). We are also thankful to Dr SocMan Ho Kimura (UCL Chemistry) for helping with XPS measurements. Dr Giuseppe Portale (University of Groningen) is also thanked for advice in performing the GISAXS analysis. The authors would like to thank Diamond Light Source for beamtime at the I07 beamline (experiments SI10488 and SI12780).

Notes and references

1. E. Roduner, Chem. Soc. Rev., 2006, 35, 583.
2. M. Haruta, T. Kobayashi, H. Sano and N. Yamada, Chem. Lett., 1987, 405–408.
3. G. J. Hutchings, J. Catal., 1985, 96, 292–295.
4. A. S. K. Hashmi and G. J. Hutchings, Angew. Chem., Int. Ed., 2006, 45, 7896–7936.
5. G. L. Bezemer, J. H. Bitter, H. P. C. E. Kuipers, H. Oosterbeek, J. E. Holewijn, X. Xu, F. Kapteijn, A. J. Van Diilen and K. P. De Jong, J. Am. Chem. Soc., 2006, 128, 3956–3964.
6. J. Silvestre-Albero, G. Rupprechter and H.-J. Freund, J. Catal., 2006, 240, 58–65.
7. S. H. Joo, J. Y. Park, J. R. Renzas, D. R. Butcher, W. Huang and G. A. Somorjai, Nano Lett., 2010, 10, 2709–2713.
8. Y. Guan, D. A. J. M. Ligthart, Ö. Pirgon-Galin, J. A. Z. Pieterse, R. A. Van Santen and E. J. M. Hensen, Top. Catal., 2011, 54, 424–438.
9. C. Chizallet, G. Bonnard, E. Krebs, L. Bisson, C. Thomazeau and P. Raybaud, J. Phys. Chem. C, 2011, 115, 12135–12149.
10. B. Roldan Cuenya and F. Behafarid, Surf. Sci. Rep., 2015, 70, 135–187.
11. B. R. Cuenya, Acc. Chem. Res., 2013, 46, 1682–1691.
12. S. M. Rogers, C. R. A. Catlow, C. E. Chan-Thaw, D. Gianolio, E. K. Gibson, A. L. Gould, N. Jian, A. J. Logsdail, R. E. Palmer, L. Prati, N. Dimitratos, A. Villa and P. P. Wells, ACS Catal., 2015, 5, 4377–4384.
13. J. P. Spatz, S. Mössmer, C. Hartmann, M. Möller, T. Herzog, M. Krieger, H. G. Boyen, P. Ziemann and B. Kabius, Langmuir, 2000, 16, 407–415.
14. D. J. Martin, D. Decarolis, R. Tucoulou, G. Martínez-Criado and A. M. Beale, Catal., Struct. React., 2017, 3, 63–70.
15. C. Nicklin, T. Arnold, J. Rawle and A. Warne, J. Synchrotron Radiat., 2016, 23, 1245–1253.
16. Y. Yu, A. Jain, A. Guillaussier, V. R. Voggu, T. M. Truskett, D.-M. Smilgies and B. A. Korgel, Faraday Discuss., 2015, 181, 181–192.
17. R. Lazzari, J. Appl. Crystallogr., 2002, 35, 406–421.
18. P. G. Jones, H. Rumpel, E. Schwarzmann, G. M. Sheldrick and H. Paulus, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1979, 35, 1435–1437.
19. L. K. Ono and B. Roldan Cuenya, J. Phys. Chem. C, 2008, 112, 4676–4686.
20. G. Guenther and O. Guillon, J. Mater. Sci., 2014, 49, 7915–7932.
21. J. A. Moulijn, A. E. Van Diepen and F. Kapteijn, Appl. Catal., A, 2001, 212, 3–16.
22. K. P. McKenna and A. L. Shluger, J. Phys. Chem. C, 2007, 111, 18848–18852.
23. W. Bu, L. Zhao, Z. Zhang, X. Zhang, J. Gao and C. Xu, Appl. Surf. Sci., 2014, 289, 6–13.
24. A. G. Sault, R. J. Madix and C. T. Campbell, Surf. Sci., 1986, 169, 347–356.
25. T. Fujitani, I. Nakamura, T. Akita, M. Okumura and M. Haruta, Angew. Chem., Int. Ed., 2009, 48, 9515–9518.
26. S. Naito and M. Tanimoto, J. Chem. Soc., Chem. Commun., 1988, 832–833.
27. D. A. Buchanan and G. Webb, J. Chem. Soc., Faraday Trans. 1, 1975, 71, 134.
28. Z. P. Liu, C. M. Wang and K. N. Fan, Angew. Chem., Int. Ed., 2006, 45, 6865–6868.
29. P. Nolte, A. Stierle, N. Y. Jin-Phillipp, N. Kasper, T. U. Schulli, H. Dosch, T. The and T. Landau, Science, 2008, 321, 1654–1658.

---

Footnote

† Electronic supplementary information (ESI) available: Synthesis methodology and details of characterisation. See DOI: 10.1039/c7cc01887h

---