Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Long range electrostatic forces in ionic liquids
Matthew A.
Gebbie
*a,
Alexander M.
Smith
b,
Howard A.
Dobbs
c,
Alpha A.
Lee
d,
Gregory G.
Warr
 e,
Xavier
Banquy
f,
Markus
Valtiner
g,
Mark W.
Rutland
*hi,
Jacob N.
Israelachvili
*c,
Susan
Perkin
*b and
Rob
Atkin
e,
Xavier
Banquy
f,
Markus
Valtiner
g,
Mark W.
Rutland
*hi,
Jacob N.
Israelachvili
*c,
Susan
Perkin
*b and
Rob
Atkin
 *j
*j
aGeballe Laboratory for Advanced Materials, Stanford University, Stanford, CA 94305, USA. E-mail: magebbie@stanford.edu
bDepartment of Chemistry, Physical & Theoretical Chemistry Laboratory, University of Oxford, Oxford, OX1 3QZ, UK. E-mail: susan.perkin@chem.ox.ac.uk
cDepartment of Chemical Engineering, University of California, Santa Barbara, CA 93106, UK. E-mail: jacob@engineering.ucsb.edu
dSchool of Engineering and Applied Sciences, Harvard University, Cambridge, MA 02138, USA
eSchool of Chemistry, F11, The University of Sydney, NSW 2006, Australia
fFaculty of Pharmacy, Universite de Montreal, Montreal, QC, Canada
gInterface Chemistry and Surface Engineering, Max Planck Institut fur Eisenforschung GmbH, Dusseldorf, 40237, Germany
hSurface and Corrosion Science, KTH Royal Institute of Technology, SE-10044 Stockholm, Sweden. E-mail: mark@kth.se
iSP Chemistry Materials and Surfaces, SE 114 86 Stockholm, Sweden
jPriority Research Centre for Advanced Fluid Interfaces, Newcastle Institute for Energy and Resources, The University of Newcastle, Australia. E-mail: rob.atkin@newcastle.edu.au
First published on 9th December 2016
Abstract
Ionic liquids are pure salts that are liquid under ambient conditions. As liquids composed solely of ions, the scientific consensus has been that ionic liquids have exceedingly high ionic strengths and thus very short Debye screening lengths. However, several recent experiments from laboratories around the world have reported data for the approach of two surfaces separated by ionic liquids which revealed remarkable long range forces that appear to be electrostatic in origin. Evidence has accumulated demonstrating long range surface forces for several different combinations of ionic liquids and electrically charged surfaces, as well as for concentrated mixtures of inorganic salts in solvent. The original interpretation of these forces, that ionic liquids could be envisioned as “dilute electrolytes,” was controversial, and the origin of long range forces in ionic liquids remains the subject of discussion. Here we seek to collate and examine the evidence for long range surface forces in ionic liquids, identify key outstanding questions, and explore possible mechanisms underlying the origin of these long range forces. Long range surface forces in ionic liquids and other highly concentrated electrolytes hold diverse implications from designing ionic liquids for energy storage applications to rationalizing electrostatic correlations in biological self-assembly.
Ions impact all aspects of modern life. The smart phones that link much of the Earth's population are powered by batteries that depend on the directed motion of large collections of ions.1 Collective ion motion will also play a key role in energy storage technologies that will enable societies to transition away from fossil fuels to greener energy sources, such as supercapacitors,2 and the correlated behaviour of ions is responsible for many biological processes that support life.3 Consequently, a complete understanding of the fundamental principles that govern the behaviour of large collections of ions would impact many branches of science and engineering, and allow ion collective motion to be predictably tuned.
This is a tremendous challenge, in large part due to the large potential energy of electrostatic interactions and long range of electrostatic interactions. In particular, analytical theories describing disordered soft matter systems, like liquid-based energy storage devices and biological systems, are sparse, and such systems are too complex to be reliably simulated.4 Increasingly, researchers are exploring the physics of ionic liquids to provide general insight into the fundamental nature of ionic correlations, as ionic liquids are comparatively simple systems that exhibit the key features of electrostatic correlations in disordered soft matter.
Ionic liquids are pure salts that are liquids at ambient conditions.5 Strong electrostatic interactions determine the key properties of ionic liquids, as for traditional high melting point salts. In contrast with traditional salts, ionic liquids are typically composed of large, asymmetric polyatomic ions with ionic radii that are about 5–10 times larger than those of monatomic ions like Li+ or K+. The large size of ionic liquid ions increases the average separation distance between cation and anion charge centers, decreasing the strength of electrostatic interactions. Concurrently, the presence of flexible and/or asymmetric ionic structures, such as alkyl chains on cations or conformational flexibility in bis(trifluoromethylsulfonyl)imide anions, introduce significant conformational and configurational entropy in ionic liquids, leading to a large number of energetically similar, and thus thermally accessible, states. Both aspects drastically suppress the melting points of ionic liquids; all of the ionic liquids discussed in this article are liquids at room temperature.
Ionic liquids exhibit a collection of properties that are of technological interest. For example, ionic liquids have extremely low vapour pressures, modest intrinsic ionic conductivities, high thermal and electrochemical stability, and are known to dissolve a wide range of chemical species, including lithium salts and polyaromatic compounds.5,6 As a consequence of this unusual range of properties, ionic liquids have significant promise for many emerging applications such as: electrochemical energy storage devices, high temperature and/or vacuum phase materials synthesis, semiconductor and superconductor gating applications, and novel self-assembly media.5–10
For many applications, the structure and properties of the electric double layer formed by ionic liquids at solid surfaces is of key importance, and has thus been the focus of a major research effort during the past decade.4 As pure salts, the consensus has traditionally been that ionic liquids have exceedingly high ionic strengths and thus very short Debye lengths.4,11 However, in 2013 Gebbie et al.12 presented force-distance data for two surfaces separated by an ionic liquid which revealed attractive forces between gold and mica surfaces extending to significantly greater distance than anticipated (Fig. 1A). Subsequently, a repulsive force of similar range was measured between two mica surfaces (Fig. 1B).13 The authors concluded that these forces are electrostatic in origin, with the implication that the ionic liquids behave as dilute electrolytes, challenging the traditional notion that ionic liquids exhibit Debye lengths that are on the order of ionic radii. Repulsive long range surfaces forces have since been measured between surfaces with the same charge in several laboratories around the globe.13–16
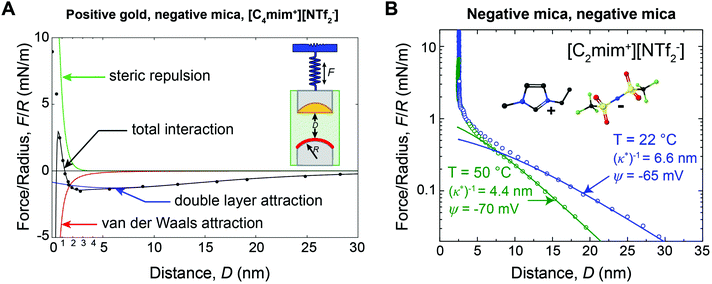 | ||
| Fig. 1 (A) SFA force-distance profile between a positive gold electrode (ΔU = +360 mV vs. OCP) and a negative mica surface across [C4mim+][NTf2−]. Data points are equilibrium forces when bringing together the surfaces. Solid lines are fitted interaction potentials, where the total interaction (black) is a superposition of long range Poisson–Boltzmann (PB) double layer attraction (blue), short range mica–gold van der Waals attraction (red) and short range steric repulsion (green). The double layer force exhibits a decay length of (κ*)−1 = 10 ± 2 nm (eqn (3)). (B) SFA measurements between two negative mica surfaces across [C2mim+][NTf2−] at room temperature (T = 22 °C) and at T = 50 °C. Data points are equilibrium forces on approach, and solid lines are fitted PB interaction potentials (eqn (2) and (3)). As the temperature is increased, (κ*)−1 decreases, consistent with the thermal disruption of electrostatic correlations and/or effective dissociation of ionic liquid ions. Figure panel (B) reprinted from M. A. Gebbie, H. A. Dobbs, M. Valtiner, and J. N. Israelachvili, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 7432–7437. | ||
Similar exponentially decaying forces have also been measured for ionic liquids mixed with a polar solvent,16 and in simple metal halide electrolytes in water at high concentration.17 Critically, this shows that the force is not a unique feature of pure ionic liquids. Thus, it is clear that long range surface forces operate between electrically charged surfaces across many different ionic liquids and concentrated electrolytes, although their origin remains the subject of debate (Fig. 2).13,16,18–20
In this article, we review experimental evidence for the existence of long range surface forces in pure ionic liquids and identify areas of consensus and division. Cases where prior experimental results stand in contrast to the recent reports of long range forces in ionic liquids are discussed, and the mechanisms that may give rise to these long range forces are described phenomenologically. Critical open questions are highlighted and potential experiments aimed at a deeper understanding of long range surface forces in ionic liquids are proposed.
Ionic liquid interfacial nanostructure
Solid surfaces perturb the nanostructure and dynamics of all liquids. In the bulk, aprotic ionic liquids with alkyl chain lengths longer than 3 carbon units, and most protic ionic liquids, have sponge-like nanostructures; only ionic liquids with very short alkyl chains exhibit charge ordering nanostructures that are reminiscent of high-temperature molten salts.21,22 Very long chain surfactant-like ionic liquids form liquid crystalline phases,23 but these are not discussed here. Ionic liquid nanostructure is solvophobic24 in origin. Electrostatic interactions drive the formation of ionic (polar) domains from which alkyl chains (nonpolar) are solvophobically excluded, and consequently cluster into nonpolar domains. These polar and nonpolar domains are dynamic and percolate throughout the bulk liquid.As for non-ionic molecular liquids,25–27 the presence of a surface perturbs the bulk liquid ordering and leads to a local, ordered nanostructure. For ionic liquids with homogeneous bulk nanostructures, the ions arrange into solvation layers, while for ionic liquids with sponge-like nanostructures, the surface flattens the sponge into a more layered order. This interfacial nanostructure gives rise to oscillating (step-like) force profiles as two surfaces approach due to the expulsion of an interfacial layer.4,24,25,28,29
Oscillations (“steps”) are measured for surface separations of between about 1 to 10 nm, and have dimensions similar to an ion pair;30,31 this indicates that the more ordered interfacial arrangements decay to the bulk structure over a few ion pair diameters (Fig. 3). Ionic liquids with longer alkyl chains have better defined bulk and interfacial nanostructures than those with shorter alkyl chains. Interfacial structure thus persists further from the surface for longer chain ionic liquids, and oscillation periods equal to two ion pairs are sometimes measured, corresponding to expulsion of a bilayer.31,32 X-ray reflectivity measurements confirm that surface ordering also occurs for an isolated interface where confinement is not a factor.33
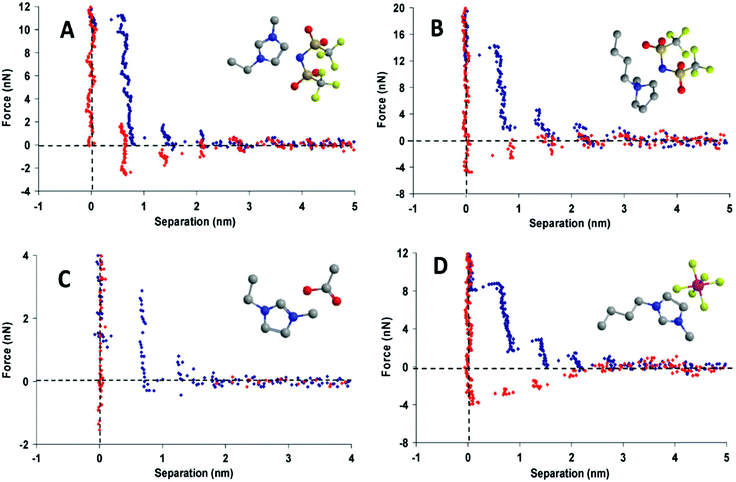 | ||
| Fig. 3 Force-distance profile for a Si3N4 AFM tip approaching (blue) and retracting from (red) a mica surface in (A) [C2mim+][NTf2−], (B) [C4mpyrr+][NTf2−], (C) [C2mim+][NTf2−], and (D) [C4mim+][PF6−]. Reproduced from ref. 24 with permission from the PCCP Owner Societies. | ||
The mechanism of structural forces in ionic liquids has the same origin as structural forces in molecular liquids, where confinement induces oscillations in molecular density, driven by packing constraints.25 Force-distance experiments do not distinguish between the limiting cases of completely charge separated ion layers, such as discrete alternating cation–anion layers, and completely charge neutral mixed ion layers; the only constraint is that the film expelled from between the surfaces during each film-thickness transition is net neutral which can be consistent with various ion arrangements. Recent studies4 suggest that most ionic liquid interfaces likely consist of ion layers that are in between these limits.
Ionic liquids are more structured at highly charged surfaces than at neutral or nonpolar surfaces4,24 and rough surfaces disrupt the formation of layered ionic liquid structures;12,34 roughness even slightly exceeding the ion dimensions can smear or eliminate interfacial forces.29,34 The number, location, and shape of oscillatory structural forces in ionic liquids are fairly insensitive to small increases in temperature. For example, as the temperature is increased from 22 °C to about 50 °C, the force needed to disrupt bound ion or molecular structures slightly decreases without resulting in a change in either the range or qualitative shape of near-surface forces.24–26
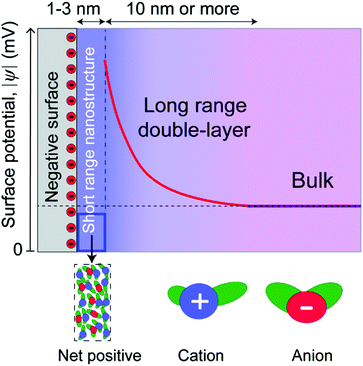
In this paper, we distinguish between near-surface forces, where surface effects are dominant, and long range forces, where the decay length is dominated by the bulk molecular properties of the liquids (Fig. 2). This is a purely conceptual distinction, as there is no physical boundary between the short and long range regimes, which are part of a continuous whole. Long range forces, when measured, involve different decay lengths, often larger, compared to the decay of surface-induced ordering, indicating that they have a different origin. These two regimes are common in some respects to both ionic liquids and dilute electrolyte solutions,35 where electric double layers are conceptualized as a near-surface Stern layer (or layers) in series with a long range “diffuse electric double layer.”
For long range electrostatic forces to be measured in an ionic liquid, some portion of the electrostatic potential of a charged surface must propagate beyond the near-surface nanostructure. Thus, it becomes important to consider the intrinsic surface charge density of the surfaces in relationship to the maximum possible packing density of the cations on that surface. Mica has been utilized in the vast majority of surface force studies to date, and mica contains an average area per negative charge site of 0.47 nm2,36 corresponding to an effective radius of 0.4 nm per site. The approximate radius of typical aprotic ionic liquid cations, using the van der Waals radius of the constituent atoms and assuming a rough averaging across the orientations and configurations available in bulk ionic liquids,4 is between 0.5–1 nm, which is slightly larger than the radius associated with negative charge sites on mica surfaces.
In contrast, protic ionic liquids can have cation radii that are less than 0.5 nm, and AFM imaging has suggested that protic ionic liquids with small ammonium cations, like ethylammonium nitrate (EAN) form surface-bound structures with a spacing that closely matches the charge sites of the underlying mica lattice.37 This may be noteworthy, as studies of EAN using the SFA38 and colloid probe AFM39,40 techniques report solely short range interaction forces at room temperature. Nonetheless, force measurements on aprotic ionic liquids in contact with mica surfaces consistently uncover the presence of long range interaction forces, where some portion of the mica surface potential necessarily propagates beyond the near surface nanostructure.
The situation is even less well resolved for surfaces other than mica. For example, Lauw et al.41 reported cation concentrations can be enhanced relative to anions in the layers of 1-butyl-1-methylpyrrolidinium ([C4mpyrr+]) bis(trifluoromethylsulfonyl)imide ([NTf2−]) at gold electrode surfaces, even over a range of positive electrochemical potentials. Thus, knowledge of surface charge alone is insufficient to predict the major ionic species that will be present adjacent to charged surfaces, and one must also carefully consider the roles played by specific ion-surface interactions and entropic effects.
Trace water can significantly impact ionic liquid near-surface nanostructure. Experiments have shown that trace water can either enhance or disrupt bound ion layers,14,31,42 possibly depending on the exact nature of the ion-surface interactions. Trace amounts of water may enhance ion layering on mica by facilitating K+ dissociation,43 but above a certain water threshold, the IL layering can be disrupted due to both packing and capillary effects;14,42–44 the details are strongly ionic liquid-dependent. At saturation, water molecules can be in excess or depleted at surfaces depending on whether the surface is hydrophilic or hydrophobic respectively, and the affinity of the ions for the surface.4
Long range forces across ionic liquids
Gebbie et al.12 first reported long range forces in ionic liquids in 2013 for [C4mim+][NTf2−] (Fig. 1A). A long range, monotonic attraction across a gold surface held at positive bias and a mica surface was measured with a characteristic exponential decay length of 10 ± 2 nm (Fig. 1A). Mica becomes negatively charged when immersed in ionic liquids, due to desorption of surface-bound potassium ions, adding a negligible K+ content to bulk ionic liquids.A weaker monotonic attraction was measured when a negative potential was applied to the gold.12 At first glance this is surprising, as a repulsion is expected between surfaces with the same charge. However, neutron reflectivity measurements41 for a structurally similar ionic liquid have shown that the first adsorbed layer can be cation rich, even at positive potentials, suggesting that [C4mim+][NTf2−] could fully screen gold surfaces, which would account for the absence of a long range repulsion. The asymmetry in the ability of cations and anions to neutralize the surface potential highlights the fact that specific ion-surface interactions and the properties of bound ion layers are critical determinants of long range forces in ionic liquids.
The presence of long range surfaces forces has since been reported in several independent laboratories13–16,37 (Fig. 4), and it is clear that long range forces do operate for several combinations of ionic liquids and charged surfaces. The magnitudes of the long range surface forces measured in ionic liquids, normalized by the probe radius of curvature, (F/R), typically fall in the range of 0.1–1 mN m−1, and the minimum F/R magnitude that can be detected in typical force measuring experiments can be lower than 0.1 mN m−1. Thus, long range forces in ionic liquids can routinely be measured via both SFA and AFM under carefully controlled conditions, as discussed in prior work.13–16,49 For comparison, long range diffuse electric double layer forces measured in mM concentration aqueous electrolyte solutions can exhibit F/R magnitudes of between 0.1–10 mN m−1, depending on the relative electrolyte concentrations and surface potentials.38
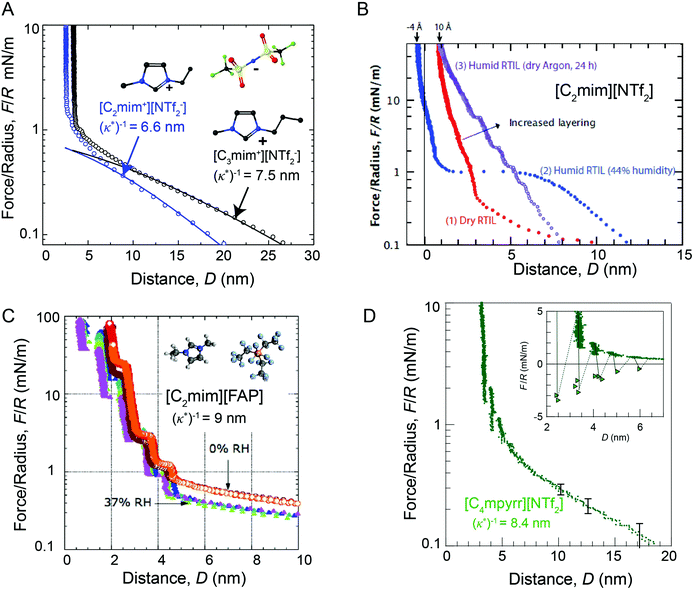 | ||
| Fig. 4 Comparison of SFA force-distance profiles between symmetric mica surfaces across differing ionic liquids and humidity conditions. Long range repulsive forces with a characteristic decay length of (κ*)−1 ∼ 5–10 nm are observed in dried ionic liquids and ionic liquids that have been exposed to relatively low humidity environments (RH ≤ 37%). Forces measured across (A) dried [C2mim+][NTf2−] (blue) and dried [C3mim+][NTf2−] (black),13 (B) dried (red), humid (blue) and semi-humid (purple) [C2mim+][NTf2−],14 (C) dried (orange, red) and semi-humid (purple, blue, green), [C2mim+][FAP−],15 and (D) dried [C4mpyrr+][NTf2−].16 Figure panel (B) reprinted with permission from H. W. Cheng et al., Adv. Mater. Interfaces, 2015, 2, 1500159. Copyright 2015 Wiley and Sons. Figure panel (C) adapted with permission from R. M. Espinosa-Marzal, A. Arcifa, A. Rossi, and N. D. Spencer, J. Phys. Chem. Lett., 2014, 5, 179–184. Copyright 2014 American Chemical Society. | ||
Long range interaction forces in ionic liquids exhibit ionic liquid-dependent exponential decay lengths in the long range, asymptotic limit, with decay lengths ranging from between about 5–10 nm for a diverse range of aprotic ionic liquids (Fig. 5).12–16 To date, the ionic liquids studied exhibit remarkably similar asymptotic interaction decay lengths, despite pronounced differences in short range ion structuring forces, implying a common underlying mechanism in the long range force regime.
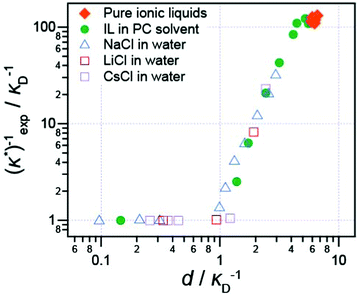
It has also been shown that the long range exponentially decaying force is not unique to pure ionic liquids, or to ionic liquids at all: Smith et al.16 studied the interaction force between two (negative) mica sheets across a wide range of ionic liquids, ionic liquids mixed with a polar solvent in varying fractions, and NaCl in water at high concentration. In every case, the force law was qualitatively similar, with oscillations at short distances, giving way to a monotonic exponentially decaying force at longer range.
The decay length of the long range part was shown to depend on ion density and the dielectric constant. Decay lengths for these high-concentration electrolytes and diluted ionic liquids are presented in Fig. 5 alongside the pure ionic liquids for comparison. When the dielectric constant of the fluid is taken into account,16 all data, including previous literature data for aqueous salt solutions, such as the LiCl solutions studied by Baimpos et al.,17 fits onto a master curve. This means that finer molecular details of the ionic liquid ions, such as the size of cation hydrocarbon substituents, do not control the fundamental nature of the long range force. The long range force is of purely electrostatic origin.
Surface properties therefore play a key role in determining the presence and magnitude of long range forces in ionic liquids, while having little impact on the long-range interaction decay length. To date, pronounced long range surface interactions have only been observed when ionic liquids are confined between, or located directly adjacent to, charged surfaces.12–16,44 Experiments with in situ electrochemical control demonstrate that interaction forces between surfaces and/or probe tips, whether attractive12 or repulsive,45 systematically increase in magnitude as the surface potential difference is increased. In contrast, the interaction decay lengths appear to be independent of the surface potential. Both the dependence of interaction strengths on surface potential and the independence of the interaction decay lengths are consistent with the conclusion that the long range force is probing a bulk correlation length, determined by bulk properties such as solution ionic strength and dielectric permittivity.
Long range forces in ionic liquids are highly sensitive to temperature. Recent SFA measurements13 show that long range interaction decay lengths for two different [CRmim+][NTf2−] ionic liquids systematically decrease as the temperature is increased from 22–75 °C. For all temperatures, the structures formed by the near-surface bound ion layers and mica surface potential remain unchanged, while the interaction decay length decreases from 6.7 ± 0.1 nm (22 °C) to 3.4 ± 0.2 nm (60 °C) for [C2mim+][NTf2−] and from 7.4 ± 0.1 nm (22 °C) to 3.5 ± 0.2 nm (74 °C) for [C3mim+][NTf2−]. It was proposed that increasing the temperature disrupts ionic correlations in bulk ionic liquids, enabling ionic liquid ions to more effectively screen surfaces over shorter distances. In contrast, forces that are purely entropic in nature would be expected to be repulsive and to grow in range as the temperature is increased.35
The presence of trace amounts of water in ionic liquids also impacts long range interaction forces, however, there are few experimental works that systematically probe the specific impact of very small fractions of water on the long range interactions. Espinosa-Marzal and colleagues15 showed that equilibrating the ionic liquid [C2mim+] tris(pentafluoroethyl)trifluorophosphate ([FAP−]) at 37% relative humidity modestly decreases the magnitude of both the long and short range forces measured between mica surfaces, without qualitatively altering the range of long range forces (Fig. 4C).
In a separate paper43 the decay length decreased with increasing humidity for a hydrophilic ionic liquid, in qualitative accordance with the dilution results of Smith et al.;16 the added water leads to an increased dielectric constant. In comparison, Cheng et al.14 show that saturating [C2mim+][NTf2−] with water at 44% relative humidity gives rise to an unexpected attractive instability between 1.5 and 5 nm (Fig. 4D), attributed to capillary bridging of the mica surfaces by water films that adsorbed at each of the hydrophilic mica–liquid interfaces. Similar long range capillary forces in water saturated [CRmim+][NTf2−] ionic liquids were recently observed by Wang et al.46 using AFM. These results show that the presence of water in ionic liquids can result in complex, and at times unexpected, changes to surface forces.14,46,47
While the presence of long range surface forces is increasingly measured for numerous combinations of ionic liquids and charged surfaces, long range interaction forces are not measured in every experiment on ionic liquids. In 1988, Horn and colleagues38 observed solely short range ion binding forces in an SFA study of the protic ionic liquid EAN between mica surfaces. Similarly, in 2010, Bou-Malham et al.48 performed an SFA study on aprotic ionic liquids where long range forces were not reported. Measurements were performed on two aprotic ionic liquids, [C4mim+] tetrafluoroborate ([BF4−]) and [C4mim+] hexafluorophosphate ([PF6−]), between mica surfaces and only short range oscillatory forces were observed. The apparent absence of long range forces in those experiments appears to be inconclusive, because the measurement of the long range force baselines required for the observation of weak long range forces is not necessary when addressing the near-surface structure that was the focus of those studies.
It remains to be shown whether an SFA experiment measuring surface forces across EAN, with high resolution and measured from very large distances would give rise to an additional weak monotonic component. Recent, AFM colloid probe measurements of EAN at room temperature yielded solely short range interaction forces,39,40 while AFM colloidal probe measurements of EAN at a significantly elevated temperature of 120 °C clearly demonstrate the presence of long range monotonic forces (Fig. 6).49 In this light, it appears unlikely that the absence of long range forces in the work of Horn et al. is due to technical difficulties.
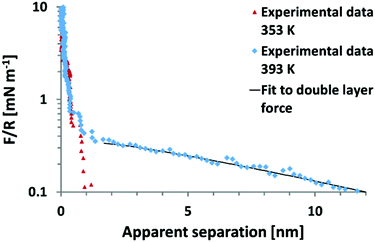 | ||
| Fig. 6 Colloid probe AFM force–distance measurements between a silica probe and mica surface across the protic ionic liquid ethyl ammonium nitrate (EAN) at 80 °C and 120 °C. In EAN, no long range forces of electrostatic origin are observed between room temperature and 80 °C.38–40 However, at 120 °C, a long range force consistent with an electrostatic double layer force is manifested.49 Reproduced from ref. 49 with permission from the Royal Society of Chemistry. | ||
The onset of a long range force at high T initially appears to contradict the temperature dependence of long range forces reported previously.13 However the temperature dependence of the long ranged force in EAN has not yet been examined. Thus, the current state of understanding for EAN is that significant increases in temperature from 22–120 °C leads to a transition from full surface charge screening at low temperatures to dilute electrolyte behaviour at 120 °C. At this stage, it is not possible to say whether this is due to changes in: (i) the ability of EAN to neutralise the surface charge at short range, the oscillatory forces are however indistinguishable from those at 80 °C as can be inferred from Fig. 6 or (ii) a change in bulk properties, for example temperature induced breakdown in the strongly hydrogen bonded, spongelike structure.
Of the other protic ILs studied, the only one to demonstrate evidence for a long ranged repulsion is dimethyl ethylammonium formate (DMEAF).37 However since this is the protic ionic liquid system with both the largest cation, and the least hydrogen bonding, this observation provides little assistance in distinguishing between these two possibilities.
Open questions and plausible origins of long range forces
The classical mean-field approach to treating electrostatic screening in electrolytes provides a useful starting point for understanding prior proposals for explaining the origin of long range forces in ionic liquids. The (formal) Debye length is defined as: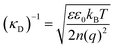 | (1) |
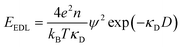 | (2) |
Typical ionic liquids have a total bulk ion concentration of about 7 M, which yields a formal Debye length on the order of 0.1 nm. This is smaller than the size of an individual ionic liquid ion and is several orders of magnitude lower than the experimentally observed decay length; it is clear that a standard application of Debye–Huckel theory could not explain the observed long range forces.
The inapplicability of the standard Debye length, (κD)−1, at such high electrolyte concentrations is unsurprising since strong ion–ion correlations exist at high ionic strengths.50,51 Poisson–Boltzmann equations, integral equation theories, and density functional theories have been developed to overcome the deficiencies in mean-field models, and these pioneering studies have been the subject of excellent reviews.50 Nonetheless, to our knowledge, these theories do not quantitatively predict a decay length that is orders of magnitude greater than the formal Debye length.
Currently, the molecular origin of long range forces in ionic liquids remains an active topic of scientific discussion and theoretical exploration, and different ways of renormalizing the parameters present in eqn (1)–(3) appear to be useful for developing intuition on ionic liquids. Specifically, the interaction decay length in ionic liquids can be framed in terms of an effective Debye length with rescaled parameters, where the formal Debye length of eqn (1), (κD)−1, is replaced by an effective Debye length in ionic liquids, (κ*)−1, shown in eqn (3).
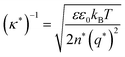 | (3) |
Renormalizing the effective ion concentration, n*
Initially, Gebbie et al.12 proposed that ionic liquids behave as very weakly dissociated, in other words dilute, ionic “solutions.” In this model, a small thermally excited population of “free ions” exist in equilibrium with a strongly correlated ionic network where each charge is neutralised by the sum of its neighbours charge, “dielectric solvent.” This conclusion was reached by interpreting the 10 nm interaction decay length reported in ref. 12 as the effective Debye length, (κ*)−1, of [C4mim+][NTf2−] at room temperature. This would indicate that less than 0.1% of the total number of ions independently contribute to electrostatic screening which was a surprising conclusion at the time.This effective Debye length was used in conjunction with the Boltzmann distribution to calculate the energetics for the effective dissociation for a virtual [C4mim+][NTf2−] ion pair within the bulk ionic liquid. It was shown12 that the effective dissociation energy determined from the measured interaction decay length was in agreement with a simple model that uses only the calculated vacuum ion pair interaction energy52 and measured low frequency dielectric permittivity53 of [C4mim+][NTf2−] (eqn (4) and (5)).
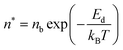 | (4) |
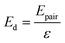 | (5) |
The agreement between this simple calculation and experimental observations12 raises the intriguing possibility that the relevant energetics for cation–anion interactions for two arbitrary ions in bulk ionic liquids can be predicted from knowledge of the ensemble average ion pair potential and ionic liquid low frequency dielectric permittivity. The permittivity is a measured property that, to first order, appears to account for the influence of electrostatic correlations, for example, ion pairing. Hence, the picture is that the majority of ionic liquid ions are strongly associated and cannot move independently, nor obey the Poisson–Boltzmann equation, leaving the ions to effectively behave as a dielectric network. This dielectric network stabilizes the presence of “free” ions and/or charged thermal excitations.
Importantly, ion pairing and/or ion aggregation in ionic liquids can give rise to an effective low frequency dielectric behaviour in bulk ionic liquids, even when pairing and/or aggregation is highly dynamic and transient, as shown very recently theoretically by Kjellander.20 This would explain why NMR diffusivity measurements fail to find evidence of long lived ion pairing in bulk ionic liquids,54 while surface forces measurements12–16 and dielectric spectroscopy measurements55 are suggestive of ionic correlation-driven aggregation. We stress that ionic aggregation and/or pairing in ionic liquids is likely a highly dynamic process.
This effective dissociation framework12 has several testable predictions and practical implications:
• First, any model of long range forces that invokes the thermal disruption of ionic correlations, an effective thermal “dissociation” of ionic liquid ions, necessitates that increases in temperature should systematically decrease the decay length of long range forces. Gebbie et al. confirmed this prediction using [C2mim+][NTf2−] and [C3mim+][NTf2−] (Fig. 1B).1 For these ionic liquids, increasing the temperature decreases the long range interaction decay length, which was interpreted as an increase in the thermally excited free ion population.
• Second, the energetics of ion “dissociation” should exhibit a temperature dependence solely through the impact of temperature on the dielectric permittivity. An analysis using the theoretical framework outlined in ref. 12 and eqn (3) and (4) under varying temperatures was carried out,1 and the dissociation energy was found to be independent of temperature for [C2mim+][NTf2−] and [C3mim+][NTf2−] up to 60 °C. This temperature independence appears to break down above 75 °C, perhaps due to changes in dielectric properties at high temperatures.
• Third, eqn (4) and (5) suggest that if one could identify two ionic liquids with similar ion pair vacuum interaction energies, Epair, but significantly different low frequency dielectric permittivities, the ionic liquid with a higher dielectric permittivity should exhibit a significantly higher degree of ionic dissociation, and resultant smaller electrostatic screening length. This experiment could be realized by maintaining the cation core of a common aprotic ionic liquid, such as the [CRmim+][NTf2−] class of ionic liquids, and comparing an alkyl-imidazolium substituted cation to an analogous imidazolium cation that incorporates a substituent with oxygen atoms or other polar groups. If confirmed, this would provide a new strategy for engineering the effective degree of dissociation of ionic liquid ions by controllably increasing (or decreasing) the ionic liquid permittivity. Hence, the cation substituents would provide functionalities that go beyond the crystal-suppressing symmetry breaking function of traditional alkyl substituents.
The ion aggregation model has been successful in describing the phenomenology and scaling of experiments on ionic liquids. Importantly, eqn (5) describes the energy required to separate charges in a pure dielectric medium with no ionic screening, thus corresponding to the limit of low free ion concentration. Models that explicitly account for screening by surrounding ions and ionic aggregates would prove beneficial for understanding ionic liquids. For multicomponent electrolyte solutions, theories must explicitly account for both dielectric properties and ionic screening. A simple mean-field model of a typical ionic liquid that explicitly considers ion-pairs as dipoles and the screened ion–ion, dipole–dipole, and dipole–ion interactions on the same footing showed that only 1/3 of ions are associated and those ion pairs have a lifetime that is comparable to the diffusive timescale.51 Further work in this direction is required to reveal the full physical picture.
Finally, we note that force distance measurements cannot be used to unambiguously define the nature of the “ions” that give rise to the measured effective Debye length. For example, theories and simulations of concentrated ionic liquid solutions56 show that neutral solvent molecules can act as effective charge carriers in highly concentrated solutions, when steric packing frustration is important. Thus, perhaps thermally excited “defects” such as localized voids which occur spontaneously due to thermal fluctuations, are charge carriers. It may also be important in this context to remember that many inert gases have significant solubilities in ionic liquids.
Renormalizing the effective ion charge, q*, and/or effective dielectric permittivity ε*
The Debye length scales as 1/q*. The bare charge of an ion is necessarily discrete. However, if a central ion is surrounded by a cloud of counterions, then some of the central ion charge is effectively compensated, causing the central ion to interact with other ions outside of the nearby counterion cloud with an effectively lowered charge. This is the basic idea behind charge renormalization, which is important for understanding interactions between charged colloids.57A rigorous formulation of similar approaches to electrolyte solutions is the subject of recent works by Kjellander20 based on the formalism of “Dressed Ion Theory” (DIT).58 Within the DIT, charge renormalization is coupled with a rescaling of the dielectric response. Essentially, the DIT formalism replaces ε in eqn (2) with a dielectric function that depends on the Debye length, ε*. Therefore, eqn (2) becomes a nonlinear equation with the possibility for multiple solutions that can be purely oscillatory, purely monotonic, or exhibit superimposed monotonic and oscillatory characteristics.
Connecting the physics of ionic liquids to other condensed matter systems
Long range forces in ionic liquids may share fundamental connections with the principles underlying electrostatic correlations in other soft matter systems. For example, the long range forces measured in ionic liquids may have an origin that is related to long range diffuse electric double layer forces in pure water, where the Debye length59,60 arises from the autoionization equilibrium (pH) of water molecules. In water, neutral water molecules form a dynamic, hydrogen bonded network, and thermal excitations drive the autoionization of water molecules into protons and hydroxide anions; the large low frequency dielectric constant of water (ε = 78 at 295 K) is responsible for stabilizing the formation of these charged thermal excitations.The physics of ionic liquids may also share conceptual similarities with the screening properties of semiconducting materials. In semiconductors, only charge carriers that are thermally excited from the valence band to the conduction band can freely move to screen electric fields under equilibrium conditions. Recently, Todorova et al.61 suggested that the autoprotolysis of water, in particular the concentrations of free hydroxyl anions and protons, can be approximated to high accuracy using defect models, in analogy to calculating defect concentrations in semiconductors. Perhaps the energetics of thermal disruption of ionic correlations in ionic liquids can also be viewed in terms of a defect model.
Notably, ionic liquids appear to exhibit key aspects of the behaviours that are traditionally associated with both dilute electrolyte solutions – long range, monotonic, exponentially decaying forces – and highly concentrated (aqueous) electrolyte solutions – short range, oscillatory forces. When charged surfaces are immersed in highly concentrated electrolyte solutions, dissolved ions form multiple bound ion layers immediately adjacent to surfaces that partially neutralize the surface charge. These bound ion layers result in the presence of oscillatory surface forces that are similar in both range and magnitude16,17,62 when compared to the short range forces that result from ionic liquid nanostructure. The longer range monotonic component of the interaction forces in concentrated aqueous electrolytes typically occur over shorter distances than measured for ionic liquids, with interaction decay lengths that range between 0.5 and 2 nm.16,17 This has been shown16 to be related to higher (bulk) low frequency dielectric permittivity of the electrolyte solutions relative to the measured low frequency dielectric permittivity measured for ionic liquids (ε = 10–15).53,63
The existence of long range forces between charged surfaces across ionic liquids should manifest itself in other ways in the properties of colloidal or particulate dispersions. While both AFM and SFA studies directly access surface forces, they both require exquisite attention to cleanliness, and this can attract the criticism that results can be affected by a comparably exquisite sensitivity to impurities.
In contrast, disperse phase systems with large surface areas are comparatively insensitive to the presence of trace impurities. We would expect long-range repulsions between silica or other well-characterised, monodisperse charged particles dispersed in ionic liquids to be reflected directly in the in their phase equilibria and osmotic pressure behaviour, and particularly the stability of colloidal crystals.64 Small angle scattering from even moderately dilute (monodisperse) particle dispersions should also exhibit structure factor effects arising from long range repulsions that could not be explained by excluded volume or solvation layer effects.65 Such approaches also facilitate the rapid and systematic exploration of environmental factors that have emerged as determinants of the long range force, whether this be temperature effects in EAN, or control over gas solubility or pressure.66,67
Stable colloidal suspensions can be prepared in ionic liquids.68 Explanations for the colloidal stability of nanoparticle suspensions in ionic liquids include the formation of stabilizing solvation layers and the presence of unscreened electrostatic interactions. We anticipate that careful future study will conclusively determine whether electrostatic interactions are operating to stabilize colloidal suspensions in ionic liquids.
More broadly, the observation of long range interactions in ionic liquids provides a series of experimental results that necessarily challenge the prevailing perspective4 on the relationship between electrostatic correlations and screening in ionic liquids and other highly concentrated electrolytes. At this point, there is solid evidence that the long range interactions measured in ionic liquids are truly equilibrium interactions, as opposed to complex time- and history-dependent dynamic effects.
The precise origin of long range forces in ionic liquids remains open, yet there are promising phenomenological theories12,13,16 as well as very recent rigorous statistical physical analyses20 implicating strong electrostatic correlations between ions. As discussed above, these frameworks appear to be broadly compatible and suggest several potentially fruitful avenues for future research, with diverse implications for ionic liquids and other highly concentrated electrolytes, from designing ionic liquids for energy storage applications, to rationalizing electrostatic correlations in biological self-assembly.
Acknowledgements
This work was supported by the US Department of Energy, Office of Basic Energy Sciences, Division of Materials Science and Engineering Award DE-FG02-87ER-45331: to M. A. G. (analysis and manuscript writing), to H. A. D. (manuscript editing and discussion), and to J. N. I. (manuscript editing and discussion). M. A. G. acknowledges funding provided by the GLAM Postdoctoral Fellowship program in the Geballe Laboratory for Advanced Materials at Stanford University. S. P. is supported by The Leverhulme Trust (RPG-2015-328) and the ERC (Starting Grant 676861 LIQUISWITCH). A. A. L. is supported by a George F. Carrier Fellowship at Harvard University. AMS is supported by a Doctoral Prize from the EPSRC. R. A. and G. W. acknowledge funding support from the Australian Research Council. X. B. acknowledges the financial supports of the CRC funding program (Tiers 2) and NSERC Discovery program. MR acknowledges support from The Knut and Alice Wallenberg Foundation for ILEAP – Ionic Liquid Lubricants Enabling Advanced Performance.References
- J. M. Tarascon and M. Armand, Nature, 2001, 414, 359–367 CrossRef CAS PubMed.
- P. Simon and Y. Gogotsi, Nat. Mater., 2008, 7, 845–854 CrossRef CAS PubMed.
- B. Eisenberg, Biophys. J., 2013, 104, 1849–1866 CrossRef CAS PubMed.
- M. V. Fedorov and A. A. Kornyshev, Chem. Rev., 2014, 114, 2978–3036 CrossRef CAS PubMed.
- T. Welton, Chem. Rev., 1999, 99, 2071–2083 CrossRef CAS PubMed.
- M. Galinski, A. Lewandowski and I. Stepniak, Electrochim. Acta, 2006, 51, 5567–5580 CrossRef CAS.
- C. F. Ye, W. M. Liu, Y. X. Chen and L. G. Yu, Chem. Commun., 2001, 2244–2245, 10.1039/b106935g.
- M. Antonietti, D. B. Kuang, B. Smarsly and Z. Yong, Angew. Chem., Int. Ed., 2004, 43, 4988–4992 CrossRef CAS PubMed.
- M. Armand, F. Endres, D. R. MacFarlane, H. Ohno and B. Scrosati, Nat. Mater., 2009, 8, 621–629 CrossRef CAS PubMed.
- J. Jeong, N. Aetukuri, T. Graf, T. D. Schladt, M. G. Samant and S. S. Parkin, Science, 2013, 339, 1402–1405 CrossRef CAS PubMed.
- M. Z. Bazant, B. D. Storey and A. A. Kornyshev, Phys. Rev. Lett., 2011, 106, 046102 CrossRef PubMed.
- M. A. Gebbie, M. Valtiner, X. Banquy, E. T. Fox, W. A. Henderson and J. N. Israelachvili, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 9674–9679 CrossRef CAS PubMed.
- M. A. Gebbie, H. A. Dobbs, M. Valtiner and J. N. Israelachvili, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 7432–7437 CrossRef CAS PubMed.
- H.-W. Cheng, P. Stock, B. Moeremans, T. Baimpos, X. Banquy, F. U. Renner and M. Valtiner, Adv. Mater. Interfaces, 2015, 2, 1500159 CrossRef.
- R. M. Espinosa-Marzal, A. Arcifa, A. Rossi and N. D. Spencer, J. Phys. Chem. Lett., 2014, 5, 179–184 CrossRef CAS PubMed.
- A. M. Smith, A. A. Lee and S. Perkin, J. Phys. Chem. Lett., 2016, 7, 2157–2163 CrossRef CAS PubMed.
- T. Baimpos, B. R. Shrestha, S. Raman and M. Valtiner, Langmuir, 2014, 30, 4322–4332 CrossRef CAS PubMed.
- A. Yochelis, Phys. Chem. Chem. Phys., 2014, 16, 2836–2841 RSC.
- A. Yochelis, J. Phys. Chem. C, 2014, 118, 5716–5724 CAS.
- R. Kjellander, Phys. Chem. Chem. Phys., 2016, 18, 18985–19000 RSC.
- J. N. A. C. Lopes and A. A. H. Padua, J. Phys. Chem. B, 2006, 110, 3330–3335 CrossRef PubMed.
- A. Triolo, O. Russina, H. J. Bleif and E. Di Cola, J. Phys. Chem. B, 2007, 111, 4641–4644 CrossRef CAS PubMed.
- J. D. Holbrey and K. R. Seddon, J. Chem. Soc., Dalton Trans., 1999, 2133–2139, 10.1039/a902818h.
- R. Hayes, G. G. Warr and R. Atkin, Phys. Chem. Chem. Phys., 2010, 12, 1709–1723 RSC.
- R. G. Horn and J. N. Israelachvili, J. Chem. Phys., 1981, 75, 1400–1411 CrossRef CAS.
- H. K. Christenson, J. Chem. Phys., 1983, 78, 6906–6913 CrossRef CAS.
- J. N. Israelachvili and R. M. Pashley, Nature, 1983, 306, 249–250 CrossRef CAS.
- S. Perkin, T. Albrecht and J. Klein, Phys. Chem. Chem. Phys., 2010, 12, 1243–1247 RSC.
- L. J. D. Frink and F. van Swol, J. Chem. Phys., 1998, 108, 5588–5598 CrossRef CAS.
- R. Atkin and G. G. Warr, J. Phys. Chem. C, 2007, 111, 5162–5168 CAS.
- S. Perkin, L. Crowhurst, H. Niedermeyer, T. Welton, A. M. Smith and N. N. Gosvami, Chem. Commun., 2011, 47, 6572–6574 RSC.
- A. M. Smith, K. R. Lovelock, N. N. Gosvami, P. Licence, A. Dolan, T. Welton and S. Perkin, J. Phys. Chem. Lett., 2013, 4, 378–382 CrossRef CAS PubMed.
- M. Mezger, H. Schroder, H. Reichert, S. Schramm, J. S. Okasinski, S. Schoder, V. Honkimaki, M. Deutsch, B. M. Ocko, J. Ralston, M. Rohwerder, M. Stratmann and H. Dosch, Science, 2008, 322, 424–428 CrossRef CAS PubMed.
- A. Sheehan, L. A. Jurado, S. N. Ramakrishna, A. Arcifa, A. Rossi, N. D. Spencer and R. M. Espinosa-Marzal, Nanoscale, 2016, 8, 4094–4106 RSC.
- J. N. Israelachvili, Intermolecular and surface forces, Academic Press, Burlington, MA, 3rd edn, 2011 Search PubMed.
- H. K. Christenson and N. H. Thomson, Surf. Sci. Rep., 2016, 71, 367–390 CrossRef CAS.
- A. Elbourne, K. Voïtchovsky, G. G. Warr and R. Atkin, Chem. Sci., 2015, 6, 527–536 RSC.
- R. G. Horn, D. F. Evans and B. W. Ninham, J. Phys. Chem., 1988, 92, 3531–3537 CrossRef CAS.
- R. A. Asencio, E. D. Cranston, R. Atkin and M. W. Rutland, Langmuir, 2012, 28, 9967–9976 CrossRef CAS PubMed.
- N. Hjalmarsson, R. Atkin and M. W. Rutland, Phys. Chem. Chem. Phys., 2016, 18, 9232–9239 RSC.
- Y. Lauw, M. D. Horne, T. Rodopoulos, V. Lockett, B. Akgun, W. A. Hamilton and A. R. Nelson, Langmuir, 2012, 28, 7374–7381 CrossRef CAS PubMed.
- R. M. Espinosa-Marzal, A. Arcifa, A. Rossi and N. D. Spencer, J. Phys. Chem. C, 2014, 118, 6491–6503 CAS.
- L. A. Jurado, H. Kim, A. Rossi, A. Arcifa, J. K. Schuh, N. D. Spencer, C. Leal, R. H. Ewoldt and R. M. Espinosa-Marzal, Phys. Chem. Chem. Phys., 2016, 18, 22719–22730 RSC.
- H. Li, R. J. Wood, F. Endres and R. Atkin, J. Phys.: Condens. Matter, 2014, 26, 284115 CrossRef PubMed.
- R. Hayes, N. Borisenko, M. K. Tam, P. C. Howlett, F. Endres and R. Atkin, J. Phys. Chem. C, 2011, 115, 6855–6863 CAS.
- Z. Wang, H. Li, R. Atkin and C. Priest, Langmuir, 2016, 32, 8818–8825 CrossRef CAS PubMed.
- H. W. Cheng, J. N. Dienemann, P. Stock, C. Merola, Y. J. Chen and M. Valtiner, Sci. Rep., 2016, 6, 30058 CrossRef CAS PubMed.
- I. Bou-Malham and L. Bureau, Soft Matter, 2010, 6, 4062 RSC.
- N. Hjalmarsson, R. Atkin and M. W. Rutland, Chem. Commun., 2016 10.1039/c6cc07396d.
- J. P. Hansen and H. Lowen, Annu. Rev. Phys. Chem., 2000, 51, 209–242 CrossRef CAS PubMed.
- A. A. Lee, D. Vella, S. Perkin and A. Goriely, J. Phys. Chem. Lett., 2015, 6, 159–163 CrossRef CAS PubMed.
- S. Tsuzuki, H. Tokuda, K. Hayamizu and M. Watanabe, J. Phys. Chem. B, 2005, 109, 16474–16481 CrossRef CAS PubMed.
- H. Weingaertner, Angew. Chem., Int. Ed., 2008, 47, 654–670 CrossRef CAS PubMed.
- H. Tokuda, S. Tsuzuki, M. A. B. H. Susan, K. Hayamizu and M. Watanabe, J. Phys. Chem. B, 2006, 110, 19593–19600 CrossRef CAS PubMed.
- V. Lockett, M. Horne, R. Sedev, T. Rodopoulos and J. Ralston, Phys. Chem. Chem. Phys., 2010, 12, 12499–12512 RSC.
- D. J. Bozym, B. Uralcan, D. T. Limmer, M. A. Pope, N. J. Szamreta, P. G. Debenedetti and I. A. Aksay, J. Phys. Chem. Lett., 2015, 6, 2644–2648 CrossRef CAS PubMed.
- S. Alexander, P. M. Chaikin, P. Grant, G. J. Morales, P. Pincus and D. Hone, J. Chem. Phys., 1984, 80, 5776–5781 CrossRef CAS.
- R. Kjellander and D. J. Mitchell, Mol. Phys., 1997, 91, 173–188 CrossRef CAS.
- H. J. Butt, Biophys. J., 1991, 60, 1438–1444 CrossRef CAS PubMed.
- U. Raviv, P. Laurat and J. Klein, J. Chem. Phys., 2002, 116, 5167–5172 CrossRef CAS.
- M. Todorova and J. Neugebauer, Phys. Rev. Appl., 2014, 1, 014001 CrossRef.
- R. M. Espinosa-Marzal, T. Drobek, T. Balmer and M. P. Heuberger, Phys. Chem. Chem. Phys., 2012, 14, 6085–6093 RSC.
- C. Daguenet, P. J. Dyson, I. Krossing, A. Oleinikova, J. Slattery, C. Wakai and H. Weingartner, J. Phys. Chem. B, 2006, 110, 12682–12688 CrossRef CAS PubMed.
- V. Reus, L. Belloni, T. Zemb, N. Lutterbach and H. Versmold, J. Phys. II, 1997, 7, 603–626 CrossRef CAS.
- D. Qiu, T. Cosgrove, A. M. Howe and C. A. Dreiss, Langmuir, 2006, 22, 546–552 CrossRef CAS PubMed.
- J. Eastoe, B. M. H. Cazelles, D. C. Steytler, J. D. Holmes, A. R. Pitt, T. J. Wear and R. K. Heenan, Langmuir, 1997, 13, 6980–6984 CrossRef CAS.
- E. W. Kaler, J. F. Billman, J. L. Fulton and R. D. Smith, J. Phys. Chem., 1991, 95, 458–462 CrossRef CAS.
- Z. He and P. Alexandridis, Phys. Chem. Chem. Phys., 2015, 17, 18238 RSC.
| This journal is © The Royal Society of Chemistry 2017 |