A five-fold interpenetrated metal–organic framework showing a large variation in thermal expansion behaviour owing to dramatic structural transformation upon dehydration–rehydration

Abstract

A five-fold interpenetrated metal organic framework (MOF) has been shown to exhibit anomalous thermal expansion due to the combined effect of hinge-like motion and sliding of individual diamondoid networks. Upon dehydration, the MOF undergoes dramatic structural changes, thereby altering its thermal expansion behaviour to a large extent.

---

Most solid materials expand along all three spatial dimensions with increasing temperature. This is known as positive thermal expansion (PTE)¹ and generally occurs due to longitudinal vibration motions. Typically, linear PTE coefficients for metals and metal oxides are in the range of 0 to 20 MK⁻¹,² but some materials also show non-positive thermal responses (e.g. negative thermal expansion (NTE)³ or zero thermal expansion (ZTE)⁴) along at least one direction. This is referred to as anomalous thermal expansion and occurs due to phenomena such as transverse vibration motions,⁵ the invar effect,⁶ and lattice-fence or hinge-like motions.⁷ Examples of anomalous thermal expansion in the literature include organic as well as metal–organic solids.⁸

Linear thermal expansion coefficients (α) can vary from small (0 < α < 20 MK⁻¹)⁹ to very large or “colossal” (|α| > 100 MK⁻¹).^8,10 It is of interest to identify materials that display anomalous thermal expansion or unusually large PTE and to then study the underlying mechanisms responsible for such behaviour. These mechanisms are often different to those observed in materials that display typical isotropic PTE and have helped to develop a general understanding of thermal expansion. This insight can be helpful in designing novel thermoresponsive materials for use in sensors and actuators.

In recent years, metal–organic frameworks (MOFs) have attracted much attention due to their novel structural diversity, flexibility and potential applications.¹¹ Furthermore, a number of MOFs such as IRMOFs,¹² cyano-MOFs^3a,5a and HKUST-1^3,13 have been reported to display isotropic negative thermal expansion. Apart from these, a number of other MOFs have displayed the unique combination of PTE, NTE and ZTE due to either hinge-like¹⁴ or stretching-tilting motions.¹⁵ In the case of interpenetrated MOFs, the occurrence of NTE is rare.^3a,5a,8a,16 It is generally presumed that interpenetration will decrease or completely suppress NTE due to the presence of extra networks that may act as physical barriers to transverse vibrations in the structure.^16,17 Herein, we report the presence of colossal uniaxial NTE in a fivefold interpenetrated MOF.

The {[Zn(FMA)(BPA)]·H₂O}_n (1·H₂O) (FMA²⁻ = fumarate, BPA = 1,2-bis-(4-pyridyl)ethane) (Scheme S1, ESI†) framework was prepared using a literature procedure.¹⁸1·H₂O crystallizes in the triclinic space group P1̄. The asymmetric unit comprises a Zn(II) ion in a distorted tetrahedral coordination environment, two crystallographically distinct half units each of FMA²⁻ and BPA, and a non-coordinated water molecule (Fig. 1a and Fig. S1, ESI†). The carboxylate groups are coordinated to the metal ion in a monodentate fashion.§ The tetrahedral metal centres are linked together via the FMA²⁻ and BPA ligands to form a three dimensional 4-connected diamondoid network (Fig. 1b). The distances between the adjacent metal ions are in the range of 9.0416(4)–13.4046(4) Å.

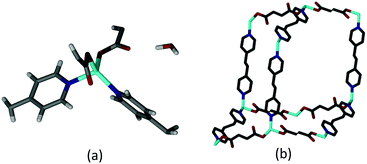Fig. 1 Perspective views of (a) the asymmetric unit of 1·H₂O and (b) a single diamondoid unit of the network (hydrogen atoms have been removed for clarity).

The void spaces of each framework are occupied by four other identical diamondoid networks such that the overall structure is fivefold interpenetrated (Fig. S2, ESI†). The mode of interpenetration is best understood as consisting of two sets of nets, one of which is twofold interpenetrated, while the other is threefold interpenetrated (Fig. S2, ESI†). This mode of interpenetration is quite rare.¹⁹ The water molecules act as bridges between the individual diamondoid networks by forming several strong O–H⋯O hydrogen bonds to the non-coordinated oxygen atoms of the FMA²⁻ ligands (Fig. 2 and Fig. S3, ESI†).

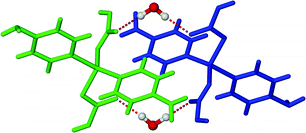Fig. 2 View of H-bonding between two diamondoid networks through guest water molecules (only selected parts of the networks are shown for clarity).

In order to investigate temperature dependent structural changes we carried out a variable temperature single-crystal X-ray diffraction (VT-SCD) experiment. Intensity data were recorded in the 100–240 K temperature range at 20 K intervals (Table S1, ESI†). Upon increasing temperature, the crystallographic a and c axes elongate, whereas the crystallographic b axis shortens (Table S2 and Fig. S4, ESI†). The crystallographic α and β angles increase to different extents, whereas γ decreases substantially upon heating (Table S3 and Fig. S5, ESI†). Since 1·H₂O crystallizes in the triclinic crystal system, the linear thermal expansion coefficients along orthogonal tensors have been determined using PASCal.²⁰

The linear thermal expansion coefficients over the temperature range 100 to 240 K are −117(5), 55(2) and 157(5) MK⁻¹ along the principal axes X1 [0.3609 −0.9319 −0.0393], X2 [0.5938 0.1319 0.7937] and X3 [−0.8798 −0.4458 0.1650], respectively (Fig. S6–S8, ESI†).

The volumetric thermal expansion coefficient of 1·H₂O is 90(2) MK⁻¹ (Fig. S9, ESI†). 1·H₂O displays colossal NTE and PTE along X1 and X3, respectively, and substantial PTE along X2. The reversibility of thermal expansion was determined by evaluating the unit cell parameters at 100 K, followed by incremental data collections at 20 K intervals up to 240 K, and then cooling the crystal again to 100 K (100K-R in the ESI†). The original and final unit cell parameters are very similar and the crystal mosaicity remains unaffected during the complete thermal cycle.

Using the VT-SCD data, the temperature dependent structural changes were examined to interpret the mechanism of thermal expansion. Upon heating, the coordination environment around the metal ion undergoes significant changes. Although the bonding angles around the Zn center undergo very slight changes (less than 2°, see Table S4, ESI†), these angular changes are associated with hinge-like motion¹⁵ within the diamondoid networks. This is more noticeable in the increase in the Zn⋯Zn distances along the [−1 2 0] and [1 0 −1] directions and shortening of the analogous distance along [0 2 1] (Table 1, Fig. 3 and Table S5, ESI†).

Table 1 List of selected non-bonding distances (in Å) within a single diamondoid network at variable temperatures for 1·H₂O

T (K)	Zn1⋯Zn2 [0 2 1]	Zn2⋯Zn3 [−1 2 0]	Zn1⋯Zn3 [1 0 −1]
100	21.5025(7)	18.8065(6)	16.1113(5)
140	21.4524(6)	18.8182(5)	16.1626(5)
180	21.3883(6)	18.8343(5)	16.2224(5)
220	21.3023(6)	18.8544(5)	16.2898(5)
240	21.2612(6)	18.8673(5)	16.3247(5)

---

Fig. 3 View of selected non-bonding distances (in Å) within a single diamondoid network at variable temperatures for 1·H₂O.

In order to understand the interplay between the individual diamondoid networks, we carefully investigated the different attractive and repulsive interactions. The attractive O–H⋯O hydrogen bonding interactions do not propagate along any principal crystallographic directions, whereas the repulsive C–H⋯H–C interactions are predominantly in the crystallographic ac plane.¶ Upon heating, the vibrational motions of the atoms increase, thereby resulting in higher steric interactions among the networks along the a and c axes. As a result, the inter-network distances increase along the crystallographic a and c axes (d1 and d3). Such motions give rise to concomitant sliding of the individual diamondoid networks, with simultaneous shrinkage of inter-network distances (d2) along the b axis (Fig. 4 and Table S6, ESI†).

Fig. 4 (a) View of various inter network distances along the crystallographic a, b and c axes (only three interpenetrated networks are shown for clarity) and (b) changes in the inter-network distances with temperature 1·H₂O.

This type of combined hinge-like motion and network sliding leads to the overall uniaxial NTE along X1 and biaxial PTE along X2 and X3. Although thermal expansion due to layer sliding alone has been described by Saha and co-workers,²¹ its simultaneous occurrence with hinge-like movement has, to the best of our knowledge, not been reported to date.

The water molecules seem to have negligible impact on the thermal expansion behaviour; the O–H⋯O hydrogen bonding interactions are strong enough to prevent significant changes in the O⋯O non-bonding distances upon change in temperature (Table S7, ESI†). Thermogravimetric analysis (TGA) of complex 1·H₂O shows continuous weight loss until 100 °C, which corresponds to the loss of non-coordinated water molecules, followed by single-step decomposition beyond 300 °C (Fig. S10, ESI†). Based on the TGA analysis, the crystals were specifically activated (at 100 °C overnight under dynamic vacuum) with a view to obtaining the dehydrated framework for comparison with its hydrated form. Remarkably, the crystals remained intact even after heating at 100 °C and SCD analysis of the activated crystals at 100 K confirms the absence of non-coordinated water molecules in the dehydrated form 1 (Fig. S11, ESI†). TGA of 1 also confirmed the absence of any residual water molecules in the activated crystals (Fig. S12, ESI†).

Although the activated framework 1 packs in the same crystal system as 1·H₂O, it undergoes a substantial structural transformation upon dehydration. In 1, the Zn(II) ions adopt a distorted octahedral environment instead of the tetrahedral geometry observed in 1·H₂O. Both of the carboxylate groups coordinate to the metal ion in a chelating mode, whereas in the case of 1·H₂O each carboxylate group has one non-coordinating oxygen atom (Fig. S13, ESI†).

Inspired by such structural variations, we investigated the possible changes in thermally-induced network dynamics upon dehydration by recording VT-SCD data for 1 using a strategy similar to that used for 1·H₂O (Table S8, ESI†). The crystallographic c axis elongates significantly as compared to a, whereas the crystallographic b axis contracts slowly upon heating from 100 K to 240 K (Fig. S14 and Table S9, ESI†). The crystallographic angle α remains relatively constant, β increases slowly and γ decreases significantly (Fig. S15 and Table S10, ESI†). Analysis of the VT-SCD unit cell parameters using PASCal²⁰ reveals that the linear thermal expansion coefficients in 1 are −48.7(6), 77(2) and 31.3(3) MK⁻¹ along X1 [0.4087 −0.9125 0.0160], X2 [−0.2453 −0.0353 −0.9688] and X3 [−0.9125 −0.3976 −0.0960], respectively (Fig. S16 and S17, ESI†).|| The overall volumetric thermal expansion coefficient of 1 is 60(3) MK⁻¹ (Fig. S18, ESI†).

All of the principal axes are nearly parallel to those of the hydrated analogue (Fig. S19, ESI†), which simplifies direct comparison of the two structures. It is noteworthy that, upon dehydration, the magnitudes of the linear thermal expansion coefficients along X1 and X3 diminish significantly by nearly ∼68 and ∼126 MK⁻¹, respectively, whereas PTE along X2 is enhanced by ∼22 MK⁻¹ (Fig. S20, ESI†).

In order to understand the thermal expansion behaviour of 1, we inspected the temperature dependent structural changes in more detail. In 1, the bonding angle O1–Zn1–N2 decreases to a lesser extent than in the hydrated analogue. Moreover, and contrary to 1·H₂O, the N1–Zn1–N2 bond angle increases in the case of 1 and a substantial decrease is observed for O1–Zn1–O3 (Table S11, ESI†). Consequently, the Zn⋯Zn distances within the diamondoid network increase along [1 0 −1], while the analogous distances along [−1 2 0] and [0 2 1] remain relatively constant. This suggests the absence of any hinge-like motion within a single network (Fig. S21 and Table S12, ESI†).

Both the ligands undergo significant conformational changes upon dehydration of 1·H₂O, thereby effecting significant changes in the thermal expansion behaviour (Scheme 1 and Fig. S22, ESI†). The torsion angles between the aliphatic parts of the FMA units coordinated to the same Zn(II) center change from 60.5(3)° to 167.9(2)°, suggesting that they undergo a syn to anti conformational change (Fig. S22, ESI†). The analogous torsion angles of BPA change from 87.7(2)° to 99.14(3)°. Concomitantly, neighbouring BPA units (parallel to the ab plane) between two individual diamondoid networks change from having a staggered to an eclipsed conformation (Scheme 1), as inferred from an increase in the torsion angle between them from 5.3(4)° to 68.3(2)°. Such conformational changes cause the BPA units to move away from one another, as evidenced by a slight increase in the centroid⋯centroid distance between the aliphatic parts of the BPA units from 5.5815(2) Å to 5.6300(1) Å. On the other hand, the conformations of neighbouring FMA units that are parallel to both the ac and bc planes remain relatively constant upon dehydration. As a consequence of dehydration, the individual diamondoid networks move further away from one another along the crystallographic c axis while they approach closer to one another along the crystallographic a and b axes (Fig. S23, Tables S6 and S13, ESI†). Hence, dehydration results in increased structural flexibility along the crystallographic c axis and more rigidity along the remaining two directions. As a result, dehydration enhances PTE along X2 and attenuates the extent of NTE and PTE along X1 and X3, respectively.

Scheme 1 Change in the coordination environment of Zn(II) centers upon loss of water molecules (top), and conformational changes upon dehydration shown along the crystallographic c axis (water molecules have been omitted for clarity) (bottom).

The absence of any thermotropic phase transition was confirmed by the absence of any notable thermal events in the differential scanning calorimetry (DSC) thermograms of both the hydrated and dehydrated forms (Fig. S24, ESI†). Upon immersing the activated crystals in water for 24 hours, 1 reverts to 1·H₂O. This is quite surprising because reverting to 1·H₂O requires the FMA²⁻ and BPA units in 1 to rotate with a concomitant change in the coordination environment of the Zn(II) metal centers from the 6- to 4-coordinate. Interestingly, the switching of structures between 1·H₂O and 1 occurs in a single-crystal to single-crystal fashion (Table S14, ESI†).²² The reversible uptake of water guest molecules prompted us to investigate other solvents such as MeOH, CHCl₃, EtOH and acetonitrile with a view to modulating the thermal expansion behaviour by altering the nature of host–guest H-bonding. Unfortunately, none of the abovementioned solvent molecules seem able to penetrate the voids of apohost 1; this is possibly due to the void spaces being too small.

To date, several MOFs have been shown to possess anomalous thermal expansion properties, but little attention has been devoted to studies on the negative linear thermal expansion behaviour of interpenetrated MOFs. We believe that the complexes 1·H₂O and 1 represent a new class of thermoresponsive interpenetrated MOFs that show anomalous NTE. Further investigation of thermal expansion behavior in interpenetrated frameworks is warranted; the effect of interpenetration as well as guest molecules leading to negative thermal expansion should be studied closely. Insights gained from such studies may facilitate the formulation of design principles for new types of thermoresponsive materials that could be useful in a wide range of applications.

The authors declare no competing financial interests.

We thank the National Research Foundation of South Africa for financial support. HA also thanks the Consolidoc fellowship program of Stellenbosch University.

Notes and references

1. N. W. Ashcroft and N. D. Mermin, Solid State Physics, Holt, Rinehart & Winston, 1976.
2. R. S. Krishnan, R. Srinivasan and S. Devanarayanan, Thermal Expansion of Crystals, Pergamon, 1979.
3. (a) A. L. Goodwin and C. J. Kepert, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 140301; (b) V. K. Peterson, G. J. Kearly, Y. Wu, A. J. Ramirez-Cuesta, E. Kemner and C. J. Kepert, Angew. Chem., Int. Ed., 2010, 49, 585.
4. (a) Y.-S. Wei, M. Zhang, P.-Q. Liao, R.-B. Lin, T.-Y. Li, G. Shao, J.-P. Zhang and X.-M. Chen, Nat. Commun., 2015, 6, 8348; (b) X. Song, Z. Sun, Q. Huang, M. Rettenmayr, X. Liu, M. Seyring, G. Li, G. Rao and F. Yin, Adv. Mater., 2011, 23, 4690; (c) S. Margadonna, K. Prassides and A. N. Fitch, J. Am. Chem. Soc., 2004, 126, 15390.
5. (a) K. W. Chapman, P. J. Chupas and C. J. Kepert, J. Am. Chem. Soc., 2005, 127, 15630; (b) W. Miller, C. W. Smith, D. S. Mackenzie and K. E. Evans, J. Mater. Sci., 2009, 44, 5441; (c) C. Lind, Materials, 2012, 5, 1125.
6. (a) M. van Schilfgaarde, I. A. Abrikosov and B. Johansson, Nature, 1999, 400, 46; (b) C. E. Guillaume, C. R. Acad. Sci., 1897, 125, 235; (c) C. E. Guillaume, Nature, 1904, 71, 134.
7. (a) L. D. DeVries, P. M. Barron, E. P. Hurley, C. Hu and W. Choe, J. Am. Chem. Soc., 2011, 133, 14848; (b) E. R. Engel, V. J. Smith, C. X. Bezuidenhout and L. J. Barbour, Chem. Commun., 2014, 50, 4238.
8. (a) A. L. Goodwin, M. Calleja, M. J. Conterio, M. T. Dove, J. S. O. Evans, D. A. Keen, L. Peters and M. G. Tucker, Science, 2008, 319, 794; (b) D. Das, T. Jacobs and L. J. Barbour, Nat. Mater., 2010, 9, 36; (c) H.-L. Zhou, Y.-B. Zhang, J.-P. Zhang and X.-M. Chen, Nat. Commun., 2015, 6, 6917; (d) S. Bhattacharya, V. G. Saraswatula and B. K. Saha, Cryst. Growth Des., 2016, 16, 277.
9. (a) J. S. O. Evans, J. Chem. Soc., Dalton Trans., 1999, 3317; (b) P. A. Tipler and G. Mosca, Physics for Scientists and Engineers, Worth Publishers, 2008, vol. 1, p. 666.
10. (a) A. D. Fortes, E. Suard and K. S. Knight, Science, 2011, 331, 742; (b) K. M. Hutchins, R. H. Groeneman, E. W. Reinheimer, D. C. Swenson and L. R. MacGillivray, Chem. Sci., 2015, 6, 4717.
11. (a) R. K. Das, A. Aijaz, M. K. Sharma, P. Lama and P. K. Bharadwaj, Chem. – Eur. J., 2012, 18, 6866; (b) H. Aggarwal, R. K. Das, P. M. Bhatt and L. J. Barbour, Chem. Sci., 2015, 6, 4986; (c) I. E. Collings, A. B. Cairns, A. L. Thompson, J. E. Parker, C. C. Tang, M. G. Tucker, J. Catafesta, C. Levelut, J. Haines, V. Dmitriev, P. Pattison and A. L. Goodwin, J. Am. Chem. Soc., 2013, 135, 7610.
12. D. Dubbeldam, K. S. Walton, D. E. Ellis and R. Q. Snurr, Angew. Chem., Int. Ed., 2007, 46, 4496.
13. Y. Wu, A. Kobayashi, G. J. Halder, V. K. Peterson, K. W. Chapman, N. Lock, P. D. Southon and C. J. Kepert, Angew. Chem., Int. Ed., 2008, 47, 8929.
14. (a) R. K. Das, H. Aggarwal and L. J. Barbour, Inorg. Chem., 2015, 54, 8171; (b) S. Henke, A. Schneemann and R. A. Fischer, Adv. Funct. Mater., 2013, 23, 5990; (c) H.-L. Zhou, R.-B. Lin, C.-T. He, Y.-B. Zhang, N. Feng, Q. Wang, F. Deng, J.-P. Zhang and X.-M. Chen, Nat. Commun., 2013, 4, 2534; (d) P. Lama, L. O. Alimi, R. K. Das and L. J. Barbour, Chem. Commun., 2016, 52, 3231.
15. P. Lama, R. K. Das, V. J. Smith and L. J. Barbour, Chem. Commun., 2014, 50, 6464.
16. Y. Wu, V. K. Peterson, E. Luks, T. A. Darwish and C. J. Kepert, Angew. Chem., Int. Ed., 2014, 53, 5175.
17. (a) A. E. Phillips, A. L. Goodwin, G. J. Halder, P. D. Southon and C. J. Kepert, Angew. Chem., Int. Ed., 2008, 47, 1396; (b) A. L. Goodwin, K. W. Chapman and C. J. Kepert, J. Am. Chem. Soc., 2005, 127, 17980.
18. H. Hwang, H.-Y. Kim, M. M. Lee, Y. J. Na, J. H. Kim, H.-C. Kim, C. Kim, S. Huh, Y. Kim and S.-J. Kim, Cryst. Growth Des., 2013, 13, 4815.
19. M. K. Sharma, P. Lama and P. K. Bharadwaj, Cryst. Growth Des., 2011, 11, 1411.
20. M. J. Cliffe and A. L. Goodwin, J. Appl. Crystallogr., 2012, 45, 1321.
21. S. Bhattacharya and B. K. Saha, Cryst. Growth Des., 2012, 12, 4716.
22. (a) H. Aggarwal, P. M. Bhatt, C. X. Bezuidenhout and L. J. Barbour, J. Am. Chem. Soc., 2014, 136, 3776; (b) S. Takamizawa, E.-I. Nakata, H. Yokoyama, K. Mochizuki and W. Mori, Angew. Chem., Int. Ed., 2003, 42, 4331.

---

Footnotes

† Electronic supplementary information (ESI) available: Synthetic procedure, detailed physical methods, detailed crystallographic information, additional figures, additional XRPD patterns. CCDC 1480758–1480780. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6cc07995d

‡ H. Aggarwal and R. K. Das have contributed equally.

§ See Fig. S1 (ESI†) for detailed criteria for assigning a Zn–O bond.

¶ O–H⋯O and C–H⋯H–C interactions have been determined using SCXRD. More detailed information on such interactions will require access to the neutron diffraction facility.

|| In the case of the dehydrated form, PASCAL analysis has revealed that the direction of the principal axes X1, X2 and X3 are [0.4087 −0.9125 0.0160], [−0.9125 −0.3976 −0.0960] and [−0.2453 −0.0353 −0.9688] respectively. However, in order to facilitate the direct comparison with its hydrated analogue, we first exchanged the coordinates of X2 and X3 and then inverted all the directions.

---