Open Access Article
Open Access ArticleVibrational blue shift of coordinated N2 in [Fe3O(OAc)6(N2)n]+: “non-classical” dinitrogen complexes†
Johannes
Lang
*,
Jennifer
Mohrbach
,
Sebastian
Dillinger
,
Joachim M.
Hewer
and
Gereon
Niedner-Schatteburg
Fachbereich Chemie and Forschungszentrum OPTIMAS, Technische Universität Kaiserslautern, 67663 Kaiserslautern, Germany. E-mail: jlang@chemie.uni-kl.de
First published on 2nd December 2016
Abstract
We present “non-classical” dinitrogen Fe(III) oxo acetate complexes in vacuo utilizing Infrared Photodissociation (IR-PD) at cryo temperatures. The IR-PD spectra reveal a blue shift of the N2 stretching vibration frequencies in the complexes. Density Functional Theory (DFT) calculations confirm the experiments and indicate strengthened N–N bonds due to pronounced σ bonding and a lack of π back donation.
The discovery of transition metal dinitrogen complexes in 19651 launched the ever growing research field of N2 coordination chemistry.2,3 One of the main goals is the conversion of N2 to ammonia under mild conditions4 by homogenous catalysis.5,6 The basic idea is to weaken N–N bonds upon coordination to enable subsequent functionalization. Precursors to N2 activation manifest by elongated N–N distances and by red shifting of stretching frequencies7,8 with respect to the vibration of the free N2 molecule. Such bond activation and vibrational red shifts have been interpreted before, e.g. in terms of the Dewar–Chatt–Duncanson (DCD) model,9 and the Blyholder surface coordination (BSC)10 model. Theoretical as well as spectroscopic investigations confirmed these interpretations.11 However, FT-IR studies on N2 coordinated to Lewis acid centers in zeolites12 and alumina13 revealed blue shifted vibrational N2 stretching frequencies (up to 24 cm−1). This indicates N–N bond strengthening rather than weakening – much beyond these established models. A similar effect has been observed in the case of isoelectronic carbon monoxide: so called “non-classical” metal carbonyl complexes14,15 exhibit blue shifted vibrational CO stretching frequencies (up to 138 cm−1).16 Gas phase studies of isolated non-classical metal carbonyl clusters17,18 proved the intrinsic molecular origin of this effect. The cause for the CO blue shift was a topic of debate19 and is now understood in terms of an interplay between π back donation and electrostatic effects.20 It is paramount to characterize the geometrical and electronic structures of such complexes in order to acquire a fundamental insight into the prevailing interactions leading to such non-classical behaviour.
The combination of Electrospray Ionization Mass Spectrometry21 (ESI-MS) and infrared (IR) laser spectroscopy is suitable for the characterization of isolated coordination complexes with defined stoichiometry. Infrared (Multiple) Photon Dissociation (IR-(M)PD) provides direct access to structural and vibrational information, both under cryogenic conditions22,23 and at room temperature.24 The experimental results and dedicated ab initio calculations are combined in order to obtain detailed insight into the geometrical structure and intrinsic properties of the isolated molecular ions.
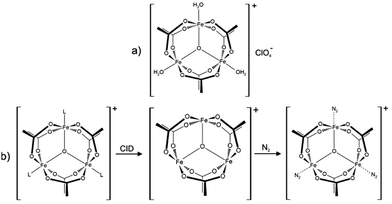
In this work we investigate isolated dinitrogen complexes [Fe3O(OAc)6(N2)n]+ (n = 1–3, OAc = CH3CO2−, cf.Scheme 1), which exhibit a significant blue shift (17 cm−1) of N2 vibrations in the complex with respect to the free N2 molecule. We examine the N2 coordination in detail to rationalize the blue shift and N–N bond strengthening. This is, to the best of our knowledge, the first report on the “non-classical” behaviour of isolated N2 complexes.
We utilize a customized Fourier Transform-Ion Cyclotron Resonance (FT-ICR)-mass spectrometer (Apex Ultra, Bruker Daltonics) equipped with an ESI ion source (Apollo 2, Bruker). We coupled the ICR cell with a KTP/KTA optical parametric oscillator/amplifier (OPO/A) IR laser system (LaserVision). Optimized minimum energy structures and linear IR absorption spectra were calculated at the B3LYP25 level of theory using cc-pVTZ basis sets26 and Stuttgart RSC 199727 effective core potential basis sets (Gaussian 0928). We present calculations with 15 unpaired alpha electrons yielding a spin multiplicity of 16 with other multiplicities (2–18) found to be significantly less stable (cf. Fig. S12, ESI†). We scale the calculated frequencies with two different scaling factors: one scaling factor (0.951) is specifically designed to elucidate N2 stretching bands in [Fe3O(OAc)6(N2)n]+. It scales the calculated N2 stretching frequencies such that a calculated free N2 stretching vibration frequency matches the experimental value29 of 2330 cm−1. This approach conveniently reveals any effects of Fe–N2 coordination on N2 stretching frequencies. A second unspecific scaling factor (0.986) is applied for all other bands below 1800 cm−1. It scales the calculated asymmetric carboxylate stretching vibration frequencies of [Fe3O(OAc)6(N2)1]+ to match our own experimental value of 1587 cm−1. Unscaled spectra are provided in the ESI† (cf. Fig. S4).
Upon spraying the sample solution and recording mass spectra in the ICR-cell, we observe a series of isotopic peaks matching convincingly with simulated isotopic patterns (cf. Fig. S1, ESI†). We assign those peaks to [Fe3O(OAc)6(L)n]+ (L = H2O, acetonitrile, acetic acid; n = 0, 1, 2, 3). Elimination of L by Collision Induced Dissociation (CID) and subsequent coordination of N2 in the hexapole at cryo temperatures (26 K) leads to the formation of [Fe3O(OAc)6(N2)n]+ (cf.Scheme 1b and Fig. S2, ESI†). Note that we observe nmax = 3, thus “titrating” the three available Fe coordination sites. The calculated Gibbs energies at various temperatures reveal N2 binding energies of 11, 9, and 8 kJ mol−1 for the first, second, and third N2 (26 K; BSSE corrected, cf. Fig. S3, ESI†). The N2 binding Gibbs energies diminish with increasing temperature, vanishing above 80 K.
We recorded IR-PD spectra of cryocooled [Fe3O(OAc)6(N2)n]+ (n = 1, 2, 3, Fig. 1, black traces) and conducted DFT simulations to obtain their linear IR absorption spectra (Fig. 1, green traces). The DFT calculations reveal optimized minimum structures as depicted in the insets of Fig. 1. We observe several bands between 1300 cm−1 and 1500 cm−1, coinciding with the predicted CH3 bending modes of the acetate ligands. While the calculated band frequencies around 1423 cm−1 and 1467 cm−1 agree well with the IR-PD spectrum, the calculated intensities differ significantly. Switching the DFT functional from B3LYP to PBE0 yields a much better match of IR intensities but significant deviations of calculated and observed vibrational frequencies (cf. Fig. S5, ESI†). Neither of these empirical functionals predicts both entities correctly. In the following we utilize the B3LYP results for further discussion.
The amount of N2 coordination (n = 1, 2, 3) has no significant influence on the frequency and intensity of the CH3 bending bands (neither in the IR-PD experiments nor in the DFT calculations). This finding likely originates from the spatial separation of the affected methyl groups from the Fe–N2 coordination sites.
We find a strong IR-PD band at 1587, 1590, and 1591 cm−1 in the cases of n = 1, 2, 3. We assign this band to carboxylic CO stretching bands of the six coordinated acetate ligands. The n = 1 CO stretching band is red shifted by ≈3–4 cm−1 with respect to the n = 2, 3 bands, and with respect to the corresponding band of the free acetate anion30 at 1591 cm−1. The DFT calculated asymmetric carboxylate stretching frequencies – scaled to match the experiment at n = 1 – reproduce well the reduced redshift of the experiments on n = 2, 3. The coordinated carboxylate groups thus sense N2 coordination through their common Fe centers. We provide an illustrative visualization of the calculated displacement vectors of these modes in Fig. S6 of the ESI.† Note that the n = 1 and 2 coordinations lift the sixfold degeneracy of these asymmetric stretching bands of the six coordinated acetate ligands. The recorded bands (slightly broadened to FWHM ≈ 7 cm−1) may well contain the predicted splittings of ≈0.5 cm−1 – yet unresolved (cf. Fig. S7, ESI†).
We observe sharp bands (FWHM ≈ 3.5 cm−1) above 2300 cm−1 revealing the IR active N2 stretching vibrations of [Fe3O(OAc)6(N2)n]+ (cf. the displacement vector visualization of these modes in Fig. S8, ESI†). Isotope labeling of the N2 molecule confirms our assignment of these IR-PD bands to the N2 stretching frequencies. We observe a red shift of the 15N–15N vibration band relative to the 14N–14N vibration band (79 cm−1; cf. Fig. S17, ESI†) and the same blue shift with respect to the free N2 in both isotopomers.
In all cases (n = 1, 2, 3) the solitary 14N2 stretching bands of the experimental IR-PD spectra shift to the blue (17–18 cm−1) with respect to the (IR inactive) stretching frequency of the free 14N2 molecule (2330 cm−1).29 These blue shifts indicate N–N bond strengthening upon coordination. Our DFT calculations predict this blue shift remarkably well (18–20 cm−1). Multiple coordinated N2 molecules have almost identical stretching frequencies. There seems to be no coupling between the N2 molecules adsorbing at distinct, equivalent Fe sites. In contrast to the carboxylate asymmetric stretching bands the N2 stretching bands shift slightly to lower frequencies with increasing n (IR-PD spectrum: 1 cm−1; DFT: 1.5 cm−1). However, in all three cases (n = 1–3) the N2 stretching band is blue shifted with respect to the free N2.
The DFT calculations reveal subtle distortions of the triangular Fe3O-core upon coordination of N2 (cf.Scheme 2 and Table S2, ESI†). Each N2 molecule binds end on to the respective Fe atom. In general, the coordination of N2 enlarges Fe–Fe distances and Fe–Ocentral bond lengths (by 0.03 Å resp. 0.01 Å) of those bonds which involve the N2 coordinating Fe-center. All the other Fe–Fe distances and Fe–Ocentral bond lengths shorten by approx. 0.03 Å or 0.01 Å. Natural Population Analysis (NPA) of [Fe3O(OAc)6(N2)n]+ (n = 0, 1, 2, 3) reveals the dependence upon n of local charge densities within the triangular Fe3O-core (cf.Scheme 2). The Fe centers gain 0.058–0.064 e electron density per coordinating N2. The non-coordinated N atoms donate 0.121–0.134 e electron density in about equal parts to the coordinating N and Fe atoms. Free, non-polar N2 molecules thus polarize and oxidize significantly upon Fe coordination, both magnitudes decreasing with n – as does the blue shift of the N2 stretching bands. Note that the N–N bond length contracts slightly upon coordination (−0.002 Å). The high positive charge on the Fe centers (1.862–1.922 e) diminishes their electron donating capability and thus inhibits the π back donation. Such charge effects seem to increase the “non-classical” effect in metal carbonyl complexes.31
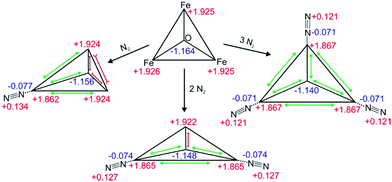 | ||
| Scheme 2 Calculated geometries and natural charge distributions of the Fe3O-core and the coordinated N2 in [Fe3O(OAc)6(N2)n]+ (n = 0, 1, 2, 3). | ||
Non covalent interaction (cf.Fig. 2 for n = 1 and Fig. S11 for n = 2, 3, ESI†) analysis reveals a rather strong attractive, but non covalent interaction between the Fe atoms and the coordinated N atoms at rather long Fe–N coordination distances of 2.451–2.501 Å (n = 1–3). At such distances the π back donation is doomed to weakness due to scant π orbital overlap. Instead, it stands to reason that σ-donation of the N2 molecule constitutes the driving force of attraction in the Fe–N2 coordination in [Fe3O(OAc)6(N2)n]+. Besides the obvious attractive Fe–N interaction, we identify repulsive interactions between the carboxylate O atoms and the coordinated N atoms.
 | ||
| Fig. 2 NCI plot of geometry optimized [Fe3O(OAc)6(N2)1]+ (cf. Fig. S10 for n = 2, 3, ESI†). The NCI plot reveals attractive interaction between the Fe center and the coordinated N atom (1) and repulsive interaction between of the O atoms and the N atom (2). | ||
Simple considerations as e.g. by the DCD and BSC models do not explain the observed blue shift of the N2 stretching vibrations upon coordination. To rationalize this effect in a fairly perspicuous way we refer to the molecular orbital (MO) diagram of N2 (cf. Scheme S1, ESI†): all bonding MOs are populated. When ruling out short range π back donation into empty anti-bonding MOs (inhibited by the net positive charge of the coordinating complex), there is a way to increase the formal N–N bond order (and thus strengthen the N–N bond and increase the stretching frequency): this is a depopulation of the antibonding 4σ* orbital into appropriate Fe centered acceptor orbitals. We have elucidated the prevailing coordination and bonding by inspection of computed molecular orbitals in [Fe3O(OAc)6(N2)n]+. Indeed, we found that the 4σ* MO of the N2 unit overlaps efficiently with MOs located at the Fe centers and at the carboxylate oxygen atoms of the [Fe3O(OAc)6]+ subunit (cf.Fig. 3 for n = 1 and Fig. S13 for n = 2, 3, ESI†). The electrons of the anti-bonding 4σ*(N2) orbital delocalize into a 4![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/char_e0d2.gif) * MO of the whole complex, whereby the 4σ*(N2) orbital polarizes towards the Fe center. Note that the node plane of 4σ*(N2) (between the N atoms) shifts somewhat towards the Fe center. The depletion of the anti-bonding electron density along the N–N bond increases the net bond order of N2 and blue shifts the N2 stretching vibration. The bonding 5σ(N2) contributes to a 5
* MO of the whole complex, whereby the 4σ*(N2) orbital polarizes towards the Fe center. Note that the node plane of 4σ*(N2) (between the N atoms) shifts somewhat towards the Fe center. The depletion of the anti-bonding electron density along the N–N bond increases the net bond order of N2 and blue shifts the N2 stretching vibration. The bonding 5σ(N2) contributes to a 5![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/char_e0d2.gif) MO of the complex. This is expected to result in N–N bond weakening counteracting the effect of 4σ*(N2) delocalization. However, 5σ(N2) receives a partial 4σ*(N2) character to form the 5
MO of the complex. This is expected to result in N–N bond weakening counteracting the effect of 4σ*(N2) delocalization. However, 5σ(N2) receives a partial 4σ*(N2) character to form the 5![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/char_e0d2.gif) MO via hybridization. The strengthening effect of 4σ*(N2) electron density delocalization thus seems to be the critical factor for the “non-classical” behavior of [Fe3O(OAc)6(N2)n]+. The involvement of the 4σ*(N2) orbital in the M–N2 bonding scheme as well as 4σ*/5σ hybridization has been suggested in the context of X-ray absorption studies of N2 adsorbed on metal surfaces.32 Inspection of all other delocalized MOs in the [Fe3O(OAc)6(N2)1]+ complex reveals a total lack of π back donation from the [Fe3O(OAc)6]+ unit to empty π*(N2) orbitals. Considering the high charge on the Fe center and the long Fe–N2 distance (see above) this seems reasonable. The N2 coordination and thus the “non-classical” behavior of [Fe3O(OAc)6(N2)n]+ originate from σ bonding effects.
MO via hybridization. The strengthening effect of 4σ*(N2) electron density delocalization thus seems to be the critical factor for the “non-classical” behavior of [Fe3O(OAc)6(N2)n]+. The involvement of the 4σ*(N2) orbital in the M–N2 bonding scheme as well as 4σ*/5σ hybridization has been suggested in the context of X-ray absorption studies of N2 adsorbed on metal surfaces.32 Inspection of all other delocalized MOs in the [Fe3O(OAc)6(N2)1]+ complex reveals a total lack of π back donation from the [Fe3O(OAc)6]+ unit to empty π*(N2) orbitals. Considering the high charge on the Fe center and the long Fe–N2 distance (see above) this seems reasonable. The N2 coordination and thus the “non-classical” behavior of [Fe3O(OAc)6(N2)n]+ originate from σ bonding effects.
Our fundamental insight into the class of “non-classical” N2–Fe complexes is remarkable in view of the industrial use of bulk iron for N2 activation and hydrogenation. It might help to advance a general understanding of dinitrogen chemistry beyond established coordination models.
This work was supported by the German Research Foundation DFG within the Transregional Collaborative Research Center SFB/TRR 88 “Cooperative effects in homo and heterometallic complexes” (3MET).
Notes and references
- M. D. Fryzuk, Chem. Commun., 2013, 49, 4866–4868 RSC.
- J. L. Crossland and D. R. Tyler, Coord. Chem. Rev., 2010, 254, 1883–1894 CrossRef CAS.
- N. Khoenkhoen, B. de Bruin, J. N. H. Reek and W. I. Dzik, Eur. J. Inorg. Chem., 2015, 567–598 CrossRef CAS.
- S. F. McWilliams and P. L. Holland, Acc. Chem. Res., 2015, 48, 2059–2065 CrossRef CAS PubMed.
- D. V. Yandulov and R. R. Schrock, Science, 2003, 301, 76–78 CrossRef CAS PubMed.
- H. Tanaka, K. Arashiba, S. Kuriyama, A. Sasada, K. Nakajima, K. Yoshizawa and Y. Nishibayashi, Nat. Commun., 2014, 5, 1–11 Search PubMed.
- N. Lehnert and F. Tuczek, Inorg. Chem., 1999, 38, 1659–1670 CrossRef CAS PubMed.
- N. Lehnert and F. Tuczek, Inorg. Chem., 1999, 38, 1671–1682 CrossRef CAS PubMed.
- J. Chatt and L. A. Duncanson, J. Chem. Soc., 1953, 2939–2947 RSC.
- G. Blyholder, J. Phys. Chem., 1964, 68, 2772–2777 CrossRef CAS.
- F. Studt and F. Tuczek, J. Comput. Chem., 2006, 27, 1278–1291 CrossRef CAS PubMed.
- K. Hadjiivanov and H. Knözinger, Catal. Lett., 1999, 58, 21–26 CrossRef CAS.
- R. Wischert, C. Coperet, F. Delbecq and P. Sautet, Chem. Commun., 2011, 47, 4890–4892 RSC.
- H. Willner and F. Aubke, Angew. Chem., Int. Ed., 1997, 36, 2402–2425 CrossRef CAS.
- A. J. Lupinetti, G. Frenking and S. H. Strauss, Angew. Chem., Int. Ed., 1998, 37, 2113–2116 CrossRef CAS.
- P. K. Hurlburt, J. J. Rack, J. S. Luck, S. F. Dec, J. D. Webb, O. P. Anderson and S. H. Strauss, J. Am. Chem. Soc., 1994, 116, 10003–10014 CrossRef CAS.
- J. Velasquez, B. Njegic, M. S. Gordon and M. A. Duncan, J. Phys. Chem. A, 2008, 112, 1907–1913 CrossRef CAS PubMed.
- A. Fielicke, G. von Helden, G. Meijer, B. Simard and D. M. Rayner, J. Phys. Chem. B, 2005, 109, 23935–23940 CrossRef CAS PubMed.
- A. S. Goldman and K. Krogh-Jespersen, J. Am. Chem. Soc., 1996, 118, 12159–12166 CrossRef CAS.
- G. Bistoni, S. Rampino, N. Scafuri, G. Ciancaleoni, D. Zuccaccia, L. Belpassi and F. Tarantelli, Chem. Sci., 2016, 7, 1174–1184 RSC.
- J. B. Fenn, Angew. Chem., Int. Ed., 2003, 42, 3871–3894 CrossRef CAS PubMed.
- N. Heine and K. R. Asmis, Int. Rev. Phys. Chem., 2014, 34, 1–34 CrossRef.
- J. Jašík, J. Žabka, J. Roithová and D. Gerlich, Int. J. Mass Spectrom., 2013, 354–355, 204–210 CrossRef.
- J. Lang, M. Gaffga, F. Menges and G. Niedner-Schatteburg, Phys. Chem. Chem. Phys., 2014, 16, 17417–17421 RSC.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- M. Dolg, H. Stoll, H. Preuss and R. M. Pitzer, J. Phys. Chem., 1993, 97, 5852–5859 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision E.01, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- K. P. Huber and G. Herzberg, Constants of Diatomic Molecules, Van Norstrand, New York, 1979 Search PubMed.
- J. D. Steill and J. Oomens, J. Phys. Chem. A, 2009, 113, 4941–4946 CrossRef CAS PubMed.
- A. M. Ricks, J. M. Bakker, G. E. Douberly and M. A. Duncan, J. Phys. Chem. A, 2009, 113, 4701–4708 CrossRef CAS PubMed.
- A. Nilsson and L. G. M. Pettersson, Surf. Sci. Rep., 2004, 55, 49–167 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cc07481b |
| This journal is © The Royal Society of Chemistry 2017 |