Open Access Article
Open Access ArticleComputational tools for the evaluation of laboratory-engineered biocatalysts
Adrian
Romero-Rivera
a,
Marc
Garcia-Borràs
b and
Sílvia
Osuna
 *a
*a
aInstitut de Química Computacional i Catàlisi and Departament de Química Universitat de Girona, Campus Montilivi, 17071 Girona, Catalonia, Spain. E-mail: silvia.osuna@udg.edu
bDepartment of Chemistry and Biochemistry, University of California, 607 Charles E. Young Drive, Los Angeles, California 90095, USA
First published on 6th September 2016
Abstract
Biocatalysis is based on the application of natural catalysts for new purposes, for which enzymes were not designed. Although the first examples of biocatalysis were reported more than a century ago, biocatalysis was revolutionized after the discovery of an in vitro version of Darwinian evolution called Directed Evolution (DE). Despite the recent advances in the field, major challenges remain to be addressed. Currently, the best experimental approach consists of creating multiple mutations simultaneously while limiting the choices using statistical methods. Still, tens of thousands of variants need to be tested experimentally, and little information is available on how these mutations lead to enhanced enzyme proficiency. This review aims to provide a brief description of the available computational techniques to unveil the molecular basis of improved catalysis achieved by DE. An overview of the strengths and weaknesses of current computational strategies is explored with some recent representative examples. The understanding of how this powerful technique is able to obtain highly active variants is important for the future development of more robust computational methods to predict amino-acid changes needed for activity.
1. Introduction
Billions of years of evolution have made enzymes superb catalysts capable of accelerating reactions by many orders of magnitude while also being compatible with life. This rate acceleration is achieved by decreasing the activation barriers of reactions, making them possible at lower temperatures and pressures. Among all known catalysts, enzymes (i.e., biocatalysts) are often the most efficient, specific and selective. Enzymes operate under mild aqueous conditions, are biodegradable and non-toxic, and their high selectivities and efficiencies reduce the number of work-up steps and provide product in higher yields. Many enzymes catalyse complex reactions in a few steps, which is in contrast to traditional catalysis that often requires many protection and deprotection steps. These advantageous characteristics of biocatalysis make enzyme-catalysed routes attractive alternatives for chemical manufacturing due to the minimization of costs and environmental advantages. The vast potential of biocatalysis is exemplified with the enzyme-catalysed synthesis of some blockbuster drugs.1–4 Indeed, biocatalysis has won 18 Presidential Green Chemistry awards since 2000 (5 awards given per year). These awards emphasize the 12 Principles of Green Chemistry, which consider environmental factors and energy efficiency among other points.The current use of biocatalysts in industry is still limited, as enzymes need to be modified to be stable for the desired pHs, temperatures, and solvents. Many chemical transformations of industrial interest do not have a natural enzyme capable of catalysing the reaction, and the biocatalyst active site is often too small for proper binding of the desired substrate. In addition, the lack of a precise understanding of enzyme catalysis makes the alteration of the natural activity of enzymes for synthetically relevant targets a tremendous challenge, even though some key factors have been identified.5–9
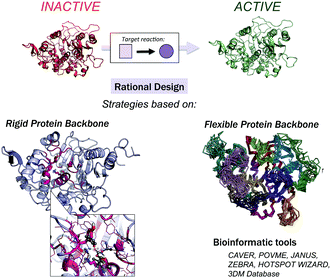
All of the available strategies for enzyme engineering consist of the following steps: (i) selection of mutation points, (ii) making the mutations, and (iii) evaluation of the new variants for activity. These can be targeted using computational and/or experimental approaches leading to rational, semi-rational or non-rational enzyme design strategies. Rational design limits the screening effort to a small number of mutations. Semi-rational strategies are based on exploiting initial desired enzymatic activities obtained by rational computational design via subsequent rounds of laboratory evolution, which is similar to the way that promiscuous side-reactions of natural enzymes are enhanced.10–12 In recent years, successful designs for a broad scope of challenging chemical transformations have been produced using semi-rational design approaches.13–22 At the other extreme, in non-rational enzyme evolution, powerful screening methods identify active variants from a large random library of mutants.
The enzyme-engineering field was revolutionized after the discovery of molecular biology methods that modify enzymes using an in vitro version of Darwinian evolution. This strategy is now commonly called Directed Evolution (DE).23–26 Initially, iterative cycles of random amino-acid changes were introduced and were followed by selection of the variants with improved thermostability, substrate specificity and enantioselectivity. Since then, many subsequent improvements have been introduced, which include protein engineering,23,27,28 gene synthesis,29 sequence analysis,30,31 bioinformatics tools,13,14,32–35 and high-throughput screening techniques, such as an ultrahigh-throughput droplet-based microfluidic screening platform.36,37 Indeed, the success of DE experiments depends on genetic diversity and on high-throughput screening or selection methods.27,36
One powerful strategy consists of combining random mutagenesis with statistics to construct mathematical models of protein sequence and function.2 This ensures the accumulation of beneficial mutations leading to the desired activity in a stepwise fashion. DE has become a powerful method to produce novel enzymes with enhanced activity, and it has the advantage that mutations can be introduced at the enzyme active site and at distal positions. The latter are found to be relevant for increasing the enzyme catalytic activity (kcat), as highlighted recently by Kell and coworkers.38 Recent examples of DE-engineered enzymes include the use of ketoreductases for the manufacture of chiral intermediates for pharmaceuticals such as atorvastatin, the active ingredient in Lipitor®, and a transaminase for the manufacture of sitagliptin, the active ingredient in Januvia®.1,3,4,39 The main drawback of DE is that little information is available as to how these mutations lead to enhanced enzyme proficiency. Many efforts are being made to rationalize how DE introduces new mutations to alter the enzyme catalytic activities.40
In this feature article, a short review of the different computational strategies that are being applied to rationally design enzymes is first presented and is followed by a more detailed overview of the available computational approaches currently used to evaluate laboratory-generated enzyme variants. Some recent representative examples are discussed to illustrate the pros and cons of the different methodologies.
2. Computational tools for the rational design of enzymes
Computational methods provide an attractive alternative to understand, model and rationally construct novel enzyme catalysis at a reduced cost. The development of robust computational strategies capable of improving and enhancing enzymatic catalysis as DE currently does is one of the most challenging and exciting roads in the biocatalysis field.41Many computational strategies have been used, and they range from the enhancement of promiscuous activities of natural enzymes employing multiple sequence and structure alignments,42,43 the simultaneous design of the entire protein backbone structure and sequence,44,45 and the (re)design of the active site of natural enzymes by mutating a subset of the active site residues while maintaining a rigid backbone.46–49 The Mayo and Hellinga labs pioneered automated computational design to create an array of (re)designed binding proteins and enzymes.46–48 Mayo converted thioredoxin into a primitive esterase with the program ORBIT, which explores the conformational and sequence space to generate the new variants.46,50 One of the most successful strategies is the Houk and Baker computational inside-out methodology that combines the structure prediction utilities in the Rosetta software (RosettaMatch51 and RosettaDesign39,40) with Quantum Mechanics (QM, i.e., theozyme).49 The proof of concept for the inside-out protocol was the successfully design of novel enzyme catalysts for the Kemp elimination,14 Retro-aldol,13 and Diels–Alder32 reactions. For extensive reviews of the inside-out protocol and designed variants, check ref. 49 and 52. An alternative to RosettaMatch is the re-design of a natural protein that already presents the desired catalytic machinery, i.e., the SABER program53 or Scaffold-Selection.54 Other strategies for matching the theozyme into a protein active site are OptGraft55 and PRODA_MATCH.56 Molecular Dynamics (MD) simulations have also been found to be the key to ranking and identifying the best enzyme mutants.57,58 Janssen and coworkers developed the CASCO (CAtalytic Selectivity by COmputational design) framework that involves high-throughput MD to engineer enzyme stereoselectivity and replace most of the experimental screening assays.59
Additional strategies have been introduced to account for some protein backbone flexibility (see Fig. 1). Smith and Kortemme implemented in Rosetta a type of conformational change observed in high-resolution structures called the ‘backrub’ move to account for some backbone flexibility.60 Baker introduced RosettaReModel, a new framework for flexible protein design.61 Other groups made use of ensembles of conformations generated using normal mode analysis,62 Discrete Molecular Dynamics (DMD) simulations,63 or by generating ensembles from small Φ/Ψ moves.64,65 DMD has been used in conjunction with QM for efficient sampling of protein chains in the study of (metallo)enzymes.66 For further techniques for sampling the conformational space in protein design check ref. 67 and 68, and for available multistate protein design strategies, check ref. 69. In addition to flexible backbone strategies, MD-based strategies have been developed to enhance Rosetta conformational sampling. Combined MD-Rosetta protocols were found to overcome some of the Rosetta sampling limitations, and MD is highly complementary to the Rosetta refinement.58,70
Other strategies have been reported in the literature for the (re)design of enzymes. OptZyme by Maranas and coworkers makes use of Transition State Analogues (TSA) to find active site mutations that minimize the interaction energy of the enzyme with TSA, rather than its substrate.71 Donald et al. developed the K* algorithm for enzyme redesign that incorporates some backbone flexibility via the backrub move and uses Dead-End Elimination (DEE)-based algorithms to find the global minimum sequence for a given backbone.72–74 To aid in the design process of allosterically controllable enzymes, Jung, Kim et al. developed an effective computational strategy to deregulate the allosteric inhibition of enzymes based on sequence evolution analysis of allosteric ligand-binding sites.75
Finally, a variety of bioinformatics and molecular modeling computational tools have been developed that target the engineering of enzyme activity, selectivity, and stability.76 POCKETOPTIMIZER developed by Malisi and coworkers can be used to alter the enzyme active site residues to improve or newly establish the binding of a small ligand.77 The ZEBRA web server attempts to systematically identify and analyse adaptive mutations.78 CAVER and POVME2 can be used to analyse tunnel dynamics in trajectories obtained by MD simulations.79,80 JANUS analyses multiple-sequence alignments to predict mutations required for inter-conversion of structurally related but functionally distinct enzymes.30 Similarly, HotSpot Wizard,31 or in the particular case of the α/β-hydrolase fold superfamily, the bioinformatic 3DM database (ABHDB), can be used to guide the design of mutations to alter the enzyme properties and functionalities.33–35 The FRESCO methodology (Framework for Rapid Enzyme Stabilization by COmputational libraries) was developed to design smart libraries for improving enzyme thermostability.81
Notwithstanding the initial successes, computationally designed enzymes perform quite poorly in comparison with natural and laboratory-engineered enzymes. This observation reflects the extremely challenging task of enzyme design itself and indicates that rational computational enzyme design is still far from being a robust and systematic strategy for designing new biocatalysts useful for manufacturing and industrial purposes. The reasons for the low activity of computationally designed enzymes are highly debated and are out of the scope of this review.15,41,82
3. Computational strategies to evaluate the catalytic proficiencies of engineered enzymes
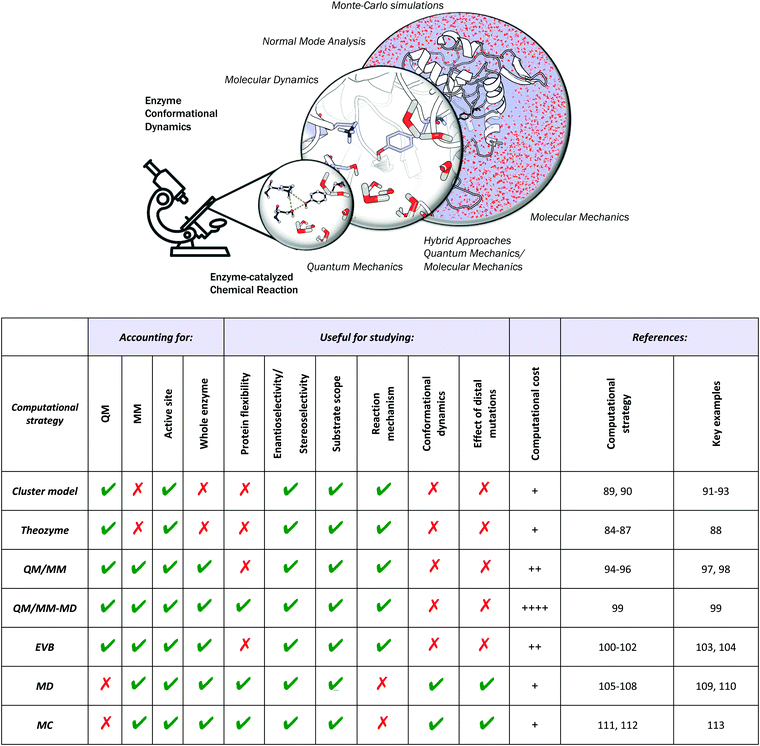
Different computational chemistry tools have been applied to understand and rationalize the role and impact new, introduced mutations have on the catalytic activities of enzymes with the final goal of improving current rational enzyme evolution protocols. Computational techniques offer the possibility to analyse, at the atomic level, how a particular mutation modifies enzymatic chemo-, regio- or stereo-selectivities, or how, for example, the substrate binding is affected due to changes in the protein conformational dynamics induced by these amino acid substitutions.In this section, a general description of the most important and applied computational strategies is reported and illustrated with different examples. All of the techniques discussed here differ in the level of resolution used to describe the protein interactions and in how they sample the enzyme conformational space (see Fig. 2).
a. Quantum mechanics calculations and quantum chemical cluster approach
Quantum Mechanics (QM) calculations include a wide range of approximations whose main objective is to solve the Schrödinger equation, providing useful information about the molecular properties and energetics of a particular chemical system. QM calculations include all the ab initio methodologies based on the Hartree–Fock approximation, semiempirical methods, and Density Functional Theory (DFT), which is currently the most extensively used QM methodology.83 Although DFT provides an accurate description of the chemical system, the associated computational cost increases exponentially when the size of the system grows. This limitation makes the treatment of an entire protein at the DFT level expensive, which explains why only a few active site residues are considered in QM-based methodologies.QM theozyme calculations have been extensively used in the framework of the inside-out protocol to computationally design new enzymes. A theozyme is a DFT-optimized, three-dimensional arrangement of amino acid side chains that are optimally disposed to stabilize the TS of the targeted reaction.49 The theozyme strategy can also be used to study enzymatic mechanisms and to unravel new biological pathways.84–87 For example, in a very recent study, this methodology was applied to elucidate the unprecedented biosynthetic pathway of penigequinolone, and a cationic epoxide rearrangement under physiological conditions was observed for the first time.88 Theozyme calculations were used to analyse and evaluate different possible reaction mechanisms catalysed by key active site residues for a new isolated enzyme (PenF), providing a clear explanation for the product formation experimentally observed. Moreover, theozyme calculations together with MD simulations have also been used by the Houk group to evaluate the catalytic performance of different DE-engineered variants as described in Section 3.d.
A popular QM strategy is the Cluster Model (CM) approach, which focuses on a well-chosen shell of amino acids from the active site of the enzyme in consideration (see Fig. 3). This methodology was developed and used more than thirty years ago by Siegbahn, despite the fact that the first application to an enzyme reaction mechanism was only achieved in 1997.91 Only those residues playing a critical role in the enzymatic mechanism are included in the cluster model. If we take a look at uses in the past, the first systems only included 20–30 atoms without imposing any constrains, which is similar to the theozyme approach described above. However, thanks to the boost in computational power, more complex systems can now be handled. Current CM calculations contain more than 200 atoms and include some atomic constraints to better mimic the protein backbone and the enzyme active site cavity. More specific information about the CM approach and details about the size of the systems and some applications can be found in ref. 89 and 90.
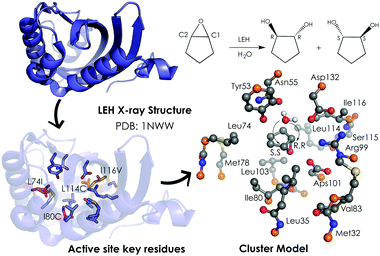 | ||
| Fig. 3 259-atom cluster model structure optimized by Himo and coworkers for LEH in ref. 92. The cluster model consisted of: Asp132–Arg99–Asp101 catalytic triad, the nucleophilic water, two hydrogen-bonded residues (Tyr53–Asn55), and different groups defining the active-site cavity, Met32, Leu35, Leu74, Met78, Ile80, Val83, Leu103, Leu114 and Ile116. The active site residues that are mutated are represented in pink (Leu74 and Ile80) and orange (Leu114 and Ile116). Atoms in orange were fixed in their X-ray coordinates. Hydrogen atoms are omitted for clarity. | ||
Since the first application of CM, a variety of studies using this methodology have been published, and most of them are related to the enzymatic reaction mechanisms.114–117 Some recent applications of CM calculations that target different mutated enzymes with the goal of rationalizing the effect of the introduced mutations (some of them via DE) will be discussed. The pros and cons that this strategy offers will be highlighted.
Limonene epoxide hydrolases (LEH) naturally catalyse the hydrolysis of limonene-1,2-epoxide to limonene-1,2-diol. However, some LEH enzymes can also accept other epoxides as substrates to yield their corresponding diols albeit with lower enantioselectivities.118 Zheng and Reetz applied DE to produce LEH variants capable of catalysing non-natural epoxide substrates (meso-cyclopentene oxide) with high enantioselectivities.118 Himo and coworkers92 studied the enantioselectivity and mutational effects using the CM approach (see Fig. 3). Some residues were truncated, and some atoms were frozen during the DFT geometry optimizations performed at B3LYP/6-31G(d,p) level of theory. Single point calculations with larger basis sets including solvent effects through the CPCM model, zero-point correction, and dispersion effects were applied afterwards. This procedure is typically used for the CM approach and yields accurate predictions of enzymatic reaction mechanisms.89,90 Their results showed in the case of the wild-type (WT) enzyme similar energy barriers for the opening of the oxirane ring, which is in agreement with the experiments that showed a small 14% ee for the R,R-product with an energy difference of 0.2 kcal mol−1. The calculations indicated that the active site cavity of the WT enzyme is quite spacious, so the cyclopentene oxide substrate can be oriented to expose both faces for the nucleophilic attack. Based on these observations, different mutations were proposed. The optimized structures of the transition states (TSs) indicated that the mutations have a direct effect on the substrate-binding pose. The proposed Leu74Ile and Ile80Cys mutations create some additional space on one side of the active site cavity, thus favoring the attack on the less hindered C2 position. This double mutant presents a lower activation barrier for the addition to C2 and, therefore, exhibits a higher selectivity towards the (R,R)-product formation. The combination of Leu114Cys and Ile116Val mutations located on the other side of the catalytic pocket make the other active site side less hindered, leading to a preference for the (S,S)-product formation (pro-R,R TS +1.4 kcal mol−1 higher in energy).
The mechanism and stereoselectivity of AMDase enzymes were also explored with CM, and a variety of substrates were employed.93 AMDase catalyses the asymmetric decarboxylation of α-aryl-α-methyl malonates. In this study, Himo and coworkers applied two different models (I and II) to analyse the substrate preferences and stereoselectivities of AMDase. The substrate used for model I was α-methyl-α-phenylmalonate (methylphenylmalonate), and methylphenylmalonate and α-methyl-α-vinylmalonate (methylvinylmalonate) for model II. The latter has a smaller size and may influence the stereoselectivity of the reaction. Model I (composed of 81 atoms) consists of Gly74, Thr75, Ser76, Tyr126, Gly189 (dioxyanion hole) and Cys188 (responsible for the protonation step of the reaction mechanism). This model lacks important residues involved in the substrate binding and is too small to accurately reproduce the experimentally observed enantioselectivities. In contrast, model II (225 atoms) also includes Pro14, Pro15, Leu40, Val43, Tyr48, Val56, Met159, and Gly190, which mimic the small and big cavities of the active site, and was able to reveal the differences in enantioselectivity for methylphenylmalonate as a substrate. The S-product has a small methyl group pointing to the more solvent-accessible pocket and a much bulkier phenyl group for the hydrophobic pocket, which is formed by Leu40, Val43, and Val156 through their side chain steric repulsion. The S-product is less stable (+14.1 kcal mol−1) than the R-product. The reaction leading to the R-product presents an activation energy of 16.2 kcal mol−1, which is in line with the experimental measurements (14–16 kcal mol−1) and the observed ee of >99%.119 The good agreement observed between the computations and experiments is due to the contribution of the extra residues included in the large model, which account for an extra hydrogen bond between the backbone amide and the carboxylate group of the Thr75 and Ser76, respectively. This study exemplifies the importance of properly selecting the cluster model size for correctly modeling the enzymatic enantio preferences. Once the best cluster model for reproducing the stereoselectivities observed for the WT enzyme is built, then it can be applied to evaluate some variants and analyse the effect of the new, introduced mutations. Some reported studies120–122 showed an enhanced enantioselectivity preference for the S-product over the natural enzyme when Gly74Cys, Cys188Ser mutations were introduced. The position of the new Cys74 residue, located at the Re face of the enediolate intermediate, was found to determine the stereochemistry of the product yielding the S-enantiomer.120–122 In the case of the smaller methylvinylmalonate substrate, the energy difference between the S-/R-products was underestimated compared to the experiments,123 demonstrating that a larger model with a more flexible binding pocket is needed to explain the enantioselectivity of the smaller substrate.
The two examples described above demonstrate that the CM approach is a powerful tool for rationalizing the effect of active site mutations on the enantioselectivity of a particular enzymatic reaction. However, CM is limited because this approach is highly dependent on the initial amino acid selection to build the CM and because the flexibility of some loops close to the active site cannot be properly considered.
b. Hybrid quantum mechanics/molecular mechanics calculations
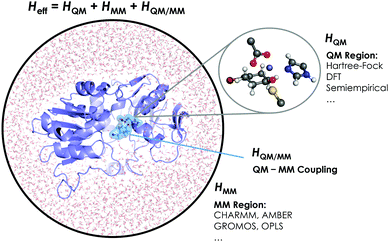
The aggregation of quantum mechanics/molecular mechanics (QM/MM) techniques reported by Warshel and Levitt94 is an extensively used technique for studying biomolecular systems and for drug design.95,96 The impact and importance of this computational strategy was meritoriously recognized in 2013 with the Nobel Prize in Chemistry.124 QM/MM methods were initially developed to allow for the study of those chemical processes that require quantum mechanical treatment, e.g., bond cleavage or bond forming reactions, but that are too large to be fully studied at a high level of theory. Thus, QM/MM calculations consist of the treatment of a small portion of the chemical system, usually the enzyme active site, using QM, and the rest of the system is described using a less rigorous but computationally more efficient level of theory, such as Molecular Mechanics (MM). MM methods use classical mechanics to model atom–atom interactions, and the energy of the system is computed using simple potential energy functions called force fields.125 In the particular case of biocatalysis, QM/MM methods allow the study of chemical reactions (i.e., bond forming/cleavage processes) involving systems of millions of atoms at an atomic resolution, explicitly considering the effects of the protein environment and solvent molecules and their influence on the reaction profile. Two of the most successful QM/MM approaches are (i) the Empirical Valence Bond (EVB) theory (see next section)100 and (ii) the molecular orbital self-consistent field (MO-SCF).126–128 The MO-SCF QM/MM approximation is based on solving the time independent Schrödinger equation using a global Hamiltonian that can be divided in three parts, as shown in Fig. 4: (i) the QM part (HQM) for the small portion of interest in the system where the chemistry takes place (fully represented at the QM level), (ii) a classical part (HMM) to treat the rest of the system and environment, and (iii) a coupling term (HQM/MM) that describes the interactions between the QM part and the MM part, which includes the electrostatic perturbation that the QM wave-function suffers due to the presence of the polarized MM environment.95,108 In this section, we will review some recent applications of the QM/MM MO-SCF methods for the study of enzymatic reactions and the effect of introduced mutations. These examples highlight how powerful this technique is for mutation analysis and prediction.Ryde and coworkers reported a comparative study evaluating the effect on both geometry and energetics of using only QM models or hybrid QM/MM.129 This paper collects all the pros and cons of using these two strategies and concluded that QM/MM calculations converge faster than QM model calculations when the same QM system size is used. Nevertheless, special care has to be taken in QM/MM calculations for treating the redistribution of charges in the junction atoms closer to the active site. QM/MM calculations have been applied to a huge range of applications in enzymatic catalysis during recent years99,130–133 and for the study of other systems and properties.95,96 We will focus our discussion on two recent publications97,98 that are based on the application of QM/MM strategies to explain and understand the changes on the enzymatic activities in mutants compared to their respective WT enzymes.
N-Methyltryptophan oxidase (MTOX) catalyses the oxidative demethylation of N-methyl-L-tryptophan (NMT) to form hydrogen peroxide, formaldehyde, and tryptophan. This family of enzymes also includes the monomeric sarcosine oxidase (MSOX). Thiel and coworkers reported97 a theoretical study of the amine oxidation step of NMT demethylation by MTOX. The level of theory used for the QM part was B3LYP-D2/6-31G(d) for structure optimization, B3LYP-D2/TZVP for energies, and the CHARMM22 force field for the MM part. The QM system includes ca. 71–72 atoms: the NMT substrate, the truncated FAD and Cys308. Two different reaction mechanisms were postulated, but the QM/MM calculations elucidated that the hydride transfer (HT) path has a more favorable energy barrier of 21.3 ± 2.3 kcal mol−1. In contrast, the alternative single-electron transfer (SET) path presented an activation energy of 34.1 ± 2.8 kcal mol−1, indicating the HT mechanism is the preferred one. Similar activation energies were obtained after including the His263 or Lys341 residues in the QM region, and relevant information about the charge of the oxygen atoms at the terminal carbon position of the substrate was obtained. When Lys341 was considered in the QM region, a change in the oxygen atom charges was observed, suggesting an important electrostatic influence imparted by that residue. However, His263Asn and Lys341Gln singly mutated variants both exhibited higher activation energies compared to the WT enzyme, and the barrier for the His263Asn mutant was substantially higher than that for the Lys341Gln mutant. The latter suggests that His263 has a more significant role for substrate binding in MTOX than in MSOX, whose mutation only decreased the rate slightly.134 The reason for this MTOX/MSOX difference probably relies on the natural substrates for both enzymes. Sarcosine is the natural substrate of MSOX, which does not possess an indole group in contrast to N-methyl-L-tryptophan and is thus lacking the possible π-cation and π-stacking interactions with Arg51 and His263. Calculations also suggested that the activation energy of the HT path increased in the case of Lys341Gln with respect to the WT, but the effect was more dramatic for the His263Asn mutation. These results were corroborated experimentally, showing a 250-fold lower MTOX activity after mutation.135 This study illustrates how QM/MM calculations are crucial to unveil the effect of key active site residues during the reaction and to determine the reasons for the differences in the rate of the process for each case.
DNA methyltransferases (DNA-MTases) are enzymes that catalyse DNA methylation. Specifically, DNA-MTases in prokariotes perform the methyl transfer from S-adenosyl-L-methionine cofactor (SAM) to an adenine (N6, position) or a cytosine nucleobase (N4 or C5 positions, see Fig. 5). A C5-MTase study was reported by Tuñón and coworkers,98 and they applied classical MD simulations and QM/MM calculations to obtain a detailed picture of the reaction mechanism. Depending on the reaction step of the mechanism, different residues were included in the QM region. The first step of the reaction corresponds to Cys81 deprotonation, and the side chains of Cys81, Ser85, and the truncated part of the DNA involved in the reaction were included in the QM region. A second possibility was explored, in which the side chain of Cys81, a water molecule and the part of the DNA involved in the reaction were considered as part of the QM system. For evaluating the methylation step of the C5 position of the nucleobase, the side chains of Glu119 and Cys81 were included, as well as the truncated part of the DNA involved in the reaction. For the β-elimination step, the same methylation QM system was used with a water molecule. In this step, the side chain of Glu119 is responsible for protonating the N3 atom of the cytosine nucleobase, and a water molecule deprotonates the C5 position. Early studies suggested that a hydroxide anion was the base in charge of deprotonating this C5. The last step of the process corresponds to the elimination of the proton located at the C5 of cytosine and the breaking of the covalent bond with Cys81. For the latter step, the same QM subsystem was used without the water molecule and the proton extracted. Based on their QM/MM calculations, they suggested that the main role of Glu119 during the methylation step is the formation of a hydrogen bond with the substrate. These results cannot, however, explain experiments where the Glu119Gln variant was found to be substantially less active than the WT, even though their actives sites are similar.136 These observations suggest that the impact of the Glu119 residue on the catalysis should be higher. QM/MM calculations for the β-elimination step showed that Glu119 plays a key role. The proton of Glu119 is transferred to the N3 position of the DNA substrate with an energy barrier of 4.8 ± 0.3 kcal mol−1. The latter induces an increased charge on the proton to be extracted and facilitates deprotonation by the water molecule. This C5 deprotonation mediated by water was more favorable than having a hydroxide anion in the enzyme active site. In the final step of the reaction mechanism, the cleavage of the C–C bond formed between the cytosine substrate and Cys81 takes place, followed by protonation of Glu119. The computed activation energy for the bond cleavage step is 4.8 ± 0.4 kcal mol−1 and 3.5 ± 0.2 kcal mol−1 for Glu119 protonation. Experiments where Glu119Ala, Glu119Gln, and Glu119Asp mutations were introduced showed a drastic decrease in the activity during the methylation step.136 This QM/MM study by Tuñón and coworkers demonstrated how important the Glu119 residue is during the whole reaction path and clarifies the effect of the Glu119 mutation on the pre-steady-state and steady-state rate constants. Additionally, they showed that a crystallographic water molecule, instead of a hydroxide anion, is responsible for the substrate C5 deprotonation. The QM/MM calculations clarified two highly debated issues of this enzymatic mechanism.
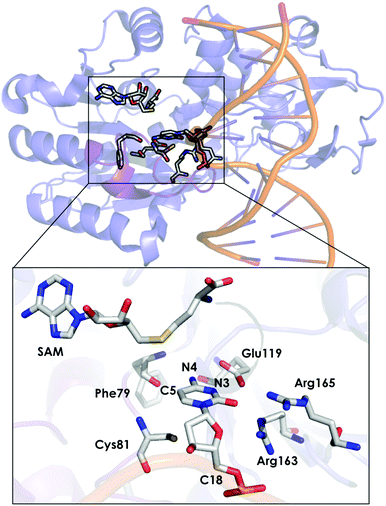 | ||
| Fig. 5 Representation of the active site of DNA methyltransferases (DNA-MTases, PDB code: 2HR1). The most important residues for the reaction are represented by sticks. | ||
The provided examples show how QM/MM calculations can help elucidate the role of certain active site residues and give some invaluable insights into the enzyme reaction mechanism. Most of these studies either consider the X-ray structure of the enzyme, as in the first provided example, or perform some classical MD simulations (see Section 3.d) to generate an ensemble of conformations from which to start the QM/MM analysis (as described in the last study provided). It is, however, recognized that enzymes are highly dynamic structures that can adopt different relevant conformational states in the course of the reaction. QM/MM calculations can also be coupled to MD simulations to properly describe the substrate conformational changes and the dynamic nature of the enzyme. In a recent perspective study by Rovira and coworkers, the importance of QM/MM-MD calculations for some carbohydrate-active enzymes was highlighted.99 In particular, they used QM/MM with the MD enhanced sampling technique metadynamics to map the conformational Free Energy Landscape (FEL). QM/MM-MD simulations have a high computational cost, which hampers their application in studying enzyme conformational dynamics.
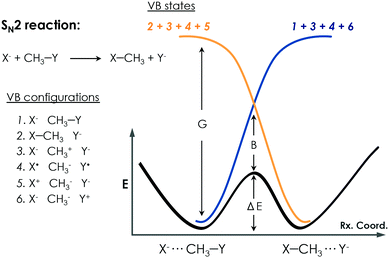
c. Empirical valence bond calculations
Warshel developed the EVB approach.100 The EVB method is a QM/MM approach that describes bond forming and breaking in a chemical reaction through diabatic states from the classical Valence Bond (VB) description of the reactants, intermediates, and products species as, shown in Fig. 6. EVB takes the energy of the different species from QM calculations and through diagonalization of the energy matrix generated obtains the eigenvalues. This procedure also allows the possibility to apply EVB to obtain the free energy profile of the studied reaction, which is a very relevant tool for the study of biocatalytic processes. A detailed description of the theory, capabilities, applications and limitations of the EVB method can be found in ref. 101 and 102. The EVB method can provide information on key residues and mutant effects.137–139 In this section, some recent applications of EVB to study enzymatic reactions and the role of new introduced mutations are summarized. The strengths and weaknesses of this technique when applied to the study of enzyme catalytic activity are highlighted and discussed.Kamerlin and coworkers applied the EVB Free Energy Perturbation/Umbrella Sampling (EVB-FEP/US) method to study the enantio- and regio-selectivity of an epoxide hydrolase (EH),103 which catalyses the hydrolysis of trans-stilbene oxide (TSO) into the corresponding diol. The system included in the EVB region was the TSO substrate, the side chain of Asp105 and His300, and the hydrolytic water molecule. The reaction mechanism consists of a nucleophilic attack of Asp105 on the epoxide, leading to the formation of an alkyl-enzyme intermediate. At this step, the side chain of His300 and the water molecule are treated as beholders because they are not involved at this stage, but they are crucial to maintaining an unbroken EVB region. The next important step consists of the hydrolysis of the alkyl-enzyme intermediate, and all the Asp105, His300, and water molecule are simultaneously involved. The R,R- and S,S-enantiomers of TSO were considered in the study as well as the nucleophilic attack on both the C1 and C2 positions of the epoxide ring. The protonation state of some residues was investigated and corroborated with experiments.140,141 A detailed analysis of the enzyme active site revealed the presence of a second His104 residue, close to the catalytic Asp105, that could be important for the reaction. They showed that having the His104 residue doubly protonated balances the charge of the otherwise negatively charged active site and leads to a physical model that accurately describes the enzyme activity and reproduces the experimental observations. They found that the nucleophilic attack preferentially occurs at the C1 position of the oxirane ring in the S,S-TSO substrate, and its activation energy is 1.7 kcal mol−1 lower than the one computed for C2. In the case of the R,R-TSO substrate, the activation barrier for the C2 attack is 3.6 kcal mol−1 lower than for the C1 position. Interestingly, the barrier for the hydrolysis step is higher when the first step occurs at C1 rather than C2, making the attack at C1 unlikely. Thus, their results suggested that the regioselectivity of the process is determined by the hydrolysis step. They also analysed the effect of some mutations. Glu35 forms a hydrogen bond with the hydrolytic water molecule, and His104 in the wild type blocks solvent access to the enzyme active site. For the R,R-TSO substrate, they observed that TSO displaces the Glu35Gln mutated residue far away from the active site, which avoids the His104 interaction, and provides useful information about the role this residue plays in the reaction. Tyr154 and Tyr235 form an oxyanion hole stabilizing the negative charge generated on the alkyl-enzyme intermediate. The single mutation of Tyr154Phe and Tyr235Phe exhibited higher barriers for both R,R- and S,S-TSO in the alkylation step compared to the WT enzyme. The His300Asn mutation slightly disrupted the active site due to the different side chain of Asn, suggesting a strong interaction between Glu35 and His104 not observed in the natural enzyme. This example demonstrates that EVB simulations can be used to unveil the most favourable protonation states of active site residues and to assess the role of the key active site residues during the reaction mechanism.
Monoamine oxidase (MAO) catalyses the oxidative deamination of monoamine neurotransmitters. Stare et al. reported an EVB study to rationalize the effect of the Ile1335Tyr mutation on the rate constant in MAO-A.104 This mutation was found to be important, as it plays a key role in determining the specificity of the MAO enzyme.142 The substrate considered was phenylethylamine (PEA), and the rate constant was computed for both the natural MAO A and the Ile1335Tyr variant. The simulation was performed on the rate limiting step of the process, which consists of the C–H bond breaking of the α-carbon atom of the amine, followed by hydrogen transfer to the N5 atom of the flavin. The two considered EVB states, i.e., the reactants and products, included the PEA substrate and the truncated flavin with a total of 36 atoms. The computed free energy activation barrier for the Ile1335Tyr mutant was 19.7 kcal mol−1, showing good agreement with experiments. The latter barrier was 1 kcal mol−1 higher than the one computed for the WT enzyme (18.6 kcal mol−1). The differences between the computed free activation energies for the WT enzyme and mutant showed good agreement with experimental measurements (difference of 0.02–0.8 kcal mol−1 depending on the snapshot considered from the MD simulation), but the difference in the rate constants was much higher because of the exponential factor. EVB calculations also revealed that the arrangements of the phenyl ring of PEA and the Phe352 residue are different in the WT compared to the mutated enzyme. In the mutant, both phenyl rings of PEA are positioned in a parallel arrangement, but in the WT enzyme, they are arranged in a quasi T-shape disposition. This fact is due to the alteration of the interactions promoted by the Ile1335Tyr mutation, which favors the parallel allying of the phenyl rings of PEA. They also suggested that another reason for the increased activation barrier comes from the increased number of water molecules around the active site due to the higher polarity of Tyr, which may decrease the activity of the mutated enzyme. In this particular example, EVB methods can be successfully applied to analyse active site residues re-arrangements induced by new, introduced mutations.
Conformational changes in the enzyme active site and flexible loops can directly affect the catalytic performance of the enzyme, and other computational techniques exist that are able to accurately sample the enzyme conformational dynamics in a more efficient way than QM/MM or EVB simulations.
d. Molecular dynamics simulations
The enzyme conformational flexibility can be analysed by means of sampling methods, such as MD simulations. In MD, ensembles of conformations are obtained by integrating equations of motion. Depending on the nature of the Hamiltonian used, they can be classified into Classical or Quantum MD simulations. Carr–Parrinello MD (CPMD)143 is the most popular approach to perform QM-MD simulations, especially when combined with QM/MM strategies that allow for applications to biomolecules.143 However, classical MD is the most used technique to study protein conformational flexibility. In this approach, both the protein and the solvent are described by a force field that is expressed by simple potentials, which can be integrated to obtain the forces on each atom, and their corresponding accelerations can be used to obtain the new velocities and positions. This yields a trajectory of the protein, which provides the enzyme conformational dynamics along with the simulation time. There are different strategies to enhance the conformational sampling that range from the use of MD-specialized hardware that produces extremely long trajectories (ANTON),105 the application of some bias to favor a given transition,106 a potential to reduce the energy barriers separating different conformational states,107 and the use of parallel ensemble MD simulations that combine several short MDs to reconstruct long time-scale processes, such as Markov State Models (MSM).144 For a recent review about the different available strategies to evaluate protein conformational flexibility check ref. 108.In this section, representative examples that highlight the importance of MD simulations to evaluate laboratory-engineered enzymes and guide the design process will be presented. In a recent study, Pande and Arnold elegantly evaluated the effect of a single mutation located in a flexible loop of the nitrating cytochrome P450 TxtE using MD simulations and MSM.145 It is interesting to emphasize that for a detailed understanding of the functional significance of the F/G loop, it was necessary to perform MD simulations on the 100 μs timescale, which is 200–2000 times longer than those previously reported for P450s.146 The included mutation in the F/G loop was found to modulate the loop dynamics and completely shifted the enzyme regioselectivity from the C4 to the C5 position of L-tryptophan (see Fig. 7A). The simulations revealed that the F/G loop can adopt two different conformations, the open state needed for substrate binding and product release and the closed-lid conformation essential for excluding water molecules from the enzyme active site and promote catalysis. By determining the transition-path (TPT)147 connecting both open- and closed-lid conformations, they could characterize the interactions that gate the transition and identify a key intermediate state. In the latter state featuring attributes from both open and closed conformations, a key His176 was identified that is hydrogen-bonded to Tyr89 and induces a partial opening of the F/G loop. The mutation of this position was hypothesized to shift the loop equilibrium towards the catalytically competent closed-lid conformational state. Site-saturation mutagenesis at position 176 indicated that the mutation of the aromatic phenylalanine, tyrosine, and tryptophan residues improved the binding of L-tryptophan and resulted in nitration at the C5 position. MD simulations, together with X-ray crystallography, indicated that the new mutants presented a 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 ratio of closed-open conformations, which was in contrast to the 50
10 ratio of closed-open conformations, which was in contrast to the 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 ratio observed for the wild-type enzyme. In addition to that, the bulky residues at position 176 forced the substrate to place the indole C5 position close to the ferric peroxynitrile, explaining the increase in regioselectivity.
50 ratio observed for the wild-type enzyme. In addition to that, the bulky residues at position 176 forced the substrate to place the indole C5 position close to the ferric peroxynitrile, explaining the increase in regioselectivity.
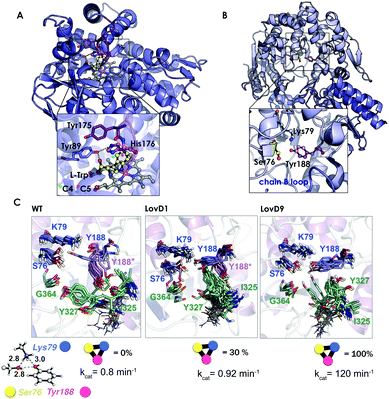 | ||
| Fig. 7 (A) Homology model of the nitrating cytochrome P450 TxtE (PDB code: 4TPO). The F/G loop is highlighted in purple, and haem, L-tryptophan and His176 are represented by balls and sticks. (B) X-ray structures for the wild-type LovD enzyme (PDB code: 3HL9). (C) Optimized quantum mechanics arrangement of the catalytic triad, Lys79 is represented as a blue sphere, Ser76 as yellow, and Tyr188 as pink. Overlay of 10 snapshots from the ANTON MD simulations for wild-type enzyme in the monomeric state; LovD1 and LovD9 together with the computed percentage of time that the catalytic triad stays in the proper arrangement for catalysis along the MD trajectory. The experimental kcat values (in min−1) are also included. | ||
In another study,109 we demonstrated the utility of all-atom unbiased microsecond MD simulations performed on the ANTON machine for rationalizing the improvement on the catalytic proficiency of some DE-engineered enzymes for the synthesis of the cholesterol-lowering drug simvastatin.
The natural enzyme studied, LovD, is an acetyltransferase that was found to catalyse the transfer of an α-methylbutyrate side chain to the C8 position of monacolin J acid (MJA) to yield lovastatin. In the natural pathway, LovD is acylated at position 176 because of its interaction with the acyl carrier protein (ACP) domain of its binding partner protein LovF. Afterwards, the α-S-methylbutyrate side chain is then regioselectively transferred to the C8 hydroxyl of MJA. Envisioning a potential enzymatic manufacturing route for the synthesis of simvastatin, 9 rounds of directed evolution were applied to yield LovD9 that accepted an unnatural acyl donor, α-dimethylbutyryl-S-methylmercaptopropionate, as a substrate and obviated the need for allosteric regulation exerted by LovF. X-ray crystallography and nanosecond-scale MD simulations were unable to provide an explanation for the increase in the catalytic activity of the last round of mutants because the catalytic residues Ser176, Tyr188, and Lys79 displayed an almost identical catalytically competent arrangement as predicted by QM (see Fig. 7B and C).
The ANTON microsecond timescale MD simulations performed on the apo monomeric state of the enzyme indicated that the introduced mutations along the DE pathway progressively stabilized the catalytically competent arrangement of the triad since the ideal QM geometry was observed with increasing frequency. The higher population of the catalytically competent conformational state suggested that the free energy of the latter conformation was gradually lowered in the DE pathway. These findings for the monomeric state of the enzyme in an explicit solvent contrasted with the MD simulations performed on the wild-type dimer X-ray structure and on a model for the LovD–LovF complex. The latter demonstrated that protein–protein interactions stabilized the QM ideal geometry of the catalytic triad for catalysis.
In other studies, short MD simulations have been found to be crucial to evaluate the effect of the included mutations on the enzyme catalytic activity, especially in cases where active site mutations have been introduced.148–151 Janssen and coworkers selected four different haloalkane dehalogenases for which experimental data on the enantioselectivity conversion of a variety of substrates was available.151 They modeled the enantioselectivity by evaluating the frequency of occurrence of Near Attack Conformations (NAC) for pairs of enantiomers during the MD simulation. NAC is defined as the conformations that deviate from the QM TS presenting angles between the reactive atoms within 20° and distances between reactive atoms of less than the sum of their van der Waals radii.110 They were able to accurately model the enantioselectivity using a cluster of short (10 ps) independent MD simulations with different initial velocities. This approach was then used to design highly stereoselective mutants of limonene epoxide hydrolase.59 Similarly, Zhou et al. created an esterase with enhanced selectivity in hydrolytic kinetic resolutions using DE and analysed the source of the enantioselectivity with X-ray crystallography and short MD simulations.150 Zhou and coworkers performed 80 nanosecond MD simulations to evaluate the effect of two mutations located at the product-release site in an epoxide hydrolase for the efficient bioresolution of bulky pharmaco substrates.148 The combination of MD simulations with the software CAVER79 were used to evaluate the effect of the included mutations on the substrate access tunnels of a dehalogenase enzyme.149 The percentage of time that the access tunnel was in an open or closed conformation was found to correlate with the catalytic activity of the variant.
These studies demonstrate how classical MD simulations coupled with QM calculations can capture enzyme conformational states key for catalysis, which cannot be elucidated by visual inspection of the X-ray data nor with high-level calculations based on an enzyme conformation taken from the crystallographic structure. MD simulations can therefore elucidate the role of both the active site and distal mutations on the catalytic activity of the enzyme. This is in contrast to the other methodologies discussed so far.
e. Monte-Carlo conformational sampling simulations
Monte-Carlo (MC) simulations are a stochastic approach to the task of generating a set of representative configurations under given thermodynamic conditions, such as temperature and volume. In the metropolis MC simulation scheme, the method randomly generates potential movements on a given structure, and the movements are accepted or rejected based on the energy of the new pose with respect to the previous structure. If the change in energy is negative, the new configuration is accepted; otherwise, depending on a probability given by a Boltzmann factor, the new structure will be discarded or selected. In contrast to MD simulations, MC gives no information about the time evolution of structural events and is inefficient for exploring the configurational space of large biomolecules.Recently, MC has been coupled with normal mode analysis methods to sample conformational changes along normal modes.111,112 PELE (Protein Energy Landscape Exploration) is a MC algorithm developed by Guallar and coworkers that subjects the ligand to random rotations and translations and perturbs the protein based on the Anisotropic Network Model (ANM).111 PELE has been successfully applied to evaluate the effect of mutations introduced via DE113,152 and has shown great promise for use in metalloenzyme designs.153 One recent example is the application of PELE combined with QM/MM calculations to unveil how substrate oxidation was improved in a DE-engineered laccase.113 The enzyme is a copper-based oxidase that reduces oxygen to water via a one-electron oxidation of a reducing substrate, 2,2′-azino-bis(3-ethylbenzo-thiazoline-6-sulfonic acid) or 2,6-dimethoxyphenol. The evolved laccase presented 5 mutations, two located in the T1 pocket, two at the substrate entrance, and an additional one on the protein surface. PELE was used to locate 20 substrate-bound structures within 5 kcal mol−1 of the lowest binding energy pose. Afterwards, QM/MM calculations were performed to evaluate the amount of spin density localized on the substrate to estimate the electron transfer reactivity. Their simulations showed that mutations introduced via DE increased the enzyme catalytic activity by enhancing the substrate binding rather than the metal redox potential. The mutations located at the enzyme active site affected the binding mode of the substrate and provided a more favorable electrostatic environment for oxidation. The same strategy was recently used to evaluate a doubly mutated peroxygenase engineered by DE for the synthesis of 1-naphtol.152
MC methodologies are, therefore, a cheap alternative to MD for evaluating enzyme conformational dynamics. However, they do not provide the time-dependence of the observed events and cannot be applied to evaluate correlated inter-residue motions.
4. Conclusions
Directed evolution has become one of the most powerful strategies to design new enzymes with high activities towards non-natural substrates or reactions. Even though the catalytic proficiencies of DE-engineered enzymes are high, the strategy is not rational because how the included mutations affect catalysis and enzyme stability has not been elucidated. This clearly limits the process since the efforts invested in optimizing a given biocatalyst cannot be further applied in other (un)related cases. In addition, DE requires an initial residual activity for the target substrate or reaction.More powerful enzyme design methods could be developed if a comprehensive understanding of the relationship between mutations and enzyme catalytic activity was achieved. In this review, the available computational approaches that can be used to elucidate the basis of DE rules of operation were presented with some recent representative examples. These can be divided into strategies that tackle: (i) the evaluation of the enzyme reaction mechanism in atomistic detail using quantum mechanics, if only certain active site residues are considered, or hybrid quantum mechanics/molecular mechanics approaches when the whole enzyme is considered; or (ii) the accurate evaluation of the conformational dynamics of the enzyme, such as molecular dynamics or Monte-Carlo simulations. Each technique presents its strengths and weaknesses, but the combination of them provides an invaluable tool to shed light on the effect of the included DE mutations on the enzyme reaction mechanism or the conformational dynamics of certain active site residues. The understanding of DE rules of operation is of the utmost importance to reach the final goal of developing more robust computational protocols to predict the amino-acid changes needed for activity. This would reduce the need for experimentally probing randomized sequences, rendering the route to novel biocatalysts much more efficient. Robust computational enzyme evolution protocols based on the discussed methodologies will, in the future, need to be developed and applied if the routine design of enzymes is to be pursued.
Acknowledgements
A. R. R. thanks the Generalitat de Catalunya for PhD fellowship (2015-FI-B-00165), M. G. B. is grateful to the European Community for CIG project (PCIG14-GA-2013-630978), and Spanish MINECO for project CTQ2014-52525-P. S. O. thanks the Spanish MINECO CTQ2014-59212-P, Ramón y Cajal contract (RYC-2014-16846), the European Community for CIG project (PCIG14-GA-2013-630978), and the funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (ERC-2015-StG-679001).Notes and references
- M. Breuer, K. Ditrich, T. Habicher, B. Hauer, M. Keßeler, R. Stürmer and T. Zelinski, Angew. Chem., Int. Ed., 2004, 43, 788–824 CrossRef CAS PubMed.
- R. J. Fox, S. C. Davis, E. C. Mundorff, L. M. Newman, V. Gavrilovic, S. K. Ma, L. M. Chung, C. Ching, S. Tam, S. Muley, J. Grate, J. Gruber, J. C. Whitman, R. A. Sheldon and G. W. Huisman, Nat. Biotechnol., 2007, 25, 338–344 CrossRef CAS PubMed.
- S. Panke and M. Wubbolts, Curr. Opin. Chem. Biol., 2005, 9, 188–194 CrossRef CAS PubMed.
- C. K. Savile, J. M. Janey, E. C. Mundorff, J. C. Moore, S. Tam, W. R. Jarvis, J. C. Colbeck, A. Krebber, F. J. Fleitz, J. Brands, P. N. Devine, G. W. Huisman and G. J. Hughes, Science, 2010, 329, 305–309 CrossRef CAS PubMed.
- S. J. Benkovic and S. Hammes-Schiffer, Science, 2003, 301, 1196–1202 CrossRef CAS PubMed.
- M. Garcia-Viloca, J. Gao, M. Karplus and D. G. Truhlar, Science, 2004, 303, 186–195 CrossRef CAS PubMed.
- S. Marti, M. Roca, J. Andres, V. Moliner, E. Silla, I. Tuñón and J. Bertran, Chem. Soc. Rev., 2004, 33, 98–107 RSC.
- Z. D. Nagel and J. P. Klinman, Nat. Chem. Biol., 2009, 5, 543–550 CrossRef CAS PubMed.
- A. Warshel, P. K. Sharma, M. Kato, Y. Xiang, H. Liu and M. H. M. Olsson, Chem. Rev., 2006, 106, 3210–3235 CrossRef CAS PubMed.
- P. A. Romero and F. H. Arnold, Nat. Rev. Mol. Cell Biol., 2009, 10, 866–876 CrossRef CAS PubMed.
- C. Jaeckel, P. Kast and D. Hilvert, Annu. Rev. Biophys., 2008, 37, 153–173 CrossRef PubMed.
- H. Renata, Z. J. Wang and F. H. Arnold, Angew. Chem., Int. Ed., 2015, 54, 3351–3367 CrossRef CAS PubMed.
- L. Jiang, E. A. Althoff, F. R. Clemente, L. Doyle, D. Rothlisberger, A. Zanghellini, J. L. Gallaher, J. L. Betker, F. Tanaka, C. F. Barbas, III, D. Hilvert, K. N. Houk, B. L. Stoddard and D. Baker, Science, 2008, 319, 1387–1391 CrossRef CAS PubMed.
- D. Rothlisberger, O. Khersonsky, A. M. Wollacott, L. Jiang, J. DeChancie, J. Betker, J. L. Gallaher, E. A. Althoff, A. Zanghellini, O. Dym, S. Albeck, K. N. Houk, D. S. Tawfik and D. Baker, Nature, 2008, 453, U190–U194 CrossRef PubMed.
- L. Giger, S. Caner, R. Obexer, P. Kast, D. Baker, N. Ban and D. Hilvert, Nat. Chem. Biol., 2013, 9, U494–U449 CrossRef PubMed.
- O. Khersonsky, G. Kiss, D. Roethlisberger, O. Dym, S. Albeck, K. N. Houk, D. Baker and D. S. Tawfik, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 10358–10363 CrossRef CAS PubMed.
- R. Blomberg, H. Kries, D. M. Pinkas, P. R. E. Mittl, M. G. Gruetter, H. K. Privett, S. L. Mayo and D. Hilvert, Nature, 2013, 503, 418–421 CrossRef CAS PubMed.
- E. A. Althoff, L. Wang, L. Jiang, L. Giger, J. K. Lassila, Z. Wang, M. Smith, S. Hari, P. Kast, D. Herschlag, D. Hilvert and D. Baker, Protein Sci., 2012, 21, 717–726 CrossRef CAS PubMed.
- J. K. Lassila, D. Baker and D. Herschlag, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 4937–4942 CrossRef CAS PubMed.
- R. Obexer, S. Studer, L. Giger, D. M. Pinkas, M. G. Gruetter, D. Baker and D. Hilvert, ChemCatChem, 2014, 6, 1043–1050 CrossRef CAS.
- X. Garrabou, T. Beck and D. Hilvert, Angew. Chem., Int. Ed., 2015, 54, 5609–5612 CrossRef CAS PubMed.
- X. Garrabou, B. I. M. Wicky and D. Hilvert, J. Am. Chem. Soc., 2016, 138, 6972–6974 CrossRef CAS PubMed.
- U. T. Bornscheuer, G. W. Huisman, R. J. Kazlauskas, S. Lutz, J. C. Moore and K. Robins, Nature, 2012, 485, 185–194 CrossRef CAS PubMed.
- J. C. Francis and P. E. Hansche, Genetics, 1972, 70, 59–73 CAS.
- S. Lutz and U. T. Bornscheuer, Protein Engineering Handbook, Wiley-VCH Verlag GmbH & Co. KGaA, 2008 Search PubMed.
- M. S. Packer and D. R. Liu, Nat. Rev. Genet., 2015, 16, 379–394 CrossRef CAS PubMed.
- R. J. Kazlauskas and U. T. Bornscheuer, Nat. Chem. Biol., 2009, 5, 526–529 CrossRef CAS PubMed.
- N. J. Turner, Nat. Chem. Biol., 2009, 5, 567–573 CrossRef CAS PubMed.
- A. Currin, N. Swainston, P. J. Day and D. B. Kell, Protein Eng., Des. Sel., 2014, 27, 273–280 CrossRef CAS PubMed.
- T. A. Addington, R. W. Mertz, J. B. Siegel, J. M. Thompson, A. J. Fisher, V. Filkov, N. M. Fleischman, A. A. Suen, C. Zhang and M. D. Toney, J. Mol. Biol., 2013, 425, 1378–1389 CrossRef CAS PubMed.
- A. Pavelka, E. Chovancova and J. Damborsky, Nucleic Acids Res., 2009, 37, W376–W383 CrossRef CAS PubMed.
- J. B. Siegel, A. Zanghellini, H. M. Lovick, G. Kiss, A. R. Lambert, J. L. Clair, J. L. Gallaher, D. Hilvert, M. H. Gelb, B. L. Stoddard, K. N. Houk, F. E. Michael and D. Baker, Science, 2010, 329, 309–313 CrossRef CAS PubMed.
- R. Kourist, H. Jochens, S. Bartsch, R. Kuipers, S. K. Padhi, M. Gall, D. Böttcher, H.-J. Joosten and U. T. Bornscheuer, ChemBioChem, 2010, 11, 1635–1643 CrossRef CAS PubMed.
- R. K. Kuipers, H.-J. Joosten, W. J. H. van Berkel, N. G. H. Leferink, E. Rooijen, E. Ittmann, F. van Zimmeren, H. Jochens, U. Bornscheuer, G. Vriend, V. A. P. Martins dos Santos and P. J. Schaap, Proteins: Struct., Funct., Bioinf., 2010, 78, 2101–2113 CAS.
- R. K. P. Kuipers, H.-J. Joosten, E. Verwiel, S. Paans, J. Akerboom, J. van der Oost, N. G. H. Leferink, W. J. H. van Berkel, G. Vriend and P. J. Schaap, Proteins: Struct., Funct., Bioinf., 2009, 76, 608–616 CrossRef CAS PubMed.
- H. Xiao, Z. Bao and H. Zhao, Ind. Eng. Chem. Res., 2015, 54, 4011–4020 CrossRef CAS PubMed.
- R. Obexer, A. Godina, X. Garrabou, P. R. E. Mittl, D. Baker, A. D. Griffiths and D. Hilvert, Nat. Chem., 2016 DOI:10.1038/nchem.2596.
- A. Currin, N. Swainston, P. J. Day and D. B. Kell, Chem. Soc. Rev., 2015, 44, 1172–1239 RSC.
- I. V. Pavlidis, M. S. Weiß, M. Genz, P. Spurr, S. P. Hanlon, B. Wirz, H. Iding and U. T. Bornscheuer, Nat. Chem., 2016, 8, 1076–1082 CrossRef CAS PubMed.
- D. C. Wedge, W. Rowe, D. B. Kell and J. Knowles, J. Theor. Biol., 2009, 257, 131–141 CrossRef PubMed.
- D. Baker, Protein Sci., 2010, 19, 1817–1819 CrossRef CAS PubMed.
- F. Duarte, B. A. Amrein and S. C. L. Kamerlin, Phys. Chem. Chem. Phys., 2013, 15, 11160–11177 RSC.
- J. A. Gerlt and P. C. Babbitt, Curr. Opin. Chem. Biol., 2009, 13, 10–18 CrossRef CAS PubMed.
- B. Kuhlman, G. Dantas, G. C. Ireton, G. Varani, B. L. Stoddard and D. Baker, Science, 2003, 302, 1364–1368 CrossRef CAS PubMed.
- S. Cooper, F. Khatib, A. Treuille, J. Barbero, J. Lee, M. Beenen, A. Leaver-Fay, D. Baker, Z. Popovic and F. Players, Nature, 2010, 466, 756–760 CrossRef CAS PubMed.
- D. N. Bolon and S. L. Mayo, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 14274–14279 CrossRef CAS PubMed.
- B. I. Dahiyat and S. L. Mayo, Protein Sci., 1996, 5, 895–903 CrossRef CAS PubMed.
- H. W. Hellinga and F. M. Richards, J. Mol. Biol., 1991, 222, 763–785 CrossRef CAS PubMed.
- G. Kiss, N. Çelebi-Ölçüm, R. Moretti, D. Baker and K. N. Houk, Angew. Chem., Int. Ed., 2013, 52, 5700–5725 CrossRef CAS PubMed , and references cited therein.
- B. I. Dahiyat and S. L. Mayo, Science, 1997, 278, 82–87 CrossRef CAS PubMed.
- A. Zanghellini, L. Jiang, A. M. Wollacott, G. Cheng, J. Meiler, E. A. Althoff, D. Rothlisberger and D. Baker, Protein Sci., 2006, 15, 2785–2794 CrossRef CAS PubMed.
- K. Świderek, I. Tuñón, V. Moliner and J. Bertran, Arch. Biochem. Biophys., 2015, 582, 68–79 CrossRef PubMed.
- G. R. Nosrati and K. N. Houk, Protein Sci., 2012, 21, 697–706 CrossRef CAS PubMed.
- C. Malisi, O. Kohlbacher and B. Höcker, Proteins: Struct., Funct., Bioinf., 2009, 77, 74–83 CrossRef CAS PubMed.
- H. Fazelinia, P. C. Cirino and C. D. Maranas, Protein Sci., 2009, 18, 180–195 CAS.
- X. Huang, K. Han and Y. Zhu, Protein Sci., 2013, 22, 929–941 CrossRef CAS PubMed.
- H. K. Privett, G. Kiss, T. M. Lee, R. Blomberg, R. A. Chica, L. M. Thomas, D. Hilvert, K. N. Houk and S. L. Mayo, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 3790–3795 CrossRef CAS PubMed.
- G. Kiss, D. Röthlisberger, D. Baker and K. N. Houk, Protein Sci., 2010, 19, 1760–1773 CrossRef CAS PubMed.
- H. J. Wijma, R. J. Floor, S. Bjelic, S. J. Marrink, D. Baker and D. B. Janssen, Angew. Chem., 2015, 127, 3797–3801 CrossRef.
- C. A. Smith and T. Kortemme, J. Mol. Biol., 2008, 380, 742–756 CrossRef CAS PubMed.
- P.-S. Huang, Y.-E. A. Ban, F. Richter, I. Andre, R. Vernon, W. R. Schief and D. Baker, PLoS One, 2011, 6, e24109 CAS.
- X. Fu, J. R. Apgar and A. E. Keating, J. Mol. Biol., 2007, 371, 1099–1117 CrossRef CAS PubMed.
- F. Ding and N. V. Dokholyan, PLoS Comput. Biol., 2006, 2, e85 Search PubMed.
- S. M. Larson, J. L. England, J. R. Desjarlais and V. S. Pande, Protein Sci., 2002, 11, 2804–2813 CrossRef CAS PubMed.
- J. A. Davey and R. A. Chica, Proteins: Struct., Funct., Bioinf., 2014, 82, 771–784 CrossRef CAS PubMed.
- M. Sparta, D. Shirvanyants, F. Ding, N. V. Dokholyan and A. N. Alexandrova, Biophys. J., 2012, 103, 767–776 CrossRef CAS PubMed.
- D. J. Mandell and T. Kortemme, Curr. Opin. Biotechnol., 2009, 20, 420–428 CrossRef CAS PubMed.
- G. D. Friedland and T. Kortemme, Curr. Opin. Struct. Biol., 2010, 20, 377–384 CrossRef CAS PubMed.
- J. A. Davey and R. A. Chica, Protein Sci., 2012, 21, 1241–1252 CrossRef CAS PubMed.
- S. Lindert, J. Meiler and J. A. McCammon, J. Chem. Theory Comput., 2013, 9, 3843–3847 CrossRef CAS PubMed.
- M. J. Grisewood, N. P. Gifford, R. J. Pantazes, Y. Li, P. C. Cirino, M. J. Janik and C. D. Maranas, PLoS One, 2013, 8, e75358 CAS.
- C.-Y. Chen, I. Georgiev, A. C. Anderson and B. R. Donald, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 3764–3769 CrossRef CAS PubMed.
- I. Georgiev and B. R. Donald, Bioinformatics, 2007, 23, i185–i194 CrossRef CAS PubMed.
- I. Georgiev, R. H. Lilien and B. R. Donald, J. Comput. Chem., 2008, 29, 1527–1542 CrossRef CAS PubMed.
- J.-S. Yang, S. W. Seo, S. Jang, G. Y. Jung and S. Kim, PLoS Comput. Biol., 2012, 8, e1002612 CAS.
- J. Damborsky and J. Brezovsky, Curr. Opin. Chem. Biol., 2014, 19, 8–16 CrossRef CAS PubMed.
- C. Malisi, M. Schumann, N. C. Toussaint, J. Kageyama, O. Kohlbacher and B. Höcker, PLoS One, 2012, 7, e52505 CAS.
- D. Suplatov, E. Kirilin, V. Takhaveev and V. Švedas, J. Biomol. Struct. Dyn., 2014, 32, 1752–1758 CAS.
- E. Chovancova, A. Pavelka, P. Benes, O. Strnad, J. Brezovsky, B. Kozlikova, A. Gora, V. Sustr, M. Klvana, P. Medek, L. Biedermannova, J. Sochor and J. Damborsky, PLoS Comput. Biol., 2012, 8, e1002708 CAS.
- J. D. Durrant, L. Votapka, J. Sørensen and R. E. Amaro, J. Chem. Theory Comput., 2014, 10, 5047–5056 CrossRef CAS PubMed.
- H. J. Wijma, R. J. Floor, P. A. Jekel, D. Baker, S. J. Marrink and D. B. Janssen, Protein Eng., Des. Sel., 2014, 27, 49–58 CrossRef CAS PubMed.
- H. Kries, R. Blomberg and D. Hilvert, Curr. Opin. Chem. Biol., 2013, 17, 221–228 CrossRef CAS PubMed.
- C. Cramer, Essentials of computational chemistry: theories and models, John Wiley & Sons, 2013 Search PubMed.
- K. Hotta, X. Chen, R. S. Paton, A. Minami, H. Li, K. Swaminathan, I. I. Mathews, K. Watanabe, H. Oikawa, K. N. Houk and C.-Y. Kim, Nature, 2012, 483, 355–U154 CrossRef CAS PubMed.
- D. J. Tantillo, J. G. Chen and K. N. Houk, Curr. Opin. Chem. Biol., 1998, 2, 743–750 CrossRef CAS PubMed.
- E. H. Krenske, A. Patel and K. N. Houk, J. Am. Chem. Soc., 2013, 135, 17638–17642 CrossRef CAS PubMed.
- G. Ujaque, D. J. Tantillo, Y. F. Hu, K. N. Houk, K. Hotta and D. Hilvert, J. Comput. Chem., 2003, 24, 98–110 CrossRef CAS PubMed.
- Y. Zou, M. Garcia-Borràs, M. Tang, Y. Hirayama, D. Li, L. Li, K. Watanabe, K. N. Houk and Y. Tang, 2016, submitted for publication.
- P. E. M. Siegbahn and F. Himo, J. Biol. Inorg. Chem., 2009, 14, 643–651 CrossRef CAS PubMed.
- P. E. M. Siegbahn and F. Himo, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 323–336 CrossRef CAS.
- P. E. M. Siegbahn and R. H. Crabtree, J. Am. Chem. Soc., 1997, 119, 3103–3113 CrossRef CAS.
- M. E. S. Lind and F. Himo, Angew. Chem., Int. Ed., 2013, 52, 4563–4567 CrossRef CAS PubMed.
- M. E. S. Lind and F. Himo, ACS Catal., 2014, 4, 4153–4160 CrossRef CAS.
- A. Warshel and M. Levitt, J. Mol. Biol., 1976, 103, 227–249 CrossRef CAS PubMed.
- H. M. Senn and W. Thiel, Angew. Chem., Int. Ed., 2009, 48, 1198–1229 CrossRef CAS PubMed.
- M. W. van der Kamp and A. J. Mulholland, Biochemistry, 2013, 52, 2708–2728 CrossRef CAS PubMed.
- B. Karasulu and W. Thiel, ACS Catal., 2015, 5, 1227–1239 CrossRef CAS.
- J. Aranda, K. Zinovjev, K. Swiderek, M. Roca and I. Tuñón, ACS Catal., 2016, 6, 3262–3276 CrossRef CAS.
- A. Ardèvol and C. Rovira, J. Am. Chem. Soc., 2015, 137, 7528–7547 CrossRef PubMed.
- A. Warshel and R. M. Weiss, J. Am. Chem. Soc., 1980, 102, 6218–6226 CrossRef CAS.
- A. Shurki, E. Derat, A. Barrozo and S. C. L. Kamerlin, Chem. Soc. Rev., 2015, 44, 1037–1052 RSC.
- S. C. L. Kamerlin and A. Warshel, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 30–45 CrossRef CAS.
- B. A. Amrein, P. Bauer, F. Duarte, A. J. Carlsson, A. Naworyta, S. L. Mowbray, M. Widersten and S. C. L. Kamerlin, ACS Catal., 2015, 5, 5702–5713 CrossRef CAS PubMed.
- G. Oanca, M. Purg, J. Mavri, J. C. Shih and J. Stare, Phys. Chem. Chem. Phys., 2016, 18, 13346–13356 RSC.
- R. O. Dror, R. M. Dirks, J. P. Grossman, H. Xu and D. E. Shaw, Annu. Rev. Biophys., 2012, 41, 429–452 CrossRef CAS PubMed.
- A. Laio and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12562–12566 CrossRef CAS PubMed.
- D. Hamelberg, J. Mongan and J. A. McCammon, J. Chem. Phys., 2004, 120, 11919–11929 CrossRef CAS PubMed.
- M. Orozco, Chem. Soc. Rev., 2014, 43, 5051–5066 RSC.
- G. Jiménez-Osés, S. Osuna, X. Gao, M. R. Sawaya, L. Gilson, S. J. Collier, G. W. Huisman, T. O. Yeates, Y. Tang and K. N. Houk, Nat. Chem. Biol., 2014, 10, 431–436 CrossRef PubMed.
- T. C. Bruice, Acc. Chem. Res., 2002, 35, 139–148 CrossRef CAS PubMed.
- A. Madadkar-Sobhani and V. Guallar, Nucleic Acids Res., 2013, 41, W322–W328 CrossRef PubMed.
- M. Rueda, P. Chacón and M. Orozco, Structure, 2007, 15, 565–575 CrossRef CAS PubMed.
- E. Monza, M. F. Lucas, S. Camarero, L. C. Alejaldre, A. T. Martínez and V. Guallar, J. Phys. Chem. Lett., 2015, 6, 1447–1453 CrossRef CAS PubMed.
- R.-Z. Liao, S.-L. Chen and P. E. M. Siegbahn, ACS Catal., 2015, 5, 7350–7358 CrossRef CAS.
- X. Li, E. M. Sproviero, U. Ryde, V. S. Batista and G. Chen, Int. J. Quantum Chem., 2013, 113, 474–478 CrossRef CAS.
- B. Manta, F. M. Raushel and F. Himo, J. Phys. Chem. B, 2014, 118, 5644–5652 CrossRef CAS PubMed.
- P. E. M. Siegbahn and M. R. A. Blomberg, FEBS Lett., 2014, 588, 545–548 CrossRef CAS PubMed.
- H. Zheng and M. T. Reetz, J. Am. Chem. Soc., 2010, 132, 15744–15751 CrossRef CAS PubMed.
- K. Miyamoto and H. Ohta, Eur. J. Biochem., 1992, 210, 475–481 CrossRef CAS PubMed.
- Y. Ijima, K. Matoishi, Y. Terao, N. Doi, H. Yanagawa and H. Ohta, Chem. Commun., 2005, 877–879 RSC.
- Y. Terao, Y. Ijima, K. Miyamoto and H. Ohta, J. Mol. Catal. B: Enzym., 2007, 45, 15–20 CrossRef CAS.
- R. Obata and M. Nakasako, Biochemistry, 2010, 49, 1963–1969 CrossRef CAS PubMed.
- K. Okrasa, C. Levy, M. Wilding, M. Goodall, N. Baudendistel, B. Hauer, D. Leys and J. Micklefield, Angew. Chem., Int. Ed., 2009, 48, 7691–7694 CrossRef CAS PubMed.
- Nobel Prizes 2013, M. Karplus, M. Levitt and A. Warshel, Angew. Chem., Int. Ed., 2013, 52, 11972 CrossRef.
- A. D. Mackerell, J. Comput. Chem., 2004, 25, 1584–1604 CrossRef CAS PubMed.
- J. Gao, Rev. Comput. Chem., 1996, 7, 119–185 CAS.
- J. Gao, Acc. Chem. Res., 1994, 29, 298–307 CrossRef.
- J. Gao and X. Xia, Science, 1992, 258, 631–635 CAS.
- S. Sumner, P. Soderhjelm and U. Ryde, J. Chem. Theory Comput., 2013, 9, 4205–4214 CrossRef CAS PubMed.
- R. Lonsdale and M. T. Reetz, J. Am. Chem. Soc., 2015, 137, 14733–14742 CrossRef CAS PubMed.
- R. P. P. Neves, P. A. Fernandes and M. J. Ramos, ACS Catal., 2016, 6, 357–368 CrossRef CAS.
- A. J. M. Ribeiro, L. Yang, M. J. Ramos, P. A. Fernandes, Z.-X. Liang and H. Hirao, ACS Catal., 2015, 5, 3740–3751 CrossRef CAS.
- A. D. Daniels, I. Campeotto, M. W. van der Kamp, A. H. Bolt, C. H. Trinh, S. E. V. Phillips, A. R. Pearson, A. Nelson, A. J. Mulholland and A. Berry, ACS Chem. Biol., 2014, 9, 1025–1032 CrossRef CAS PubMed.
- G. H. Zhao, H. Song, Z. W. Chen, F. S. Mathews and M. S. Jorns, Biochemistry, 2002, 41, 9751–9764 CrossRef CAS PubMed.
- A. Ilari, A. Bonamore, S. Franceschini, A. Fiorillo, A. Boffi and G. Colotti, Proteins: Struct., Funct., Bioinf., 2008, 71, 2065–2075 CrossRef CAS PubMed.
- F.-K. Shieh and N. O. Reich, J. Mol. Biol., 2007, 373, 1157–1168 CrossRef CAS PubMed.
- L. Mones, W.-J. Tang and J. Florian, Biochemistry, 2013, 52, 2672–2682 CrossRef CAS PubMed.
- A. Sharir-Ivry, R. Varatharaj and A. Shurki, Chem. – Eur. J., 2015, 21, 7159–7169 CrossRef CAS PubMed.
- J. Aqvist and S. C. L. Kamerlin, ACS Catal., 2016, 6, 1737–1743 CrossRef.
- L. T. Elfstrom and M. Widersten, Biochem. J., 2005, 390, 633–640 CrossRef PubMed.
- A. Thomaeus, J. Carlsson, J. Aqvist and M. Widersten, Biochemistry, 2007, 46, 2466–2479 CrossRef CAS PubMed.
- R. M. Geha, I. Rebrin, K. Chen and J. C. Shih, J. Biol. Chem., 2001, 276, 9877–9882 CrossRef CAS PubMed.
- R. Car and M. Parrinello, Phys. Rev. Lett., 1985, 55, 2471–2474 CrossRef CAS PubMed.
- G. R. Bowman, V. S. Pande and F. Noé, An Introduction to Markov State Models and Their Application to Long Timescale Molecular Simulation, Springer, 2014 Search PubMed.
- S. C. Dodani, G. Kiss, J. K. B. Cahn, Y. Su, V. S. Pande and F. H. Arnold, Nat. Chem., 2016, 8, 419–425 CrossRef CAS PubMed.
- H. Zhang, C. Kenaan, D. Hamdane, G. H. B. Hoa and P. F. Hollenberg, J. Biol. Chem., 2009, 284, 25678–25686 CrossRef CAS PubMed.
- E. Weinan and E. Vanden-Eijnden, J. Stat. Phys., 2006, 123, 503–523 CrossRef.
- X.-D. Kong, S. Yuan, L. Li, S. Chen, J.-H. Xu and J. Zhou, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 15717–15722 CrossRef CAS PubMed.
- V. Liskova, D. Bednar, T. Prudnikova, P. Rezacova, T. Koudelakova, E. Sebestova, I. K. Smatanova, J. Brezovsky, R. Chaloupkova and J. Damborsky, ChemCatChem, 2015, 7, 648–659 CrossRef CAS.
- J. Ma, L. Wu, F. Guo, J. Gu, X. Tang, L. Jiang, J. Liu, J. Zhou and H. Yu, Appl. Microbiol. Biotechnol., 2013, 97, 4897–4906 CrossRef CAS PubMed.
- H. J. Wijma, S. J. Marrink and D. B. Janssen, J. Chem. Inf. Model., 2014, 54, 2079–2092 CrossRef CAS PubMed.
- P. Molina-Espeja, M. Cañellas, F. J. Plou, M. Hofrichter, F. Lucas, V. Guallar and M. Alcalde, ChemBioChem, 2016, 17, 341–349 CrossRef CAS PubMed.
- V. Sáez-Jiménez, S. Acebes, V. Guallar, A. T. Martínez and F. J. Ruiz-Dueñas, PLoS One, 2015, 10, e0124750 Search PubMed.
| This journal is © The Royal Society of Chemistry 2017 |