Isomeric control of the mechanical properties of supramolecular filament hydrogels

Abstract

Supramolecular filament hydrogels are an emerging class of biomaterials that hold great promise for regenerative medicine, tissue engineering, and drug delivery. However, fine-tuning of their bulk mechanical properties at the molecular level without altering their network structures remains a significant challenge. Here we report an isomeric strategy to construct amphiphilic peptides through the conjugation of isomeric hydrocarbons to influence the local viscoelastic properties of their resulting supramolecular hydrogels. In this case, the packing requirements of the chosen isomeric hydrocarbons within the supramolecular filaments are dictated by their atomic arrangements at the molecular and intermolecular levels. Atomistic molecular dynamics simulations suggest that this design strategy can subtly alter the molecular packing at the interface between the peptide domain and the hydrophobic core of the supramolecular assemblies, without changing both the filament width and morphology. Our results from wide-angle X-ray scattering and molecular simulations further confirm that alterations to the intermolecular packing at the interface impact the strength and degree of hydrogen bonding within the peptide domains. This subtle difference in the isomeric hydrocarbon design and their consequent packing difference led to variations in the persistence length of the individual supramolecular filaments. Microrheological analysis reveals that this difference in filament stiffness enables the fine-tuning of the mechanical properties of the hydrogel at the macroscopic scale. We believe that this isomeric platform provides an innovative method to tune the local viscoelastic properties of supramolecular polymeric hydrogels without necessarily altering their network structures.

---

Introduction

The mechanical properties of materials are known as the key features that affect their functionality. The rigidity of scaffolding materials, for instance, is a known physical cue that can impact cellular behaviour at various levels.^1–7 Such synthetic matrices can be constructed by employing molecular self-assembly as the fundamental principle, in which the building blocks associate spontaneously into filamentous assemblies through non-covalent interactions.^8–14 This strategy highlights the connections between the molecular design of the underlying building blocks and the resulting properties of their supramolecular assemblies, thus providing a possibility of controlling the mechanical properties from the very bottom-up.^15–19 In general, the mechanical properties of these supramolecular matrices are the combinative consequence of several factors, including the stiffness and entanglement/alignment of the filaments, mesh size (largely determined by the concentration of the building units), as well as the presence of other additives such as multivalent ions or other types of molecules.^20–23 Oftentimes, it is difficult to decouple the individual effects of each factor from the overall combinative effect, and this in turn causes complications in interpreting the results of interfacing these supramolecular hydrogels with the cells of interest. In this study, we report a strategy to tune the local viscoelastic properties of supramolecular filament networks without inducing any variations in the mesh size and salt concentration.

Supramolecular one-dimensional (1D) nanostructures can be formed by the self-assembly of amphiphilic molecules that intrinsically adopt strong, directional intermolecular interactions, such as hydrogen bonding or π–π interactions.²⁴ These 1D supramolecular structures are regarded as semi-flexible filaments that can further entangle to form a 3D network.^25–29 MacKintosh et al. showed that for solutions of entangled semi-flexible filaments (such as F-actins), the storage modulus G′ scales as G′ ∼ κ²/k_BTξ⁻²L_e⁻³.²⁰ Here, κ is the semi-flexible chain bending modulus, ξ is the mesh size of the network related to the monomer concentration, L_e is the chain entanglement length, k_B is the Boltzmann constant, and T is the temperature. The overall stiffness of such supramolecular networks is often controlled by varying the bulk concentration of the monomers.³⁰ While this approach usually enhances the mechanical strength of the matrix, it is complicated by simultaneous changes in the mesh size because both ξ and L_e are dependent on the concentration.³¹ In particular, when L_e ≥ ξ and the persistence length l_p ∼ κ/k_BT ≥ ξ, it is found that L_e ∼ (κ/k_BT)^1/5(ac_A)^−2/5, where c_A is the concentration of the monomers of size a, and that 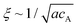.^32,33 Thus, for semi-flexible networks with L_e ≥ ξ and the persistence length l_p ≥ ξ, the storage modulus G′ scales with the concentration as G′ ∼ κ(κ/k_BT)^2/5(ac)^11/5.²⁰ For example, the persistence length l_p of biological filaments (such as F-actin) can be related to the linear mass density λ_p of the filament such that l_p ∼ (Y/4πk_BTρ_m²)λ_p², where Y is the Young's modulus of the filament and ρ_m is the mass per unit volume.³⁴ These studies suggest that it is theoretically possible to use the bending modulus, κ, to tune the mechanical properties of semi-flexible filament networks without affecting other network parameters such as mesh size and monomer concentration.

Inspired by these pioneering studies, herein we present a peptide-based supramolecular platform that utilizes isomeric hydrocarbons to dictate the mechanical properties of supramolecular filament networks through the modulation of the bending modulus of individual filaments. This strategy highlights the control of the persistence length of individual filaments—not through the variation of the linear mass density of the filament, a common mechanism for biological filaments found in nature—but through the modulation of the strength of the filament interface due to differences originating from intermolecular packing and hydrogen bonding. This strategy offers an effective means to tune the mechanical properties of semi-flexible networks at the molecular level. Given the rapidly growing interest in peptide-based supramolecular hydrogels,^17,35–45 we believe that our findings have broad implications for their biomedical applications in regenerative medicine and drug delivery.

Results and discussion

Molecular design and assembly

We conjugated a series of isomeric alicyclic groups to an identical peptide segment to imbue the necessary overall amphiphilicity for self-assembly under aqueous conditions (Fig. 1A). The differences in atomic arrangements offer different molecular packing requirements within the hydrophobic/hydrophilic interfacial area, further affecting the mechanical properties of the respective supramolecular networks while ensuring identical surface functionality and similar pore/mesh size at a fixed monomer concentration (the mesh size is a function of the monomer size and concentration in such networks).²⁰ This miktoarm star peptide platform includes a β-sheet adopting the peptidic domain GNNQQNY (originated from the yeast prion Sup35),⁴⁶ an oligoproline segment, and a cyclic hydrocarbon segment.⁴⁷ The designed peptides MASP2, MASP3, and MASP4 carried a cyclopentylpropionyl, a cyclohexylacetyl or a cycloheptanecarboxyl group, respectively (Fig. 1A). The details of molecular synthesis, purification and characterization can be found in ESI, S1–S2 and Fig. S1–S3.† MASP1, an analogue of the MASP series, which bears a linear but not cyclic hydrocarbon, has been reported previously in an effort devoted to developing enzymatically degradable supramolecular filaments.⁴⁷ Since MASP1 contains two more hydrogen atoms than MASP2–4 and thus cannot be considered as an isomer, its assembly behaviour is not discussed in detail. Specifically, the three chosen isomeric building units possess different ring sizes—five, six and seven carbons—with the remaining methylenes acting as spacer groups between the ring and carboxyl—two, one and zero carbons, respectively. These differences are expected to alter the packing within the hydrophilic/hydrophobic interfacial environment of the assemblies (Fig. 1B). We utilized atomistic molecular dynamics simulations of the pre-assembled filaments (Fig. 1C) to reveal that while the core dimensions of the filament remain unchanged, the increasing ring size of the isomer ultimately alters the molecular packing at the interface. This difference in packing leads to a variation in hydrogen bonding within the filament corona and also a calculated variation in interfacial tension while maintaining the same diameter of the three assemblies, ultimately causing a variation in the persistence length of single filaments on the order of 250–4000 nm.

Fig. 1 Design of self-assembling peptides with isomeric hydrocarbons which form supramolecular filament networks. (A) Chemical structures of the designed peptides investigated in this study and the estimation of the ring size of the cycloalkyl chain in the peptides of interest. The ring size in 3D space was estimated by using MarvinSpace and ChemAxon. (B) Schematic representation of the self-assembling process of peptides into supramolecular filament networks. (C) A snapshot of the supramolecular filament of MASP4 after 100 ns of simulation. The peptide domain, cycloheptane ring, oligoproline segment, and water within 10 Å of the peptide are displayed in green, yellow, pink, and cyan, respectively.

Nanostructure characterization

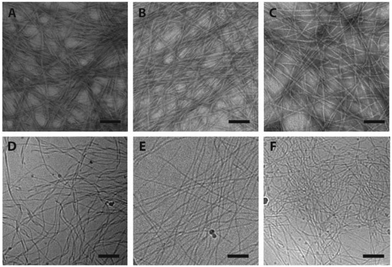
The supramolecular nanostructures formed by the self-assembly of each isomeric peptide were characterized by transmission electron microscopy (TEM) and cryogenic-TEM (cryo-TEM) (Fig. 2). When dissolved in water (pH 4.5), all the three designed molecules were found to associate into filamentous assemblies of ∼10 nm in width, while the length could reach several microns after one day of incubation at a concentration of 1% (w/v, 2.1 mM). Circular dichroism (CD) spectroscopy reveals that all the designed peptides showed characteristic absorption of polyproline type II-like (PPII) secondary structures (strong negative peak at 205 nm, very weak positive peak at 235 nm) (Fig. 3A). The expected characteristics of β-sheet conformation of the Sup35 segments were not explicitly revealed in the CD spectra, potentially due to their weaker absorption intensity relative to the PPII-like conformation stemming from the oligoproline segment.⁴⁷ It is noteworthy that MASP1 revealed a very similar assembly behaviour in water, forming filamentous assemblies with a PPII-like peptide conformation.⁴⁷ Wide angle X-ray scattering (WAXS), however, could confirm the presence of β-sheets for all the designed peptides (Fig. 3B–D). The reflective peaks at ∼4.7 Å are indicative of the typical spacing of hydrogen bonds among the neighbouring peptides. Notably, MASP3 and MASP4 exhibited a more diffusive peak at 4.7 Å than that of MASP2, an observation that is very likely linked to the molecular packing of the isomeric hydrocarbons, which will be expounded in the later discussion. The β-sheet conformation is considered crucial for the formation and propagation of filamentous nanostructures.^48,49

Fig. 2 TEM and cryo-TEM micrographs of the supramolecular filaments. The assembled filaments formed by MASP2 (A, D), MASP3 (B, E) and MASP4 (C, F) in Milli-Q water (pH 4.5) were observed in TEM imaging (upper panels) and cryo-TEM imaging (bottom panels). The regular TEM specimens were negatively stained with 2% uranyl acetate. Peptide concentration = 2.1 mM. All bars = 200 nm.

Fig. 3 Secondary structural analysis and measurements of the critical aggregation concentration of isomeric peptides used in this study. (A) CD spectra of MASP2–4. Spectra were recorded for 0.167% (w/v) solutions that were instantly diluted from 1% (w/v) solutions. (B–D) WAXS patterns of MASP2–4 at 2% (w/v). The reflective peaks at ∼4.7 Å (indicated by the arrows) correspond to the spacing of intermolecular hydrogen bonds in a β-sheet. (E–G) Determination of the CAC values of peptides by Nile red encapsulation for MASP2 (E), MASP3 (F) and MASP4 (G); the transition of I₆₃₅/I₆₆₀ indicated the intensity surge of Nile red when exposed in hydrophobic environments when the peptide concentration exceeds the CAC value. The obtained CAC values for MASP2, MASP3 and MASP4 were ∼40 μM in 0.1 M MES buffer (pH 4.5). Data are presented as mean ± standard deviation (n = 3).

The mesh/pore size is dependent only on the size and concentration of the monomer that forms the supramolecular filaments.²⁰ In the case reported here, the isomeric peptides differ only in the hydrocarbons and are structurally identical in the dominant peptidic segment. Hence, the monomer sizes among MASP2–4 should be approximately the same, and thus at the same monomer concentration the mesh size of their resulting networks should be identical for all the three molecules. However, given that there exists a dynamic equilibrium between the monomers and the assembled filaments and only these assembled monomers actually contribute to the network mesh size, it is important to assess the critical aggregation concentration (CAC) of the building blocks. The CAC value of each molecule was thus measured by incubating the peptide solutions of various concentrations with a reporter dye Nile red.⁵⁰ Nile red is a hydrophobic dye that exhibits a blue-shifted fluorescence emission with enhanced intensity when exposed to hydrophobic environments.^51,52 Each isomeric peptide solution (in MES buffer, pH 4.5) at various concentrations was mixed with a fixed content of Nile red, and then the emergence of the blue-shifted emission upon encapsulation within the hydrophobic cores was carefully monitored as the peptide concentration surpasses the CAC value (ESI S3 and Fig. S4†). The transition concentration was determined by plotting the ratio of the emission maximum of Nile red in hydrophobic environments (λ_max: 635 nm) to that under aqueous conditions (λ_max: 660 nm) against the bulk peptide concentrations. Our results suggested that the CAC values of MASP2, MASP3, and MASP4 are very similar and are in the range of ∼50 μM at pH 4.5 (Fig. 3E–G). These results implied that MASP2, MASP3, and MASP4 would have the same proportion of building blocks remaining in the assembled state at a given bulk concentration. Since our results from TEM imaging (Fig. 2) have demonstrated that there were no distinguishable morphological differences between the filament length and width, we speculate that the mesh size of the resulting hydrogels would be essentially the same for all MASPs at the investigated concentrations (∼4.2 mM) in the limit of low filament bundling.

Molecular dynamics simulation

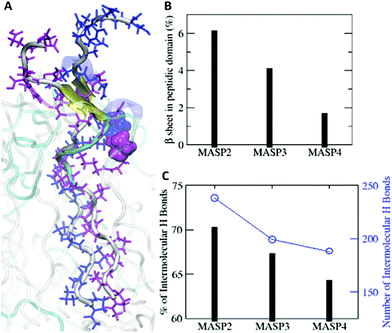
Simulations have become an indispensable tool to investigate the structure of peptide-amphiphile filamentous assemblies.^53–55 We subsequently performed atomistic molecular dynamics (MD) simulations to provide molecular-level insight into the differences of atomic arrangements in the molecular packing and accordingly the mechanical properties of the supramolecular filaments (ESI S4†).^56,57 Three pre-assembled MASP supramolecular filaments were simulated for 100 ns, allowing the interfacial density profile to relax and the peptides to form β-sheets along the filament axis. Each system was pre-assembled into an 8-layered fibril with 9 monomers per layer. The systems were neutralized by Cl⁻ ions and solvated in a water box. The force field used in the MD simulations was AMBER ff99SB.⁵⁸ The force field for the hydrocarbon segments of the MASPs was parameterized using the general AMBER force field (GAFF)⁵⁹ with the atomic partial charges assigned by using VCharge v1.01 (VeraChem, LLC),⁶⁰ and the TIP3P model⁶¹ was employed for water. Atomistic MD simulations were carried out using a parallel molecular dynamics code NAMD2.⁶² All systems were simulated in the NPT ensemble at 1 atm and 310 K for 100 ns with full periodic boundary conditions (see the ESI† for additional simulation methods).

The radial density profile was calculated for each component of the simulated MASPs to examine the correlation between the ring size of the cycloalkyl chain and the molecular packing (Fig. 4), with their filamentous nanostructures shown in Fig. S5.† These results showed that the filament widths (∼12 nm) were nearly identical between MASP2, MASP3, and MASP4 filaments (Fig. 4D), consistent with our experimental observations from TEM imaging. We did notice a difference in the molecular packing among the peptides. However, this difference in packing did not propagate to the inner hydrophobic core of the oligoproline segments. The radial density profile showed that the density of the isomeric hydrocarbons of the MASP2 filaments exhibited a peak shifted towards the location of the peptide domain, compared with the density of the isomeric hydrocarbons of the MASP3 and MASP4 filaments. Furthermore, the peak density of the isomeric hydrocarbon of MASP2 (∼0.8 g cm⁻³) is lower when compared with the peak density of the isomeric hydrocarbons of the MASP3 and MASP4 filaments (∼1.05 g cm⁻³), indicating that the hydrocarbon density is distributed across a larger radius (Fig. 4E). In contrast, the onset of the hydrocarbon density of the MASP4 filaments in particular was shifted towards the inner hydrophobic core (∼15 Å), compared with that of its MASP2 counterpart (∼20 Å).

Fig. 4 Molecular dynamics simulation of the density profile of each component in assembled filaments. Snapshots (A, B), positions of hydrocarbon segments (C) and the radial density profile (D–G) of each MASP component in preassembled filaments after molecular dynamics simulation for 100 ns. The peptide domain, hydrocarbon segment (denoted as R in Fig. 1A), and oligoproline segment are displayed in red, green and blue, respectively, in the top (A) and side (B) view of the preassembled MASP4 filament. Cycloalkyl rings of MASP2 and MASP4 in the filaments are highlighted in red and blue, respectively, in (C). The density profile is averaged over the last 50 ns.

The difference could be rooted in the varied ring size, as well as the variations in the length and flexibility of the isomeric hydrocarbons. Since the cyclopentylpropionyl group of MASP2 possesses a smaller ring, it could possibly extend further due to its two alkyl carbons outside of the ring structure providing extra flexibility in comparison with the cyclohexylacetyl or cycloheptanecarboxyl groups on MASP3 or MASP4, respectively. Moreover, this increased flexibility could allow the hydrocarbon tails to adopt conformations that are more favourable toward efficient β-sheet formation compared with the MASP4 filaments. The two cyclopentyl rings of neighbouring MASP2 molecules would be more distant from the peptide backbones, causing less steric restrictions between the neighbouring MASP2 molecules and allowing them to be spatially close to form tighter intermolecular hydrogen bonds, as shown in Fig. 5A. The formation of β-sheets and intermolecular hydrogen bonds at the simulation timescale was also evaluated, finding that there was a corresponding reduction of β-sheet formation in the peptide domain as the ring size was increased (Fig. 5B). Likewise, both the total number of hydrogen bonds and the fraction of intermolecular hydrogen bonds to the total hydrogen bonds in the MASPs decreased in a similar fashion (Fig. 5C).

Fig. 5 Molecular dynamics simulation of the β-sheet formation. (A) A snapshot of β-sheet formation in simulation. Two MASP2 monomers are highlighted in blue and magenta. These two MASP2 monomers form β-sheets (yellow arrows). Cyclopentyl rings are displayed in a van der Waals model with the corresponding colours. (B) Percentages of β-sheets in the peptide domain of MASP2, MASP3, and MASP4. (C) Percentages of the intermolecular hydrogen bonds for the three studied conjugates. In panel (C), the total numbers and percentages of intermolecular hydrogen bonds (H bonds) are presented in blue circles and black bars, respectively.

Microrheological measurements

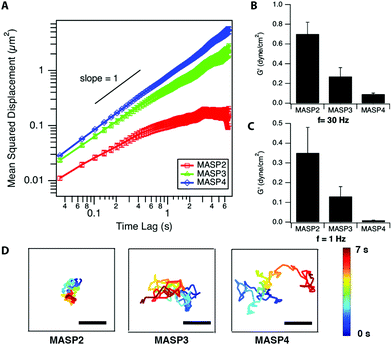
The local viscoelastic properties of the resulting supramolecular materials were determined using particle-tracking microrheology. Unlike the conventional macrorheology, the particle-tracking rheology provides the information of local stiffness in the materials at the submicron to micron scale.^63–65 The viscoelastic properties are determined by tracking the movement of the probing particles trapped within the studied viscoelastic materials, in which the fluctuation of filaments governs the motion of embedded particles and reveals the stiffness/flexibility of the surrounding materials. The mean-squared displacement (MSD), the critical parameter in microrheology, of the embedded particles can be described by using the generalized Stokes–Einstein equation.^65–67 For viscoelastic materials, the MSD of the embedded particles follows the relationship 〈Δr²〉 ∝ t^α, where α is the logarithmic slope of MSD versus time lag.^64–66 At a fixed molar concentration (4.2 mM; 1 wt% for MASP2–4), the ensemble-averaged MSD of the probing particles in the resulting scaffolds showed the trend, MSD_MASP2 < MSD_MASP3 < MSD_MASP4, at all monitored timescales (Fig. 6A). The logarithmic slopes of MSD vs. time lag, α, of the probing particles ranged between zero and unity, suggesting the sub-diffusive behaviour of each hydrogel (Fig. S6†). The diffusion coefficient, D, is calculated from the MSD by using D = MSD/4t.

Fig. 6 Microrheological analysis of the hydrogels formed by submitted MASP2–4. (A) Mean-squared displacement versus time lag probing particles embedded within 1% (w/v) MASP2, MASP3 and MASP4. (B–C) Calculated storage modulus G′ according to the MSD profile at two chosen frequencies, 30 Hz (B) and 1 Hz (C). (D) Representative trajectories of the movement of the centre of a single probing particle embedded within MASP2, MASP3, and MASP4 scaffolds. All bars = 1 μm. Data are presented as the ensemble average ± standard error.

de Gennes and co-workers have proposed that the motion of a particle of diameter d through a network of average mesh size ξ is an activated process dictated by the activation energy, which is determined by the elastic free energy associated with the expansion of a mesh formed by Gaussian chains.^32,69 The estimation for the diffusion coefficient D can be derived as follows:

D = D₀ exp(−β(d/ξ)^δ) (1)

where D₀ is the diffusion coefficient of the spheres in pure solvent and β is the dimensionless coefficient expected to be on the order of one. For non-cross-linked networks, the exponent δ is 2.0. By using the prediction on the scaling of the average mesh size in semi-dilute solutions with the polymer concentration c, and the approximation ξ ∝ c^−1/2 for rod-like macromolecules,³³ de Gennes and Schmidt and co-workers^32,68,69 have derived the following relationship:

D(c_A,d) = D(0,d)exp(−β′d²c_A) (2)

where the constant β′ has the dimension length/mass. This conclusion could further lead to another derivation , which stated the same dependence of ξ on the concentration as we previously introduced 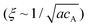. Moreover, it is implied that more factors besides the monomer size can determine the mesh size ξ, which can be captured by fitting the diffusion data. Here, D₀ is calculated directly from the Stokes–Einstein equation, D₀ = k_BT/6πηr, with the dynamics viscosity of water η = 8.90 × 10⁻³ dyn s cm⁻² and the particle radius r = 0.5 μm. By plugging this D₀ and the experimental diffusion coefficient D into the above equation, we estimated the constant β′. Assuming β ≈ 1, as Schmidt and co-workers suggested, the mesh size ξ was estimated: approximately 1219 nm, 793 nm, and 580 nm for MASP2, MASP3, and MASP4, respectively. The storage modulus (G′) could be calculated by using the generalized Stokes–Einstein equation, showing a trend of G′_MASP2 > G′_MASP3 > G′_MASP4 at two frequencies (1 Hz and 30 Hz) (Fig. 6B and C).

Discussion

According to the theory depicted by MacKintosh et al., the storage modulus G′ ∼ κ(κ/k_BT)^2/5(ac)^11/5 for sterically entangled semi-flexible networks.²⁰ The persistence length l_p could be approximated by the MacKintosh scaling, when using the estimated values of mesh size derived previously and applying the relationship between the bending modulus κ and the persistence length l_p (κ ∼ l_pk_BT). Using a = ∼4.7 Å, the corresponding spacing of the hydrogen bonds of β-strands in the neighbouring peptides observed in WAXS for all designed peptides, l_p values were approximately 14 112 nm, 1995 nm and 340.5 nm for MASP2, MASP3, and MASP4, respectively by calculation. While the mesh size exhibited a 52% reduction from MASP2 to MASP4, the persistence length plummeted for 98%. For MASP2 and MASP3, the estimated persistence lengths were much larger than their mesh sizes, and therefore they can be regarded as networks composed of semi-flexible chains. However, this expectation did not hold for MASP4 since its estimated persistence length l_p was not longer than its mesh size ξ, which suggests that some of the assumptions for β and ξ can be further clarified in future studies.

Since the l_p values for MASP2–4 were calculated, the interfacial tension could also be roughly calculated by using the following relationship for a D*-dimensional object when the rigidity is κ = Φγd_c^4−D* ∼ l_pk_BT, in which Φ is an interfacial coupling constant, γ is the interfacial tension, and d_c is the diameter of the hydrophobic core.⁷⁰ The interfacial coupling constant Φ ≈ 0.05 is found for cylindrical block copolymer filomicelles.⁷⁰ Using D* = 1 and d_c = 8 nm together with the previously mentioned Φ, we obtained the interfacial tension γ ≈ 2267 pN nm⁻¹, 320 pN nm⁻¹, and 55 pN nm⁻¹ for MASP2, MASP3, and MASP4, respectively. The estimated γ values for MASP2/MASP3 were greater than the typical interfacial tension values, suggesting the necessity for characterization of the interfacial coupling constant Φ of the assemblies in our design platform, which could be obtained with further characterization of the mechanical properties through both experiment and simulation.⁷¹ One way to interpret this phenomenon is to use the Gibbs adsorption equation, log γ/log C = −2.303 ΓRT, where C is the concentration, R is the gas constant, T is the temperature, and Γ is the number of moles of the component adsorbed per unit area (mol m⁻²). The higher local density of the hydrocarbon segment of MASP3 and MASP4 compared to that of MASP2 at the peak radius (Fig. 4B) might partially contribute to their lower interfacial tension. Thus, we showed that the conjugation of isomeric hydrocarbons induced a variation in the expected interfacial tension, and that their packing in the interfacial region of the self-assembled structures subsequently leads to differences in the bending rigidity and the storage modulus. From the microrheological results, the larger the conjugated cycloalkyl group in the amphiphilic peptides, the larger the magnitude of the MSD. This was also evident from the representative trajectories of an embedded particle in MASP2, MASP3, and MASP4, in which the probing particles display a larger displacement over a 7-second period when trapped in the relatively weaker hydrogel formed by MASP4 (Fig. 6D).

A number of previous reports have detailed the use of different peptide sequences to construct peptide-based hydrogels to control the mechanical properties, yet these reported instances are often accompanied by changes in surface chemistry or fundamental self-assembling behaviour due to the alteration of the peptide segments. For instance, Gooch and co-workers reported that the storage modulus of peptide hydrogels could decrease by a factor of ∼4.8 after incorporating a RGD segment into their peptidic building blocks.⁷² In another study, an enzymatic cleavable peptide was included within the building units to form hydrogels, leading to the reduction of storage moduli from >300 kPa to 43 Pa.⁷³ Although using isomeric peptides as building blocks or incorporating different hydrophobic side chains have both shown to be possible strategies to control the morphology of the assembled structures,^74,75 the use of this rationale to control the mechanical properties has been scarcely reported. Most recent work has focused on the biophysical consequences of the materials after modifying the amino acid order in the peptidic domains. For example, an interesting study reported by Pashuck et al. utilized a series of peptide amphiphiles with different combinations of valine/alanine to construct hydrogels with different mechanical properties, and further demonstrated that the intensity of β-sheet signals in the circular dichroism spectra was associated with the stiffness of the hydrogels.⁷⁶ A recent study conducted by Schneider and co-workers has shown that a single amino acid change in a 20-amino acid peptide, APC1, could provide drastic differences in rheological behaviours (such as the sol–gel transition and shear-thin recovery).⁷⁷ These examples stressed the control of mechanical properties from the peptidic domains, and the origin of stiffness change was due to the order of intermolecular interactions among the side chains of the amino acids. Recently, Tantakitti et al. showed that the mechanical properties (governed by hydrogen bonding along the filament at the amino acid level) can be modulated due to the strength of the local salt concentration.⁷⁸

In our case, the reported design platform keeps the peptide segment unchanged among all the designed building blocks to guarantee the same surface functionality, without changing the local electrostatic environment and with a similar contour length per filament. From our microrheological results, we observed a trend of lower stiffness of hydrogels when conjugating large-ring bearing side chains to the peptide segments. As stated previously, the mesh/pore size of all peptides in this study was similar at a fixed bulk concentration. Therefore, it was unlikely that the stiffness variations of MASP2–4 hydrogels were due to the differences in the mesh/pore size. Interestingly, the results from microrheological studies were in good correlation with our results of peptide secondary conformation study and prediction of simulation. A reported study has suggested that the alignment of hydrogen bonds in peptide amphiphiles can dictate the mechanical stiffness of hydrogels, showing that increased stiffness could originate from the ordered β-sheet formation along the length of the fibre.⁷⁶ Experimentally, we have observed a reduction of the ordered β-sheet structure in WAXS when a bulkier hydrocarbon was incorporated into the peptide. This is complemented by our data from molecular simulations that suggest that the observed shift in mechanical properties for these MASP filaments could arise from cooperative effects due to (1) the shift in hydrocarbon locations towards the inner hydrophobic core with the increase in ring size, and (2) decrease in the degree of hydrogen bond formation within the peptide domain and subsequent decrease in β-sheet formation (due to the increase in the hydrocarbon ring size). The experimental observations from WAXS and microrheology can be traced down to the molecular design, where the size of the ring of the isomeric hydrocarbons alters the packing in the hydrophilic/hydrophobic interfacial environments in the filaments without causing alterations in the surface chemistry.

Conclusions

In conclusion, we have developed an isomeric platform to construct 3D matrices that allows control over the local viscoelastic properties without affecting other material parameters, an ability that originates from the bottom-up design of synthetic peptides. Since such peptide-based hydrogels are relatively clean systems for further applications compared with many naturally occurring matrices, the fine-tuning of the local mechanical properties will be highly effective if these synthetic materials are applied in cell culture. We believe this design rationale could also be an effective means to construct synthetic materials with an aim to elucidate or differentiate the roles of local mechanical properties and geometric sensing in directing cell behaviors with controlled surface chemistry and mesh size.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

S. M. L. and H. C. would like to gratefully acknowledge the National Science Foundation (NSF) 1506937 for support. D. W. acknowledges the funding support from National Cancer Institute (U54CA143868 and R01CA174388). We also acknowledge the NSF for the purchase of the MALDI-ToF mass spectrometer used in this work. We also acknowledge NSF XSEDE resources under grant number TG-CHE130099 and a grant of computer time from the City University of New York High Performance Computing Center under NSF Grants CNS-0855217, CNS-0958379 and ACI-1126113. M. K. would also like to acknowledge partial support by the Rosemary O'Halleran scholarship.

Notes and references

1. D. E. Discher, P. Janmey and Y. L. Wang, Science, 2005, 310, 1139–1143.
2. A. J. Engler, S. Sen, H. L. Sweeney and D. E. Discher, Cell, 2006, 126, 677–689.
3. J. W. Shin and D. E. Discher, Nat. Mater., 2012, 11, 662–663.
4. A. Zemel, F. Rehfeldt, A. E. X. Brown, D. E. Discher and S. A. Safran, Nat. Phys., 2010, 6, 468–473.
5. M. P. Lutolf and J. A. Hubbell, Nat. Biotechnol., 2005, 23, 47–55.
6. M. P. Lutolf, P. M. Gilbert and H. M. Blau, Nature, 2009, 462, 433–441.
7. B. Trappmann and C. S. Chen, Curr. Opin. Biotechnol., 2013, 24, 948–953.
8. J. M. Lehn, Angew. Chem., Int. Ed. Engl., 1990, 29, 1304–1319.
9. G. M. Whitesides and B. Grzybowski, Science, 2002, 295, 2418–2421.
10. T. F. A. De Greef, M. M. J. Smulders, M. Wolffs, A. Schenning, R. P. Sijbesma and E. W. Meijer, Chem. Rev., 2009, 109, 5687–5754.
11. T. Aida, E. W. Meijer and S. I. Stupp, Science, 2012, 335, 813–817.
12. A. E. X. Brown, R. I. Litvinov, D. E. Discher, P. K. Purohit and J. W. Weisel, Science, 2009, 325, 741–744.
13. J. H. Ortony, C. J. Newcomb, J. B. Matson, L. C. Palmer, P. E. Doan, B. M. Hoffman and S. I. Stupp, Nat. Mater., 2014, 13, 812–816.
14. T. Shimada, N. Sakamoto, R. Motokawa, S. Koizumi and M. Tirrell, J. Phys. Chem. B, 2012, 116, 240–243.
15. H. Acar, S. Srivastava, E. J. Chung, M. R. Schnorenberg, J. C. Barrett, J. L. LaBelle and M. Tirrell, Adv. Drug Delivery Rev., 2017, 110, 65–79.
16. J. D. Hartgerink, E. Beniash and S. I. Stupp, Science, 2001, 294, 1684–1688.
17. B. F. Lin, K. A. Megley, N. Viswanathan, D. V. Krogstad, L. B. Drews, M. J. Kade, Y. C. Qian and M. V. Tirrell, J. Mater. Chem., 2012, 22, 19447–19454.
18. Y. C. Yu, P. Berndt, M. Tirrell and G. B. Fields, J. Am. Chem. Soc., 1996, 118, 12515–12520.
19. S. M. Zhang, M. A. Greenfield, A. Mata, L. C. Palmer, R. Bitton, J. R. Mantei, C. Aparicio, M. O. de la Cruz and S. I. Stupp, Nat. Mater., 2010, 9, 594–601.
20. F. C. MacKintosh, J. Käs and P. A. Janmey, Phys. Rev. Lett., 1995, 75, 4425–4428.
21. J. C. Stendahl, M. S. Rao, M. O. Guler and S. I. Stupp, Adv. Funct. Mater., 2006, 16, 499–508.
22. B. Ozbas, K. Rajagopal, L. Haines-Butterick, J. P. Schneider and D. J. Pochan, J. Phys. Chem. B, 2007, 111, 13901–13908.
23. Y. Li, Y. Sun, M. Qin, Y. Cao and W. Wang, Nanoscale, 2015, 7, 5638–5642.
24. F. J. M. Hoeben, P. Jonkheijm, E. W. Meijer and A. Schenning, Chem. Rev., 2005, 105, 1491–1546.
25. A. Aggeli, M. Bell, N. Boden, J. N. Keen, P. F. Knowles, T. C. B. McLeish, M. Pitkeathly and S. E. Radford, Nature, 1997, 386, 259–262.
26. B. Ozbas, K. Rajagopal, J. P. Schneider and D. J. Pochan, Phys. Rev. Lett., 2004, 93, 4.
27. J. Y. Huh and E. M. Furst, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 031802.
28. V. Castelletto, I. W. Hamley and P. J. F. Harris, Biophys. Chem., 2008, 138, 29–35.
29. M. C. Branco, F. Nettesheim, D. J. Pochan, J. P. Schneider and N. J. Wagner, Biomacromolecules, 2009, 10, 1374–1380.
30. R. A. Hule, R. P. Nagarkar, A. Altunbas, H. R. Ramay, M. C. Branco, J. P. Schneider and D. J. Pochan, Faraday Discuss., 2008, 139, 251–264.
31. R. H. Colby, M. Rubinstein and J. L. Viovy, Macromolecules, 1992, 25, 996–998.
32. C. F. Schmidt, M. Baermann, G. Isenberg and E. Sackmann, Macromolecules, 1989, 22, 3638–3649.
33. P. G. Degennes, P. Pincus, R. M. Velasco and F. Brochard, J. Phys., 1976, 37, 1461–1473.
34. D. H. Boal, Mechanics of the Cell, Cambridge University Press, 2012.
35. E. J. Chung, Y. Cheng, R. Morshed, K. Nord, Y. Han, M. L. Wegscheid, B. Auffinger, D. A. Wainwright, M. S. Lesniak and M. V. Tirrell, Biomaterials, 2014, 35, 1249–1256.
36. C. J. Newcomb, S. Sur, J. H. Ortony, O. S. Lee, J. B. Matson, J. Boekhoven, J. M. Yu, G. C. Schatz and S. I. Stupp, Nat. Commun., 2014, 5, 3321.
37. G. A. Silva, C. Czeisler, K. L. Niece, E. Beniash, D. A. Harrington, J. A. Kessler and S. I. Stupp, Science, 2004, 303, 1352–1355.
38. D. S. Chu, D. L. Sellers, M. J. Bocek, A. E. Fischedick, P. J. Horner and S. H. Pun, Biomater. Sci., 2015, 3, 41–45.
39. Y. J. Chuah, Y. Peck, J. E. J. Lau, H. T. Heec and D. A. Wang, Biomater. Sci., 2017, 5, 613–631.
40. G. Cinar, A. Ozdemir, S. Hamsici, G. Gunay, A. Dana, A. B. Tekinay and M. O. Guler, Biomater. Sci., 2017, 5, 67–76.
41. D. Kalafatovic, M. Nobis, N. Javid, P. Frederix, K. I. Anderson, B. R. Saunders and R. V. Ulijn, Biomater. Sci., 2015, 3, 246–249.
42. J. E. P. Sun, B. Stewart, A. Litan, S. J. Lee, J. P. Schneider, S. A. Langhans and D. J. Pochan, Biomater. Sci., 2016, 4, 839–848.
43. P. D. Tatman, E. G. Muhonen, S. T. Wickers, A. O. Gee, E. S. Kim and D. H. Kim, Biomater. Sci., 2016, 4, 543–554.
44. M. N. M. Walter, A. Dehsorkhi, I. W. Hamley and C. J. Connon, Biomater. Sci., 2016, 4, 346–354.
45. Z. Q. Yu, Z. Cai, Q. L. Chen, M. H. Liu, L. Ye, J. Y. Ren, W. Z. Liao and S. W. Liu, Biomater. Sci., 2016, 4, 365–374.
46. R. Nelson, M. R. Sawaya, M. Balbirnie, A. O. Madsen, C. Riekel, R. Grothe and D. Eisenberg, Nature, 2005, 435, 773–778.
47. Y.-A. Lin, Y.-C. Ou, A. G. Cheetham and H. Cui, Biomacromolecules, 2014, 15, 1419–1427.
48. M. W. West, W. Wang, J. Patterson, J. D. Mancias, J. R. Beasley and M. H. Hecht, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 11211–11216.
49. A. Aggeli, I. A. Nyrkova, M. Bell, R. Harding, L. Carrick, T. C. B. McLeish, A. N. Semenov and N. Boden, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 11857–11862.
50. Y.-A. Lin, Y.-C. Ou, A. G. Cheetham and H. Cui, ACS Macro Lett., 2013, 2, 1088–1094.
51. P. Greenspan, E. P. Mayer and S. D. Fowler, J. Cell Biol., 1985, 100, 965–973.
52. E. R. Gillies, T. B. Jonsson and J. M. J. Frechet, J. Am. Chem. Soc., 2004, 126, 11936–11943.
53. Y. S. Velichko, S. I. Stupp and M. O. de la Cruz, J. Phys. Chem. B, 2008, 112, 2326–2334.
54. O. S. Lee, S. I. Stupp and G. C. Schatz, J. Am. Chem. Soc., 2011, 133, 3677–3683.
55. S. Tsonchev, A. Troisi, G. C. Schatz and M. A. Ratner, Nano Lett., 2004, 4, 427–431.
56. M. Kang, P. Zhang, H. Cui and S. M. Loverde, Macromolecules, 2016, 49, 994–1001.
57. M. Kang, H. Cui and S. M. Loverde, Soft Matter, 2017, 13, 7721–7730.
58. V. Hornak, R. Abel, A. Okur, B. Strockbine, A. Roitberg and C. Simmerling, Proteins, 2006, 65, 712–725.
59. J. M. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174.
60. M. K. Gilson, H. S. R. Gilson and M. J. Potter, J. Chem. Inf. Comput. Sci., 2003, 43, 1982–1997.
61. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935.
62. J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kale and K. Schulten, J. Comput. Chem., 2005, 26, 1781–1802.
63. F. C. MacKintosh and C. F. Schmidt, Curr. Opin. Colloid Interface Sci., 1999, 4, 300–307.
64. T. A. Waigh, Rep. Prog. Phys., 2005, 68, 685–742.
65. D. Wirtz, Ann. Rev. Biophys., 2009, 38, 301–326.
66. T. G. Mason, K. Ganesan, J. H. vanZanten, D. Wirtz and S. C. Kuo, Phys. Rev. Lett., 1997, 79, 3282–3285.
67. T. G. Mason and D. A. Weitz, Phys. Rev. Lett., 1995, 74, 1250–1253.
68. D. Langevin and F. Rondelez, Polymer, 1978, 19, 875–882.
69. P. G. de Gennes, P. Pincus and R. M. Velasco, personal communication, quoted in D. Langevin, F. Rondelez, Polymer, 1978, 19, 875 edn.
70. P. Dalhaimer, F. S. Bates and D. E. Discher, Macromolecules, 2003, 36, 6873–6877.
71. B. M. Discher, H. Bermudez, D. A. Hammer, D. E. Discher, Y.-Y. Won and F. S. Bates, J. Phys. Chem. B, 2002, 106, 2848–2854.
72. M. D. Stevenson, H. Piristine, N. J. Hogrebe, T. M. Nocera, M. W. Boehm, R. K. Reen, K. W. Koelling, G. Agarwal, A. L. Sarang-Sieminski and K. J. Gooch, Acta Biomater., 2013, 9, 7651–7661.
73. K. M. Galler, L. Aulisa, K. R. Regan, R. N. D'Souza and J. D. Hartgerink, J. Am. Chem. Soc., 2010, 132, 3217–3223.
74. H. G. Cui, A. G. Cheetham, E. T. Pashuck and S. I. Stupp, J. Am. Chem. Soc., 2014, 136, 12461–12468.
75. J. A. Lehrman, H. G. Cui, W. W. Tsai, T. J. Moyer and S. I. Stupp, Chem. Commun., 2012, 48, 9711–9713.
76. E. T. Pashuck, H. Cui and S. I. Stupp, J. Am. Chem. Soc., 2010, 132, 6041–6046.
77. D. J. Smith, G. A. Brat, S. H. Medina, D. D. Tong, Y. Huang, J. Grahammer, G. J. Furtmuller, B. C. Oh, K. J. Nagy-Smith, P. Walczak, G. Brandacher and J. P. Schneider, Nat. Nanotechnol., 2016, 11, 95–102.
78. F. Tantakitti, J. Boekhoven, X. Wang, R. V. Kazantsev, T. Yu, J. Li, E. Zhuang, R. Zandi, J. H. Ortony, C. J. Newcomb, L. C. Palmer, G. S. Shekhawat, M. O. de la Cruz, G. C. Schatz and S. I. Stupp, Nat. Mater., 2016, 15, 469–476.

---

Footnotes

† Electronic supplementary information (ESI) available: Detailed experimental and simulation procedures of molecular synthesis, characterization, and computation. See DOI: 10.1039/c7bm00722a

‡ These authors contributed equally.

---