Ultrafast laser-probing spectroscopy for studying molecular structure of protein aggregates†
Huihun
Jung‡
ab,
Chester J.
Szwejkowski‡
c,
Abdon
Pena-Francesch‡
ab,
John A.
Tomko
c,
Benjamin
Allen
ade,
Şahin Kaya
Özdemir
f,
Patrick
Hopkins
*c and
Melik C.
Demirel
 *abd
*abd
aCRAFT Center, Materials Research Institute, Pennsylvania State University, University Park, PA 16802, USA. E-mail: mdemirel@engr.psu.edu; Tel: +814 863-2270
bEngineering Science and Mechanics Department, Pennsylvania State University, University Park, PA 16802, USA
cDepartment of Mechanical and Aerospace Engineering, University of Virginia, Charlottesville, VA 22904, USA. E-mail: phopkins@virginia.edu; Tel: +434-982-6005
dHuck Institutes of Life Sciences, Pennsylvania State University, University Park, PA 16802, USA
eDepartment of Biochemistry and Molecular Biology, Pennsylvania State University, University Park, PA 16802, USA
fDepartment of Electrical and Systems Engineering, Washington University, St. Louis, MO 63130, USA
First published on 27th February 2017
Abstract
We report the development of a new technique to screen protein aggregation based on laser-probing spectroscopy with sub-picosecond resolution. Protein aggregation is an important topic for materials science, fundamental biology as well as clinical studies in neurodegenerative diseases and translation studies in biomaterials engineering. However, techniques to study protein aggregation and assembly are limited to infrared spectroscopy, fluorescent assays, immunostaining, or functional assays among others. Here, we report a new technique to characterize protein structure–property relationship based on ultrafast laser-probing spectroscopy. First, we show theoretically that the temperature dependence of the refractive index of a protein is correlated to its crystallinity. Then, we performed time-domain thermo-transmission experiments on purified semi-crystalline proteins, both native and recombinant (i.e., silk and squid ring teeth), and also on intact E. coli cells bearing overexpressed recombinant protein. Our results demonstrate, for the first time, relative quantification of crystallinity in real time for protein aggregates. Our approach can potentially be used for screening an ultra-large number of proteins in vivo. Using this technique, we could answer many fundamental questions in structural protein research, such as the underlying sequence-structure relationship for protein assembly and aggregation.
Introduction
Predicting the folding and self-assembly outcomes of an amino-acid sequence remains one of the great unsolved problems in biology.1 For globular proteins, this problem can be addressed readily if an existing structure can be leveraged for homology modeling.2,3 However, a large subset of protein sequence space forms a variety of insoluble assemblies, and the self-assembly behavior of such sequences has important ramifications in fields ranging from human disease to materials engineering.4 Insoluble protein assemblies are often characterized by long-range-ordered molecular structures (e.g., β-sheets, coiled coils, or triple helices) that arise due to repetitive amino-acid sequences and that impact function broadly. Hence, experimental methods to characterize the structures of these assemblies are of critical importance. Traditional techniques for probing protein structure include Fourier transform infrared spectroscopy (FTIR), circular dichroism (CD), dynamic light scattering (DLS), fluorescence spectroscopy, nuclear magnetic resonance (NMR), cryo-electron microscopy (cryo-EM), small-angle X-ray scattering (SAXS), and X-ray crystallography.5 However, there remains an urgent need for fast and efficient techniques that can screen the properties of large numbers of protein sequences with minimal sample volume or in living cells.6Thermo-reflectance techniques measure the thermal properties of any material by probing the change in reflectivity due to the change in its temperature using an ultrafast pump and probe optics.7 The fundamental assumption of this technique is that the measured reflectivity of the probe is related to the temperature change induced by the modulated pump pulses.8 In the last decade, this technique has emerged as powerful thermometry platform to measure and interrogate the thermal properties of a wide range of bulk materials and nanosystems.9 This technique was used to interrogate the thermal and optical responses of chemically cross-linked global proteins, but ultrafast thermo-reflectance based techniques never been reported for structural proteins or living systems, to the best of our knowledge.
Here, we report a new technique to characterize protein crystallinity based on ultrafast laser-probing spectroscopy. The time-domain thermo-transmission (TDTT) technique10 enables screening of proteins in milliseconds, a feat that would be impossible to achieve with existing approaches such as fluorescence, immunostaining, or functional assays.11 We studied three different semi-crystalline proteins and showed that crystallinity correlates quantitatively with transient thermo-optic response. Moreover, we demonstrated that the TDTT technique works qualitatively in vivo by measuring the thermo-optical properties of overexpressed proteins in E. coli.
Results and discussion
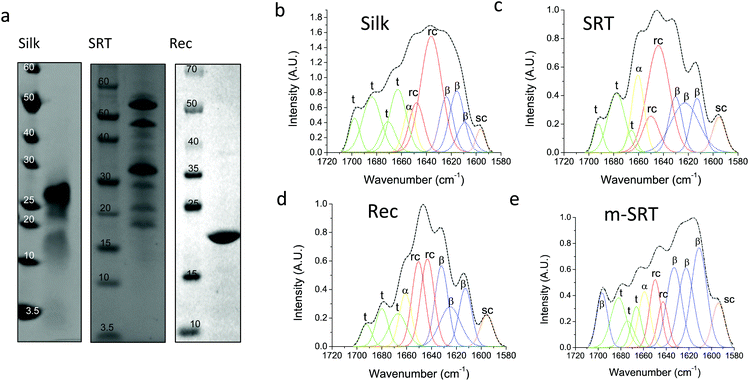
Silk12 and squid ring teeth (SRT)13 are semi-crystalline proteins that form flexible, biodegradable, and thermally and structurally stable materials. The semi-crystalline morphology of these proteins, which originates from their β-sheet secondary structures, enables genetic tuning of their physical properties.14 Silk and SRT protein complexes are composed of several proteins of varying molecular weight.15 However, this heterogeneity renders variability in physical properties of such samples. Therefore, we also studied a recombinant SRT16 protein (Rec) with a unique molecular weight (i.e., 18 kDa) that forms a monodisperse sample. Native SRT17 and silk18 proteins were extracted from the tentacles of Loligo vulgaris and cocoons of Bombyx mori respectively. The proteins were dissolved in organic solvents and processed for deposition of pure protein films as described in Methods section. The recombinant 18 kDa SRT protein16 was identified by a combination of RNA-sequencing, protein mass spectroscopy, and bioinformatics (i.e., transcriptome assembly), and then produced via recombinant expression in E. coli. The molecular weight of the proteins is confirmed by sodium dodecyl sulfate-polyacrylamide gel electrophoresis (SDS-PAGE), shown in Fig. 1a. Both silk and SRT provide a rich molecular architecture that can micro-phase separate to form amorphous GLY (glycine, leucine and tyrosine) -rich and crystalline β-sheet regions with crystalline domain dimensions of 2–3 nm. However, SRT proteins show diverse variable AVSTH (alanine, valine, serine, threonine and histidine)-rich domains in their crystal-forming sequences,4 while silk protein is made up of highly ordered β-sheet stacks containing oligomers of GAGAGS repeats.19 In order to provide crystallinity values for benchmarking against TDTT measurements, we analyzed samples of silk, SRT, Rec and m-SRT (methanol treated SRT) proteins by X-ray diffraction (XRD, Fig. S1†) and Fourier transform infrared spectroscopy (FTIR, Fig. 1b–e). Of all the absorption bands in the FTIR spectrum of proteins, the amide-I band (1600–1700 cm−1 region) is the most intense and the most characteristic. The amide I band is mainly originated by the stretching vibration of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond and it is directly related to the backbone conformation due to the hydrogen bonding of the carbonyl group. A quantitative analysis of the secondary structure in the proteins of interest is performed by Fourier self-deconvolution signal processing and curve-fitting as described in the methods below. Individual absorption bands are assigned to secondary structure elements according to the literature: a triplet of bands in the 1600–1635 cm−1 region and one band at 1697 cm−1 are attributed to β-sheet, two bands in 1645–1650 cm−1 to random coil, one band at 1661 cm−1 to α-helix and three bands in 1668–1692 cm−1 to turn structures. The secondary structure fraction (Table 1) is estimated from the band area, and the crystallinity of the proteins is taken as the percentage β-sheet content. Silk, SRT and Rec films exhibited increasing crystallinity in that order. Highly crystallinity SRT sample was prepared by treating SRT films with methanol, which has been reported to aid in β-sheet formation in silk.20
O bond and it is directly related to the backbone conformation due to the hydrogen bonding of the carbonyl group. A quantitative analysis of the secondary structure in the proteins of interest is performed by Fourier self-deconvolution signal processing and curve-fitting as described in the methods below. Individual absorption bands are assigned to secondary structure elements according to the literature: a triplet of bands in the 1600–1635 cm−1 region and one band at 1697 cm−1 are attributed to β-sheet, two bands in 1645–1650 cm−1 to random coil, one band at 1661 cm−1 to α-helix and three bands in 1668–1692 cm−1 to turn structures. The secondary structure fraction (Table 1) is estimated from the band area, and the crystallinity of the proteins is taken as the percentage β-sheet content. Silk, SRT and Rec films exhibited increasing crystallinity in that order. Highly crystallinity SRT sample was prepared by treating SRT films with methanol, which has been reported to aid in β-sheet formation in silk.20
| Silk protein (%) | SRT protein (%) | Rec protein (%) | m-SRT protein (%) | |
|---|---|---|---|---|
| β-Sheet | 24 | 34 | 38 | 57 |
| Random coil | 36 | 36 | 34 | 16 |
| α-Helix | 6 | 12 | 10 | 8 |
| Turns | 34 | 18 | 18 | 19 |
The temperature dependence of the refractive indices (i.e., thermo-optic coefficient) of the proteins was reported earlier based on optical cavity measurements.21 In general, the thermo-optic coefficient can be written as a function of density change and temperature change, dn/dT = (∂n/∂ρ)T(∂ρ/∂T) + (∂n/∂T)ρ = −(ρ∂n/∂ρ)Tα + (∂n/∂T)ρ, where ρ is the density, α is the coefficient of thermal expansion. The first term on the right side of the equation is the volume-dependent thermal response, which is related to thermal expansion. The second term, on the other hand, is the volume independent thermal response that is solely determined by the electronic structure of the material. We previously measured the thermal expansion coefficient, α, for all protein samples (−95 × 10−6 ± 7 × 10−6 K−1 for SRT proteins and −300 × 10−6 ± 10 × 10−6 K−1 for silk). Apparent negative thermal expansion coefficients are not surprising for structural proteins. For rubbery materials, the thermal expansion coefficient depends on the strain. In general, the total expansion is obtained by adding the expansion coefficient, α, to the unstressed material, α′ = α − ε/T. For example, a natural rubber stretched three times of its length gives a contribution of about −10−2 K−1 at room temperature.22 Similarly, silk shrinks significantly in size when hydrated due to inter-domain stresses (i.e., super-contraction of amorphous domains) in the native form.23
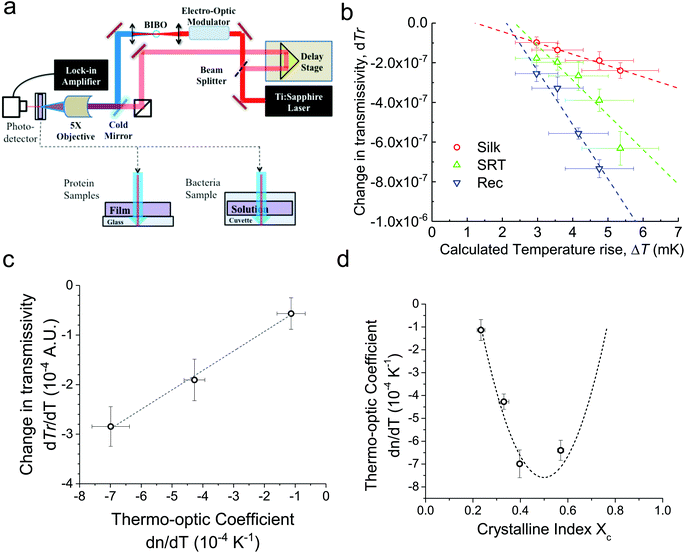
For conventional polymers, the volume independent index change, ∂n/∂Tρ, is small enough to be ignored. Hence, Zhang et al.24 showed a linear relationship between dn/dT and α values by ignoring the volume independent term for conventional polymers. We measured the changes in the ultrafast absorption properties due to changes in temperature using time-domain thermo-transmission (TDTT) (Fig. 2a). TDTT is centered upon concepts of ultrafast laser pump–probe spectroscopy, where, in TDTT, the measured transmission signal is related to the temporal decay of the probe pulse due to the transient energy density and transport mechanisms induced from the modulated pump pulse. The pump is used to trigger a rapid thermal process in the sample and the probe beam is used to examine the excited relaxation dynamics and energy changes of the excited volume. The temporal evolution of this process is monitored by varying the relative delay time between the pump and probe pulses. While the rapid absorption of the pump pulse leads to both temperature changes and thermal expansion, these signatures of the optical changes of the sample are separable in the time domain.25 The characteristic signatures of the temporal thermal response are a rapid exponential decay in ∼2 ps after laser absorption, representing nonequilibrium redistribution and coupling among thermal carriers, followed by a slower exponential decay, representing the change in the absorption of the sample that is linearly related to temperature (i.e., diffusive thermal transport).7
Our measurements are performed outside the picosecond interval, which also ensures that our measurements avoid any non-linear optical effects from simultaneous pump and probe absorption in the sample. Using transmission geometry to detect the transient absorption changes,26 our measurements on three different proteins are then related to the volume independent term of the thermo-optic coefficient, as described in ESI (Fig. S2a–c†). We benchmark our measurements and analysis using a thin gold film (Fig. S2d†), as the thermo-optic coefficients of gold films have been extensively characterized.27
First, monitoring the volume-independent thermotransmissivity signal as a function of pump-laser power shows linear relationships with distinct slopes for each of the different protein materials (Fig. 2b). These data are used to compute the thermo-transmission coefficient of each sample, which are related to the thermo-optic coefficients of the same materials (Fig. 2c).21 Plotting the thermo-transmission coefficients calculated from the experimental data for the tested proteins as a function of crystallinity revealed that the thermo-optic coefficient becomes more negative with increasing crystallinity index of the protein (Fig. 2d). Considering the Fresnel and Beer laws (see derivation in Appendix), an analytical relationship can be derived dn/dT = [az(n + 1)3∝/4(n − 1)Xc(1 − Xc)], where a is the extinction coefficient, z is the film thickness, and Xc is the crystallinity index (Fig. 2d), which agrees well with the experimental data.
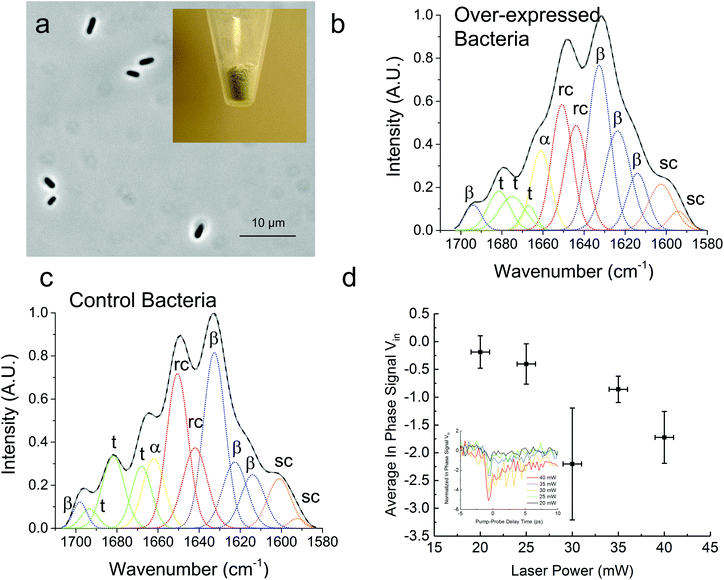
In Fig. 3, we demonstrate that the TDTT technique could work qualitatively in vivo by measuring the relative temperature changes in thermo-transmission properties of overexpressed recombinant protein SRT protein in E. coli. FTIR analysis of the overexpressed E. coli (Fig. 3a) reveals higher β-sheet content (48%) compared to purified recombinant 18 kDa protein (38%) (Fig. 3b) as shown in Table 2. Typical total protein concentration in E. coli is estimated as 190 mg mL−1, which corresponds to dry weight of 55% or volumetric composition of 40%.28 Hence, larger β-sheet content in E. coli compared to purified recombinant film is expected. On the other hand, as a negative control, we also performed FTIR studies (Fig. 3c) on the same empty vector strain of E. coli, which shows 6% lower β-sheet content (42%) compared to overexpressed E. coli. We attribute this difference to overexpressed SRT protein, which should contribute 6–8% increase to β-sheet content given that overexpression yields 15–20% excess recombinant SRT protein in E. coli. These results are also consistent with the TDTT results (Fig. 3d). Although the TDTT data in bacterial measurements cannot be converted into exact crystallinity values, it is clear that the thermo-transmissivity response correlates linearly with the incident laser power (∼ temperature shift). Note, due to the fact that these TDTT data were collected on E. coli samples suspended in water, the absolute absorption, and hence quantitative temperature rise, was not able to be calculated accurately, thus, qualitative TDTT trends as a function of incident laser power are reported in Fig. 3.
| Overexpressed bacteria (%) | Control bacteria (%) | |
|---|---|---|
| β-Sheet | 48 | 42 |
| Random coil | 30 | 31 |
| α-Helix | 9 | 9 |
| Turns | 13 | 18 |
Conclusion
We report the development of a novel optical spectroscopy technique to characterize the nanoscale morphology of structural proteins. We also show theoretically that the reflectivity measurement is correlated to the protein crystallinity via the thermo-optic coefficient. As we show here, time-resolved changes in the refractive index of semicrystalline proteins vary as a function of temperature, and the strength of this effect correlates with crystallinity. Ultimately, this allows us to quantify rapidly the crystallinity of a protein sample using time-domain thermo-transmission spectroscopy by decoupling volumetric thermal expansion from its structural response at room temperature. Our approach can potentially be used for screening an ultra-large number of proteins in vivo. The size of the library for these proteins is simply limited by the fluidic and electronic components of the sorting since the TDTT technique operates in the order of picoseconds. If this screening technique is achieved, we could answer many fundamental questions in protein research, such as the underlying sequence–structure relationship for structural proteins. Successful development of this technique for proteins will have a significant impact on multiple applications in various fields (e.g., materials science, synthetic biology, metabolic engineering, agriculture, prion based diseases) and open new avenues of protein research.29Materials and methods
Native squid ring teeth (SRT) and silk
European common squid (Loligo vulgaris) were caught from the coast of Tarragona (Spain). The squid ring teeth (SRT) were removed from the tentacles, immediately soaked in deionized water and ethanol mixture (7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0
0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :30 ratio v/v) and vacuum dried in a desiccator. Silk cocoons were purchased from Amazon, Inc., and we followed the protocol reported earlier.30
:30 ratio v/v) and vacuum dried in a desiccator. Silk cocoons were purchased from Amazon, Inc., and we followed the protocol reported earlier.30
Expression and recombinant squid ring teeth (Rec) proteins
The SRT protein family is comprised of SRTs of different size that exhibit different physical properties. Heterologous expression of the smallest (∼18 kDa) SRT protein extracted from Loligo vulgaris was performed using the protocols described earlier.16 Briefly, the full length sequence was cloned into Novagen's pET14b vector system and transformed into E. coli strain BL21(DE3). Recombinant SRT expression was achieved with a purity of ∼90% and an estimated yield of ∼50 mg L−1. The size of the protein was confirmed via sodium dodecyl sulfate-polyacrylamide gel electrophoresis (SDS-PAGE).Protein gel preparation
0.2 mg of SRT or silk is dissolved in 1 mL of 5% acetic acid/2 M urea solution, and subjected to sodium dodecyl sulfate polyacrylamide gel electrophoresis (SDS-PAGE) for protein separation. The protein gels were stained with Coomassie blue dye.Protein casting
SRT solution (either recombinant or native protein) was prepared by dissolving 50 mg mL−1 of protein in hexafluoro-2-propanol (HFIP). The SRT solution was sonicated for 1 hour and vacuum-filtered in a 4–8 μm mesh size filter. Silk fibroin solution was prepared following a previously reported protocol.30 20 μL of protein solution were poured on 1 × 1 cm Al-coated (80 nm) silica glass substrates and were ambient-dried in the fume hood overnight, resulting in protein films with approximately 25 μm in thickness. Aluminum coated (80 nm) silica glass substrates were used in pump–probe transient absorption measurements, and microscope glass slide substrates were used in spectroscopic characterization. Methanol treated samples were immersed in methanol for 2 hours and dried in the fume hood overnight.Spectroscopic characterization
XRD: X-Ray Diffraction (Wide Angle X-ray Scattering, WAXS) data were collected in a Rigaku DMAX-Rapid II Microdiffractometer (wavelength λ = 0.154 nm) using a Cu Kα source and a 30 μm collimator with 10 minute exposure at 50 kV and 40 mA. The crystallinity index was calculated as the ratio of the area of crystal peaks to the total area by fitting the Lorentz-corrected WAXS intensity data using Gaussian functions. Data analysis was performed with MDI Jade X-ray diffraction software and OriginPro 8.5 software.ATR-FTIR (attenuated total reflectance Fourier transform infrared spectroscopy): Spectral data were collected (Thermo Scientific Nicolet 6700 FT-IR) under attenuated total reflection (diamond crystal) mode using Happ-Genzel apodization with 4 cm−1 resolution from 400 to 4000 cm−1. For each spectrum, 256 scans were co-added. Fourier self-deconvolution (FSD) and second derivative evaluation of the amide I band (1580–1706 cm−1) were performed using the OMNIC software (Thermo Scientific, v7.3). Second derivatives were obtained from the original amide I spectra and a nine-point Savitsky–Golay smoothing filer of polynomial degree 5 was applied. FSD was performed with Lorentzian line shape with 25 cm−1 bandwidth and an enhancement factor of 2. Individual bands were fitted to the deconvoluted spectra and were assigned to secondary structural components as previously reported. The number and position of the fitted bands were obtained from the second derivative spectra, where the minima in the second derivative spectra corresponded to the fitted band maxima in the deconvoluted spectra. Gaussian curve fitting was performed in OriginPro 8.5 software by using a nonlinear least-squares method. First, the initial band positions (taken from the second derivatives) were fixed and the width and height were left as free parameters. Then, the band positions were allowed to change within a ±1 cm−1 range using the built-in Levenberg–Marquardt algorithm. The relative areas of the single bands were used in the secondary-structure composition calculations.
Pump–probe transient absorption measurements (time domain thermotransmission – TDTT)
A Ti:Sapphire laser (Spectra-Physics, Tsunami) is used for time domain transmissivity measurements. Laser characteristics were 800 nm central wavelength, 10 nm bandwidth, 90 fs pulse duration, and 80 MHz reputation rate. The beam is split into two paths (pump and probe paths) by a polarizing beam splitter (PBS) and the pump is frequency doubled to 400 nm wavelength, pump: 7.5 mW (average power of pump modulated at 8.8 MHz using a sinusoidal envelope), probe: 4 mW of average power. The pump beam power was varied to change the relative temperature rise in the samples during TDTT measurements. The beam size 14 micron for the probe and 34 micron for the pump with synchronous sampling via mechanical delay stage. The transmittance signal is digitalized using a Thorlabs DET10A Si Detector and a Zurich Instruments UHFLI digital lock-in amplifier. The resulting locked-in voltage is on the order of 10−6 V; data was collected up to pump–probe time delays of 5.5 ns, with variation and noise of 1 nV and 0.2 μV respectively. The bandwidth of the detector was 1 GHz. The delay between pump and probe is mechanically controlled using Newport Optical Delay Line Kit. A combination of LabView and MatLab programs (developed in-house) were used to analyze the data.Author contributions
MCD conceived the idea and derived structure–property equations. MCD, SKO, PEH and BDA planned and supervised the research. APF fabricated the protein films and performed spectroscopic characterization, CJS and JAT performed the pump–probe transient absorption measurements, and HJ worked on the cloning, recombinant expression and purification of proteins. All authors contributed to writing and revising the manuscript, and agreed on the final content of the manuscript.Additional information
The authors declare no competing financial interests. Correspondence and requests for materials should be addressed to PEH and MCD.Appendix: Derivation of structure–property equation for TTDT measurements
Starting with Fresnel equation: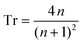 | (1) |
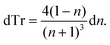 | (2) |
Thus, the measured change in transmissivity via TDTT is directly related to the change in the index of refraction. Therefore, dTr/dT∝dn/dT.
Beer Law states a relationship between absorbance and concentration (or crystalline and amorphous fractions, Xc and Xa respectively, for polymers):
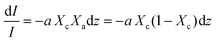 | (3) |
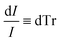 | (4) |
Combining Fresnel (2) and Beer Law (3) results in:
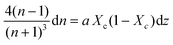 | (5) |
Dividing both sides by dT (infinitesimal temperature),
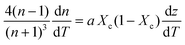 | (6) |
Inserting coefficient of thermal expansion as a function of thickness, z,
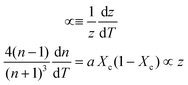 | (7) |
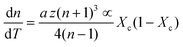 | (8) |
Acknowledgements
MCD, BDA, APF, and HJ were supported by the Army Research Office under grant no. W911NF-16-1-0019, and Materials Research Institute of the Pennsylvania State University. PEH, CJS, and JAT were supported by the Army Research Office under grant No. W911NF-16-1-0320. We thank Mr Huzeyfe Yilmaz for providing thermo-optic coefficient for proteins studied in this manuscript.References
- S. B. Dev, Prog. Biophys. Mol. Biol., 2015, 117, 232–239 CrossRef PubMed.
- M. A. Marti-Renom, A. C. Stuart, A. Fiser, R. Sánchez, F. Melo and A. Šali, Annu. Rev. Biophys. Biomol. Struct., 2000, 29, 291–325 CrossRef CAS PubMed.
- T. Schwede, J. Kopp, N. Guex and M. C. Peitsch, Nucleic Acids Res., 2003, 31, 3381–3385 CrossRef CAS PubMed.
- M. C. Demirel, M. Cetinkaya, A. Pena-Francesch and H. Jung, Macromol. Biosci., 2015, 15, 300–311 CrossRef CAS PubMed.
- T. L. Blundell and L. N. Johnson, Protein Crystallography, Academic Press, 1976 Search PubMed.
- C. V. Robinson, A. Sali and W. Baumeister, Nature, 2007, 450, 973–982 CrossRef CAS PubMed.
- D. G. Cahill, Rev. Sci. Instrum., 2004, 75, 5119–5122 CrossRef CAS.
- P. E. Hopkins, J. R. Serrano, L. M. Phinney, S. P. Kearney, T. W. Grasser and C. T. Harris, J. Heat Transfer, 2010, 132, 081302 CrossRef.
- D. G. Cahill, W. K. Ford, K. E. Goodson, G. D. Mahan, A. Majumdar, H. J. Maris, R. Merlin and S. R. Phillpot, J. Appl. Phys., 2003, 93, 793–818 CrossRef CAS.
- O. M. Wilson, X. Hu, D. G. Cahill and P. V. Braun, Phys. Rev. B: Condens. Matter, 2002, 66, 224301 CrossRef.
- R. Pepperkok and J. Ellenberg, Nat. Rev. Mol. Cell Biol., 2006, 7, 690–696 CrossRef CAS PubMed.
- G. H. Altman, F. Diaz, C. Jakuba, T. Calabro, R. L. Horan, J. Chen, H. Lu, J. Richmond and D. L. Kaplan, Biomaterials, 2003, 24, 401–416 CrossRef CAS PubMed.
- M. Nixon and P. N. Dilly, Symp. Zool. Soc. London, 1977, 38, 447–511 Search PubMed.
- H. Jung, A. Pena-Francesch, A. Saadat, A. Sebastian, D. H. Kim, R. F. Hamilton, I. Albert, B. D. Allen and M. C. Demirel, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 6478–6483 CrossRef CAS PubMed.
- V. Sariola, A. Pena-Francesch, H. Jung, M. Çetinkaya, C. Pacheco, M. Sitti and M. C. Demirel, Sci. Rep., 2015, 5, 13482 CrossRef PubMed.
- A. Pena-Francesch, S. Florez, H. Jung, A. Sebastian, I. Albert, W. Curtis and M. C. Demirel, Adv. Funct. Mater., 2014, 24, 7401–7409 CrossRef CAS.
- A. Pena-Francesch, B. Akgun, A. Miserez, W. Zhu, H. Gao and M. C. Demirel, Adv. Funct. Mater., 2014, 24, 6227–6233 CrossRef CAS.
- D. N. Rockwood, R. C. Preda, T. Yücel, X. Wang, M. L. Lovett and D. L. Kaplan, Nat. Protoc., 2011, 6, 1612–1631 CrossRef CAS PubMed.
- T. Lefèvre, M.-E. Rousseau and M. Pézolet, Biophys. J., 2007, 92, 2885–2895 CrossRef PubMed.
- X. Hu, D. Kaplan and P. Cebe, Macromolecules, 2006, 39, 6161–6170 CrossRef CAS.
- H. Yilmaz, A. Pena-Francesch, L. Xu, R. Shreiner, H. Jung, S. H. Huang, S. K. Ozdemir, M. C. Demirel and L. Yang, SPIE Proc., 2016, 974501, DOI:10.1117/12.2214245.
- C. Y. Ho and R. E. Taylor, Thermal Expansion of Solids, ASM International, 1998 Search PubMed.
- J. M. Gosline, M. W. Denny and M. E. DeMont, Nature, 1984, 309, 551–552 CrossRef CAS.
- Z. Zhang, P. Zhao, P. Lin and F. Sun, Polymer, 2006, 47, 4893–4896 CrossRef CAS.
- C. S. Gorham, K. Hattar, R. Cheaito, J. C. Duda, J. T. Gaskins, T. E. Beechem, J. F. Ihlefeld, L. B. Biedermann, E. S. Piekos and D. L. Medlin, Phys. Rev. B: Condens. Matter, 2014, 90, 024301 CrossRef.
- S. S. Chou, B. Kaehr, J. Kim, B. M. Foley, M. De, P. E. Hopkins, J. Huang, C. J. Brinker and V. P. Dravid, Angew. Chem., Int. Ed., 2013, 125, 4254–4258 CrossRef.
- P. E. Hopkins, Phys. Rev. B: Condens. Matter, 2010, 81, 035413 CrossRef.
- R. Milo and R. Phillips, Cell Biology by the Numbers, Garland Science, 2015 Search PubMed.
- J. Nielsen, M. Fussenegger, J. Keasling, S. Y. Lee, J. C. Liao, K. Prather and B. Palsson, Nat. Chem. Biol., 2014, 10, 319–322 CrossRef CAS PubMed.
- S. Kim, A. N. Mitropoulos, J. D. Spitzberg, H. Tao, D. L. Kaplan and F. G. Omenetto, Nat. Photonics, 2012, 6, 818–823 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6an02570f |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2017 |