Broadband absorption spectroscopy for rapid pH measurement in small volumes using an integrated porous waveguide

Abstract

Broadband absorption spectroscopy integrated with microfluidics is widely used to measure the pH of samples available in small volumes. Single pass absorption spectroscopy, however, suffers from poor minimum detectable absorption coefficient because the optical path length is determined by the physical dimensions of microchannels. As a result, either large amounts of indicator dyes are added or instrumentally complex techniques are used to determine sample pH. This work addresses these limitations by the integration of metal-clad leaky waveguide (MCLW) with microfluidics to perform broadband absorption spectroscopy. The MCLW consisted of a porous agarose waveguide with an estimated thickness and swelling ratio values of 1.405 ± 0.009 μm and 20.96 ± 0.65% respectively coated onto a titanium layer 32.8 ± 0.43 nm thick on a glass slide. MCLW permits obtaining absorption spectra over most of the wavelength range of the visible region (i.e. 450 nm to 700 nm) with a speed of 12.5 spectra per second using 3.2 nl of sample. The minimum detectable decadic absorption coefficient measured using MCLW was 0.43 cm⁻¹, which is intermediate between single pass absorption spectroscopy and instrumentally complex techniques such as broadband cavity enhanced absorption spectroscopy and whispering gallery mode resonators.

---

1. Introduction

Broadband absorption spectroscopy combined with microfluidics is a powerful tool for studying reaction kinetics, and quantitation and often identification of analytes.^1–15 Another important application of the technique is to determine pH of samples,^16–19 which is among the most frequently measured analytical quantities in areas including biological and chemical sciences, as well as environmental, food and pharmaceutical quality control.^20–26 To measure sample pH without having to add large amounts of indicator dyes, which can introduce perturbations in sample pH, it is essential to be able to perform absorption measurements with high sensitivity. The minimum detectable absorption coefficient of single pass absorption spectroscopy is, however, limited by the physical dimensions of microchannels.^27,28 Thus, broadband cavity enhanced absorption spectroscopy (BBCEAS),^29–34 liquid core waveguides (LCWs),^35–38 whispering gallery mode (WGM) resonators^39–41 and anti-resonant reflecting optical waveguides (ARROWs)^42,43 have been integrated with microfluidics. The limitations of these techniques include one or more of instrumental complexity, elaborate fabrication methods, narrowband measurements and limited spatial and/or temporal resolution.

Previously, we described metal-clad leaky waveguide (MCLW) integrated with microfluidics to perform absorption spectroscopy with improved minimum detectable absorption coefficient.⁴⁴ MCLW was fabricated on a glass substrate by vacuum deposition of a metal layer (typically titanium) and then a spin-coated agarose waveguide. Light was partially confined in the waveguide by total internal and Fresnel reflection at the waveguide-sample and waveguide-substrate interfaces respectively. A peak in reflectivity was observed at the resonance angle (the angle at which light couples strongly into the waveguide) and its intensity was a function of scattering and absorption losses in and on the waveguide. As agarose is porous, the absorbing species diffuses into the waveguide and hence light confined in the waveguide as well as in the evanescent field above the waveguide interacts with it. This is in contrast to non-porous waveguides where only the evanescent field interacts with the absorbing species. Hence, the detection sensitivity and LOD of porous waveguides is about three times better than non-porous waveguides. Our previous work, however, required mechanical scanning of the angle of the white light source and spectrophotometer detector because of the dispersive nature of MCLW, which meant that at a given angle only a limited range of wavelengths could be coupled into the waveguide. As a result of the mechanical movement, this method was slow and, because of the external spectrophotometer, gave quite noisy spectra. Overall, this method required about 16 seconds to acquire a complete spectrum and gave a minimum detectable absorption coefficient of 26.4 cm⁻¹. Using a monochromatic source, a 650 nm semiconductor laser, a photodiode detector and mechanical scanning improved the minimum detectable absorption coefficient to 0.16 cm⁻¹ but still required 3.33 s to acquire the required reflectivity data. Although the laser source considerably improved the detection limit, the single wavelength means that this method is not suitable for all absorbing species and cannot aid in identification.

In the work described here, the external spectrophotometer was replaced by a transmission grating and camera and using an input white light wedge beam all the information required to generate an absorption spectrum was obtained without any mechanical movement, thus allowing spectra to be generated much more rapidly. The camera integration time was only 80 ms, potentially allowing 12.5 spectra to be acquired per second. The improved signal-to-noise of this instrumental setup resulted in a minimum detectable absorption coefficient of 0.43 cm⁻¹, a 60-fold improvement over the previous setup. This work was carried out using bromothymol blue (BTB) solutions (rather than methylene blue solutions used previously) as an exemplar analyte because of the following: firstly, it permits studying the feasibility of using MCLW to perform absorption spectroscopy between 450 nm and 700 nm (i.e. over the entire visible range). Secondly, the absorption spectrum of BTB solution is pH sensitive, which allows investigating the suitability of MCLW to determine sample pH. Thirdly, unlike methylene blue, BTB does not form aggregates. Thus, the use of BTB solutions is better suited to build models for estimating the waveguide parameters such as swelling ratio, refractive index and thickness.

2. Experimental

2.1 Chemicals and materials

1 mm thick glass slides were purchased from VWR (Leicestershire, UK). Sulfuric acid, hydrogen peroxide, titanium, sodium phosphate monobasic monohydrate, sodium phosphate dibasic dodecahydrate, phosphoric acid, sodium hydroxide (1.0 M), glutaraldehyde (25%), bovine serum albumin (BSA), poly-ethylene glycol (PEG) and BTB (95%) were purchased from Sigma-Aldrich (Gillingham, UK). Ultrapure™ LMP agarose was obtained from Life Technologies (Paisley, UK). Glycerol was obtained from Fisher (Loughborough, UK).

2.2 MCLW device fabrication

Glass squares of ∼25.4 mm by 25.4 mm were cleaned in piranha solution (should be used with caution) and then coated with titanium using an e-beam evaporator (Auto500, Edwards, Crawley, UK). 0.2 g of agarose in 10 ml water was heated in a microwave oven until fully dissolved. Subsequently, 12.5 μl of 25% (v : v) glutaraldehyde was added and allowed to react for 30 min at 95 °C. The solution was spin coated on a glass slide with titanium layer at a speed of 2250 rpm for 30 s. The plate used to make a flow cell was 38 mm by 42 mm, consisted of a recessed Y-shaped cavity with a 4 mm wide and 0.2 mm deep channel and a groove 1 mm wide and 0.75 mm deep to mount an O-ring. The plate was placed on the MCLW chip and was held in place using a water-cooled fixture maintained at 20 °C clamped on top.

2.3 Instrumentation

Fig. 1 illustrates the instrumentation used to perform MCLW based absorption spectroscopy. A BK7 equilateral prism (Qioptic Photonics, Denbighshire, UK) was used to couple light in and out of the MCLW device. The light source (fibre-coupled tungsten-halogen lamp, Ocean Optics, Duiven, Netherlands) and camera (PL-B781, Pixelink, Ottowa, Canada) were mounted on rails, which were connected to goniometers to control their angular position. An assembly of achromatic doublet, heat filter and polariser was used to obtain a TE-polarised collimated beam limited to the visible region. Light was passed through a cylindrical lens (100YE25, Comar Optics Ltd, Cambridge, UK) to obtain a wedge-shaped beam with a wedge angle of ∼14° in air or ∼9° in the prism. The output of the MCLW was passed through a transmission grating (GT25-03, Thorlabs, Newton, USA) and a 100 mm focal length achromatic doublet (100DQ25, Comar Optics Ltd, Cambridge, UK) to focus it onto the camera.

Fig. 1 (a) Instrumentation used to test the MCLW device, (b) plan and (c) side views of the arrangement (where ‘x’ and ‘y’ refers to the camera coordinates, and the flow cell is not shown in (b) and (c) for clarity).

The relationship between camera pixel and wavelength was determined by introducing interference filters of known wavelength in the path of incident light and recording the corresponding pixel position of the reflected light. The relationship between the camera pixel number and wavelength is given by:

N = 6232.32 − 8.9504λ (1)

where N is the pixel number and λ the wavelength in nm. The camera integration time was set to 80 ms. Refractive indices of the solutions were measured using a Bellingham and Stanley RFM900 automatic refractometer with an accuracy of ±1 × 10⁻⁵. Fluids were pumped through the flow cell using a peristaltic pump at a flow rate of 0.2 ml min⁻¹. Unless stated otherwise, sodium phosphate buffer of concentration of 35 mM (with a corresponding ionic strength of ∼100 mM) and pH 8.22 was used.

2.4 Methodology to estimate of swelling ratio, refractive index and thickness of agarose waveguide

As shown in Table 1, the MCLW was modelled as a four layer structure in an in-house written transfer matrix program where BTB was or was not present.

Table 1 Model parameters (where t_Ti and t_agarose are thickness of titanium and agarose respectively, and rest of the symbols are defined in text)

Layer	Thickness (μm)	Material	Refractive index
1	10	NBK7	n glass − 0.000000i
2	Unknown (tTi)	“Ti”	Unknown (nTi − kTii)
3	Unknown (tagarose)	Agarose + (BTB)	Unknown
4	10	Buffer + (BTB)	n buffer − kdyei

---

The wavelength dependent refractive indices of glass (n_glass) and buffer (n_buffer) were built into the program using either tabulated Sellmeier coefficients or cubic spline interpolation of refractive index data in literature.^45–47 Literature sources disagree quite significantly on the complex refractive index of titanium (n_Ti − k_Tii); ranging from 1.9634–3.0625i (ref. 46) to 2.6140–3.6080i (ref. 48) at 589 nm, and hence was treated as an unknown parameter. Single pass absorption spectroscopy was used to determine the wavelength dependent molar extinction coefficients (ε, in M⁻¹ cm⁻¹) of BTB solutions, which were substituted in eqn (2) to determine the corresponding imaginary refractive index.

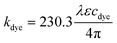where k_dye is the imaginary refractive index of BTB, c_dye is the concentration of BTB in buffer (in this case, 250 μM) and λ is the wavelength in m. The real refractive index of rehydrated (n_agarose) agarose at each wavelength is given by the following expression:where c_agarose is the concentration of the original agarose solution (w : v), n_buffer is the refractive index of buffer and Δn is the refractive index increment for pure agarose with respect to buffer. The refractive index values for pure agarose were obtained from literature.⁴⁵ In the absence of BTB in the buffer, the imaginary refractive index of agarose (k_scattering) was a result of scattering caused by the gel's porous structure. In the presence of BTB in the buffer, the imaginary refractive index of the waveguide had an additional component because of absorption losses introduced by the diffusion of the dye in the waveguide. This additional imaginary refractive index component was determined by scaling the k_dye by a factor of (c_dye,w/c_dye) where c_dye,w is the concentration of the dye in the waveguide and was treated as an unknown parameter. All the unknown parameters in Table 1 were determined using the simplex method developed by Nelder and Mead.⁴⁹ The pore size distribution in agarose films were estimated experimentally by irrigating MCLW with solutions of species of different molecular weights and recording shifts in the reflectivity peak.

3. Results and discussion

3.1 Estimation of swelling ratio, refractive index and thickness of agarose waveguide

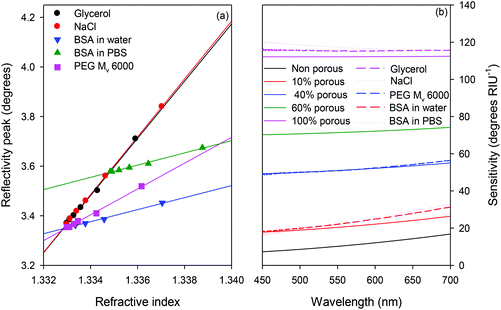
The thickness and refractive index of the titanium layer were estimated to be 32.8 ± 0.43 nm and 1.938 ± 0.009 − (1.001 ± 0.007)i respectively suggesting that the deposited film likely contained some titanium oxide and nitride.⁵⁰ The thickness (t_agarose) and swelling ratio (S) of the agarose waveguide was estimated to be 1.405 ± 0.009 μm and 20.96 ± 0.65% respectively. The imaginary refractive index of agarose because of scattering losses (k_scattering) was estimated to be (2.14 ± 0.16) × 10⁻⁴. Finally, the concentration of BTB in the waveguide (c_{dye, w}) was estimated to be 573 ± 48 μM. No systematic variation in the concentration of BTB in the waveguide was found with pH, but it was higher than in the buffer (in this case, c_dye was 250 μM), indicating that there was an interaction between the agarose and dye that was independent of pH over the range studied.

Fig. 2 shows that the refractive index sensitivity of MCLW was ∼25% and ∼55% lower for PEG (M_v: 6000) and BSA respectively compared to small molecules such as glycerol and NaCl. Further, as shown in Fig. 2(b), the refractive index sensitivity of larger molecules (e.g. PEG and BSA) is a stronger function of wavelength than small molecules (e.g. glycerol and NaCl). This observation can be explained by considering that the smaller species are present in both the waveguide and the evanescent field, but the larger species are at least partially excluded from the waveguide. The fraction of light in the evanescent field increases with increasing wavelength, thus increasing the sensitivity of the MCLW to species in the evanescent field as the wavelength increases. If the species is present in both the waveguide and evanescent field, the sensitivity is largely independent of wavelength. A comparison of theoretical and experimental refractive index sensitivities of MCLW (see Fig. 2(b)) suggests that the waveguide is 10% porous to BSA, 40% to PEG and 100% to glycerol and NaCl. This in turn implies that the pore size distribution is such that only 10% of the pores are bigger than BSA, 40% bigger than PEG and all are bigger than glycerol or NaCl. A more accurate determination of the pore size distribution in these agarose films would require a wide range of different molecular weight PEGs.

Fig. 2 A plot of (a) reflectivity peak versus refractive index at 589.4 nm and (b) comparison of theoretical (solid lines) and experimental (dashed or dotted lines) refractive index sensitivity versus wavelength of MCLW for different solutions.

It is proposed that the pore size distribution in agarose waveguides is much smaller than gels formed for electrophoresis separation because of the spin coating process used to make the waveguides. The normal process for agarose to form gels is by forming helices and then bundles of helices, which branch and subsequently join with other bundles of helices to make an interconnected network with large pores.⁵¹ It is proposed that the spin coating process results in two competing processes occurring simultaneously: gelation and dehydration; producing films that are not as porous as the original wet gel. Atomic force microscopy of wet agarose gels^52,53 has shown that the pore size follows a power law with concentration, leading to a pore size estimate of ∼128 nm for a 21% swelled (∼10.5% w/v) gel. This expected pore size is considerably larger than BSA, but experimentally the gel is not porous to the protein, thus supporting the conclusion that the combination of spin coating and dehydration/rehydration dramatically reduces the pore size of agarose.

3.2 Broadband absorption spectroscopy using MCLW for pH measurement

Fig. 3 is a typical output of MCLW and clearly shows that a single reflectivity peak was observed in the wavelength range between 450 nm and 700 nm, which implies that the MCLW supported a single optical mode in the wavelength range investigated. The resonance angle of the MCLW irrigated with buffer is 63.09° at 615 nm. Further, the resonance angle increases by 0.4° as the wavelength decreases from 700 nm to 450 nm.

Fig. 3 Typical output of MCLW irrigated with buffer (where ‘x’ is wavelength and ‘y’ is angle of incidence).

Plots of normalised peak reflectivity values versus wavelength for cases when the MCLW was irrigated with buffer and 250 μM BTB solution are shown in Fig. 4, and were used to determine the dye's absorption spectra. Reflections from surfaces resulted in interference effects, which were observed as modulations in intensity values. The absorbance maxima of the dye obtained using MCLW and single pass absorption spectroscopy were comparable (615–617 nm for former versus 616–618 nm for latter), but the peak shape was slightly different to that obtained using single pass absorption spectroscopy because the optical path length in the MCLW varies with wavelength. The wavelength resolution of the MCLW was ∼16 nm compared to 1 nm for the spectrophotometer. The wavelength resolution was mainly determined by the collimation of the input beam; using a 400 μm core diameter optical fibre, a 63 mm focal length collimating lens and a 100 mm focal length output lens gives a theoretical wavelength resolution of 19 nm. Reducing the fibre core diameter would improve collimation and hence wavelength resolution, but at the expense of much reduced light intensity. This in turn would require longer integration times to obtain spectra.

Fig. 4 Normalised peak reflectivity values or absorption versus wavelength obtained using (i) MCLW and (ii) single pass absorption spectroscopy.

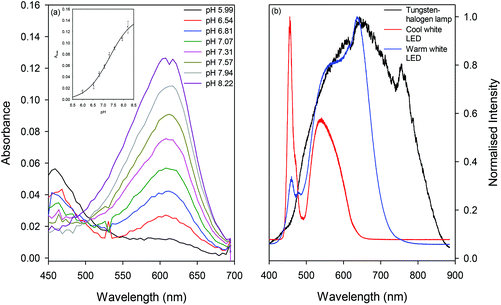
The absorption spectra of BTB solution obtained using MCLW, which is provided in Fig. 5(a), shows that the wavelength maximum of the basic form of the dye is at 612 nm. The corresponding literature reported value is 615–616.^54–56 The reported value for the wavelength maximum of the acidic form of the dye is around 415 nm,⁵⁶ but could not be observed in the spectra obtained using MCLW because of the low intensity of the tungsten halogen lamp at short wavelengths (see Fig. 5(b)). As shown in the inset in Fig. 5(a), the relationship between the absorbance maximum, A_max, and pH was sigmoidal and is given by eqn (4) (r² of 0.996).

Fig. 5 (a) Absorbance spectra of 250 μM BTB solutions of ionic strength of 100 mM at different pH obtained using MCLW (where the inset shows absorbance maximum versus pH) and (b) wavelength dependent intensity of light sources investigated in this work.

The pK_a of BTB solution was, therefore, determined to be 7.31 ± 0.15, which is in accordance with the literature reported value of 7.2 for BTB solutions prepared in buffers of ionic strength of 100 mM.^57,58 A well-defined isosbestic point, however, could not be obtained because of the low intensity of the tungsten halogen lamp at short wavelengths resulting in poor signal to noise ratio in that wavelength region. Other light sources such as cool and warm white LEDs (W57L5111P and M57L5111P, Roithner Lasertechnik, Vienna, Austria) were also investigated, but both had low intensity around 500 nm (as shown in Fig. 5(b)). This gap straddles the isosbestic point of BTB, making the signal-to-noise ratio at these wavelengths markedly worse. Further, the warm white LED converts more of the output of the blue LED to red and green at the expense of lower overall intensity and hence required an integration time of 200 ms to probe the MCLW. Supercontinuum sources would cover the entire wavelength range with high intensity, but are generally subject to temporal fluctuations in intensity which would also worsen the signal-to-noise ratio. As a compromise between stability, wavelength range and intensity the tungsten halogen source was the optimum choice.

In summary, this work demonstrated the suitability for performing broadband absorption spectroscopy and its application to determine sample pH using MCLW. The ability to perform broadband spectroscopy using MCLW integrated with microchannels means that very small sample volumes can be probed. In this case, the volume of the sample probed was 3.2 nl, based on the width of the channel (4 mm), the propagation length of the mode (∼0.4 mm) and the thickness of the waveguide plus the penetration depth of the evanescent field (1.65 + 0.35 μm). In addition, as the entire absorption spectrum was obtained, the absorption maximum can be determined even if the absorption peak shifts as a result of changes in solvent composition. Further, based on the error bars on the absorbance maximum, MCLW permits determining sample pH with a resolution of ∼0.12 ± 0.03 between pK_a −0.5 and pK_a +0.5 of the indicator dye used. The pH resolution obtained using MCLW is comparable to that of solid-state metal oxide electrodes and ISFETs. In comparison to latter approaches, however, MCLW is beneficial because it does not require physical contact with the sample, patterning of multiple materials and fabrication of electrodes at multiple locations to obtain spatial information. Additionally, MCLW offers rapid response time (80 ms versus 1 s) and does not require repeated calibration.^59,60 Although this is lower resolution than a calibrated glass pH electrode, it is adequate for probing small sample volumes in microfluidic devices for applications where continuous and rapid monitoring of pH is required.⁵⁹

3.3 Minimum detectable absorption coefficient of MCLW

It is useful to determine the lowest concentration of BTB that can be used to determine the minimum detectable absorption coefficient of MCLW because it governs the minimum concentration of an indicator dye that can be added to determine the sample pH. The absorption spectrum of different concentrations of BTB solutions as well as peak absorbance (A_max) versus dye concentration (c_dye) are provided in Fig. 6. The relationship between the two is linear and given by A_max = 1.148 × 10⁻³c_dye + 5.058 × 10⁻⁴ (r² = 0.998) where c_dye is in μM.

Fig. 6 Absorption spectrum of different concentrations of BTB solutions in 100 mM ionic strength phosphate buffer, pH 8.22, obtained using MCLW (where the inset shows absorbance maximum versus BTB concentration).

The LOD of MCLW for BTB solution was 15.49 μM, which corresponds to a minimum detectable decadic absorption coefficient of 0.43 cm⁻¹. This minimum detectable absorption coefficient is about five times better than that achievable using single pass absorption spectroscopy and was obtained with an integration time of 80 ms.³⁴ The lower LOD of MCLW compared to single pass absorption spectroscopy means that lower dye concentrations can be used for pH sensing, resulting in smaller pH perturbations of weakly buffered samples. For example, addition of 15.49 μM BTB to water increases the sample pH by 0.17 versus 0.46 for 77.45 μM dye. Compared to BBCEAS using integrated mirrors, the minimum detectable absorption coefficient is two times higher (0.43 versus 0.23 cm⁻¹) but the temporal resolution of MCLW is 125 times better (80 ms versus 10 s).³⁴ In comparison to WGM resonators,^39–41 MCLW is instrumentally less complex and does not need to be fabricated at the locations to be sensed. Finally, MCLW is easily fabricated using techniques such as spin coating, integrated with planar microfluidic flow cells and probed using free space optics.

4. Conclusions

This work for the first time demonstrates the suitability of a metal-clad leaky waveguide (MCLW) integrated with microfluidics to perform broadband absorption spectroscopy to determine pH in small sample volume. The MCLW consists of a porous waveguide (in this case, agarose) deposited on a titanium coated glass slide. The porous nature of the waveguide is beneficial because the sample diffuses into the waveguide and hence light confined in the waveguide as well as in the evanescent field above the waveguide interacts with it. The presence of the metal layer permit visualisation of the resonance angle of the MCLW. The intensity of reflectivity peak at the resonance angle is a function of wavelength dependent extinction coefficient of the sample, and hence is used to determine the absorption spectrum of the sample. In the case of a sample consisting of a pH sensitive dye, the absorption spectrum is related to the sample pH. Modelling of the MCLW was carried out using an in-house transfer matrix program with integrated simplex optimisation to adjust the model parameters to obtain a best fit to the experimental data. Modelling of the device with simplex optimisation was able to determine the agarose layer thickness (1.405 ± 0.009 μm), swelling ratio (20.96 ± 0.65%), BTB concentration in the waveguide (573 ± 48 μM) and the thickness and complex refractive index of the titanium layer (32.8 ± 0.43 nm and 1.938 ± 0.009 − (1.001 ± 0.007)i respectively). The MCLW provides a wavelength and temporal resolution of ∼16 nm and 80 ms respectively. MCLW provides a limit of detection of 15.5 μM for the pH indicator dye BTB, which corresponds to a minimum detectable decadic absorption coefficient of 0.43 cm⁻¹. This is intermediate between single pass absorption spectroscopy and more instrumentally complex techniques such as BBCEAS and WGM resonators.

References

1. J. E. Noble and M. J. A. Bailey, in Guide to Protein Purification, ed. R. R. Burgess and M. P. Deutscher, 2nd edn, 2009, vol. 463, pp. 73–95.
2. C. Cordella, I. Moussa, A. C. Martel, N. Sbirrazzuoli and L. Lizzani-Cuvelier, J. Agric. Food Chem., 2002, 50, 1751–1764.
3. F. C. Jentoft, in Advances in Catalysis, ed. B. C. Gates and H. Knozinger, 2009, vol. 52, pp. 129–211.
4. D.-B. Hou, J. Zhang, L. Chen, P.-J. Huang and G.-X. Zhang, Spectrosc. Spectral Anal., 2013, 33, 1839–1844.
5. R. A. Schoonheydt, Chem. Soc. Rev., 2010, 39, 5051–5066.
6. D. J. Beebe, G. A. Mensing and G. M. Walker, Annu. Rev. Biomed. Eng., 2002, 4, 261–286.
7. A. J. deMello, Nature, 2006, 442, 394–402.
8. P. S. Dittrich and A. Manz, Nat. Rev. Drug Discovery, 2006, 5, 210–218.
9. D. Mark, S. Haeberle, G. Roth, F. von Stetten and R. Zengerle, Chem. Soc. Rev., 2010, 39, 1153–1182.
10. G. M. Whitesides, Nature, 2006, 442, 368–373.
11. R. Ren, Z. Wen, S. Cui, Y. Hou, X. Guo and J. Chen, Sci. Rep., 2015, 5, 10714.
12. A. Azam and S. S. Babkair, Int. J. Nanomed., 2014, 9, 2109–2115.
13. R. Zmijan, M. Carboni, L. Capretto, E. Stulz and X. Zhang, RSC Adv., 2014, 4, 14569–14572.
14. S. Mohr, K. Fisher, N. S. Scrutton, N. J. Goddard and P. R. Fielden, Lab Chip, 2010, 10, 1929–1936.
15. J. Halliwell and C. Gwenin, Toxins, 2013, 5, 1381–1391.
16. L. Florea, C. Fay, E. Lahiff, T. Phelan, N. E. O'Connor, B. Corcoran, D. Diamond and F. Benito-Lopez, Lab Chip, 2013, 13, 1079–1085.
17. A. Q. Maclin, M. D. Kim, S. A. Dergunov, E. Pinkhassik and E. Lindner, Electroanalysis, 2015, 27, 733–744.
18. S. deMarcos and O. S. Wolfbeis, Anal. Chim. Acta, 1996, 334, 149–153.
19. Z. F. Ge, C. W. Brown, L. F. Sun and S. C. Yang, Anal. Chem., 1993, 65, 2335–2338.
20. M. Tantama, Y. P. Hung and G. Yellen, J. Am. Chem. Soc., 2011, 133, 10034–10037.
21. K. Hammer, B. Schneider, K. Kulinski and D. E. Schulz-Bull, Estuarine, Coastal Shelf Sci., 2014, 146, 24–32.
22. S. J. Taylor and R. Clemente, J. Hum. Nutr. Diet., 2005, 18, 371–375.
23. R. A. V. Rossel and C. Walter, Geoderma, 2004, 119, 9–20.
24. V. M. Stippl, A. Delgado and T. M. Becker, High Pressure Res., 2002, 22, 757–761.
25. J. R. Anderson, C. Borggaard, A. J. Rasmussen and L. P. Houmoller, Meat Sci., 1999, 53, 135–141.
26. J. C. Hung, J. Nucl. Med., 2002, 43, 1495–1506.
27. B. Kuswandi, Nuriman, J. Huskens and W. Verboom, Anal. Chim. Acta, 2007, 601, 141–155.
28. P. J. Viskari and J. P. Landers, Electrophoresis, 2006, 27, 1797–1810.
29. S. E. Fielder, A. Hese and A. A. Ruth, Rev. Sci. Instrum., 2005, 76, 023107.
30. M. Islam, L. N. Seetohul and Z. Ali, Appl. Spectrosc., 2007, 61, 649–658.
31. S.-S. Kiwanuka, T. Laurila and C. F. Kaminski, Anal. Chem., 2010, 82, 7498–7501.
32. S. R. T. Neil, C. M. Rushworth, C. Vallance and S. R. Mackenzie, Lab Chip, 2011, 11, 3953–3955.
33. L. van der Sneppen, G. Hancock, C. F. Kaminski, T. Laurila, S. R. Mackenzie, S. R. T. Neil, R. Peverall, G. A. D. Ritchie, M. Schnippering and P. R. Unwin, Analyst, 2010, 135, 133–139.
34. C. M. Rushworth, G. Jones, M. Fischlenchner, E. Walton and H. Morgan, Lab Chip, 2014, 15, 711–717.
35. T. Dallas and P. K. Dasgupta, Trends Anal. Chem., 2004, 23, 385–392.
36. A. Datta, I. Y. Eom, A. Dhar, P. Kuban, R. Manor, I. Ahmad, S. Gangopadhyay, T. Dallas, M. Holtz, F. Temkin and P. K. Dasgupta, IEEE Sens. J., 2003, 3, 788–795.
37. M. P. Duggan, T. McCreedy and J. W. Aylott, Analyst, 2003, 128, 1336–1340.
38. C. Gooijer, G. P. Hoornweg, T. de Beer, A. Bader, D. J. van Iperon and U. A. T. Brinkman, J. Chromatogr. A, 1998, 824, 1–5.
39. S. L. Westcott, J. Zhang, R. K. Shelton, N. M. K. Bruce, S. Gupta, S. L. Keen, J. W. Tillman, L. B. Wald, B. N. Strecker, A. T. Rosenberger, R. R. Davidson, W. Chen, K. G. Donovan and J. V. Hryniewicz, Rev. Sci. Instrum., 2008, 79, 033106.
40. A. Nitkowski, A. Baeumner and M. Lipson, Biomed. Opt. Express, 2011, 2, 271–277.
41. A. Nitkowski, L. Chen and M. Lipson, Opt. Express, 2008, 16, 11930–11936.
42. F. Prieto, L. M. Lechuga, A. Calle, A. Llobera and C. Domínguez, J. Lightwave Technol., 2001, 19, 75–83.
43. N. J. Goddard, J. Hulme, C. Malins, K. Singh and P. R. Fielden, Analyst, 2002, 127, 378–382.
44. R. Gupta, B. Bastani, N. J. Goddard and B. Grieve, Analyst, 2013, 138, 307–314.
45. J. Podesva, O. Prochazka and A. Medin, Polymer, 1995, 36, 4967–4970.
46. A. D. Rakić, A. B. Djurišic, J. M. Elazar and M. L. Majewski, Appl. Opt., 1998, 37, 5271–5283.
47. M. Polyanskiy, Refractive index database, http://refractiveindex.info/?shelf=glass&book=BK7&page=SCHOTT, accessed 14th February, 2016.
48. P. B. Johnson and R. W. Christy, Phys. Rev. B: Condens. Matter, 1974, 9, 5056–5070.
49. J. A. Nelder and A. R. Mead, Computer J., 1965, 7, 308–313.
50. S. Mahmoud, J. Mater. Sci., 1987, 22, 3693–3697.
51. S. Boral and H. B. Bohidar, Polymer, 2009, 50, 5585–5588.
52. N. Pernodet, M. Maaloum and B. Tinland, Electrophoresis, 1997, 18, 55–58.
53. M. Maaloum, N. Pernodet and B. Tinland, Electrophoresis, 1998, 19, 1606–1610.
54. J. B. Puschett, B. S. Rao, B. M. Karandikar and K. Matyjaszewski, Talanta, 1991, 38, 335–338.
55. E. Klotz, R. Doyle, E. Gross and B. Mattson, J. Chem. Educ., 2011, 88, 637–639.
56. R. H. Byrne, Anal. Chem., 1987, 59, 1479–1481.
57. G. S. Patterson, J. Chem. Educ., 1999, 76, 395–398.
58. A. Stangelmayer, I. Klimant and O. S. Wolfbeis, Fresenius' J. Anal. Chem., 1998, 362, 73–76.
59. M. Yuqing, C. Jianrong and F. Keming, J. Biochem. Biophys. Methods, 2005, 63, 1–9.
60. W.-D. Huang, H. Cao, S. Deb, M. Chiao and J. C. Chiano, Sens. Actuators, A, 2011, 169, 1–11.

---