Open Access Article
Open Access ArticleRole of micropillar arrays in cell rolling dynamics†
Kisoo
Kim
a,
Junemo
Koo
a,
SangJun
Moon
*b and
Won Gu
Lee
*a
aDepartment of Mechanical Engineering, College of Engineering, Kyung Hee University, Republic of Korea. E-mail: termylee@khu.ac.kr; Fax: +82-31-202-8106; Tel: +82-31-201-3321
bSchool of Mechanical and Nuclear Engineering, Ulsan National Institute of Science and Technology, Republic of Korea. E-mail: nanobiomems@gmail.com
First published on 24th October 2016
Abstract
In this study, we present a role of arrayed micropillar structures in cell rolling dynamics. Cell rolling on a ligand coated surface as a means of cell separation was demonstrated using a micropillar-integrated microfluidic channel. This approach allows the separation of cells according to characteristic surface properties, regardless of cell size. In these experiments, different moving trajectories of the cells between a ligand-coated micropost structure and a 1% BSA coated micropost structure were observed using sequential images. Based on the analysis of the angle of travel of cells in the trajectory, the average angles of travel on the ligand-coated microposts were 1.5° and −3.1° on a 1% BSA-coated micropost structure. The overall force equivalent applied to a cell can be analyzed to predict the cell rolling dynamics when a cell is detached. These results show that it will be possible to design chip geometry for delicate operations and to separate target cells. Furthermore, we believe that these control techniques based on a ligand coated micropillar surface can be used for enhancing cell rolling-based separation in a faster and more continuous manner.
Introduction
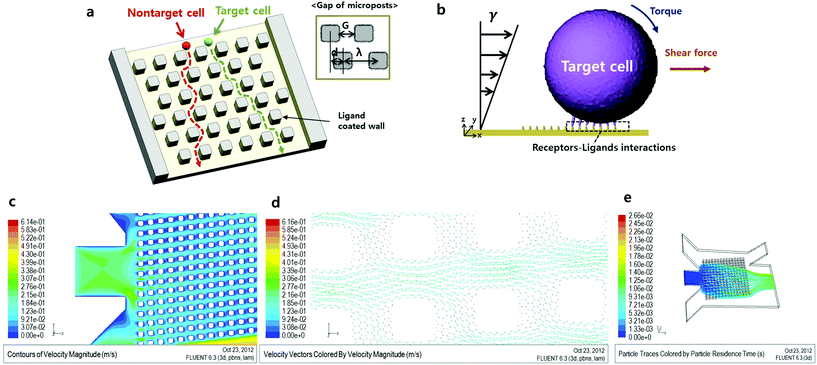
Numerous cell sorting methods have been recently developed for various applications.1–6 These methods use various discriminating parameters, such as fluorescence, cell size and the cell surface properties. However, cell sorting techniques using these parameters have several limitations with respect to cell separation.7 For instance, fluorescence labeling techniques have annoying steps, such as sample preparation steps before the assay and the need to remove labeling materials after the assay. Label-free cell separation methods, like the cell size based technique, do not require these additional steps. However, the cell size based technique has the limitation that it is impossible to separate size-overlapped cells. To overcome these limitations, a novel cell sorting technique based on cell rolling has been developed.8,9 Cell rolling is a characteristic phenomenon that occurs as a result of interactions between surface affinities caused by cell receptor–surface ligand bonding and shear fluid flow. Regardless of the cell size, this approach can separate cells using only characteristic surface properties. Consequently, this approach is useful for discriminating blood cell lines or stem cell lines. Also, many studies using leukocytes,10 CD34+ bone marrow cells11 and mesenchymal stem cells (MSCs)12 have been conducted using this method. However, it is difficult to observe interactions between cells and the ligand-coated wall in previously developed assays. There has been a need to develop methods that are more time efficient by reducing the length of time the cell and the wall interact.In this study, we describe a combinational cell sorting method in which cell trajectories are shifted in a micropillar-integrated microfluidic channel, as shown in Fig. 1a. Based on numerical analysis results of our proposed microfluidic chip, the trajectories of the particles demonstrated that non-target cells do not interact with the microposts, because of the hydrodynamic force exerted on the gap between microposts. Using these design parameters, an analysis of the force of cell rolling was conducted in a microfluidic environment. A microfluidic chip was coated with an HL-60 cell ligand, recombinant human P-selectin, as a positive control and a second device was coated with 1% BSA (bovine serum albumin) as a negative control. We anticipated that the HL-60 cells in the ligand-coated microposts and in the 1% BSA coated microfluidic channel would have different trajectories and we were able to verify this. Also, using sequential images, we analyzed the average trajectory angle of cells and the cell rolling effect in a micropillar array.
Model description
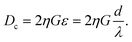 | (1) |
In this formula, η is the variable used to correct the non-uniform profile of the fluid formed by the micropillar. Also, η depends on the spacing factor, ε, and specific η value is acquired using the graph by assuming a parabolic flow profile.14 Based on the formula, Dc has to be greater than 11 μm since the target HL-60 cell which we want to separate has a 10 to 11 μm diameter. However, when the Dc value increases, the target cell will be able to flow along the pathway intended for non-target cells. Consequently, we set an 11 μm for Dc. The G factor, the width between micropillars, was set as twice the target cell diameter, 20 μm, in order to prevent blocking of cells by the micropillar. We then calculated the shift value, ‘d’, between the micropillar array lines. As a result, d was 5 μm when G was 20 μm and, naturally, λ becomes 40 μm.
 | (2) |
When there is a difference in velocity between fluid and a particle, the drag force acts on the particle to decrease it. The drag force is a function of the fluid density, ρ, fluid velocity, 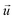 , particle velocity,
, particle velocity, 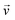 , the frontal area of the particle, A, as well as the drag coefficient CD which depends on the particle Reynolds number, as shown in eqn (3). The particle Reynolds number is defined as
, the frontal area of the particle, A, as well as the drag coefficient CD which depends on the particle Reynolds number, as shown in eqn (3). The particle Reynolds number is defined as 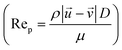 , where D and μ represent the particle diameter and dynamic viscosity of the fluid.
, where D and μ represent the particle diameter and dynamic viscosity of the fluid.
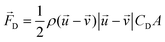 | (3) |
When a particle accelerates in fluid, the fluid accelerated in the opposite direction by reaction. The corresponding force is called the virtual mass force as shown in eqn (4).
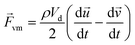 | (4) |
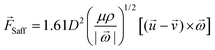 | (5) |
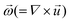 is the rotational velocity vector. The particle could either rise up or sink down depending on the angle between the relative velocity and the rotational velocity vector.
is the rotational velocity vector. The particle could either rise up or sink down depending on the angle between the relative velocity and the rotational velocity vector.
The pressure difference across a particle could arise due to the particle rotation caused by external forces other than the velocity gradient, and the resulting force is called the Magnus lift force as shown in eqn (6).
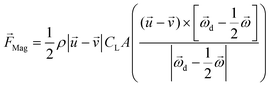 | (6) |
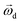 is the rotational velocity vector of the particle, and CL is the lift coefficient due to rotation and is a function of the spin rate defined as
is the rotational velocity vector of the particle, and CL is the lift coefficient due to rotation and is a function of the spin rate defined as 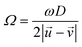 .
.
| Fbinding = f(R,Tc,Ac), | (7) |
| Tc = f(Kc,r,NL,Nm,Am,l), | (8) |
However, the study by Lomakina et al. showed that the cortical tension is predictable using the reaction force from the substrate, Freac.18 The formula is shown below:
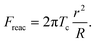 | (9) |
Based on the idea, the shear force which affects a cell rolling can be optimized according to the application. In our model, since the shear force can affect a stream line position of non-target cells, the shear force can be optimized with the angle of the pillar post array. Also, the receptor–ligand binding force affects the efficiency of cell attachment and the displacement of cells. This binding force can be varied dynamically by the deformation of the cell.19 To observe the effect of each parameter, we conducted experiments in a controlled manner of external flow field and cell-post interaction.
Materials and methods
Numerical analysis
Fig. 1c and d show the contour and vector plot of velocity in the microchannel respectively, where the fluid seems to prefer to flow along a slanted direction along the array of posts, and the fluid between posts in the slanted direction tends to flow downwards (+x, −y). To predict an appropriate flow rate for cell rolling on the micropost, three parameters which are shear stress, the location of average velocity and fluid viscosity should be calculated for the flow rate. In a previous study, rolling of a model cell, HL-60, was stably achieved at 2.5 to 3.5 dyne per cm2 shear force on P-selectin coated areas.8 Also, as shown in Fig. 1d, the shape of the fluid profile is roughly parabolic between the microposts. This indicates that the position of average velocity is located about one half and half the gap of the microposts. The velocity of fluid, v, is 0.00138 m s−1 can be calculated with the conditions of three flow parameters where the shear force substitutes 3 dyn cm−2, the position of average velocity is 5 μm, and the fluid viscosity of buffer, μ, is 0.00108 kg m−1 s−1. Multiplication of the velocity and area results in the amount of flow, 0.06624 μL min−1.
Particle pathway analysis using numerical model
The trajectories of non-target cells were calculated using the Lagrangian particle tracking method in Fluent 6.3 assuming one-way coupling between the particle and fluid flow, which presumes that fluid flow affects particle motion but not the other way around. The proposed model reflects the design factor of deterministic lateral displacement, so the effect influenced by the cell may be negligible.Furthermore, the solution was assumed to be dilute so that the effect of collision between particles was neglected. Using the velocity field obtained, the trajectories of particles with 10 μm in diameter and the same density of blood cells, 1058 kg m−3, released at the center port of the inlets were traced as shown in Fig. 1c. The released particles were spread over the array of posts at the expansion of the port, and they moved down (−y) as they crossed the array of posts due to the velocity field profile.
Using the above described conditions, Fig. 1e shows particle trajectories and separation paths. Particles from the inlet spread into the system uniformly and passed by the micropillars. Most of the particles moved in the right lower direction (+x, −y) and exited through the outlet. To confirm the vector of velocity, we observe the direction of fluid flow expressed by the vectors. As shown in Fig. 1e, the vertical space between the micropillars made the fluid flow in the right direction (x-axis), but the fluid went down. Thus, non-target cells followed the direction of the fluid (+x, −y).
Microfluidic chip fabrication
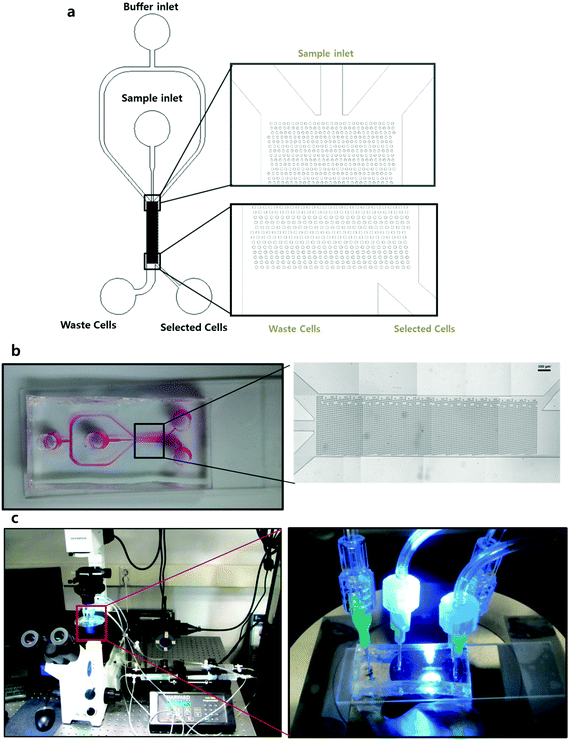
The designed microfluidic chip was constructed with polydimethylsiloxane (PDMS) using a soft lithography method. The computer-aided design (CAD) print was used to make a photo mask as shown in Fig. 2a, and a photo resister coated 4′′ Si wafer was used as a master mold. To fabricate the PDMS chip, the well mixed PDMS soluble material was poured onto the Si wafer and baked in a 90 °C oven for 40 minutes. After the detachment of PDMS, 2 mm diameter holes were punched to make two inlets for the sample and buffer, and two outlets for non-target cells and target cells. The final PDMS chip was attached to a slide glass using an oxidized plasma device. The image of Fig. 2b shows the stitched images obtained using microscopy and the overall scheme of the microfluidic chip. This image demonstrates that at an aspect ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, the micropillars are aligned and configured without bending on the chip.
2, the micropillars are aligned and configured without bending on the chip.
During these processes, a bending phenomenon can occur on the micropillars, as shown in ESI Fig. S2a.† There are two main reasons why bending occurs. First, when the PDMS chip mold is peeled from the Si wafer, the shear force can be exerted on the micropillars. However, this problem can be solved by relocating the structure of the PDMS chip to face upward when cutting a PDMS chip. Second, when a PDMS chip is attached to the slide, pressure is exerted on the micropillar patterned area. For this reason, during the process of sticking the PDMS chip onto the slide, pressure should be applied to the area where the pattern does not exist.
Ligand coating
The target HL-60 cell ligand, recombinant human P-selectin/CD62P, was purchased from R&D Systems (Minnesota, USA). The concentration of P-selectin used was 1.5 μg mL−1, based on previous representative research.8 Also, many studies were successfully conducted in the closed and open systems by using this condition.9,15,20 The P-selectin solution was injected into the completed PDMS chip using an injection pump, and the chip was incubated at room temperature for three hours. After that, the P-selectin injected chip and a negative control group were washed with 1% BSA (bovine serum albumin). When 1% BSA is injected into the chip, the materials suspended in the solution will accumulate at the entrance of the channel inlet as shown in ESI Fig. S2b.† Because the 1% BSA solution contains a number of floating substances, the 1% BSA was filtered through a porous cellulose equipped steric cup to eliminate the materials suspended in the fluid.21 Using this procedure, we were able to minimize the number of floating materials and prevent blockage of the inlet.Cell preparation
Since, the rolling mechanism of HL-60 as a suspension cell line is well-defined in many studies,22–24 we used this cell line for the reliable experiment. The target HL-60 cells (a human WBC cell line) were purchased from the Korean cell line bank (Seoul, Korea). The medium was composed of a mixture of RPMI 1640 (with L-glutamine, 25 mM HEPES), 10% FBS (fetal bovine serum) and 1% penicillin–streptomycin (penicillin–streptomycin, P/S). HL-60 cells were incubated in this medium at 37 °C and in 5% CO2. After three days, cells were divided at a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 ratio. The cell passage number was between 5 and 20. Cells were centrifuged at 1300 rpm (246g) for 5 min, and diluted in DPBS to achieve a cell concentration of between 105 and 106 cells mL−1. The average diameter of HL-60 cells using Image J was 10.678 μm (ESI Fig. S3†).
3 ratio. The cell passage number was between 5 and 20. Cells were centrifuged at 1300 rpm (246g) for 5 min, and diluted in DPBS to achieve a cell concentration of between 105 and 106 cells mL−1. The average diameter of HL-60 cells using Image J was 10.678 μm (ESI Fig. S3†).
Experimental procedure
After ligand coating on the chip and cell preparation, four 20 mL syringes (the buffer and cell loaded syringes, and two empty syringes for the discrimination of the selected and waste cells) were mounted on the PHD2000 injection pump (Harvard Apparatus, USA). Additionally, the ligand coated chip was placed on the observation instruments, which included an IX71 inverted fluorescence microscope (Olympus, Japan) and a CCD camera (Zeiss, Germany), to allow for the observation of cell movement. Subsequently, the fluid flow of cells and the buffer solution were injected at 72 μL min−1 into the chip through the injection pump. A negative control group was also used in an equivalent experiment.Image analysis of the cell rolling pathway
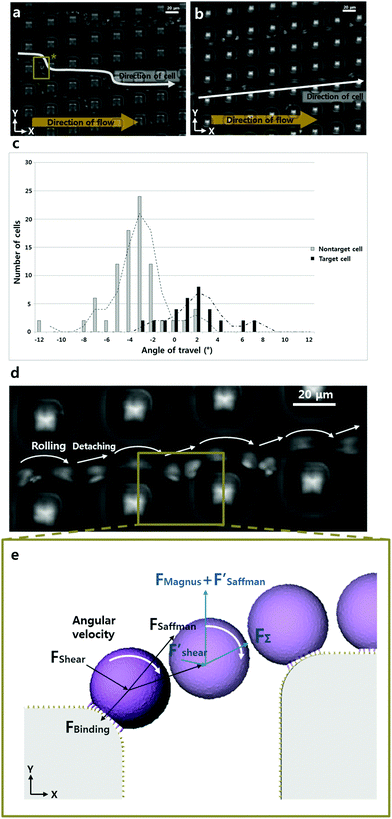
To observe the path of a sample cell, we captured 14 frames over 7 seconds. To acquire the average angle of the cell trajectories, we captured serial pictures with a 0.2 second interval (ESI Fig. S4†). 100 pictures were taken over 20 seconds and analyzed using the MTrack J (Image J) freeware to establish the pathway taken by the cells.Results and discussion
Analytical results on the effect of the arrayed geometry of micropillars on cell rolling and separation
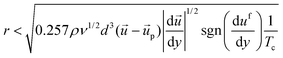 | (10) |
After detachment, a cell is affected by the Magnus lift force according to the angular velocity, Saffman lift force and shear force. Since the influence of the Saffman lift force decreases when a cell is away from the wall, it becomes insignificant. Based on the simulation result shown in Fig. 1d, the direction of the shear force is towards the lower right side (+x, −y) at the location between the micropillars. So, the Magnus lift force and Saffman lift force are together larger than the shear force and the cell moves to the upper right side (+x, +y). We can express the minimum value of the fluid velocity, if we divide the y axis value of the shear force.
| Fshear,y = B·Fshear | (11) |
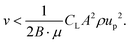 | (12) |
Moreover, through displacement observation of rolling cells in the P-selectin coated microfluidic channel shown in Fig. 3b and d, we identified the velocity of cell rolling as ∼50 μm s−1. This result indicates that this microfluidic chip is more efficient in the speed aspect than in the previous research.9 That is because our method uses a smaller contact length with the cell ligand than the contact length used in other methods.
Conclusions
In summary, we developed a modified cell separation method using the cell rolling effect in a micropillar integrated microfluidic channel. This method is a useful approach to distinguish different cells of the same size using differences in cell surface characteristics. Before performing the experiment, we conducted a simulation to validate the proposed microfluidic chip. By predicting the fluid velocity and the particle path, we found that when a hydrodynamic force was applied the non-target cells moved toward the waste outlet. After coating the device with a ligand or 1% BSA, the HL-60 cell trajectories after injection into the fabricated PDMS chip which has two different surface conditions, revealed that the cell trajectories in the P-selectin coated micropillars and 1% BSA micropillars had different path angles. In particular, in the P-selectin coated microposts, we observed that cells move along the array of micropillars by repeated detachment and attachment to the micropillars. Additionally, we analyzed this phenomenon through the analysis of the forces applied on a single cell. Using this analysis, we obtained the contact length when a cell surface interaction is broken and the minimum value of fluid velocity is required to overcome shear stress at the location between the micropillars. We believe that our proposed design using the cell rolling effect and our analysis will contribute to research on cell manipulation techniques in biology. Furthermore, this model will be potentially useful for biomedical applications such as cell-based therapy, point-of-care testing and cell sorting techniques in research laboratories.Acknowledgements
This study was supported by a grant of the Korean Health Technology R&D Project, Ministry of Health & Welfare, Republic of Korea (HI14C1632, HI15C1027). This research was also supported by the National Research Foundation of Korea (NRF-2016R1A1A1A05005348).Notes and references
- H. Yun, K. Kim and W. G. Lee, Cell manipulation in microfluidics, Biofabrication, 2013, 5(2), 022001 CrossRef PubMed.
- C. W. Shields, C. D. Reyes and G. P. Lopez, Microfluidic cell sorting: a review of the advances in the separation of cells from debulking to rare cell isolation, Lab Chip, 2015, 15(5), 1230–1249 RSC.
- E. L. Jackson and H. Lu, Advances in microfluidic cell separation and manipulation, Curr. Opin. Chem. Eng., 2013, 2(4), 398–404 CrossRef PubMed.
- J. Chen, J. Li and Y. Sun, Microfluidic approaches for cancer cell detection, characterization, and separation, Lab Chip, 2012, 12(10), 1753–1767 RSC.
- P. Sajeesh and A. K. Sen, Particle separation and sorting in microfluidic devices: a review, Microfluid. Nanofluid., 2014, 17(1), 1–52 CrossRef.
- M. Ohlin, et al., Temperature-controlled MPa-pressure ultrasonic cell manipulation in a microfluidic chip, Lab Chip, 2015, 15(16), 3341–3349 RSC.
- W. Zhao, et al., Label-Free Microfluidic Manipulation of Particles and Cells in Magnetic Liquids, Adv. Funct. Mater., 2016, 26(22), 3916–3932 CrossRef.
- S. Choi, J. M. Karp and R. Karnik, Cell sorting by deterministic cell rolling, Lab Chip, 2012, 12(8), 1427–1430 RSC.
- S. Choi, et al., A cell rolling cytometer reveals the correlation between mesenchymal stem cell dynamic adhesion and differentiation state, Lab Chip, 2014, 14(1), 161–166 RSC.
- S. Hong, et al., Covalent immobilization of p-selectin enhances cell rolling, Langmuir, 2007, 23(24), 12261–12268 CrossRef PubMed.
- A. W. Greenberg and D. A. Hammer, Cell separation mediated by differential rolling adhesion, Biotechnol. Bioeng., 2001, 73(2), 111–124 CrossRef PubMed.
- T. Yamaoka and A. Mahara, Cell rolling column in purification and differentiation analysis of stem cells, React. Funct. Polym., 2011, 71(3), 362–366 CrossRef.
- J. A. Davis, et al., Deterministic hydrodynamics: Taking blood apart, Proc. Natl. Acad. Sci. U. S. A., 2006, 103(40), 14779–14784 CrossRef PubMed.
- D. W. Inglis, et al., Critical particle size for fractionation by deterministic lateral displacement, Lab Chip, 2006, 6(5), 655–658 RSC.
- R. Karnik, et al., Nanomechanical control of cell rolling in two dimensions through surface patterning of receptors, Nano Lett., 2008, 8(4), 1153–1158 CrossRef PubMed.
- X. J. Zheng, et al., Cell receptor and surface ligand density effects on dynamic states of adhering circulating tumor cells, Lab Chip, 2011, 11(20), 3431–3439 RSC.
- S. Bose, et al., A Semianalytical Model to Study the Effect of Cortical Tension on Cell Rolling, Biophys. J., 2010, 99(12), 3870–3879 CrossRef PubMed.
- E. B. Lomakina, et al., Rheological analysis and measurement of neutrophil indentation, Biophys. J., 2004, 87(6), 4246–4258 CrossRef PubMed.
- Z. Y. Luo, et al., Two-dimensional numerical study of flow dynamics of a nucleated cell tethered under shear flow, Chem. Eng. Sci., 2014, 119, 236–244 CrossRef.
- C. H. Lee, et al., Examining the lateral displacement of HL60 cells rolling on asymmetric P-selectin patterns, Langmuir, 2011, 27(1), 240–249 CrossRef PubMed.
- X. Cui, et al., A volumetric meter chip for point-of-care quantitative detection of bovine catalase for food safety control, Anal. Chim. Acta, 2016, 935, 207–212 CrossRef PubMed.
- L. Wu, et al., Impact of carrier stiffness and microtopology on two-dimensional kinetics of P-selectin and P-selectin glycoprotein ligand-1 (PSGL-1) interactions, J. Biol. Chem., 2007, 282(13), 9846–9854 CrossRef PubMed.
- W. C. Chang, L. P. Lee and D. Liepmann, Biomimetic technique for adhesion-based collection and separation of cells in a microfluidic channel, Lab Chip, 2005, 5(1), 64–73 RSC.
- C. Dong and X. X. Lei, Biomechanics of cell rolling: shear flow, cell-surface adhesion, and cell deformability, J. Biomech., 2000, 33(1), 35–43 CrossRef PubMed.
- I. Wong and C. M. Ho, Surface molecular property modifications for poly(dimethylsiloxane) (PDMS) based microfluidic devices, Microfluid. Nanofluid., 2009, 7(3), 291–306 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6an01506a |
| This journal is © The Royal Society of Chemistry 2017 |