Stability, electronic structures and thermoelectric properties of binary Zn–Sb materials

Abstract

We report first principles studies of the binary Zn–Sb phases in relation to thermoelectric properties and chemical stability. We identify the unknown structure of the Zn₃Sb₂ phase using particle swarm optimization, finding a tetragonal structure different from the hexagonal Mg₃Sb₂ and the hexagonal or cubic Ca₃Sb₂ phases. All the phases are found to be semiconducting with bandgaps in the range of 0.06–0.77 eV. This semiconducting behavior is understood in Zintl terms as a balance between the Zn : Sb and Sb³⁻ : ½(Sb₂)⁴⁻ ratios in the stable crystal structures. With the exception of Zn₃Sb₂, which has a small gap, all the compounds have electronic properties favorable for thermoelectric performance.

---

1 Introduction

Thermoelectric (TE) devices can directly convert between electrical and thermal energies for cooling or heating or to recover waste heat. These materials have traditionally had an important role in energy conversion, especially portable refrigeration devices, and power generation especially for space crafts.^1–3 They are increasingly seen as having the potential to make important contributions to energy technology more generally^3–5 and have additionally attracted fundamental interest due to the connection with topological insulators and the possibility of new types of thermoelectrics.^5–9 Furthermore there has been interest in transient thermoelectric effects.^10–15 A key challenge for enabling applications is to improve the TE properties of the active materials.

Efficiency plays a central role in energy technology. In the case of TE, this is limited by a figure of merit ZT = σS²T/k, where σ is the electrical conductivity, S is the thermopower, k is the thermal conductivity, and T is the absolute temperature. A good TE material should have excellent electrical transport properties, measured by the TE power factor (PF = S²σ) and also a low thermal conductivity k.

Caillat et al. found a high ZT of 1.3 at 970 K in p-type β-Zn₄Sb₃ in 1997.¹⁶ The high performance combined with the relatively inexpensive, environmentally acceptable composition stimulated considerable interest. Four compounds in the narrow range of 50–60 atomic% of Zn were reported in the binary Zn–Sb phase diagram: ZnSb is a stoichiometric compound with a well characterised crystal structure (CdSb-type)¹⁷ and stable up to 822 K. Zn₄Sb₃ displays temperature dependent polymorphism, with a β–α transition at approximately 250 K.^18,19 Two phases of Zn₈Sb₇ have been reported, α and β.^20,21 Zn₃Sb₂ is metastable and has been reported without any crystal structure solution.²² Interestingly, the experimental values and temperature dependences of S and σ are very similar for ZnSb, β-Zn₄Sb₃ and β-Zn₈Sb₇. What makes the β-phase special is the exceptionally low thermal conductivity, which is as low as that expected for glass-like materials. The presence of the interstitial Zn atoms in the β-phase crystal structures is the key to the low lattice thermal conductivity.^20,23 There have been several studies of electrical and transport properties for β-Zn₄Sb₃, α-Zn₈Sb₇ and ZnSb,^24–32 including first principles studies of the electronic structures of these binaries^26,30–32 and the related Zintl phases SrZn₂Sb₂ and YbZn₂Sb₂. However, the other phases have not been studied in similar detail. Here we report detailed first-principles calculations to establish the electronic structures of Zn–Sb binary system compounds, elucidate the structures and bonding, and to assess their thermoelectric potential.

2 Computational methodology

Full structure optimizations were performed using the projector augmented wave (PAW)³³ method with generalized approximation (GGA) of Perdew–Burke–Ernzerhof (PBE) as implemented in the VASP code.³⁴ Following a series of test calculations a plane-wave cutoff of 360 eV and k-point meshes of spacing 2π × 0.03 Å⁻¹ or better were adopted. In all of the calculations the convergence limit was set to 1 × 10⁻⁴ eV Å⁻¹ for the force and 1 × 10⁻⁵ eV Å⁻¹ for the energy. Standard GGA methods underestimate the band gaps due to the presence of artificial self-interaction and the absence of the derivative discontinuity in the exchange–correlation potential.^35,36 We used the modified Becke Johnson (MBJ)³⁷ potential to obtain more accurate bandgaps and optical properties. This potential generally improves the accuracy of the gap values relative to experiments. For example, the band gaps calculated using MBJ potential for ZnSb and β-Zn₄Sb₃ (0.60 and 0.77 eV, respectively) are much closer to experimental values (0.61 and 0.8 eV^38,39) than PBE values (0.15 and 0.4 eV).

This is important for predicting the thermoelectric properties, as the thermopower in particular can be strongly reduced by spurious bipolar effects from underestimated band gaps. However, the MBJ potential does not have a corresponding energy functional and therefore cannot be used to predict the structures. Therefore we use the PBE functional, which is designed to produce reliable total energies and structures, but not band gaps, to obtain crystal structures, and then do calculations with the MBJ potential to obtain band structures and transport properties. We did not include the spin–orbit coupling (SOC) effect in transport calculations since it shows a negligible effect on the electronic structures of the studied system. The values of the gaps are given in Table 1 along with calculated transport coefficients at 400 K. The available experimental and calculated data are listed for comparison. The transport coefficients are discussed for each compound in the sections below.

Table 1 Calculated indirect and direct bandgaps E_g (in eV), as well as thermopowers S (in μV K⁻¹) and power factor divided by scattering time σS²/τ (in 10¹⁰ W K⁻² ms) at a temperature of 400 K and a carrier concentration of 10²⁰ cm⁻³. The available experimental (Exp.) and calculated (Cal.) results are listed for comparison; for S, the data for comparison are: ZnSb at a carrier concentration of 0.75 × 10²⁰ cm⁻³ at a temperature of 400 K from ref. 29, and 1 × 10²⁰ cm⁻³ at 600 K from ref. 31; β-Zn₄Sb₃ at 4.9 × 10²⁰ cm⁻³ at 400 K from ref. 29, and 0.75 × 10²⁰ cm⁻³ at 400 K from ref. 26; α-Zn₈Sb₇ at 4.7 × 10²⁰ cm⁻³ at 400 K from ref. 29

Compound	E g (indirect)	E g (direct)	S (400 K, 10^20 cm^−3)	σS ^2/τ (400 K, 10^20 cm^−3)
ZnSb	0.60	0.88	98	7.3
	0.61(Exp.)^38		90(Cal.)^29
	0.56(Cal.)^31		135(Cal.)^31
α-Zn4Sb3	0.68	0.77	205	14.5
	0.77		161
β-Zn4Sb3	0.8(Exp.)^39	0.81	110(Cal.)^29	15.9
	0.3(Cal.)^30		180(Cal.)^26
α-Zn8Sb7	0.71	0.76	164	7.5
			142(Cal.)^29
β-Zn8Sb7	0.61	0.61	129	8.1
Zn3Sb2	0.06	0.1	109	6.9

---

In order to demonstrate the validity of using the MBJ potential, we calculate the optical spectra shown in Fig. 1. The onset of absorption is at 0.85 eV. The experimental onset of strong absorption transition is at approximately 1.05 eV. We find noticeable anisotropy in the optical absorption, very close to the onset. It shows significantly stronger absorption for polarization along c, in accord with the experiment.³⁸ We predict that this anisotropy switches at higher energy so that the strongest absorption is for polarization along a in the range 2–4 eV.

Fig. 1 Optical spectra of ZnSb calculated by using the MBJ functional.

The transport calculations were done using the BoltzTraP program.⁴⁰ We used approximately 5000 k-points in the irreducible Brillouin Zone, with the constant relaxation time approximation. The necessary crystal structure and eigen-energies were obtained from VASP results by using MBJ potential. This approach uses a rigid band approximation. This is generally valid for semiconductors that have good conductivity when doped, as is the case for the Zn–Sb phases (note that strong band distortion upon doping is indicative of strong electronic scattering by dopants). It is also consistent with spectroscopic measurements for some of these phases in relation to prior density functional calculations.^30–32 Going beyond the rigid band approximation would require knowledge of the specific doping elements and defects that occur in actual samples.

Previous studies on the phase diagram of the zinc-antimony system have reported compound Zn₃Sb₂.^41,42 But it is metastable and crystals amorphize over time, which impedes its structure and property characterization. We performed a crystal structure prediction for Zn₃Sb₂via global minimization of free energy surfaces as implemented in the CALYPSO code, which searches for the stable structures of the given compounds. Using particle swarm optimization (PSO) the most stable structures based on the chemical composition can be found. Importantly, this approach is unbiased by already known structures.^43,44 In this sense it differs from approaches such as those used in most materials genome projects, for example, the materials project,⁴⁵ where known structures and structure types are generally relied upon. The advantage of the PSO approach is that it can find structures that were previously unknown, while on the other hand it requires calculations for many structures during the global optimization. Structure searching was performed at zero pressure with simulation cells consisting of 1–4 formula units (f.u.). This global optimization involved density functional relaxations of approximately 1500 distinct structures to find the ground state. The most stable predicted structure was then further optimized using VASP as described above. This calculation adds the structure and energy of Zn₃Sb₂ to the phase diagram.

3 Structure and phase diagram

We consider all Zn–Sb binary materials for which structures have been reported and Zn₃Sb₂ with a predicted structure. Orthorhombic ZnSb (space group Pbac) was reported in 1948.¹⁷ It may be regarded as an arrangement of Zn centered, vertex and corner sharing Sb₄ tetrahedra (quasitetrahedral close-packing), as shown in Fig. 2a. The formal valence state of Sb is −2, and it has the appearance of a classical Zintl phase with Sb present as (Sb₂)⁴⁻ dimers. The ZnSb₄ tetrahedra are linked by Sb–Sb bonds. We note that such Sb–Sb dumbbells have been implicated in the low thermal conductivity of the Zn₄Sb₃ phase.⁴⁶

Fig. 2 Crystal structure of (a) ZnSb, (b) predicted Zn₃Sb₂ structure with CALYPSO, (c) α-Zn₄Sb₃, (d) β-Zn₄Sb₃, Zn2, Zn3, and Zn4 are interstitial atoms, (e) α-Zn₈Sb₇, (f) β-Zn₈Sb₇, Zn8, Zn10 are interstitial atoms.

The low temperature α-phase and high temperature β-phase of Zn₄Sb₃ were considered in this work. The unit cell of β-Zn₄Sb₃ is rhombohedral (space group R3̄C) and contains three distinct atomic positions (36 Zn, 18 Sb1, and 12 Sb2 amounting to a Zn_3.6Sb₃ stoichiometry). The atoms on the Sb1 site are free Sb³⁻ while those on the Sb2 site form (Sb₂)⁴⁻ dimers, according to the Zintl-Klemm concept.⁴⁷ The problem posed by apparent deviation from the nominal composition was solved by Snyder et al.²³ They found a high degree of disorder in the Zn substructure of β-Zn₄Sb₃, and in particular interstitial Zn atoms distributed on three partially occupied general sites in space group R3̄C (36f). Additionally, the regular framework position (also 36f) displayed a considerable occupational deficiency with only 0.89–0.9 of the sites filled. Based on this, the framework of β-Zn₄Sb₃ for our calculations was constructed in the following way:^48,49 first, a rhombohedral primitive cell was built with full occupancy of Zn1, Sb1 and Sb2 sites resulting in the Zn₁₂Sb₁₀ stoichiometry. Then we removed two Zn atoms from the main site (Zn1) and inserted three different Zn interstitials in the Zn2, Zn3 and Zn4 sites, respectively, while maximizing the distance between interstitial atoms to minimize the total energy.²⁵ We considered all the possible configurations and chose the lowest total energy one. The final structure is shown in Fig. 2d. Below about 250 K β-Zn₄Sb₃ transforms into α-Zn₄Sb₃, which somewhat surprisingly has a completely ordered structure with a crystallographic composition of Zn₁₃Sb₁₀ for fully occupied sites.¹⁹ The structure of α-Zn₄Sb₃ is triclinic, but is often described with a C-centred cell (i.e. C1̄). Here, the interstitial Zn atoms are located on two fully occupied sites, and the main Zn site is also fully occupied (Fig. 2c).¹⁸

β-Zn₈Sb₇ is a new metastable compound whose synthesis was reported in 2015.²⁰ It crystallizes in a noncentrosymmetric orthorhombic space group Pmn21. Twenty-four Zn atoms are distributed over 6 fully occupied crystallographic sites, while the remaining 8 Zn atoms are distributed over 4 sites with partial occupancies. It contains 10 (Sb₂)⁴⁻ dumbbells and 8 isolated Sb³⁻ anions, which is similar to Zn₁₃Sb₁₀. Each Zn atom is surrounded by distorted tetrahedra with sharing of common edges. The distances of the reported Zn7–Zn8 and Zn9–Zn10 sites are in the range of 1.2–1.4 Å. This indicates that only one of two possible Zn atoms is present. Thus, we use one Zn8 atom to replace the nearest Zn7 atom, similarly for Zn9 and Zn10. The final crystal structure with the lowest total energy is shown in Fig. 2f. The α-Zn₈Sb₇ phase was reported as Zn_1+δSb (with δ = 0.068) with a space group P1̄.²¹ It has an ordered structure with an ideal stoichiometry of Zn₈Sb₇ and few Zn defects in it. We adopt its ideal full occupancy structure in our calculation (Fig. 2e).

We performed variable-cell prediction simulations using the PSO methodology for Zn₃Sb₂ at 0 GPa. The lowest energy structure was chosen, as shown in Fig. 2b. Its crystal structure is tetragonal (space group P4̄21m, Z = 2), with lattice parameters a = 7.090 Å and c = 4.777 Å. Sb occupies the 4e (1.134, 0.634, 0.738) sites, while Zn atoms are at the 4e sites (1.134, 0.634, 0.738) and 2d sites (0, 0, 0.5). All Sb in this structure are isolated Sb³⁻ anions, with no bonds between Sb atoms. We note that this structure differs from the hexagonal and cubic structures of Mg₃Sb₂ and Ca₃Sb₂. Each Sb atom is exclusively surrounded by six Zn atoms (at distances between 2.65 and 2.82 Å, similar to the known structures for β-Zn₄Sb₃ 2.7–2.8 Å, for α-Zn₄Sb₃ 2.67–2.75 Å, for β-Zn₈Sb₇ 2.64–2.87 Å, and 2.56–2.92 Å for the α-Zn₈Sb₇ phase). Each ZnSb₄ tetrahedron shares a common Sb atom with another five tetrahedra.

It is perhaps surprising that Zn₃Sb₂ has a different structure than hexagonal Mg₃Sb₂. However, we note that the electronegativity of Zn is significantly higher than Mg, which suggests chemical differences. We carefully checked the result by performing all-electron calculations for Zn₃Sb₂ in the fully relaxed Mg₃Sb₂ structure and our predicted tetragonal ground state structure. These calculations were done using the general potential linearized augmented planewave (LAPW) method⁵⁰ as implemented in the WIEN2k code.⁵¹ We used highly converged basis sets based on the accurate LAPW augmentation, plus local orbitals to treat semicore states. We added additional local orbitals to improve the accuracy for the Zn d state.⁵² Spin–orbit was included in these calculations. We find that our predicted tetragonal structure is lower in energy by 0.25 eV per formula unit. This means that the tetragonal structure is strongly preferred over the Mg₃Sb₂ structure for Zn₃Sb₂.

We calculated the formation energy with respect to the elements for six configurations. As plotted in Fig. 3, the formation enthalpies of all the configurations are negative. In order to analyze phase stability at 0 K, we constructed the convex hull of formation enthalpy, as illustrated by the solid lines in Fig. 3. Here we included the SOC effect. ZnSb is the most stable system with a formation energy of approximately 27 meV per atom. The data shown for the interstitial β-phase structures are for the lowest formation energy structure out of all those that we built. A structure whose formation enthalpy lies above the convex hull, which can be considered as a global stability line, is metastable or unstable. The formation enthalpies of Zn₄Sb₃, Zn₈Sb₇ and Zn₃Sb₂ are above the convex hull. As expected, the interstitial frameworks of β-phases are less stable than those of the ordered α-phases, but they still have a negative energy of formation (4.5 meV per atom for β-Zn₄Sb₃, 6 meV per atom for β-Zn₈Sb₇). Surprisingly the α-phase is unstable with respect to the decomposition into ZnSb and Zn.^21,53 The predicted structure of Zn₃Sb₂ has a little lower formation enthalpy (8 meV per atom). Without the SOC the formation energies are a little lower. But this does not change the stability situation for the Zn–Sb binary system.

Fig. 3 Calculated enthalpy of formation as a function of Zn concentration.

4 Electronic and transport properties

The calculated band structures and total and projected density of states (DOS) obtained with MBJ potential are shown in Fig. 4–9a. The Fermi levels are set to the top of the valence band. The results show that the MBJ method performs consistently better than PBE-GGA and produces band gaps that are in excellent agreement with the experimental values. This is in accord with prior results for other non-d-electron semiconductors.^54,55 All the band structures shown are indirect band gap except β-Zn₈Sb₇. The PDOS show that the valence bands are formed from Zn p, Sb s, and Sb p hybridized states. The conduction band is characterized mainly by 4s-electrons of zinc which are hybridized with 5p-electrons of antimony. The total density of states show a similar shape and magnitude of the valence band edges of Zn₄Sb₃ and Zn₈Sb₇, which suggests a similar hole carrier effective mass and similar electronic properties. It is remarkable that in spite of the different Zn–Sb ratios and crystal structures, all these compounds show similar electronic structures. This is an example of the robustness of the Zintl concept for the Zn–Sb system, specifically the balance between the Zn : Sb and the Sb³⁻ : ½(Sb₂)⁴⁻ ratios.

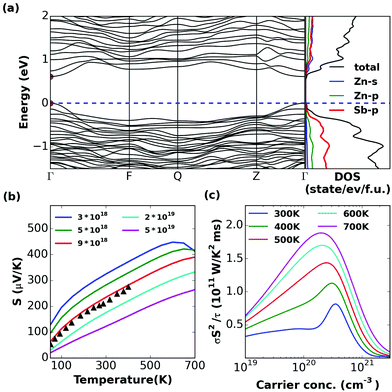
Fig. 4 Calculated (a) band structure and (partial) density of states, (b) thermopower (S) versus temperature at different carrier concentrations (with different colorful lines), and (c) power factor divided by scattering time (σS²/τ) versus carrier concentration at different temperatures (with different colorful lines) for ZnSb. In (a) the band edges are marked by red circles and in (b) experimental values (ref. 56) are shown with triangles for comparison.

Fig. 5 Calculated (a) band structure and (partial) density of states, (b) S and (c) σS²/τ of α-Zn₄Sb₃. Experimental values reported in ref. 57 are shown with triangles for comparison.

Fig. 6 Calculated (a) band structure and (partial) density of states, (b) S (c) σS²/τ of β-Zn₄Sb₃. Experimental values reported in ref. 16 are plotted with triangles.

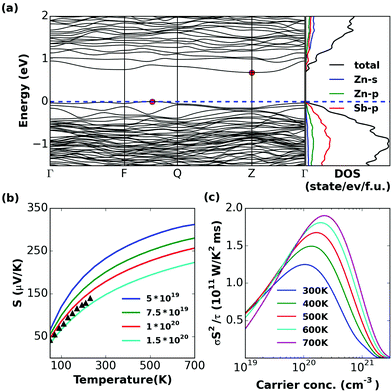
Fig. 7 Calculated (a) band structure and (partial) density of states, (b) S and (c) σS²/τ of α-Zn₈Sb₇.

Fig. 8 Calculated (a) band structure and (partial) density of state, (b) S (c) σS²/τ of β-Zn₈Sb₇. Experimental values reported in ref. 20 are shown with triangles for comparison.

Fig. 9 Calculated (a) band structure and (partial) density of states, (b) S and (c) σS²/τ of Zn₃Sb₂.

Here we focus on the p-type, since experimentally all these compounds form as the p-type. We performed calculations of the thermopower as a function of temperature and the p-type doping level with Boltzmann theory in the CSTA with rigid bands. We also show S²σ/τ as a function of carrier concentration at different temperatures. This is the power factor divided by the scattering time, τ, which is an undetermined parameter that can depend on both doping and temperature. Generally τ decreases with both temperature and carrier concentration, though the carrier concentration dependence is often weaker than the τ dependence. The validity of these approaches can be established by studying the agreement between theoretical results and experimental data shown in Fig. 4–6 and 8 and is discussed further in the text.

ZnSb

The valence bands are nearly parabolic at the band edge. We show the thermopower of ZnSb at carrier concentrations (10¹⁸–10¹⁹ cm⁻³), which are in general accord with experimental data⁵⁶ although the experimental carrier concentration needs to be established in order to determine how close the accord is (Fig. 4b). It should be noted that in ZnSb it has been proven that it is difficult to achieve hole concentrations above 10¹⁹ cm⁻³. The peak σS²/τ lies in the range of 1 × 10²⁰ to 4 × 10²⁰ cm⁻³ (Fig. 4c). It is highly likely that ZT for ZnSb can be significantly increased if the carrier concentration can be increased.

Zn₄Sb₃

At the edge of the valence bands, we find heavier bands for the α phase than the β phase, resulting in higher DOS near the VBM (Fig. 5 and 6a), which should lead to a little larger thermopower in p-type materials. They display similar band gap E_g = 0.68 and 0.77 eV, respectively. The latter agrees well with the experimental value E_g = 0.8 eV³⁹ for the β phase. The thermopower value of the α phase is indeed a little higher than the β phase in our calculation (Fig. 5 and 6b). Experimental measurements of S for α-Zn₄Sb₃ are only available for temperatures below 250 K.⁵⁷ One can see that our interstitial structures can get thermopowers in accord with the experiment again with the caveat of the carrier concentration.¹⁶ The doping level at 300–700 K corresponding to the peak σS²/τ lies in the range of 1 × 10²⁰ to 4 × 10²⁰ cm⁻³ for the α phase and 2 × 10²⁰ to 9 × 10²⁰ cm⁻³ for the β phase (Fig. 5 and 6c), again implying that the peak ZT is likely to be at high carrier concentration.

Zn₈Sb₇

The band structure of α-Zn₈Sb₇ shows that it is an indirect band gap semiconductor, with E_g = 0.71 eV. Disordered β-Zn₈Sb₇ has a direct band gap, with E_g = 0.61 eV. They have very similar transport properties. The doping level at 300–700 K corresponding to the peak σS²/τ lies in the range of 1 × 10²⁰ to 4 × 10²⁰ cm⁻³ for both α and β phases (Fig. 7 and 8c). It was found that the thermopower values of the disordered β-phase and the ordered α-phase of Zn₄Sb₃ and Zn₈Sb₇ were very similar. Hence, the key to the outstanding thermoelectric properties of the β-phase lies in the exceptionally low thermal conductivity, which is as low as that for glass-like materials combined with its favorable electronic properties.

Zn₃Sb₂

A narrow band gap of 0.06 eV separates the valence states to the conduction states. The electronic structure of Zn₃Sb₂ exhibits the charge carrier pockets with light bands near the VBM and CBM, which leads to low thermopower. As predicted the light band at the edge of bands indeed leads to a low thermopower for Zn₃Sb₂ (Fig. 9b). The very small gap suggests that this phase will not be a good thermoelectric at least at room temperature and above. This is also seen in the thermopower, which shows strong bipolar effects.

5 Conclusions

The β-phases of Zn₈Sb₇ and Zn₄Sb₃ have complex crystal structures. These structures challenge crystallography because of the presence of site disorder for the Zn atoms. In this work, we have proposed structural models of β-phases, which are close to experimental studies. All binary Zn/Sb compounds are narrow-gap semiconductors. We have analysed the phase stability, electronic structure, optical property of ZnSb and transport properties by means of first principles density functional theory and Boltzmann transport calculations. Additionally, we have searched for the Zn₃Sb₂ structure using the PSO method. This yields a structure different from the hexagonal structure of Mg₃Sb₂, reflecting the different chemistries of Zn and Mg. In terms of the formation energy, this phase is comparable to Zn₈Sb₇ and Zn₄Sb₃. In thermodynamic stability analysis, they are all metastable phases.

A similar shape and magnitude of the total density of states in the valence band edge of Zn₄Sb₃ and Zn₈Sb₇ lead to similar thermopower values. The thermopower data and transport properties from our calculations show that Zn₃Sb₂ should not be a good candidate for thermoelectric materials at room temperature and above. The existing experimental results show the best performance for β-Zn₄Sb₃. This material has a reasonable band gap, shows multiple valence bands sufficiently near the band edge to influence the thermoelectric behavior and importantly has a low thermal conductivity characteristic of the β-phases. However, our results also show that there is still room for improvement in ZT of the β phases by optimization of carrier concentration. A comparison of the compounds in terms of the balance between σ/τ and S at 400 K and a carrier concentration of 10¹⁹ cm⁻³ as well as the doping dependence of S is given in Fig. 10.

Fig. 10 (a) Electrical conductivity divided by scattering time (σ/τ) versus thermopower (S) calculated at a temperature of 400 K and a carrier concentration of 10¹⁹ cm⁻³, and (b) thermopower versus carrier concentration calculated at a temperature of 400 K for different phases of the Zn–Sb materials. In (b) the available experimental and calculated data from the previous work by Pomrehn et al. (ref. 29), Toberer et al. (ref. 57), Caillat et al. (ref. 16), and Wang et al. (ref. 20) are shown for comparison; for the scatters, consistent colors with those of lines are used for the same phases.

Finally it is interesting to note that although some gaps are small, all the compounds are semiconducting. This is a reflection of the Zintl concept in those phases, especially the balance between the Zn : Sb and Sb³⁻ : ½(Sb₂)⁴⁻ ratios reflecting stabilization or destabilization of (Sb₂)⁴⁻ polyanions according to the amount of charge available from the Zn²⁺cations. We note that several of these phases are underdoped for thermoelectric performance. The flexibility of these compounds in terms of carrier compensation via the Sb³⁻ : ½(Sb₂)⁴⁻ ratio poses a challenge for achieving the optimum doping level. The solution to this problem may lead to significantly better ZT in the Zn–Sb phases.

Acknowledgements

The authors acknowledge funding support from the Recruitment Program of Global Youth Experts in China and special funds for talent development in Jilin Province. Part of calculations was performed in the high performance computing center of Jilin University. Work of D. J. S is supported by S3TEC an Energy Frontier Research Center funded by the Department of Energy, Office of Science, Basic Energy Sciences under award DE-SC0001299/DE-FG02-09ER46577.

References

1. H. J. Goldsmid and R. W. Douglas, Br. J. Appl. Phys., 1954, 5, 386–390.
2. C. Wood, Rep. Prog. Phys., 1988, 51, 459–540.
3. L. E. Bell, Science, 2008, 321, 1457–1461.
4. G. Chen, M. S. Dresselhaus, G. Dresselhaus, J.-P. Fleurial and T. Caillat, Int. Mater. Rev., 2003, 48, 45–66.
5. J. Yang, L. Xi, L. Wu, X. Shi, L. Chen, J. Yang, W. Zhang, C. Uher and D. J. Singh, NPJ Comput. Mater., 2016, 2, 15015.
6. L. Muchler, F. Casper, B. Yan, S. Chadov and C. Felser, Phys. Status Solidi RRL, 2012, 7, 91–100.
7. H. Shi, D. Parker, M. H. Du and D. J. Singh, Phys. Rev. Appl., 2015, 3, 014004.
8. Y. Xu, Z. Gan and S. C. Zhang, Phys. Rev. Lett., 2014, 112, 226801.
9. G. Xing, J. Sun, K. P. Ong, X. Fan, W. Zheng and D. J. Singh, APL Mater., 2016, 4, 053201.
10. M. Sasaki, H. Negishi and M. Inoui, J. Appl. Phys., 1986, 59, 796–802.
11. S. Walia, R. Weber, S. Sriram, M. Bhaskaran, K. Latham, S. Zhuiykov and K. Kalantar-Zadeh, Energy Environ. Sci., 2011, 4, 3558–3564.
12. S. Walia, R. Weber, S. Balendhran, D. Yao, J. T. Abrahamson, S. Zhuiykov, M. Bhaskaran, S. Sriram, M. S. Strano and K. Kalantar-Zadeh, Chem. Commun., 2012, 48, 7462–7464.
13. S. Walia, S. Balendhran, P. Yi, D. Yao, S. Zhuiykov, M. Pannirselvam, R. Weber, M. S. Strano, M. Bhaskaran, S. Sriram and K. Kalantar-Zadeh, J. Phys. Chem. C, 2013, 117, 9137–9142.
14. S. Walia, R. Weber, K. Latham, P. Petersen, J. T. Abrahamson, M. S. Strano and K. Kalantar-Zadeh, Adv. Funct. Mater., 2011, 21, 2072–2079.
15. S. Walia, S. Balenhran, H. Nili, S. Zhuiykov, G. Rosengarten, Q. H. Wang, M. Bhaskaran, S. Sriram, M. S. Strano and K. Kalantar-Zadeh, Prog. Mater. Sci., 2013, 50, 1443–1489.
16. T. Caillat, J.-P. Fleurial and A. Borshchevsky, J. Phys. Chem. Solids, 1997, 58, 1119–1125.
17. K. E. Almin, Acta Chem. Scand., 1948, 2, 400–407.
18. Y. Mozharivskyj, Y. Janssen, J. L. Harringa, A. Kracher, A. O. Tsokol and G. J. Miller, Chem. Mater., 2006, 18, 822–831.
19. J. Nylén, M. Andersson, S. Lidin and U. Häussermann, J. Am. Chem. Soc., 2004, 126, 16306–16307.
20. J. Wang and K. Kovnir, J. Am. Chem. Soc., 2015, 137, 12474–12477.
21. C. S. Birkel, E. Mugnaioli, T. Gorelik, U. Kolb, M. Panthöfer and W. Tremel, J. Am. Chem. Soc., 2010, 132, 9881–9889.
22. F. Adjadj, E.-d. Belbacha, M. Bouharkat and A. Kerboub, J. Alloys Compd., 2006, 419, 267–270.
23. G. J. Snyder, M. Christensen, E. Nishibori, T. Caillat and B. B. Iversen, Nat. Mater., 2004, 3, 458–463.
24. P. H. M. Böttger, S. Diplas, E. Flage-Larsen, Ø. Prytz and T. G. Finstad, J. Phys.: Condens. Matter, 2011, 23, 265502.
25. F. Cargnoni, E. Nishibori, P. Rabiller, L. Bertini, G. J. Snyder, M. Christensen, C. Gatti and B. B. Iversen, Chem. – Eur. J., 2004, 10, 3861–3870.
26. S.-G. Kim, I. I. Mazin and D. J. Singh, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 6199–6203.
27. S. Wang, H. Li, D. Qi, W. Xie and X. Tang, Acta Mater., 2011, 59, 4805–4817.
28. U. Häussermann and A. S. Mikhaylushkin, Dalton Trans., 2010, 39, 1036–1045.
29. G. S. Pomrehn, E. S. Toberer, G. J. Snyder and A. van de Walle, J. Am. Chem. Soc., 2011, 133, 11255–11261.
30. A. N. Qiu, L. T. Zhang and J. S. Wu, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 035203.
31. K. Niedziolka, R. Pothin, F. Rouessac, R. M. Ayral and P. Jund, J. Phys.: Condens. Matter, 2014, 26, 365401.
32. P. H. M. Bottger, S. Diplas, E. Flage-Larsen, O. Prytz and T. G. Finstad, J. Phys.: Condens. Matter, 2011, 23, 265502.
33. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
34. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
35. J. P. Perdew and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048–5079.
36. L. Sham and M. Schlüter, Phys. Rev. Lett., 1983, 51, 1888–1891.
37. F. Tran and P. Blaha, Phys. Rev. Lett., 2009, 102, 226401.
38. H. Komiya, K. Masumoto and H. Fan, Phys. Rev., 1964, 133, A1679–A1684.
39. M. Vaida, N. Duteanu and I. Grozescu, J. Serb. Chem. Soc., 2016, 81, 323–332.
40. G. K. Madsen and D. J. Singh, Comput. Phys. Commun., 2006, 175, 67–71.
41. B. DeWitt and H. Seltz, J. Am. Chem. Soc., 1939, 61, 3170–3173.
42. M. Boström and S. Lidin, J. Alloys Compd., 2004, 376, 49–57.
43. Y. Wang, J. Lv, L. Zhu and Y. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 094116.
44. Y. Wang, J. Lv, L. Zhu and Y. Ma, Comput. Phys. Commun., 2012, 183, 2063–2070.
45. A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002.
46. W. Schweika, R. P. Hermann, M. Prager, J. Person and V. Keppens, Phys. Rev. Lett., 2007, 99, 125501.
47. G. A. Papoian and R. Hoffmann, Angew. Chem., Int. Ed., 2000, 39, 2408–2448.
48. E. Toberer, K. Sasaki, C. Chisholm, S. Haile, W. Goddard and G. Snyder, Phys. Status Solidi RRL, 2007, 1, 253–255.
49. S. Wang, X. Tan, G. Tan, X. She, W. Liu, H. Li, H. Liu and X. Tang, J. Mater. Chem., 2012, 22, 13977–13985.
50. D. J. Singh and L. Nordstrom, Planewaves Pseudopotentials and the LAPW Method, Springer, Berlin, 2nd edn, 2006.
51. P. Blaha, K. Schwarz, G. Madsen, D. Kvasnicka and J. Luitz, in WIEN2k, An Augmented Plane Wave+Local Orbitals Program for Calculating Crystal Properties, K. Schwarz, Tech. Univ. Wien, Austria, 2001.
52. D. Singh, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 6388–6392.
53. A. S. Mikhaylushkin, J. Nylén and U. Häussermann, Chem. – Eur. J., 2005, 11, 4912–4920.
54. D. J. Singh, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 205102.
55. D. Koller, F. Tran and P. Blaha, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195134.
56. D. Eklöf, A. Fischer, Y. Wu, E.-W. Scheidt, W. Scherer and U. Häussermann, J. Mater. Chem. A, 2013, 1, 1407–1414.
57. T. Souma, G. Nakamoto and M. Kurisu, J. Alloys Compd., 2002, 340, 275–280.

---