Open Access Article
Open Access ArticleGold nanoparticle superlattices: correlating chemiresistive responses with analyte sorption and swelling†
Natalia
Olichwer
,
Andreas
Meyer
,
Mazlum
Yesilmen
and
Tobias
Vossmeyer
*
Institute of Physical Chemistry, University of Hamburg, Grindelallee 117, 20146 Hamburg, Germany. E-mail: tobias.vossmeyer@chemie.uni-hamburg.de
First published on 10th August 2016
Abstract
Chemiresistive and in situ GISAXS (grazing-incidence small-angle X-ray scattering) measurements were performed simultaneously on superlattices self-assembled from 1-dodecanethiol (DDT)-stabilized gold nanoparticles (GNPs, 4 nm). When dosed with vapors (1000–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm) of toluene, 4-methyl-2-pentanone and 1-propanol, the GNP superlattice films responded with reversible increases in both the interparticle distance and resistance. Additionally, the mass uptake due to analyte sorption was determined microgravimetrically. Comparing the partition coefficients, chemiresistive sensitivities and GISAXS-measured swelling for the three solvent vapors revealed the same trends, which were consistent with the solubility match between DDT and the analyte. GISAXS-measured swelling and swelling deduced from microgravimetry showed remarkable agreement for 4-methyl-2-pentanone and toluene, whereas only a fraction of sorbed 1-propanol induced swelling. This suggests that due to the poor affinity of 1-propanol to DDT a significant amount deposited unselectively on the films' surface or within voids, where it is ineffective for swelling. The experimentally obtained data for analyte sorption and swelling were used to calculate the responses according to the commonly used chemiresistor model based on thermally activated charge transport. The comparison between calculated and measured responses demonstrated that the model can predict the chemiresistive responses to the analytes only qualitatively, i.e. with a precision of one order of magnitude and for 1-propanol with reversed direction. To enable a deeper understanding of the sensing mechanism and more precise predictions of the sensor characteristics, investigations into the microporosity of the assemblies and permittivity changes of the organic medium during analyte sorption are recommended as next experimental steps.
000 ppm) of toluene, 4-methyl-2-pentanone and 1-propanol, the GNP superlattice films responded with reversible increases in both the interparticle distance and resistance. Additionally, the mass uptake due to analyte sorption was determined microgravimetrically. Comparing the partition coefficients, chemiresistive sensitivities and GISAXS-measured swelling for the three solvent vapors revealed the same trends, which were consistent with the solubility match between DDT and the analyte. GISAXS-measured swelling and swelling deduced from microgravimetry showed remarkable agreement for 4-methyl-2-pentanone and toluene, whereas only a fraction of sorbed 1-propanol induced swelling. This suggests that due to the poor affinity of 1-propanol to DDT a significant amount deposited unselectively on the films' surface or within voids, where it is ineffective for swelling. The experimentally obtained data for analyte sorption and swelling were used to calculate the responses according to the commonly used chemiresistor model based on thermally activated charge transport. The comparison between calculated and measured responses demonstrated that the model can predict the chemiresistive responses to the analytes only qualitatively, i.e. with a precision of one order of magnitude and for 1-propanol with reversed direction. To enable a deeper understanding of the sensing mechanism and more precise predictions of the sensor characteristics, investigations into the microporosity of the assemblies and permittivity changes of the organic medium during analyte sorption are recommended as next experimental steps.
Introduction
Since Wohltjen and Snow1 demonstrated the first chemiresistors based on assemblies of ligand-stabilized gold nanoparticles (GNPs) in 1998, numerous studies reported on the chemiresistive properties and applications of a variety of nanoparticle based composites.2 These materials differ for example in the metal,3–6 shape7 and size8–11 of the particle core as well as the length5,12,13 and chemical nature of the ligands. Most commonly used ligands include simple or functionalized aliphatic or aromatic thiols8,14–19 and dithiols.11,13,20,21 Many studies emphasized the tunability of chemical selectivity by varying the ligands' structural parameters, which is a great advantage of such sensors. Along with other intriguing characteristics such as high sensitivity, fast and reversible responses, low detection limits and low power consumption GNP-based chemiresistors are promising candidates for advanced applications in environmental monitoring,22–25 personnel security26–28 and biomedical diagnostics.29–31While target specific optimization progresses rapidly, the underlying sensing mechanism still remains only vaguely understood. For discussing the response characteristics most studies take into consideration a sensing mechanism based on thermally activated charge transport32 according to the following equation:33
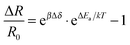 | (1) |
According to the model represented by eqn (1) two effects have to be accounted for when the sensor film is exposed to analyte vapors.2,33 On the one hand, due to sorption of analyte within the organic matrix the film swells and the enlarged tunneling distances increase the resistance. On the other hand, the permittivity of the ligand matrix changes. Using ligands with low permittivity the adsorption of more polar analytes reduces the activation energy causing the resistance to drop. This bidirectionality of the sensor response as a result of the interplay between swelling and permittivity increase has been addressed in multiple works.8,10,12,19,21,35 For example, while the chemiresistive responses are usually positive, indicating that swelling is the dominant effect, it could be shown that rigidly cross-linked nanoparticle films respond with a decrease in resistance to analyte sorption.21 Presumably, in these films the permittivity change becomes the overriding effect of the transduction mechanism.
In most previous studies the response characteristics of GNP-based chemiresistors have been discussed qualitatively referring to eqn (1). So far, only few studies aimed at a more detailed understanding of the sensing mechanism by taking into account either the gravimetrically measured amount of sorbed analyte,33 the distribution of sorbed analyte measured by neutron reflectometry,36 or the swelling of the sensor films measured by ellipsometry,19 environmental scanning electron microscopy (E-SEM),37 or X-ray scattering techniques.38–40 Small-angle X-ray scattering (SAXS) techniques (including GISAXS) have been shown to be powerful methods for studying sorption-38–40or strain-induced41–43changes in the interparticle distances. For example, Ibañez and coworkers39 dosed coatings of tetraoctylammonium bromide-stabilized gold nanoparticles with solvent vapors and monitored in situ the interparticle distance changes by GISAXS.
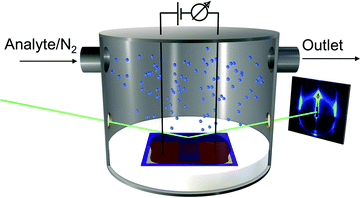
To enable reliable measurements of only subtle interparticle distance changes – induced at relatively low vapor concentrations – the use of highly ordered nanoparticle films, providing well-resolved SAXS signals, is most suitable. Recently, Pileni and coworkers38,44 reported on the assembly of highly ordered, supercrystalline films from 1-dodecanethiol (DDT)-capped GNPs. Using SAXS techniques they were able to measure reversible swelling when exposing the films to toluene vapors.38 Here, we followed this approach to measure sorption-induced changes in interparticle distances when dosing supercrystalline GNP films with different solvent vapors in the concentration range 1000–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm. Simultaneously, we recorded the films' chemiresistive responses and, additionally, the amount of sorbed analyte was quantified using quartz crystal microbalances (QCM). To take into account the influence of permittivity changes, solvents with significantly different permittivities were used as analytes. As detailed in the following, these measurements allowed us to assess quantitatively the influence of analyte sorption and film swelling on the chemiresistive responses and to reevaluate the commonly used chemiresistor model according to eqn (1).
000 ppm. Simultaneously, we recorded the films' chemiresistive responses and, additionally, the amount of sorbed analyte was quantified using quartz crystal microbalances (QCM). To take into account the influence of permittivity changes, solvents with significantly different permittivities were used as analytes. As detailed in the following, these measurements allowed us to assess quantitatively the influence of analyte sorption and film swelling on the chemiresistive responses and to reevaluate the commonly used chemiresistor model according to eqn (1).
Experimental
Materials
Chloro(triphenylphosphine)gold(I) (98%) was purchased from ABCR. All other chemicals were purchased from Aldrich. They were all of analytical grade and used as received.Synthesis of gold nanoparticles
1-Dodecanethiol (DDT)-stabilized gold nanoparticles were prepared following the method by Pileni and coworkers,44 which is based on the synthesis developed by Stucky and coworkers.45 A solution of 5 mmol tert-butylamine borane complex in 2 mL toluene and a solution of 0.25 mmol chloro(triphenylphosphine)gold(I) and 500 μL 1-dodecanethiol in 25 mL toluene were mixed at 100 °C and stirred for 5 min. After the solution cooled down to room temperature the particles were precipitated twice or three times by adding 5 to 20 mL ethanol. The samples were centrifuged at 5095 × g and −10 °C. The precipitates were dried under nitrogen and dispersed in ∼5 mL toluene.Deposition of nanoparticle films
For SEM, GISAXS and chemiresistor measurements the samples were prepared by dropping a concentrated GNP solution (c∼10−2 mmol L−1) onto a silicon wafer. The samples dried under ambient conditions and were used the next day. For electrical measurements the sample was deposited onto silicon substrates (thermal oxide layer 500 nm) with interdigitated gold electrode structures (50 finger pairs, gap: 10 μm, overlap: 1.8 mm, thickness: 50 nm or 100 nm). To enable GISAXS measurements simultaneously with chemiresistive measurements the GNP films covered the electrodes as well as some mm2 of blank silicon wafer next to the electrodes for positioning the X-ray spot. The QCM substrates were coated on both sides using a more diluted solution (c∼10−3 mmol L−1).Transmission electron microscopy (TEM)
TEM images of GNPs were measured with a Philips CM 300, kV, LaB6 microscope. The gold nanoparticle solution was diluted in a solution of DDT in toluene (c∼10−3 mol L−1) in order to prevent the particles from coalescing on the grid during TEM measurements. 10 μL of this solution were then dropped onto a carbon coated copper grid and measured after solvent evaporation. For size determination ∼1000 particles were evaluated using the software ImageJ.Scanning electron microscopy (SEM)
SEM images of the GNP films deposited onto silicon substrates were recorded using a LEO-1550 (Carl Zeiss) field-emission scanning electron microscope. For imaging cross sections of the films, the coated wafers were cleaved.Grazing-incidence small-angle X-ray scattering (GISAXS)
These experiments were performed using our in-house SAXS apparatus equipped with an Incoatec™ X-ray source IμS and Quazar Montel optics. The wavelength of the X-ray probe was 0.154 nm and the focal spot size at the sample position was 0.6 mm2. The samples were mounted on a high resolution motorized goniometer and the incident angle was set to 0.3°. The sample-detector distance was 1.6 m. The patterns were recorded with a Rayonix™ SX165 CCD-Detector and the accumulation time per GISAXS measurement was 600 s. The evaluation of the data was carried out using the software Scatter.46,47Thermogravimetric analysis (TGA)
This analysis of the gold nanoparticle assemblies was performed in a temperature range of 25 °C to 800 °C using the Mettler Toledo TGA 1. The heating rate was 10 °C min−1 and the nitrogen flow was 20 mL min−1. For the TGA measurements the gold nanoparticle solution was filled into aluminum oxide cups (∼70 μL). The solvent evaporated under ambient conditions over night. The dry mass was ca. 3 mg.Dose–response measurements with solvent vapors
The chemiresistor responses were measured by supplying a constant current of 100 nA (Keithley Sourcemeter 2601A) and recording the change in voltage (Keithley Multimeter 2002) when dosing the sensors with the analyte vapors after purging the test chamber with zero gas (nitrogen 5.0). Test vapors were generated using a commercial programmable calibration system (Kalibriersystem Modell CGM 2000, Umwelttechnik MCZ). As carrier gas nitrogen 5.0 was used. For the experiments three different test chambers were employed: one for simple chemiresistor measurements (aluminum, ∼10 mL), one equipped with Kapton windows for the in situ GISAXS and chemiresistor measurements (stainless steel, PTFE, ∼100 mL) and one allowing to perform QCM and chemiresistor measurements in parallel (PTFE, ∼20 mL). The flow through the sensor test chambers was set to a rate of 400 mL min−1. All experiments were carried out at room temperature. Solvent sorption on the GNP-coated QCMs was recorded as the shift of the resonant frequency Δfs upon analyte sorption. The resonant frequency f of the QCMs (AT-cut polished with gold electrodes, resonance frequency: 10 MHz, KVG Quartz Crystal Technology GmbH) was obtained from the impedance spectra of the QCMs which were measured using an Agilent E5100A Network Analyzer. Here, the QCM is represented by a four-element equivalent circuit. From the frequency shift the mass of sorbed analyte Δm was calculated according to the Sauerbrey equation:48 | (2) |
Results and discussion
1. Preparation of GNP superlattice films and structural characterization
DDT-stabilized GNPs with a core diameter of ∼4 nm were prepared by the reduction of chloro(triphenylphosphine)gold(I) with tert-butylamine borane complex in the presence of DDT, as originally described by Stucky and coworkers45 and later modified by Pileni and coworkers.44 This method provides GNPs with extremely narrow size distributions (standard deviation <10%). A representative TEM image of these GNPs is shown in Fig. 1a (size histograms and additional TEM images are provided in the ESI,† Fig. S1). Table 1 lists the TEM measured core diameters D with standard deviations for the three GNP batches used in our in situ GISAXS/chemiresistor experiments.| Sample | D (nm) | δ (nm) | r eff (nm) | ρ sl (g cm−3) |
|---|---|---|---|---|
| GNP1 | 3.7 ± 0.2 | 1.9 | 2.8 | 4.8 |
| GNP2 | 3.9 ± 0.2 | 2.1 | 3.0 | 4.6 |
| GNP3 | 3.7 ± 0.2 | 2.3 | 3.0 | 4.0 |
Using SAXS techniques, Pileni and coworkers44 studied in detail how GNPs prepared by above mentioned method self-assemble as thin film GNP superlattices. Here, we prepared such highly ordered GNP films by drop casting the nanoparticle suspensions onto silicon substrates. Fig. 1b and c show SEM images of the as-deposited films. The sharp pattern observed in the Fourier transformation (Fig. 1d) of the SEM image confirms the highly ordered arrangement of closely packed nanocrystals.
Because the motivation of this study was to measure simultaneously swelling of GNP superlattice films by GISAXS and their chemiresistive responses the substrates used for film deposition had defined areas for positioning the X-ray spot and for contacting the films via interdigitated electrodes. Scheme 1 shows the experimental setup used for in situ GISAXS/chemiresistor measurements.
Fig. 2a shows a representative GISAXS pattern of a GNP superlattice film measured under nitrogen at ambient temperature. Further examples are provided in the ESI† (Fig. S2). While the reflections in qy-direction are due to the 2-dimensional hexagonal arrangement of the particles, the ring-shaped scattering with its center at qz = 0 and qy = 0 is the SAXS signature of the 3-dimensional arrangement of GNPs. The lack of prominent reflections within this ring indicates the presence of supercrystalline domains with predominantly random orientations. From these ring-shaped patterns we extracted the SAXS curves using the software Scatter.46,47 This was done by performing line cuts from center-to-edge of the pattern along regions without the vertical GISAXS reflections and integrating along the ring over a defined section, as indicated by the red lines in Fig. 2a. The obtained SAXS curve shown in Fig. 2b displays the integrated SAXS intensities at q values in the range of ∼0.6 to ∼2.2. This curve with a main peak at q∼1.28 and a second minor peak at q∼1.5 reveals that the GNPs formed an fcc superlattice, in accordance with previous findings of Pileni and coworkers.44 For comparison, the calculated scattering curves of the fcc and bcc lattices are also displayed in Fig. 2b.
 | ||
| Fig. 2 (a) GISAXS pattern of the GNP superlattice film prepared from sample GNP2. (b) SAXS intensity profile extracted from the GISAXS pattern and calculated curves of fcc and bcc lattices. | ||
The calculated SAXS curve of the fcc lattice returned the center-to-center distance between nearest neighbor GNPs. In general, the center-to-center distance deduced from GISAXS measurements was found in reasonable agreement with the center-to-center distance extracted from the Fourier transform of SEM images, assuming an fcc lattice with the (111)-plane aligned with the substrate surface.
It is to note that the diameters of the gold cores obtained from the SAXS analysis are somewhat larger than the observed diameters in TEM images. As detailed in the ESI† we attribute this difference mainly to texture effects, which affect the intensity ratio of the reflections. Therefore, the edge-to-edge distance δ between nearest neighbor GNP cores was calculated by subtracting the TEM-measured GNP core size D from the GISAXS-measured center-to-center distance. The edge-to-edge distances δ determined for the three GNP films used in the in situ GISAXS/chemiresistor experiments were fairly similar, as shown by the corresponding values listed in Table 1.
Scheme 2 shows a model of the supercrystalline nanocrystal arrangement. Considering a length of 1.8 nm49 of the fully stretched 1-dodecanethiol ligand the measured interparticle distances δ between 1.9 and 2.3 nm (Table 1) indicate significant interdigitation of the DDT alkyl chains with differences in the degree of interdigitation between the three GNP superlattice films. We tentatively attribute such differences to subtle variations in the density of ligands bound to the nanocrystals' surface.
 | ||
| Scheme 2 Superlattice formed by DDT-stabilized gold nanoparticles with effective radius reff = D/2 + δ/2. | ||
In a perfect fcc superlattice of DDT-stabilized GNPs 74% of available space is filled with spheres of radius reff comprising the gold core and parts of the ligand shell with the thickness δ/2 forming the superlattice (Scheme 2). The reff values determined for the three GNP films investigated are listed in Table 1. In the following we assume that the remaining 26% are filled with ligands extending into the interstitial sites. Taking into account the volume fraction of gold (using the TEM-measured size of the gold cores) and assuming that all remaining volume of the superlattice is occupied by DDT, the densities ρsl of the assemblies were calculated as detailed in the ESI.† The obtained values, which are used for considerations outlined below, are listed in Table 1. It is to note that the calculated mass fractions of gold and DDT, which are based on GISAXS and TEM measurements are in remarkable agreement with results of thermogravimetric measurements, as described in the ESI† (Table S1 and Fig. S6).
2. GNP Superlattice films dosed with solvent vapors: sorption, swelling and chemiresistive responses
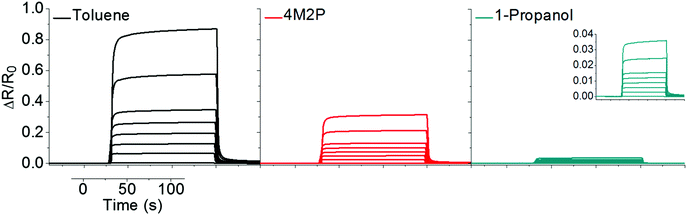
Sorption measurements were performed by dosing the GNP-coated QCM substrates with vapors of toluene, 4-methyl-2-pentanone (4M2P) and 1-propanol, in the concentration range 50–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm. These analytes differ significantly in permittivity, see Table 2, but have similar vapor pressures (29, 21 and 20 mbar at 20 °C respectively),21 ensuring that differences in partitioning are mainly based on the films' chemical selectivity. In a set of preliminary experiments we also tested the responses of GNP films to water vapor. However, because these measurements revealed only marginal chemiresistive responses, with no swelling discernable in GISAXS experiments, we did not consider water as a relevant analyte in our present study. In all experiments nitrogen 5.0 was used as carrier gas. During vapor exposure the resonance frequency decreased and, as seen by the transients depicted in Fig. 3, sorption of all three analytes was remarkably fast (t90 5 to 35 s) and reversible.
000 ppm. These analytes differ significantly in permittivity, see Table 2, but have similar vapor pressures (29, 21 and 20 mbar at 20 °C respectively),21 ensuring that differences in partitioning are mainly based on the films' chemical selectivity. In a set of preliminary experiments we also tested the responses of GNP films to water vapor. However, because these measurements revealed only marginal chemiresistive responses, with no swelling discernable in GISAXS experiments, we did not consider water as a relevant analyte in our present study. In all experiments nitrogen 5.0 was used as carrier gas. During vapor exposure the resonance frequency decreased and, as seen by the transients depicted in Fig. 3, sorption of all three analytes was remarkably fast (t90 5 to 35 s) and reversible.
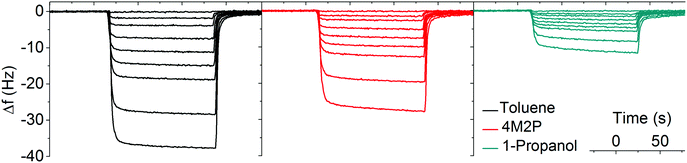 | ||
Fig. 3 Typical QCM responses to toluene (black), 4M2P (red) and 1-propanol (green). The vapor concentrations were 50, 500, 1000, 2000, 3000, 4000, 5000, 7500, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm. 000 ppm. | ||
Using the Sauerbrey equation48 (eqn (2)) the measured frequency shift was used to calculate the mass of sorbed analyte. Fig. 4 shows the sorption isotherms obtained by plotting the relative mass uptake of the films as a function of vapor concentration. A linear correlation is recognized for all three analytes with the slope (i.e. the sensitivity) decreasing in the order toluene > 4M2P > 1-propanol. This trend in sensitivity is qualitatively consistent with the solubility match between the nonpolar hydrophobic dodecyl residues of the DDT ligands and these analytes.
The partition coefficients K = Cf/Cv, representing the ratio of analyte concentration Cf in the film and Cv in the vapor phase, are listed in Table 2. Similar partition coefficients for sorption of toluene have previously been reported in the case of disordered films from 1-octanethiol-stabilized GNPs (core size of 4.3 nm), K∼1000,33 and 1-dodecanethiol-stabilized GNPs (core size ∼3 nm), K∼1500.50
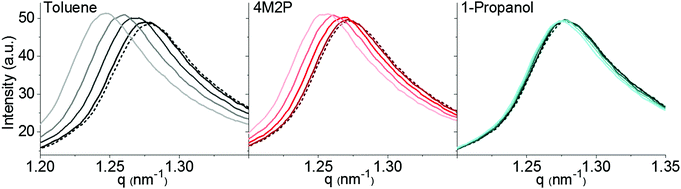
Here, our objective was to measure distance changes in GNP superlattices upon sorption of solvent vapor via in situ GISAXS and to correlate these changes with simultaneously recorded chemiresistive responses. In order to study sorption-induced distance variations also at vapor concentrations below 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm, it was necessary to capture even subtle variations in the interparticle distances. Therefore, the intended experiments required highly ordered particle arrangements providing sharp SAXS/GISAXS signatures. Fig. 5 shows the shift of the (111)-reflection observed when dosing a GNP superlattice film (sample GNP3) with vapors of toluene, 4M2P and 1-propanol at four different concentrations (1000, 4000, 7000 and 10
000 ppm, it was necessary to capture even subtle variations in the interparticle distances. Therefore, the intended experiments required highly ordered particle arrangements providing sharp SAXS/GISAXS signatures. Fig. 5 shows the shift of the (111)-reflection observed when dosing a GNP superlattice film (sample GNP3) with vapors of toluene, 4M2P and 1-propanol at four different concentrations (1000, 4000, 7000 and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm). While the exposure to toluene and 4M2P vapor caused increasing shifts of the scattering curves to smaller q values with increasing vapor concentration, only marginal shifts were induced by 1-propanol vapor. It is to note that the observed shifts of the scattering curves were essentially reversed when purging the cell with nitrogen as shown exemplarily in Fig. S8 (ESI†). The trends shown in Fig. 5 were reproduced when repeating the measurements with two other superlattice films, which were prepared from different GNP batches (see Table 1). Experimental data of these measurements are provided in the ESI† (Fig. S9). In addition to the shift of the (111)-reflection seen in Fig. 5 (and Fig. S9, ESI†) a slight increase in intensity is observed when dosing the films with increasing concentrations of toluene or 4M2P vapor. An analysis of the scattering curves indicates that this increase in signal intensities results from the superposition of the reflection with the underlying form factor function, which increases with decreasing q-values.
000 ppm). While the exposure to toluene and 4M2P vapor caused increasing shifts of the scattering curves to smaller q values with increasing vapor concentration, only marginal shifts were induced by 1-propanol vapor. It is to note that the observed shifts of the scattering curves were essentially reversed when purging the cell with nitrogen as shown exemplarily in Fig. S8 (ESI†). The trends shown in Fig. 5 were reproduced when repeating the measurements with two other superlattice films, which were prepared from different GNP batches (see Table 1). Experimental data of these measurements are provided in the ESI† (Fig. S9). In addition to the shift of the (111)-reflection seen in Fig. 5 (and Fig. S9, ESI†) a slight increase in intensity is observed when dosing the films with increasing concentrations of toluene or 4M2P vapor. An analysis of the scattering curves indicates that this increase in signal intensities results from the superposition of the reflection with the underlying form factor function, which increases with decreasing q-values.
For determining the change in interparticle distance upon exposure to analyte vapor the scattering curves were fitted46,47 to determine the nearest-neighbor-distances in the dry and in the analyte loaded films. Fig. 6 shows the increase in interparticle distance as a function of applied vapor concentration. As already indicated by the scattering curves shown in Fig. 5, the effectiveness of the vapors to swell the films decreased in the order toluene > 4M2P ≫ 1-propanol. While for 4M2P the interparticle distance increased linearly with vapor concentration, a slight deviation from linear behavior was observed for toluene. Here, the data points are in best agreement with a monoexponential growth function. Taking into account the observed linear increase of mass uptake with increasing vapor concentration (Fig. 4) and assuming isotropic swelling one might expect the increase of the interparticle distance to follow a cube root function (see eqn (S16) in the ESI†). However, because the volume added by sorbed analyte is very small compared to the initial film volume, a linear approximation for the correlation between swelling and vapor concentration should be well applicable. The slight deviation from linear behavior observed for toluene sorption may hint at sorption processes being more complex than accounted for by a simple additive and isotropic volume increase.
 | ||
| Fig. 6 Changes in interparticle distances measured while dosing the GNP films with vapors of toluene (black), 4M2P (red) and 1-propanol (green) at various concentrations. The data points show averages of measurements performed with the three GNP superlattice films prepared from samples GNP1, GNP2 and GNP3 (Table 1). The individual data sets are provided in the ESI† (Fig. S10). For toluene a monoexponential fit-function was used, whereas a linear function was fitted to the data referring to 4M2P. Because the swelling observed for 1-propanol vapor was only marginal and the scattering of corresponding data points was relatively strong, no fit-function was applied for this analyte. | ||
At the highest concentration of toluene vapor (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm) the interparticle distance increased by ∼0.12 nm. For comparison, Pileni and coworkers38 investigated very similar superlattices comprised of DDT-stabilized GNPs with a core diameter of 5 nm. They reported interparticle distance increments between ∼0.4 to ∼0.7 nm when exposing the films to nearly saturated (∼37
000 ppm) the interparticle distance increased by ∼0.12 nm. For comparison, Pileni and coworkers38 investigated very similar superlattices comprised of DDT-stabilized GNPs with a core diameter of 5 nm. They reported interparticle distance increments between ∼0.4 to ∼0.7 nm when exposing the films to nearly saturated (∼37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 ppm at 25 °C) toluene vapor. Taking into account the considerably lower vapor concentrations used in our study the results reported here are in reasonable agreement with these earlier findings.
500 ppm at 25 °C) toluene vapor. Taking into account the considerably lower vapor concentrations used in our study the results reported here are in reasonable agreement with these earlier findings.
In our present study, two sets of experiments were performed to investigate the chemiresistive responses of superlattice films when dosing them with vapors of toluene, 4M2P and 1-propanol in the concentration range 50–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm.
000 ppm.
In the first set of experiments the duration of each vapor exposure was set to 120 s. Fig. 7 shows a series of typical chemiresistor responses. In agreement with the sorption characteristics measured by microgravimetry (Fig. 3) the responses were quick, with t90 times <8 s, and fully reversible. Furthermore, all responses showed an increase in resistance, which was highest for toluene (∼90% at 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm), significantly lower for 4M2P (∼30% at 10
000 ppm), significantly lower for 4M2P (∼30% at 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm) and one order of magnitude lower in the case of 1-propanol (∼4% at 10
000 ppm) and one order of magnitude lower in the case of 1-propanol (∼4% at 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm). Thus, the observed chemical selectivity is qualitatively in agreement with the gravimetrically measured mass loadings and GISAXS-measured swelling. However, compared to the gravimetric measurements (Fig. 3) the differences in response amplitudes observed between the three analytes are clearly more pronounced in the case of the chemiresistors. This behavior will be discussed in detail below when we conflate the different response characteristics to gain a more comprehensive picture of the sensing mechanism.
000 ppm). Thus, the observed chemical selectivity is qualitatively in agreement with the gravimetrically measured mass loadings and GISAXS-measured swelling. However, compared to the gravimetric measurements (Fig. 3) the differences in response amplitudes observed between the three analytes are clearly more pronounced in the case of the chemiresistors. This behavior will be discussed in detail below when we conflate the different response characteristics to gain a more comprehensive picture of the sensing mechanism.
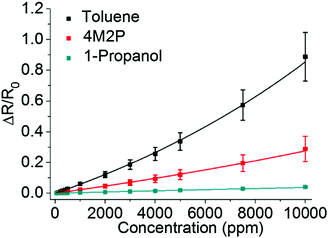
Fig. 8 shows the response isotherms of the GNP superlattice-based chemiresistors. In contrast to cross-linked GNP films,11 the response amplitudes did not saturate with increasing vapor concentrations. Instead, the isotherms for toluene and 4M2P suggest an exponential increase with ascending analyte concentration. The responses to 1-propanol were too faint to clearly discern this trend. The sensitivities determined as the slopes of linear fits of the isotherms in the range 50–1000 ppm were 6 × 10−5 ppm−1 for toluene, 2 × 10−5 ppm−1 for 4M2P and 4 × 10−6 ppm−1 for 1-propanol. Regarding toluene vapor, similarly curved response isotherms have been reported previously for chemiresistors based on disordered assemblies of DDT-stabilized GNPs.17
In the second set of experiments the chemiresistive responses were sampled simultaneously with the GISAXS signals. For these experiments the setup illustrated in Scheme 1 was used. Due to the geometric requirements of the GISAXS measurements the volume of the sensor test chamber was much larger (∼100 mL) than in the first set of experiments and fairly long vapor exposures (20 min) were necessary to ensure sufficiently long integration times for the GISAXS measurements. Therefore, the acquired chemiresistive responses were somewhat retarded as the larger cell volume required longer purge times. However, the response amplitudes and, thus, the obtained response isotherms were practically identical to those obtained by first set of experiments. Representative response transients and the response isotherms obtained in the second set of chemiresistor measurements are provided in the ESI† (Fig. S12 and S10).
3. Correlation of chemiresistive responses, sorption and swelling – revisiting the chemiresistor model
 | ||
| Fig. 9 Interparticle distance changes as a function of vapor concentration. Black data points (Δδ) refer to GISAXS measurements whereas the red data points (Δδqcm) were generated using the QCM-measured mass of sorbed analyte. The black data points represent mean values referring to measurements of three GNP superlattice films prepared from samples GNP1, GNP2, and GNP3 (Table 1 and Fig. 6). The red data points are based on the data shown in Fig. 4. | ||
As an interim conclusion, our correlation of film swelling extracted from QCM data with swelling measured by GISAXS suggests that with decreasing affinity of the analyte to the ligand matrix, the analyte molecules are sorbed less selectively to sites provided within the ligand matrix. While the nonpolar toluene and 4M2P molecules are absorbed mainly within the nonpolar ligand matrix and cause significant swelling, the protic polar 1-propanol molecules are adsorbed rather unselectively on the films' surface or within voids, where they do not contribute to film swelling. This interpretation is supported by a previously conducted neutron reflectometry study on sorption of solvent vapors in dendrimer cross-linked GNP films.36 When exposing those films to vapors of solvents with orthogonal solubility the formation of a wetting layer on top of the film was observed, while the bulk of the film remained essentially solvent free.
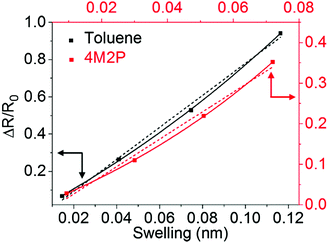 | ||
| Fig. 10 Chemiresistive response amplitudes vs. swelling (Δδ). Linear (dotted lines) and monoexponential functions (solid lines) were fitted to the data. The data points are mean values referring to the three GNP superlattice films prepared from samples GNP1, GNP2 and GNP3. The same data were also used for the presentation in Fig. 6 and 11. The complete set of individual data is shown in Fig. S10 in the ESI.† | ||
 | (3) |
For calculating the activation energy, the permittivity of the analyte swollen ligand matrix εsw was estimated as the volume-weighted average of the permittivity of the ligand εDDT and the analyte εana.33,66 The individual permittivities εana are listed in Table 2. For 1-dodecanethiol two different values of εDDT were used for the calculations, i.e. the reported permittivities of 2.051 and 2.652 for alkanethiols. The volume of sorbed analyte, which was used for calculating εsw was obtained from the QCM measurements (Fig. 4) and denoted as Vana,qcm. Alternatively, the volume of sorbed analyte was calculated from swelling determined by GISAXS and denoted as Vana,gis. Details of the calculations can be found in the ESI.† The resulting permittivities are referred to as εsw,qcm and εsw,gis, respectively. In the latter case only the volume fraction of analyte is considered, which contributed to film swelling, i.e. which was sorbed within the ligand matrix. The chemiresistive responses, which were calculated using eqn (1) and (3) with either εsw,qcm or εsw,gis, are referred to as ΔR/R0,εqcm and ΔR/R0,εgis. Fig. 11 and Fig. S13 (ESI†) show ΔR/R0,εqcm (blue squares) and ΔR/R0,εgis (red diamonds/squares) calculated with εDDT = 2.6 and εDDT = 2.0, respectively, in comparison to the measured sensor responses ΔR/R0 (black squares).
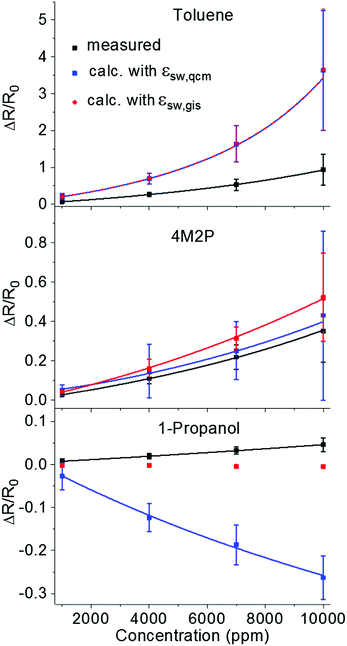 | ||
| Fig. 11 Measured and calculated chemiresistive responses according to eqn (1) and (3) to toluene (top), 4M2P (middle) and 1-propanol (bottom) plotted vs. vapor concentration. For calculating the response amplitudes ΔR/R0,εqcm (blue squares) and ΔR/R0,εgis (red diamonds/squares) the GISAXS-measured swelling Δδ (see Fig. 6) and the volume-weighted average permittivity of the analyte swollen ligand matrix, εsw,qcm or εsw,gis, respectively, were used. εsw,qcm and εsw,gis were calculated based either on QCM or GISAXS data, respectively, and using εDDT = 2.6. The data points represent averages obtained from three films prepared using the GNP samples GNP1, GNP2 and GNP3. The individual data sets are shown in Fig. S10 (ESI†). The curves fitted to the data (solid and dashed lines) serve as guide to the eye and were generated using the chemiresistor model based on eqn (1) and (3), as detailed in the ESI† (Fig. S13). For 1-propanol the fit to the ΔR/R0,εgis data was omitted due to scattering of the GISAXS data. | ||
Qualitatively, the calculated response isotherms show the same trends as the measured isotherms: the response amplitudes decrease in the order toluene > 4M2P > 1-propanol.
For toluene ΔR/R0,εqcm and ΔR/R0,εgis are superimposed because Vana,qcm and Vana,gis, which were used to calculate the permittivity, are very similar (Fig. 9) and, in addition, the low permittivity of toluene renders the effect of the permittivity change on the sensor response negligible. Thus, the sensor responses result nearly exclusively from the swelling effect. However, the calculated responses are significantly higher (by a factor of ∼3) compared to the measured responses. Similar findings have been reported by Steinecker et al.33 and Digianantonio et al.40 for different kinds of solvents and water, respectively.
Steinecker et al.33 studied the chemiresistive responses of coatings comprised of 1-octanethiol-stabilized GNPs when exposed to different solvent vapors. They estimated both swelling and permittivity changes of the analyte/ligand matrix using exclusively QCM data. The observed deviation between measured and calculated responses was attributed to pore-filling, which attenuates film swelling and, thereby, explains the lower responses measured. In contrast, our results from QCM and GISAXS data suggest that, at least in the case of highly ordered superlattice GNP films, the volume increase upon toluene sorption translates nearly quantitatively into a change in interparticle distances (Fig. 9). Thus, the deviation between calculated and measured responses observed in our present study cannot be attributed to pore filling.
Using SAXS techniques Digianantonio et al.40 studied wires of tris(2,4-dimethyl-5-sulfonatophenyl)phosphine-stabilized GNPs with ∼15 nm core size. They measured the relative resistance changes ΔR/R0 simultaneously with changes in the center-to-center-distances when exposing the wires to humidity. Their calculation of the relative resistance changes showed a good match with the experimentally determined responses after correcting the SAXS measured center-to-center distance changes Δδ by a factor of 0.2 to 0.4. However, it is to note that in their analysis the Arrhenius term of eqn (1) including sorption-induced changes in the ligand shell's permittivity was not taken into account.
As in the case of toluene vapor, Vana,qcm and Vana,gis are similar for sorption of 4M2P leading to comparable values for ΔR/R0,εqcm and ΔR/R0,εgis. Using εDDT = 2.6 the calculated responses are in fairly good agreement with the measured responses, as shown in Fig. 11. Exchanging the permittivity of the ligand matrix by εDDT = 2.0 enhances the influence of the analyte's permittivity on the response, leading to more pronounced deviation from the measured chemiresistive responses. The countervailing swelling and permittivity effect render the calculated responses slightly negative or positive (−10−2 to 10−2, see Fig. S13 in the ESI†).
As shown in Fig. 11 and Fig. S13 (ESI†) using the QCM data for calculating the permittivity changes induced by 1-propanol sorption suggests negative ΔR/R0,εqcm responses in the range ∼−10−1, in contrast to the measured slightly positive responses (∼10−2 range). Here, the swelling Δδ observed by GISAXS was actually below 0.01 nm. In this range the influence of swelling on the response is negligible and the chemiresistive response is dominated by the counteracting effect of increasing permittivity. Taking into account the QCM-measured analyte volume Vana,qcm for calculating the permittivity increase assumes that all gravimetrically measured 1-propanol contributes to this change in permittivity. Therefore, this calculation suggests negative chemiresistive responses significantly deviating from the slightly positive responses measured. However, as pointed out above, it is likely that only a fraction of 1-propanol was absorbed within the GNP superlattice and, thus, only a small amount of gravimetrically detected analyte contributed to changes in the dielectric environment of the conduction paths. Accordingly, when calculating the increase in permittivity based on the GISAXS-measured analyte volume Vana,gis the obtained responses ΔR/R0,εgis were close to zero, giving much better agreement with the measured responses ΔR/R0.
Summary and conclusions
In this study we analyzed the chemiresistive responses of GNP superlattice films by measuring in situ sorption-induced swelling via GISAXS. Further, microgravimetry was used to compare observed swelling with the uptake of sorbed analyte volume and to account for the change in permittivity of the organic matrix. Inserting the experimentally determined changes of the interparticle distances and permittivity into eqn (1) and (3) described the measured chemiresistive responses of the films only qualitatively. In the case of toluene the calculated responses can be brought into agreement with the experimental values by reducing the GISAXS-measured swelling by a factor of 0.45. This deviation is possibly due to reduced swelling of the film close to the film/substrate interface, where the mobility of the particles is more restricted.67 In the case of the more polar analyte 4M2P the responses returned by the model were in fairly good agreement with the measured resistance changes when using a relative permittivity of 2.6 for the ligand matrix. However, when substituting this value by 2.0 the model suggests stronger deviations with partly negative chemiresistive responses (ESI†). For the protic polar 1-propanol the model suggested negative responses. In contrast, the experimentally determined responses were slightly positive. In part, this discrepancy can be explained by taking into account that essentially no swelling was observed by GISAXS, suggesting that 1-propanol was mainly sorbed within pores and/or as a wetting layer on top of the coating without affecting the charge transport.To further develop our understanding of the sensing mechanism, it is necessary to gain a more detailed picture on the molecular structure of the films, the ligand arrangement and the sizes and size distribution of micropores. To this end we are currently exploring the pore structure of superlattice GNP films using positron annihilation lifetime spectroscopy. Additionally, measurements of sorption-induced variations of the GNPs' dielectric environment (correlated with GISAXS and microgravimetry) could provide interesting data for further evaluating and refining the currently used model for GNP based chemiresistors.
Acknowledgements
The authors thank Mr Hendrik Schlicke for technical assistance regarding the QCM measurements. Mr Andreas Kornowski, Mr Stefan Werner and Mr Robert Schön are acknowledged for measuring TEM and SEM images. We thank Ms Katrin Rehmke and Mr Stefan Bleck (Institute for Technical and Macromolecular Chemistry, University of Hamburg) for TGA measurements. Mateusz Olichwer is acknowledged for supporting the preparation of graphical artwork.References
- H. Wohltjen and A. W. Snow, Anal. Chem., 1998, 70, 2856–2859 CrossRef CAS.
- F. J. Ibañez and F. P. Zamborini, Small, 2011, 8, 174–202 CrossRef PubMed.
- F. J. Ibañez and F. P. Zamborini, ACS Nano, 2008, 2, 1543–1552 CrossRef PubMed.
- F. J. Ibañez and F. P. Zamborini, J. Am. Chem. Soc., 2008, 130, 622–633 CrossRef PubMed.
- L. Wang, X. Shi, N. N. Kariuki, M. Schadt, G. R. Wang, Q. Rendeng, J. Choi, J. Luo, S. Lu and C.-J. Zhong, J. Am. Chem. Soc., 2007, 129, 2161–2170 CrossRef CAS PubMed.
- Y. Joseph, B. Guse, A. Yasuda and T. Vossmeyer, Sens. Actuators, B, 2004, 98, 188–195 CrossRef CAS.
- E. Dovgolevsky, U. Tisch and H. Haick, Small, 2009, 5, 1158–1161 CAS.
- A. W. Snow, M. G. Ancona and D. Park, Langmuir, 2012, 28, 15438–15443 CrossRef CAS PubMed.
- L. Wang, J. Luo, J. Yin, H. Zhang, J. Wu, X. Shi, E. Crew, Z. Xu, Q. Rendeng, S. Lu, M. Poliks, B. Sammakia and C.-J. Zhong, J. Mater. Chem., 2010, 20, 907–915 RSC.
- L. Han, D. R. Daniel, M. M. Maye and C.-J. Zhong, Anal. Chem., 2001, 73, 4441–4449 CrossRef CAS PubMed.
- N. Olichwer, E. W. Leib, A. H. Halfar, A. Petrov and T. Vossmeyer, ACS Appl. Mater. Interfaces, 2012, 4, 6151–6161 CAS.
- E. García-Berríos, T. Gao, M. D. Woodka, S. Maldonado, B. S. Brunschwig, M. W. Ellsworth and N. S. Lewis, J. Phys. Chem. C, 2010, 114, 21914–21920 Search PubMed.
- Y. Joseph, I. Besnard, M. Rosenberger, B. Guse, H.-G. Nothofer, J. M. Wessels, U. Wild, A. Knop-Gericke, D. Su, R. Schlögl, A. Yasuda and T. Vossmeyer, J. Phys. Chem. B, 2003, 107, 7406–7413 CrossRef CAS.
- J. Bryant-Genevier, K. Scholten, S. K. Kim and E. T. Zellers, Sens. Actuators, B, 2014, 202, 167–176 CrossRef CAS.
- M. Segev-Bar, A. Landman, M. Nir-Shapira, G. Shuster and H. Haick, ACS Appl. Mater. Interfaces, 2013, 5, 5531–5541 CAS.
- C.-L. Li, Y.-F. Chen, M.-H. Liu and C.-J. Lu, Sens. Actuators, B, 2012, 169, 349–359 CrossRef CAS.
- J. Im, S. K. Sengupta, M. F. Baruch, C. D. Granz, S. Ammu, S. K. Manohar and J. E. Whitten, Sens. Actuators, B, 2011, 156, 715–722 CrossRef CAS.
- E. García-Berríos, T. Gao, J. C. Theriot, M. D. Woodka, B. S. Brunschwig and N. S. Lewis, J. Phys. Chem. C, 2011, 115, 6208–6217 Search PubMed.
- H.-L. Zhang, S. D. Evans, J. R. Henderson, R. E. Miles and T.-H. Shen, Nanotechnology, 2002, 13, 439–444 CrossRef CAS.
- S. Shan, W. Zhao, J. Luo, J. Yin, J. C. Switzer, P. Joseph, S. Lu, M. Poliks and C.-J. Zhong, J. Mater. Chem. C, 2014, 2, 1893–1903 RSC.
- Y. Joseph, A. Peic, X. Chen, J. Michl, T. Vossmeyer and A. Yasuda, J. Phys. Chem. C, 2007, 111, 12855–12859 CAS.
- L. J. Hubble, J. S. Cooper, A. Sosa-Pintos, H. Kiiveri, E. Chow, M. S. Webster, L. Wieczorek and B. Raguse, ACS Comb. Sci., 2015, 17, 120–129 CrossRef CAS PubMed.
- J. S. Cooper, B. Raguse, E. Chow, L. Hubble, K.-H. Müller and L. Wieczorek, Anal. Chem., 2010, 82, 3788–3795 CrossRef CAS PubMed.
- N. Garg, A. Mohanty, N. Lazarus, L. Schultz, T. R. Rozzi, S. Santhanam, L. Weiss, J. L. Snyder, G. K. Fedder and R. Jin, Nanotechnology, 2010, 21, 405501 CrossRef PubMed.
- Q. Zhong, W. H. Steinecker and E. T. Zellers, Analyst, 2009, 134, 283–293 RSC.
- J. Lee, S. Mubeen, C. M. Hangarter, A. Mulchandani, W. Chen and N. V. Myung, Electroanalysis, 2011, 23, 2623–2628 CrossRef CAS.
- L. K. Wright and E. T. Zellers, Analyst, 2013, 138, 6860–6868 RSC.
- S. K. Kim, D. R. Burris, H. Chang, J. Bryant-Genevier and E. T. Zellers, Environ. Sci. Technol., 2012, 46, 6065–6072 CrossRef CAS PubMed.
- R. Vishinkin and H. Haick, Small, 2015, 11, 6142–6164 CrossRef CAS PubMed.
- M. S. Webster, J. S. Cooper, E. Chow, L. J. Hubble, A. Sosa-Pintos, L. Wieczorek and B. Raguse, Sens. Actuators, B, 2015, 220, 895–902 CrossRef CAS.
- J. Luo, J. Luo, L. Wang, X. Shi, J. Yin, E. Crew, S. Lu, L. M. Lesperance and C.-J. Zhong, Sens. Actuators, B, 2012, 161, 845–854 CrossRef CAS.
- R. H. Terrill, T. A. Postlethwaite, C. H. Chen, C. D. Poon, A. Terzis, A. Chen, J. E. Hutchison, M. R. Clark, G. Wignall, J. D. Londono, R. Superfine, M. Falvo, C. S. Johnson, E. T. Samulski and R. W. Murray, J. Am. Chem. Soc., 1995, 117, 12537–12548 CrossRef CAS.
- W. H. Steinecker, M. P. Rowe and E. T. Zellers, Anal. Chem., 2007, 79, 4977–4986 CrossRef CAS PubMed.
- W. P. Wuelfing, S. J. Green, J. J. Pietron, D. E. Cliffel and R. W. Murray, J. Am. Chem. Soc., 2000, 122, 11465–11472 CrossRef CAS.
- J. Im, A. Chandekar and J. E. Whitten, Langmuir, 2009, 25, 4288–4292 CrossRef CAS PubMed.
- N. Krasteva, R. Krustev, A. Yasuda and T. Vossmeyer, Langmuir, 2003, 19, 7754–7760 CrossRef CAS.
- C. Kunstmann-Olsen, D. Belić, D. F. Bradley, M. P. Grzelczak and M. Brust, Chem. Mater., 2016, 28, 2970–2980 CrossRef CAS.
- Y. Wan, N. Goubet, P.-A. Albouy, N. Schaeffer and M.-P. Pileni, Langmuir, 2013, 29, 13576–13581 CrossRef CAS PubMed.
- M. C. Dalfovo, L. J. Giovanetti, J. M. Ramallo-López, R. C. Salvarezza, F. G. Requejo and F. J. Ibañez, J. Phys. Chem. C, 2015, 119, 5098–5106 CAS.
- L. Digianantonio, M. Gauvin, T. Alnasser, D. Babonneau, B. Viallet, J. Grisolia, G. Viau, A. Coati, Y. Garreau and L. Ressier, J. Phys. Chem. C, 2016, 120, 5848–5854 CAS.
- P. Siffalovic, L. Chitu, K. Vegso, E. Majkova, M. Jergel, M. Weis, S. Luby, I. Capek, J. Keckes, G. A. Maier, A. Satka, J. Perlich and S. V. Roth, Nanotechnology, 2010, 21, 385702 CrossRef CAS PubMed.
- N. Decorde, N. M. Sangeetha, B. Viallet, G. Viau, J. Grisolia, A. Coati, A. Vlad, Y. Garreau and L. Ressier, Nanoscale, 2014, 6, 15107–15116 RSC.
- K. Vegso, M. Jergel, P. Siffalovic, M. Kotlar, Y. Halahovets, M. Hodas, M. Pelletta and E. Majkova, Sens. Actuators, A, 2016, 241, 87–95 CrossRef CAS.
- N. Goubet, J. Richardi, P.-A. Albouy and M.-P. Pileni, Adv. Funct. Mater., 2011, 21, 2693–2704 CrossRef CAS.
- N. Zheng, J. Fan and G. D. Stucky, J. Am. Chem. Soc., 2006, 128, 6550–6551 CrossRef CAS PubMed.
- S. Förster, L. Apostol and W. Bras, J. Appl. Crystallogr., 2010, 43, 639–646 CrossRef.
- S. Förster, A. Timmann, M. Konrad, C. Schellbach, A. Meyer, S. S. Funari, P. Mulvaney and R. Knott, J. Phys. Chem. B, 2005, 109, 1347–1360 CrossRef PubMed.
- G. Sauerbrey, Z. Phys., 1959, 155, 206–222 CrossRef CAS.
- C. D. Bain, E. B. Troughton, Y.-T. Tao, J. Evall, G. M. Whitesides and R. G. Nuzzo, J. Am. Chem. Soc., 1989, 111, 321–335 CrossRef CAS.
- J. W. Grate, D. A. Nelson and R. Skaggs, Anal. Chem., 2003, 75, 1868–1879 CrossRef CAS PubMed.
- K. Slowinski, R. V. Chamberlain, C. J. Miller and M. Majda, J. Am. Chem. Soc., 1997, 119, 11910–11919 CrossRef CAS.
- M. D. Porter, T. B. Bright, D. L. Allara and C. E. D. Chidsey, J. Am. Chem. Soc., 1987, 109, 3559–3568 CrossRef CAS.
- K. Bian, J. J. Choi, A. Kaushik, P. Clancy, D.-M. Smilgies and T. Hanrath, ACS Nano, 2011, 5, 2815–2823 CrossRef CAS PubMed.
- B. W. Goodfellow, M. R. Rasch, C. M. Hessel, R. N. Patel, D.-M. Smilgies and B. A. Korgel, Nano Lett., 2013, 13, 5710–5714 CrossRef CAS PubMed.
- D. S. Sidhaye and B. L. V Prasad, Chem. Mater., 2010, 22, 1680–1685 CrossRef CAS.
- X. M. Lin, C. M. Sorensen and K. J. Klabunde, J. Nanopart. Res., 2000, 2, 157–164 CrossRef CAS.
- D. Zanchet, M. S. Moreno and D. Ugarte, Phys. Rev. Lett., 1999, 82, 5277–5280 CrossRef CAS.
- Y. Yu, A. Jain, A. Guillaussier, V. R. Voggu, T. M. Truskett, D.-M. Smilgies and B. A. Korgel, Faraday Discuss., 2015, 181, 181–192 RSC.
- J. E. Martin, J. P. Wilcoxon, J. Odinek and P. Provencio, J. Phys. Chem. B, 2000, 104, 9475–9486 CrossRef CAS.
- M. P. Pileni, Acc. Chem. Res., 2012, 45, 1965–1972 CrossRef CAS PubMed.
- T. Geyer, P. Born and T. Kraus, Phys. Rev. Lett., 2012, 109, 128302 CrossRef PubMed.
- A. Courty, J. Richardi, P.-A. Albouy and M.-P. Pileni, Chem. Mater., 2011, 23, 4186–4192 CrossRef CAS.
- H. AlQahtani, M. Sugden, D. Puzzovio, L. Hague, N. Mullin, T. Richardson and M. Grell, Sens. Actuators, B, 2011, 160, 399–404 CrossRef CAS.
- S. D. Evans, S. R. Johnson, Y. L. Cheng and T. Shen, J. Mater. Chem., 2000, 10, 183–188 RSC.
- B. Abeles, P. Sheng, M. D. Coutts and Y. Arie, Adv. Phys., 1975, 24, 407–461 CrossRef CAS.
- A. M. Kummer, A. Hierlemann and H. Baltes, Anal. Chem., 2004, 76, 2470–2477 CrossRef CAS PubMed.
- Y. Joseph, B. Guse, T. Vossmeyer and A. Yasuda, J. Phys. Chem. C, 2008, 112, 12507–12514 CAS.
Footnote |
| † Electronic supplementary information (ESI) available: TEM images of the gold nanoparticles, SEM, GISAXS and TGA data of the GNP superlattice films, chemiresistive response transients to different vapors, measured and calculated chemiresistive response isotherms, details on calculations. See DOI: 10.1039/c6tc02412b |
| This journal is © The Royal Society of Chemistry 2016 |