The structure, chemistry and magnetic properties of FePbBiO₄

Abstract

The compound FePbBiO₄ has been synthesised and has a tetragonal structure (P4₂/mbc, a = 8.48924(9) Å, c = 6.10597(8) Å) that is closely related to FeSb₂O₄. It provides the first example of a compound with this structure that (a) contains only trivalent ions (here Fe³⁺) within the chains of edge-linked octahedra and (b) accommodates Bi³⁺ in the walls of the channels formed between the chains of octahedra. FePbBiO₄ orders antiferromagnetically with a Néel temperature of 24 K; neutron diffraction reveals A-type magnetic order with moments oriented perpendicular to [001]. The magnetic moment of Fe³⁺ at 4 K is 3.74(6) μ_B, slightly lower than that commonly observed for this cation in well-ordered magnetic oxides.

---

1 Introduction

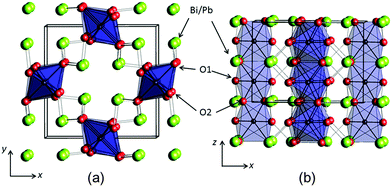
The mineral schafarzikite, FeSb₂O₄, has been reported to be tetragonal (P4₂/mbc, a = 8.62 Å and c = 5.91 Å)¹ with one-dimensional features: chains of edge-linked FeO₆ octahedra are aligned along [001] and enclose parallel channels. This is illustrated in Fig. 1 for the detailed structure of the new compound reported here, FePbBiO₄ (or Fe(PbBi)₂O₄), where one Pb²⁺ and one Bi³⁺ ion have replaced two Sb³⁺ ions. In FeSb₂O₄, therefore, Sb³⁺ ions link the FeO₆ octahedra via their apical (O1) and equatorial (O2) ligands and form SbO₃ trigonal pyramids. The Sb³⁺ lone pairs (e) are directed into the channels and provide pseudo-tetrahedral SbO₃e coordination. Strong intrachain magnetic exchange (primarily direct orbital overlap between adjacent Fe²⁺ ions) results in A-type magnetic order (Fig. 2a) below the Néel temperature, T_N = 46 K.^2,3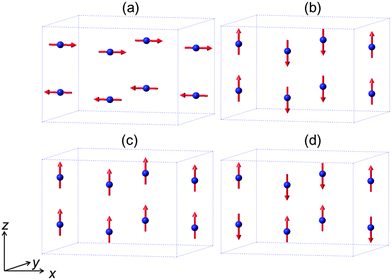

Fig. 1 The structure of FePbBiO₄ structure viewed (a) along [001] and (b) approximately along [010]. Fe – black within blue octahedra, Pb/Bi – large green spheres, O – red spheres (O1 apical and O2 equatorial).

Fig. 2 The four possible collinear spin alignments generating the basic observed magnetic structures for MSb₂O₄ phases: (a) A-type, (b) C-type, (c) F-type and (d) G-type.

Related MSb₂O₄ materials (M = magnetic transition metal) are known for M = Mn, Co, Ni, Cu and Zn.^4–8 All order magnetically at low temperatures except for CuSb₂O₄, which appears to show no long range order above 2 K,⁹ and ZnSb₂O₄, which is diamagnetic. Whereas the phases with M = Mn, Fe display predominantly A-type magnetic order (Fig. 2a), the M = Co, Ni phases are C-type antiferromagnets (Fig. 2b).^1,10,11 It has been suggested that the nature of the direct exchange within the chains – size of cation, M–M separation distance and occupancy of the t_2g orbitals – is responsible for the change in magnetic order.^11,12 The 90° M–O–M intrachain exchange is expected to be ferromagnetic but weak for all ions in the series Mn⋯Ni. However, Mn²⁺ and Fe²⁺ experience strong direct antiferromagnetic exchange because the t_2g orbitals are relatively diffuse; this allows overlap of orbitals on adjacent cation sites to give an antiferromagnetic groundstate. Across the series from Mn to Ni, the d-orbitals contract and the t_2g orbitals fill up both of which weaken the direct exchange such that intrachain ferromagnetic order occurs to give, overall, C-type order. In confirmation of these basic principles, the change in magnetic order for the series Fe_xCo_1−xSb₂O₄ and Mn_xCo_1−xSb₂O₄, 0 ≤ x ≤ 1 has recently been reported and shows a gradual change from A-type to C-type as x decreases.¹²

Attempts to functionalise some materials by creating mixed M²⁺/M³⁺ oxidation states have been reported via substitution of Pb²⁺ for Sb³⁺ for M = Mn, Fe and Co.^11,13,14 However, only for M = Fe is oxidation of the transition metal favoured over oxidation of Sb³⁺ to Sb⁵⁺.¹³ Even for this system, FeSb_2−xPb_xO₄, pure crystalline products were obtained only for x ≤ 0.7 and no phase containing 100% Fe³⁺ (requiring equal amounts of +2 and +3 charged lone pair cations) has been reported. The magnetic properties of such a material are of interest because the direct exchange would be expected to be weaker than in the Fe²⁺ compound, FeSb₂O₄, such that the resultant magnetic order is not simple to predict. It is also strange that no schafarzikite-type phase containing Bi³⁺ ions has been reported since the ionic radius of Bi³⁺ (1.03 Å) is intermediate between those of Pb²⁺ (1.19 Å) and Sb³⁺ (0.76 Å); these data are for 6-coordinate ions since data are not given for 3-coordination.¹⁵ In the present study, we examined the use of the similarly sized cations Pb²⁺ and Bi³⁺ and we report the successful synthesis, structure, magnetic properties and chemistry of the resultant product FePbBiO₄: the first schafarzikite compound to contain only +3 cations within the chains of octahedra and the first to contain Bi³⁺ cations.

2 Experimental

A polycrystalline sample of FePbBiO₄ was synthesised by heating an intimate mixture of pre-dried Fe₂O₃ (99%, Aldrich), PbO (99.9%, Aldrich) and Bi₂O₃ (99.9%, Aldrich) in the appropriate stoichiometric amounts. The mixture was heated in air for two periods of 7 h at 650 °C in an alumina boat.

X-Ray powder diffraction (XRPD) data were collected on a Bruker D8 diffractometer (PSD: Lynxeye, Cu-K_α1, Ge monochromator) in planar transmission mode. Neutron powder diffraction (NPD) data were collected on diffractometer D2B, ILL, Grenoble at temperatures of 300, 20, 16 and 4 K. The wavelength was calibrated using XRPD refinement data on the same sample to give λ = 1.5923 Å. The ILL data used for the refinements were extracted from only the centre of the detectors to provide greater peak resolution.

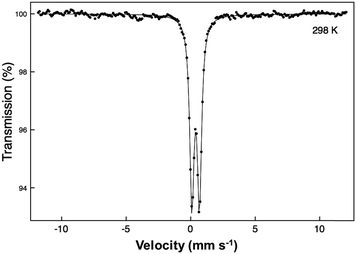
A ⁵⁷Fe Mössbauer spectrum was recorded at 298 K with a constant acceleration spectrometer in transmission geometry using a ca. 400 MBq ⁵⁷Co/Rh source. To avoid the effects of excessive absorption by the presence of Pb and Bi, a sample enriched to 10% ⁵⁷Fe was synthesised. The drive velocity was calibrated with the ⁵⁷Co/Rh source and a natural iron foil. The chemical isomer shift data are reported relative to that of metallic iron at 298 K.

The Rietveld method¹⁶ was used to refine the nuclear and magnetic structures of FePbBiO₄ with the aid of the general structures analysis system (GSAS)¹⁷ and EXPGUI interface.¹⁸ Background intensity was modelled using a shifted Chebyschev polynomial with 25 terms, while peak shapes were modelled using a pseudo-Voigt function. Isotropic displacement parameters were assigned to Fe³⁺ and the equatorial O2, but anisotropic parameters were used for Pb²⁺/Bi³⁺ and the apical O1. The magnetic structure was modelled using a second unit cell (P1) containing only magnetic cations, with appropriate constraints applied to the magnetic moments to conform to a given model. The unit cell dimensions of the magnetic phase were constrained to those of the nuclear unit cell.

Magnetic susceptibility data were acquired using a Quantum Design MPMS SQUID under field cooled (FC) and zero field cooled (ZFC) conditions with an applied field of 100 Oe. No corrections for diamagnetism were applied since they are too small to provide a significant effect. A cooling and heating rate of 10 K min⁻¹ was used, with measurements taken in ‘Sweep’ mode. The polycrystalline sample (∼70 mg) was contained in a gelatin capsule, within a plastic straw.

3 Results and discussion

3.1 Crystal structure

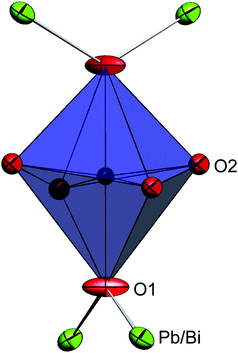
The synthesised FePbBiO₄ was dark brown and stable in air up to the melting point at ∼700 °C. The ambient temperature Mössbauer spectrum, Fig. 3, shows a single Fe³⁺ doublet with a chemical isomer shift, δ, of 0.39 mm s⁻¹ and quadrupole splitting, Δ, of 0.59 mm s⁻¹. These values are typical of octahedral Fe³⁺ and confirm that the synthesis yields a product for which 100% of the Fe is present as Fe³⁺. XRPD data revealed the product to be single phase with a tetragonal, P4₂/mbc, structure which is indicative of the schafarzikite structure. The unit cell parameters determined from Rietveld refinement against X-ray data were subsequently used to calibrate the NPD data, against which the structure was refined. The refined structural parameters are given in Table 1 for data obtained at ambient temperature and 4 K. The relevant diffraction profiles corresponding to the refinement based on ambient temperature data are shown in Fig. 4. The Bi and Pb ions were found to be randomly distributed on the channel wall site; it was found that this position and the apical O1 site had higher than expected isotropic displacement parameters (IDPs). Allowing anisotropy resulted in strongly anisotropic parameters (ADPs) as shown in Table 1. These values are attributed to the presence of both Pb²⁺ and Bi³⁺: the charge and size differences, as discussed in the Introduction, result in local displacements of the cations and the O1 ions, to which they are bonded. The effects of the ADPs are highlighted in Fig. 5, which focuses on this region of the structure. The local displacements of Pb/Bi towards or away from the bonded O1 are indicated, and O1 moves in a perpendicular direction so that the Fe–O1 bond distance will not change significantly. The displacements allow optimisation of the bonding requirements according to whether Pb²⁺ or Bi³⁺ is bonded to a particular O1 site. Table 2 gives important bond distances and angles and also provides bond valence sums (BVS)¹⁹ for the cations and the full structure is shown in Fig. 1.

Fig. 3 The ambient temperature ⁵⁷Fe Mössbauer spectrum of FePbBiO₄.

Table 1 Refined structural parameters from NPD data from FePbBiO₄ at 300 K and 4 K (the latter are given in italics)

Atom	Site	x	y	z	U iso (or Ueq) × 100/Å^2
P42/mbc: a = 8.48925(9) (8.4725(2)) Å, c = 6.10597(8) (6.1004(2)) Å, volume = 440.04(1) (437.90(3)) Å^3. Rwp = 0.036 (0.056); χ^2 = 4.19 (8.98).a Anisotropic displacement parameters (all × 100/Å^2) are given.
Fe	4d	0.0	0.5	0.25	0.91(3)
					0.58(4)
Pb/Bi	8h	0.1541(1)	0.1570(1)	0.0	1.65^a
		0.1547(2)	0.1558(2)	0.0	1.13
O1	8g	0.6686(1)	0.1686(1)	0.25	2.74^a
		0.6687(2)	0.1687(2)	0.25	1.86
O2	8h	0.0930(2)	0.6303(2)	0.0	1.34(3)
		0.0916(3)	0.6313(3)	0.0	0.70(5)

---

Atom	U 11	U 22	U 33	U 12	U 13	U 23
Pb/Bi	1.27(6)	2.10(6)	1.59(4)	0.21(4)	0.0	0.0
	0.68(9)	1.58(10)	1.13(8)	0.23(6)	0.0	0.0
O1	3.54(6)	3.54(6)	1.14(6)	−2.40(7)	−0.99(5)	0.99(5)
	2.52(9)	2.52(9)	0.52(11)	−1.51(12)	−0.66(10)	−0.66(5)

---

Fig. 4 Fitted neutron powder diffraction profiles at 300 K showing observed data (red crosses), calculated (green line) and difference (purple line). Reflection markers are shown below the diffraction profiles.

Fig. 5 Ion displacements represented by contours enclosing 70% of the neutron scattering.

Table 2 Significant bond distances, bond valence sums (BVS) and angles at 300 K

Bond		Distance/Å	BVS
Fe	–O1	2.024(1) [×2]		2.83
	–O2	2.0435(9) [×4]
Pb/Bi	–O1	2.1298(10)…[×2]	Pb^2+ 2.79		Bi^3+ 2.65
	–O2	2.159(2)

---

Bond	Angle/°
O1–Fe–O1	180.0(0)
O1–Fe–O2	83.71(4) [×4]
	96.29(4) [×4]
O2–Fe–O2	83.34(5) [×2]
	98.05(5) [×2]
O1–Pb/Bi–O1	91.57(5)
	90.89(5) [×2]

---

The unit cell volume (440.0 ų, Table 1) is similar to that of FeSb₂O₄ (439.5 ų),¹³ which reflects a balance in the effects of replacing Fe²⁺ with the smaller Fe³⁺ whilst, at the same time, substituting the larger Pb²⁺/Bi³⁺ combination for Sb³⁺. However, a contraction occurs along a and an expansion along c (for FeSb₂O₄: a = 8.6157(1) Å, c = 5.9207(1) Å).¹³ This effect is universally seen when oxidation occurs at the octahedral intrachain cation owing to enhanced electrostatic repulsions across the common edges of the linked octahedra.

Although the BVS for Fe³⁺ is close to that expected (Table 2), the determined Pb/Bi site provides a highly “overbonded” location for Pb²⁺ whereas Bi³⁺ would be somewhat “underbonded”. However, these values are to be expected since they are determined from the average Pb/Bi and O ionic positions and are consistent with the ADP values, which represent an attempt to model the distribution of the average scattering from the O, Pb and Bi nuclei. Because of the electrostatic repulsion between Fe³⁺ cations within the chains of edge-linked octahedra along [001], the octahedra are extended in this direction; this provides O2–Fe–O2 equatorial angles of 83.34(5)° (where the angle bisector is parallel to [001]) and 98.05(5)° (where the bisector is perpendicular to [001]).

3.2 Magnetic properties

Magnetic susceptibility (χ) data for FePbBiO₄ are shown in Fig. 6a and suggest a simple paramagnetic-antiferromagnetic transition with a Néel temperature of 24 K; a small divergence between the FC and ZFC susceptibilities below T_N is possibly due to a slight canting of the moments. Fig. 6b shows the variation of 1/χ with temperature, which is exactly linear such that it is difficult to differentiate the data points and the least squares fit; the material therefore strictly obeys the Curie–Weiss law: the slope corresponds to an effective moment of μ_eff = 5.870(1) μ_B and the intercept on the temperature axis gives the Weiss constant, θ = −97(1) K. As expected for a d⁵ high spin cation, for which there is zero orbital contribution to the magnetic moment, the moment is in excellent agreement with the spin-only moment of 5.92 μ_B. As is usual for materials with this structure, −θ is significantly greater than T_N; this may be rationalised since θ will reflect the average exchange energy (intrachain and interchain) at temperatures above T_N, whereas T_N is determined largely by the weaker interchain exchange interactions.¹²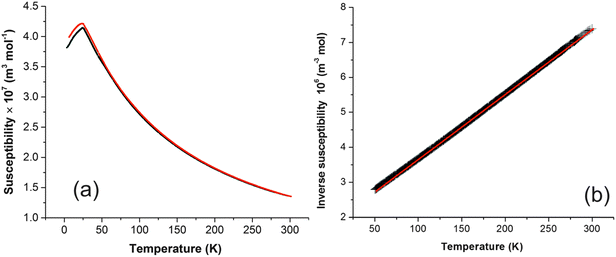

Fig. 6 (a) Plot of magnetic susceptibility against temperature for FePbBiO₄ (FC data red, ZFC data black). (b) Plot of inverse susceptibility against temperature (data are black, linear fit is red).

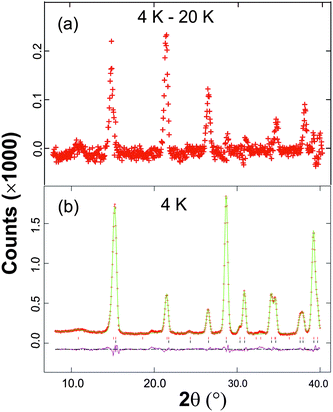
The low temperature magnetic order was explored by collecting NPD data sets at 4 K, 16 K and 20 K. The nuclear structural parameters at 4 K are given in Table 1 and show no major changes compared with those at 300 K. Symmetry allows a range of magnetically ordered structures. Fig. 2 shows the basic types of magnetic order that have been observed for MSb₂O₄ materials, but the actual order in these materials can be complex, with contributions from more than one of the types of order shown in Fig. 2.¹² A separate magnetic phase with P1 symmetry was therefore used in the low temperature refinements to allow complete flexibility. The principal order observed was found to be A-type with moments aligned along [100], A_x, or the equivalent A_y. Although a small C_z component was observed for the largest overall moment (at the lowest temperature, 4 K), at higher temperatures no significant evidence for this was apparent. The refined moments are given in Table 3, where μ_x gives the A-type moment and μ_z the C-type component. The mixture of A_x and C_z components at 4 K corresponds to a small rotation of the moments by 6.3(8)° away from the x-axis towards the z-axis. The NPD profiles at 300 K and 4 K are compared in Fig. 7 for 2θ < 40°, where strong magnetic scattering is observed.

Table 3 Magnetic data for FePbBiO₄ from NPD refinements

Temperature/K	μ x /μB	μ z /μB	μ total/μB
4	3.72(5)	0.41(7)	3.74(6)
16	3.17(6)	0	3.17(6)
20	2.70(7)	0	2.70(7)

---

Fig. 7 (a) The difference between the observed NPD profiles at 4 K and 20 K demonstrating the areas of large magnetic scattering. (b) Fitted neutron powder diffraction profiles at 4 K for 2θ < 40 K: observed data (red crosses), calculated (green line) and difference (purple line). Reflection markers for the magnetic and nuclear unit cells are shown in red and black, respectively.

The NPD data show that FePbBiO₄ and FeSb₂O₄ display the same principal magnetic order: A_x-type with antiferromagnetic order within the chains of FeO₆ octahedra. However, the overall exchange interactions appear to be weaker for FePbBiO₄, since T_N (24 K) is significantly lower than that for FeSb₂O₄, 46 K.^2,3 The Fe³⁺⋯Fe³⁺ direct exchange is probably weaker in FePbBiO₄ because of the more contracted d-orbitals of Fe³⁺. It is also likely that the extended interchain covalent exchange pathway (Fe–O–Pb/Bi–O–Fe) is reduced in energy. Given the increased size of Co²⁺ compared with Fe³⁺, it is a little surprising that CoSb₂O₄ displays C-type order¹¹ (with ferromagnetic order within a given chain of octahedra) whereas FePbBiO₄ is A-type, which is normally associated with strong direct exchange. This feature can be rationalised by the difference in electron configurations within the t_2g orbitals participating in the direct exchange: (t_2g)⁵ and (t_2g),³ respectively. In contrast to Fe³⁺, where all t_2g–t_2g overlaps will result in antiferromagnetic exchange, for Co²⁺ both antiferromagnetic and ferromagnetic exchange interactions are present depending on the electron occupancy of the overlapping orbitals; this will reduce the overall tendency for antiferromagnetic chain order.

The refined magnetic moment at 4 K, 3.74(6) μ_B, is lower than the ideal value of 5 μ_B for Fe³⁺. However, the value is similar to values normally seen for Fe³⁺ compounds, and the reduced moment is caused by zero-point quantum mechanical effects and ligand-to-metal electron transfer inherent to covalence within the Fe–O bonds.

The overall magnetic moments are plotted against temperature in Fig. 8. The Néel temperature from the susceptibility measurements has been included and the resulting four data points fit well to the Brillouin function 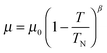where the Néel temperature, T_N, is fixed at 24 K, μ₀ is the zero-point moment and β is an exponent that is linked to the nature of the transition. In this case, fitting the data results in the parameters: μ₀, = 3.89(4) μ_β, and β = 0.20(1). Although lower than that normally found for magnetic order in isotropic materials (for which β is usually ca. 0.3), β is typical for low dimensional systems and is similar to the value of 0.18 reported for FeSb₂O₄.³

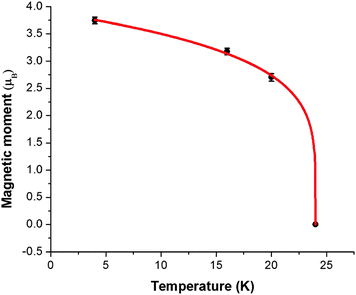Fig. 8 Variation of ordered magnetic moment (●) with temperature fitted to a Brillouin function (red line).

4 Conclusions

Tetragonal FePbBiO₄ has been synthesised and its unit cell shows a contraction along a and an expansion along c compared with that of FeSb₂O₄. These changes are the result of enhanced electrostatic repulsion between the Fe³⁺ cations within the chains of octahedra oriented along [001]. The Bi³⁺ and Pb²⁺ ions are randomly distributed on the sites which form the walls of the channels within the structure, and their bonding preferences result in small differences to their ionic positions; these are reflected in the atomic ADP values. Below the Néel temperature (24 K), FePbBiO₄ displays A-type antiferromagnetic order with moments perpendicular to [001]. The magnetic moment of Fe³⁺ at 4 K is 3.74(6) μ_B, slightly lower than expected for this cation in well-ordered magnetic oxides.

Acknowledgements

We thank EPSRC for financial support of this research (EP/L014114/1) and EPSRC, EU and ILL for the provision of NPD facilities. We are grateful to Dr Emma Suard for assistance in collecting the NPD data and Dr Martin Lees for the use of a SQUID at the Department of Physics, University of Warwick. The X-ray diffractometers used in this research were obtained through Birmingham Science City: Creating and Characterising Next Generation Advanced Materials (West Midlands Centre for Advanced Materials Project 1), with support from Advantage West Midlands (AWM) and part funded by the European Regional Development Fund (ERDF). Data associated with the results shown in this paper are accessible from the University of Birmingham Archive: http://epapers.bham.ac.uk/2162/.

References

1. J. A. Gonzalo, D. E. Cox and G. Shirane, Phys. Rev., 1966, 147, 415.
2. F. Varret, P. Imbert, A. Gerard and F. Hartmann-Boutron, Solid State Commun., 1968, 6, 889.
3. R. Chater, J. R. Gavarri and A. W. Hewat, J. Solid State Chem., 1985, 60, 78.
4. G. Tammann, Z. Anorg. Allg. Chem., 1925, 149, 21.
5. E. Koyama, I. Nakai and K. Nagashima, Nippon Kagaku Kaishi, 1979, 6, 793.
6. J. R. Gavarri, G. Calvarin and B. Chardon, J. Solid State Chem., 1983, 47, 132.
7. H. T. Witteveen, Solid State Commun., 1971, 9, 1971.
8. S. Ståhl, Ark. Kern. Min. Geol., 1943, 17B, 1.
9. M. T. Atanasova, A. M. Strydom, C. J. H. Schutte, L. C. Prinsloo and W. W. Focke, J. Mater. Sci., 2014, 49, 3497.
10. J. R. Gavarri and A. W. Hewat, J. Solid State Chem., 1983, 49, 14.
11. B. P. de Laune and C. Greaves, J. Solid State Chem., 2012, 187, 225.
12. J. Cumby, B. P. de Laune and C. Greaves, J. Mater. Chem. C, 2016, 4, 201.
13. M. J. Whitaker, R. D. Bayliss, F. J. Berry and C. Greaves, J. Mater. Chem., 2011, 21, 14523.
14. A. M. Abakumov, M. G. Rozova, E. V. Antipov, J. Hadermann, G. Van Tendeloo, M. V. Lobanov, M. Greenblatt, M. Croft, E. V. Tsiper, A. Llobet, K. A. Lokshin and Y. S. Zhao, Chem. Mater., 2005, 17, 1123.
15. R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751.
16. H. M. Rietveld, J. Appl. Crystallogr., 1969, 2, 65.
17. A. C. Larson and R. B. Von Dreele, General Structural Analysis System (GSAS), Los Alamos National Laboratory LAUR, 1994, pp. 86–748.
18. B. H. Toby, J. Appl. Crystallogr., 2001, 34, 210.
19. I. D. Brown and D. Altermatt, Acta Crystallogr., Sect. B: Struct. Sci., 1985, 41, 244.

---