 Open Access Article
Open Access ArticleThe quantum mechanics derived atomistic mechanism underlying the acceleration of catalytic CO oxidation on Pt(110) by surface acoustic waves†
Qi
An
a,
Jin
Qian
a,
Robert R.
Nielsen
a,
Luca
Sementa
b,
Giovanni
Barcaro
b,
Fabio R.
Negreiros
b,
Alessandro
Fortunelli
ab and
William A.
Goddard III
*a
aMaterials and Process Simulation Center (MSC), California Institute of Technology, Pasadena, CA 91125, USA. E-mail: wag@wag.caltech.edu
bCNR-ICCOM and IPCF, Consiglio Nazionale delle Ricerche, via Giuseppe Moruzzi 1, 56124, Pisa, Italy
First published on 14th June 2016
Abstract
Experimental evidence that surface acoustic waves (SAW) can significantly enhance the rate of catalytic oxidation of CO to CO2 over the Pt(110) catalyst surface [S. Kelling et al., Faraday Disc., 1997, 107, 435–444] is examined using quantum mechanics (QM) simulations. First we determined the QM based mechanism for the O2-rich régime of the reaction, and the energy landscape of CO interacting with an O-covered reconstructed Pt(110) surface at both static and dynamic levels, but in the absence of SAW. We then utilized ab initio molecular dynamic (AIMD) simulations to determine how SAW might modify the kinetics. We focus here on the short (picosecond time scale) shock spikes induced by switching of domains in the piezoelectric driver on which the catalyst is deposited. We find that SAW-induced spikes promote dynamic changes in the diffusion and desorption, from which we estimate the influence of SAW on CO oxidation rate over Pt(110). We find good agreement with the experimentally observed catalytic enhancement by SAW. With an atomistic mechanism in place one can now consider how to use SAW to enhance other catalytic reactions.
1. Introduction
A great deal of progress has been made in improving catalytic processes through clever use of ligands, surface preparations, solvents, combined with external variables of temperature and pressure. However, major challenges still exist in improving the activity, selectivity and operating conditions for catalytic processes that are of fundamental importance in the energy and environment fields, such as the conversion of petroleum and biomass, water splitting to convert light or fields into energy (H2), CO2 reduction to generate fuels, and NH3 synthesis (Haber–Bosch).1,2 Alternative, non-conventional approaches exploiting novel external electric, magnetic, or mechanical fields are being investigated to enlarge the parametric space for catalysis.3,4We became particularly interested in several experimental studies reporting promising results of acoustic wave enhanced catalysis (AWEC). One experiment used a 100 nm Pd film deposited on a 1 mm LiNbO3 to generate acoustic waves at the resonant frequencies of the crystal (3.4 MHz, in thickness extension mode or TERO) on the Pd film exposed to a recirculating mixture of ethanol (EtOH) and O2. The acoustic waves led to accelerated ethanol oxidation to acetaldehyde by 1880-fold with no effect on oxidative dehydrogenation (ODH) to ethene. In contrast, exposing a Pd catalyst to TERO excitation substantially accelerates (by a factor of 6) ethanol decomposition to ethylene (ODH) but has no effect on the rate of acetaldehyde production.5 No atomistic mechanism has been proposed to explain this puzzling chemistry. Similarly, surface science studies demonstrated that CO oxidation to CO2 (the COox reaction) over the Pt(110) surface was enhanced sufficiently by surface acoustic waves (SAW) to increase the maximum CO pressure for rapid oxidation by 20%.6 Again, no atomistically based understanding is available of how SAW can couple to such catalytic processes sufficiently to induce dramatic increases the rates. Thus, there is no guide for identifying which catalytic processes can be accelerated using this new AWEC approach. Indeed altering conditions sometimes leads to no AWEC or even a decrease in the catalytic rates.7 Clearly to utilize AWEC to design improved catalysts requires an atomistic mechanism to rationalize these experiments.
As a first step in developing an atomistic understanding of how AW might modify rates of catalysis, we chose to examine the effect of SAW on the catalytic oxidation of CO with O2 on the Pt(110) catalyst surface.6 COox/Pt(110) has been studied extensively because when CO and O2 pressures are comparable one observes oscillatory patterns in both space and time (this reaction was the first example of such behavior in the field of heterogeneous catalysis).8 First we carried out quantum mechanics (QM) computations at the PBE level of Density Function Theory (DFT) to develop an understanding of the underlying reaction mechanisms without SAW. Then we used QM to understand how SAW might increase the COox efficiency. We found good agreement of this new mechanism for AWEC with the surface science experiments.
We consider that homogeneous strain fluctuations at 20 MHz and with wave length of 200 μm are unlikely to affect significantly the COox reaction energy landscape. However, we are aware that flipping the domains in the piezoelectric SAW driver can lead to short (picosecond) shock spikes. Thus we investigated how such shocks propagating to the catalyst surface might couple to diffusion, desorption, and reactive phenomena to modify the rates. We model this phenomenon using ab initio molecular dynamics (AIMD) simulations combined with a kinetic model we derived from the QM studies of the COox/Pt(110) reaction. This allows us to estimate the influence of SAW on COox catalytic efficiency. Indeed we find that the predicted SAW enhancement is in good agreement with experiment. This provides an atomistic mechanism that can now be used to design new applications for which SAW might dramatically increase selectivity, produce novel reaction products, or decrease the required temperature or pressure compared to traditional approaches.
2. Computational methodology
We carried out density functional theory (DFT) quantum mechanics using the Perdew–Burke–Ernzerhof (PBE) generalized gradient exchange–correlation (xc) functional,11 a plane wave basis set, and the projected augmented-wave method to simplify the description of atomic cores.12 For technical reasons we use two different codes: Quantum Espresso13 for DFT geometry optimizations and Nudged Elastic Band (NEB)14 evaluation of energy barriers, and VASP15 for the AIMD simulations. We validated that the results of the two codes coincide quantitatively for selected static cases.We found that a kinetic energy cutoff of 500 eV for the plane wave expansions gives excellent convergence of the total energies, energy differences, and structural parameters in structure optimization. The same energy cutoff was applied in both the static DFT and AIMD calculations. The Monkhorst–Pack grid (3 × 3 × 2) in the k-space was used in both the DFT and AIMD simulations. For the DFT simulations, our convergence criteria were: a 1 × 10−5 eV energy difference for solving the electronic wave function and 1 × 10−3 eV Å−1 force for structure optimization. For the AIMD simulations, our convergence criteria were: a 1 × 10−5 eV energy difference for solving the electronic wave function. The spin-restricted KS solvers were used in the AIMD simulations, and the symmetry was not constrained.
We first optimized the bulk Pt system leading to a lattice parameter of 2.82 Å in agreement with the experimental value of 2.78 Å. Then we created a 3 × 2 supercell along the “a” and “b” direction and constructed a five layer slab along the c direction with 20 Å vacuum. The bottom two Pt layers were fixed during the AIMD simulations. To validate that a 5-layer slab is sufficient, we also calculated the CO absorption energy on the facet sites for a 7-layer slab with 0.83 ML oxygen coverage. The CO absorption energy changed by only 0.01 eV suggesting that the 5-layer slab is sufficient.
The AIMD simulation procedures were as follows. First the systems were heated at a constant rate from 10 to 300 K over 10 ps. Then the systems were equilibrated at 300 K for 1 ps using the NVT (constant volume, constant temperature, and constant number of atoms) ensemble. Next, we heated the system from 300 to 1700 K uniformly over 5 ps. Finally the system was equilibrated at 1700 K for 5 ps before the shock simulations. The time constant for the Nose–Hoover thermostat was 0.1 ps. The time step 1 fs was used for integrating the equation of motion.
To mimic the spikes in the SAW experiments, we introduced a relatively strong shock by displacing the Pt atoms of two bottom layers by 0.5 Å further away from the unfixed layers but keeping them frozen. The intensity of the shock thus may possibly be stronger than that in the SAW experiments but it allows us to observe possible effects of a shock within the short time of a few picoseconds practical for AIMD simulations. This shock increases the potential energy of the supercell typically by 5.5 eV and the temperature of the system by ≈300 K (as shown in Fig. S2 of the ESI†). We applied a microcanonical (NVE) ensemble during the shock simulation. Further computational details are provided in the ESI.†
3. Results and discussion
3.1 Reaction mechanisms without SAW
The experimental apparatus used in ref. 6 is shown in Fig. 1a: an interdigital transducer is composed of a single-crystal piezoelectric film of 1 mm thickness covered on both sides with 500 nm-thick platinum layers exposing the (110) surface. This was obtained by growing Pt on a NaCl substrate, then dissolving the ionic substrate on top of a piezoelectric film to which the Pt layer is cold-welded. This was followed by sputtering and annealing the resulting composite system to obtain the proper surface orientation. In this apparatus, the Pt layers lie perpendicular to the propagation path of the SAW, acting simultaneously as catalysts and as electrodes for generating SAW at the surface of the underlying piezoelectric. The SAW frequency is 18.8 to 19.8 MHz with an applied power up to 1 W. Doppler measurements show that the SAW produces surface oscillations that extend up to 20 nm perpendicular to the catalyst surface6 with a longitudinal wave length of 200 μm, implying a homogeneous strain of ∼10−4.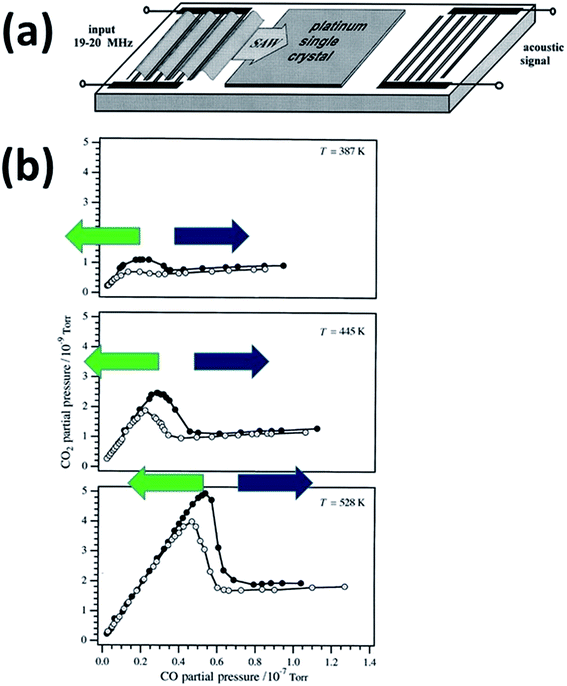 | ||
| Fig. 1 (a) Schematic picture of the interdigital transducer device used by Kelling6 to test the effect of SAW on heterogeneous catalysis. (b) Measurements of COox reaction rate: CO2 partial pressure as a function of CO pressure with a constant baseline O2 pressure PO2 = 1.2 × 10−7 Torr at three different temperatures: from top to bottom in order of increasing temperature from T = 387, T = 445 and T = 528 K, and with SAW excitation off (white) or on (black). Green and blue arrows have been added to highlight the transition from CO-poor (green) to CO-rich (blue) régimes. Adapted with permission from ref. 6. © Royal Society of Chemistry (1997). | ||
The COox reaction in ref. 6 was studied over the temperature range between T = 387 and T = 528 K, with a constant baseline O2 pressure PO2 = 1.2 × 10−7 Torr. The CO pressure was increased from zero to PCO = 8 × 10−8 Torr, while the evolving CO2 pressure (PCO2) was measured in the presence and absence of SAW excitation, as shown in Fig. 1b. Two COox régimes are apparent in Fig. 1b:
• The CO-poor régime in which PCO2 changes linearly as a function of PCO, with a proportionality factor around ≈0.1 weakly dependent upon the temperature. In this régime Low-Energy Electron Diffraction (LEED) characterization showed a (1 × 2) reconstructed pattern.9
• The CO-rich régime for PCO higher than a temperature-dependent threshold, where the COox reaction rate decreased dramatically, saturating at a plateau whose value also depends upon temperature. In these CO-rich conditions the (1 × 2) reconstruction of the Pt(110) surface is lifted. At CO coverages higher than ≈0.20 monolayers (ML, calculated relative to the density of Pt atoms in the (1 × 1) surface) the strong interaction of CO with Pt leads to the (1 × 1) unreconstructed surface.9,10
• The transition from the linear to the plateau régime of COox occurs when PCO is large enough that the CO coverage exceeds ≈0.2 ML.
When the SAWs are turned on, the above qualitative picture does not change, however the SAW increases the PCO threshold at which the cross-over to a pressure-independent régime occurs by roughly 20%. That is, the SAW extends the high-efficiency non-oscillatory linear régime by 20% (together with a weak increase in the PCO2 plateau for the CO-rich region). Thus the effect of SAW on COox/Pt(110) is homologous to increasing the temperature of the transition by ≈35 K. However the experiments were carefully conducted to exclude any significant increase in the sample temperature under the given conditions (upper bound of <5 K), thus leaving open the question of the origin of the SAW-induced catalytic enhancement.
To gain insight into the atomistic mechanisms of these effects, we focused on the high-efficiency, O2-rich or CO-poor branch of the COox reaction. Experimentally the bare Pt(110) surface exhibits the well-known (1 × 2) missing row reconstruction, formed by erasing every second topmost [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] row of Pt atoms.16 This reconstruction is preserved under O2-rich conditions17 in which the surface is covered with O adatoms, as schematically depicted in Fig. 2a for the Pt(110) surface with an oxygen-coverage of 1 ML (a CO molecule adsorbed on top of Pt rows is also shown in this figure). Note that the O adatoms are located in bridge/hollow sites of the fcc(111)-like facets that characterize the Pt(110) reconstructed surface.18 For temperature in the range 387 to 528 K and PO2 = 1.2 × 10−7 Torr the actual oxygen coverage is ∼0.85 ML.19 Thus we consider that a Pt(110) (3 × 2) cell with one O adatom missing represents a realistic model of Pt(110) at an O-coverage = 0.83 ML as shown in Fig. 2b. Under static long-time conditions and higher PO2, the O adatoms self-organize into a (11 × 2) 0.91 ML superstructure17 that is weakly favorable thermodynamically.20 But we expect that this ordered structure does not occur under the disordering influence of CO. Other quantities that will be used in the following are:
0] row of Pt atoms.16 This reconstruction is preserved under O2-rich conditions17 in which the surface is covered with O adatoms, as schematically depicted in Fig. 2a for the Pt(110) surface with an oxygen-coverage of 1 ML (a CO molecule adsorbed on top of Pt rows is also shown in this figure). Note that the O adatoms are located in bridge/hollow sites of the fcc(111)-like facets that characterize the Pt(110) reconstructed surface.18 For temperature in the range 387 to 528 K and PO2 = 1.2 × 10−7 Torr the actual oxygen coverage is ∼0.85 ML.19 Thus we consider that a Pt(110) (3 × 2) cell with one O adatom missing represents a realistic model of Pt(110) at an O-coverage = 0.83 ML as shown in Fig. 2b. Under static long-time conditions and higher PO2, the O adatoms self-organize into a (11 × 2) 0.91 ML superstructure17 that is weakly favorable thermodynamically.20 But we expect that this ordered structure does not occur under the disordering influence of CO. Other quantities that will be used in the following are:
• Under the above conditions the experimental dissociative sticking probability for O2 molecule onto Pt(110) is ∼0.03 {Fig. 1 of ref. 21}.
• In contrast the dissociative sticking probability of O2 onto the bare (1 × 2)-reconstructed Pt(110) surface at T around 500 K is ≈0.3 (see Fig. 2 of ref. 22).
• The CO sticking coefficient onto the bare (1 × 2)-reconstructed Pt(110) surface is about 0.6.22
We also calculated the NEB energy barrier for O-hole diffusion to be 0.88 eV at 0.83 ML coverage. Thus an O-adatom can jump from one site to the next will take place in 3 × 10−4 s at T = 528 K, implying that O-adatom diffusion is fast in these conditions.
We next investigated CO interaction with the Pt(110)-(1 × 2) at various O-coverages. At 1 ML O-coverage we find that CO adsorbs on-top of the ridge of [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] rows (see Fig. 2a for a schematic depiction) with a very weak absorption enthalpy of 0.1 eV, so very little CO is on the ridge at ∼500 K. We anticipate that our DFT results as reported below are in general consistent with both experiment and previous theoretical results.20,23 However, one important difference we find with respect to previous computational studies is for the Eley–Rideal (ER) mechanism (the process in which a CO molecule hits a 1 ML-O-covered reconstructed Pt(110) surface and picks up an O adatom thus producing CO2). To investigate this process in detail, we carried out the following calculations:
0] rows (see Fig. 2a for a schematic depiction) with a very weak absorption enthalpy of 0.1 eV, so very little CO is on the ridge at ∼500 K. We anticipate that our DFT results as reported below are in general consistent with both experiment and previous theoretical results.20,23 However, one important difference we find with respect to previous computational studies is for the Eley–Rideal (ER) mechanism (the process in which a CO molecule hits a 1 ML-O-covered reconstructed Pt(110) surface and picks up an O adatom thus producing CO2). To investigate this process in detail, we carried out the following calculations:
• We established an upper bound of 0.55 eV for the ER barrier, by carrying out NEB calculations along a path between an initial state in which CO is adsorbed on top of a [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] ridge and a final state corresponding to the 0.83 ML-covered Pt(110) surface plus gas-phase CO2 (as illustrated in Fig. 2c).
0] ridge and a final state corresponding to the 0.83 ML-covered Pt(110) surface plus gas-phase CO2 (as illustrated in Fig. 2c).
• For COox at 1 ML O-coverage, we carried out a systematic scan of the potential energy surface to find an energy barrier for ER of ≈0.4 to 0.5 eV, depending on the CO path.
• In contrast, Pedersen predicted a high (>1.1 eV) energy barrier for this process.20
A second difference we find with respect to previous theoretical studies is that
• We predict an even smaller COox barrier (≈0.3 eV) for an ER mechanism at low (0.25 ML) O-coverage. This is consistent with the most recent experimental evidence for COox on Pt(111), according to which the COox reactivity increases in the order: α-PtO2 < Pt–O surface oxide [similar to 1 ML O-covered Pt(110)] < single O adatom.24
• In contrast, the previously predicted the lowest COox energy barrier was only 0.3 eV for the PtO2 [10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] oxide phase,20 which is not consistent with the experiments in which the COox barrier is smaller at low O-coverage.
0] oxide phase,20 which is not consistent with the experiments in which the COox barrier is smaller at low O-coverage.
At 0.83 ML O-coverage, we find that CO adsorbs on top of a [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] row ridge next to the O-hole with an absorption energy of 0.53 eV, but we find that it is much more favorable (an adsorption energy of 1.52 eV) to adsorb in the hollow fcc(111)-like site left empty by the missing O adatom, as illustrated in the left-hand-side of Fig. 2d. In this site, CO can react with an adjacent O adatom to produce CO2via a Langmuir–Hinshelwood (LH) mechanism, a process illustrated in Fig. 2d. This decreases the total energy by 0.62 eV, leading to an energy barrier of 1.34 eV and an Arrhenius prefactor of 1.06 × 1013 Hz.
0] row ridge next to the O-hole with an absorption energy of 0.53 eV, but we find that it is much more favorable (an adsorption energy of 1.52 eV) to adsorb in the hollow fcc(111)-like site left empty by the missing O adatom, as illustrated in the left-hand-side of Fig. 2d. In this site, CO can react with an adjacent O adatom to produce CO2via a Langmuir–Hinshelwood (LH) mechanism, a process illustrated in Fig. 2d. This decreases the total energy by 0.62 eV, leading to an energy barrier of 1.34 eV and an Arrhenius prefactor of 1.06 × 1013 Hz.
The value of 1.34 eV that we calculate for the energy barrier for COox in the LH path at 0.83 ML O-coverage is close to the value of the barrier for CO desorption (1.52 eV). We explain this as due to the repulsion between CO and adsorbed O-atoms that we find in this system. The small difference between the CO adsorption energy and the LH COox energy barrier (0.18 eV) suggests that the COox/Pt(110) reaction is dominated by a competition between these two different processes for the experimental conditions of interest (see the discussion below). The ER and LH mechanisms are both viable under the given conditions, however the ER mechanism has a much lower energy barrier (<0.5 eV) than the LH barrier (1.3 eV) while LH is favored by low pressure (low impinging rate). We note that CO2 adsorption on Pt(110) at various O-coverages has been tested and found to be unfavorable with respect to CO2 evolution, so that no formation of CO2 nor CO3 (carbonate) adsorbed species is expected, a result quite different for other metal heterogeneous catalysts.25
The picture emerging from these calculations is in excellent agreement with precise spectroscopic experimental characterization under reaction conditions,26 which show the existence of two régimes for COox:
• A low-PCO/high-rate branch where the reacting CO species is adsorbed on the Pt surface and embedded within an O-rich environment (it was proved experimentally that bridging CO is absent) of fully developed Pt oxides or subsurface oxygen.
• And a high-PCO/low-rate branch.
At low O-coverage (or high CO coverage) the energy landscape for CO adsorption changes again. First, as mentioned above, the ER COox barrier drops to ≈0.3 eV at 0.25 ML O-coverage. Concurrently, CO adsorption changes both the site and energetics: as illustrated schematically in Fig. 2e, the CO adsorption energy is 1.77 eV at the on-top site of the ridge of [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] rows, far from the O adatom. This strongly non-linear dependence of the CO + O energetics on the Pt(110) surface observed experimentally is expected since it is ultimately the origin of well-known oscillatory behavior of the COox process on this heterogeneous catalyst.8
0] rows, far from the O adatom. This strongly non-linear dependence of the CO + O energetics on the Pt(110) surface observed experimentally is expected since it is ultimately the origin of well-known oscillatory behavior of the COox process on this heterogeneous catalyst.8
Finally, our calculations show that O2 dissociation on the reconstructed surface occurs only when two adjacent sites are empty (in agreement with previous studies23). In this case the O2 molecule binds with an adsorption energy of 0.72 eV, and goes through a saddle point with an energy barrier of 0.54 eV to form O-adatoms at two nearest-neighbor sites, as illustrated schematically in the left-hand-side, middle and right-hand-side, respectively, of Fig. 2f for a (2 × 2) unit cell at 0.5 ML O-coverage. In contrast, in the absence of two adjacent vacant sites the probability of O2 dissociation is negligible,23 in agreement with experiment.19
For convenience of the reader, we summarize the results of static DFT calculations in Fig. S3 and S4 of the ESI.†
3.2 SAW-induced catalytic effects
Having clarified the energy landscape of CO over O-covered Pt(110)-(1 × 2) surface from static DFT calculations, we now explore how SAW-induced effects can affect the catalytic rates.SAWs produce a homogeneous strain of the Pt lattice, as determined by Doppler experiments.27 However in agreement with previous studies28 we calculate that a sizable strain (of the order of 1–2%) is necessary to induce sufficiently large changes in adsorption energetics to influence catalytic rates. This strain is 100 times larger than observed for homogeneous SAW modulations of the surface (of the order of 10−4, as noted above).
Also in agreement with previous studies29 we find that electric fields of the order of a few V nm−1 would be necessary to change the adsorption and reaction energetics sufficiently to explain the observed increase in catalytic efficiency. For example, we calculate that an electric field of 1 V nm−1 changes the CO adsorption energy on Pt(110) by 0.015 eV. This suggests that a field of at least 6 V nm−1 would be required to produce a sizable effect of 0.09 eV. Such high electric fields are not expected under the SAW conditions, since many unobserved phenomena would be triggered at much lower field values.30 Moreover such fields are unrealistic considering the thickness and screening of the Pt metallic layer, which would attenuate the electric field down to values ∼1000 times smaller than required.6
The effects of SAW-induced homogeneous strain on diffusion31 can also be excluded as well as the major cause of the observed increase in COox efficiency, since the diffusion energy barriers are also sizable (the barrier to O-diffusion is 0.88 eV) and thus appreciably modified only by much larger values of the strain.
The presence of structural defects might enhance SAW effects, but which kind of defects? Local defects are not visible in PEEM experiments6 in the low-P(CO), highly efficient, linear-régime branch of COox reaction. An interesting hint comes from the observation that the SAW-enhanced catalysis does not occur on the pristine sample, but only after an incubation time.6 A more thorough characterization27 ascertained that during the incubation time the surface begins to exhibit damage, with the Pt layers developing cracks, while Pt-species down to single Pt atoms are scattered away from the damaged surface onto the surrounding of the sample. In particular, a model for generating cracks by phase shift of the acoustic waves was proposed, in which sudden “spikes” or “riggles” develop at the surface of the Pt layer due to interference of SAW. This effect is similar to that of shock wave that we investigated previously in a different context.32
To obtain information about the atomistic processes produced by a shock wave at the Pt(110) surface, we constructed a model Pt(110) 17 nm-thick slab (7170 atoms) and used the ReaxFF reactive force field33 with parameters specifically derived for Pt systems34 to investigate the impact of this slab against a hard wall. Snapshots and the velocity distribution from this simulation in Fig. S1† and 3 show the effects of a shock wave generated at one end of the slab as it propagates through the slab to reflect off the opposite free (110) surface. We observe that the impinging wave produces a temporary flattening of the surface as one most notable effect. To translate this result into a first-principles AIMD dynamics simulation of a reactive system, we devised the following computational procedure:
 | ||
| Fig. 3 Positions and velocity distribution along shock direction (Vz component) for the atoms near the free surface from ReaxFF simulations of the collision of a Pt(110) slab against a hard wall positioned at extreme right-hand-side of the picture (see also Fig. S1†). Each snapshot captures the systems at increasing times from top to bottom. The times are 3.4, 3.9, 4.1, 4.2 ps from top to bottom [color coding for velocity distribution (unit: km s−1)]. | ||
• We took a (3 × 2) cell of a 0.88 nm-thick Pt(110) slab covered on one side by co-adsorbed CO and O. Here we used 1 adsorbed CO molecule and 5 O adatoms (0.83 ML O-coverage) as in the left-most panel of Fig. 2(d).
• We carried out ab initio molecular dynamics (AIMD) after first equilibrating the system at 300 K for 10 ps.
• Then to model the effect of phase-shifted SAW we extended the two bottom Pt layers by 0.5 Å from the rest of the system (as suggested by the ReaxFF shock wave simulations in Fig. 3), fixed them, and carried out a final NVE AIMD calculation at a temperature of 1700 K (since AIMD simulations can only be done for few ps, a high temperature is needed to observe dynamic phenomena).
We find that without SAW no reactive event is observed on the equilibrated CO & O-covered Pt(110) surface over the period of 10 ps, even at this high temperature. However with the SAW we observed that several dynamic processes are triggered in the AIMD simulations (a movie of a representative trajectory is included in the ESI†). The temperature and the internal energy changes of the system under SAW conditions are displayed in Fig. S2,† and show an increase in the temperature by ≈300 K due to SAW shock wave. Here we see:
• CO diffusion (also in the form of a Pt–CO unit as illustrated in Fig. 4a). This occurred 4 times in the 7 simulations.
 | ||
| Fig. 4 Snapshots from AIMD simulations illustrating the dynamic processes thereby extracted: (a) CO diffusion (also in the form of a Pt–CO unit); (b) Pt–CO detachment; (c) COox reaction. | ||
• Pt–CO detachment (Fig. 4b). This occurred in 5 of the 7 simulations.
• COox reaction (Fig. 4c and the ESI movie†). This occurred in 3 of the 7 simulations.
These simulations provide a rational for the experimentally observation.
First, CO diffusion is found to be facile, both as a CO molecule and as a Pt–CO unit, as illustrated in Fig. 4a. In particular, CO interacts strongly with the less coordinated Pt atoms so that a Pt–CO unit rather than a single CO molecule can sometimes desorb from the surface. We note in this connection that our computational approach predicts an adsorption energy of 2.0 eV for CO on top of a ridge of the bare reconstructed Pt(110) surface at zero O-coverage. This value is in very good agreement with the 1.9 eV estimate from calorimetric experiments in the limit of low coverage (see Fig. 1 in ref. 22) but is much larger than the estimate of 1.56 eV from surface temperature35 and molecular beam modulation36 techniques. This discrepancy can be reconciled by noting that the CO molecule in the pre-desorption state acquires a significant entropic free-energy component from libration modes, a component that is absent in the equilibrium configuration. From a previous analysis37 we derive that this increases the Arrhenius prefactor of CO desorption by a factor ≈102 with respect to values typical for surface processes. Indeed in ref. 37 the desorption of CO from a Ni(110) surface was considered. Using a classical stochastic diffusion equation for the distance between the C atom and the surface and assuming that the adsorbed CO molecule can transform energy from the bending (librational) mode of the O atom about the Ni–C bond into translational kinetic energy, an Arrhenius expression for the rate of CO desorption was obtained differing from a standard one only in the pre-exponential factor which turned out to be ≈1015 instead of ≈1013 as predicted from the characteristic frequency of the adsorbate–surface interaction potential. The increase in librational entropy singled out in the CO-over-Ni(110) case is typical for CO desorption. Thus, we use the same estimated number for our CO-over-Pt(110). This produces an apparent decrease of the CO adsorption energy under dynamic condition that is not expected in static experiments such as temperature-stimulated desorption experiments. This point (usually neglected in the analysis of these experiments via the Redhead equation) will be important in the kinetic analysis below.
Second, we observe detachment of Pt in our simulations, not as a Pt atom but as the more stable Pt–CO unit (Fig. 4b). This rationalizes the experimental observation of Pt-species down to single Pt atoms scattered away from the damaged surface into the regions surrounding the sample.6 This is thus qualitatively in agreement with the presence of stochastic spikes at the surface.
Third, the SAW-induced spikes in our AIMD simulations eventually promote COox reactions (Fig. 4c). Interestingly this occurs via an ER-like mechanism in which CO first shifts from (111)-facet adsorption to on-top [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] ridge adsorption, from which it descends back to the O-covered (111)-like surface to pick up an O adatom and produce gas-phase CO2. This is similar to the results of our scan of the potential energy surface at the static DFT level for the ER COox mechanism (see above). This excellent agreement between static DFT and dynamic AIMD simulations corroborates both observations.
0] ridge adsorption, from which it descends back to the O-covered (111)-like surface to pick up an O adatom and produce gas-phase CO2. This is similar to the results of our scan of the potential energy surface at the static DFT level for the ER COox mechanism (see above). This excellent agreement between static DFT and dynamic AIMD simulations corroborates both observations.
3.3 Kinetic model
We can now quantify our analysis. The highly efficient régime of the COox reaction is suppressed at high P(CO) by the competition between O2 dissociation vs. CO adsorption sticking probabilities turning in favor of CO, which eventually covers and poisons the surface. We know from experiment8 that the switch between low-P(CO) and high-P(CO) régimes occurs when CO-coverage is about 0.2 ML. We define the following simplified kinetic model:| ġCO = ge × ICO × SCO − gCO × [gO × RCOox + Rdes] | (1) |
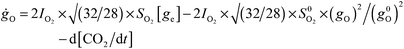 | (2) |
 | (3) |
| d[CO2]/dt = SER × ICO × gO + gCO × gO × RCOox | (4) |
| ge = coverage of empty sites in ML | (5) |
| gO = coverage of O-adatoms in ML | (6) |
| g0O = O-coverage in the absence of CO = 0.85 ML [ref. 19] | (7) |
| gCO = coverage of CO in ML | (8) |
| ICO = impingement rate of CO | (9) |
| IO2 = impingement rate of O2 | (10) |
| SCO = sticking coefficient of CO on an empty site = 0.6 [ref. 22] | (11) |
| SO2[ge] = dissociative sticking coefficient of O2 = 0.3 (ref. 22) × {probability of adjacent empty sites}[ge] | (12) |
| {Probability of adjacent empty sites}[ge] = 2[(n − 1)/n] × (ge)2 × {1 + (n − 2)(n − 3/2)/100} | (13) |
 | (14) |
| SER = probability of an Eley–Rideal COox reactive event = 0.093 | (15) |
| RCOox = COox LH reaction rate = 1.06 × 1013 × exp[−1.34 eV/kBT] | (16) |
| Rdes = CO desorption rate = 100 × 1.06 × 1013 × exp[−1.52 eV/kBT] | (17) |
| d[CO2]/dt = rate of CO2 production | (18) |
Formula (13) predicts that in the absence of CO at g0e = 1 − g0O = 0.15 ML the probability of two empty adjacent sites is ≈0.116 so that SO2[ge] = 0.3 × 0.116 ≈ 0.03 in keeping with experiment.21
Note that we have ġCO + ġe + ġO = 0, as it should be since gCO + ge + gO = 1.
The Eley–Rideal SER sticking coefficient is estimated as ≈0.093 to ensure consistency with experiment21 and with the observed approximately linear behavior of the rate of CO2 production as a function of PCO in CO-poor conditions (see Fig. 1).
Some numbers derived from this analysis are as follows:
(1) The O2 impingement rate IO2 corresponds to one collision every 54 s per surface site at PO2 = 1.2 × 10−7 Torr and T = 528 K. The rate of O2 dissociation is obtained by multiplying this number times the dissociative sticking coefficient, which is about 0.03 at ge = 0.15 ML (in the absence of CO).21
(2) The CO adsorption rate is given by the CO impingement rate (ICO, related to the O2 impingement rate times the ratio of pressures and the square root of mass ratio) times the sticking coefficient of CO onto an empty site (0.6 [ref. 6]) times the fraction of empty sites. This leads to ∼one event every several 102 seconds per surface site under operating conditions.
(3) The rate for the COox reaction of adsorbed CO molecules is given in eqn (1)–(4) as the product of O-coverage times CO-coverage (gO × gCO) times the COox LH reaction rate, which is determined by an Arrhenius formula with a prefactor (1.06 × 1013 Hz) and an activation energy (1.34 eV) as calculated at the DFT level (see above).
(4) The rate of CO desorption is instead determined by an Arrhenius formula with a prefactor calculated as 100 times the prefactor for LH COox36 and a DFT-calculated activation energy (1.52 eV, see above).
Clearly the formula for the COox LH reaction rate [=gO × gCO × RCOox] holds for CO molecules adsorbed within an environment of O-adatoms as in Fig. 2c. This model is realistic as long as the rate of CO desorption and LH COox is slower than the CO adsorption rate, which under the given conditions is certainly true up to T = 445 K.
However at T = 528 K we find that CO desorption and LH COox become much faster (time-scale of seconds) than CO adsorption (time-scale of hundreds of seconds). This corresponds to a different régime in which CO would not poison the surface, because CO in the gas phase becomes thermodynamically more stable than CO adsorbed on the Pt(110) surface within an environment of O-adatoms. In such a régime, CO that was adsorbed on-top of the ridge of [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] rows in the low O-coverage regions becomes the dominant species (see Fig. 2e), with an adsorption energy increasing from 1.52 eV (Fig. 2d, left-hand-side) to 1.77 eV (Fig. 2e). This is sufficiently large to stabilize it against CO in the gas phase. In this régime adsorbed CO will reorganize in patches or islands with a low O-coverage. From these different adsorption sites CO will jump onto a fcc(111)-like facet next to an O adatom to produce CO2via a LH mechanism. In a first approximation we take this into account in the kinetic model described above by assuming an equilibrium between CO on-top of [1
0] rows in the low O-coverage regions becomes the dominant species (see Fig. 2e), with an adsorption energy increasing from 1.52 eV (Fig. 2d, left-hand-side) to 1.77 eV (Fig. 2e). This is sufficiently large to stabilize it against CO in the gas phase. In this régime adsorbed CO will reorganize in patches or islands with a low O-coverage. From these different adsorption sites CO will jump onto a fcc(111)-like facet next to an O adatom to produce CO2via a LH mechanism. In a first approximation we take this into account in the kinetic model described above by assuming an equilibrium between CO on-top of [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] ridges and CO next to an O-adatom, and then using the same kinetic formulae eqn (1)–(18) with RCOox and Rdes modulated by the Boltzmann factor = exp[−(1.77 − 1.52 eV)/kBT]. This will then be assumed in the following analysis.
0] ridges and CO next to an O-adatom, and then using the same kinetic formulae eqn (1)–(18) with RCOox and Rdes modulated by the Boltzmann factor = exp[−(1.77 − 1.52 eV)/kBT]. This will then be assumed in the following analysis.
Assuming now steady-state conditions we set: ġCO = ġe = ġO = 0, and we solve the resulting eqn (1)–(3) subject to the constraint gCO + ge + gO = 1. The solution is not analytic due to the presence of higher powers in the unknowns, but we obtained results numerically. To give a qualitative but realistic idea of the solution of this model, we note that, setting eqn (1) = 0, we obtain:
| gCO = ge × ICO × SCO/[gO × RCOox + Rdes] | (19) |
Now, considering that gO does not change much under the given conditions (ranging between 0.85 and 0.65 ML), formula (19) predicts that the number of surface sites covered by CO is simply proportional to the number of empty sites. Note that the coefficient of proportionality is basically given by the ratio between the rate of impingement vs. that of surface processes, where the quantities ICO, SCO, RCOox, Rdes, are either constant or known as function of temperature and pressure, see formulae (9)–(18) above. The precise numerical solution of the kinetic model provides us with the following estimates.
At P(O2) = 1.2 × 10−7 Torr and T = 445 K, we predict that gCO ≈ 0.2, and thus the predicted switch between low-P(CO) and high-P(CO) régimes, at PCO = 0.43 × 10−7 Torr, which can be compared with the experimental value of 0.23 × 10−7 Torr.
At P(O2) = 1.2 × 10−7 Torr and T = 528 K, we predict that gCO ≈ 0.2 at PCO = 0.73 × 10−7 Torr, which can be compared with the experimental value of 0.45 × 10−7 Torr.
We also predict that the ratio between P(CO2) and P(CO) in steady state is around 0.11 to 0.12, which is close to the experimental value of ≈0.1 (see Fig. 1).
Considering the approximations involved, the intrinsic uncertainties of DFT predictions, and the sensitivity of the system kinetics to variations in the input parameters, the proposed picture is at least semi-quantitatively consistent with experiment. Indeed, if we simply increase the value of the energy barrier for the COox LH reaction and CO desorption by 0.026 eV (i.e., changing them from 1.34 eV to 1.366 eV and from 1.52 eV to 1.546 eV, respectively), we predict a PCO threshold = 0.23 × 10−7 Torr at T = 445 K and = 0.424 × 10−7 Torr at T = 528 K, respectively, which match very well the experimental values of 0.23 × 10−7 Torr and 0.45 × 10−7 Torr, respectively.
We now consider the SAW case. The AIMD simulations suggest that turning on SAW activates several dynamic processes, as discussed above. It is not easy to quantify the corresponding effect on the CO oxidation process because the AIMD simulation must be run at elevated temperature to observe dynamic processes in the time scale of ab initio molecular dynamics (few ps), even in the presence of SAW excitation. Thus our statistics are necessarily limited by the computational effort associated with AIMD simulations. Moreover processes such as Pt–CO desorption generates fresh new catalyst surface that can drastically change the energy landscape of the reaction. Nevertheless, the present findings can be summarized as follows.
• First, we do not observe any reactive or desorption processes during the 10 ps AIMD control runs in the absence of SAW stimulation.
• Second, considering all the AIMD NVE runs (i.e., for a total simulation time of 25 ps) we observe 3 LH COox events, 4 CO desorption events, and 1 Pt–CO desorption event. Here the time scales of LH COox and desorption are different: CO or Pt–CO desorption occur on average within the first 1.8 ps, whereas LH COox events occur on average after 4.3 ps. In other words, the first effect of the SAW spike is to desorb CO with high probability. However, even if the spike does not succeed in desorbing CO in the first 1.8 ps, the energy lingering in the system (recall that we conduct NVE simulations) can promote LH COox reaction with a probability of about 40–50% after 4.3 ps.
To translate these observations into quantitative estimates of the effect of SAW on the efficiency of the COox catalytic process, we consider for simplicity only the SAW increase in CO desorption. The total area of the catalyst used in the experiment is 0.4 × 0.4 mm9 which (at gCO ≈ 0.2) corresponds to ≈3 × 1011 surface sites. Each SAW cycle occurs with a frequency around 20 MHz, which we assume may produce several shock events. If we assume that each SAW cycle produces – say – 7 CO desorption events over the whole area of the catalyst, this will increase the CO desorption rate by ≈20%. Thus the ratio of surface processes [gO × RCOox + Rdes] with respect to the CO impingement rate in eqn (19) will shift the PCO threshold at which the switch between low-P(CO) and high-P(CO) régimes occurs. In particular, assuming 7 CO desorption events per SAW cycle, the switch between the two régimes in the presence of SAW stimulation is predicted to occur for
• P(CO) = 0.30 × 10−7 Torr when T = 445 K and
• P(CO) = 0.51 × 10−7 Torr when T = 528 K, respectively.
This can be compared to the experimental values of
• P(CO) = 0.29 × 10−7 Torr when T = 445 K and
• P(CO) = 0.54 × 10−7 Torr when T = 528 K.
Thus, despite the several approximations involved in the present analysis and uncertainties in predicted energetics, we conclude that our proposed mechanism is in semi-quantitative agreement with experiment, thus providing a consistent atomistic mechanistic understanding and rationalization.
4. Conclusions and perspectives
In summary, we present here a QM-based theoretical analysis and assessment of the experimentally observed surface-acoustic-wave (SAW)-induced enhancement of the COox/Pt(110) reaction.6,9,27 Our AIMD simulations lead to atomistic mechanisms for SAW to enhance such dynamic processes as diffusion, desorption, and reaction, that are accelerated by the several short shocks during each cycle of the SAW. This spectrum of SAW induced fluctuations in the surface concentrations indicates a decoupling of the degrees of freedom related to space and velocity that is qualitatively different from that of thermal fluctuations. That is, the SAW can increase fluctuations in localized regions of space while keeping fluctuations in velocity averaged over large distances basically constant.This development of an atomic mechanism is a necessary step to start exploiting the SAW approach to modulate and control surface effects. We find that short picosecond shocks from domain flipping transitions during the SAW 20MHx cycle provide the possibility of delivering localized packets of energy to specific, performance-limiting mechanistic steps (in the present case the desorption of the CO poisoning species) to provide a novel means to affect local atomistic level modulations that can alter catalytic rates. This mechanism provides a basis for selecting other catalyst processes that might be dramatically enhanced with SAW.
For example, we considered here a continuous film deposited on the piezoelectric surface. However, this should apply equally for polycrystalline samples as those used in Inoue's experiments5 provided that there are pathways for the shock to propagate to the catalytic surface. To extend this concept to such high surface area materials as catalyst nanoparticles on inactive porous supports, it would be important to ensure that the shock propagation can proceed from the piezoelectric surface to the catalyst surface. Highly anisotropic materials seem especially appealing in this respect.
However, a major challenge in making this AWEC approach effective will be to achieve precise control of AW-induced dynamical processes, that avoids dispersion of SAW energy into purely thermal dissipation or (worse) unwanted side-processes such as scattering of Pt atoms as in the COox/Pt(110) case here investigated. One intriguing possibility in this respect might be surface nanopatterning via deposition of size-selected nanoclusters from the gas phase that might control the grain size, morphology, and boundaries to focus and control the shocks at the catalytic surfaces.
Acknowledgements
This work was funded by the U.S. Department of Energy's Advanced Research Projects Agency-Energy (ARPA-E) under contract number DE-AR0000552.References
- C. Marcilly, J. Catal., 2003, 216, 47–62 CrossRef CAS.
- J. N. Galloway, F. J. Dentener, D. G. Capone and E. W. Boyer, et al. , Biogeochemistry, 2004, 70, 153–226 CrossRef CAS.
- A. Assion, T. Baumert, M. Bergt, T. Brixner, B. Kiefer, V. Seyfried, M. Strehle and G. Gerber, Science, 1998, 282, 919–922 CrossRef CAS PubMed.
- B. J. Sussman, D. Townsend, M. Y. Ivanov and A. Stolow, Science, 2006, 314, 278–281 CrossRef CAS PubMed.
- Y. Inoue, Surf. Sci. Rep., 2007, 62, 305–336 CrossRef CAS.
- S. Kelling, T. Mitrelias, Y. Matsumoto, V. P. Ostanin and D. A. King, Faraday Discuss., 1997, 107, 435–444 RSC.
- S. J. Reese, D. H. Hurley and H. W. Rollins, Ultrason. Sonochem., 2006, 13, 283–286 CrossRef CAS PubMed.
- R. Imbihl and G. Ertl, Chem. Rev., 1995, 95, 697–733 CrossRef CAS.
- S. Kelling, S. Cerasari, H. H. Rotermund, G. Ertl and D. A. King, Chem. Phys. Lett., 1998, 293, 325–330 CrossRef CAS.
- T. Gritsch, D. Coulman, R. J. Behm and G. Ertl, Phys. Rev. Lett., 1989, 63, 1086–1089 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17978 CrossRef.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. Chiarotti, M. Cococcioni and I. Dabo, et al. , J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- A. M. Lahee, W. Allison, R. F. Willis and K. H. Reider, Surf. Sci., 1983, 126, 654–660 CrossRef CAS.
- S. Helveg, W. X. Li, N. C. Bartelt, S. Horch, E. Lægsgaard, B. Hammer and F. Besenbacher, Phys. Rev. Lett., 2007, 98, 115501 CrossRef CAS PubMed.
- G. Binnig, H. Rohrer, C. Gerber and E. Weibel, Surf. Sci., 1983, 131, L379–L384 CrossRef CAS.
- N. Freyer, M. Kiskinova, G. Pirug and H. P. Bonzel, Surf. Sci., 1986, 166, 206–220 CrossRef CAS.
- T. M. Pedersen, W. X. Li and B. Hammer, Phys. Chem. Chem. Phys., 2006, 8, 1566–1574 RSC.
- A. V. Walker, B. Kloetzer and D. A. King, J. Chem. Phys., 1998, 109, 6879–6888 CrossRef CAS.
- C. E. Wartnaby, A. Stuck and Y. Y. Yeo, J. Phys. Chem., 1996, 100, 12483–12488 CrossRef CAS.
- T. Zhu, S.-G. Sun, R. A. van Santen and E. J. M. Hensen, J. Phys. Chem. C, 2013, 117, 11251–11257 CAS.
- D. Miller, H. S. Casalongue, H. Bluhm, H. Ogasawara, A. Nilsson and S. Kaya, J. Am. Chem. Soc., 2014, 136, 6340–6347 CrossRef CAS PubMed.
- F. R. Negreiros, L. Sementa, G. Barcaro, S. Vajda, E. Aprà and A. Fortunelli, ACS Catal., 2013, 2, 1860–1864 CrossRef.
- J. H. Miners, S. Cerasari, V. Efstathiou, M. Kim and D. P. Woodruff, J. Chem. Phys., 2002, 117, 885–896 CrossRef CAS.
- S. Kelling, N. Saito, Y. Inoue and D. A. King, Appl. Surf. Sci., 1999, 150, 47–57 CrossRef CAS.
- M. W. Wu and H. Metiu, J. Chem. Phys., 2000, 113, 1177–1183 CrossRef CAS.
- N. Bonnet, I. Dabo and N. Marzari, Electrochim. Acta, 2014, 121, 210–214 CrossRef CAS.
- W. Steurer, S. Surnev, F. P. Netzer, L. Sementa, F. R. Negreiros, G. Barcaro, N. Durante and A. Fortunelli, Nanoscale, 2014, 6, 10589–10595 RSC.
- A. Cut, V. Y. Zaitsev and L. V. Zhigilei, J. Phys. Chem. C, 2013, 117, 9252–9258 Search PubMed.
- Q. An, S. V. Zybin, W. A. Goddard III, A. Jaramillo-Botero, M. Blanco and S.-N. Luo, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 220101 CrossRef.
- A. C. T. van Duin, S. Dasgupta, F. Lorant and W. A. Goddard III, J. Phys. Chem. A, 2001, 105, 9396–9409 CrossRef CAS.
- C. F. Sanz-Navarro, P. O. Astrand, D. Chen, M. Ronning, A. C. T. van Duin, T. Jacob and W. A. Goddard III, J. Phys. Chem. A, 2008, 112, 1392–1402 CrossRef CAS PubMed.
- J. R. Engstrom and W. H. Weinberg, Surf. Sci., 1998, 201, 145–170 CrossRef.
- J. Fair and R. J. Madix, J. Chem. Phys., 1980, 73, 3480 CrossRef CAS.
- A. Redondo, Y. Zeiri and W. A. Goddard III, Phys. Rev. Lett., 1982, 49, 1847–1850 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Computational details of DFT and AIMD simulations, illustration of the ReaxFF simulation and an AIMD trajectory as a movie. See DOI: 10.1039/c6ta03669d |
| This journal is © The Royal Society of Chemistry 2016 |

