Fluoride substitution in sodium hydride for thermal energy storage applications

Abstract

The solid-state solutions of NaH_xF_1−x (x = 1, 0.95, 0.85, 0.5) have been investigated to determine their potential for thermal energy applications. Thermal analyses of these materials have determined that an increase in fluorine content increases the temperature of hydrogen release, with a maximum rate of desorption at 443 °C for NaH_0.5F_0.5 compared to 408 °C for pure NaH, while pressure–composition–isotherm measurements have established a ΔH_des of 106 ± 5 kJ mol⁻¹ H₂ and ΔS_des of 143 ± 5 J K⁻¹ mol⁻¹ H₂, compared to 117 kJ mol⁻¹ H₂ and 167 J K⁻¹ mol⁻¹ H₂, respectively, for pure NaH. While fluorine substitution actually leads to a decrease in the stability (enthalpy) compared to pure NaH, it has a larger depressing effect on the entropy that leads to reduced hydrogen equilibrium pressures. In situ powder X-ray diffraction studies have ascertained that decomposition occurs via enrichment of fluorine in the NaH_xF_1−x composites while, unlike pure NaH, rehydrogenation is easily achievable under mild pressures. Further, cycling studies have proven that the material is stable over at least seven hydrogen sorption cycles, with only a slight decrease in capacity while operating between 470 and 520 °C. Theoretically, these materials may operate between 470 and 775 °C and, as such, show great potential as thermal energy storage materials for concentrating solar thermal power applications.

---

Introduction

Currently, the population of the world is increasing by 80 million people per year, which, along with technological growth, puts a tremendous strain on global energy production.¹ Even if fossil fuel reserves were not dwindling, alternative energy sources are unquestionably required and many renewable energy projects are underway globally. Some of the largest projects involve the construction of concentrating solar-thermal power (CSP) stations that harvest the sun's energy in the form of heat that is used directly to produce electricity.² In order to produce electricity at night time or during periods of low sunlight, thermal energy storage has been implemented at a number of these stations including a state-of-the-art 110 MW plant in Nevada called the Crescent Dunes Solar Energy Plant.² Using molten NaNO₃/KNO₃ salts, this station has the capacity to store 10 h of thermal energy at full load for electricity production.

Molten salts are the first generation of thermal energy storage materials used for CSP and, as such have their drawbacks including low heat storage capacity, large volumes, high costs, and an operating temperature that is limited to 565 °C.³ Metal hydrides are thermochemical heat storage materials and have 5–30 times the energy density of molten salts and have the potential to reduce the heat storage costs of next generation CSP.^4,5 Recent discussion of this topic has identified a range of high temperature metal hydrides that have the potential to operate at temperatures far exceeding those of molten salts (∼565 °C), supercritical-CO₂ (650 °C), and also the next generation of power tower technology (650–800 °C),^6,7 although reversibility and cost are the key issues to solve.^8–13

Fluorine stabilised metal hydrides have recently been proposed for high-temperature thermal storage.³ The comparable ionic size of the hydride and fluoride ions and the structural similarity of their compounds were recognised before the 1960s,¹⁴ with recent studies determining that fluorine substitution leads to increased thermal stability while also reducing system costs. For instance, NaMgH₂F releases hydrogen at 545 °C at a pressure of 10 bar compared to 493 °C for NaMgH₃.^15,16 Though NaMgH₂F has a lower heat storage capacity compared to other Mg-based hydrides, its higher operating temperature and thermal stability results in a lower system installed cost.^8,15,17

It was originally theorised that a solid solution between NaH and NaF would be unlikely to form due to the relatively large difference in lattice constant and Born–Haber lattice energies between NaH and NaF.¹⁴ However, recent ab initio calculations and Calphad modelling have predicted that the enthalpy of mixing between NaH and NaF is slightly negative (∼2 kJ mol⁻¹) and a single solid solution is obtainable.¹⁸ At the same time, the authors of ref. 18 predicted that fluorine substitution will increase the equilibrium decomposition temperature. In this study, NaH has been mixed with NaF to successfully form solid solutions of NaH_xF_1−x and their thermal decomposition, thermodynamics, and reversibility determined by PCI (pressure–composition–isotherm), TPD (temperature programmed desorption) and XRD (powder X-ray diffraction) analysis. These results have been directly compared to NaH, a material that to date has negligible reversibility, despite having superior thermal stability compared to other binary hydrides for CSP applications.⁹

Experimental

All handling of chemicals and sealable milling canisters was undertaken in an argon-atmosphere Mbraun Unilab glovebox in order to minimise oxygen (O₂ < 1 ppm) and water (H₂O < 1 ppm) contamination. NaH (95%, Sigma-Aldrich) and NaF (99.99%, Sigma-Aldrich) were milled at various ratios (Table 1) inside an Across International Planetary Ball Mill (PQ-N04) employing tempered steel vials and balls in an Ar atmosphere. A ball-to-powder mass ratio of 30 : 1 was employed, with a total milling time of 3 h at a speed of 400 rpm. Following milling, the samples were generally annealed under a H₂ pressure of 40 bar at 460 °C for 6 days.

Table 1 Structural and thermal properties of NaH_xF_1−x mixtures. Esd's of lattice parameters and H occupancies of the 4b site are in parentheses

NaH/NaF molar ratio	NaH/NaF weight ratio	Lattice parameter (Å)	H occupancy	Max H2 release (°C)	Desorbed H2 (theoretical) (wt%)	Reabsorbed H2 (wt%)	Fraction of desorbed H2 reabsorbed (%)
100 : 0	100 : 0	4.8814(2)	1	408	3.53(4.20)	0.2	5.7
95 : 5	92 : 8	4.8642(2)	0.908(1)	413	3.24(3.85)	0.32	9.9
85 : 15	76 : 24	4.8305(2)	0.7904(8)	417	2.43(3.20)	0.36	14.8
70 : 30	57 : 43	4.7856(4)	0.595(1)	430	1.82(2.40)	0.88	48.4
50 : 50	36 : 64	4.7407(2)	0.449(2)	443	1.11(1.53)	0.70	63.1
0 : 100	0 : 100	4.63419(3)	0	—	—	—	—

---

Ex situ powder X-ray diffraction (XRD) was performed using a Bruker D8 Advance diffractometer (Cu Kα radiation) utilising XRD sample holders covered with a poly(methylmethacrylate) (PMMA) airtight bubble to prevent oxygen/moisture contamination during data collection. The PMMA bubble results in a broad hump in XRD patterns centred at ∼20° 2θ. The powder was mixed with 10 wt% Si (−325 mesh, 99%, Aldrich) as an internal reference to accurately determine sample displacement errors. Data was acquired over a 2θ range of 20–80°, with step size of 0.02° and count time of 1 s per step. In situ synchrotron powder X-ray diffraction (SR-XRD) was performed at the Australian Synchrotron in Melbourne, Australia.¹⁹ NaH/NaF powder was loaded in a quartz capillary (outer diameter 0.7 mm, wall thickness 0.01 mm) and mounted in a sample holder with Swagelok tube fittings while inside a glove box filled with purified argon (<1 ppm O₂ and H₂O). The sample holder was then connected to a H₂ gas filling/vacuum manifold, and the capillary heated with a hot air blower with a heating rate of 5 °C min⁻¹, under a 1 bar H₂ atmosphere. One-dimensional SR-XRD patterns (monochromatic X-rays with λ = 0.824890 Å) were continuously collected using a Mythen microstrip detector²⁰ with an exposure time of 27 s. The capillary was oscillated 120° during exposure to improve the powder averaging. Diffraction patterns were quantitatively analysed with the Rietveld method²¹ using TOPAS (Bruker-AXS). The low atomic number of hydrogen usually presents difficulties for Rietveld refinement of hydrogen containing phases. However, the occupancy of hydrogen and fluorine can be readily obtained for NaH_xF_1−x solid solutions due to dramatic changes in diffracted peak intensities that occurs upon fluorine substitution for hydrogen (Fig. S1†).

The composition of NaH_xF_1−x materials after hydrogen sorption experiments were estimated by comparing the lattice parameters determined from lab-based XRD to the lattice parameters and composition determined from SR-XRD. For the room temperature measurements, a linear fit of the lattice parameters of the annealed NaH_xF_1−x powders (Table 1) against H : F ratios was generated. Above room temperature compositions were determined by firstly constructing a linear fit of the lattice parameters during thermal expansion of each annealed material from room temperature to 430 °C collected during in situ SR-XRD measurements. Quadratic expressions were then constructed from the lattice parameters against H : F ratios over the whole temperature range. This allowed the determination of NaH_xF_1−x composition by SR-XRD from the in situ SR-XRD data.

The hydrogen sorption properties were examined by measuring Pressure–Composition–Isotherms (PCI) between 450 °C and 520 °C with a computer controlled Sieverts/volumetric apparatus previously described.²² The digital pressure transducer (Rosemount 3051S) has a precision and accuracy of 14 mbar, whilst room temperature measurements were recorded using a 4-wire platinum resistance temperature detector (RTD). The sample temperature was monitored using a K-type thermocouple that was calibrated by the manufacturer to be accurate within 0.1 °C at 419 °C. Above ∼420 °C, the permeation of hydrogen directly through the walls of the stainless steel sample cell becomes an issue and the measured hydrogen content at each PCI data point has to be corrected for this loss. A full explanation of the correction method has previously been explained in detail.¹⁵

Hydrogen sorption cycling studies were carried out utilising the same apparatus as for the PCI experiments. In order to inhibit Na evaporation during the experiment, the NaH_xF_1−x sample was loaded inside an Fe tube (wall thickness of 0.025 cm, inner diameter of 0.45 cm).^23,24 The bottom of the Fe tube was crimped tube placed inside the reactor vessel. To allow the sample to fully absorb and desorb hydrogen during cycling, 3 bar H₂ was applied to the vessel before cycling between 520 °C (P_eq(H₂) ∼ 3.1 bar) and 472 °C (P_eq(H₂) ∼ 1.1 bar) for 6 h per step for a total of 7 repetitions.

Temperature Programmed Desorption (TPD) experiments were carried out using an identical apparatus to those described in the PCI measurements, although the experimental conditions were altered. Prior to heating the samples in a closed system, the vessel was kept in vacuo. Samples were heated from room temperature to 550 °C at 2 °C min⁻¹ followed by an isothermal stage for 40 min. The vessel was then allowed to cool under its own thermal dissipation rate. The sample masses were chosen such that they each contained the same quantity of hydrogen.

Results and discussion

Synthesis

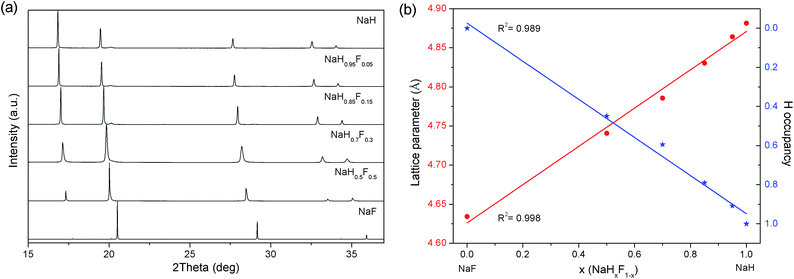
NaH and NaF powders were ball-milled in various ratios (Table 1) and annealed at 460 °C for six days under 40 bar H₂. The resultant powders were analysed by SR-XRD (Fig. 1a) and the data refined using the Rietveld method (Fig. S1 and Table S1†) indicating that neither starting materials were present (Table S2†). NaH and NaF exist in the crystallographic space group Fm3̄m with lattice parameters of 4.8814(2) and 4.63419(3) Å, respectively (after milling and annealing). The increase in lattice parameters between NaF to NaH is due to the increase of bond length between the Na and respective anion (Na–F = 2.308 Å, Na–H = 2.445 Å).^25,26 Consequently, each product consisted of a single phase, which also indexed to the space group Fm3̄m, with the refined lattice parameters residing between those of the pure alkali metal salts (Table 1). As expected, a solid-solution has been produced in the form of NaH_xF_1−x where the H and F are randomly distributed on the 4b site. The hydrogen positions and occupancies within metal hydrides are usually difficult to determine via XRD. However, partial substitution of hydrogen for fluorine results in strong changes in peak intensity that can be used to elucidate the hydrogen occupancy (Fig. S1 and Table S1†). Plotting the lattice parameters and H occupancy against the initial NaH/NaF fractions exhibits a linear correlation (Fig. 1b) that obeys Vegard's law.²⁷ As such, lattice parameters (LP) increase directly with NaH ratio providing us with eqn (1), which can subsequently aid with deducing the composition of materials after hydrogen sorption cycles.

LP = 0.0024 × (NaH mole fraction) + 4.6277 (1)

Fig. 1 SR-XRD patterns (a) and refined lattice parameters and H occupancies (b) of NaH_xF_1−x mixtures. λ = 0.824890 Å, T = 27 °C.

It is noted that this correlation could be slightly improved by the use of a quadratic function, but a linear correlation allows for a simplistic approach to determine the approximate composition of the solid solutions. Overall the R² value for the linear fit was 0.998, while the R² value for the polynomial fit was 0.9998. On a side note, the refined H occupancies appear to be consistently lower than the as-milled NaH/NaF fractions. This could be attributed to the greater X-ray scattering of F compared to H. This scenario may have also arisen from the difference in purity between the NaH (95%) and NaF (>99.99%) starting materials. Even though the purchased NaH was labelled as 95% pure, Rietveld refinement of a ball milled and annealed sample (in order to replicate the method used to synthesise the NaH_xF_1−x mixtures) indicated a presence of 12 wt% NaOH (Table S2 and Fig. S1†). Therefore, the use of lattice parameters to estimate the H/F composition is more efficient than the refined H occupancies of the materials.

Annealing the samples under a H₂ atmosphere is essential to attain a solid-solution; merely milling the materials results in diffraction peaks for the NaF and NaH starting materials (Fig. S2†). Annealing was initially conducted on the as-milled NaH_0.5F_0.5 at 300 °C, under 30 bar H₂ for three days, where a wide variety of NaH_xF_1−x compositions were observed including 7 wt% NaF, 40 wt% NaH_0.25F_0.75 and 54 wt% NaH_0.57F_0.43 (Table S3†). H₂ pressure is often used for annealing at these temperatures in order to avoid hydrogen desorption from NaH.

Subsequent annealing at 460 °C for a total of six days resulted in a single phase when analysed by laboratory based XRD. Further analysis of the sample (annealed for 6 days) by SR-XRD showed asymmetric broadening of the diffraction peaks that indicates that the sample was not quite fully homogenous and that small proportions of higher F containing species were present (although not measureable by laboratory XRD analysis) (Fig. S3†). Further annealing of the sample under 1 bar H₂ was inadvertently monitored by in situ SR-XRD, where one single phase was finally observed at ∼140 °C (Fig. 4a). To investigate this result, ex situ annealing was conducted on the as-milled material at 200 °C, under 1 bar H₂ or 1 bar Ar for 24 h. It was assumed that excess H₂ pressure may inhibit the reaction between NaH and NaF, as observed previously with NaBH₄ and NaCl mixtures.²⁸ As such, after XRD, a reduction in solid-state solution production was achieved by employing milder annealing conditions, with ∼44 wt% NaF being present under both reaction atmospheres (Fig. S2 and Table S3†). It is therefore understood that at 200 °C the reaction atmosphere does not affect the reaction outcome, although increased temperatures promote the formation of the solid-state solution. One explanation for the additional annealing that occurred during the in situ XRD is that the material has already been subjected to an annealing cycle and so much lower diffusion distances are required to produce a single-phase solid solution.

Thermal desorption studies

To ascertain the relative stabilities of the NaH_xF_1−x samples, TPD analysis was carried out. In conventional TPD experiments, the desorbed gases are measured by Mass Spectrometry or by acquiring the partial pressure as the gases are removed from the system under reduced pressure.^29,30 In this experiment, the gases were desorbed into a closed system and the incremental pressure changes used to determine the rate of gas desorption (Fig. 2). A small enough quantity of material was used so as not to reach atmospheric pressure and hence limit the possibility of thermodynamic inhibition. The first notable aspect is that the theoretical H₂ capacity for each NaH_xF_1−x composition was not obtained (Fig. 2a and Table 1). It is normal for the theoretical capacity not to be achieved due to impurities in the sample and H₂ permeation through the vessel walls (even though a correction coefficient was implemented).¹⁶ The rate of H₂ release dramatically decreases as the fraction of NaF increases, as does the onset temperature of H₂ desorption. To accurately determine the temperature of the maximum rate of H₂ release, the first derivative of the desorbed wt% was calculated (Fig. 2b and Table 1). It is clear that the addition of NaF considerably increases the temperature of desorption of NaH; NaH_0.5F_0.5 has a maximum H₂ release rate at 443 °C, while NaH has a maximum at 408 °C. In fact, the maximum release rate temperature increases linearly with increasing NaF. This is the desired effect, although for NaH_0.5F_0.5, the hydrogen capacity is only 36% of pure NaH (Table 1). Further addition of NaF will ultimately decrease the H₂ capacity to such an extent as to make it inadequate for thermal energy applications.

Fig. 2 TPD analysis of NaH_xF_1−x samples (heating rate = 2 °C min⁻¹). (a) H₂ desorption during heating and cooling (→ indicates direction of experimental data). (b) Rate of H₂ desorption during heating.

One interesting inference from the TPD data is that the addition of fluorine allows the NaH_xF_1−x systems to reabsorb H₂. NaH is renowned for having negligible H₂ reversibility even at increased pressures.⁸ The maximum pressure of desorbed gas obtained in these experiments was 0.86 bar for NaH while the NaH_xF_1−x systems never reached above 0.8 bar. At these pressures H₂ was reabsorbed by the NaH_xF_1−x systems during cooling and the relative quantity increased with increasing NaF fraction (Fig. 2a and Table 1). NaH_0.5F_0.5 reabsorbed 0.7 wt% H₂, which is 63% of the total quantity of H₂ desorbed. Once the temperature decreased to ∼350 °C the absorption halted, presumably due to kinetic limitations, and so it is feasible that full reabsorption could be achieved provided the temperature is maintained above ∼350 °C. The only factor inhibiting maximum H₂ reabsorption is the loss of Na content during the experiment, as the high vapour pressure of molten sodium metal causes its distillation.^23,24 In fact, virtually no Na was observed by XRD in the remaining NaH_0.5F_0.5 after the TPD measurement. In addition, the lattice parameter of 4.723 Å for the NaH_xF_1−x phase suggests a composition of NaH_0.4F_0.6 (using eqn (1)); a loss of 20 mol% of NaH.

Hydrogen desorption PCI measurements were performed on NaH_0.5F_0.5 between 450 °C and 520 °C in order to determine the thermodynamics of hydrogen release (Fig. 3a). It is evident from the four curves that desorption occurs in a single step, although the sloping plateaux are consistent with the hydrogen existing as a randomly distributed solid-solution rather than a stoichiometric hydride phase.¹⁵ The lack of flat plateaux is a disadvantage from an engineering perspective where absorption and desorption of hydrogen at a constant equilibrium pressure is ideal. One major setback to sloping equilibrium pressures is that the operational pressures for which full reversibility is achievable become wider as lower pressures are required for full dehydrogenation while higher pressures are required for full hydrogenation. A lab-based work-around for this situation is to increase the volume of the reactor and extend the temperature differential between desorption and absorption. Upon scale up, engineering considerations will have to be made to avoid excessively large reactor volumes.

Fig. 3 PCI analysis of NaH_0.5F_0.5 at selected temperatures (a) and van't Hoff plot of respective H₂ desorption equilibrium pressures (b).

To determine the thermodynamics of hydrogen release, van't Hoff plots were constructed (Fig. 3b). The enthalpy (ΔH_des) and entropy (ΔS_des) were determined via two methods. The first, simply involved determining the pressure at −0.55 wt% of H₂ content. This gave ΔH_des = 106 kJ mol⁻¹ H₂ and ΔS_des = 143 J K⁻¹ mol⁻¹ H₂ with an associated R² factor of 0.997 (Fig. 3b). The second method involved numerically fitting each PCI curve with a quadratic function (Fig. S4†) so that ΔH_des and ΔS_des could be determined over the whole range of compositions (Fig. S5†). The van't Hoff plots for hydrogen desorption values below −0.9 wt% showed a poor fit and were not considered further. The poor fits are possibly due to small errors in the calculated leak rates that accumulate over the course of the desorption measurements that may compound at lower pressures. As a result, at 0.55 wt% H₂, ΔH_des = 109 kJ mol⁻¹ H₂ and ΔS_des = 147 J K⁻¹ mol⁻¹ H₂ with an associated R² factor of 0.989 for method 2. The inconsistency observed between the two methods is likely due to the numerical fitting of the data, although systematic errors can be attributed to fluctuations in temperature during the experiment and hydrogen diffusion through the cell.¹⁵ As such, an error of ±5 can placed on both ΔH_des and ΔS_des. The reported values will use the result from method 1 due to the improved R² factor. Therefore, ΔH_des = 106 ± 5 kJ mol⁻¹ H₂ and ΔS_des = 143 ± 5 J K⁻¹ mol⁻¹ H₂.

To put these values into context, for pure NaH, ΔH_des = 117 kJ mol⁻¹ H₂, and ΔS_des = 167 J K⁻¹ mol⁻¹ H₂.³¹ A decrease in ΔH_des and ΔS_des in NaH_0.5F_0.5 of ∼11 kJ mol⁻¹ H₂ of ∼24 J K⁻¹ mol⁻¹ H₂ respectively denotes that the equilibrium pressure at which decomposition occurs is significantly lower than that of NaH. Subsequently, the temperature of decomposition of NaH_0.5F_0.5 can be increased without significantly increasing the pressure requirements. For CSP applications this is ideal and also in terms of the aim of this study. As mentioned in the introduction, an ideal operating temperature for these systems is between 550 and 800 °C,^6,7,9 while reduction in operating pressure at these temperatures will also significantly reduce infrastructure costs and, in turn, safety concerns.

Utilising the numerical fits of the PCI data and the derived van't Hoff plots (Fig. S4†), the variation in desorption enthalpy and entropy as a function of hydrogen content can be established (Fig. S5†). During decomposition, ΔH_des appears to increase linearly between −0.3 and −0.9 wt% H₂ from 106 to 113 kJ mol⁻¹ H₂. At the same time, ΔS_des appears to be parabolic in nature, with an increase from 144 J K⁻¹ mol⁻¹ H₂ at −0.3 wt% H₂ until a maximum of 147 J K⁻¹ mol⁻¹ H₂ at −0.7 wt% H₂. This is followed by a decrease to 146 J K⁻¹ mol⁻¹ H₂ by −0.9 wt% H₂. Although this is only a small change in ΔH_des and ΔS_des, it is still significant and may help to explain the sloping nature of the PCI curve. Often, just prior to decomposition of a material to another material (often with a different crystal structure) a flat equilibrium plateau is observed. In this NaH_xF_1−x system, the starting material and final product have the same Fm3̄m space group. During the decomposition process of NaH_0.5F_0.5, H₂ is gradually desorbed forming a product with a larger F content but with the same structure; H and F share the same 4b atomic site, while Na is also lost through evaporation. Accordingly, the thermodynamics of decomposition change over the course of the experiment.

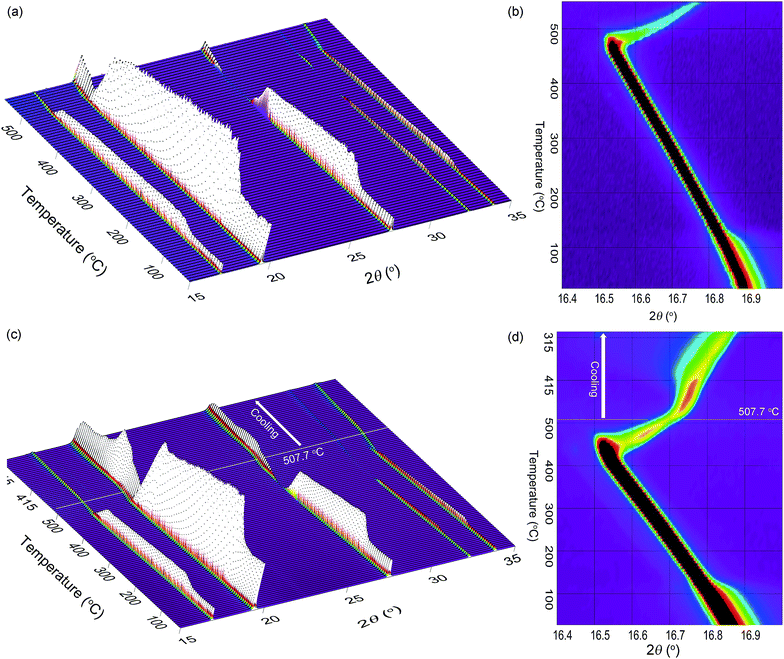
In situ XRD studies of NaH_0.5F_0.5

The in situ XRD data is useful for explaining the process of decomposition (Fig. 4 and S6†). During heating from room temperature to 434 °C, the lattice is observed to expand from 4.7407(2) to 4.83633(9) Å (Fig. 4a and b). At ∼430 °C, the shift in peak position to smaller angles, that is associated with thermal expansion, halts and the peaks decrease in intensity and shift to higher angles on further heating. This decrease in the lattice parameters indicates a substantial enrichment of fluorine within in the structure. In fact, during decomposition, the pattern can only be modelled assuming that a range of compositions co-exist. By 485 °C, the composition of the material ranges from NaH_0.48F_0.52 (2 wt%) to NaH_0.34F_0.66 (42 wt%) but by ∼542 °C the final composition ranged from NaH_0.26F_0.74 (3 wt%) to NaH_0.2F_0.8 (44 wt%). Total decomposition was not observed due to obliteration of the quartz capillary. As such, no pure phase of NaF is detected nor Na (due to Na being in its molten state). This result indeed corroborates the variation in thermodynamic properties observed during the PCI experiment as being due to a variation in composition during decomposition.

Fig. 4 (a) In situ SR-XRD of NaH_0.5F_0.5 during heating to 542 °C and (b) an expanded view of the (111) reflection highlighting the changes during desorption of H₂. (c) In situ SR-XRD of NaH_0.5F_0.5 during heating to 507.7 °C and cooling and (d) an expanded view of the (111) reflection highlighting the changes during desorption and absorption of H₂ (5 °C min⁻¹, 1 bar H₂, λ = 0.824890 Å).

In a similar in situ XRD experiment, heating of the system was halted at 507.7 °C and the material allowed to cool at 5 °C min⁻¹ under 1 bar H₂ in order to replicate the conditions during the TPD experiments (Fig. 4c and d and S7†). The sample continues to decompose as the sample cools to ∼470 °C where the composition of the sample ranges from NaH_0.29F_0.71 (5 wt%) to NaH_0.25F_0.75 (56 wt%) (Fig. S7†). By ∼442 °C rehydrogenation of the sample is progressing, with a composition ranging from NaH_0.33F_0.67 (2 wt%) to NaH_0.27F_0.73 (64 wt%). Hydrogenation continues over the course of cooling with a final composition of NaH_0.58F_0.42 (2 wt%) and NaH_0.3F_0.7 (51 wt%) at 98 °C. One perceptible observation is the wide spread of compositions produced during hydrogenation, when in most cases one single phase of a material forms over time.^32,33 Furthermore, at 98 °C, the final composition of the material contains 2 wt% NaH_0.58F_0.42, which has a greater hydrogen content than the NaH_0.5F_0.5 starting material. This is attributed to the mobility of Na during the decomposition process away from the hot zone which prevents the even formation of NaH_0.5F_0.5. Nevertheless, this experiment illustrates the enhanced reversibility of this system compared to that of pure NaH and reiterates the results of the TPD experiment.

Cycling studies

A sample of NaH_0.5F_0.5 was cycled seven times between 475 and 525 °C (Sieverts apparatus) to explore its extended reversibility and to determine its feasibility for technological applications (Fig. 5a). To ensure that Na did not evaporate during decomposition, the sample was loaded into a thin walled Fe tube.^23,24 While heating the sample to 475 °C the initial pressure was set to 10 bar to inhibit decomposition. The pressure was then reduced to 3 bar and the temperature ramped to 525 °C. During the consecutive cycles, no significant decrease in capacity was observed. The material desorbed a maximum of 0.72 wt% H₂ and reabsorbed 0.5 wt% H₂.

Fig. 5 Cycling of NaH_0.5F_0.5 between 470 and 520 °C (a) and SR-XRD characterisation of the final product (b). λ = 0.824890 Å.

The fact that full reversibility was not achieved is due to the sloping equilibrium plateau pressure determined during the PCI experiments (Fig. 3a). An initial pressure of 3 bar H₂ was used to ensure that the H₂ pressure was above the equilibrium pressure at 475 °C and hence guarantee absorption. At 525 °C the equilibrium pressure should have reached ∼4.2 bar (for 0.9 wt% desorption) although this system did not pass 3.5 bar upon desorption, but absorption at 475 °C would also cease at 1.5 bar (for 0.9 wt% absorption). As such, as the H₂ leaked through the reactor walls, the drop in pressure inhibited full absorption of H₂ into the material to the full extent it exhibited on the first two cycles.

This result determined that the sample is reversible and most importantly that the Fe tube inhibited the evaporation of Na. That being said, SR-XRD analysis of the final sample in the hydrogenated state indicated that total rehydrogenation had not occurred (Fig. 5b). Profile analysis of the pattern allowed for the determination of the lattice parameters of the contained phases and hence the composition of the material. Using eqn (1), the composition is determined to be a mixture of NaH_0.21F_0.79 (10 wt%), NaH_0.33F_0.67 (45 wt%), NaH_0.36F_0.64 (24 wt%). In addition, NaHF₂ was not observed in the powder product as it is thermodynamically unstable in the presence of Na and/or NaH.³⁴

Although the time allotted for the final hydrogen absorption step was not as prolonged as the six previous hydrogenation steps, Na is deemed to have evaporated from the sample as no Na was determined by XRD, as such better crimping of the sample is required, especially if a technological application is to be found.

Technological application of NaH_xF_1−x

The substantial improvement in the reversible hydrogenation capacity of NaH by the formation of NaH_xF_1−x solid-state has been undertaken to make NaH remotely reversible.⁸ Addition of NaF increases the temperature of decomposition to 440 °C (max H₂ release) compared to 408 °C for pure NaH. At the same time, ΔH_des and ΔS_des of 106 ± 5 kJ mol⁻¹ H₂ and 143 ± 5 J K⁻¹ mol⁻¹ H₂ for NaH_0.5F_0.5 is reduced compared to pure NaH. Although a reduction in the ΔH_des compared to NaH is not ideal, ΔS_des decreases substantially more with F substitution than does the ΔH_des. Hence the H₂ equilibrium pressure is substantially decreased with only a minor decrease in the enthalpy. Overall, these factors bode well for the integration of these materials into thermal energy applications.

In comparison to other materials considered for thermal energy applications, NaH_0.5F_0.5 is especially competitive in regards to the operating temperature (Table 2). For instance, in CSP applications an ideal operating temperature range is between 550 and 800 °C.^6,7,9 As such, the operational properties of NaH_0.5F_0.5 lead to a greater plant efficiency. The higher reaction enthalpy of NaH_0.5F_0.5 compared to MgH₂, for instance, decreases the overall hydrogen mass required to generate an equivalent electrical output and therefore decreases the heat transfer area of the systems. Furthermore, the lower hydrogen mass requirement decreases the quantity of the low temperature hydride,^{8–10,15,17,37} which is the most expensive component of the coupled system.³⁷ These factors counteract the decreased theoretical hydrogen capacity for NaH_0.5F_0.5, which is lower than the majority of the materials listed in Table 2. One major advantage of NaH_0.5F_0.5 is the cost of the materials. It is estimated that NaH costs US$ 4.8 per kg⁻¹, while NaF costs ∼US$ 1.2 per kg⁻¹.³⁸ This translates to a cost of ∼US$ 10 per kW h_th for NaH_0.5F_0.5, while NaH would cost ∼US$ 12 per kW h_th, a decrease of 17%. For a CSP plant which would require thousands of tons of material to operate, this is a vast saving.

Table 2 Properties of selected metal hydrides and calculated operating temperatures between 1 and 150 bar^a

Material	Theoretical H2 capacity (wt%)	ΔHdes (kJ mol^−1 H2)	Operating range (°C)	Theoretical thermal storage capacity (kJ kg^−1)
a Pressures noted correspond to calculated fugacities (pressure = fugacity/compressibility of H2). b Maximum temperature unachievable due to sintering.^36
NaH0.5F0.5	1.53	106	470–775	803
NaMgH2F	2.95	96.8 (ref. 15)	431–738	1416
NaMgH3 – 1 step	4.01	86.6 (ref. 16)	382–683	1721
NaH	4.20	116.8 (ref. 31)	426–659	2434
NaBH4	10.67	100.4 (ref. 34)	511–890	5709
MgH2	7.66	74 (ref. 35)	282–534^b	2811
Mg2FeH6	5.47	77 (ref. 35)	304–564	2090

---

Other than the relatively low hydrogen capacity of NaH_0.5F_0.5, the major drawback is the sloping plateau observed from the PCI measurements (Fig. 3). This causes the operational pressures for which full reversibility is achievable to become wider as lower pressures are required for full dehydrogenation, while higher pressures are required for full hydrogenation. A work-around for this situation is to increase the volume of the reactor and extend the temperature differential between desorption and absorption.

Another disadvantage is the distillation of Na upon decomposition. As decomposition occurs, the Na vapour will agglomerate in the cooler parts of the reactor bed. As such, the reversibility of the material decreases as segregation occurs. This will ultimately lead to NaF rich areas of material. Means to prevent Na loss from the reactor bed have been identified (such as Fe membranes that are permeable to H₂ at high temperatures but not Na vapour) but this will require engineering of this solution on a large scale suitable for CSP application. To prevent NaF segregation and increase H capacity, the use of lower fractions of NaF may be beneficial. This is to be developed in a future publication. The assessment of long term cycling of these materials will also determine the overall effects of these detrimental properties.

Conclusions

The solid-state solutions of NaH_xF_1−x (x = 1, 0.95, 0.85, 0.5) have been investigated to determine their potential for thermal energy applications. Thermal desorption measurements have determined that the temperature for maximum hydrogen desorption of NaH_0.5F_0.5 is 443 °C, releasing 1.3 wt% H₂ (theoretical: 1.5 wt% H₂), while pure NaH decomposes at 408 °C. PCI measurements indicate a sloping single-step hydrogen desorption curve with a plateau mid-point enthalpy of 106 ± 5 kJ mol⁻¹ H₂ and an entropy of desorption of 143 ± 5 J K⁻¹ mol⁻¹ H₂. These values are decreased in comparison to 117 kJ mol⁻¹ H₂ and 167 J K⁻¹ mol⁻¹ H₂, respectively, for pure NaH. While the fluorine substitution actually leads to a decrease in the stability (enthalpy) compared to pure NaH, it has a larger depressing effect on the entropy that leads to reduced hydrogen equilibrium pressures. The solid state solutions of NaH_xF_1−x are reversible compared to pure NaH and are shown to absorb hydrogen below 1 bar H₂, above 350 °C. Cycling of NaH_0.5F_0.5 has been investigated over seven cycles and although the theoretical capacity is not met, capacity is not greatly reduced. Despite the relatively modest thermal storage capacity compared to other metal hydrides, the high enthalpy and operating temperatures of NaH_xF_1−x means that substantially less hydrogen is required for generating electric power compared to other metal hydrides for solar thermal storage. As such, these low cost (∼US$ 10 per kW h_th for NaH_0.5F_0.5) materials hold great potential as thermal energy storage materials for concentrating solar thermal power applications.

Acknowledgements

The authors acknowledge the financial support of the Australian Research Council (ARC) for ARC Linkage grant LP120101848, LP150100730 and ARC LIEF grants LE0989180 and LE0775551, which enabled the XRD and gas sorption studies to be done. We would like to thank the project teams at the Australian Synchrotron Powder Diffraction Beam Line.

Notes and references

1. Worldometers, Worldometers, http://www.worldometers.info/world-population/, accessed January 19, 2016.
2. M. Fellet, C. E. Buckley, M. Paskevicius and D. A. Sheppard, MRS Bull., 2013, 38, 1012–1013.
3. D. A. Sheppard, T. D. Humphries and C. E. Buckley, Mater. Today, 2015, 18, 414–415.
4. D. N. Harries, M. Paskevicius, D. A. Sheppard, T. Price and C. E. Buckley, Proc. IEEE, 2012, 100, 539–549.
5. E. S. Freeman, J. Phys. Chem., 1956, 60, 1487–1493.
6. US Department of Energy, D.O.E. ARPA-E High Energy Advanced Thermal Storage – DE-FOA-0000471, https://arpa-e-foa.energy.gov/FileContent.aspx?FileID=79a5de09-8bfd-4590-9cb4-e42578248d90, accessed March 21, 2016.
7. SunShot Vision Study, Chapter 5: Concentrating Solar Power: Technologies, Cost, and Performance, US Department of Energy, US Department of Energy, 2012.
8. D. A. Sheppard, T. D. Humphries and C. E. Buckley, Appl. Phys. A, 2016, 122, 406.
9. D. A. Sheppard, M. Paskevicius, T. D. Humphries, M. Felderhoff, G. Capurso, J. Bellosta von Colbe, M. Dornheim, T. Klassen, P. A. Ward, J. A. Teprovich, C. Corgnale, R. Zidan, D. M. Grant and C. E. Buckley, Appl. Phys. A, 2016, 122, 395.
10. P. A. Ward, C. Corgnale, J. A. Teprovich, T. Motyka, B. Hardy, D. A. Sheppard, C. E. Buckley and R. Zidan, Appl. Phys. A, 2016, 122, 462.
11. Q. Lai, M. Paskevicius, D. A. Sheppard, C. E. Buckley, A. W. Thornton, M. R. Hill, Q. Gu, J. Mao, Z. Huang, H. K. Liu, Z. Guo, A. Banerjee, S. Chakraborty, R. Ahuja and K.-F. Aguey-Zinsou, ChemSusChem, 2015, 8, 2789–2825.
12. M. Paskevicius, D. A. Sheppard, K. Williamson and C. E. Buckley, Energy, 2015, 88, 469–477.
13. M. Felderhoff, R. Urbanczyk and S. Peil, Green, 2013, 3, 113–123.
14. C. E. Messer, J. Solid State Chem., 1970, 2, 144–155.
15. D. A. Sheppard, C. Corgnale, B. Hardy, T. Motyka, R. Zidan, M. Paskevicius and C. E. Buckley, RSC Adv., 2014, 4, 26552–26562.
16. D. A. Sheppard, M. Paskevicius and C. E. Buckley, Chem. Mater., 2011, 23, 4298–4300.
17. P. A. Ward, C. Corgnale, J. A. Teprovich, T. Motyka, B. Hardy, B. Peters and R. Zidan, J. Alloys Compd., 2015, 645, S374–S378.
18. E. R. Pinatel, M. Corno, P. Ugliengo and M. Baricco, J. Alloys Compd., 2014, 615(1), S706–S710.
19. K. S. Wallwork, B. J. Kennedy and D. Wang, Synchrotron Radiation Instrumentation: Ninth International Conference on Synchrotron Radiation Instrumentation, 2007.
20. B. Schmitt, C. Brönnimann, E. Eikenberry, F. Gozzo, C. Hörmann, R. Horisberger and B. Patterson, Nucl. Instrum. Methods Phys. Res., Sect. A, 2003, 501, 267–272.
21. R. A. Young and R. A. Young, The Rietveld Method, Oxford University Press, 1995.
22. M. Paskevicius, D. A. Sheppard and C. E. Buckley, J. Am. Chem. Soc., 2010, 132, 5077–5083.
23. D. M. Banus, J. J. McSharry and E. A. Sullivan, J. Am. Chem. Soc., 1955, 77, 2007–2010.
24. W. Klostermeier and E. U. Franck, Ber. Bunsen-Ges. Phys. Chem., 1982, 86, 606–612.
25. Y. Shirako, Y. G. Shi, A. Aimi, D. Mori, H. Kojitani, K. Yamaura, Y. Inaguma and M. Akaogi, J. Solid State Chem., 2012, 191, 167–174.
26. C. G. Shull, E. O. Wollan, G. A. Morton and W. L. Davidson, Phys. Rev., 1948, 73, 842–847.
27. A. R. Denton and N. W. Ashcroft, Phys. Rev. A, 1991, 43, 3161–3164.
28. D. B. Ravnsbæk, L. H. Rude and T. R. Jensen, J. Solid State Chem., 2011, 184, 1858–1866.
29. R. Cvetanovic and Y. Amenomiya, Adv. Catal., 1967, 17, 103–149.
30. T. D. Humphries, G. N. Kalantzopoulos, I. Llamas-Jansa, J. E. Olsen and B. C. Hauback, J. Phys. Chem. C, 2013, 117, 6060–6065.
31. F. D. Manchester and A. San-Martin, Phase Diagrams of Binary Hydrogen Alloys, ASM International, Ohio, 2000.
32. T. D. Humphries, M. B. Ley, C. Frommen, K. T. Munroe, T. R. Jensen and B. C. Hauback, J. Mater. Chem. A, 2015, 3, 691–698.
33. T. D. Humphries, J. W. Makepeace, S. Hino, W. I. F. David and B. C. Hauback, J. Mater. Chem. A, 2014, 2, 16594–16600.
34. Outukumpu, Chemistry Software, Houston, 9th edn, 2006.
35. A. Reiser, B. Bogdanovic and K. Schlichte, Int. J. Hydrogen Energy, 2000, 25, 425–430.
36. B. Bogdanović, H. Hofmann, A. Neuy, A. Reiser, K. Schlichte, B. Spliethoff and S. Wessel, J. Alloys Compd., 1999, 292, 57–71.
37. C. Corgnale, B. Hardy, T. Motyka, R. Zidan, J. Teprovich and B. Peters, Renewable Sustainable Energy Rev., 2014, 38, 821–833.
38. Metal Prices.com, http://www.metalprices.com/metal/magnesium/magnesium-99-9-usa, accessed 15 June 2016.

---

Footnote

† Electronic supplementary information (ESI) available: XRD analysis of annealed NaH_xF_1−x materials; van't Hoff plots of NaH_0.5F_0.5; variation of ΔH and ΔS as function of hydrogen desorption; composition of NaH_0.5F_0.5 as a function of temperature measured by in situ XRD. See DOI: 10.1039/c6ta03623f

---