Water adsorption behaviour of CAU-10-H: a thorough investigation of its structure–property relationships

Abstract

Aluminium isophthalate CAU-10-H [Al(OH)(benzene-1,3-dicarboxylate)]·nH₂O exhibits water adsorption characteristics which make it a promising adsorbent for application in heat-exchange processes. Herein we prepared a stable coating of this MOF and evaluated its long-term stability under closed-cycle conditions for 10 000 water adsorption and desorption cycles, which are typical lifetimes for adsorption heat storage (AHS) applications. No degradation of the adsorption capacity could be observed which makes CAU-10-H the most stable MOF under these humid cycling conditions reported until now. Moreover, thermophysical properties like thermal conductivity and heat of adsorption were directly measured. In order to identify the structural features associated with the adsorption behaviour, the structural differences between the dry and the water loaded CAU-10-H were studied by Rietveld refinements and second harmonic generation (SHG) microscopy. The observed transition of space group symmetry from I4₁ to I4₁/amd between the humid and dry forms is induced by the adsorption/desorption of water into/out of the MOF channels. This originates from a torsional motion around the C–C bond between the carboxylate groups and the aromatic ring in half of the linker molecules. These observations are in excellent agreement with molecular dynamics simulations which confirm the energetic benefit of this transition.

---

Introduction

Metal–organic frameworks (MOFs) have been extensively studied with regard to various potential applications.¹ Due to their high porosity, they hold promise as storage and release adsorbents.² Their variable composition and tunable surface chemistry³ make these solids interesting materials for catalysis.⁴ MOFs have as well been incorporated into sensing devices.⁵ A possible application which came into focus, because of the promising application, is the use of MOFs as adsorbents in adsorption heat transformation, i.e., adsorption heat pumps (AHPs) and adsorption chillers (ACs).^6–8

For a good performance of AHPs or ACs, the (water) vapor uptake should occur in a pressure range between 0.1 and 0.4 p/p₀. The adsorption capacity should be higher than 0.2 g g⁻¹ with a steep adsorption step and a small hysteresis for not losing sensible heat. The regeneration temperature should not be higher than 120 °C and cycle stability under these adsorption/desorption conditions should guarantee a material lifetime of several years.

Compared to classical compression chillers, adsorption systems are thermally driven. By the adsorption into a porous material the working fluid is removed from the gas phase and subsequently evaporation from the liquid reservoir takes place. Hence, in analogy to an electrically driven compressor used in refrigerators it can be seen as a “thermal compressor”.^9–11 In order to remove the working fluid from the porous material, heat is used as driving energy. Compared to absorption systems (e.g. salt solutions), low temperature heat can be used in adsorption systems.¹² By the use of recently developed MOFs as porous materials, driving temperatures below 75 °C seem to be manageable, thus allowing access to lower energy driving sources. However, while several compounds were investigated regarding their water vapour sorption characteristics,^8,13–20 it was also observed that only very few materials withstand the harsh conditions imposed during repeated water adsorption and desorption cycles, which is a prerequisite for their applicability.^7,20 Long-term multi-cycle water stability is mainly observed for MOFs of the MIL-series.^14–19,21 For example, aluminium fumarate can be subjected to 4500 adsorption/desorption cycles without decomposition.²² Another MOF showing promising stability is the aluminium isophthalate CAU-10-H (Fig. 1); it shows a small reversible structural change during adsorption and no loss in crystallinity or porosity after 700 water vapour adsorption/desorption cycles.²³ Remarkably, both materials are based on infinite chains of AlO₆-octahedra and exhibit square shaped one-dimensional channels.^24,25 The underlying mechanism and the structure dependence caused by the adsorption of guest molecules are not yet fully understood. With regard to the intended application in a sorption chiller or a heat pump, further investigations need to be conducted, namely shaping and further stability tests under a closed water vapour atmosphere, accompanied by evaluation of the thermophysical properties.

Fig. 1 PXRD patterns of CAU-10-H after coating (red), after 10 000 cycles (blue). For comparison, the simulated PXRD pattern of the hydrated structure is shown (black).

Thus, herein we report a detailed analysis of this promising MOF including heat capacity (c_p), thermal conductivity and long-term stability measurements, as well as further structural analysis by means of in situ powder X-ray diffractometry (PXRD) during water adsorption studies, Rietveld refinement and second harmonic generation microscopy. Experimental investigations are complemented by molecular simulations in order to understand the structural transition and structure–property relationships.

Furthermore, we present an appropriate binder based coating of CAU-10-H on a metallic layer, which has been exposed to an application-oriented multi-cycle water adsorption/desorption test of 10 000 cycles, which is to the best of our knowledge currently the highest water vapour sorption cycle number a MOF has successfully withstood.

Experimental

Sample preparation

CAU-10-H was synthesized and activated according to an adapted literature procedure²⁴ using Al₂(SO₄)₃·18H₂O as the metal source (Bernd Kraft) and isophthalic acid (Aldrich Chemistry). In contrast to the standard procedure, a round bottom glass flask has been used to prepare larger amounts of CAU-10-H (see ESI† for details).

Coatings were prepared following a previously published procedure,²⁶ slightly modified and adapted for use with CAU-10-H. 2.085 g of dehumidified CAU-10-H were mixed with 1.408 g of Silikophen® P 50/300 and 6.437 g of xylene. The resulting dispersion was stirred and homogenised in an ultra-sonic bath for 20 min. Subsequently, the dispersion was manually applied with a pipette on 50 × 50 mm² aluminium plates (AlMg3 alloy). After drying at RT, the coated plates were heated to 200 °C and cured at this temperature for 2 h. The achieved coating has a mass of 0.253 g with a thickness of approximately 300 μm (see Fig. S1 and S2 in the ESI† for SEM images of the coating).

Characterization

Pore volume and surface area. The pore volume and surface area were obtained by N₂ adsorption isotherm analysis performed on a Quantachrome® Nova at 77 K, after vacuum degassing (120 °C/24 h).

Powder X-ray diffraction (PXRD) analysis. Powder X-ray diffraction (PXRD) analysis was performed on a Bruker D8 Advance diffractometer with DaVinci™ design, using Cu-Kα radiation from a Cu anode tube at 40 kV/40 mA with a Ni filter in Bragg Brentano geometry. An MRI TC-humidity chamber, coupled to a humidified nitrogen flow generated by an Ansyco® humidifier, was used for controlled humidity and in situ PXRD cycle experiments. An XYZ Newport stage was used for coated sheets.

In situ PXRD. In situ PXRD cycle experiments were done with the sample held at 40 °C and cycled between a wet (40% r.H.) and dry (0% r.H.) nitrogen flow. After every cycle, the powder diffractogram was recorded.

High-resolution PXRD data for Rietveld refinement. High-resolution PXRD data for Rietveld refinement were acquired from samples which were loaded into capillaries and sealed either under ambient conditions (hydrated form) or sealed after evacuation at 0.1 mbar and heating to 200 °C (dry form). The data were collected using a STOE Stadi-P diffractometer equipped with a Mythen detector using monochromated Cu Kα1 radiation. The software used for indexing and refinements was TOPAS.²⁷ The structural data for this paper have been deposited with the Cambridge Crystallographic Data Center (CCDC-numbers 1454066 and 1454067).

In situ second harmonic generation (SHG) microscopy. In situ second harmonic generation (SHG) microscopy was used to study structural phase transitions upon desorption and adsorption. A customized inverted wide-field Olympus microscope which is described elsewhere^28,29 coupled to a femtosecond pulsed InSight DeepSee laser operating at a wavelength of 800 nm was used. For the in situ adsorption and desorption, a RH95 Linkam Humidity controller was mounted on the microscope.

Water adsorption characteristics. Water adsorption characteristics were measured as isotherms and isobars using a custom-built Rubotherm thermobalance with enhanced measuring load and cell geometry to allow measurements on coated samples (for details see ref. 26).

Hydrothermal cycle stability. Hydrothermal cycle stability was investigated by short cycle experiments under isobaric conditions (5.6 kPa H₂O vapour) between 140 °C and 40 °C within the Rubotherm thermobalance. This allowed the in situ detection of possible initial degradation during the first cycles. Advanced long term hydrothermal stability to 10 000 full cycles was acquired within a custom-made closed cycle apparatus, consisting of a vacuum chamber under a pure water vapour atmosphere of 1.2 kPa. The samples are fixed on a heat exchanger plate connected to an alternating flow of hot and cold water in order to enable heating at 120 °C and cooling at 20 °C within 90 seconds.

Prior to and after the treatment, the water uptake of the samples at 40 °C and 5.6 kPa was measured within the thermobalance to identify possible loading degradation.

Computer modelling

The unit cell of CAU-10-H was calculated by means of the PXRD data to obtain the fractional coordinates and their occupancy probabilities. Then, implementation of the symmetry operations of the I4₁/amd crystallographic space group led to the final unit cell atomic coordinates. Molecular dynamics (MD) simulations were conducted on both the dehydrated and water-loaded CAU-10-H up to 20 ns at 300 K in the isothermal constant-stress ensemble (N, S, T) to account for the sorbent cell's volume and shape fluctuations according to a combination of the isenthalpic constant-stress method of Parrinello and Rahman,³⁰ and the thermostat algorithm of Nosé.³¹ However, results based on the Andersen conventional isobaric algorithm,³² wherein only the pressure tensor is taken into account, namely crystal transformations remain inhibited, are also presented in the ESI† for comparison. The calculated structure was modelled as a fully flexible framework; the parameters for the potential functions are detailed in the ESI.† Furthermore, regarding the particular mobility of the ligands of the material, two model options were tested: a stiff version by imposing torsional potentials on them, and another one enabling quasi-free rotation around the C–C bonds of the linker carboxylate groups (Fig. S5 in ESI†). However, only the latter version predicts the structural transition of the CAU cell upon water adsorption; also, it captures the linker dynamics upon water adsorption with respect to the second harmonic generation (SHG) microscopy experiments of this work. Although the scope of the modelling work of this article is not the derivation of a strict force field for this sorbent, one could conclude that a realistic representation for its linkers definitely opts for flexible states. The guest water interactions were described by the SPC/E model.³³ The water model was kept rigid by constraining the two bond lengths and the angle between them by means of the SHAKE³⁴ algorithm.

Results

Water uptake and stability characteristics under closed system conditions

Coating preparation was successful as the crystal structure of CAU-10-H is preserved, as proven by PXRD measurements (Fig. 1). Furthermore, the sample showed good accessibility for water, as the maximum water uptake of the coated sample was determined at 0.26 g g⁻¹ (g water per g of coating (CAU-10-H + binder)) at p/p₀ = 0.76 (Fig. 2).

Fig. 2 Water desorption isobar at 5.6 kPa_H2O of CAU-10-H powder (red) and coated AlMg3-plate (black).

This corresponds approximately to 76–79% of the maximum pure powder capacity (i.e. 0.33–0.34 g g⁻¹) at maximal loading. This is in good agreement with the MOF content of approximately 76 wt% within the coating calculated from the initial composition. Thus, it can be concluded that the coating formulation does not impede the accessibility of the micropores.

With regard to hydrothermal stability, cycle experiments were first performed in the thermobalance, as strong degradation of MOFs typically occurs during the initial cycles.²² Thus, the coated samples were tested under closed-system conditions.

A very small degradation is visible in these 7 cycles, as shown in Fig. 3. The maximal water sorption capacity in the beginning is 0.264 g g⁻¹ whereas after 7 cycles 0.261 g g⁻¹ is observed. The total capacity loss amounts to 0.003 g g⁻¹, 2.3%. In addition, the dry mass decreases from 0.253 g to 0.252 g which leads to a very small loss of 0.001 g or 0.4%. This can be attributed to a small rearrangement in the crystal or occupation of active sites by water which is then bound too strong to free these sites under cycle conditions. Also the loss in dry mass could be due to the sublimation of unreacted linkers under cycle conditions. This effect is stabilized after some cycles.

Fig. 3 In situ hydrothermal cycles of the CAU-10-H coatings under a pure water vapour atmosphere at 5.6 kPa. The sample was thermally cycled between 40 °C and 140 °C. Loading in blue and temperature in red.

Following these very promising initial results, the sample passed 10 000 water adsorption/desorption cycles in the custom-made cycle test rig. In contrast to the thermobalance, this setup does not allow an in situ determination of the water uptake. Thus, the uptake capacity was measured after 1000, 5000 and 10 000 cycles within the thermobalance. No loss of uptake capacity, within the measurement error, was observed (see Fig. 4).

Fig. 4 Comparison of the uptake capacity prior to cycle treatment, after 1000 and after 10 000 adsorption/desorption cycles.

In addition, the powder X-ray diffractogram before and after 10 000 adsorption/desorption cycles showed that all reflections are preserved and no change in crystallinity is visible (Fig. 2).

In situ PXRD structural stability investigation upon water adsorption/desorption

With regard to the known structural change upon adsorption of guest molecules, especially water, adsorption/desorption experiments were conducted under in situ PXRD observation (Fig. 5). After 20 cycles, there are no changes in the PXRD pattern; the reflections of the material show the same intensity as those of the fresh powder. In addition, no increase of amorphous background is visible.

Fig. 5 20 adsorption (blue)/desorption (red) cycles of CAU-10-H with in situ XRD observation. For clarity, only the first 3 cycles and last 3 cycles are shown.

These results are in line with the cycling results by thermogravimetry leading to the conclusion that there is no degradation of the material.

Rietveld refinements of the wet and dry structures

The in situ measurements at different relative humidity values unambiguously prove a phase transition between the known non-centrosymmetric form of CAU-10-H and a not yet reported dry, centrosymmetric conformation. Although the structure of hydrated CAU-10-H has been reported previously, the structure was revaluated since better PXRD data could be obtained. In the light of these results, high-resolution PXRD data were analyzed and crystal structures of the dry and wet forms were obtained by Rietveld refinement, taking also into account the results of SHG-microscopy (see below). For details on the experimental procedure, please see ESI.†

The most relevant parameters of the refinement are summarized in Table 1. The asymmetric units, relevant bond distances and the final Rietveld plots are given in the ESI.†

Table 1 Final parameters of the Rietveld refinements

CAU-10-H	-H2O	-dry
Space group	I41	I41/amd
a = b [Å]	21.2928(4)	21.5214(7)
c [Å]	10.7305(3)	10.3218(4)
V [Å^3]	4865.0(2)	4780.7(4)
R WP/%	6.8	4.3
R Bragg/%	3.2	0.6
GoF	1.54	1.03
Wavelength	Cu Kα1	Cu Kα1

---

In situ SHG structural transition observation upon water desorption and adsorption

Using Second Harmonic Generation (SHG) microscopy, non-centrosymmetric to centrosymmetric transitions can be observed, as only non-centrosymmetric crystals generate an SHG signal, whereas centrosymmetric structures cannot.³⁵ To study the effect of guest water molecules on the crystal structure, the SHG intensity of CAU-10-H was recorded in situ upon variation of relative humidity. Fig. 6 shows clearly that a phase transition occurs upon adsorption and desorption of water. The centrosymmetric to non-centrosymmetric phase transition sets in at 20% relative humidity. This value corresponds to the water adsorption starting point on the adsorption isotherm, as reported by Reinsch et al.²⁴ Therefore, it can be concluded that adsorbed water molecules cause the structure to be organized non-centrosymmetrically, whereas the absence of H₂O leaves the structure centrosymmetric.

Fig. 6 In situ SHG intensity measurement at 26 °C of CAU-10-H with increasing relative humidity of H₂O (adsorption branch, solid line) and subsequent decreasing relative humidity of H₂O (desorption branch, dashed line).

Structure description

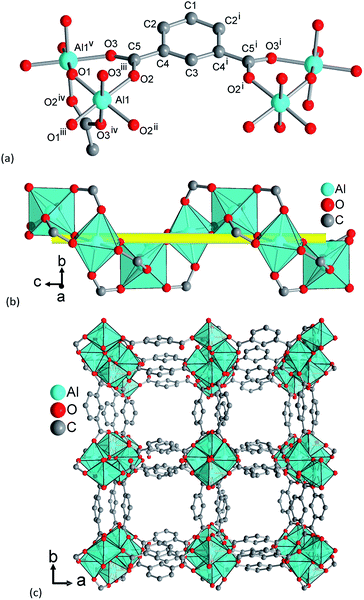
The framework structure of CAU-10-H is formed by the interconnection of fourfold helical chains of cis-corner sharing {AlO₆} octahedra by isophthalate linker molecules (1,3-benzenedicarboxylate). Four oxygen atoms in each polyhedron originate from four different coordinating carboxylate groups while two cis standing hydroxide ions induce the helical shape of the inorganic building unit. The organic moieties connect each chain to four adjacent inorganic units and thus square shaped one dimensional channels are formed (Fig. 7).

Fig. 7 Structural elements in CAU-10-H dry: (a) extended asymmetric unit with full Al coordination spheres and full ligand bridging mode. Symmetry transformations (i) = 1 − x, y, z; (ii) = x, −y, −z; (iii) = 0.25 + y, 0.25 − x, −0.25 + z; (iv) = 0.25 + y, −0.25 + x, 0.25 − z; (v) = 0.25y, −0.25 + x, 0.25 + z. (b) The inorganic building unit, a fourfold helical chain of cis vertex-sharing AlO₆ polyhedra winding around the fourfold axis (yellow line). (c) The 3D framework structure exhibiting square shaped one dimensional channels.

Adjacent chains in the framework exhibit different orientations; thus, half the helices are 4₁ helices while the other half represents 4₃ helices. Due to the high symmetry of the structure, all linker molecules are arranged in an identical fashion. They are arranged pairwise with centroid–centroid distances between the aromatic rings of 3.62(2) Å, indicating π-stacking interactions between the aromatic moieties. The resulting minimum diagonal distance of the channels based on the vdW-radii of the framework is thus approximately 3.6 Å.

Upon dehydration/rehydration, no bonds are broken and the observed phase transition can be attributed to conformational changes which result from coordination of water molecules. The differences in the crystal structures and, thus, in space group symmetry are due to slight rotations around the C–C bond of the carboxylate groups. These torsions are much stronger in the hydrated form compared to the dry form. Although the accuracy of the refined structure is limited due to the absence of single crystal diffraction data, this can be well observed in the refined crystal structures. In the structure of CAU-10-H, only half a linker molecule is present in the asymmetric unit and the averaged value for the O–C–C–C torsion angle is 13.5°. In the crystal structure of CAU-10-H-H₂O (Fig. 8), two complete linker molecules are present in the asymmetric unit. For one of the molecules, this angular tension is apparently relaxed and O–C–C–C torsion angles with average values of 14.3° and 2.5° are observed. The other linker molecule is more stressed than in the dry state and the O–C–C–C angles amount up to 33.5° and 33.8°. These latter linker molecules also point more strongly into the framework channels narrowing their minimum distance from 3.6 Å to only 2.4 Å. This is also accompanied by the slight tilting of the inorganic building units around their symmetry axis.

Fig. 8 Structural elements in CAU-10-H H₂O: (a) extended asymmetric unit with full Al coordination spheres and full ligand bridging mode. Symmetry transformations (i) = 0.5 − y, x, −0.25 + z; (ii) = 0.5 − x, 0.5 − y, −0.5 + z; (iii) = y, 0.5 − x, 0.25 + z; (iv) = 0.5 − x, 0.5 − y, 0.5 + z; (v) = 0.5 + y, 1 − x, −0.25 + z; (vi) = 1.5 − x, 0.5 − y, −0.5 + z; (vii) = 1 − y, −0.5 + x, 0.25 + z; (viii) = 1.5 − x, 0.5 − y, 0.5 + z. (b) The inorganic building unit, a fourfold helical chain of cis vertex-sharing AlO₆ polyhedra winding around the fourfold axis (yellow line). (c) The 3D framework structure exhibiting square shaped one dimensional channels. Crystal water molecules are omitted for clarity.

This structural change is induced by the adsorption of water molecules. These are found close to the bridging OH-groups (shortest O–O distance 2.80(2) Å and 2.94(2) Å) but also close to coordinating carboxylate oxygen atoms (2.85(2) Å and 2.95(2) Å). Several other close proximities can be observed between the guest molecules inside the pores (for details see ESI†). These structural changes affect the unit cell parameters and upon hydration the unit cell volume is increased by ≈1.7% due to an anisotropic expansion. While the a and b parameters decrease upon hydration from 21.52 to 21.29 Å, the c axis is expanded from 10.32 to 10.73 Å.

Thermophysical characteristics

Heat capacity and conductivity of the coated material. The heat capacity and conductivity of CAU-10-H have been measured for the powder as pressed pellets and for the coated sample (Fig. 9).

Fig. 9 Diffusivity in mm² s⁻¹ (black), thermal conductivity in W m⁻¹ K⁻¹ (red) and heat capacity in J g⁻¹ K⁻¹ (blue) of CAU-10-H (solid line) and coated CAU-10-H (dashed lines).

The heat capacity for the pure powder is in the range of 1.3 J g⁻¹ K⁻¹ at RT up to 1.7 J g⁻¹ K⁻¹ at 150 °C, which is higher compared to the reported literature data for MOFs.^22,36,37 The thermal conductivity has been determined to be 0.08 W m⁻¹ K⁻¹ and the diffusivity to be 0.07 mm² s⁻¹ showing the characteristics of a porous material. These values are lower for the coated sample, with a heat capacity of 1.25 J g⁻¹ K⁻¹, a thermal conductivity of 0.03 W m⁻¹ K⁻¹ and a diffusivity of 0.05 mm² s⁻¹. This is probably because the binder lowers the thermophysical characteristics of the coated material compared to the pure material.

Heat of adsorption. The isosteric heat ΔH was calculated from the adsorption isotherms reported by Fröhlich et al.,²³ using the Clausius–Clapeyron equation,³⁸
where R is the universal gas constant, p is the numerical value of the equilibrium pressure and T is the temperature in K.

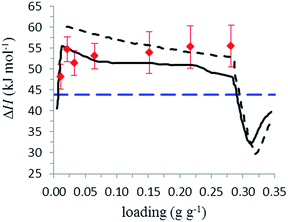
For the calculation, the three isotherms were transformed into a form with the relative loading in mol H₂O over absolute pressure in Pa. The loading of the first isotherm was split into 1000 steps. For each step, pressures of the three isotherms with the same loading were calculated using linear interpolation between the measurement points, resulting in a list with 1000 loadings and the corresponding three pressures. For every step, the natural logarithm of the three pressures was plotted against the reciprocal temperatures of the isotherms 1/T, and a linear fit between the points was made. The slope of this straight line is ΔH_ads/R. Fig. 10 shows the calculated heat of adsorption and desorption against the loading in g g⁻¹. ΔH_ads starts at approximately 56 kJ mol⁻¹ at low loadings, with a plateau of slightly over 50 kJ mol⁻¹ between 0.06 and 0.28 g g⁻¹, and falls under the evaporation enthalpy of H₂O when capillary pore condensation begins. The calculated heat of desorption ΔH_des shows a similar shape with higher values between 60 kJ mol⁻¹ and 52 kJ mol⁻¹ between 0.03 and 0.28 g g⁻¹. The decrease in ΔH_ads above 0.28 g g⁻¹ is due to a change from adsorption to pore condensation. The rise in ΔH_ads before 0.03 g ⁻¹ is accounted by uncertainties in the measurement.

Fig. 10 Isosteric heats: calculated from experimental adsorption (solid line) and desorption (short dashed line) isotherms and computed during MD simulations (see text below and red points); the long dashed line points to the evaporation enthalpy of H₂O at STP.³⁹

Molecular dynamics computer simulations

The simulated IR spectrum of CAU-10-H was computed by means of the Fourier transform of the correlation function of the dipole moment vectors⁴⁰ using the quasi free modelling for the linkers; the latter option proved to be in acceptable agreement with the experimentally measured spectrum (Fig. S9†). Details on adapting the Dreiding generic force field to this sorbent with respect to the experimental spectrum and the derivation of the partial charges of the host atoms are given in the ESI.†

The molecular dynamics revealed a “flapping” motion of the benzene rings around the C–C bonds of the linker carboxylate groups (Fig. S5†), thus taking conformations between two extrema with the one being almost parallel (state I) and the other being vertical (state II) to the channel axis, so that conformations of the linkers approaching the state I or II can widen or narrow, respectively, the effective path-width of the channels.

In Fig. 11, the correlation probabilities between the dihedral angles φ₁ and φ₂ denoting the motion of the carboxylate group relative to the aromatic ring (Fig. S5†) are presented, over the total number of ligands (sixteen ligands per unit cell), for both the bare and water-loaded materials at 0.032 and 0.303 g g⁻¹. It is shown that in the dry material the most probable conformations are achieved when the aromatic rings tend to lie almost parallel along the z-direction. It is worth mentioning that simulation can predict a spectrum of angle values in addition to the experimentally measured average of 13.5°.

Fig. 11 MD calculations: correlation probabilities of the dihedral angles φ₁ and φ₂ for the CAU-10-H ligands attaining two conformation extrema (top), for the dry (middle), and the water-loaded material at 0.303 g g⁻¹ (bottom); Gibbs free energy profile of the transition I to II (most bottom).

The above situation changes gradually upon water adsorption, in the sense that the increasing guest concentration gives rise to two distinct sets of conformations between the vicinity of states I and II separated by a lower probability region, thus forming a free energy barrier of about 3k_BT, where k_B = 1.3806 × 10⁻²³ J K⁻¹ is the Boltzmann constant; presumably this is a consequence of steric hindrance phenomena at higher loadings up to saturation. Furthermore, the Gibbs free energy profile, G(φ_a), a = 1, 2, shown in the same figure for the first dihedral, was calculated over a sequence of angles between states I and II by

G(φ_a) = −k_BT ln[ρ(φ_a)/ρ] + const

where
The vector r^N constitutes the sampled configurational space through the set of N total degrees of freedom for the system guest plus host. The above ratio is actually a mean value of a delta distribution, sampled over the states of the (N, P, T) ensemble under the prescribed pressure, P (loading), and T, therefore defining the probability density, ρ(φ_a), a = 1, 2, of having a ligand conformation at the angle φ_o, with dimensions [rad⁻¹]; this quantity is normalized by the uniform probability density, ρ = 1/ω, over the totally sampled angle, ω, so that to become dimensionless in the logarithm.

The MD simulations in the N, S, T ensemble by means of the quasi free ligand version predict an anisotropic structural transition of the unit cell upon water adsorption. In particular, the unit cell contracts in the [100] and [010] directions and expands at the same time in the [001] direction, resulting in a volume increase of approximately 1.9% close to saturation. This finding may be attributed to the aforementioned ligand preferred conformation with increasing water loading. The average unit cell edges were calculated for the water uptakes of 0.005, 0.011, 0.022, 0.032, 0.065, 0.151, 0.216, 0.281, 0.303 and 0.368 g g⁻¹ as illustrated in Fig. 12. It is also observed that at saturation where the system becomes much congested the unit cell starts expanding, thus explaining the predicted increase of the a and b axes. The variation of the three angles of the unit cell shown in the same figure was also recorded during the run, showing no deviation from the 90 degrees on the average for a fully equilibrated MD trajectory.

Fig. 12 Computed length evolution of the a, b and c axes (top), and α, β, and γ angles of the CAU-10-H unit cell (bottom), induced by the water adsorption during an MD trajectory, as a function of loading for 0.005, 0.011, 0.022, 0.032, 0.065, 0.151, 0.216, 0.281, 0.303 and 0.368 g g⁻¹.

We found that the guest molecules are primarily adsorbed in the proximity of the AlO₆ polyhedra via hydrogen bonding to the O1 and H7 atoms of the bridging OH groups and the O2 and O3 oxygen atoms of the carboxylate groups (see Fig. S5 and calculated radial distribution functions in Fig. S10†). As loading increases further, the guest–guest interactions dominate as a result of the hydrogen bonding, therefore, giving rise to water clusters which may exert steric effects on the linkers that alter their position (Fig. 11, S11 and S12†); this phenomenon leads to a distortion of the CAU framework. It must be stressed here that the anisotropic structural transition is not observed when imposing torsional potential on all dihedral angles controlling the motion of the CAU-10-H linkers (see Fig. S7 and S8†). This finding supports the result that this anisotropic structural transition of the CAU cell can be mainly attributed to the ligand reorientations upon water sorption. The predicted isosteric heats of water from MD in the CAU sorbent were calculated after developing a Widom type scheme⁴¹ using the following equation for the loadings shown in Fig. 10.

r_t represents the degrees of freedom of the test water molecule and Δ[scr V, script letter V](r_t; r^N) stands for the potential energy change of the system energy, [scr V, script letter V](r^N, ψ^N), upon the insertion of a test sorbate molecule.

In other words, the above equation entails: firstly, an ensemble average of the change in potential energy (and its Boltzmann factor) brought about by the random insertion of a “ghost” (test) water molecule, namely, interacting with the host atoms and guest molecules without perturbing the current configuration; the average is carried out over the states (snapshots) of the system as they are created during the MD trajectory. And secondly, evaluation of a spatial integral over a sequence of random insertions and orientations of this test molecule within the current CAU volume is carried out at each state. The described averages are denoted by 〈…〉_W. f_b is the fugacity of the bulk phase; at low pressures it becomes pressure, hence the derivative in the above equation decays.

It must be stressed that in our simulations the equation above represents the configurational part of the differential heat of sorption since it is related to the configurational part of internal energy, namely the potential energy, [scr V, script letter V].

Cooling performance

The water adsorption data were transformed according to the Dubinin–Astakhov approach leading to the following equation for the equilibrium loading capacity as a function of the adsorption potential:⁴²
where the adsorption potential is given by

The transformation leads to a fairly smooth characteristic curve with a steep step between 200 J g⁻¹ and 250 J g⁻¹ of the adsorption potential. By the use of this rough thermodynamic model, the potential of the working pair water/CAU-10-H has been evaluated under different boundary conditions.

At first, the sensitivity of the uptake capacity with regard to the desorption conditions, i.e., the condenser and desorption temperatures, was calculated. As shown in Fig. 13, the CAU-10-H can be easily regenerated by a very low desorption temperature. Even at a high condenser temperature of 35 °C, a desorption temperature less than 75 °C is sufficient to completely dry the material. With lower condenser temperature, the required driving temperatures decrease with a minimum of 70 °C at a condenser temperature of 27 °C.

Fig. 13 Projection of the uptake capacity versus the chilling and heat rejection temperatures, showing a very broad plateau with maximum uptake capacity for a large range of boundary conditions.

In addition to the desorption conditions, the sensitivity for the adsorption conditions, i.e. the heat rejection and the chilling temperatures (evaporator), was evaluated. As can be seen in Fig. 14, CAU-10 performs best either at heat rejection temperatures below 30 °C and/or for evaporator temperatures above 10 °C with almost the maximum uptake of approximately 0.32 g g⁻¹. Surprisingly, nearly the whole uptake capacity can be achieved with heat rejection temperatures below 30 °C for almost the whole range of chilling temperatures. In addition, the full uptake can be achieved even at a very high heat rejection temperature of 35 °C, if the chilling temperatures can be increased above temperatures of 12 °C. Thus, this working pair is highly interesting for very low driving heat cooling applications.

Fig. 14 Calculation of uptake capacity vs. desorption temperature and condensing temperature. As illustrated by the red line, CAU-10-H can be completely dried at all typical condenser temperatures used in cooling application with a desorption temperature less than 75 °C.

As this field of application is not accessible by current state-of-the-art materials, CAU-10-H clearly closes a gap, thus allowing new adsorption chilling applications.

Conclusions

The results described herein demonstrate that CAU-10-H remains stable during several thousand adsorption and desorption cycles with water as working fluid.

Due to its thermophysical characteristics, it is a suitable adsorbent for application in adsorptive cooling application with water as the working fluid. The water uptake of 0.26 g g⁻¹ for the coated sample (0.34 g g⁻¹ for the bulk) is lower compared to that of other very good performing and stable MOFs, like aluminium-fumarate coating (0.35 g g⁻¹). Other MOFs with higher water capacities like UiO-66 (0.45 g g⁻¹) or MIL-100 (Fe 0.65 g g⁻¹, Al 0.36 g g⁻¹) lack stability upon cycling. The successful coating procedure, the high stability up to 10 000 cycles under working conditions, the nearly perfect shape of the isotherm and the high uptake capacity make CAU-10-H the best performing MOF for heat pump applications reported until now.

For a successful market introduction, it will be necessary to develop an industrially more feasible and scalable route for its synthesis. The structural transition which was characterised in detail indicates that the flexibility of this material is dominated by a torsional motion within the linker molecule, which nevertheless does not lower the stability of the MOF. Since this is the second MOF demonstrating such long-term stability and since the first MOF with such properties (aluminium fumarate) is also based on Al³⁺, we assume that Al-based MOFs are the most promising MOF adsorbents for application in water based heat pumps. One major challenge in the future will be the development of better MOF adsorbents in which the stability is preserved while the capacity and therefore the amount of converted energy are increased.

Acknowledgements

The authors would like to thank Linkam for lending them the demo version of the RH95 Humidity Controller. Financial support from the German Federal Ministry of Education and Research and the Greek General Secretariat of Research and Technology within the German-Greek joint project WASSERMOD under grant 03SF0469B, and the project Optimat under grant 03SF0492A/C as well as support by the Fraunhofer Zukunftsstiftung under grant HARVEST are gratefully acknowledged. Georg Hagelstein is thanked for the SEM measurements. Also Albina Holz and Konstantin Gradwohl are thanked for their work in the laboratory. KM and DDV are grateful to Belspo for funding in the IAP project Functional Supramolecular Systems. MvdV and DDV are grateful for the financial support from the Hercules Foundation. GKP acknowledges the supercomputing centre of the Greek General Secretariat of Research and Technology, “ARIS”.

Notes and references

1. (a) C. Janiak and J. K. Vieth, New J. Chem., 2010, 34, 2366–2388; (b) A. U. Czaja, N. Trukhan and U. Muller, Chem. Soc. Rev., 2009, 38, 1284–1293; (c) C. Janiak, Dalton Trans., 2003, 2781.
2. (a) H. Wu, Q. Gong, D. H. Olson and J. Li, Chem. Rev., 2012, 112, 836–868; (b) L. J. Murray, M. Dincă and J. R. Long, Chem. Soc. Rev., 2009, 38, 1294–1314; (c) J. R. Li, R. J. Kuppler and H. C. Zhou, Chem. Soc. Rev., 2009, 38, 1477–1504; (d) M. P. Suh, H. J. Park, T. K. Prasad and D. W. Lim, Chem. Rev., 2012, 112, 782–835.
3. M. Eddaoudi, D. F. Sava, J. F. Eubank, K. Adil and V. Guillerm, Chem. Soc. Rev., 2015, 44, 228–249.
4. A. Corma, H. Garcia and F. X. Llabres i Xamena, Chem. Rev., 2010, 110, 4606–4655.
5. O. Shekhah, J. Liu, R. A. Fischer and C. Wöll, Chem. Soc. Rev., 2011, 40, 1081–1106.
6. (a) Y. I. Aristov, B. Dawoud, I. S. Glaznev and A. Elyas, Int. J. Heat Mass Transfer, 2008, 51, 4966–4972; (b) M. F. de Lange, K. J. F. M. Verouden, T. J. H. Vlugt, J. Gascon and F. Kapteijn, Chem. Rev., 2015, 115, 12205–12250; (c) S. K. Henninger, F. Jeremias, H. Kummer and C. Janiak, Eur. J. Inorg. Chem., 2012, 2625–2634; (d) C. Janiak and S. K. Henninger, Chimia, 2013, 67, 419–424; (e) J. Canivet, A. Fateeva, Y. Guo, B. Coasne and D. Farrusseng, Chem. Soc. Rev., 2014, 43, 5594–5617.
7. F. Jeremias, D. Fröhlich, C. Janiak and S. K. Henninger, New J. Chem., 2014, 38, 1846–1852.
8. S. K. Henninger, H. A. Habib and C. Janiak, J. Am. Chem. Soc., 2009, 131, 2776–2777.
9. (a) J. V. Veselovskaya, R. E. Critoph, R. N. Thorpe, S. Metcalf, M. M. Tokarev and Y. Aristov, Appl. Therm. Eng., 2010, 30, 1188–1192; (b) Z. Tamainot-Telto, S. J. Metcalf and R. E. Critoph, Int. J. Refrig., 2009, 32, 727–733; (c) A. A. Askalany, M. Salem, I. M. Ismael, A. H. H. Ali, M. G. Morsy and B. B. Saha, Renewable Sustainable Energy Rev., 2013, 19, 565–572; (d) K. Habib, B. B. Saha, A. Chakraborty, S. T. Oh and S. Koyama, Appl. Therm. Eng., 2013, 50, 1582–1589; (e) Y. I. Aristov, Appl. Therm. Eng., 2012, 42, 18–24; (f) R. Wang and R. Oliveira, Prog. Energy Combust. Sci., 2006, 32, 424–458; (g) B. B. Saha, A. Chakraborty, S. Koyama and Y. I. Aristov, Int. J. Heat Mass Transfer, 2009, 52, 516–524; (h) B. B. Saha, A. Chakraborty, S. Koyama, K. Srinivasan, K. C. Ng, T. Kashiwagi and P. Dutta, Appl. Phys. Lett., 2007, 91, 111902.
10. (a) L. G. Gordeeva, A. Freni, Y. I. Aristov and G. Restuccia, Ind. Eng. Chem. Res., 2009, 48, 6197–6202; (b) Y. I. Aristov, M. M. Tokarev, A. Freni, I. S. Glaznev and G. Restuccia, Microporous Mesoporous Mater., 2006, 96, 65–71; (c) B. Dawoud and Y. Aristov, Int. J. Heat Mass Transfer, 2003, 46, 273–281; (d) Y. I. Aristov, Int. J. Refrig., 2009, 32, 675–686; (e) I. A. Simonova, A. Freni, G. Restuccia and Y. I. Aristov, Microporous Mesoporous Mater., 2009, 122, 223–228; (f) Y. I. Aristov, J. Chem. Eng. Jpn., 2007, 40, 1242–1251; (g) Y. I. Aristov, Appl. Therm. Eng., 2013, 50, 1610–1618.
11. (a) Y. I. Aristov, G. Restuccia, G. Cacciola and V. N. Parmon, Appl. Therm. Eng., 2002, 22, 191–204; (b) N. C. Srivastava and I. W. Eames, Appl. Therm. Eng., 1998, 18, 707–714.
12. R. Z. Wang, Z. Z. Xia, L. W. Wang, Z. S. Lu, S. L. Li, T. X. Li, J. Y. Wu and S. He, Energy, 2011, 36, 5425–5439.
13. (a) T. Birsa Čelič, M. Mazaj, N. Guillou, E. Elkaïm, M. El Roz, F. Thibault-Starzyk, G. Mali, M. Rangus, T. Čendak, V. Kaučič and N. Zabukovec Logar, J. Phys. Chem. C, 2013, 117, 14608–14617; (b) G. W. Peterson, J. B. DeCoste, T. G. Glover, Y. Huang, H. Jasuja and K. S. Walton, Microporous Mesoporous Mater., 2013, 179, 48–53; (c) H. Jasuja and K. S. Walton, Dalton Trans., 2013, 42, 15421–15426; (d) H. Jasuja, J. Zang, D. S. Sholl and K. S. Walton, J. Phys. Chem. C, 2012, 116, 23526–23532; (e) G. E. Cmarik, M. Kim, S. M. Cohen and K. S. Walton, Langmuir, 2012, 28, 15606–15613; (f) P. M. Schoenecker, C. G. Carson, H. Jasuja, C. J. J. Flemming and K. S. Walton, Ind. Eng. Chem. Res., 2012, 51, 6513–6519; (g) F. Jeremias, V. Lozan, S. Henninger and C. Janiak, Dalton Trans., 2013, 42, 15967–15973; (h) M. F. de Lange, C. P. Ottevanger, M. Wiegman, T. J. H. Vlugt, J. Gascon and F. Kapteijn, CrystEngComm, 2015, 17, 281–285.
14. J. J. Low, A. I. Benin, P. Jakubczak, J. F. Abrahamian, S. A. Faheem and R. R. Willis, J. Am. Chem. Soc., 2009, 131, 15834–15842.
15. J. Ehrenmann, S. K. Henninger and C. Janiak, Eur. J. Inorg. Chem., 2011, 471–474.
16. A. Khutia, H. U. Rammelberg, T. Schmidt, S. Henninger and C. Janiak, Chem. Mater., 2013, 25, 790–798.
17. M. Wickenheisser and C. Janiak, Microporous Mesoporous Mater., 2015, 204, 242–250.
18. M. Wickenheisser, A. Herbst, R. Tannert, B. Milow and C. Janiak, Microporous Mesoporous Mater., 2015, 215, 143–153.
19. M. Wickenheisser, T. Paul and C. Janiak, Microporous Mesoporous Mater., 2016, 220, 258–269.
20. N. C. Burtch, H. Jasuja and K. S. Walton, Chem. Rev., 2014, 114, 10575–10612.
21. F. Jeremias, A. Khutia, S. K. Henninger and C. Janiak, J. Mater. Chem., 2012, 22, 10148–10151.
22. F. Jeremias, D. Fröhlich, C. Janiak and S. K. Henninger, RSC Adv., 2014, 4, 24073–24082.
23. D. Fröhlich, S. K. Henninger and C. Janiak, Dalton Trans., 2014, 43, 15300–15304.
24. H. Reinsch, M. A. van der Veen, B. Gil, B. Marszalek, T. Verbiest, D. de Vos and N. Stock, Chem. Mater., 2013, 25, 17–26.
25. E. Alvarez, N. Guillou, C. Martineau, B. Bueken, B. Van de Voorde, C. Le Guillouzer, P. Fabry, F. Nouar, F. Taulelle, D. de Vos, J.-S. Chang, K. H. Cho, N. Ramsahye, T. Devic, M. Daturi, G. Maurin and C. Serre, Angew. Chem., Int. Ed., 2015, 54, 3664–3668.
26. H. Kummer, G. Füldner and S. K. Henninger, Appl. Therm. Eng., 2015, 85, 1–8.
27. Topas Academics 4.2, Coelho Software, 2007.
28. M. A. van der Veen, B. F. Sels, D. E. De Vos and T. Verbiest, J. Am. Chem. Soc., 2010, 132, 6630–6631.
29. M. A. van der Veen, J. van Noyen, B. F. Sels, P. A. Jacobs, T. Verbiest and D. E. De Vos, Phys. Chem. Chem. Phys., 2010, 12, 10688–10692.
30. M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182.
31. S. Nosé, J. Chem. Phys., 1984, 81, 511.
32. (a) H. C. Andersen, J. Chem. Phys., 1980, 72, 2384; (b) E. Pantatosaki, G. Megariotis, A.-K. Pusch, C. Chmelik, F. Stallmach and G. K. Papadopoulos, J. Phys. Chem. C, 2012, 116, 201–207.
33. H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271.
34. J.-P. Ryckaert, G. Ciccotti and H. J. Berendsen, J. Comput. Phys., 1977, 23, 327–341.
35. T. Verbiest, K. Clays and V. Rodriguez, Second-order nonlinear optical characterization techniques. An introduction, CRC Press, Boca Raton, 2009.
36. M. Kandiah, M. H. Nilsen, S. Usseglio, S. Jakobsen, U. Olsbye, M. Tilset, C. Larabi, E. A. Quadrelli, F. Bonino and K. P. Lillerud, Chem. Mater., 2010, 22, 6632–6640.
37. V. Guillerm, F. Ragon, M. Dan-Hardi, T. Devic, M. Vishnuvarthan, B. Campo, A. Vimont, G. Clet, Q. Yang, G. Maurin, G. Férey, A. Vittadini, S. Gross and C. Serre, Angew. Chem., Int. Ed., 2012, 51, 9267–9271.
38. P. W. Atkins, Physikalische Chemie, Wiley-VCH, Weinheim, 3rd edn, 2001.
39. R. H. Perry, D. W. Green and J. O. Maloney, Perry's Chemical Engineers' Handbook, McGraw-Hill, New York, 7th edn, 1997.
40. R. G. Gordon, in Advances in Magnetic Resonance, Elsevier, 1968, vol. 3, pp. 1–42.
41. P. D. Kolokathis, E. Pantatosaki and G. K. Papadopoulos, J. Phys. Chem. C, 2015, 119, 20074–20084.
42. (a) S. K. Henninger, M. Schicktanz, P. Hügenell, H. Sievers and H.-M. Henning, Int. J. Refrig., 2012, 35, 543–553; (b) F. Stoeckli, Russ. Chem. Bull., 2001, 50, 2265–2272; (c) M. Dubinin, J. Colloid Interface Sci., 1967, 23, 487–499.

---

Footnote

† Electronic supplementary information (ESI) available: CAU-10-H synthesis and characterization details, Rietveld refinement, modelling details and CIF files reported in this paper. CCDC 1454066 and 1454067. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6ta01757f

---