Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Crystal structure and proton conductivity of BaSn0.6Sc0.4O3−δ: insights from neutron powder diffraction and solid-state NMR spectroscopy†
Francis G.
Kinyanjui‡
 *a,
Stefan T.
Norberg
a,
Christopher S.
Knee
a,
Istaq
Ahmed
a,
Stephen
Hull
b,
Lucienne
Buannic
c,
Ivan
Hung
d,
Zhehong
Gan
d,
Frédéric
Blanc
ef,
Clare P.
Grey
ce and
Sten G.
Eriksson
a
*a,
Stefan T.
Norberg
a,
Christopher S.
Knee
a,
Istaq
Ahmed
a,
Stephen
Hull
b,
Lucienne
Buannic
c,
Ivan
Hung
d,
Zhehong
Gan
d,
Frédéric
Blanc
ef,
Clare P.
Grey
ce and
Sten G.
Eriksson
a
aDepartment of Chemical and Biological Engineering, Chalmers University of Technology, SE-412 96 Gothenburg, Sweden
bThe ISIS Facility, STFC Rutherford Appleton Laboratory, Didcot, Oxfordshire OX11 0QX, UK
cDepartment of Chemistry, State University of New York, Stony Brook, NY 11790-3400, USA
dCenter of Interdisciplinary Magnetic Resonance, National High Magnetic Field Laboratory, 1800 East Paul Dirac Drive, Tallahassee, Florida 32310, USA
eDepartment of Chemistry, University of Cambridge, Lensfield Road, Cambridge, CB2 1EW, UK
fDepartment of Chemistry and Stephenson Institute for Renewable Energy, University of Liverpool, Crown Street, Liverpool, L69 7ZD, UK
First published on 2nd March 2016
Abstract
The solid-state synthesis and structural characterisation of perovskite BaSn1−xScxO3−δ (x = 0.0, 0.1, 0.2, 0.3, 0.4) and its corresponding hydrated ceramics are reported. Powder and neutron X-ray diffractions reveal the presence of cubic perovskites (space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) with an increasing cell parameter as a function of scandium concentration along with some indication of phase segregation. 119Sn and 45Sc solid-state NMR spectroscopy data highlight the existence of oxygen vacancies in the dry materials, and their filling upon hydrothermal treatment with D2O. It also indicates that the Sn4+ and Sc3+ local distribution at the B-site of the perovskite is inhomogeneous and suggests that the oxygen vacancies are located in the scandium dopant coordination shell at low concentrations (x ≤ 0.2) and in the tin coordination shell at high concentrations (x ≥ 0.3). 17O NMR spectra on 17O enriched BaSn1−xScxO3−δ materials show the existence of Sn–O–Sn, Sn–O–Sc and Sc–O–Sc bridging oxygen environments. A further room temperature neutron powder diffraction study on deuterated BaSn0.6Sc0.4O3−δ refines the deuteron position at the 24k crystallographic site (x, y, 0) with x = 0.579(3) and y = 0.217(3) which leads to an O–D bond distance of 0.96(1) Å and suggests tilting of the proton towards the next nearest oxygen. Proton conduction was found to dominate in wet argon below 700 °C with total conductivity values in the range 1.8 × 10−4 to 1.1 × 10−3 S cm−1 between 300 and 600 °C. Electron holes govern the conduction process in dry oxidizing conditions, whilst in wet oxygen they compete with protonic defects leading to a wide mixed conduction region in the 200 to 600 °C temperature region, and a suppression of the conductivity at higher temperature.
m) with an increasing cell parameter as a function of scandium concentration along with some indication of phase segregation. 119Sn and 45Sc solid-state NMR spectroscopy data highlight the existence of oxygen vacancies in the dry materials, and their filling upon hydrothermal treatment with D2O. It also indicates that the Sn4+ and Sc3+ local distribution at the B-site of the perovskite is inhomogeneous and suggests that the oxygen vacancies are located in the scandium dopant coordination shell at low concentrations (x ≤ 0.2) and in the tin coordination shell at high concentrations (x ≥ 0.3). 17O NMR spectra on 17O enriched BaSn1−xScxO3−δ materials show the existence of Sn–O–Sn, Sn–O–Sc and Sc–O–Sc bridging oxygen environments. A further room temperature neutron powder diffraction study on deuterated BaSn0.6Sc0.4O3−δ refines the deuteron position at the 24k crystallographic site (x, y, 0) with x = 0.579(3) and y = 0.217(3) which leads to an O–D bond distance of 0.96(1) Å and suggests tilting of the proton towards the next nearest oxygen. Proton conduction was found to dominate in wet argon below 700 °C with total conductivity values in the range 1.8 × 10−4 to 1.1 × 10−3 S cm−1 between 300 and 600 °C. Electron holes govern the conduction process in dry oxidizing conditions, whilst in wet oxygen they compete with protonic defects leading to a wide mixed conduction region in the 200 to 600 °C temperature region, and a suppression of the conductivity at higher temperature.
1. Introduction
During the past three decades proton conducting ceramics have been widely studied due to their high ionic conductivities in the intermediate temperature region of 300–600 °C. In particular these materials have been proposed to be used as proton conducting electrolytes in protonic ceramic fuel cells (PCFC). The lower operating temperature of PCFCs would provide substantial advantages over solid oxide fuel cells (SOFC) based on oxide ion-conducting electrolytes. The higher operating temperatures of SOFCs, usually 700–900 °C, have limited their technological development due to high system costs, performance degradation rates, slow start-up and shutdown cycles. For example, in the 700–900 °C temperature range, the use of chromium containing interconnector steels might cause chromium poisoning of the electrodes1 and shorten the lifetime of the cell. Reduced start-up times and relaxed matching of the thermal expansion coefficients of the various fuel cell components are additional benefits that accompany the lowering of the operating temperature.Acceptor doped perovskites provide many eligible systems for proton conducting electrolytes, e.g. BaZr1−xYxO3−δ,2–4 BaCe1−xYxO3−δ,2 SrCe1−xYxO3−δ,5 BaZr1−xYbxO3−δ (ref. 6) all with 0 ≤ x ≤ 0.2, and BaZr1−xInxO3−δ (ref. 7) with 0 ≤ x ≤ 1. Below 700 °C, BaZr1−xYxO3−δ possesses a bulk proton conductivity greater than the best oxide ion conductors.2 Proton incorporation is reliant on the formation of oxygen vacancies in a process commonly referred to as acceptor doping in the A2+B4+O32− type perovskites. Here, a portion of the tetravalent cations at the B-site is substituted by trivalent dopant cations resulting in the formation of charge compensating oxygen vacancies in the system. This process can be described using Kröger–Vink notation for Sc-doped BaSnO3 with Sc3+ doped on the Sn4+ site as:
 | (1) |
 corresponding to a Sc3+ ion sitting on a Sn site with a negative charge, and
corresponding to a Sc3+ ion sitting on a Sn site with a negative charge, and 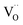 to an oxygen vacancy with two positive charges. When in contact with a H2O bearing gas the oxygen vacancies
to an oxygen vacancy with two positive charges. When in contact with a H2O bearing gas the oxygen vacancies  are filled via the following reaction:
are filled via the following reaction: | (2) |
 corresponding to a OH− ion sitting on a O lattice site with a positive charge.
corresponding to a OH− ion sitting on a O lattice site with a positive charge.
However, in oxidizing conditions and in some systems, electronic holes can instead compensate for the vacancies via the following equation leading to p-type hole (h˙) conduction:
 | (3) |
Under low oxygen partial pressures the following mechanism can occur yielding n-type electronic conduction:
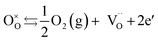 | (4) |
Significant proton conduction has been reported in substituted stannate phases such as BaIn0.5Sn0.5O2.75,8 Ba2YSnO5.5,9 BaSn1−xMxO3−δ with M = Sc, Y, In and Gd, x = 0.125 (ref. 10) and x = 0.25 (ref. 11) and BaSn1−xYxO3−δ (0 ≤ x ≤ 0.5).12 More recently, Li and Nino reported on proton conductivity of BaSn0.9M0.1O3−δ (M = In, Lu, Er and Y) in oxidising and reducing conditions,13 whilst Bévillon et al.14 used a density functional theory approach to probe the energy landscape of the proton in substituted BaSn1−xMxO3−x/2.
In this study, BaSn1−xScxO3−δ was selected as the system of interest as the recent studies highlighted above have established acceptor doped BaSnO3 as a promising alternative candidate to the more widely studied BaZrO3 and BaCeO3 systems. Scandium was chosen here as the dopant as it has an ionic radius that is only slightly larger than that of tin (0.745 Å and 0.69 Å for Sc3+ and Sn4+ respectively in 6-fold coordination).15 We report the preparation and characterisation of the BaSn1−xScxO3−δ series with 0 ≤ x ≤ 0.4 via PXRD and solid-state NMR techniques, and a more detailed study of the highest accepter doped sample, BaSn0.6Sc0.4O3−δ. While the location of the oxygen vacancies was determined by 119Sn, 45Sc, and 17O multinuclear solid-state NMR spectroscopy by investigating the presence of Sn and Sc cations with various coordination numbers, the position of the deuteron ions in D2O treated BaSn0.6Sc0.4O3−δ was found by neutron powder diffraction (NPD). Finally, the electrical conductivity was studied using electrochemical impedance spectroscopy (EIS) recorded under different atmospheres to reveal the temperature dependence of the dominating charge carriers.
2. Experimental
2.1. Synthesis
BaSn1−xScxO3−δ with x = 0, 0.1, 0.2, 0.3 and 0.4 were synthesized by a solid state reaction using stoichiometric amounts of BaCO3 (Merck 99%), SnO2 (Sigma-Aldrich 99.9%), and Sc2O3 (Sigma-Aldrich 99.9%). The reactants were weighed and finely mixed to a paste using a mortar and pestle and ethanol before heating at 1000 °C for 8 h. The powders were then ball milled to a fine powder for 8 h in a Teflon milling house with ethanol using a planetary ball mill and zirconium milling balls. The powders were then dried and pressed into pellets, and subsequently reacted at 1200 °C for 72 h before being ball milled, pelletized and heated again at 1455 °C for 24 h. The sintered pellets were thereafter milled into a fine powder to give the as-prepared samples. All the heating steps were performed under an oxygen gas flow.Hydration of BaSn1−xScxO3−δ was performed by heating the powders with a stoichiometric amount of D2O, calculated to correspond to the complete filling of oxygen vacancies, in a hydrothermal bomb at 225 °C for 12 h. Drying of samples for NMR and NPD measurements was performed by treating at 900 °C for 8 h under vacuum. 17O NMR data were collected on samples that have been enriched in 17O by heating the freshly dried samples (1 h at 950 °C under vacuum) under 50% 17O enriched O2 gas (Isotec, 99%) for 2 days at 950 °C.
Conductivity measurements on a sample of BaSn0.6Sc0.4O3−δ were performed on a 16 mm diameter, 72% dense pellet (made by uni-axially pressing of powders at 8 tons) which was sintered at 1455 °C for 24 h. The pellet was then coated on both faces with platinum paste, heated for 2 h at 1000 °C to remove the organic component of the paste, and finally, treated for 7 days in a furnace at 300 °C with a vapour saturated N2 gas flow (p(H2O) ≈ 0.40 atm) to give a pre-hydrated sample.
2.2. X-ray powder diffraction (PXRD)
PXRD data for the as-prepared samples were collected on a Bruker AXS D8 ADVANCE VARIO X-ray powder diffractometer (CuKα1 = 1.54058 Å) equipped with a LynxEye detector and a germanium (111) primary monochromator. The step size used was 0.050° with a collection time of 0.7 s per step in the 27° to 72° 2-theta range.2.3. Neutron powder diffraction (NPD)
NPD data were collected at room temperature on dried BaSnO3, dried BaSn0.6Sc0.4O3−δ and D2O treated BaSn0.6Sc0.4O3−δ samples using the Polaris16 instrument at the ISIS neutron facility, and subsequently analysed using the GSAS17,18 software package. Data from two detector banks were used for the structure refinements, i.e. the backscattering detector bank covering scattering angles of 130° < 2θ < 160°, and a d-spacing range of 0.2 < d (Å) < 3.2, with a resolution of Δd/d ∼ 5 × 10−3, and the 90° detector bank (85° < 2θ < 95°; 0.3 < d (Å) < 4.1; Δd/d ∼ 7 × 10−3). Data were collected for approximately 9 h for the D2O treated BaSn0.6Sc0.4O3−δ sample and 1 h for the dried samples.Rietveld refinements18–20 included the following parameters: a scale factor, the cubic lattice parameter a, background parameters describing a reciprocal interpolar function, isotropic thermal vibration parameters for the cation sites, uBa, uSn/Sc, and anisotropic parameters for the oxygen site, u11, u22 = u33 and 4 profile parameters describing Gaussian and Lorentzian contributions to the Bragg peak profiles in the cubic space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. Ba was set at 1b (½, ½, ½), Sn/Sc at 1a (0, 0, 0) and O at 3d (½, 0, 0). Ahmed et al.21 reported the likelihood of the deuteron being located at the 24k (0.55, 0.20, 0) crystallographic site for BaZr0.5In0.5O2.5(OD)0.5 and this was used as a starting point in the analysis of the data from the deuterium containing sample.
m. Ba was set at 1b (½, ½, ½), Sn/Sc at 1a (0, 0, 0) and O at 3d (½, 0, 0). Ahmed et al.21 reported the likelihood of the deuteron being located at the 24k (0.55, 0.20, 0) crystallographic site for BaZr0.5In0.5O2.5(OD)0.5 and this was used as a starting point in the analysis of the data from the deuterium containing sample.
2.4. Solid-state NMR
119Sn NMR spectra were acquired at 11.7 T on a wide bore Oxford 500 MHz Varian Infinity Plus spectrometer using a 3.2 mm HX Chemagnetics probehead tuned to 186.26 MHz. The BaSnO3 (dried) and BaSn1−xScxO3−δ samples (in vacuum dried and D2O treated forms) were packed under nitrogen gas atmosphere in 3.2 mm zirconia rotors, which were then spun at a spinning frequency νr = 20 kHz. 119Sn single pulse experiments were carried out using a π/2 pulse width of 2 μs (i.e. at an rf field amplitude of νSn1 = 125 kHz) and a recycle delay of 70 s allowing full relaxation of the 119Sn spins. Chemical shifts were externally referenced to SnO2 at −604.3 ppm.High field 45Sc NMR experiments were performed at 19.6 T on a ultra-narrow bore Bruker DRX 830 MHz spectrometer at the National High Magnetic Field Laboratory, Tallahassee, Florida, USA using a home-built 1.8 mm single channel probe22 tuned to 202.44 MHz. All samples were packed inside 1.8 mm rotors, spun at a spinning frequency νr of 33.333 kHz, and short recycle delays of 0.2 s allowing full relaxation of the 45Sc spins were used for the 1D spectra. t1 rotor synchronized two-dimensional (2D) triple-quantum MAS (TQMAS) experiments23–25 were performed using a shifted-echo pulse sequence and the Soft-Pulse-Added-Mixing (SPAM) enhancement pulse.26 Hard and soft pulses were performed at radio-frequency (rf) field amplitudes of νSc1 = 150 kHz and approximately νSc1 = 20 kHz, respectively. Chemical shifts were externally referenced to a 1 M solution of Sc(NO3)3 in water at 0.0 ppm.
17O NMR experiments were carried out on a 17.6 T wide bore Bruker Avance 750 MHz spectrometer equipped with a 4 mm HXY (in double resonance mode) probehead and operating at 101.72 MHz. All samples were packed inside 4 mm rotors and spun at a spinning frequency νr of 15 kHz. 17O one-dimensional spectra were recorded using a one pulse sequence with selective pulse widths of π/6 = 0.6 μs and at an rf field amplitude of νO1 = 50 kHz. t1 rotor synchronized two-dimensional (2D) TQMAS experiments were performed using the z-filtered pulse sequence.27 Hard and soft pulses were performed at rf field amplitudes of νO1 = 50 kHz and approximately νO1 = 10 kHz, respectively. The recycle delays were set to 5 s for all experiments. Chemical shifts were externally referenced to water at 0.0 ppm.
All data were processed with MatLab and MatNMR.28
2.5. Impedance spectroscopy
A ProboStat™ (NorECs AS, Norway) cell coupled to a Solartron 1260 frequency response analyser in standalone mode was used to collect electrochemical impedance data. Data collection was between 1 Hz and 1 MHz at 1 V rms amplitude between 150 and 1000 °C in steps of 50 °C with an equilibration time of 30 minutes before data collection. Data was collected for BaSn0.6Sc0.4O3−δ in the following sequence: pre-hydrated sample heating and cooling in dry Ar gas, wet (humidified) Ar gas cooling, wet O2 gas on cooling, and finally dry O2 gas on cooling. Two silica tubes, one inside the other, were used to cover the cell, and two P2O5 gas traps before the cell were used to ensure dry gas conditions within the cell. A dense mullite–alumina tube was used in conjunction with a water bubbler at ambient temperature to provide wet gas (p(H2O) ≈ 0.025 atm) within the cell.3. Results
3.1. X-ray diffraction
Fig. 1 shows the PXRD pattern for all dried BaSn1−xScxO3−δ samples (x = 0.0, 0.1, 0.2, 0.3 and 0.4). These data reveal that all samples are highly crystalline and the patterns indicate that the phases adopt a cubic perovskite structure (space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) across the range of compositions. The cell parameters, obtained from profile fitting using Jana2006,29 increased with increase of dopant fraction in agreement with the Sc3+ ionic radius (0.745 Å) being larger than Sn4+ (0.69 Å).15 Close inspection of the data revealed evidence of peak shoulders at 2θ ≈ 44°, 54° for the x = 0.1, 0.2 and 0.3 samples. This behaviour was rationalised in terms of phase segregation into BaSnO3 and a BaSn1−xScxO3−δ phase comparatively rich in scandium in order to preserve the overall stoichiometry of the initial sample reactants. This behaviour was not apparent for the x = 0.4 sample, and its cell parameter of 4.1367(1) Å showed a significant enlargement compared to the value of 4.1156(1) Å determined for un-doped BaSnO3. BaSn0.6Sc0.4O3−δ, which showed the highest incorporation of scandium based on the PXRD results, was therefore selected for further study via neutron diffraction and impedance measurements.
m) across the range of compositions. The cell parameters, obtained from profile fitting using Jana2006,29 increased with increase of dopant fraction in agreement with the Sc3+ ionic radius (0.745 Å) being larger than Sn4+ (0.69 Å).15 Close inspection of the data revealed evidence of peak shoulders at 2θ ≈ 44°, 54° for the x = 0.1, 0.2 and 0.3 samples. This behaviour was rationalised in terms of phase segregation into BaSnO3 and a BaSn1−xScxO3−δ phase comparatively rich in scandium in order to preserve the overall stoichiometry of the initial sample reactants. This behaviour was not apparent for the x = 0.4 sample, and its cell parameter of 4.1367(1) Å showed a significant enlargement compared to the value of 4.1156(1) Å determined for un-doped BaSnO3. BaSn0.6Sc0.4O3−δ, which showed the highest incorporation of scandium based on the PXRD results, was therefore selected for further study via neutron diffraction and impedance measurements.
 | ||
| Fig. 1 (a) PXRD patterns collected on dried BaSn1−xScxO3−δ samples with the indicated cell parameters in Ångstroms. (b) Comparison of the cell parameters for the dried and as prepared BaSn1−xScxO3−δ samples with values reported by Wang et al.,10,11 and Cerda et al.30 | ||
3.2. Neutron diffraction
The NPD data for BaSn0.6Sc0.4O3−δ presented in Fig. 2 revealed that a minor Sc2O3 impurity phase was present in the vacuum dried sample. The large neutron scattering lengths of scandium (12.29 fm) and oxygen (5.803 fm) compared to their relatively weaker X-ray scattering powers could explain why this minor phase was detected in the neutron pattern (Fig. 2) but was not visible in the PXRD patterns (Fig. 1). The Sc2O3 peaks are not visible in the NPD of deuterated BaSn0.6Sc0.4O3−δ where only a single, deuteron containing, perovskite phase is present. | ||
| Fig. 2 NPD patterns of vacuum dried and deuterated BaSn0.6Sc0.4O3−δ. Black filled circles indicate reflections arising from a small amount of Sc2O3. | ||
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m crystal system, and Sc2O3 were included into the Rietveld analysis of the dried sample, phase 1, 2 and 3 respectively. The weight fractions of these three phases obtained from the refinement were 95.55(1) wt%, 3.34(8) wt% and 1.11(1) wt%, respectively (Fig. S1†). The Sn
m crystal system, and Sc2O3 were included into the Rietveld analysis of the dried sample, phase 1, 2 and 3 respectively. The weight fractions of these three phases obtained from the refinement were 95.55(1) wt%, 3.34(8) wt% and 1.11(1) wt%, respectively (Fig. S1†). The Sn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sc site occupancy in the dominant perovskite phase 1 was reciprocally linked and refined to give a small increase in the Sn
Sc site occupancy in the dominant perovskite phase 1 was reciprocally linked and refined to give a small increase in the Sn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sc ratio, with 0.666(2) and 0.334(2) site occupancies for Sn and Sc, respectively. The overall sample stoichiometry was consistent with the initial 0.6 Sn and 0.4 Sc molar fractions. Modelling the oxygen atoms with an anisotropic displacement parameter (ADP) significantly reduced the values of the χ2 goodness of fit parameter from 15.66 to 10.86. Simultaneous refinement of the oxygen ADP and occupancy was not deemed reliable due to the high degree of correlation between these two variables. Hence the occupancy of the oxygen site in phase 1 was set to 0.944 as would be expected for a dried sample with a BaSn0.666Sc0.334O3−δ composition with a final χ2 value of 6.372. The final agreement to the data is shown in the supplementary data (Fig. S1†). Note that for simplicity we continue to refer to this sample as BaSn0.6Sc0.4O3−δ, despite the slightly lower Sc content of the perovskite phase.
Sc ratio, with 0.666(2) and 0.334(2) site occupancies for Sn and Sc, respectively. The overall sample stoichiometry was consistent with the initial 0.6 Sn and 0.4 Sc molar fractions. Modelling the oxygen atoms with an anisotropic displacement parameter (ADP) significantly reduced the values of the χ2 goodness of fit parameter from 15.66 to 10.86. Simultaneous refinement of the oxygen ADP and occupancy was not deemed reliable due to the high degree of correlation between these two variables. Hence the occupancy of the oxygen site in phase 1 was set to 0.944 as would be expected for a dried sample with a BaSn0.666Sc0.334O3−δ composition with a final χ2 value of 6.372. The final agreement to the data is shown in the supplementary data (Fig. S1†). Note that for simplicity we continue to refer to this sample as BaSn0.6Sc0.4O3−δ, despite the slightly lower Sc content of the perovskite phase.
| Refinement parameters | Dry BaSnO3 | BaSn0.6Sc0.4O3−δ | |
|---|---|---|---|
| Dry | Deuterated | ||
| a Occupancies refined to slightly larger than 1, and therefore fixed to 1. b Due to correlation between the oxygen site ADP and occupancy this value was not refined in final stages, instead it was fixed to the value determined by the amount of refined scandium x = 0.334 (oxygen fraction = (3 − (0.334/2))/3). c Occupancy of the deuterium site was fixed to reflect a deuterium content consistent with complete filling of the oxygen vacancies. d The refined unit cell parameter was 4.11457(17) Å. | |||
| a (Å) | 4.11588(2) | 4.13549(1) | 4.15716(2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| U iso (Å 2 ) × 100 | |||
| Ba | 0.416(4) | 0.614(5) | 1.200(5) |
| Sn/Sc | 0.231(3) | 0.712(6) | 1.057(4) |
| O U11 | 0.294(8) | 0.334(11) | 0.498(8) |
| O U22–U33 | 0.923(6) | 1.201(7) | 1.261(5) |
| D (x, y, 0) | 0.579(3), 0.217(3), 0 | ||
| D (x, y, 0) Uiso | 11.3(4) | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Occupancy | |||
| Ba (0.5, 0.5, 0) | 1.0a | 1.0a | 1.0a |
| Sn (0, 0, 0) | 1.0a | 0.666(2) | 0.6 |
| Sc (0, 0, 0) | — | 0.334(2) | 0.4 |
| O (0.5, 0, 0) | 1.0 | 0.944b | 1.0a |
| D (x, y, 0) | — | — | 0.0167c |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Bond distances (Å) | |||
| 12 × Ba–O | 2.91037(1) | 2.92423(1) | 2.93956(1) |
| 6 × Sn/Sc–O | 2.05794(1) | 2.06774(1) | 2.07858(1) |
| 1 × O–D | — | 0.959(12) | |
| 1 × O–D(1−y, x, z) | 2.109(7) | ||
| 1 × O–D(−y, x, z) | 2.680(6) | ||
| 2 × O–D(1+z, y, −x) | 2.862(9) | ||
| χ 2 | 48.16 | 6.37 | 12.84 |
| R wp (%) | 0.0314 | 0.0283 | 0.0124 |
| R p (%) | 0.0360 | 0.0441 | 0.0169 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Phases (wt%) | |||
| Main | 100 | 95.55(1) | 100 |
| Sc2O3 | — | 1.11(1) | — |
| BaSnO3 | — | 3.34(8)d | — |
| Variables | — | 26 | 47 |
3.3. Solid-state NMR
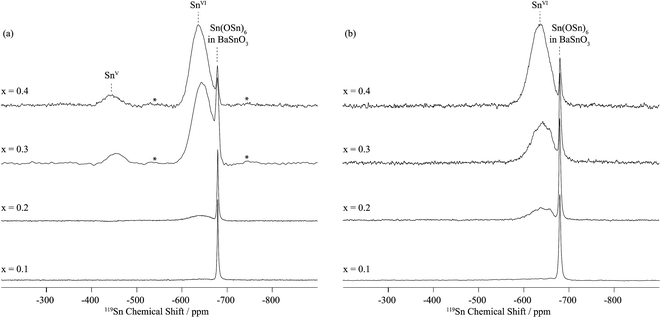
In dry Sc-substituted BaSnO3, a new set of 119Sn resonances with intensity proportional to Sc concentration appears at around −640 ppm (Fig. 4a). This feature is assigned to tin in six fold environments surrounded by at least one scandium cation based on previous NMR studies of the related Y-doped BaSnO3 materials.32 In this system, the six-coordinated Sn cations with various numbers of Y ions in their first cationic coordination shells, i.e. Sn(OSn)5(OY), Sn(OSn)4(OY)2, Sn(OSn)3(OY)3, etc. could be individually observed, the 119Sn resonance shifting by +27 to +34 ppm per added Y ion. Here the 119Sn spectra of Sc-doped BaSnO3 lacks such sharp, resolved features, most likely due to a smaller frequency shift per Sc ion added to the vicinity of the Sn nuclei. Indeed the ionic radius of Sc3+ in 6-fold coordination (0.745 Å) is much closer to the one of Sn4+ (0.69 Å) in comparison to Y3+ (0.90 Å) leading to smaller local distortions in the case of Sc substitution and therefore smaller frequency shifts. A weak but sharp BaSnO3 resonance is seen in all four samples (x = 0.1, 0.2, 0.3 and 0.4) at −679 ppm most likely due to a separate BaSnO3 impurity phase; the weakest BaSnO3 resonance was seen for x = 0.4, consistent with the low phase fraction obtained in the NPD refinement of this phase (Fig. 2 and S1†).
A second broad resonance, centered at −450 ppm (Fig. 4a), is assigned to five-coordinated Sn environments in line with a shift to higher frequency going from six to five-fold Sn coordination,31,32 a trend generally observed for a number of nuclei.33
On hydrothermal D2O treatment of dry BaSn1−xScxO3−δ (Fig. 4b), the 119Sn NMR resonance at −450 ppm, associated with the five-coordinated Sn environments, totally disappears, which is consistent with its assignment, and shows complete reaction of the oxygen vacancies 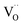 with D2O during hydration to form six-coordinated Sn environments (experimentally observed at −636 ppm). The sharp −679 ppm resonance is also seen, providing evidence for BaSnO3 environments although no sign of an impurity phase was detected in the NPD data, presumably due to its low concentration.
with D2O during hydration to form six-coordinated Sn environments (experimentally observed at −636 ppm). The sharp −679 ppm resonance is also seen, providing evidence for BaSnO3 environments although no sign of an impurity phase was detected in the NPD data, presumably due to its low concentration.
 | ||
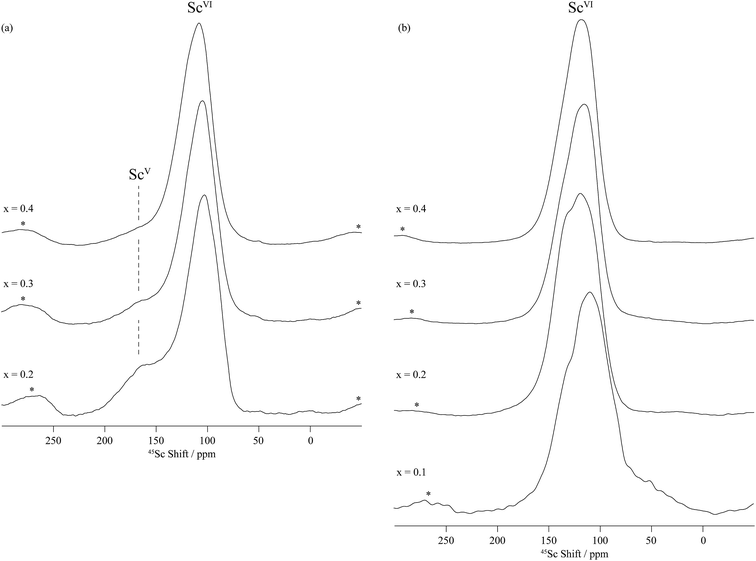
| Fig. 6 Two-dimensional sheared triple-quantum 45Sc MAS spectra of (a) dry BaSn0.6Sc0.4O3−δ and (b) deuterated BaSn0.6Sc0.4O3−δ obtained at 19.6 T with a MAS frequency of 33.33 kHz. 9600 transients were accumulated for each of the 24 (for (a)) and 16 (for (b)) t1 increments at a recycle delay of 0.4 s. Top: anisotropic skyline projection (the 45Sc MAS NMR single pulse spectra are given in Fig. 5 and S3†). Left: isotropic skyline projection of the TQMAS spectra. ScVI and ScV denote six and five coordinated scandium environments, respectively. | ||
Two sets of resonances are clearly observed in the F1 vertically projected spectra of the dry BaSn0.6Sc0.4O3−δ sample at shifts of approximately 125 and 225 ppm (Fig. 6) demonstrating the presence of two different scandium environments. Extraction of the shifts of these resonances in the horizontal F2 dimension allow isotropic chemical shifts values of around 120 and 200 ppm to be extracted (see Table 2) and assigned to 6- and 5-coordinated scandium environments, respectively, based on previous study by Stebbins et al.,34 our previous work on the BaZr1−xScxO3−δ series,35 and Takamura et al.'s recent hydration study of 10% mol Sc-substituted BaZrO3.36 The 5-coordinated Sc environment which has a very large linewidth (leading to a quadrupolar coupling of around 20 MHz) is ascribed to the presence of an oxygen vacancy in the 1st coordination shell of a Sc atom.
| Site | Environment | δ iso/ppm | C Q/MHz | η Q |
|---|---|---|---|---|
| a 45Sc and 17O NMR parameters were determined from the peak positions in the TQMAS spectra at 19.6 and 17.6 T, respectively (see ESI).25 b Not applicable. c Data from ref. 32. d Not measured experimentally. | ||||
| Dry BaSnO 3 | ||||
| Sn | SnVI(OSn)6 | −679 | —b | |
| Sc | —b | |||
| Oc | SnVI–O–SnVI | 152 | 6.1 | 0.0 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Dry BaSn 0.6 Sc 0.4 O 3−δ | ||||
| Sn | SnVI(OSn)6 in BaSnO3 | −679(1)31 | —b | |
| SnVI | −640(10) | |||
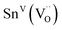
|
−450(10) | |||
| Sc | ScVI | 120(5) | 7(2) | 0.7(3) |
| ScV | 199(7) | 20(2) | 0.0(1) | |
| O | Sn–O–Sn | 203(5) | 8(1) | —d |
| Sn–O–Sc | 248(10) | 3(1) | —d | |
| Sn–O–Sc | 261(8) | 3(1) | —d | |
| Sc–O–Sc | 420 | 5(1) | —d | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Hydrothermally D 2 O treated BaSn 0.6 Sc 0.4 O 3−δ | ||||
| Sn | SnVI(OSn)6 in BaSnO3 | −679(1)31 | —b | |
| SnVI | −636(10) | |||
| Sc | ScVI | 122(5) | 7(2) | 0.8(1) |
| O | —d | |||
Upon hydrothermal D2O treatment, the oxygen vacancies are filled by protonic (deuterons) and OD defects resulting in the loss of the 5-coordinated Sc as revealed by the 45Sc NMR spectra given in Fig. 5b and S4–S6b.† These spectra are now dominated by resonances centered at around 125 ppm and corresponding to 6-coordinated Sc only (Table 2). In fact, more than one 6-coordinated Sc environments are often visible in the 45Sc MQMAS spectra of deuterated BaSn1−xScxO3−δ, and are assigned to ScO6 (as in the dry samples) and ScO5(OD) environments (i.e. 6-coordinated scandium in the vicinity of a protonic defect).
Note that the Sc2O3 impurity seen by NPD was not observed by 45Sc NMR of dry BaSn0.6Sc0.4O3−δ (Fig. 6a). This is attributed to the very small amount of Sc2O3 (1.11%, Table 1), which is probably below the NMR detection limit, and to the fact that the two 6-coordinated Sc sites in Sc2O3 have isotropic chemical shifts of 108 and 128 ppm,34 very close to the value for 6-coordinated Sc in this sample. The lack of resolution might therefore also prevent its observation.
3.4. Impedance spectroscopy
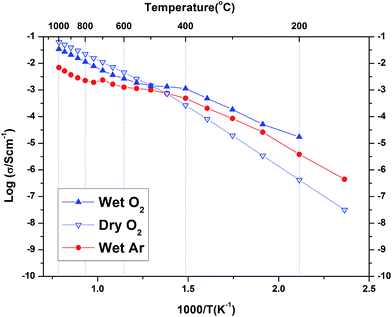
Fig. 8 shows the complex plane plot of the pre-hydrated BaSn0.6Sc0.4O3−δ sample on heating at 100 °C in dry Ar. Two time constants are observed, including one in the high frequency region near the origin; the data is modelled using two (RQ) elements, representing a resistor and constant phase element in parallel, connected in series. The derived capacitances were 1.17 × 10−11 F cm−2 and 8.14 × 10−9 F cm−2 consistent with bulk and grain boundary processes, respectively. The feature at the lowest frequencies is attributed to electrode processes. For the initial heating and cooling data, it was possible to separate bulk and grain boundary conductivity in this manner at temperatures below approximately 400 °C. At higher temperatures, and for the other atmospheres and thermal protocols, the data were analysed using a similar approach but here the distinction between bulk and grain boundary was not as clear and only the total conductivity (bulk + grain boundary) could be extracted.The conductivity data collected for BaSn0.6Sc0.4O3−δ under Ar consisted of three regions (see Fig. 9). Region I between 800–1000 °C has O2− anions or possibly electron holes as the dominant charge carriers, while region II, between 400 and 800 °C is characteristic of the growing influence of protons and displays a characteristic plateau39 that reflects the simultaneously varying proton concentration and proton mobility. Region III, at T ≤ 400 °C, is dominated by proton charge carriers. Comparison of the conductivity under dry Ar vs. dry O2 conditions reveals that the sample possesses significantly higher conductivity, approximately one order of magnitude greater, under oxidizing conditions throughout the entire temperature interval as evident in Fig. 10. Conductivity under wet oxygen and above 450 °C was found, unexpectedly, to be lower than that in dry oxygen (Fig. 11).
 | ||
| Fig. 10 A comparison of the total conductivity of BaSn0.6Sc0.4O3−δ under dry Ar gas and dry O2 gas. The activation energies below 400 °C were 0.95 eV and 0.90 eV respectively. | ||
4. Discussion
4.1. Phase formation
The cell parameters extracted from the PXRD results of the as-synthesized BaSn1−xScxO3−δ (x = 0.0, 0.1, 0.2, 0.3, 0.4) samples were found to increase with the level of Sc3+ dopant content. This expansion is expected as it reflects the greater ionic radius of Sc3+ (0.745 Å, 6-fold coordination) in comparison to Sn4+ (0.69 Å).15 Additionally, samples with dopant concentrations in the range x = 0.1–0.3, contained peak shoulders in their XRD patterns, which were attributed to a level of phase segregation. These results were in agreement with the 119Sn NMR data which revealed the presence of sharp Sn(OSn)6 environments similar to that observed in BaSnO3 (Fig. S2†).The cell parameters obtained in this paper for BaSn1−xScxO3−δ are visibly lower than those reported by Wang and co-workers,10,11 (Fig. 1b) but for BaSnO3 our reported value is still higher than the value of 4.1140 Å reported by both Roth et al.40 and Cerda et al.30 Anomalous behaviour has been reported for Sc3+ doped BaZrO3 (ref. 41) system with samples sintered at a lower temperature having a larger unit cell parameter when compared to samples sintered at higher temperatures. Hiraiwa et al.41 demonstrate this behaviour is unique to the Sc3+ dopant and is contrary to the behaviour of other dopants for BaZrO3. However no hypothesis exists yet to explain this behaviour.
Although BaSn0.6Sc0.4O3−δ was initially found to be phase pure by PXRD, subsequent NPD data revealed the presence of some Sc2O3, and hence the possible presence of BaSnO3 in the dried BaSn0.6Sc0.4O3−δ sample. Indeed, very weak intensities, seen as shoulders on the main perovskite peaks, were visible in the NPD pattern (Fig. S1†) and the refined cell parameter obtained for the minor BaSnO3 component of 4.11457(17) Å showed good agreement with that of the dried BaSnO3 sample (a = 4.11588(2) Å). This was confirmed by the presence of the typical Sn(OSn)6 resonance at −679 ppm in the 119Sn NMR data.
On hydrothermal treatment of BaSn0.6Sc0.4O3−δ with D2O, the minor Sc2O3 impurity was not observed in the NPD data, possibly indicating the complete solubility of the Sc2O3 into the perovskite structure is obtained under these conditions; a small signal characteristic of the local Sn environment present in BaSnO3 was still observed by 119Sn NMR (Fig. S2†). The significant difference in melting points of SnO2 (1630 °C) and Sc2O3 (2485 °C) reactants suggests that different cation diffusion rates are likely to be a contributing factor for the observed sample inhomogeneity across the BaSn1−xScxO3−δ series. The solution based synthesis approaches utilised by Wang et al.10 and Buannic et al.32 in the preparation of BaSn1−xYxO3−δ (0.0 ≤ x ≤ 0.5) may be expected to help overcome this issue, although we note that the presence of undoped BaSnO3 was also reported for BaSn0.9Y0.1O3−δ.32
4.2. Deuteron site
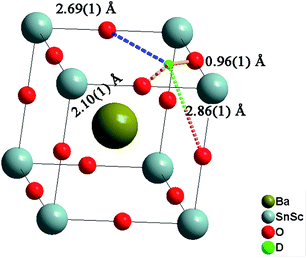
The deuteron site of the hydrothermally D2O treated BaSn0.6Sc0.4O3−δ sample was successfully refined by Rietveld analysis. The deuteron atomic coordinates at the 24k site were x = 0.579(3) and y = 0.217(3) resulting in an average O–D bond distance of 0.96(1) Å, in good agreement with literature values.21,42 The local environment around a deuteron occupying the 24k site is illustrated in Fig. 12 and shows three O–D interatomic distances of relevance for the proton transfer step towards acceptor oxygen ions, the closest being at 2.11(1) Å. It is clear that the local proton configuration is highly anisotropic and these results are in good agreement with experimental studies of related, highly substituted, perovskites, BaZr0.5In0.5O2.75 (ref. 21) and BaSn0.5In0.5O2.75.43 The presence of a similar next nearest O–D interaction at ∼2.15 Å was also recently found for BaTi0.5In0.5O2.53(OD)0.44 from reverse Monte Carlo analysis of total scattering neutron diffraction data.44 These findings are in line with theoretical45–47 and experimental48,49 studies that revealed a clear tendency for protons to relax towards the dopant ions. The proximity of the second nearest oxygen atom indicates a tendency for enhanced hydrogen bonding interactions that will influence the proton diffusion. Whilst hydrogen bonding is expected to increase the likelihood of success for a proton transfer between neighbouring oxygen ions, the re-orientation step necessary for long range diffusion, involves breaking of the same H-bonds. It is therefore presently unclear what the full implications of the deuteron site are for migrating protons.Both the D2O treated and the vacuum dried samples showed large and highly anisotropic ADPs for the oxygen site. This indicates significant static disorder of the oxygen ions as previously found21 and it is important to stress that the refined structural models will represent a long range, time averaged, picture.
The diffraction data for the deuterated BaSn0.6Sc0.4O2.8 sample revealed an increase in the cell parameter, a, compared to the as-prepared sample (Table 1). This lattice expansion is due to the filling of oxygen vacancies by larger hydroxyl (OD) groups and was similar in magnitude to that reported in related perovskites.39,50 The hydration process was also clearly reflected in the solid-state NMR data. The presence of a five-coordinate Sn and Sc peaks in the spectra of the dry BaSn0.6Sc0.4O2.8 sample confirmed the existence of oxygen vacancies 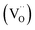 and the loss of these signals upon hydrothermal D2O treatment confirmed their subsequent filling.
and the loss of these signals upon hydrothermal D2O treatment confirmed their subsequent filling.
4.3. Local Sn and Sc environments
The fine structure observed for the contribution of each Y dopant cation in Sn(OSn)6−z(OY)z (0 ≤ z ≤ 0.4) environment in the 119Sn NMR spectra of the related BaSn1−xYxO3−δ phases31,32 is not observed here for BaSn0.6Sc0.4O3−δ (Fig. 4 and S2†). Additionally, a signal associated with Sn(OSn)6 environments persists for the highly substituted Sc sample whereas it is absent for BaSn0.6Y0.4O2.8 and BaSn0.5Y0.5O2.75.32 This suggests that there is greater disorder at the B-site and/or smaller changes in the specific local environments due to the much closer ionic radii of 6-fold coordinated Sn4+ (0.69 Å) and Sc3+ (0.745 Å) vs. 6-fold Y3+ (0.96 Å).15 More importantly, the presence of noticeable concentrations of Sn–O–Sn and Sc–O–Sc environments, as revealed by 17O NMR on 17O enriched BaSn0.6Sc0.4O3−δ, confirms the absence of significant Sn/Sc ordering; for strict ordering and x = 0.5, only the Sc–O–Sn environment should be present, analogous to the behaviour of BaSn0.5Y0.5O2.75 (Ba2SnYO5.5).32 For x < 0.5 this environment dominates, with lower concentrations of Sn–O–Sn environments being present, their concentration increasing with decreasing Sc content. For x = 0.1 and 0.2, the ratio of Sn(OSn)6−n(OSc)n with n > 0 to Sn(OSn)6 sites is low but increases dramatically for x = 0.3 and 0.4, the amount of segregated BaSnO3 being minimum for the latter. There is a possibility that Sn, if hosting Sc in its vicinity, has a preference for hosting a high number of Sc, i.e. Sn(OSn)6−n(OSc)n with n ≥ 3. In such case, the concentration of Sn(OSn)6−n(OSc)n with n ≥ 3 would be small for x = 0.1 and 0.2 and, combined to a broad resonance (as seen for x = 0.3 and 0.4), would yield to a very weak signal. This hypothesis is corroborated by the recurring segregation of a non-negligible amount of BaSnO3, by the presence of a fair number of Sn–O–Sc bonds, and by the limited amount of Sc–O–Sc linkages as observed by 17O (Fig. 7) for x = 0.1 and 0.2. The greater size difference between Y3+ and Sn4+ drives a stronger tendency for ordering of the B-site cations that becomes nearly perfect with alternating Sn–O–Y–O–Sn linkages in BaSn0.5Y0.5O2.75 (Ba2SnYO5.5) as demonstrated by the existence a single main resonance at 259 ppm for Sn–O–Y moieties in the 17O NMR spectra.32 While some preferential cationic arrangement is possibly occurring in BaSn1−xScxO3−δ, it is not as predominant as in BaSn1−xYxO3−δ.The one-dimensional 45Sc NMR spectra of dry BaSn0.8Sc0.2O3−δ (Fig. 5) reveals a clear signal for five coordinated Sc, whilst the 119Sn data show no signal of 5-coordinated Sn for the x = 0.1 and 0.2 samples. Taken together, this strongly implies that oxygen vacancies are preferentially found in between or near Sc cations at low doping levels (x ≤ 0.2). These findings agree with the results of Buannic et al.,35 Oikawa et al.36,51 (for x ≤ 0.1) on the related BaZr1−xScxO3−δ system that suggested a tendency for the amount of 5 coordinated Sc to increase with doping level for x ≤ 0.2. Interestingly, the one-dimensional 45Sc NMR spectra reveal that the ratio of ScV to ScVI decreases as the Sc content increases above x = 0.2. A notable difference between the BaSn1−xScxO3−δ and BaZr1−xScxO3−δ systems is the level of dopant solubility which reaches a maximum for BaZr1−xScxO3−δ at x ≈ 0.2,35 whereas the scandium incorporation level reaches x ≈ 0.35 for the nominal x = 0.4 BaSn1−xScxO3−δ sample based on the Sc site occupancy refined from neutron diffraction analysis for the dry material (Table 1). Buannic et al.,35 speculated earlier that the avoidance of energetically unfavourable Sc–O–Sc linkages, that are expected to become more numerous in systems where B-site ordering does not occur, may be a driving force for phase segregation into Sc2O3 and BaZr1−xScxO3−δ with lower x. The present NMR findings for BaSn0.6Sc0.4O3−δ, showing coexistence of Sn(OSn)6 and SnO5 coordinations and low levels of ScO5 (in comparison to the x = 0.2 sample), therefore points towards a relative abundance of  local environments in comparison with a purely statistical cation and vacancy distribution. Possibly the Sn4+ ion is more flexible with respect to oxygen vacancies than Zr4+, and this plays a role in facilitating a relatively higher scandium incorporation into the perovskite matrix.
local environments in comparison with a purely statistical cation and vacancy distribution. Possibly the Sn4+ ion is more flexible with respect to oxygen vacancies than Zr4+, and this plays a role in facilitating a relatively higher scandium incorporation into the perovskite matrix.
In summary, consideration of all the NMR data reveals an intricate picture in relation to the local B-site environments. The picture that emerges is nonetheless consistent with the formation of increasing levels of oxygen vacancies upon acceptor doping and the tendency for partial phase segregation, probably on nanometric-length scales, observed during the phase formation of the BaSn1−xScxO3−δ series as discussed above.
4.4. Conductivity
The conductivity of BaSn0.6Sc0.4O3−δ reveals a complex dependency on pO2 and pH2O. In dry, proton free, conditions the material reveals a major p-type contribution that is similar in magnitude to that reported recently for a related, highly acceptor doped, BaTi0.5Sc0.5O3−δ.52 The behaviour is also comparable to Ba2SnYO5.5,9 BaSn1−xYxO3−δ (ref. 12) and BaZr0.8Y0.2O3−δ (ref. 53) for which hole conduction dominates at high p(O2) and high T. This enhanced conductivity can be rationalised through the partial filling of oxygen vacancies resulting in the formation of mobile electron holes as described in eqn (3) above.Compared with the dry gas conditions, the conductivity under wet gas conditions (Ar or O2), and that obtained from the initial heating run in dry Ar on the pre-hydrated sample, were significantly higher in the intermediate temperature region of 150–650 °C (200–450 °C in wet O2) due to protons acting as the main charge carriers. Above 650 °C the conductivity obtained under wet and dry Ar were very similar as the material had probably dehydrated. This is characteristic of several related proton-conducting systems9,54 and reflects a transition to predominant oxide ion as protonic defects become unstable at higher T. Remarkably, at T > 450 °C under oxidizing conditions (Fig. 10), the conductivity is lower under wet gas compared to dry gas, although overall it still remains significantly higher than under wet Ar. This can be rationalised on the basis of the strong p-type character of the material that leads to a competition between holes and protons in wet oxidising conditions. A combination of the two reactions described by eqn (2) and (3) above would result in the consumption of holes in the presence of water vapour as per eqn (5) below.
 | (5) |
This consumption of holes depletes the number of available h˙ charge carriages and hence lowers the total conductivity at T > 450 °C to values below those of the dry oxygen condition. This kind of behaviour has been observed for BaZr0.9−xPrxGd0.1O3−δ where highly mobile electron holes (h˙) were found to dominate conductivity even to very low temperatures and in wet conditions.55 It is clear that within the T range ∼400–600 °C, BaSn0.6Sc0.4O3−δ displays significant mixed proton and electron conduction in wet oxygen, indicating potential suitability as a cathode material for PCFCs.
Table 3 lists a summary of obtained conductivity parameters for a number of acceptor doped BaSnO3 and BaTiO3 systems reported in the literature. For BaSn0.6Sc0.4O3−δ, it was possible to separate a bulk contribution for the initial heating run of the pre-hydrated sample at temperatures up to 350 °C. As apparent from the impedance data shown in Fig. 8 and the Arrhenius plot presented in Fig. 9, the total protonic conductivity is dominated by the highly resistive grain boundaries at relatively low temperatures. The bulk proton conduction in fact reaches a very high value of ∼2 × 10−3 S cm−1 at 350 °C (Fig. 9). The activation energy of bulk proton conductivity of BaSn0.6Sc0.4O3−δ, estimated from the heating cycle of the pre-hydrated sample in the T range 100 to 250 °C, was 0.40(1) eV. This shows reasonable agreement with the 0.52 eV reported for both of the more lightly Sc substituted BaSnO3 phases10,56 but is closer to the 0.38 eV and 0.34 eV reported for bulk proton conduction in BaSn0.875Y0.125O3−δ (ref. 10) and BaSn0.75Y0.25O3−δ,56 respectively. The bulk activation energies reported by Wang et al. for BaSn1−xYxO3−δ (0.05 ≤ x ≤ 0.375)12 are approximately 0.1 eV lower than the 0.51 eV reported for bulk proton conductivity in Ba2YSnO5.5 (ref. 9) suggesting that the long range B-site ordering found in this phase is not beneficial to proton migration. Our present findings for BaSn0.6Sc0.4O3−δ support this trend in as much as a low (0.40 eV) activation energy for bulk proton mobility is observed. Direct comparison of bulk activation energies is, however, not straightforward and values extracted from impedance data may also reflect partial contributions from, for example, defect formation enthalpies, dopant to proton trapping and the effects of grain boundaries. Therefore, although the trend from the data on acceptor doped BaSnO3 (Table 3) seemingly supports more facile bulk proton diffusion in disordered systems we avoid drawing wider conclusions in regards to the impact of B-site ordering on proton mobility in perovskites.
| Material | E a protonic (total)/eV | E a protonic (bulk)/eV | Total conductivity (protonic) in wet gas/S cm−1 | Ref. |
|---|---|---|---|---|
| BaSn0.9In0.1O3−δ | — | 0.54 | 1.3 × 10−3 (4% H2/96% N2 500 °C) | 11 |
| BaSn0.875Sc0.125O3−δ | 0.87 | 0.52 | 4 × 10−4(Ar, 500 °C) | 10 |
| BaSn0.75Sc0.25O3−δ | 0.73 | 0.52 | 8 × 10−4 (Ar, 500 °C) | 56 |
| BaSn0.6Sc0.4O3−δ | 0.7–0.67 | 0.40 | 1.07 × 10−3 (Ar, 600 °C) | This work |
| BaSn0.9Y0.1O3−δ | — | 0.49 | 4 × 10−5 (4% H2/96% N2 500 °C) | 13 |
| BaSn0.875Y0.125O3−δ | 0.72 | 0.38 | 2.3 × 10−4 (Ar, 500 °C) | 10 |
| BaSn0.75Y0.25O3−δ | 0.66 | 0.34 | 7 × 10−4 (Ar, 500 °C) | 12 |
| BaSn0.5Y0.5O2.75 (Ba2YSnO5.5 double perovskite structure) | — | 0.51 | 1.3 × 10−3 (bulk) (N2, 600–400 °C) | 9 |
| BaTi0.8Sc0.2O3−δ (6 H hexagonal structure) | 0.80 | 0.77 | 1 × 10−5 (Ar, 400 °C) | 58 |
| BaTi0.5Sc0.5O3−δ | 0.46 | 0.22 | 2.89 × 10−4 (Ar, 550 °C) | 52 |
| BaTi0.3Sc0.7O3−δ | 0.48 | — | 2 × 10−3 (Ar, 600 °C) | 58 |
| BaTi0.5In0.5O3−δ | 0.48 | — | 2.1 × 10−4 (Ar, 500 °C) | 59 |
| BaTi0.2In0.8O3−δ | — | 0.42 | 1.1 × 10−3 (450 −600 °C) | 57 |
The activation energies for the total protonic conduction of BaSn0.6Sc0.4O3−δ lie in the range 0.67–0.70 eV in wet Ar which is lower than the 0.87 eV recently reported for BaSn0.875Sc0.125O3−δ,10 and closer to the 0.73 eV obtained for BaSn0.75Sc0.25O3−δ.56 The total proton conductivity of 1.07 × 10−3 S cm−1 obtained for BaSn0.6Sc0.4O3−δ in wet Ar at 600 °C is similar to that of BaIn0.8Ti0.2O2.6 (ref. 57) and BaTi0.3Sc0.7O3−δ,58 and is significantly higher than that reported previously for BaSn1−xScxO3−δ with lower scandium contents.10,11 This behaviour probably reflects the greater proton concentration in the more highly doped system. A trend of increasing proton conduction with increasing dopant concentration might be emerging from Table 3. Ultimately, however, it is the proton mobility, and understanding how it is influenced by factors such as the level of B-site cation ordering and the chemical nature of the ions, that is critical in order to obtain new materials with significantly enhanced proton conductivity.
5. Conclusions
Scandium substitution of the tin site within BaSnO3 has been achieved by solid-state synthesis. Some degree of phase segregation was observed in the dry materials but it has largely disappeared in the BaSn0.6Sc0.4O2.8 sample after D2O treatment. Analysis of X-ray and neutron diffraction data has indicated an average cubic symmetry of space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and the deuteron position was successfully located at the 24k site (0.579(3), 0.217(3), 0) from Rietveld analysis. 119Sn solid-state NMR revealed a series of local tin environments consistent with 6 and 5 coordinate Sn environments and BaSnO3 impurities. The resonance from the 6-coordinate site is broad indicating a wide range of Sn environments differing in the number of Sn and Sc cation in the 1st B-site cation coordination shell. This behaviour is very different to the structure of BaSn1−xYxO3−δ with a high concentration of yttrium, in which Y–O–Sn ordering occurs. The five-coordinated Sn is observed at high Sc doping levels (x ≥ 0.4), confirming the presence of oxygen vacancies nearby tin. Conversely, the 45Sc NMR data showed the existence of intense peaks for five-coordinated Sc, the relative fraction of five to six-coordinated Sc increasing with decreasing Sc content, suggesting preferential trapping of oxygen vacancies in between or near Sc cations at lower Sc concentrations. For all compositions, the five coordinated Sc and Sn environments vanished after hydration as OH groups filled the available oxygen vacancies.
m and the deuteron position was successfully located at the 24k site (0.579(3), 0.217(3), 0) from Rietveld analysis. 119Sn solid-state NMR revealed a series of local tin environments consistent with 6 and 5 coordinate Sn environments and BaSnO3 impurities. The resonance from the 6-coordinate site is broad indicating a wide range of Sn environments differing in the number of Sn and Sc cation in the 1st B-site cation coordination shell. This behaviour is very different to the structure of BaSn1−xYxO3−δ with a high concentration of yttrium, in which Y–O–Sn ordering occurs. The five-coordinated Sn is observed at high Sc doping levels (x ≥ 0.4), confirming the presence of oxygen vacancies nearby tin. Conversely, the 45Sc NMR data showed the existence of intense peaks for five-coordinated Sc, the relative fraction of five to six-coordinated Sc increasing with decreasing Sc content, suggesting preferential trapping of oxygen vacancies in between or near Sc cations at lower Sc concentrations. For all compositions, the five coordinated Sc and Sn environments vanished after hydration as OH groups filled the available oxygen vacancies.
BaSn0.6Sc0.4O3−δ was found to be predominantly a p-type conductor under oxidizing atmospheres with proton conduction dominating at lower temperatures. The competition between holes and protons results in a suppression of the conductivity at T > 450 °C in wet oxidizing conditions in comparison to dry oxygen. This mixed ionic and electron hole conduction means that the material could be utilized in gas separation membrane applications or cathodes of proton conducting fuel cells. The current study showed that highly scandium substituted BaSnO3 supports very high bulk proton conductivity, comparable to that reported for Y-doped BaZrO3 and the double perovskite Ba2YSnO5.5. It is suggested that further work on the material should focus on the growth of large grained samples in order to reduce grain boundary resistance, and investigate the chemical stability of the material under CO2 atmospheres. Given the present findings, solution synthesis routes aiming to create a more homogeneous mixing of the B-site ions at the atomic level are also of potential interest.
Authors' contribution
I. A., S. G. E., S. T. N. conceptualized and planned the project, F. G. K., I. A. synthesized the samples. F. G. K. did EIS experiments and EIS data analysed with C. S. K., F. G. K., I. A., S. T. N., S. H., S. G. E. performed neutron data collection and structural analysis. L.B. prepared the 17O enriched materials. L. B., I. H., Z. G. and F. B. carried out the NMR experiments. L. B., F. B. and C. P. G. performed analysis of the NMR data. The manuscript was written with contribution from all co-authors.Acknowledgements
The authors thank the Swedish Energy Agency (Energimyndigheten) and the Swedish Research Council (Vetenskapsrådet) for project funding. The UK Science and Technology Facilities Council, STFC, is thanked for allocating beam time at the ISIS Facility. The National High Magnetic Field Laboratory is supported through the National Science Foundation Cooperative Agreement (DMR-0084173) and by the State of Florida. L. B., F. B. and C. P. G. thank the NSF via grant DMR0804737 and NYSTAR for support. F. B. also thanks the EU Marie Curie actions FP7 for an International Incoming fellowship (grant no. 275212) and the University of Liverpool for funding. C. P. G. thanks the European Research Council for an Advanced Fellowship. We thank Dr Boris Itin for technical assistance with the NMR measurements at 17.6 T at New York Structural Biology Center, New York City, NY.References
- S. P. Jiang and Y. D. Zhen, Solid State Ionics, 2008, 179, 1459–1464 CrossRef CAS.
- K. D. Kreuer, Annu. Rev. Mater. Res., 2003, 33, 333–359 CrossRef CAS.
- Y. Yamazaki, R. Hernandez-Sanchez and S. M. Haile, Chem. Mater., 2009, 21, 2755–2762 CrossRef CAS.
- E. Fabbri, D. Pergolesi and E. Traversa, Chem. Soc. Rev., 2010, 39, 4355–4369 RSC.
- H. Iwahara, T. Esaka, H. Uchida and N. Maeda, Solid State Ionics, 1981, 3–4, 359–363 CrossRef CAS.
- R. C. T. Slade, S. D. Flint and N. Singh, Solid State Ionics, 1995, 82, 135–141 CrossRef CAS.
- A. Manthiram, J. F. Kuo and J. B. Goodenough, Solid State Ionics, 1993, 62, 225–234 CrossRef CAS.
- T. Schober, Solid State Ionics, 1998, 109, 1–11 CrossRef CAS.
- P. Murugaraj, K. D. Kreuer, T. He, T. Schober and J. Maier, Solid State Ionics, 1997, 98, 1–6 CrossRef CAS.
- Y. Wang, A. Chesnaud, E. Bevillon, J. Yang and G. Dezanneau, Int. J. Hydrogen Energy, 2011, 36, 7688–7695 CrossRef CAS.
- Y. Wang, A. Chesnaud, E. Bévillon, J. Xiong and J. Yang, J. Alloys Compd., 2013, 555, 395–401 CrossRef CAS.
- Y. Z. Wang, A. Chesnaud, E. Bevillon and G. Dezanneau, Solid State Ionics, 2012, 214, 45–55 CrossRef CAS.
- L. P. Li and J. C. Nino, Int. J. Hydrogen Energy, 2013, 38, 1598–1606 CrossRef CAS.
- É. Bévillon, J. Hermet, G. Dezanneau and G. Geneste, J. Mater. Chem. A, 2014, 2, 460–471 Search PubMed.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- S. Hull, R. I. Smith, W. I. F. David, A. C. Hannon, J. Mayers and R. Cywinski, Phys. B, 1992, 180–181, 1000–1002 CrossRef.
- R. B. V. D. A. C. Larson, Los Alamos National Laboratory Report, LAUR 86-748 Search PubMed.
- B. H. Toby, J. Appl. Crystallogr., 2001, 34, 210–213 CrossRef CAS.
- H. M. Rietveld, J. Appl. Crystallogr., 1969, 2, 65–71 CrossRef CAS.
- L. B. McCusker, R. B. Von Dreele, D. E. Cox, D. Louer and P. Scardi, J. Appl. Crystallogr., 1999, 32, 36–50 CrossRef CAS.
- I. Ahmed, C. S. Knee, M. Karlsson, S. G. Eriksson, P. F. Henry, A. Matic, D. Engberg and L. Börjesson, J. Alloys Compd., 2008, 450, 103–110 CrossRef CAS.
- Z. Gan, P. L. Gor'kov, W. W. Brey, P. J. Sideris and C. P. Grey, J. Magn. Reson., 2009, 200, 2–5 CrossRef CAS PubMed.
- L. Frydman and J. S. Harwood, J. Am. Chem. Soc., 1995, 117, 5367–5368 CrossRef CAS.
- A. Medek, J. S. Harwood and L. Frydman, J. Am. Chem. Soc., 1995, 117, 12779–12787 CrossRef CAS.
- J.-P. Amoureux and M. Pruski, in eMagRes, John Wiley & Sons, Ltd, 2007, DOI:10.1002/9780470034590.emrstm0319.pub2.
- Z. Gan and H. T. Kwak, J. Magn. Reson., 2004, 168, 346–351 CrossRef CAS PubMed.
- J.-P. Amoureux, C. Fernandez and S. Steuernagel, J. Magn. Reson., Ser. A, 1996, 123, 116–118 CrossRef CAS PubMed.
- J. D. van Beek, J. Magn. Reson., 2007, 187, 19–26 CrossRef CAS PubMed.
- M. Dusek, V. Petricek and L. Palatinus, Acta Crystallogr., Sect. A: Found. Crystallogr., 2006, 62, s46 Search PubMed.
- J. Cerda, J. Arbiol, G. Dezanneau, R. Diaz and J. R. Morante, Sens. Actuators, B, 2002, 84, 21–25 CrossRef CAS.
- N. J. Clayden, C. M. Dobson and A. Fern, J. Chem. Soc., Dalton Trans., 1989, 843–847, 10.1039/DT9890000843.
- L. Buannic, F. Blanc, D. S. Middlemiss and C. P. Grey, J. Am. Chem. Soc., 2012, 134, 14483–14498 CrossRef CAS PubMed.
- K. J. D. MacKenzie and M. E. Smith, Multinuclear Solid-State Nmr of Inorganic Materials, Elsevier, 2002 Search PubMed.
- N. Kim, C.-H. Hsieh and J. F. Stebbins, Chem. Mater., 2006, 18, 3855–3859 CrossRef CAS.
- L. Buannic, F. Blanc, I. Hung, Z. H. Gan and C. P. Grey, J. Mater. Chem., 2010, 20, 6322–6332 RSC.
- I. Oikawa and H. Takamura, Chem. Mater., 2015, 27, 6660–6667 CrossRef CAS.
- N. Kim and C. P. Grey, Science, 2002, 297, 1317–1320 CAS.
- S. E. Ashbrook and M. E. Smith, Chem. Soc. Rev., 2006, 35, 718–735 RSC.
- I. Ahmed, S. G. Eriksson, E. Ahlberg, C. S. Knee, P. Berastegui, L. G. Johansson, H. Rundlof, M. Karlsson, A. Matic, L. Borjesson and D. Engberg, Solid State Ionics, 2006, 177, 1395–1403 CrossRef CAS.
- R. S. Roth, J. Res. Natl. Bur. Stand. (U. S.), 1957, 58, 75 CrossRef CAS.
- C. Hiraiwa, D. Han, A. Kuramitsu, A. Kuwabara, H. Takeuchi, M. Majima and T. Uda, J. Am. Ceram. Soc., 2013, 96, 879–884 CrossRef CAS.
- E. Kendrick, K. S. Knight, M. S. Islam and P. R. Slater, Solid State Ionics, 2007, 178, 943–949 CrossRef CAS.
- T. Ito, T. Nagasaki, K. Iwasaki, M. Yoshino, T. Matsui, N. Igawa and Y. Ishii, Solid State Ionics, 2007, 178, 13–17 CrossRef CAS.
- S. T. Norberg, S. M. Rahman, S. Hull, C. S. Knee and S. G. Eriksson, J. Phys.: Condens. Matter, 2013, 25, 454214 CrossRef PubMed.
- M. Karlsson, M. E. Björketun, P. G. Sundell, A. Matic, G. Wahnström, D. Engberg, L. Börjesson, I. Ahmed, S. Eriksson and P. Berastegui, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 1–7 Search PubMed.
- C. Shi and M. Morinaga, J. Comput. Chem., 2006, 27, 711–718 CrossRef CAS PubMed.
- S. J. Stokes and M. S. Islam, J. Mater. Chem., 2010, 20, 6258–6264 RSC.
- Y. Yamazaki, F. Blanc, Y. Okuyama, L. Buannic, J. C. Lucio-Vega, C. P. Grey and S. M. Haile, Nat. Mater., 2013, 12, 647–651 CrossRef CAS PubMed.
- F. Blanc, L. Sperrin, D. Lee, R. Dervisoglu, Y. Yamazaki, S. M. Haile, G. De Paepe and C. P. Grey, J. Phys. Chem. Lett., 2014, 5, 2431–2436 CrossRef CAS PubMed.
- I. Sosnowska, R. Przeniosło, W. Schäfer, W. Kockelmann, R. Hempelmann and K. Wysocki, J. Alloys Compd., 2001, 328, 226–230 CrossRef CAS.
- I. Oikawa, M. Ando, Y. Noda, K. Amezawa, H. Kiyono, T. Shimizu, M. Tansho and H. Maekawa, Solid State Ionics, 2011, 192, 83–87 CrossRef CAS.
- S. M. H. Rahman, I. Ahmed, R. Haugsrud, S. G. Eriksson and C. S. Knee, Solid State Ionics, 2014, 255, 140–146 CrossRef CAS.
- K. Nomura and H. Kageyama, Solid State Ionics, 2007, 178, 661–665 CrossRef CAS.
- I. Ahmed, S. G. Eriksson, E. Ahlberg, C. S. Knee, H. Gotlind, L. G. Johansson, M. Karlsson, A. Matic and L. Borjesson, Solid State Ionics, 2007, 178, 515–520 CrossRef CAS.
- A. Magrasó, C. Frontera, A. E. Gunnæs, A. Tarancón, D. Marrero-López, T. Norby and R. Haugsrud, J. Power Sources, 2011, 196, 9141–9147 CrossRef.
- Y. Wang, PhD Doctorate, Ecole Centrale Paris, Chine, 2009.
- E. Quarez, S. Noirault, M. T. Caldes and O. Joubert, J. Power Sources, 2010, 195, 1136–1141 CrossRef CAS.
- S. M. Rahman, S. T. Norberg, C. S. Knee, J. J. Biendicho, S. Hull and S. G. Eriksson, Dalton Trans., 2014, 43, 15055–15064 RSC.
- S. M. H. Rahman, C. S. Knee, I. Ahmed, S. G. Eriksson and R. Haugsrud, Int. J. Hydrogen Energy, 2012, 37, 7975–7982 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Rietveld fit of dry BaSn0.6Sc0.4O3−δ sample (Fig. S1). 119Sn (Fig. S2), 45Sc (Fig. S3–S6) and 17O (Fig. S7) spectra of all materials as a function of Sc doping concentration, 45Sc MQMAS of deuterated BaSn0.9Sc0.1O3−δ (Fig. S4), 45Sc MQMAS of dry and deuterated BaSn0.8Sc0.2O3−δ (Fig. S5), 45Sc MQMAS of dry and deuterated BaSn0.7Sc0.3O3−δ (Fig. S6), 17O MQMAS of 17O enriched BaSn0.8Sc0.2O3−δ and BaSn0.6Sc0.4O3−δ (Fig. S8). See DOI: 10.1039/c5ta09744d |
| ‡ Present address: Department of Materials, University of Oxford, OX1 3PH Oxford, UK, E-mail: E-mail: francis.kinyanjui@materials.ox.ac.uk, Tel: +44 (0)1865 612765. |
| This journal is © The Royal Society of Chemistry 2016 |