Relating side chain organization of PNIPAm with its conformation in aqueous methanol

Abstract

Combining nuclear magnetic resonance (NMR), dynamic light scattering (DLS), and μs long all-atom simulations with two million particles, we establish a delicate correlation between increased side chain organization of PNIPAm and its collapse in aqueous methanol mixtures. We find that the preferential binding of methanol with PNIPAm side chains, bridging distal monomers along the polymer backbone, results in increased organization. Furthermore, methanol–PNIPAm preferential binding is dominated by hydrogen bonding. Our findings reveal that the collapse of PNIPAm is dominated by enthalpic interactions and that the standard poor solvent (entropic) effects play no major role.

---

1 Introduction

Polymer conformations in solvent mixtures often exhibit puzzling and paradoxical behavior. One such phenomenon is co-non-solvency that occurs when two competing (miscible) good solvents for a polymer are mixed together, as a result the same polymer collapses within intermediate solvent–cosolvent mixing ratios in bulk^1–9 and near surfaces.^10,11 One popular system that shows co-non-solvency is the conformational behavior of poly(N-isopropylacrylamide) (PNIPAm) in aqueous alcohol mixtures. Even when the phenomenon is usually associated with PNIPAm,^1–4 the name co-non-solvency was first coined when polystyrene chains were dissolved in a mixture of cyclohexane and DMF solution.¹² Interestingly, not only PNIPAm and polystyrene, rather a large number of polymers can exhibit the phenomenon of co-non-solvency.^13–18 Furthermore, these systems present both LCST and UCST temperature effects. This suggests that the effect, unlike the common chemical believe, is not “only” restricted to polymers exhibiting LCST behavior and thus is independent of specific chemical details.

The microscopic origin of the puzzling coil–globule–coil transition is a matter of intense debate. Here extensive experimental,^1–5,9 theoretical^6,8,19–21 and computer simulations^4,7,8,22 studies have been performed. On the experimental side, studies have employed infrared spectra, light scattering and neutron scattering.^1–5,9 In some cases, also in conjunction with analytical theory^1,5 and parameter estimation for interaction strength.⁹ On the theory side, ever since the first theoretical work employing the Flory–Huggins theory,¹ several analytical works have been proposed to explain co-non-solvency based on the cooperativity effect,⁶ particle based theory,⁸ Flory–Huggins lattice model at high polymer concentrations,²⁰ and the off-lattice statistical model,²¹ to name a few. Furthermore, former simulations are mostly limited to a few studies.^4,7,8 In this context, using a semi-grand canonical molecular dynamics approach, two of us have previously shown that PNIPAm has a significantly higher affinity (or preferential binding) towards methanol than towards water by a factor of ∼4k_BT per monomer.⁷ This is further exemplified by potential of mean force (PMF) calculations, where a clear preferential interaction of methanol with PNIPAm was observed.²³ This indicates that the polymer collapse in miscible good solvents, such as water and methanol for PNIPAm, is dictated by the relative (enthalpic) interaction strengths between methanol–PNIPAm and water–PNIPAm. Recently, it has been shown that the effect of co-non-solvency can also be observed in tertiary butyl alcohol in methanol–water mixtures, that is driven by enthalpic interactions.²⁴ Furthermore, the enthalpically driven collapse of PNIPAm is against the common understanding of standard poor solvent collapse of LCST polymers, where solvent entropy gain plays a crucial role in polymer collapse. Furthermore, because a wide variety of polymers show the co-non-solvency phenomenon when dissolved in appropriate mixtures of solvents, a unified concept of co-non-solvency was proposed within a generic approach.^8,19 Therefore, simple Lennard-Jones (LJ) interactions between monomer–(co)solvent are sufficient to explain the co-non-solvency effect at constant temperature^8,19 and more effects,^25,26 while ignoring all chemical details that often only contribute to a mere numerical prefactor. However, LJ representation of a (co)solvent bead may represent several methanol and/or water molecules.⁸

What makes the co-non-solvency of PNIPAm an interesting and puzzling effect is that concepts known from the conventional polymer science often are insufficient to describe the phenomenon. For example: (1) a polymer collapses when the solvent quality remains good or even gets increasingly better by the addition of better cosolvent,^7,8 (2) standard poor solvent collapse or entropic effects are irrelevant, (3) the phenomenon is independent of any underlying LCST or UCST temperature behavior of polymers,^13–19 and (4) is driven by large (local) concentration fluctuations of different solvent components near the polymer,¹⁹ making the mean-field description unsuitable. In this work, we revisit the phenomenon of co-non-solvency of PNIPAm in aqueous methanol mixtures by combining nuclear magnetic resonance (NMR), dynamic light scattering (DLS) and μs long, two million particles all-atom simulations. Note that we have used all-atom simulation instead of a semi-grand canonical setup.⁷ This is because in the case of a good solvent chain, the chain extension covers almost a full simulation domain consisting of ∼30 nm box boundary. To better correlate the different approaches, we match the polymer length N_l to be similar, in the unit of persistence length [small script l]_p, which was chosen as N_l ∼ 100[small script l]_p. Our results provide experimental support for the claims presented in the four points mentioned above.

The remainder of the paper is organized as follows: in Section 2 we briefly state the methodology for simulations, material synthesis and experimental measurements. Section 3 presents results and discussion. Finally we draw our conclusions in Section 4.

2 Materials, models and methods

2.1 Nuclear magnetic resonance measurements

The H-NMR experiments^27,28 were measured with a 5 mm triple resonance TXI ¹H/¹³C/¹⁵N probe equipped with a z-gradient on an 850 MHz Bruker AVANCE III system. For proton spectra, 128 transients were used with a 9.5 μs long 90° pulse and a 17 600 Hz spectral width together with a recycling delay of 5 s. The temperature was regulated at 298.3 K and calibrated with a standard ¹H methanol NMR sample using the Topspin 3.1 software (Bruker). Temperature was controlled with a VTU (variable temperature unit) and an accuracy of ±0.1 K.

Diffusion Ordered NMR Spectroscopy (DOSY-NMR) experiments were performed with a gradient strength of 5.350 G mm⁻¹ on a Bruker Avance-III 850 NMR Spectrometer. The gradient strength of probes was calibrated by using a sample of ²H₂O/¹H₂O at a defined temperature and compared with the theoretical diffusion coefficient of ²H₂O/¹H₂O (values taken from Bruker diffusion manual) at 298.3 K.

The diffusion delay time (Δ), Bruker term D₂O was optimized for the TXI probe for 60 ms, while the gradient pulse length was kept at 1.6 ms. The optimization was realized by comparing the remaining intensity of the signals at 2% and 95% gradient strengths. The intensity loss of the echo was in the range of 90%. Using longer diffusion time causes a loss of signal intensity (from the echo) due to a short spin lattice relation time T₁, which was determined with the inversion recovery method²⁷ before diffusion measurements.

The diffusion measurements were done with a 2D DOSY sequence²⁹ by incrementing in 16 linear steps from 2% to 100% with the TXI probe. The calculation of the diffusion value was automatically done with the mono exponential function:³⁰

where I(G) and I(0) are the intensities of the signals with and without gradient, γ the gyromagnetic ratio of the nucleus (¹H in these measurements), G is the gradient strength, δ the duration of the pulse field gradient (PFG), D the diffusion value in m² s⁻¹ and Δ the “diffusion time” between the beginning of the two gradient pulses. The relaxation delay between the scans was 3 s.

The 2D sequence for diffusion measurement used double stimulated echo with three spoil gradients for convection compensation and with an eddy current delay of 5 ms for reduction^31,32 (acronym Bruker pulse program: dstebpgp3s). The spin–spin relaxation times T₂ were obtained via the CPMG method (Carr–Purcell–Meiboom–Gill)^33,34 using eight different increments. In the experiment, the time between the inversion (180° pulse) and the read pulse (90° pulse) is incremented in eight steps and the quantitative analysis of the eight integrals (from the eight increments) exponentially fitted.

2.2 Size exclusion chromatography and light scattering

2.2.1 Size exclusion chromatography. For relative molecular weight determinations, a PSS SECcurity Agilent 1260 Infinity Setup (Polymer Standards Service GmbH (PSS)) was used, including a column set from PSS (2× GRAM 1000, 1× GRAM 100, particle size 10 μm) maintained at 60 °C, a UV (270 nm) and an RI detector. The eluent was DMF (containing 1 gL⁻¹ LiBr) with a flow rate of 1 mL min⁻¹. The RI detector signal was used and the molecular weights are relative to linear polystyrene (PS) standards provided by Polymer Standards Service (PSS). Relative M_w values agreed within 5% (high M_w range) to 10% (low M_w range) with absolute M_w values obtained by static light scattering (SLS).

2.2.2 Light scattering measurements. All light scattering experiments were performed on a commercially available instrument from ALV GmbH consisting of an electronically controlled goniometer and an ALV-5004 multiple tau full-digital correlator (320 channels). A HeNe laser with a wavelength of 632.8 nm and an output power of 25 mW (JDS Uniphase, Type 1145P) was utilized as a light source. All solutions were filtered through Millex-LCR 0.45 μm filters (Merck Millipore), directly into quartz light scattering cuvettes (inner diameter 18 mm), which were cleaned before in a Thurmond apparatus with distilled acetone. All light scattering measurements were carried out, similar to the NMR measurements, at a temperature of 25 °C. For the dynamic light scattering (DLS) experiments, PNIPAm samples were dissolved at a concentration of 1 gL⁻¹ in pure water and in pure methanol. The z-average diffusion coefficients were determined after angular dependent measurements and averaging the apparent diffusion coefficients. The refractive index increment of each sample in methanol was determined with a Michelson interferometer.

2.3 PNIPAm samples and synthesis

Three different PNIPAm samples were used for our experiments. These include a commercial PNIPAm from Sigma-Aldrich [cat # 535311-10G]. Using light scattering and size exclusion chromatography, we estimate absolute molecular weight M_w and poly dispersity (PDI) to be M_w (SLS) = 293 kDa, M_w (GPC) = 309 kDa, and PDI = 2.69. N_l value is estimated using the equation N_l = (M_w/PDI)/M₀, where M₀ is the NIPAm formula weight. This corresponds to N_l = 962 (sample PNIPAM-963). Furthermore, we have prepared two PNIPAm samples by RAFT polymerization giving chain lengths bracketing that corresponding to N_l ∼ 100[small script l]_p to better correlate all-atom simulations and experimental observations (details will be described in the next section).

Before starting the polymerization procedure, N-isopropyl acrylamide (NIPAm, Acros, 99%) was recrystallized three times in series by adding a benzene solution (∼30% NIPAm by weight) to an approximate 12-fold excess of pentane at room temperature. 4,4′-Azobis(4-cyanovaleric acid) (ACVA, Aldrich, ≥98%,), 4-((((2-carboxyethyl)thio)carbonothioyl)thio)-4-cyanopentanoic acid (BM1433, >95%, boron molecular) and all other materials were purchased from commercial sources and utilized as received.

2.3.1 Reversible addition–fragmentation chain-transfer polymerization of PNIPAm. Sample 1 (PNIPAM-207) with N_l = 207: NIPAm, BM1433, and ACVA were combined in a molar ratio of 250 : 1 : 0.4 in a 25 mL Shlenk tube and pump/purged 3 times with vacuum/argon. DMF (anh) was added via syringe to give a 20% by weight NIPAm solution that was sparged with argon for 30 minutes while cooling in ice. The reaction was initiated by placing in a 60 °C bath, and aliquots were taken via syringe at time intervals to estimate conversion by NMR and molecular weight by GPC. After 10 hours (∼80% conversion by NMR), the solution was cooled in ice and the polymer precipitated 3 times by dripping into rapidly stirring ether (from MeOH for 2nd and 3rd cycle), and the resulting pale yellow solid dried under reduced pressure. ¹H NMR (850 MHz, D₂O) δ: 3.90 (br, 1H), 2.20–1.90 (br, overlapping, 1H), 1.80–1.34 (br, overlapping, 2H), 1.16 (br, 6H). M_w (GPC): 26.5 kDa, PDI = 1.13. Prior to precipitation M_w (GPC) = 18.6 kDa, PDI = 1.4.

Sample 2 (PNIPAM-288) with N_l = 288: conducted as above, but with NIPAM, BM1433, and ACVA in a molar ratio of 500 : 1 : 1 and reaction stopped at 60% conversion. ¹H NMR identical to PNIPAM-207. M_w (GPC): 39.8 kDa, PDI = 1.22. Prior to precipitation M_w (GPC) = 30.2 kDa, PDI = 1.4.

2.4 All-atom simulations

We employ all atom molecular dynamics simulations using GROMACS package.³⁵ We use the Gromos96 force field³⁶ for methanol, the SPC/E water model³⁷ and the force field parameters for PNIPAm are taken from ref. 4. The temperature is set to 298 K using velocity rescaling with a coupling constant 0.5 ps.³⁸ The electrostatics are treated using Particle Mesh Ewald.³⁹ The interaction cutoff is chosen as 1.0 nm. The time step for the simulations is set to 2 fs. Initial equilibration of every configuration is performed at ambient pressure for 20 ns, where the pressure coupling is done using a Berendsen barostat⁴⁰ with a coupling time of 0.5 ps. The final configuration of constant pressure simulations, with equilibrated density, is used for canonical simulations.

We choose a PNIPAm chain of length N_l = 256 that corresponds to ∼100[small script l]_p, with [small script l]_p being the persistence length of a PNIPAm chain. Note that an atactic PNIPAm chain has [small script l]_p ∼ 2–3 monomers. We choose five different methanol mole fractions x_m in MD simulations. In Table 1 we present our system parameters. The production runs are performed for at least 1 μs long MD trajectory each. During the production run observables such as gyration radius R_g and structure factor S(q) are calculated. In Fig. 1 we present the time evolution of R_g for three different x_m. It can be seen that the structure is rather stable over long simulation time scales.

Table 1 System sizes for the simulations performed in this study. Here, N is the total number of solvent molecules, N_w is the number of water molecules, N_m is the number of methanol molecules, x_m is the methanol mole fraction, L_box the equilibrated box length, and chain gyration radius R_g

x m	N	N w	N m	L box (nm)	R g (nm)
0.10	7.0 × 10^5	6.3 × 10^5	0.7 × 10^5	28.3	2.53
0.25	6.0 × 10^5	4.5 × 10^5	1.5 × 10^5	28.1	2.28
0.60	5.0 × 10^5	2.0 × 10^5	3.0 × 10^5	28.6	5.22
0.80	5.0 × 10^5	1.0 × 10^5	4.0 × 10^5	29.8	6.24
1.00	6.0 × 10^5	0	6.0 × 10^5	32.8	7.37

---

Fig. 1 Time evolution of polymer gyration radii R_g for three different methanol mole fractions x_m. The results are shown for a chain length N_l = 256 and at temperature T = 298 K.

3 Results and discussions

3.1 PNIPAm conformation in aqueous methanol revisited

We first revisit PNIPAm conformation in water and methanol mixtures. In Fig. 2 we show R_g as a function of x_m. We have also included the data from the earlier generic simulations corresponding to N_l = 100[small script l]_p.⁸ It can be appreciated that, by matching [small script l]_p between the all-atom and previous generic simulations, we obtain a very good (almost quantitative) agreement. Furthermore, Fig. 2 also suggests that 1σ ∼ 1 nm. This can be rationalized as follows: in our generic model [small script l]_p ∼ 1 monomer, whereas for a PNIPAm chain [small script l]_p ∼ 2.5–3 monomers or ∼1 nm. This leads to a mapping of 2.5–3 NIPAm monomers onto one generic bead. Since the size of a generic monomer is 1σ, thus our observation of 1σ ∼ 1 nm is a reasonably good estimate. To make comparison with the empirical data, we have estimated PNIPAm radii by both DOSY NMR and DLS measurements on three PNIPAm samples of varying sizes. For this purpose, we have used samples PNIPAm-207 or N_l ∼ 207 = 83[small script l]_p and PNIPAm-288 or N_l ∼ 288 = 115[small script l]_p. Fig. 2 contains the experimental data for PNIPAm-207 that show a similar trend as the all-atom and the generic simulations. A slight quantitative variation in R_g is because of the difference in N_l's between experiment and all-atom simulations, which varies by ∼15[small script l]_p. As the R_g for the smaller PNIPAm samples is below that can be accurately determined by SLS (i.e., R_g < 10 nm), we obtain hydrodynamic radii R_h from diffusion coefficient data (DLS and DOSY NMR) using the Stokes–Einstein–Sutherland relation.^41,42R_h is then translated into R_g using the expressions R_g = 1.5R_h for coil conformations and R_g = (3/5)^1/2R_h for globule.^43,44 Note that we present experimental data of R_g for the well defined collapsed structures and expanded chain conformations. Near the transition region 0.25 < x_m < 1.0, we do not present data because of the nontrivial relation between R_h and R_g.

Fig. 2 Gyration radius R_g as a function of methanol mole fraction x_m. Results are shown for R_g obtained from all-atom simulations for a chain of length N_l = 256 ∼ 100[small script l]_p and experimental measurements for N_l ∼ 207 ∼ 83[small script l]_p (sample PNIPAm-207). For the pure water (x_m = 0.0) and pure methanol (x_m = 1.0) we use the data obtained from dynamic light scattering (DLS). For the collapsed structure at x_m = 0.1 and 0.25, we present the data calculated using nuclear magnetic resonance (NMR). For comparison, we also include data from our previous generic simulations⁸ with N_l ∼ 100[small script l]_p and an analytical expression presented in eqn (2). Arrows are the indicative of the corresponding y-axis of the corresponding data set.

Having shown the results for the collapse–swelling–collapse transition, we now want to briefly explain the origin of this reentrant transition. In this context, it was previously shown that the initial collapse at lower x_m values are due to preferential binding of methanol molecules with the PNIPAm chain.⁷ Therefore, when a small amount of methanol molecules is added, these molecules try to bind to more than one monomer acting as sticky contacts between distal monomers along the polymer backbone. This tendency leads to the formation of segmental loops along the backbone initiating the process of polymer collapse. When the x_m exceeds a certain concentration, so that the system can overcome the solvent translational entropy, the polymer re-opens after complete decoration of the polymer with methanol molecules. In this case, conformational entropy contributes to a logarithmic correction¹⁹ and, therefore, only leads to a weak effect on describing the overall phenomenon, which is otherwise dominated by enthalpy. The methanol molecules forming enthalpically driven sticky contacts between distal monomer units were termed as bridging cosolvent and their fractions defined as ϕ_B.⁸ The analytical expression for ϕ_B¹⁹ can be converted into gyration radius using an argument using the formulation¹⁹ based on,^43,44

where R⁰_g is the gyration radius for x_m = 0. Here [scr V, script letter V] is the magnitude of the negative excluded volume −|[scr V, script letter V]|, which can be estimated from the simulations and analytical theory.⁸ Note that ϕ_B gives the direct measure of [scr V, script letter V] using the relation [scr V, script letter V] = 100ϕ_B(x_c). Furthermore, an analytical expression can be derived for ϕ_B using a Langmuir like adsorption isotherm taking into account the competitive displacement of both solvent and cosolvent.⁸ In Fig. 2 we also include R_g estimated using eqn (2). It can be seen that the experimental, all-atom simulation and generic simulation data can be well described by the analytical theory. Suggesting a reasonable correlation between the phenomena of co-non-solvency and the bridging scenario proposed earlier.⁸

Fig. 3 shows a scaling plot of R_g obtained from all-atom simulations and from NMR and DLS measurements of the three polymer samples included in this work. For comparison we have also included data taken from the published literature.^3,7 It can be appreciated that the data from different N_l obtained from different methods falls within the universal scaling law, further showing a nice quantitative agreement between different methods.

Fig. 3 Gyration radius R_g as a function of chain length N_l. Results are shown for coil (at x_m = 1.0) and globule (at x_m = 0.1) conformations. Data for R_g are obtained from different experiments, simulations and also from published work from the literature, as described in the legend. Symbols are respective data and the lines are power law fits shown in the legend. For coil conformation R_g ∝ N_l^3/5 and for globular conformations R_g ∝ N_l^1/3.

3.2 Good solvent collapse

One of the most intriguing features of this phenomenon is that PNIPAm collapses in good solvent. This makes the polymer conformation completely decoupled from the thermodynamic solvent quality (see chemical potential data in ref. 7). Therefore, we expect the chains to maintain a self avoiding walk statistics between the bridging points, i.e. an exponent of ν = 3/5. A quantity that best describes the polymer conformation is the static structure factor S(q), which usually requires very long simulation trajectories and also long chain lengths. In this context, thus far all-atom simulations are mostly limited to oligomer systems (consisting of N_l = 20–40 to 8–16[small script l]_p). In this work, we calculate S(q) for a collapsed chain at x_m = 0.1 over last 0.5 μs long all-atom MD run for N_l = 256 ∼ 100[small script l]_p. In Fig. 4 we show S(q), which shows a cross over from an approximate q^−5/3 scaling between 4 nm⁻¹ ≤ q ≤ 10 nm⁻¹ (or corresponding length scale of 1.6 nm ≥ [small script l] ≥ 0.62 nm) to a q⁻⁴ scaling for q ≤ 4 nm⁻¹. This suggests that – while a PNIPAm chain remains globally collapsed, it consists of rather large good solvent blobs with typical sizes of [small script l] ∼ 1.3 nm.

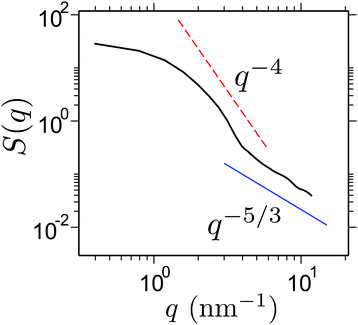Fig. 4 Static structure factor S(q) of a collapsed PNIPAm structure at x_m = 0.1. For the calculations of S(q) we only consider the alkane backbone of a PNIPAm chain.

3.3 Folded PNIPAm structure and side chain organization

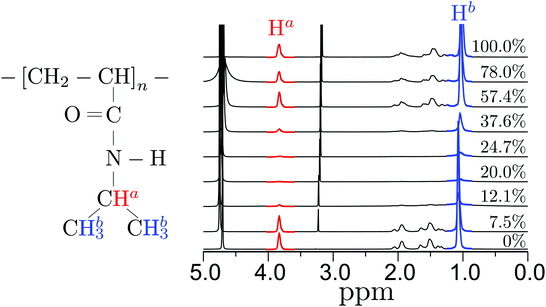
We have used solution NMR to monitor side chain dynamics of PNIPAm as a function of x_m (predeuterated MeOD in D₂O). Typical ¹H NMR spectra are presented in Fig. 5. All the signals decrease in area and broaden with increasing x_m between 7.5% ≤ x_m ≤ 37.6% and then again increases when x_m ≥ 37.6%. The decrease in area and broadening of the signals indicate slowing dynamics, which can be reflected in spin–spin relaxation times T₂, as also reported by others as a means to map out polymer collapse.⁴⁸ The T₂ values for the H^a signal plotted in Fig. 6, as a function of x_m, give the expected clear signature of the coil–globule–coil scenario as a result of the side chains becoming less mobile when the polymer is in the collapsed state.

Fig. 5 Left panel shows schematic representation of a monomer of PNIPAm. In NMR experiments we identify the rigidity of H^a and H^b indicated in this schematic. Right panel presents nuclear magnetic resonance (NMR) spectra highlighting H^a and H^b hydrogens as indicated in the left panel. Results are shown for different methanol mole fractions x_m, starting from pure water x_m = 0.0 (or 0%) to pure methanol x_m = 1.0 (or 100%). The signal around 3.75 ppm corresponds to H^a and H^b peak appears around 1.10 ppm. Note that for clear representation of the data, we have aligned the peak positions of H^a. We have used Sigma Aldrich sample of PNIPAm-962.

Fig. 6 In-plane relaxation time T₂ of H^a hydrogen as a function of methanol mole fractions x_m. The data is obtained by integrating the intensity peak around 3.75 ppm in Fig. 5.

The data from the NMR experiments also suggests that the side group rigidity of a PNIPAm chain is because of the fact that a PNIPAm collapses in a way that the inner core of the folded structure is occupied by the side groups. MD simulations also support this claim for a collapsed structure. In this context, as described earlier, when there is preferential binding of PNIPAm with methanol, it is expected to observe methanol encapsulation within a collapsed structure of PNIPAm. Therefore, it is important to monitor if the side chain rich inner core also has methanol molecules sitting in between. For this purpose, we have performed a separate set of NMR experiments to identify preferential binding of the methanol molecules with PNIPAm chains.

3.4 Preferential adsorption of methanol on PNIPAm and solvent intake

To experimentally observe the preferential interaction of the PNIPAm with methanol, we have used a concept where preferential PNIPAm–methanol binding⁷ can lead to local aggregation of methanol near the polymer structure that leads to depletion away from the polymer, see a schematic in Fig. 7(a). For this purpose we have prepared a NMR tube separated into two compartments by a membrane filter, see Fig. 7(b). Both compartments contain 15% aqueous methanol, and 1.188 g PNIPAM was added to the upper compartment. This essentially becomes an osmosis experiment, with quantitative ¹H-NMR spectra collected to monitor changes in solvent composition in the lower compartment, from which solvent uptake by the PNIPAM can be estimated. For all different time dependent proton spectra, the same phase correction, baseline and integration parameters (integral width for the proton and methyl group of methanol) were applied.

Fig. 7 Part (a) presents a schematic representation of the concept where local aggregation of cosolvents near a polymer lead to depletion away from the macromolecular structure. Part (b) shows a schematic showing the 5 mm tube with external reference capillary, a sealing function and a paper filter in the center that separates PNIPAM from bulk aqueous methanol mixture at the bottom. Part (c) presents the amount of excess methanol molecules encapsulated by the PNIPAm collapsed sample as measured from the depletion of methanol in the lower part of the NMR tube. Here 3% of methanol is with respect to the initial 15% of the methanol content.

In Fig. 7(c) we present the amount of depleted methanol in the lower panel of the NMR tube in Fig. 7(b) that is engulfed by the PNIPAm sample in the upper panel of the NMR tube. The measurements were conducted over sixteen days. It can be seen that the methanol increases by ∼3% in the polymer system within the first 3–4 days. Beyond 4 days, solvent intake data shows a plateau suggesting no evaporation of methanol from the airtight experimental setup. Note that a rather large polymer concentration is needed in the upper panel of Fig. 7(b) to observe any significant solvent intake. The solvent intake, as observed in our NMR experiments, further supports our earlier claim that preferential adsorption of the methanol with PNIPAm drives the polymer collapse.⁷ This scenario can be further validated by looking into the potential of mean force (PMF) between PNIPAm–methanol and PNIPAm–water calculated using the umbrella sampling.^23,45,46 In Fig. 8 we show PMF between different PNIPAm–(co)solvent pairs, which show a clear signature of preferential enthalpic interactions between PNIPAm–methanol. Furthermore, in a given polymer, the energy density within the solvation volume is dictated not only the interaction energy, but also by the sizes of the solvent (methanol and water in this case). Therefore, it should still be mentioned that the enthalpic interactions (or bridging) are usually not given by a single methanol molecule, rather a few collectively lead to sticky contacts.⁸

Fig. 8 Potential of mean force v(r) showing NIPAm–methanol and NIPAm–water interaction strengths for two different pressures. Simulations are performed at a temperature of 298 K and the data is taken from ref. 23.

The window of PNIPAm collapse, or the LCST behavior, is strongly dependent on the temperature of the systems.^1,2 Here, it is important to mention that – just because a polymer exhibits an LCST behavior, it does not suggest that the polymer collapse at a constant T should also be driven enhanced solvent entropy by the addition of methanol in water. Our arguments are based on the claim that the interaction asymmetry between PNIPAm–methanol and PNIPAm–water dictate PNIPAm collapse in aqueous methanol mixture.⁸ The smaller the asymmetry, the narrower the window of polymer collapse.¹⁹ To elucidate that a PNIPAm collapses because of interaction asymmetry, we have calculated PMF between NIPAm–water and NIPAm–methanol for T = 278 K. The data is shown in Fig. 9. As expected, at a reduced T the asymmetry in interactions also reduces, making the background binary fluid homogeneous for the polymer. This can not facilitate a polymer to collapse in a binary mixture. Interestingly previous experiments^1,2 have shown that the PNIPAm remains in coil state for T = 278 K, thus showing a nice correlation capturing the temperature effects between the earlier experiments^1,2 and our simulations.

Fig. 9 Same as Fig. 8. But for a temperature T = 278 K.

3.5 Mechanism of polymer collapse

Lastly we want to comment on the possible mechanism of cosolvent bridging leading to PNIPAm collapse in aqueous methanol mixtures. In this context, it is already presented in the previous section and consistent with previous work,⁷ that there is a preferential binding of PNIPAm with methanol. To further illustrate the bridging scenario driven by preferential adsorption, we calculate the number of hydrogen bonds n_H-bond/N_l between a methanol molecules and a NIPAm monomer using all-atom simulations. In Fig. 10(a) we show n_H-bond/N_l as a function of x_m. In the range 0.10 ≤ x_m ≤ 0.25, NIPAm shows a strong tendency of hydrogen bonding with the methanol molecules that is evident from the maximum deviation from the expected linear behavior.⁴ Without attempting to describe any specific geometry or arrangement of H-bond donor and acceptors, we can assume the –OH end of the methanol points towards the PNIPAm amide linkage, such that the CH₃ of methanol now forms part of the local solvent accessible surface previously defined by the amide group. The sticky contacts could then be formed between these CH₃ groups and the isopropyl group of a distal NIPAm unit (see Fig. 10(b)), or between multiple CH₃ groups of bound methanol molecules (see Fig. 10(c)). Note that in Fig. 10(b) and (c), for simplicity of representation, we only highlight hydrogen bonds between hydrogen of methanol and the oxygen of NIPAm amide groups that we expect to be most dominant. However, it should be mentioned that there might be several more scenarios. For example, there is a possibilities of bonding between methanol oxygen and hydrogen of the amide group and methanol hydrogen with nitrogen of the amide groups. Furthermore, it should also be mentioned that a single CH₃ interaction with isopropyl group is ∼k_BT, which may not sound as a large enough interaction strength. However, these methanol mediated sticky contacts are each likely facilitated by a few methanol molecules making the sticky contact attraction strength of the order of several ∼k_BT and not only by a single methanol molecule, as simplified in the schematics shown in Fig. 10(b) and (c). Here we want to emphasize that the solvation properties are intimately linked to the energy density within the solvation volume. Hence, not only dictated by the individual interaction strengths, but also related to number of (co)solvent particles within the solvation volume. Therefore, if one can reduces the energy density within the solvation volume, such that the solvent–cosolvent interaction contrast also reduces, one should expect to see narrower window of collapse. Indeed, it had been experimentally observed that for larger alcohols (such as ethanol or propanol) window of collapse reduces by ∼30–40% in comparison to methanol.⁴⁷

Fig. 10 Part (a) shows number of hydrogen bonds n_H-bond/N_l between a methanol molecule and a monomer of PNIPAm as a function of methanol mole fraction x_m. The dashed red line is the linear extrapolation. Data is shown for all-atom simulations of chain length N_l = 256 and for the temperature T = 298 K. Parts (b) and (c) present schematic of two possible scenarios of bridging methanol molecules, which we expect to be most relevant.

4 Conclusions

We have revisited the co-non-solvency of PNIPAm in aqueous methanol mixtures. For this purpose, we have combined nuclear magnetic resonance and dynamics light scattering experiments with the all-atom molecular dynamics simulations, complementing our earlier studies of generic simulations⁸ and analytical theory.¹⁹ These findings strongly support that the initial collapse at lower methanol concentration is due to the methanol–PNIPAm enthalpic (bridging) effects and the reopening at larger methanol concentrations is entropic. Furthermore, preferential PNIPAm–methanol binding leads to increased organization of the PNIPAm side chains, which is intimately linked to the global conformational behavior of PNIPAm in aqueous methanol mixtures.

While we study a specific system of PNIPAm in aqueous methanol mixture, our proposed mechanism of PNIPAm collapse at lower methanol concentrations provide a natural explanation to other phenomena, such as the initial collapse of PNIPAm in aqueous urea mixtures.^48,49 Where the collapse was proposed is initiated by hydrogen bonded bridging of urea molecules between two NIPAm monomers that are far along the polymer backbone.

It should also be mentioned that when dealing with polymer physics and/or the thermodynamics of polymer solutions, two key considerations, out of several, are absolutely needed to make any reasonable comparison to experimental data: (1) a polymer should be studied and not an oligomer and (2) time scale of simulations compared to the polymer relaxation time. In this context, our simulations of μs long trajectory of a N_l = 100[small script l]_p chain consisting of two million particles is the largest all-atom simulations performed on this PNIPAm based systems. A reasonably good agreement between all-atom simulations and experiments complementing earlier generic simulations, suggests that the co-non-solvency phenomenon is indeed driven by enthalpy.⁸

Acknowledgements

D. M. thanks Burkhard Dünweg, Martin Müser, Kostas Ch. Daoulas, Paulo A. Netz, Robinson Cortes-Huerto, and Torsten Stühn for countless stimulating discussions, Jens-Uwe Sommer for useful discussions during the SOMATAI-2016 meeting in Crete that motivated us to calculate Fig. 9 and Adam Moule for useful discussion regarding the methanol mediated sticky contacts and NMR experiments. We thank Robert Graf for stimulating discussions regarding NMR technique. Furthermore, we gratefully acknowledge the assistance of Christine Rosenauer with the DLS and GPC measurements. We thank Stefan Spang for preparing the NMR tube for the second set of NMR experiments. M. D. W., T. E. O., and C. M. M. acknowledges hospitality at the Max-Planck Institut für Polymerforschung, where this work was initiated and performed. We thank Robinson Cortes-Huerto, Takahiro Okhuma, and Torsten Stühn for critical reading of the manuscript.

References

1. H. G. Schild, M. Muthukumar and D. A. Tirrell, Macromolecules, 1991, 24, 948–952.
2. F. M. Winnik, H. Ringsdorf and J. Venzmer, Macromolecules, 1990, 23, 2415–2416.
3. G. Zhang and C. Wu, Phys. Rev. Lett., 2001, 86, 822–825.
4. J. Walter, J. Sehrt, J. Vrabec and H. J. Hasse, J. Phys. Chem. B, 2012, 116, 5251–5259.
5. H. Kojima, F. Tanaka, C. Scherzinger and W. Richtering, J. Polym. Sci., Part B: Polym. Phys., 2013, 51, 1100–1111.
6. F. Tanaka, T. Koga and F. M. Winnik, Phys. Rev. Lett., 2008, 101, 028302.
7. D. Mukherji and K. Kremer, Macromolecules, 2013, 46, 9158–9163.
8. D. Mukherji, C. M. Marques and K. Kremer, Nat. Commun., 2014, 5, 4882.
9. K. Kyriakos, M. Philipp, C.-H. Lin, M. Dyakonova, N. Vishnevetskaya, I. Grillo, A. Zaccone, A. Miasnikova, A. Laschewsky, P. Mller-Buschbaum and C. M. Papadakis, Macromol. Rapid Commun., 2016, 37, 420–425.
10. M. Richter, M. Hunnenmörder and R. von Klitzing, Colloid Polym. Sci., 2014, 292, 2439–2452.
11. Y. Yu, M. Cirelli, B. D. Kieviet, E. S. Kooij, G. J. Vancso and S. de Beer, Polymer, 2016 DOI:10.1016/j.polymer.2016.08.029.
12. B. A. Wolf and M. M. Willms, Makromol. Chem., 1978, 179, 2265–2277.
13. A. Hiroki, Y. Maekawa, M. Yoshida, K. Kubota and R. Katakai, Polymer, 2001, 42, 1863–1867.
14. R. Lund, L. Willner, J. Stellbrink, A. Radulescu and D. Richter, Macromolecules, 2004, 37, 9984–9993.
15. B. E. Read, Trans. Faraday Soc., 1960, 56, 382–390.
16. M. Ohkura, T. Kanaya and K. Kaji, Polymer, 1992, 33, 3686–3690.
17. Y. Kiritoshi and K. Ishihara, J. Biomater. Sci., Polym. Ed., 2002, 13, 213–224.
18. Y. Kiritoshi and K. Ishihara, Sci. Technol. Adv. Mater., 2003, 4, 93–98.
19. D. Mukherji, C. M. Marques, T. Stuehn and K. Kremer, J. Chem. Phys., 2015, 142, 114903.
20. J. Dudowicz, K. F. Freed and J. F. Douglas, J. Chem. Phys., 2015, 143, 131101.
21. Y. A. Budkov, A. L. Kolesnikov, N. N. Kalikin and M. G. Kiselev, EPL, 2016, 114, 46004.
22. F. R. Rupero, T. Hajari and N. van der Vegt, J. Phys. Chem. B, 2015, 119, 15780–15788.
23. T. E. deOliveira, P. A. Netz, D. Mukherji and K. Kremer, Soft Matter, 2015, 11, 8599–8604.
24. K. Mochizuki, S. R. Pattenaude and D. Ben-Amotz, J. Am. Chem. Soc., 2016, 138, 9045–9048.
25. J. Heyda, A. Muzdalo and J. Dzubiella, Macromolecules, 2013, 46, 1231–1238.
26. S. de Beer, E. Kutnyanszky, P. M. Schön, G. J. Vancso and M. H. Müser, Nat. Commun., 2014, 5, 3781.
27. A. Jerschow and N. Mueller, J. Magn. Reson., Ser. A, 1996, 123, 222–225.
28. A. Jerschow and N. Mueller, J. Magn. Reson., Ser. A, 1997, 125, 372–375.
29. M. Holz and H. Weingartner, J. Magn. Reson., 1991, 92, 115.
30. J. E. Tanner, J. Chem. Phys., 1970, 50, 2523.
31. D. H. Wu, A. D. Chen and C. S. Johnson, J. Magn. Reson., Ser. A, 1995, 115, 260–264.
32. K. F. Morris and C. S. Johnson, J. Am. Chem. Soc., 1992, 114, 3139–3141.
33. H. Y. Carr and E. M. Purcell, Phys. Rev., 1954, 94, 630.
34. S. Meiboom and D. Gill, Rev. Sci. Instrum., 1958, 29, 688–691.
35. S. Pronk, S. Pall, R. Schulz, P. Larsson, P. Bjelkmar, R. Apostolov, M. R. Shirts, J. C. Smith, P. M. Kasson, D. van der Spoel, B. Hess and E. Lindahl, Bioinformatics, 2013, 29, 845–854.
36. W. F. van Gunsteren, S. R. Billeter, A. A. Eising, P. H. Hünenberger, P. Krüger, A. E. Mark, W. R. P. Scott and I. G. Tironi, Gromos43a1, Hochschulverlag AG an der ETH Zurich, 1996, pp. 1–1402.
37. H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271.
38. G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101.
39. U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. A. Pedersen, J. Chem. Phys., 1995, 103, 8577.
40. H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684.
41. W. Sutherland, Philos. Mag., 1905, 9, 781.
42. A. Einstein, Ann. Phys., 1905, 322, 549.
43. P.-G. de Gennes, Scaling Concepts in Polymer Physics, Cornell University Press, London, 1979.
44. J. Des Cloizeaux and G. Jannink, Polymers in Solution: Their Modelling and Structure, Clarendon Press, Oxford, 1990.
45. M. Sprik and G. Ciccoti, J. Chem. Phys., 1998, 109, 7737.
46. J. Kahlen, L. Salimi, M. Sulpizi, C. Peter and D. Donadio, J. Phys. Chem. B, 2014, 118, 3960.
47. R. O. P. Costa and R. F. S. Freitas, Polymer, 2002, 43, 5879–5885.
48. J. Wang, B. Liu, G. Ru, J. Bai and J. Feng, Macromolecules, 2016, 49, 234–243.
49. L. B. Sagle, Y. Zhang, V. A. Litosh, X. Chen, Y. Cho and P. S. Cremer, J. Am. Chem. Soc., 2009, 131, 9304–9310.

---