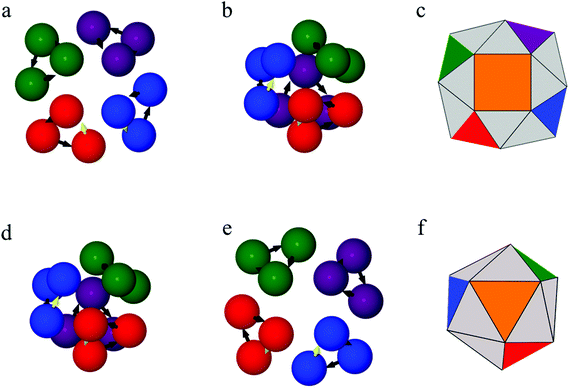Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Supracolloidal reconfigurable polyhedra via hierarchical self-assembly†
Daniel
Morphew
and
Dwaipayan
Chakrabarti
 *
*
School of Chemistry, University of Birmingham, Edgbaston, Birmingham B15 2TT, UK. E-mail: d.chakrabarti@bham.ac.uk
First published on 18th November 2016
Abstract
Enclosed three-dimensional structures with hollow interiors have been attractive targets for the self-assembly of building blocks across different length scales. Colloidal self-assembly, in particular, has enormous potential as a bottom-up means of structure fabrication exploiting a priori designed building blocks because of the scope for tuning interparticle interactions. Here we use computer simulation study to demonstrate the self-assembly of designer charge-stabilised colloidal magnetic particles into a series of supracolloidal polyhedra, each displaying a remarkable two-level structural hierarchy. The parameter space for design supports thermodynamically stable polyhedra of very different morphologies, namely tubular and hollow spheroidal structures, involving the formation of subunits of four-fold and three-fold rotational symmetry, respectively. The spheroidal polyhedra are chiral, despite having a high degree of rotational symmetry. The dominant pathways for self-assembly into these polyhedra reveal two distinct mechanisms – a growth mechanism via sequential attachment of the subunits for a tubular structure and a staged or hierarchical pathway for a spheroidal polyhedron. These supracolloidal architectures open up in response to an external magnetic field. Our results suggest design rules for synthetic reconfigurable containers at the microscale exploiting a hierarchical self-assembly scheme.
1 Introduction
Self-assembly of colloidal particles offers a low-cost, scalable route to the bottom-up fabrication of three-dimensional structures because of the scope for tuning interparticle interactions.1 Recent years have seen remarkable progress in the synthesis of a wide variety of complex colloidal particles,2–4 which interact via a multitude of forces.5 Thanks to this progress, hierarchical self-assembly for synthetic anisotropic colloidal building blocks, though still at an early stage of exploration, promises to open up routes to structural complexity at an unprecedented level.6–8 While examples of structural hierarchies in nature are abundant,9 encoding structural hierarchy for man-made functional materials has been elusive. This multiscale design problem faces a significant challenge to overcome any kinetic traps that may arise, especially in the presence of relatively strong interactions between anisotropic colloidal building blocks in certain directions.7 Understanding the pathways for hierarchical self-assembly is thus crucial to mitigate this challenge.10,11Hollow structures find a myriad of practical applications predominantly for their ability to encapsulate guests and thus have been targets for self-assembly at different length scales.12–16 We recently explored a biomimetic design route to hollow spheroidal structures at the microscale,7 drawing inspiration from the intricate self-assembly of spheroidal shells with icosahedral symmetry observed for many viral capsids in the realm of nature.17 These spheroidal shells exhibit a spectacular structural hierarchy, where the surface curvature emerges from the edge-sharing of polygons, as in the so-called Platonic and Archimedean solids.18 Our approach to produce hollow spheroidal structures exploited designer colloidal magnetic particles, which, for size-selected clusters, formed thermodynamically stable polyhedra: a polyhedron of octahedral symmetry, topologically equivalent to the snub cube, for N = 24 particles and a polyhedron of icosahedral symmetry, topologically equivalent to the snub dodecahedron, for N = 60. In a remarkable display of structural hierarchy, the colloidal magnetic particles formed uniform triangular subunits at an intermediate level, while the ordered arrangement of these planar trimers at the next level resulted in the formation of each of these polyhedra with emergent faces.7 It is relevant to note here that the snub cube and snub dodecahedron are the only two Archimedean solids, which are chiral, despite having a high degree of rotational symmetry.18 Together with the snub tetrahedron, they complete the set of convex snub polyhedra.18 See Table S1 in the ESI† for some geometric features of this set of polyhedra.
Our designer building blocks, which included a permanent point-dipole shifted away from the centre,7 closely resemble the micron-sized colloidal magnetic particles, synthesised using a single-domain hematite cube inclusion underneath the surface of an organosilica polymer sphere.19 When the range of the electrostatic repulsion between these colloidal particles was reduced by modulating the salt concentration of the medium, the particles were indeed found to form planar trimers. However, the direction of the dipole moment within the magnetic cube was not known with certainty in this experimental system.20 In the building blocks that we considered the point-dipole was directed radially outward and thus the building blocks were cylindrically symmetric.7 In fact, magnetic particles with off-centred dipoles have drawn special interest in computer simulation studies,7,20–23 relevant to the synthesis of a variety of exotic colloidal magnetic particles in recent years.19,24–26
As captured by our designer colloidal magnetic particles,7 the trimers were the dominant structural motifs in the experimental study by Sacanna et al.19 However, the formation of tetramers was also occasionally observed in this experimental system.27 In this context, a relevant question is whether we can design structural hierarchy with tetramers at the intermediate level. Another particularly pertinent question relates to the mechanism of self-assembly when it results in structural hierarchy at multiple levels. These questions provided the motivation for the present contribution, where we also intended to examine the possibility of encoding self-assembly of designer colloidal magnetic particles into the snub tetrahedron or its topological equivalent. In relation to the mechanism of hierarchical self-assembly, we intended to investigate, in particular, whether or not the emergence of structural hierarchy at multiple levels involves hierarchical pathways, i.e. proceeds in stages.28
In order to address these questions, we employed a sophisticated structure prediction tool, a rare-event simulation technique and a Monte Carlo simulation method. Here we demonstrate the self-assembly of designer charge-stabilised colloidal magnetic particles with off-centred dipoles into a series of reconfigurable supracolloidal polyhedra and elucidate distinct kinetic pathways for self-assembly into two of these polyhedra of very different morphologies. These polyhedra each display a remarkable two-level structural hierarchy involving either a tetramer or a trimer at the intermediate level. The rest of this paper is organised as follows. Section 2 describes the model and methods before the results are presented with discussion in Section 3. Finally, the concluding section presents a summary with an outlook.
2 Model and methods
2.1 Model
We employed the widely-used one-component description for our colloidal system with an effective potential. The spherical magnetic particles that we considered in this study interact with each other via the Yukawa potential describing the screened electrostatic repulsion that offers the charge-stabilisation. The magnetic interactions are described within a point-dipole approximation; a permanent point-dipole is placed away from the centre of the spherical core in a rigid framework. The potential energy V for a cluster of N charge-stabilised colloidal magnetic particles in the presence of a magnetic field is then given by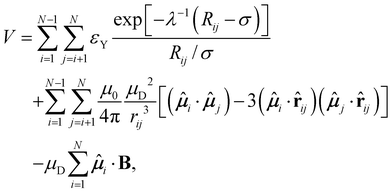 | (1) |
![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) i is the unit vector defining the direction of the dipole moment of the latter, whose magnitude is μD, μ0 is the permeability of free space, and rij is the separation vector: rij = ri − rj with magnitude rij, so that the unit vector
i is the unit vector defining the direction of the dipole moment of the latter, whose magnitude is μD, μ0 is the permeability of free space, and rij is the separation vector: rij = ri − rj with magnitude rij, so that the unit vector ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij = rij/rij. In the Yukawa description of screened electrostatic repulsion, λ−1 is the inverse Debye screening length and εY is the so-called contact potential. The units of energy and length are chosen as the Yukawa parameters εY and σ, respectively. The direction of the external field B = (0,0,B), when applied, was held fixed along the z-axis of the space-fixed frame. The magnetic dipole μD is given in reduced units of (4πεYσ3/μ0)1/2 and the magnetic field strength B is in [εYμ0/(4πσ3)]1/2. The model parameters are then the inverse Debye screening length λ−1, the strength of the dipole μD, the separation d between the location of the point-dipole and the centre of the particle, the angle θ between the direction of the dipole moment
ij = rij/rij. In the Yukawa description of screened electrostatic repulsion, λ−1 is the inverse Debye screening length and εY is the so-called contact potential. The units of energy and length are chosen as the Yukawa parameters εY and σ, respectively. The direction of the external field B = (0,0,B), when applied, was held fixed along the z-axis of the space-fixed frame. The magnetic dipole μD is given in reduced units of (4πεYσ3/μ0)1/2 and the magnetic field strength B is in [εYμ0/(4πσ3)]1/2. The model parameters are then the inverse Debye screening length λ−1, the strength of the dipole μD, the separation d between the location of the point-dipole and the centre of the particle, the angle θ between the direction of the dipole moment ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) i and the shift vector ri − Ri, and the magnetic field strength B. The shift distance is expressed in terms of a dimensionless ratio α = 2d/σ, where σ is the length scale in terms of which the Yukawa potential is defined, offering an estimate of the size of the particle in the absence of a hard core. In our previous study,7 we considered the θ = 0° case, where the point-dipole points radially outward.
i and the shift vector ri − Ri, and the magnetic field strength B. The shift distance is expressed in terms of a dimensionless ratio α = 2d/σ, where σ is the length scale in terms of which the Yukawa potential is defined, offering an estimate of the size of the particle in the absence of a hard core. In our previous study,7 we considered the θ = 0° case, where the point-dipole points radially outward.
The colloidal magnetic particles were treated as rigid bodies. The translational coordinates for the centre of the particles were represented by the Cartesian coordinates and the rotational coordinates by an angle-axis representation,29 unless specified otherwise. The gradients and the Hessian were obtained analytically whenever necessary.
2.2 Global optimisation
We used basin-hopping (BH) global optimisation method,30,31 as implemented in GlOSP,32 to characterize the putative global minimum on the potential energy landscape (PEL) for each cluster size. This method is based on a hypersurface deformation that provides a reduced configuration space spanned by local minima on the PEL without changing the energies of any of these minima.31 The reduced configuration space was explored by proposing random steps in both the rigid-body translational and rotational coordinates from the current minimum, followed by local geometry optimisation to a minimum. For geometry optimisation to a minimum, the limited-memory Broyden–Fletcher–Goldfarb–Shanno (LBFGS) algorithm was used.33 The proposed step was accepted or rejected on the basis of a Metropolis criterion, using the relative energies of the two local minima and a fictitious temperature. In this method, the step sizes are much larger than those typically used in Monte Carlo simulations of thermodynamic properties to ensure that the transformed PEL is explored efficiently. For each cluster size, five independent BH global optimisation runs were performed starting from random initial configurations and the lowest minimum found was proposed as the putative global minimum. In this study, the global minima are presented with high confidence level with 100% convergence up to N = 21. For N = 24, the tetramer with four-fold rotational symmetry, as shown in Fig. 1b, were used as a rigid building block to improve the efficiency of search. The global minimum thus obtained was relaxed for the individual colloidal magnetic particles with θ = 90° by removing the constraints.2.3 Rare-event simulation
In order to obtain kinetic pathways for structural transitions, we employed discrete path sampling (DPS),34 as implemented in the software PATHSAMPLE,35 which drives the program OPTIM.36 The DPS approach to rare-event simulation relies upon recursive use of geometry optimisation to grow a database of minima and transition states. In this method, an initial path between two selected minima, generally consisting of a series of intervening transition states and minima, is determined by repeated use of double-ended transition state searches. The doubly nudged elastic band (DNEB) algorithm37,38 is used to identify transition state candidates, which are then accurately refined using hybrid eigenvector-following techniques.39 The eigenvalue shifting technique is used for treatment of the six degrees of freedom associated with overall translation and rotation in transition state searches. The technique uses analytic expressions for the corresponding Hessian eigenvectors with zero eigenvalues. The DNEB implementation uses a discrete representation of the band in terms of a set of images, obtained by an incremental approach to quaternion interpolation algorithm Slerp.40The two minima reached by (approximate) steepest-descent paths leaving a transition state parallel and anti-parallel to the eigenvector with the unique negative eigenvalue define its connectivity. For local minimisations the limited-memory Broyden–Fletcher–Goldfarb–Shanno (LBFGS) algorithm of Liu and Nocedal is used.33,41 Discrete paths are then generated systematically from the initial connected path to grow the database by adding all the distinct minima and transition states found during successive connection-making attempts for pairs of minima selected using a missing connection algorithm.42 The addition of new stationary points to the database critically depends on reliable identification of permutation-inversion isomers. The discrete path that makes the largest contribution to the two-state rate constant within a steady-state approximation for the intervening minima is extracted from the DPS database using a network formulation43via Dijkstra's shortest-path algorithm44 by choosing suitable edge weights.34
2.4 Monte Carlo simulations
A series of Monte Carlo (MC) simulations were performed within two different constraining spherical volumes starting from five independent configurations. In a given run, the reduced temperature of the system of Ns = 4 rigid building blocks was gradually decreased. For each rigid body, the translational degrees of freedom were represented by the Cartesian coordinates of the geometric centre and a quaternion representation was used to describe the orientational degrees of freedom.45 The step sizes in both translational and orientational space were adapted to secure an average acceptance ratio of 0.45 except at relatively high reduced temperatures. At each temperature, simulations were run at least for 109 MC cycles (2 × 109 cycles at low temperatures), each of which consisted of Ns single-particle moves in both translational and orientational space; half of these cycles were used for equilibration. Here T* is the reduced temperature given by T* = kBT/εY.3 Results and discussion
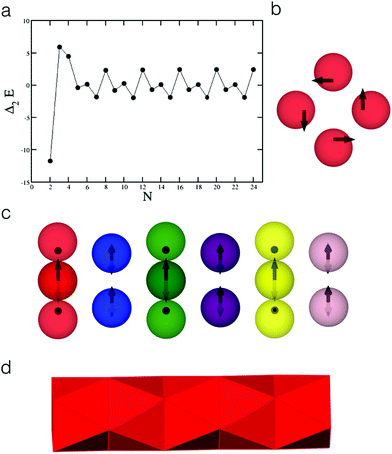
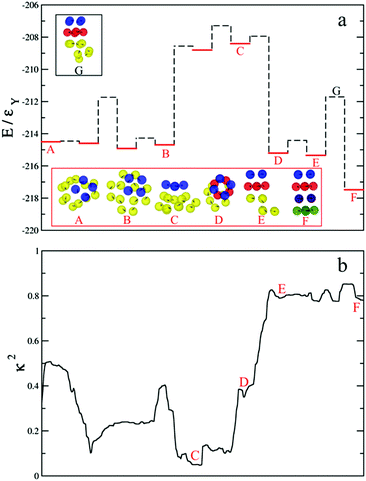
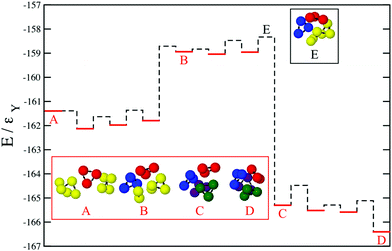
In our quest for hierarchical self-assembly via tetramers, square planar units appeared to be plausible secondary building blocks, which could support a flux-closure arrangement of dipoles, as opposed to tetrahedra. We therefore considered the θ = 90° case and varied the parameter α in particular. By employing basin-hopping global optimisation,30,31 we characterised the global minima on the PELs for clusters of these colloidal particles as the thermodynamically favoured structures especially at low reduced temperatures. Fig. 1a shows the second finite difference of the potential energy for the global minimum as a function of the cluster size N, Δ2E(N) for N = 2–24. Here Δ2E(N) = Vmin(N − 1) + Vmin(N + 1) − 2Vmin(N), where Vmin(N) is the potential energy of the global minimum for a cluster of N particles. The plot corresponds to the following set of parameters: θ = 90°, α = 0.3, μD = 2 and λ−1 = 25. The plot features pronounced peaks for certain values of N, indicating especially stable structures for the corresponding cluster sizes. It is then evident that the structures for the cluster sizes, which are integer multiples of 4, are especially stable. This could be a sign of structural hierarchy, which was indeed confirmed by the inspection of the structures. Fig. 1b exhibits the 4-particle global minimum for the aforementioned parameter set. The global minimum in this case is indeed a square planar unit, stabilised by the dipoles arranged in a flux closure state. The disposition to form tetrameric subunits continued with increasing N. These square planar subunits stack on top of each other to form a tubular structure in a striking display of structural hierarchy as evident in Fig. 1c for N = 24. As N increases in integer multiples of 4, the number of square planar subunits grows resulting in an increase in the length of the tube and the global minima are of D4d symmetry. The polyhedral representation in Fig. 1d shows the triangular faces that are emergent from this hierarchical self-assembly and clearly demonstrates the anti-prismatic arrangement.We characterised a dominant pathway for the self-assembly into the tubular structure for N = 16 by employing discrete path sampling approach to rare event simulation.29,34,46 The energy profile of the dominant pathway for the self-assembly starting from a high-energy, relatively disordered minimum that we obtained in this case is shown in Fig. 2a; see Movie 1 in the ESI† for the complete pathway. This pathway involves the formation of the square planar units as the secondary building blocks and demonstrates that as the square planar subunits are formed, they attach to a growing tubular structural motif practically one by one (D, E and F in Fig. 2a). These subunits are stabilised by the dipoles in a flux-closure state; the transformation from E to F involves a relatively high energy barrier due to the reorganisation of the dipoles within the final two subunits to attain the flux-closure state. Thus the main feature for this pathway for hierarchical self-assembly is that the assembly at both the levels proceed simultaneously to eventually produce a two-level structural hierarchy. The relative shape anisotropy parameter κ2 for a cluster, bounded between 0 and 1, provides an estimate of its shape anisotropy.47κ2 = 0 for a spherically symmetric distribution and κ2 = 1 for a perfectly linear arrangement. The evolution of κ2 along the self-assembly pathway into the tubular structure, shown in Fig. 2b, highlights the progressive increase in κ2 with the quasi one-dimensional growth caused by the sequential attachment of the tetrameric subunits to the tubular motif as they are formed.
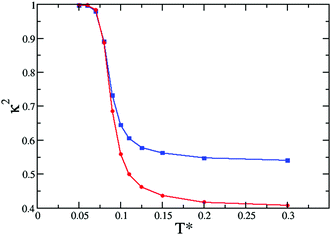
In order to assess whether the thermodynamically stable tubular structure is kinetically accessible and is thus likely to be self-assembled under appropriate experimental conditions, we carried out Monte Carlo simulations wherein the reduced temperature T* was gradually reduced from a finite value. Since the pathway, shown Fig. 2a, suggests that the hierarchical self-assembly into the tubular structure is most likely to proceed via the formation of the square planar units, Monte Carlo simulations were performed with the secondary building blocks, shown in Fig. 1b, modelled as rigid units. Such an approach allowed single-particle moves to be used effectively in a multiscale problem. Fig. 3 shows the evolution of the parameter κ2 as a function of the reduced temperature; the gradual growth of κ2 to unity indicates the formation of increasingly quasi one-dimensional structure. Note that for a perfectly tubular structure, the centres of the rigid secondary building blocks are co-linear, for which κ2 = 1.
We next sought the design rule for the snub tetrahedron, the smallest member of the set of convex snub polyhedra. In our quest for the snub tetrahedron, we focused on the cluster of N = 12 cylindrically symmetric (i.e. θ = 0°) colloidal magnetic particles. While the global minimum on the PEL is a bowl structure (Fig. 4a), we identified a spheroidal structure that is topologically equivalent to the snub tetrahedron as a low-lying minimum (Fig. 4b). Both of these structures exhibit a two-level structural hierarchy, where planar triangular subunits stabilised by a flux-closure arrangement of the point-dipoles serve as secondary building blocks (vide Fig. S1 in the ESI†). It is the organisation of these secondary building blocks that results in an open or a closed structure. Analysis of the energetics for these structures reveals that a nearly anti-parallel arrangement of the dipoles in neighboring secondary building blocks is energetically favoured (representative examples are shown in Fig. 4a, b and also in Fig. S2 in the ESI† for clarity) and is a key factor in determining the low energy structures. Such interactions, though fewer in number for the bowl structure compared to the spheroidal structure, are of sufficient strength to make the bowl structure the global minimum on the PEL. The angle ϕ between the dipoles for such pairs is closer to the perfect anti-parallel arrangement in the bowl structure (see Table S2 in the ESI†).
The above analysis led us to vary the parameter θ for our designer building blocks and investigate the structures and energetics. This choice also appeals in the context of the uncertainty in the direction of the dipole moment within the magnetic cube used in the synthesis of colloidal magnetic particles reported in ref. 19. For θ = 10°, the propensity for hierarchical self-assembly was retained with the triangular subunits in the flux-closure arrangement formed at the first level of organisation. In fact, the triangular subunit is more stable when θ = 10° as compared to θ = 0° due to a decrease in the separation between the dipoles within the subunit. For N = 12, we indeed find the global minimum to be a spheroidal structure (Fig. 4d) that is topologically equivalent to the snub tetrahedron as evident in Fig. 4f. Note that it is chiral with tetrahedral symmetry. In this case, the interactions between the dipoles in the anti-parallel arrangements in neighbouring secondary building blocks are sufficient in strength in the spheroidal structure, though they are still weaker than those in the bowl structure (Fig. 4e), to stabilize the spheroidal structure, and in fact, cause it to be the global minimum on the PEL. The details of the energetics are given in Table S3 in the ESI.†
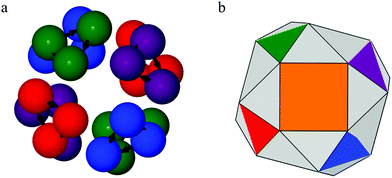
It was then relevant to investigate whether the designer colloidal magnetic particles with θ = 10° formed the other two convex snub polyhedra for appropriate size selected clusters. To this end, we considered N = 24 and N = 60. In the case of N = 24, the ground state structure for the cluster is indeed a convex polyhedron of octahedral (O) symmetry, displaying two-level structural hierarchy, as shown in Fig. 5. This polyhedron is composed of 32 triangular faces and 6 square faces and is topologically equivalent to the snub cube, a chiral Archimedean solid. Eight of the triangular faces (shown in distinct colors) originate from the colloidal particles forming triangular subunits of three-fold rotational symmetry. The other triangular faces (shown in light gray) and the square faces (shown in orange) emerge from the hierarchical self-assembly of these triangular subunits. The emergent triangular faces have slightly different edge lengths, making the polyhedron topologically equivalent to the snub cube. In the case of N = 60, however, we have not observed such a spheroidal structure to be the ground state. A polyhedron topologically equivalent to the snub dodecahedron and thus of icosahedral symmetry would have an emergent face of five-fold symmetry. For our designer colloidal magnetic particles with θ = 10°, we have found that for N = 15 a bowl structure with such an emergent face is not the global minimum. Instead, the global minimum in this case corresponds to a configuration, containing a polyhedron that is topologically equivalent to the snub tetrahedron plus an additional trimeric subunit (vide Fig. S3 in the ESI†). This is in line with our observation for N = 60.
Finally, we characterised the dominant pathway to the hollow spheroidal structure of tetrahedral symmetry, topologically equivalent to the snub tetrahedron, as shown in Fig. 4d. It was of interest to compare pathways to two distinct polyhedra that both exhibit two-level structural hierarchies with different types of subunits formed at the intermediate level.7Fig. 6 shows the energy profile of the dominant pathway that we have obtained for the self-assembly to the spheroidal structure, which is the smallest in this series, starting from a relatively high-energy, disordered minimum. The complete self-assembly pathway is shown in Movie 2 in the ESI.† This self-assembly pathway suggests that the pathway is hierarchical, where the two-level organisation proceeds stage-wise. In the first stage, trimers stabilised by the arrangement of dipoles in a flux-closure state are formed. These trimers act as the secondary building blocks for the subsequent stage and the next level of assembly is driven by the stability arising from the anti-parallel arrangements of the dipoles between the secondary building blocks. Through the second stage of assembly the trimers retain their integrity, invoking a high degree of cooperativity. The energy barriers involved in the second stage of assembly are therefore relatively low. However, the element of cooperativity is likely to result in relatively high entropy costs in the free-energy barriers.
When subjected to an external magnetic field, the tubular structures collapse above a threshold field. For example, the ground state structure for the N = 16 cluster with θ = 90° was found to be a zig-zag chain, where the dipoles are parallel to the field direction, as shown in Fig. 7. For a nonzero value of θ, such a zig-zag configuration is favoured over a linear configuration by the dipolar interactions due to a smaller separation between the adjacent point-dipoles in the former case. The structures can thus be reconfigured by the application of an external magnetic field above a threshold. The ability to reconfigure an enclosed structure is especially attractive when it is hollow and spheroidal for the design of responsive containers that can encapsulate guests and release them on demand.
The colloidal magnetic particles we have considered in the present study are in close correspondence with the colloidal magnetic particles, synthesised using iron oxide inclusions located underneath the surface of organosilica polymer spheres.19 Reasonable estimates for the parameters can be obtained in real units by using εY = 4.1 × 10−21 J (of the order of kBT at room temperature) and σ = 10−6 m. Corresponding to these values, we have in real units μD ∼ 4 × 10−16 A m2, B ∼ 2 × 10−4 T, and λ = 40 nm, all well within the experimentally accessible regime.19 The control of the colloidal charge number allows for the value of the Yukawa contact potential εY to be modulated by an order of magnitude.48
4 Conclusions
The present computer simulation study has identified a series of polyhedra as the ground state structures for size-selected clusters of designer charge-stabilised colloidal magnetic particles, each with an embedded point-dipole at an off-centred location. In particular, we have identified square anti-prismatic tubular structures and spheroidal polyhedra as the ground state structures for the design space that we investigated. A remarkable feature of these supracolloidal polyhedra of distinct morphologies is that they all exhibit two-level structural hierarchies, via either tetramers or trimers in the intermediate level. The subunits formed at the intermediate level have the dipoles in flux-closure arrangements in either case. The shift of the dipole relative to the centre, described by the parameter α, and the angle θ between the dipole vector and the radial shift vector are the two critical parameters that determine whether these subunits have four-fold or three-fold rotational symmetry and hence the overall morphology. We have thus been able to design structural hierarchies via tetramers in a controlled way.In our quest for the snub tetrahedron, we have found the angle θ to be a critical parameter to determine the stability of a topological variant of the snub tetrahedron relative to the bowl structure on the PEL. In particular, for θ = 10°, we observed the ground state structures, which are topologically equivalent to the snub tetrahedron (N = 12) and the snub cube (N = 24), two of the three convex snub polyhedra that exist. The third member of this set is the snub dodecahedron, which is of icosahedral symmetry; for N = 60, we observed the ground state structure that is topologically equivalent to the snub dodecahedron in the case of θ = 0°, but not for θ = 10°. On the other hand, for θ = 0°, a snub polyhedral structure (topologically equivalent) is also the ground state structure for N = 24, but not for N = 12. It is important to note here that the internal angle for the emergent regular faces in this series of topologically equivalent snub polyhedra varies from 60° to 108° from the snub tetrahedron to the snub dodecahedron. It is plausible that this angular range is too wide for these emergent faces be supported by our designer colloidal magnetic particles for a single value of θ for these polyhedra to be the ground state structures for appropriate size-selected clusters. Another striking feature is that the spheroidal polyhedra, which are formed via the formation of triangular subunits at the intermediate level, are chiral, despite having a high degree of rotational symmetry.
It is intriguing that the dominant kinetic pathways, which we characterised for the self-assembly into two distinct supracolloidal polyhedra, present very different mechanisms for emergent two-level structural hierarchies, presumably due to the distinct morphologies of these polyhedra. These pathways provide especially distinct routes depending upon whether organisation at different levels proceeds simultaneously or sequentially. In the former case, higher-order building blocks are formed one by one and attach to a growing structural motif corresponding to the next level of organisation; in the latter, higher-order building blocks are all formed before the next level of organisation proceeds.28 The spheroidal structures can be underpinned by only certain numbers of triangular subunits commensurate with closed shells. In contrast, the square planar subunits, which serve as the secondary building blocks, can directly stack up to form the tubular structures. It is likely that these structural features of the assemblages resulted in the distinct mechanisms that we observed. The formation of the spheroidal structure proceeds via a hierarchical pathway where the requisite number of triangular subunits are produced in the first stage before the organisation of these secondary building blocks takes place. The tubular structure is instead formed via a growth mechanism involving sequential attachment of the secondary building blocks as they are formed. It is noteworthy that cooperative particle dynamics are crucial for the hierarchical pathway, and the corresponding free-energy barrier is likely to have a considerable entropy contribution. The mechanistic understanding of the self-assembly pathways will be critical to our ability to effectively control these dynamical pathways.10,11
These supracolloidal polyhedra can serve as microscale containers, the practical applications of which primarily arise from their ability to encapsulate guests. Our results demonstrate a feasible design space for the experimental realisation of such 3-dimensional hollow structures, exploiting a hierarchical self-assembly scheme. Additionally, we provide possible guidelines for controlling the morphology in terms of the two parameters α and θ, in particular. The responsiveness of these containers to an applied magnetic field is a particularly attractive feature that allows these containers to be opened and closed on demand. The spheroidal polyhedra that we characterised offer confined space enclosed by well-defined facets in a chiral environment, extending the features of metal–organic frameworks to the microscale,12,49 and are thus likely to offer a further range of potential applications in catalysis and separation.50 For these applications, the ability to select the size of the cluster will be especially crucial.
We thank Dr Stefano Sacanna for stimulating discussions. This work was supported by the Engineering and Physical Sciences Research Council of the UK and the University of Birmingham.
References
- G. M. Whitesides and M. Boncheva, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 4769–4774 CrossRef CAS.
- S. C. Glotzer and M. J. Solomon, Nat. Mater., 2007, 6, 557–562 CrossRef PubMed.
- F. Li, D. P. Josephson and A. Stein, Angew. Chem., Int. Ed., 2011, 50, 360–388 CrossRef CAS PubMed.
- S. Sacanna, M. Korpics, K. Rodriguez, L. Colón-Meléndez, S.-H. Kim, D. Pine and G.-R. Yi, Nat. Commun., 1688, 2013, 4 Search PubMed.
- Y. Min, M. Akbulut, K. Kristiansen, Y. Golan and J. Israelachvili, Nat. Mater., 2008, 7, 527–538 CrossRef PubMed.
- K. Miszta, J. de Graaf, G. Bertoni, D. Dorfs, R. Brescia, S. Marras, L. Ceseracciu, R. Cingolani, R. van Roij, M. Dijkstra and L. Manna, Nat. Mater., 2011, 10, 872–876 CrossRef CAS PubMed.
- D. Morphew and D. Chakrabarti, Nanoscale, 2015, 7, 8343–8350 RSC.
- J. Zhang, E. Luijten and S. Granick, Annu. Rev. Phys. Chem., 2015, 66, 581–600 CrossRef CAS PubMed.
- P. Fratzl and R. Weinkamer, Prog. Mater. Sci., 2007, 52, 1263–1334 CrossRef CAS.
- S. Whitelam and R. L. Jack, Annu. Rev. Phys. Chem., 2015, 66, 143 CrossRef CAS PubMed.
- W. M. Jacobs and D. Frenkel, J. Am. Chem. Soc., 2016, 138, 2457–2467 CrossRef CAS PubMed.
- L. R. MacGillivray and J. L. Atwood, Angew., Chem. Int. Ed., 1999, 38, 1018–1033 CrossRef CAS.
- A. D. Dinsmore, M. F. Hsu, M. G. Nikolaides, M. Marquez, A. R. Bausch and D. A. Weitz, Science, 2002, 298, 1006–1009 CrossRef CAS PubMed.
- Y. He, T. Ye, M. Su, C. Zhang, A. E. Ribbe, W. Jiang and C. Mao, Nature, 2008, 452, 198–201 CrossRef CAS PubMed.
- C. H. J. Evers, J. A. Luiken, P. G. Bolhuis and W. K. Kegel, Nature, 2016, 534, 364–368 CrossRef PubMed.
- Y. Hsia, J. B. Bale, S. Gonen, D. Shi, W. Sheffler, K. K. Fong, U. Nattermann, C. Xu, P.-S. Huang, R. Ravichandran, S. Yi, T. N. Davis, T. Gonen, N. P. King and D. Baker, Nature, 2016, 535, 136–139 CrossRef CAS PubMed.
- D. L. Caspar and A. Klug, Cold Spring Harbor Symp. Quant. Biol., 1962, 27, 1–24 CrossRef CAS PubMed.
- P. R. Cromwell, Polyhedra, Cambridge University Press, Cambridge, 1997 Search PubMed.
- S. Sacanna, L. Rossi and D. J. Pine, J. Am. Chem. Soc., 2012, 134, 6112–6115 CrossRef CAS PubMed.
- A. A. Abrikosov, S. Sacanna, A. P. Philipse and P. Linse, Soft Matter, 2013, 9, 8904–8913 RSC.
- S. Kantorovich, R. Weeber, J. J. Cerda and C. Holm, Soft Matter, 2011, 7, 5217–5227 RSC.
- M. Klinkigt, R. Weeber, S. Kantorovich and C. Holm, Soft Matter, 2013, 9, 3535–3546 RSC.
- A. B. Yener and S. H. L. Klapp, Soft Matter, 2016, 12, 2066–2075 RSC.
- L. Baraban, et al. , Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 031407 CrossRef PubMed.
- S. K. Smoukov, S. Gangwal, M. Marquezbc and O. D. Velev, Soft Matter, 2009, 5, 1285–1292 RSC.
- J. Yan, S. C. Bae and S. Granick, Adv. Mater., 2015, 27, 874–879 CrossRef CAS PubMed.
- S. Sacanna, Private Communication, 2016.
- T. K. Haxton and S. Whitelam, Soft Matter, 2013, 9, 6851–6861 RSC.
- D. Chakrabarti and D. J. Wales, Phys. Chem. Chem. Phys., 2009, 11, 1970–1976 RSC.
- Z. Li and H. A. Scheraga, Proc. Natl. Acad. Sci. U. S. A., 1987, 84, 6611–6615 CrossRef CAS.
- D. J. Wales and J. P. K. Doye, J. Phys. Chem. A, 1997, 111, 5111–5116 CrossRef.
- D. Chakrabarti, GlOSP: A program for global optimisation for structure prediction, 2015 Search PubMed.
- D. Liu and J. Nocedal, Mathematical Programming, 1989, 45, 503–528 CrossRef.
- D. J. Wales, Mol. Phys., 2002, 100, 3285–3306 CrossRef CAS.
- D. J. Wales, http://www-wales.ch.cam.ac.uk/PATHSAMPLE, PATHSAMPLE: A driver for OPTIM to create stationary point databases using discrete path sampling and perform kinetic analysis.
- D. J. Wales, http://www-wales.ch.cam.ac.uk/OPTIM/, OPTIM: A program for optimising geometries and calculating reaction pathways.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 1999, 111, 7010–7022 CrossRef CAS.
- S. A. Trygubenko and D. J. Wales, J. Chem. Phys., 2004, 120, 2082–2094 CrossRef CAS PubMed.
- L. J. Munro and D. J. Wales, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 3969–3980 CrossRef CAS.
- X. Li, Journal of Graphics, GPU, and Game Tools, 2007, 12, 1–6 CrossRef.
- J. Nocedal, Math. Comput., 1980, 35, 773–782 CrossRef.
- J. M. Carr and D. J. Wales, J. Phys. Chem. B, 2008, 112, 8760–8769 CrossRef CAS PubMed.
- D. A. Evans and D. J. Wales, J. Chem. Phys., 2004, 121, 1080–1090 CrossRef CAS PubMed.
- E. W. Dijkstra, Numerische Mathematlk, 1959, 1, 269–271 CrossRef.
- J.-Y. Trosset and H. A. Scheraga, J. Comput. Phys., 1999, 20, 412–427 CAS.
- D. Chakrabarti, H. Kusumaatmaja, V. Rühle and D. J. Wales, Phys. Chem. Chem. Phys., 2014, 16, 5014–5025 RSC.
- D. N. Theodorou and U. W. Suter, Macromolecules, 1985, 18, 1206–1214 CrossRef CAS.
- A.-P. Hynninen and M. Dijkstra, Phys. Rev. Lett., 2005, 94, 138303 CrossRef PubMed.
- Y. Inokuma, M. Kawano and M. Fujita, Nat. Chem., 2011, 3, 349–358 CrossRef CAS PubMed.
- N. Yanai and S. Granick, Angew. Chem., Int. Ed., 2012, 51, 5638–5641 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Supplementary figures are provided along with movies for pathways. See DOI: 10.1039/c6sm01615d |
| This journal is © The Royal Society of Chemistry 2016 |