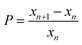Open Access Article
Open Access ArticleProbing the mystery of Liesegang band formation: revealing the origin of self-organized dual-frequency micro and nanoparticle arrays†
Rita
Tóth
*a,
Roché M.
Walliser
b,
István
Lagzi
c,
Florent
Boudoire
ab,
Marcel
Düggelin
b,
Artur
Braun
 a,
Catherine E.
Housecroft
b and
Edwin C.
Constable
b
a,
Catherine E.
Housecroft
b and
Edwin C.
Constable
b
aLaboratory for High Performance Ceramics, Empa, Swiss Federal Laboratories for Materials Science and Technology, 8600, Überlandstrasse 129, Dübendorf, Switzerland. E-mail: Rita.Toth@empa.ch; ritatoth1113@gmail.com
bDepartment of Chemistry, University of Basel, Spitalstrasse 51, 4056 Basel, Switzerland
cDepartment of Physics, Budapest University of Technology and Economics, 1111, Budafoki út 8, Budapest, Hungary
First published on 2nd September 2016
Abstract
Periodic precipitation processes in gels can result in impressive micro- and nanostructured patterns known as periodic precipitation (or Liesegang bands). Under certain conditions, the silver nitrate–chromium(VI) system exhibits the coexistence of two kinds of Liesegang bands with different frequencies. We now present that the two kinds of bands form independently on different time scales and the pH-dependent chromate(VI)–dichromate(VI) equilibrium controls the formation of the precipitates. We determined the spatial distribution and constitution of the particles in the bands using focused ion beam-scanning electron microscopy (FIB-SEM) and scanning transmission X-ray spectromicroscopy (STXM) measurements. This provided the necessary empirical input data to formulate a model for the pattern formation; a model that quantitatively reproduces the experimental observations. Understanding the pattern-forming process at the molecular level enables us to tailor the size and the shape of the bands, which, in turn, can lead to new functional architectures for a range of applications.
Introduction
Periodic precipitation (or Liesegang phenomenon)1–4 is a manifestation of self-organization controlled by the diffusion and reaction of two or more chemical species resulting in a visually impressive periodic precipitation pattern5 due to the non-equilibrium nature of the thermodynamic processes involved. These reactions do not follow the traditional chemical kinetics tendency, i.e. they do not reach equilibrium by the shortest path, and they have even been considered as the precursors of life processes.6 Remarkably, this pattern also has a “quantum property” since from its macroscopic parameters, such as the molecular weight of the precipitate product (M), the “speed of diffusion” (ν) and the periodicity of the pattern (λ) the value of Planck's constant (h) can be obtained.7 Liesegang pattern formation has gained recent attention as it allows the assembly of meso- and micro-structured architectures.1–4,8 Solution processing offers a viable alternative to epitaxial methods for the preparation of hierarchical materials, and bottom-up approaches offer the promise of engineering heterogeneous micro- and nanostructured materials by the self-assembly or self-organization of molecular building blocks.1,2 These periodic precipitation processes typically occur in gels, which prevent both the sedimentation of colloids and hydrodynamic instabilities that might destroy chemical structures. Typically, one ionic component (the inner electrolyte) is placed in the gel and the second component (the outer electrolyte) diffuses from a solution or another gel; pattern formation is then driven by a diffusively propagating chemical front. Depending on the gel structure and the geometry of the system, a variety of patterns can be observed including regular Liesegang bands, revert type bands, dendrites with fractal structure, dynamic precipitation waves and the coexistence of the so-called primary and secondary patterns.9–14 In the latter structure, two types of patterns are superimposed with different frequencies in the classical AgNO3/K2Cr2O7/gelatin system.14 Interestingly, a similar dual-frequency structure was also found in PbCrO4 Liesegang bands that obey the revert spacing law.13 No study has yet been published which provides experimental evidence and a mechanism for the formation of such patterns. For the rational design of these dual-frequency microstructures, it is essential to understand their physico-chemical origin and the factors controlling their frequency. This paper describes experimental investigations of the formation mechanism of the precipitate patterns in the AgNO3/K2Cr2O7/gelatin system and we show that the two kinds of patterns form on different time scales independent of each other; the chromate–dichromate equilibrium governs the precipitate formation. We reveal the chemical composition of the bands using scanning transmission X-ray spectro-microscopy, and we demonstrate the spatial distribution of the precipitate particles inside the bands using focused ion beam scanning electron microscopy (FIB-SEM). In addition, we show that the number and the type of the bands can easily be tailored by the pH of the system. To support our concept, we have developed a model containing the chromate–dichromate equilibrium along with the precipitation reactions and the results are in very good agreement with the experimental findings.We selected the AgNO3/K2Cr2O7/gelatin system because this is the oldest traditional Liesegang system. In addition, silver dichromate finds some application as an oxidation catalyst15 and we envisaged the potential for the self-assembly of electrocatalytic microreactors.
Results and discussion
Precipitate bands were obtained by a stamping method14 in which an agarose gel stamp loaded with AgNO3 was placed onto a gelatin film containing K2Cr2O7 along with varying concentrations of aqueous NH4OH. The AgNO3 from the stamp diffuses into the gelatin and forms micro- and nanoparticle precipitate bands centered around the stamp contact. Under certain conditions, two types of precipitate bands are superimposed in the pattern: fairly wide bands (height: 1.2–25 μm, width: 10–40 μm) with a relatively large wavelength (spacing: 10–90 μm) and thin, densely packed bands (height: 30–200 nm, width: 1–3 μm, spacing 1–2 μm) (Fig. 1). | ||
| Fig. 1 SEM micrograph of a typical dual-frequency precipitate pattern in the AgNO3/K2Cr2O7/gelatin system. | ||
The focus of this paper is to understand why and how the two kinds of precipitate bands form in the classical AgNO3–K2Cr2O7 system. Since this is the prototypical Liesegang system, a deeper understanding of the dual-frequency pattern formation in this system will enable the design of these complex precipitate bands in other chemical systems.
To investigate the constitution of the bands, quantitative chemical information with a spatial resolution below 100 nm is required. Since the bands are composed of mesoscopic particles, XRD for phase analysis can be ruled out. We used scanning transmission X-ray spectromicroscopy (STXM), which provides detailed spectroscopic information at high spatial resolution. STXM can spatially map the electronic structure and the chemical state of the pattern by near-edge X-ray absorption fine structure (NEXAFS) spectroscopy.16–19
Spectroscopic investigations
STXM micrographs of the dual-frequency pattern formed in 400–500 nm thin gelatin films spin-coated onto 200 nm thin silicon nitride membranes were acquired over length scales from 250 μm to 20 nm at energies covering the chromium L2,3-edges (corresponding to 2p1/2 and 2p3/2 atomic orbitals), the oxygen K1-edge (1s) and the silver M4,5-edges (3d3/2 and 3d5/2). STXM micrographs at the Cr L3-edge (2p3/2, 576.2 eV) together with a 3D laser scanning micrograph of the pattern clearly show the high frequency bands in and also between the large bands (Fig. 2).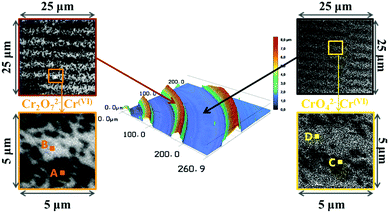 | ||
| Fig. 2 Liesegang precipitation bands formed in a ∼500 nm thin gelatin film. In the middle: 3D laser scanning micrograph of the periodic bands and its surrounding area. Left side: STXM micrographs of the fine detail of bands (top: 125 nm pixels, bottom: 50 nm pixels). Right side: STXM micrographs of the fine detail of the area between two bands (top: 125 nm pixels, bottom: 50 nm pixels). The STXM micrographs were measured at 576.2 eV, corresponding to absorption by Cr. A–D shows the positions where STXM spectra were recorded (Fig. 3). | ||
Fig. 3 shows the average of 100 spectra (100 × 20 nm × 20 nm areas) at positions A, B, C and D of a dual-frequency pattern shown in Fig. 2, on a band of a pattern which contains only large bands (E), as well as the spectra of reference materials (gelatin, K2Cr2O7, K2CrO4, Cr2O3, Ag and AgNO3). The Cr L3,2 spectra present two sets of features in the L3 region (570–579 eV) and the L2 region (580–590 eV) (Fig. 3a). The strong similarity between spectra A, E and the reference Cr(VI) spectrum20 confirms that in the precipitation bands, chromium is present as Cr(VI). In spectra B and C, the L2 peak (∼584 eV) is shifted slightly to lower energy and resembles the Cr(III) reference spectrum20,21 indicating that the area between the large bands contains Cr(III). It is worth noting that the X-ray beam contains some spectral contamination from Cr(III), which is present in the synchrotron beamline optics. In addition, the gelatin could act as a reducing agent and generate some Cr(III). We conclude that the precipitate contains Cr(VI) but when very small amounts of precipitate are present, the signature of Cr(III) from the aforementioned source becomes spectrally prevalent.
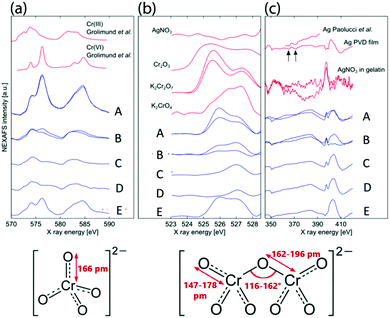 | ||
| Fig. 3 STXM spectra. (a) Cr L3,2 edges, (b) O K edge and (c) Ag M edge average spectra (blue curves) of 10 square areas of 20 nm × 20 nm on the fine structure of a large band (A), background between the fine structure in the band (B), on the fine structure between bands (C) and background where no precipitation occurred (D). Spectra E were taken on a band in a pattern which only contained the large bands. As references (red curves) for (a) we added Cr(III) and Cr(VI) spectra from ref. 20, for (b) we acquired K2Cr2O7, K2CrO4 and AgNO3 spectra and used Cr2O3 spectrum from ref. 21. For references for the silver edge spectra (c) we used AgNO3 in a gelatin film, our physical vapor deposited Ag film and a polycrystalline Ag sample.22 Structural properties of the chromate and dichromate anions were taken from ref. 23. | ||
This, however, does not yet reveal whether the bands contain chromate or dichromate ion. Both chromate and dichromate contain Cr(VI), but the bond lengths and angles about the Cr in the dichromate ion vary to a certain extent (Fig. 3). Fig. 3b shows the oxygen 1s spectra of the abovementioned regions. In spectra A, B and E, the two peaks suggest that the precipitate in the large bands contains dichromate. The peaks are narrower than in K2Cr2O7, possibly due to interaction with Ag+ ions. The peaks in spectra C and D are similar to the K2CrO4 reference spectrum, indicating that the high frequency thin bands between the large bands contain CrO42− ions. Smaller amounts of CrO42− ions are also found between these bands. Lastly, Fig. 3c shows the Ag M4,5 edge spectra; while the peaks corresponding to the M4,5 edges at 368 eV and 374 eV are clearly visible (arrows) on the Ag reference spectra,22 they are not observed in any of the precipitate spectra. The broad, flat peak in the range of the Ag M4,5 edges suggests that silver is present throughout the entire pattern, although a contribution from the nitrogen K edge peak at ∼405 eV is anticipated. Nitrogen is present in the gelatin, in the substrate (Si3N4 window) and in the outer electrolyte AgNO3.
As a conclusion of the NEXAFS results, the analysis of the Cr 2p multiplet spectra shows that the precipitates consist of Cr(VI). The O K pre-edge results reveal that the large bands contain Cr2O72− ions and the area between the large bands, including the high frequency thin bands, contains CrO42− ions. Since the Ag M edge spectra show that silver is present in the precipitate bands, we conclude that the precipitate in the large bands is Ag2Cr2O7 and in the small bands it is Ag2CrO4. It is noteworthy, that the Ag edge spectra also suggest the presence of Ag–N bonds in the high frequency bands causing the peak at 398 eV (see later discussion), while this peak is absent from the spectrum of the low frequency, large band when high frequency bands do not form (E).
Vertical spatial distribution of precipitate particles
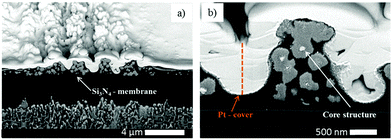
Additional information about the structure and constitution of the precipitate particles was obtained from a cross section of the pattern by FIB-SEM24 (Fig. 4a) and energy-dispersive X-ray spectroscopy (EDX). With these techniques we wanted to answer the question whether the particles form throughout the entire thickness of the gelatin film or only on top of the film. When the two kinds of bands coexist, their profile gives the impression that the smaller bands are formed on the top of the large bands. Is this really the case or do the small bands form in the whole depth of the large bands? SEM image of a FIB-cut cross-section slice of a large band shows that the precipitate particles form within the whole thickness of the gelatin film (Fig. 4b). It is evident from Fig. 4c and d that the small bands also span the whole depth of the gelatin film. However, the precipitate particles in close proximity of the large band peak are at least one magnitude larger than the particles at the edges of the large band. It is even easier to see the spatial distribution of the precipitate particles in a very thin (∼2 μm) gelatin film (Fig. 5). In Fig. 5a the whole depth of the film is split into high frequency, thin bands and the bands are composed of micro- and nanoparticles. A further magnified SEM-FIB image reveals a lighter colored core structure inside the particles (Fig. 5b). EDX measurements (Fig. S1, ESI†) indicate that the core has a higher silver content than the surrounding material which has a silver![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) chromium ratio of approximately 1
chromium ratio of approximately 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.
1.
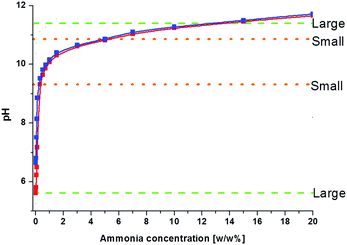
pH effect
We observed that the size and the frequency, as well as the number of the Liesegang bands, depend on the pH of the system. Without NH4OH (pH = 6.2), only large, low frequency bands form. When NH4OH was added to the gelatin film stepwise, we observed large band formation between pH = 6.3 and pH = 11.8. The small, high frequency bands also appeared in coexistence with the large bands between pH = 9.3 and pH = 10.8 (Fig. 6); the large bands contain an accumulation of thinner, high frequency bands as seen in Fig. 1. With increasing pH, the probability of small band formation increases, while the number of large bands decreases. Above pH = 11.8, band formation is not possible since the gelatin does not form a gel. We know from the STXM measurements that the large precipitate bands are silver dichromate, and the thin bands are composed of silver chromate. We propose that the precipitation process is controlled by the chromate–dichromate equilibrium reaction (1).25,26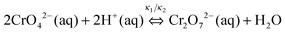 | (1) |
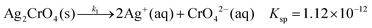 | (2) |
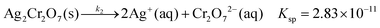 | (3) |
The higher the initial pH, the more the chromate–dichromate equilibrium is shifted towards the chromate side (see chemical equilibrium diagram in Fig. S2, ESI†). This is also apparent from the color change of the gelatin/K2Cr2O7/NH4OH solution; at higher pH the solution becomes yellow as opposed to the orange color of the solution without NH4OH. As a result, at higher pH fewer dichromate ions remain to form large bands. Therefore, with increasing pH, the number of the large bands decreases and consequently, the spacing coefficient increases. This is calculated from the spacing between consecutive bands using:
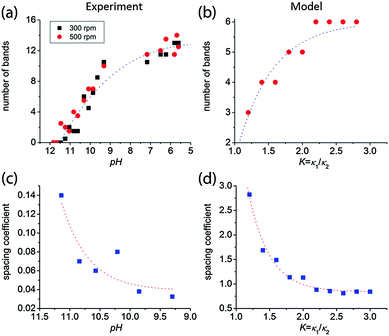 | ||
| Fig. 7 The number of large bands decreases with increasing pH both in experiments (a) and model calculations (b). In (a) the red circles and the black rectangles correspond to gelatin films prepared with 500 rpm and 300 rpm spin coating speeds, respectively. The spacing of the bands increases with increasing pH both in experiments (c) and model calculations (d). We used the same parameter set in the numerical simulations as in Fig. 8. | ||
We also studied systems where the gelatin contained potassium chromate instead of potassium dichromate. The same pH dependence was observed with only a slight pH shift (blue and red curves in Fig. 6), due to the buffering effect of the gelatin. Without added gelatin and base we measured pH values of 4.22 and 8.66 for 0.01 M K2Cr2O7 and 0.01 M K2CrO4 solutions, respectively, but when 10% gelatin is added, the pH changes to 6.2 and 6.6. It shows that the type of the initial chromium(VI) species ions (chromate or dichromate) has only an insignificant effect on the pattern formation.
The STXM Ag M edge spectra showed an Ag–N bond signature peak at 398 eV in the high frequency bands, but this peak was absent from the spectrum of the low frequency, large band (Fig. 3c, curve E). At higher ammonia concentrations, diammine silver(I),27 (aqueous [Ag(NH3)2][NO3]), can form from AgNO3 and NH4OH. If [Ag(NH3)2]+ plays a crucial role in band formation, bands should not form when KOH is used instead of ammonia. As both kinds of bands formed in the system containing KOH, [Ag(NH3)2]+ formation does not have a role in band formation. The Ag–N bond signature may also originate from the amino groups in gelatin which coordinate Ag+ in an alkaline milieu.
Model and simulation
Knowing the constitution of the bands and the relevant chemical equilibria, we developed a reaction–diffusion model based on the Cahn–Hilliard phase separation scenario28 to understand the periodic precipitation phenomenon. Our kinetic model contains 5 species, namely AgNO3 (A), K2CrO4 (B1), K2Cr2O7 (B2), and two precipitates, Ag2CrO4 (C1) and Ag2Cr2O7 (C2):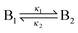 | (4) |
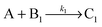 | (5) |
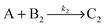 | (6) |
| δta = DΔa − k1ab1 − k2ab2 | (7) |
| δtb1 = DΔb1 − k1ab1 − κ1b1 + κ2b2 | (8) |
| δtb2 = DΔb2 − k2ab2 + κ1b1 − κ2b2 | (9) |
| δtm1 = −λ1Δ(ε1m1 − γm13 + σΔm1) + k1ab1 | (10) |
| δtm2 = −λ2Δ(ε2m2 − γm23 + σΔm2) + k2ab2 | (11) |
![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) = (ch + cl)/2 and λ, ε, γ and σ are parameters of the Cahn–Hilliard equation.30,31Eqn (7)–(11) were solved numerically using the “method of lines” technique on a uniform 1D grid with appropriate boundary (no-flux boundary conditions for all species except for A at the junction point of the electrolytes), where for species A a Neumann-type boundary condition was applied: (a|x=0(t) = a0) and initial conditions (a(t = 0, x) = 0, b1(t = 0, x) = b10, b2(t = 0, x) = b20, m1(t = 0, x) = m2(t = 0, x) = 0). The equations were integrated in time by the forward Euler method. The grid spacing and the time step were 1.0 and 0.04, respectively.
= (ch + cl)/2 and λ, ε, γ and σ are parameters of the Cahn–Hilliard equation.30,31Eqn (7)–(11) were solved numerically using the “method of lines” technique on a uniform 1D grid with appropriate boundary (no-flux boundary conditions for all species except for A at the junction point of the electrolytes), where for species A a Neumann-type boundary condition was applied: (a|x=0(t) = a0) and initial conditions (a(t = 0, x) = 0, b1(t = 0, x) = b10, b2(t = 0, x) = b20, m1(t = 0, x) = m2(t = 0, x) = 0). The equations were integrated in time by the forward Euler method. The grid spacing and the time step were 1.0 and 0.04, respectively.
The results of the model are in very good agreement with our experimental findings. Fig. 8 shows experimental and calculated profiles at two different pH values. At pH = 5.7 large, low frequency bands form, while at pH = 10.1 very thin, densely packed bands can be observed. Here the chromate–dichromate equilibrium (1) is shifted towards CrO42−, a trend accurately reproduced by the model calculation. When κ1 >κ2 in eqn (4), the equilibrium is shifted towards Cr2O72− and strong, low density bands form. However, when the equilibrium is shifted towards CrO42−, K = κ1/κ2 decreases and the high frequency bands coexist with the large, low frequency bands. The number of the bands can also be controlled by the pH in the theoretical model similarly to the experiments. Fig. 7 illustrates how the number of bands decreases and consequently, the spacing between them increases with decreasing K = κ1/κ2 in agreement with the experimental findings.
Silver core structure
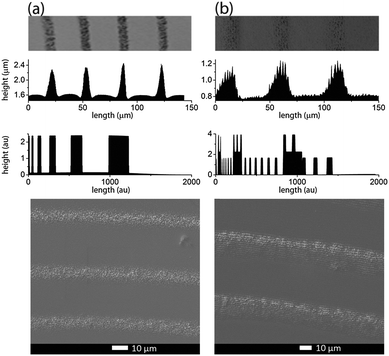
Real time band formation was monitored by digital video recording of the precipitation process. The experimental setup and the time lapse photographs taken from the video are presented in the ESI† (Fig. S3 and S4). The video demonstrates that the bands are fixed at their location once they are formed. More interestingly, they also reveal that a milky/off-white material forms at the propagation front of the diffusing outer electrolyte preceding the large band formation (Fig. S4, ESI†). SEM images of this area of the precipitate pattern show small, densely packed bands (Fig. 9). The area which is covered by these bands is much wider than the wavelength of the large bands. It is reasonable to assume that these small bands form from the white material we have seen in the video.SEM-FIB images and EDX analysis revealed that the precipitate particles contain a high silver ratio core. We propose that the white precipitate in the propagation front seen in the video contains silver nanoparticles which are formed from the invading outer electrolyte on a different time scale (faster), before the precipitation reaction between the inner and outer electrolyte occurs. We reported previously8 that in a system containing the same AgNO3 invading electrolyte, however, only NH4OH (no chromate) in the gelatin film, similar high frequency small bands form at pH > 7.2 and the bands are composed of Ag/Ag2O particles. Fig. S5 (ESI†) clearly demonstrates that the morphological parameters of this highly periodic pattern and the high frequency bands found in the classical system are almost identical. We used the same experimental conditions, the only difference between the two systems was the lack of potassium dichromate in one of the gelatin films. In the silver nitrate/ammonium hydroxide/gelatin system (Fig. S5 left, ESI†) we determined an average band height of 40–90 nm, a FWHH of 2.0 μm and a spacing of 3.15 μm (measured from the maximum of one peak to the maximum of the neighbouring peak). In the propagation front of the classical Liesegang system containing dichromate ions (Fig. S5 right, ESI†) we found an average band height of 40–80 nm, a FWHH of 2.1 μm and a spacing of 3.4 μm. SEM-FIB cross sections, made at approximately the same distance (350 μm) from the stamping core, revealed that the size of the particles forming the bands is the same in the two systems.
Remarkably, it was also found that the cores of the particles in the bands of the classical system (Fig. 10b and d) are almost identical in shape and size as the nanoparticles found in the silver nitrate/ammonium hydroxide/gelatin system (Fig. 10a and c). As the core structures were found in both the large and small bands formed in the classical dichromate Liesegang system, it is rational to assume that the silver containing nanoparticles formed in the reaction front serve as nucleation sites for the Ag2Cr2O7 and Ag2CrO4 precipitates at high pH. As the Ag2CrO4 precipitate is less soluble than Ag2Cr2O7 (eqn (2) and (3)), first this nucleates on the silver particles in the small bands, and later Ag2Cr2O7 builds upon them forming the large bands. For this reason, much larger particles are observed in close proximity to the peak of the large bands in the SEM-FIB cross-section micrographs. This also explains why the STXM measurements show mainly Ag2Cr2O7 precipitate in the large bands even when they are split into small bands and in contrast, the small bands between the large bands appear to contain Ag2CrO4 precipitate. The two precipitates can form consecutively and both of them can be present at the same time due to their different solubilities.
It has already been suggested by Holba32 and Ramaiah33 that secondary (small) precipitation band formation precedes the primary (large) band growth, but it was thought that the latter is a result of the coarsening and strengthening of the secondary bands. However, from our results it is clear that the chemical composition of the two types of precipitation bands is different; therefore they must form independently from each other. We assume that the white precipitate forming first at the reaction front creates the fundamental structure for the two kinds of bands, before silver chromate/dichromate grow around the silver containing core particles. Similar coexistence of larger and finer bands was observed by Karam et al.13 in the Pb(NO3)2/K2CrO4/agar system. However, this system follows a reverted spacing law, i.e. the spacing between large bands decreases with the distance from the contact area of the two electrolytes, as opposed to the classical Ag2Cr2O7 system we used, where the spacing increases as we get further from the contact area. This difference implies a different formation mechanism which is, according to the authors, related to the light sensitivity of the PbCrO4 precipitate.
Conclusions
We investigated the formation mechanism of a unique, dual-frequency precipitate pattern in the AgNO3/K2Cr2O7/gelatin system. Our X-ray spectroscopy measurements demonstrated that the chemical composition of the large, low frequency and the small, high frequency bands are Ag2Cr2O7 and Ag2CrO4, respectively. We showed with a focused ion beam scanning electron microscope that the precipitate micro- and nanoparticles form in the whole thickness of the gelatin film. The SEM-FIB images also revealed that the larger bands split up into much thinner bands throughout the entire depth of the large bands. In addition, we demonstrated that pH is the process parameter to tailor the number and the type of the bands. With increasing pH, the number and the height of the bands decrease, while their spacing increases and there is an optimal pH range where the two kinds of bands coexist. We proposed that the pattern formation is governed by the pH dependent chromate–dichromate equilibrium. To support our theory, we formulated a model containing the chromate–dichromate equilibrium and the precipitation reactions and the results are in qualitative agreement with the experimental findings. We showed by FIB-SEM imaging and EDX measurement that the precipitate particles contain a high silver ratio core, which we assume to form on a different timescale. The silver/silver oxide particles form first from AgNO3 and NH4OH due to the gelatin's reducing ability producing a high frequency band structure.8 These particles then serve as nucleation sites for the less soluble Ag2CrO4 precipitate which grows a shell on the particles. The formed larger particles follow the pattern of the high frequency bands. The Ag2Cr2O7 precipitate forms the larger bands built on top of the small bands at a later time scale.With the gained knowledge from our investigations of the “classical” Liesegang system, we are now able to understand the formation of the bands. This helps us to control the formation as well as the size and the shape of the bands. Now we can tailor the system for potential low cost structures adapted to a wide range of applications e.g. production of nanowires/bands, surface enhancement of catalytically active materials, as well as diffraction gratings.
Experimental section
Gelatin film preparation
The gelatin films (10% w/w) containing the inner electrolyte (0.01 M K2Cr2O7 or 0.01 M K2CrO4) and a base (ammonia 0.3% w/w) were spin coated on X-ray-transparent, 200 nm thin silicon nitride membranes (Silson Ltd) at a speed of 300–500 rpm and were dried for 24 hours in the dark at ambient temperature. The pH dependence of the reaction was tested by varying the amount of the added base.Stamp preparation/stamping
Agarose solution (6% w/w, prepared with degased MilliQ water) was heated in a microwave oven and poured on a pre-shaped PDMS mask containing 500 μm diameter holes. The degassed and cooled agarose film was removed from the mask, cut into 0.4 cm × 0.4 cm pieces and soaked in AgNO3 solution (0.3 M) for 2 days. The soaked stamps were dried on a filter paper for 2–6 minutes and placed on the gelatin films for 2 hours.Imaging
Images of the formed periodic patterns were acquired using a 3D Laser Scanning Microscope (Keyence VK-X200), which uses a violet laser with 408 nm at 0.95 mW. The resolution for the profile (height) measurements is 0.5 nm.SEM (scanning electron microscopy), SEM-FIB (scanning electron microscopy-focused ion beam) and EDX (energy-dispersive X-ray spectroscopy) measurements were performed on a FEI Helios Nano Lab 650 at ZMB (Zentrum Mikroskopie der Universität Basel, Basel Switzerland) on the same samples, which have been analyzed before by STXM. The STXM sample holder was mounted onto a SEM sample holder. The whole setup was then sputter-coated with a 30 nm platinum layer to increase conductivity.
STXM (scanning transmission X-ray spectro-microscopy) measurements were performed on the PolLux beamline of the Swiss Light Source, Paul Scherrer Institute (Villigen, Switzerland).17–19 The images and spectra were acquired at photon energies covering the chromium L-edge (565 eV to 800 eV), the oxygen K-edge (500 eV to 600 eV) and the silver M-edge (340 eV to 420 eV). The silver energy range also contains the nitrogen K edge (395 eV to 403 eV), which presents some interference due to the nitrogen present in the gelatin and the silicon nitride membranes supporting the samples and the Fresnel zone-plate focusing optic of the STXM instrument. We also recorded spectra of several reference materials, such as K2Cr2O7, K2CrO4, Ag and AgNO3. An empty hole of the sample holder and a pure gelatin film were also scanned as a background for the sample and reference materials measurements. Background subtraction, normalizations and absorbance calculations for the STXM data were performed using custom Matlab procedures.
Acknowledgements
Financial support for R. T. from the Marie Heim-Vögtlin grant (No. PMPDP2-139698/1) and for R. W. and F. B. from the Swiss National Science Foundation (SNF) (No. 200021-137868) is gratefully acknowledged. I. L. acknowledges the financial support of the Hungarian Scientific Research Fund (OTKA K104666). We thank Swiss Light Source, Villigen, for the allocation of synchrotron radiation beamtime at PolLux endstation and we are grateful to B. Watts and J. Raabe at Swiss Light Source whose outstanding efforts have made these experiments possible. The PolLux end station was financed by the German Minister für Bildung und Forschung (BMBF) through contracts 05KS4WE1/6 and 05KS7WE1. A. B. is grateful to A. P. Hitchcock (McMaster Univ.) for advice on planning the STXM experiment.Notes and references
- B. A. Grzybowski, K. J. M. Bishop, C. J. Campbell, M. Fialkowski and S. K. Smoukov, Soft Matter, 2005, 1, 114 RSC.
- H. Yan, Y. Zhao, C. Qiu and H. Wu, Sens. Actuators, B, 2008, 132, 20 CrossRef CAS.
- B. A. Grzybowski and C. J. Campbell, Mater. Today, 2007, 10, 38 CrossRef CAS.
- S. C. Müller and J. Ross, J. Phys. Chem. A, 2003, 107, 7997 CrossRef.
- R. E. Liesegang, Naturwiss. Wochenschr., 1896, 11, 353 Search PubMed; E. Nakouzi and O. Steinbock, Sci. Adv., 2016, 2, 1 Search PubMed.
- S. Leduc, Mechanism of Life, Rebman Ltd, London, 1911 Search PubMed.
- R. Fürth, Z. Phys., 1933, 81, 143–162 CrossRef.
- R. M. Walliser, R. Tóth, I. Lagzi, D. Mathys, L. Marot, A. Braun, C. E. Housecroft and E. C. Constable, RSC Adv., 2016, 6, 28388 RSC.
- A. Volford, F. Izsák, M. Ripszám and I. Lagzi, Langmuir, 2007, 23, 961 CrossRef CAS PubMed.
- M. Al-Ghoul, T. Ghaddar and T. Moukalled, J. Phys. Chem. B, 2009, 113, 11594 CrossRef CAS PubMed.
- L. M. Barge, K. H. Nealson and J. Petruska, Chem. Phys. Lett., 2010, 493, 340 CrossRef CAS.
- J. Petruska and L. M. Barge, Chem. Phys. Lett., 2013, 556, 315 CrossRef CAS.
- T. Karam, H. El-Rassy and R. Sultan, J. Phys. Chem. A, 2011, 115, 2994 CrossRef CAS PubMed.
- (a) S. K. Smoukov, I. Lagzi and B. Grzybowski, J. Phys. Chem. Lett., 2011, 2, 345 CrossRef CAS; (b) S. K. Smoukov, A. Bitner, J. Campbell, K. Kandere-Grzybowska and B. A. Grzybowski, J. Am. Chem. Soc., 2005, 127, 17803 CrossRef CAS PubMed.
- B. M. Abu-Zied, Appl. Catal., A, 2000, 198, 139–153 CrossRef CAS.
- H. Ade, X. Zhang, S. Cameron, C. Costello, J. Kirz and S. Williams, Science, 1992, 258, 972–975 CAS.
- U. Frommherz, J. Raabe, B. Watts, R. Stefani and U. Ellenberger, AIP Conf. Proc., 2010, 1234, 429 CrossRef.
- U. Flechsig, C. Quitmann, J. Raabe, M. Böge, R. Fink and H. Ade, AIP Conf. Proc., 2007, 879, 505 CrossRef CAS.
- J. Raabe, et al. , Rev. Sci. Instrum., 2008, 79, 113704 CrossRef CAS PubMed.
- D. Grolimund, et al. , J. Synchrotron Radiat., 1999, 6, 612 CrossRef CAS PubMed.
- J. W. Chiou, et al. , Appl. Surf. Sci., 2011, 257, 4863 CrossRef CAS.
- G. Paolucci, A. Santoni, G. Comelli, K. Prince and R. Agostino, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44(19), 888 CrossRef.
- M. R. Sundberg, J. Valo, R. Uggla and M. Melnik, ICA, 2012, 383, 164 CAS.
- S. Reyntjens and R. Puers, J. Micromech. Microeng., 2001, 11, 287 CrossRef CAS.
- G. Michel and R. Machiroux, J. Raman Spectrosc., 1983, 14, 2 CrossRef.
- R. C. Weast, CRC Handbook of Chemistry and Physics, CRC Press, 58th edn, 1977–1978, B-255 Search PubMed.
- L. F. Gorup, E. Longo, E. R. Leite and E. R. Camargo, J. Colloid Interface Sci., 2011, 360, 355 CrossRef CAS PubMed.
- J. W. Cahn and J. E. Hilliard, J. Chem. Phys., 1958, 28, 258 CrossRef CAS.
- T. Antal, M. Droz, J. Magnin and Z. Rácz, Phys. Rev. Lett., 1999, 83, 2880 CrossRef CAS.
- S. Thomas, I. Lagzi, F. Molnár and Z. Rácz, Phys. Rev. Lett., 2013, 110, 078303 CrossRef PubMed.
- A. Volford, I. Lagzi, F. Molnár and Z. Rácz, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 055102(R) CrossRef PubMed.
- V. Holba, Colloid Polym. Sci., 1989, 267, 456 CAS.
- C. V. Raman and K. Subba Ramaiah, Proc. - Indian Acad. Sci., Math. Sci., 1939, 9, 455–466 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: EDX spectra, video monitoring setup, comparison of AgNO3/NH4OH/gelatin and the classical AgNO3/K2Cr2O7/NH4OH/gelatin Liesegang systems, chemical equilibrium diagram for chromate–dichromate equilibrium. See DOI: 10.1039/c6sm01564f |
| This journal is © The Royal Society of Chemistry 2016 |